Assessment of Streamflow Simulation for a Tropical Forested Catchment Using Dynamic TOPMODEL—Dynamic fluxEs and ConnectIvity for Predictions of HydRology (DECIPHeR) Framework and Generalized Likelihood Uncertainty Estimation (GLUE)
Abstract
1. Introduction
2. Materials and Methods
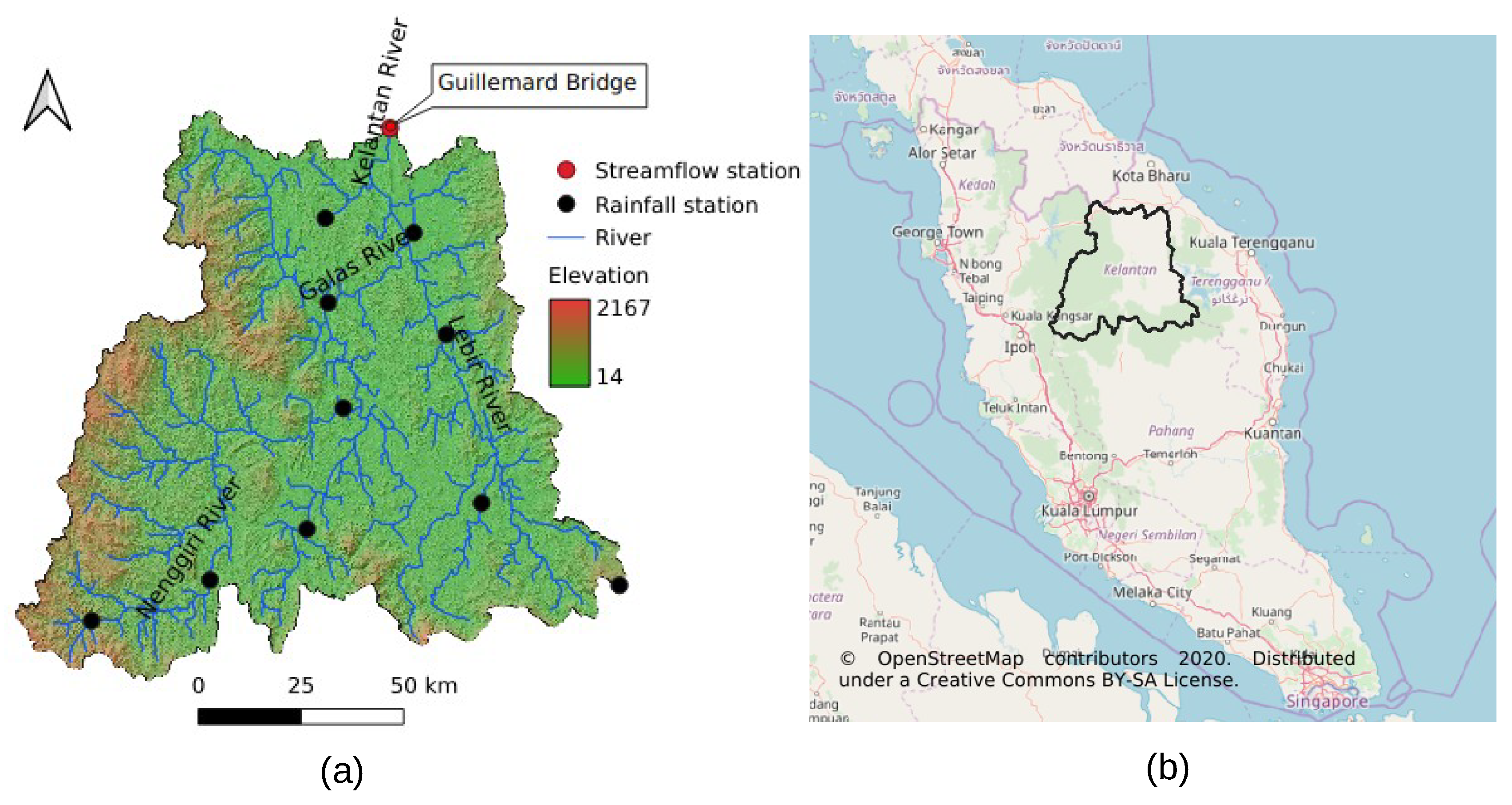
2.1. Study Area
2.2. Input Data
2.3. The Concept and the Framework of the Rainfall Runoff Model
2.4. GLUE Analysis
3. Results and Discussion
- Topographic classifier: three slope classes, three area classes, and five elevation classes
- 10 Rainfall grid classes—gauges data gridded after Thiessen polygon applied
- 29 Potential evapotranspiration grid classes
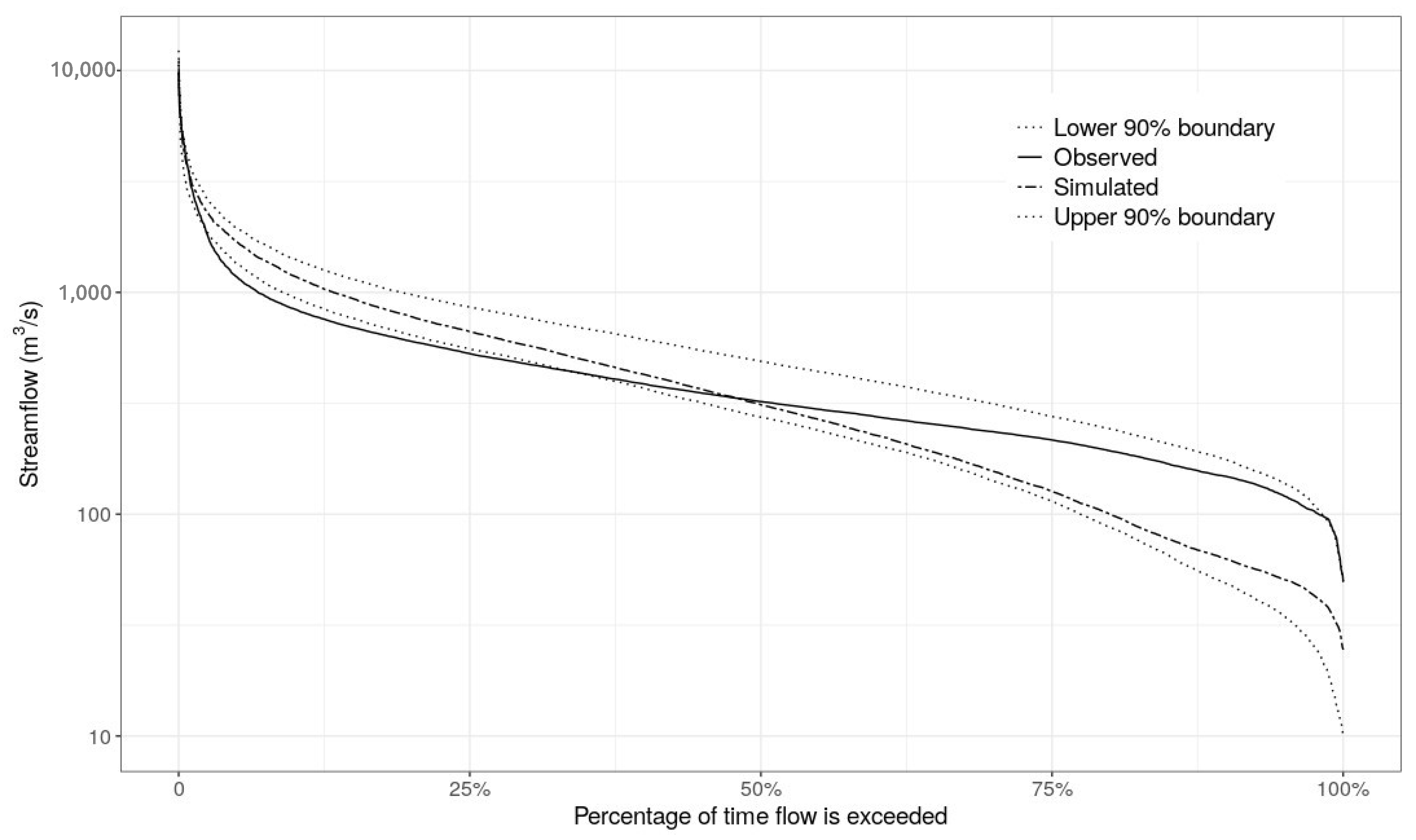
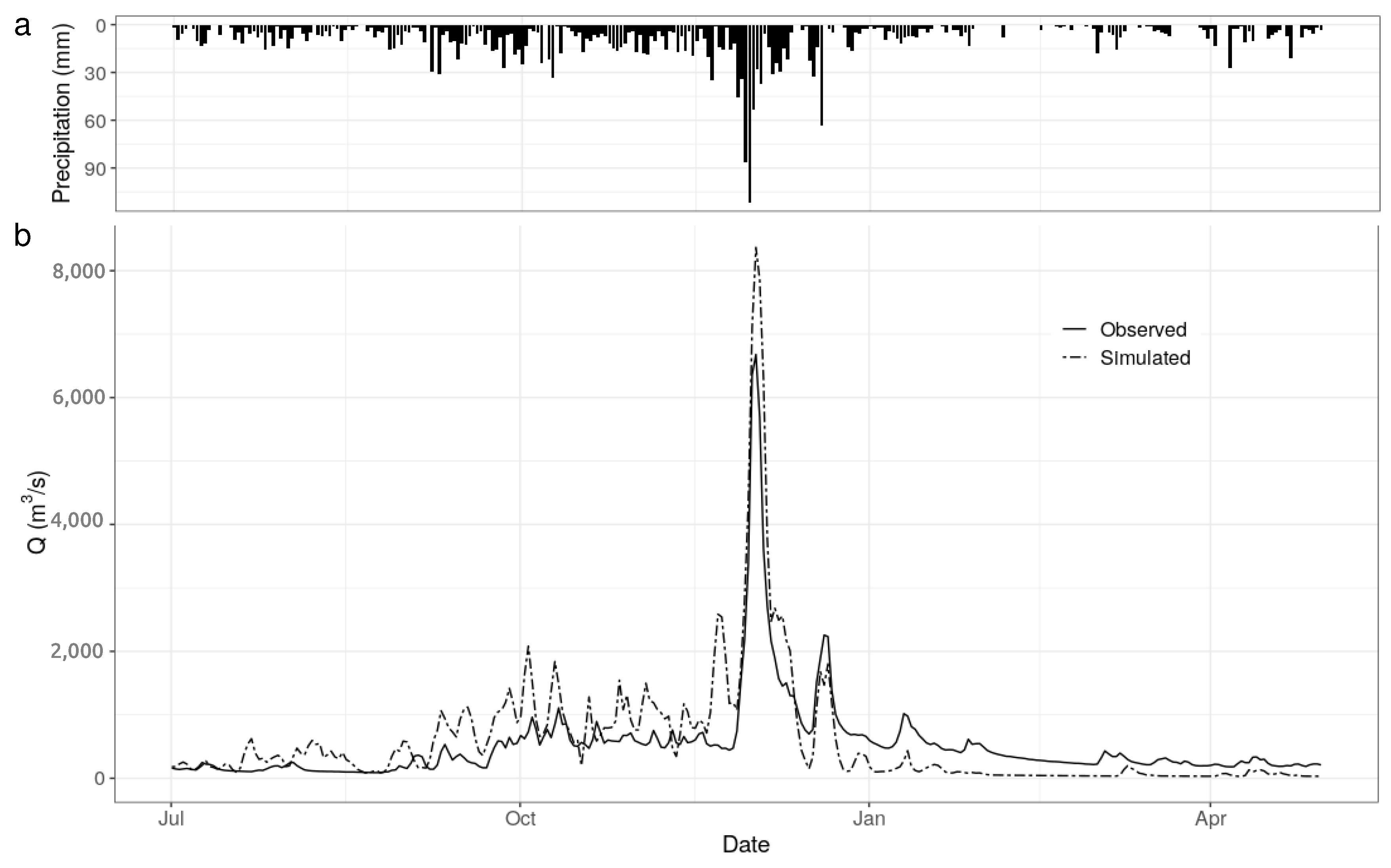
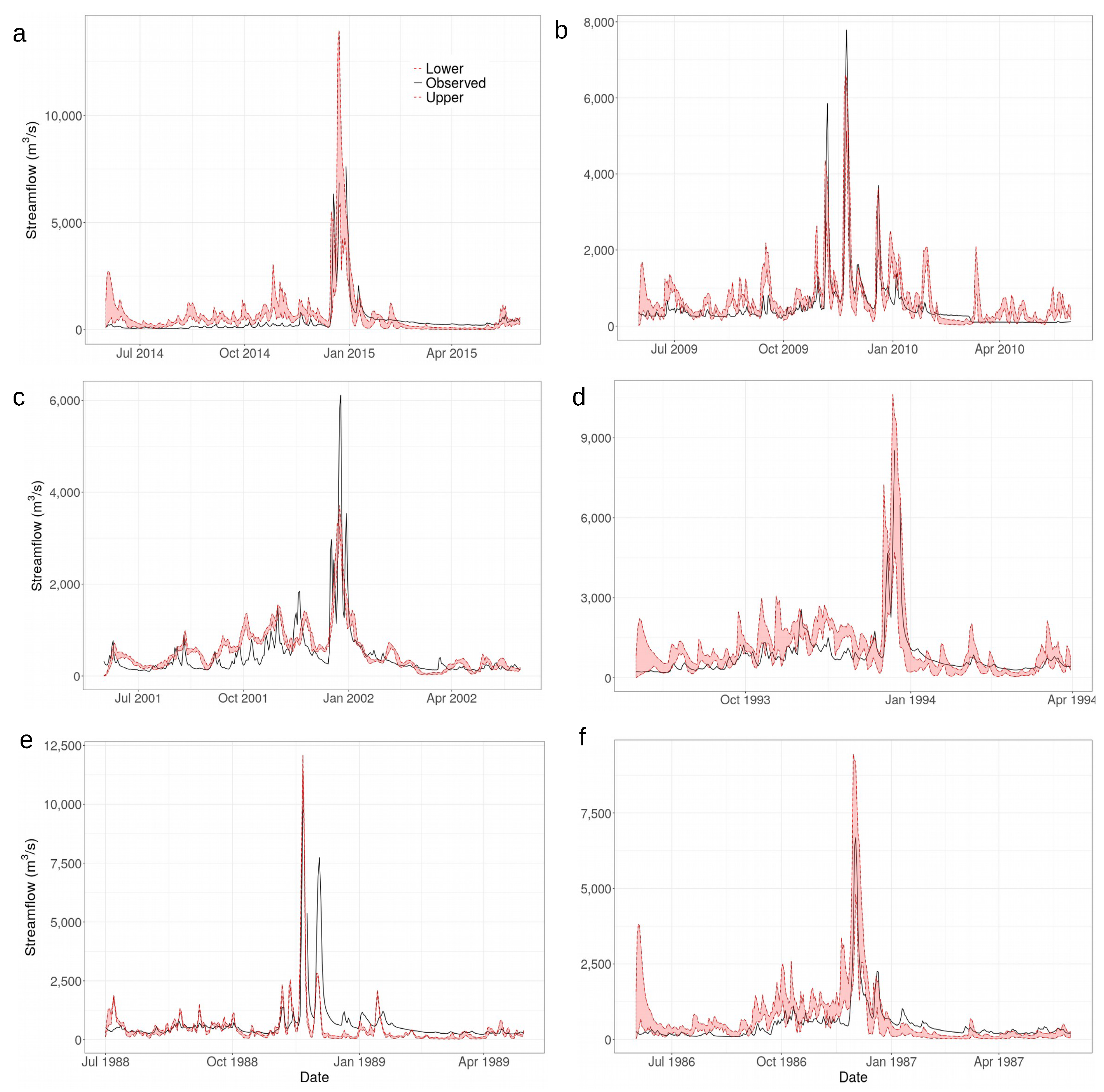
3.1. Streamflow Simulation and Model Performance
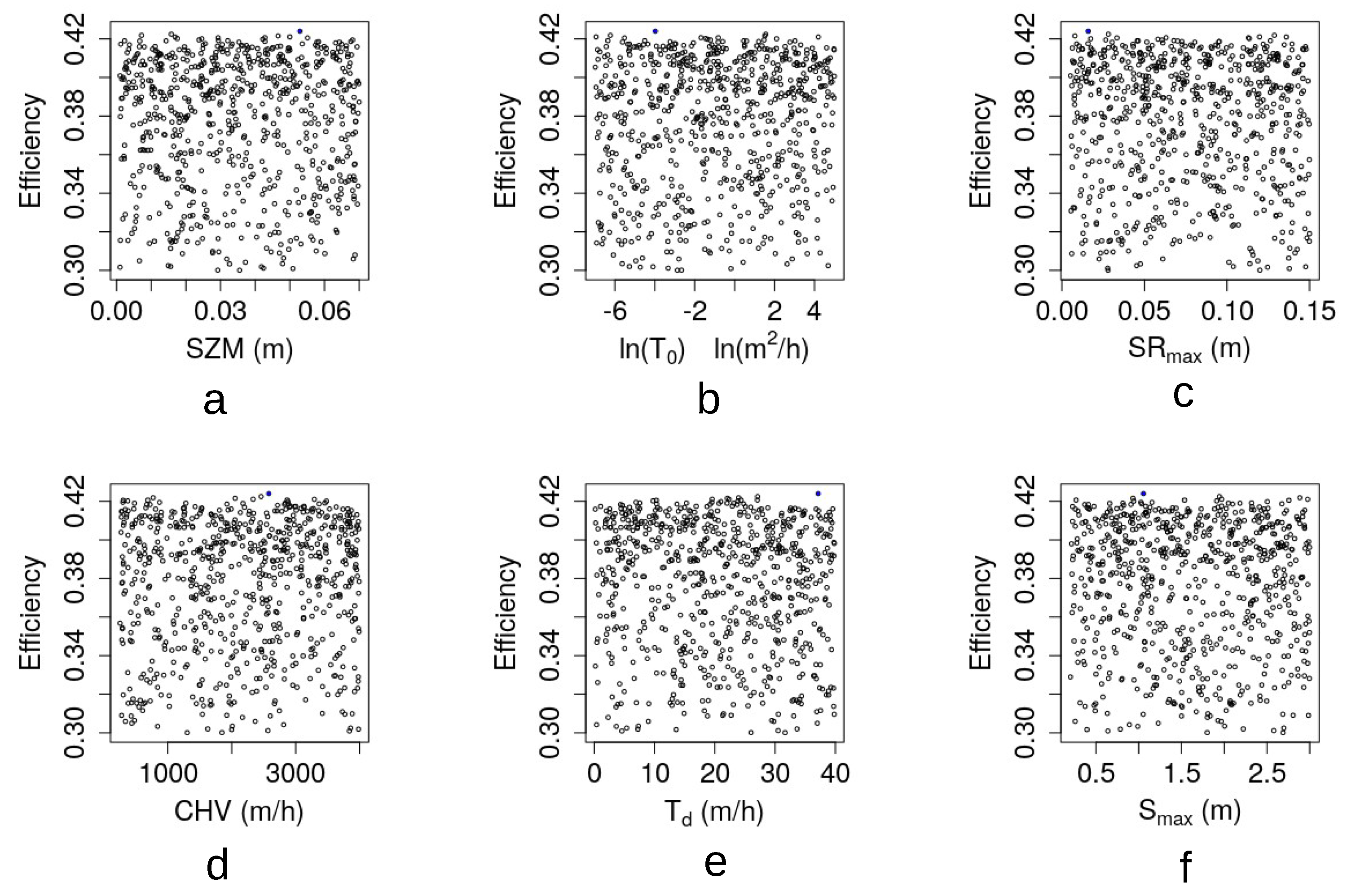
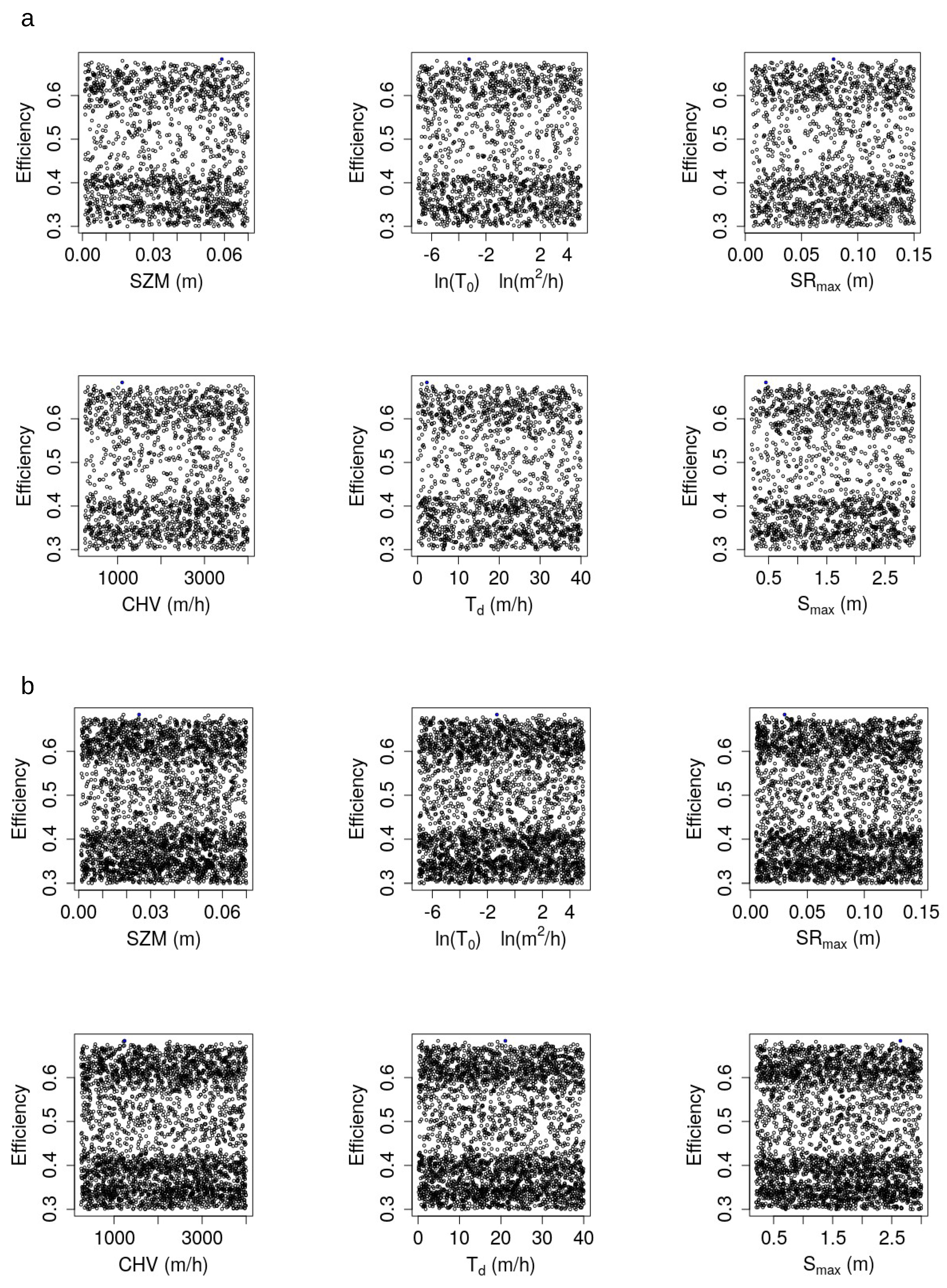
3.2. Analysis of Model Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DECIPHeR | Dynamic fluxEs and ConnectIvity for Predictions of Hydrology |
| DEM | Digital Eelevation Model |
| DID | The Department of Irrigation and Drainage |
| DTA | Digital Terrain Analysis |
| FDC | Flow Duration Curve |
| GLEAM | Global Land Evaporation Amsterdam Model |
| GLUE | Generalized Likelihood Uncertainty Estimation |
| HRU | Hydrological Response Unit |
| IFAS | Integrated Flood Analysis System |
| NSE | Nash Sutcliffe Efficiency |
| SCS-CN | Soil Conservation Service Curve Number |
| SRTM | Shuttle Radar Topography Mission |
| USGS | United State Geological Survey |
References
- Sivapalan, M.; Takeuchi, K.; Franks, S.; Gupta, V.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.; Mendiondo, E.; O’connell, P.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Silberstein, R. Hydrological models are so good, do we still need data? Environ. Model. Softw. 2006, 21, 1340–1352. [Google Scholar] [CrossRef]
- Singh, V.P.; Frevert, D.K. Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publication: Lone Tree, CO, USA, 2002. [Google Scholar]
- Merz, R.; Parajka, J.; Blöschl, G. Scale effects in conceptual hydrological modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.; Dwarakish, G. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An overview of rainfall-runoff model types. In International Congress on Environmental Modelling and Software; Brigham Young University: Provo, UT, USA, 2018. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley & Sons: Oxford, UK, 2011. [Google Scholar]
- Uhlenbrook, S.; Seibert, J.; Leibundgut, C.; Rodhe, A. Prediction uncertainty of conceptual rainfall-runoff models caused by problems in identifying model parameters and structure. Hydrol. Sci. J. 1999, 44, 779–797. [Google Scholar] [CrossRef]
- Fenicia, F.; Kavetski, D.; Savenije, H.H. Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Seibert, J. Conceptual Runoff Models-Fiction or Representation of Reality; Acta Universitatis Upsaliensis: Uppsala, Sweden, 1999. [Google Scholar]
- Campling, P.; Gobin, A.; Beven, K.; Feyen, J. Rainfall-runoff modelling of a humid tropical catchment: The TOPMODEL approach. Hydrol. Process. 2002, 16, 231–253. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. A dynamic topmodel. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Metcalfe, P.; Beven, K.; Freer, J. Dynamic TOPMODEL: A new implementation in R and its sensitivity to time and space steps. Environ. Model. Softw. 2015, 72, 155–172. [Google Scholar] [CrossRef]
- Coxon, G.; Freer, J.; Lane, R.; Dunne, T.; Knoben, W.J.; Howden, N.J.; Quinn, N.; Wagener, T.; Woods, R. DECIPHeR v1: Dynamic fluxEs and ConnectIvity for Predictions of HydRology. Geosci. Model Dev. 2019, 12. [Google Scholar] [CrossRef]
- Buytaert, W.; Reusser, D.; Krause, S.; Renaud, J.P. Why can’t we do better than Topmodel? Hydrol. Process. Int. J. 2008, 22, 4175–4179. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.M.; Mcintyre, N.R.; Wheater, H.S. Catchment scale hydrological modelling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Lee, S.U.; Batchelder, R. Appraisal of the generalized likelihood uncertainty estimation (GLUE) method. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Montanari, A. What do we mean by ‘uncertainty’? The need for a consistent wording about uncertainty assessment in hydrology. Hydrol. Process. Int. J. 2007, 21, 841–845. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K. Environmental Modelling: An Uncertain Future; Routledge: London, UK, 2010. [Google Scholar]
- Page, T.; Beven, K.J.; Freer, J.; Neal, C. Modelling the chloride signal at Plynlimon, Wales, using a modified dynamic TOPMODEL incorporating conservative chemical mixing (with uncertainty). Hydrol. Process. Int. J. 2007, 21, 292–307. [Google Scholar] [CrossRef]
- Montanari, A. Large sample behaviors of the generalized likelihood uncertainty estimation (GLUE) in assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Gil, E.G.; Tobón, C. Hydrological modelling with TOPMODEL of Chingaza páramo, Colombia. Rev. Fac. Nac. Agron. Medellín 2016, 69, 7919–7933. [Google Scholar]
- Buytaert, W.; Beven, K. Models as multiple working hypotheses: Hydrological simulation of tropical alpine wetlands. Hydrol. Process. 2011, 25, 1784–1799. [Google Scholar] [CrossRef]
- Suliman, A.H.A.; Katimon, A.; Darus, I.Z.M.; Shahid, S. TOPMODEL for streamflow simulation of a tropical catchment using different resolutions of ASTER DEM: Optimization through response surface methodology. Water Resour. Manag. 2016, 30, 3159–3173. [Google Scholar] [CrossRef]
- Chappell, N.A.; Bidin, K.; Sherlock, M.; Lancaster, J. Parsimonious spatial representation of tropical soils within dynamic, rainfall-runoff models. In Forests, Water and People in the Humid Tropics; Cambridge University Press: Cambridge, UK, 2004; pp. 756–769. [Google Scholar]
- Chappell, N.A.; Franks, S.W.; Larenus, J. Multi-scale permeability estimation for a tropical catchment. Hydrol. Process. 1998, 12, 1507–1523. [Google Scholar] [CrossRef][Green Version]
- Peters, N.E.; Freer, J.; Beven, K. Modelling hydrologic responses in a small forested catchment (Panola Mountain, Georgia, USA): A comparison of the original and a new dynamic TOPMODEL. Hydrol. Process. 2003, 17, 345–362. [Google Scholar] [CrossRef]
- Suliman, A.H.A.; Gumindoga, W.; Katimon, A. Semi-distributed rainfall-runoff modeling utilizing ASTER DEM in Pinang Catchment of Malaysia. Sains Malays. 2014, 43, 1379–1388. [Google Scholar]
- Gumindoga, W.; Rientjes, T.; Haile, A.; Dube, T. Predicting streamflow for land cover changes in the Upper Gilgel Abay River Basin, Ethiopia: A TOPMODEL based approach. Phys. Chem. Earth Parts A/B/C 2014, 76, 3–15. [Google Scholar] [CrossRef]
- Arenas-Bautista, M.C.; Arboleda-Obando, P.F.; Duque-Gardeazabal, N.; Saavedra-Cifuentes, E.; Donado, L.D. Hydrological Modeling in Tropical Regions via TopModel. Study Case: Central Sector of the Middle Magdalena Valley-Colombia. Preprints 2018. [Google Scholar] [CrossRef]
- Takeuchi, K.; Ao, T.; Ishidaira, H. Introduction of block-wise use of TOPMODEL and Muskingum-Cunge method for the hydroenvironmental simulation of a large ungauged basin. Hydrol. Sci. J. 1999, 44, 633–646. [Google Scholar] [CrossRef]
- Magome, J.; Gusyev, M.; Hasegawa, A.; Takeuchi, K. River discharge simulation of a distributed hydrological model on global scale for the hazard quantification. In Proceedings of the 21st International Congress on Modelling and Simulation (MODSIM2015), Broadbeach, Australia, 29 November–4 December 2015; pp. 1593–1599. [Google Scholar]
- Jaafar, A.S.; Sidek, L.M.; Basri, H.; Zahari, N.M.; Jajarmizadeh, M.; Noor, H.M.; Osman, S.; Mohammad, A.H.; Azad, W.H. An overview: Flood catastrophe of Kelantan watershed in 2014. In ISFRAM 2015; Springer: Singapore, 2016; pp. 17–29. [Google Scholar] [CrossRef]
- Butler, R. High Deforestation Rates in Malaysian States Hit by Flooding. Mongabay, 19 January 2015. [Google Scholar]
- Shakirah, J.A.; Sidek, L.; Hidayah, B.; Nazirul, M.; Jajarmizadeh, M.; Ros, F.; Roseli, Z. A Review on Flood Events for Kelantan River Watershed in Malaysia for Last Decade (2001–2010). In Proceedings of the IOP Conference Series: Earth and Environmental Science, Putrajaya, Malaysia, 23–25 February 2016; IOP Publishing Ltd.: Bristol, UK, 2016; Volume 32, p. 012070. [Google Scholar] [CrossRef]
- Ahmad Shafuan, M.F. Runoff Estimation Using SCS CN Method For Kelantan River Basin. In Proceedings of the International Conference on Water Resources, Bayview Hotel, Langkawi, Malaysia, 24–25 November 2015. [Google Scholar] [CrossRef]
- Hafiz, I.; Sidek, L.; Basri, H.; Fukami, K.; Hanapi, M.; Livia, L.; Jaafar, A. Integrated flood analysis system (IFAS) for Kelantan river basin. In Proceedings of the 2014 IEEE 2nd International Symposium on Telecommunication Technologies (ISTT), Langkawi, Malaysia, 24–26 November 2014; pp. 159–162. [Google Scholar]
- Saadatkhah, N.; Tehrani, M.H.; Mansor, S.; Khuzaimah, Z.; Kassim, A.; Saadatkhah, R. Impact assessment of land cover changes on the runoff changes on the extreme flood events in the Kelantan River basin. Arab. J. Geosci. 2016, 9, 687. [Google Scholar] [CrossRef]
- Basarudin, Z.; Adnan, N.A.; Latif, A.R.A.; Tahir, W.; Syafiqah, N. Event-based rainfall-runoff modelling of the Kelantan River Basin. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Kuching, Malaysia, 26–29 August 2013; Volume 18, p. 012084. [Google Scholar]
- Adnan, N.A.; Atkinson, P. Disentangling the effects of long-term changes in precipitation and land use on hydrological response in a monsoonal catchment. J. Flood Risk Manag. 2018, 11, S1063–S1077. [Google Scholar] [CrossRef]
- Woodward, D.E.; Hawkins, R.H.; Hjelmfelt, A.; Van Mullem, J.; Quan, Q.D. Curve number method: Origins, applications and limitations. In Proceedings of the US Geological Survey Advisory Committee on Water Information–Second Federal Interagency Hydrologic Modeling Conference, Las Vegas, NV, USA, 28 July–1 August 2002. [Google Scholar]
- Nasr, A.; Bruen, M. Development of neuro-fuzzy models to account for temporal and spatial variations in a lumped rainfall–runoff model. J. Hydrol. 2008, 349, 277–290. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’CONNOR, K.M.; Nasr, A.E. A comparative study of three neural network forecast combination methods for simulated river flows of different rainfall—Runoff models. Hydrol. Sci. J. 2007, 52, 896–916. [Google Scholar] [CrossRef]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep Learning Data-Intelligence Model Based on Adjusted Forecasting Window Scale: Application in Daily Streamflow Simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Wong, C.; Venneker, R.; Uhlenbrook, S.; Jamil, A.; Zhou, Y. Variability of rainfall in Peninsular Malaysia. Hydrol. Earth Syst. Sci. Discuss. 2009, 6, 5471–5503. [Google Scholar] [CrossRef]
- Jabatan Penerangan. Available online: http://pmr.penerangan.gov.my (accessed on 10 June 2017).
- USGS. Earth Explorer. SRTM/Shuttle Radar Topography Mission 1 Arc-Second Digital Terrain Elevation Data-Global. Available online: https://earthexplorer.usgs.gov/ (accessed on 10 November 2017).
- Ludwig, R.; Schneider, P. Validation of digital elevation models from SRTM X-SAR for applications in hydrologic modeling. ISPRS J. Photogramm. Remote Sens. 2006, 60, 339–358. [Google Scholar] [CrossRef]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Gonzalez Miralles, D.; Holmes, T.; De Jeu, R.; Gash, J.; Meesters, A.; Dolman, A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Beven, K. TOPMODEL: A critique. Hydrol. Process. 1997, 11, 1069–1085. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, L.; Chen, T.; Di Baldassarre, G. Analysis of parameter uncertainty in hydrological and sediment modeling using GLUE method: A case study of SWAT model applied to Three Gorges Reservoir Region, China. Hydrol. Earth Syst. Sci. 2012, 16, 121–132. [Google Scholar] [CrossRef]
- Harmel, R.D.; Smith, P.K.; Migliaccio, K.W. Modifying goodness-of-fit indicators to incorporate both measurement and model uncertainty in model calibration and validation. Trans. ASABE 2010, 53, 55–63. [Google Scholar] [CrossRef]
- Freer, J.; Beven, K.; Ambroise, B. Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach. Water Resour. Res. 1996, 32, 2161–2173. [Google Scholar] [CrossRef]
- Searcy, J.K.; Hardison, C.H. Double-Mass Curves; Number 1541; US Government Printing Office: Washington, DC, USA, 1960.
- Heng, C.L. Groundwater utilisation and management in Malaysia. In Proceedings of the 41 st CCOP Annual Session, Tsukuba, Japan, 15–18 November 2004; p. 83. [Google Scholar]
- Chong, F.; Tan, D.N. Hydrogeological Activities in Peninsular Malaysia and Sarawak; Geological Society of Malaysia: Kuala Lumpur, Malaysia, 1986; Volume 2, pp. 827–842. [Google Scholar]
- Brutsaert, W. Long-term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Noguchi, S.; Nik, A.R.; Yusop, Z.; Tani, M.; Sammori, T. Rainfall-runoff responses and roles of soil moisture variations to the response in tropical rain forest, Bukit Tarek, Peninsular Malaysia. J. For. Res. 1997, 2, 125–132. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Freund, E.R.; Zappa, M.; Kirchner, J.W. Averaging over spatiotemporal heterogeneity substantially biases evapotranspiration rates in a mechanistic large-scale land evaporation model. Hydrol. Earth Syst. Sci 2020, 24, 5015–5025. [Google Scholar] [CrossRef]
- Martens, B.; De Jeu, R.A.; Verhoest, N.E.; Schuurmans, H.; Kleijer, J.; Miralles, D.G. Towards Estimating Land Evaporation at Field Scales Using GLEAM. Remote Sens. 2018, 10, 1720. [Google Scholar] [CrossRef]
- Alias, N.E.; Mohamad, H.; Chin, W.Y.; Yusop, Z. Rainfall analysis of the Kelantan big yellow flood 2014. J. Teknol. 2016, 78. [Google Scholar] [CrossRef]
- Azlee, A. Worst floods in Kelantan, confirms NSC. Retrieved January 2015, 5, 2017. [Google Scholar]
- Ghorbani, K.; Wayayok, A.; Abdullah, A.F. Simulation of flood risk area in Kelantan watershed, Malaysia using numerical model. J. Teknol. 2016, 78, 51–57. [Google Scholar] [CrossRef]
- Freer, J.E.; McMillan, H.; McDonnell, J.; Beven, K. Constraining dynamic TOPMODEL responses for imprecise water table information using fuzzy rule based performance measures. J. Hydrol. 2004, 291, 254–277. [Google Scholar] [CrossRef]
- Fronzi, D.; Tazioli, A. Groundwater and flood events in different hydrogeological periods: A case study in the Aspio river (Marche Region). Ital. J. Eng. Geol. Environ. 2019, 1. [Google Scholar] [CrossRef]
| Parameter | Description | Lower Limit | Upper Limit |
|---|---|---|---|
| [m] | Form of exponential decline in conductivity | 0.001 | 0.07 |
| [m h] | Effective lateral saturated transmissivity | −7 | 5 |
| [m] | Maximum root zone storage | 0.005 | 0.15 |
| [m] | Initial root zone deficit | 0 | 0.01 |
| [m h] | Unsaturated zone time delay | 0.1 | 40 |
| [m h] | Channel routing velocity | 250 | 4000 |
| [m] | Maximum effective deficit of subsurface saturated zone | 0.2 | 3 |
| Peak | Simulation Range (Year-Month) | Rainfall-Runoff Ratio (Q/P) | Highest Recorded Peak (m3/s) | Numerical Goodness of Fit for the Highest Rank of Parameter Set | Measurement to Fall inside the GLUE Uncertainty Limits (%) | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 2014-06/2015-05 | 0.40 | 7613.5 | 0.68 | 0.74 | 448.18 | −21.0 | 14.52 |
| 2 | 2012-06/2013-03 | 0.36 | 6215.5 | 0.17 | 0.34 | 826.43 | −49.6 | NA |
| 3 | 2009-06/2010-05 | 0.50 | 7786.0 | 0.70 | 0.75 | 423.43 | −18.5 | 28.76 |
| 4 | 2007-06/2008-05 | 0.67 | 8028.4 | 0.25 | 0.62 | 638.94 | 6.4 | NA |
| 5 | 2001-06/2002-05 | 0.50 | 6111.8 | 0.40 | 0.64 | 392.20 | −14.1 | 13.97 |
| 6 | 1993-08/1994-03 | 0.57 | 8533.7 | 0.72 | 0.75 | 478.00 | −12.8 | 38.68 |
| 7 | 1988-07/1989-04 | 0.64 | 9775.1 | 0.32 | 0.48 | 772.83 | 30.5 | 17.10 |
| 8 | 1986-06/1987-05 | 0.45 | 6680.5 | 0.78 | 0.81 | 434.26 | −16.0 | 23.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fadhliani; Zulkafli, Z.; Yusuf, B.; Nurhidayu, S. Assessment of Streamflow Simulation for a Tropical Forested Catchment Using Dynamic TOPMODEL—Dynamic fluxEs and ConnectIvity for Predictions of HydRology (DECIPHeR) Framework and Generalized Likelihood Uncertainty Estimation (GLUE). Water 2021, 13, 317. https://doi.org/10.3390/w13030317
Fadhliani, Zulkafli Z, Yusuf B, Nurhidayu S. Assessment of Streamflow Simulation for a Tropical Forested Catchment Using Dynamic TOPMODEL—Dynamic fluxEs and ConnectIvity for Predictions of HydRology (DECIPHeR) Framework and Generalized Likelihood Uncertainty Estimation (GLUE). Water. 2021; 13(3):317. https://doi.org/10.3390/w13030317
Chicago/Turabian StyleFadhliani, Zed Zulkafli, Badronnisa Yusuf, and Siti Nurhidayu. 2021. "Assessment of Streamflow Simulation for a Tropical Forested Catchment Using Dynamic TOPMODEL—Dynamic fluxEs and ConnectIvity for Predictions of HydRology (DECIPHeR) Framework and Generalized Likelihood Uncertainty Estimation (GLUE)" Water 13, no. 3: 317. https://doi.org/10.3390/w13030317
APA StyleFadhliani, Zulkafli, Z., Yusuf, B., & Nurhidayu, S. (2021). Assessment of Streamflow Simulation for a Tropical Forested Catchment Using Dynamic TOPMODEL—Dynamic fluxEs and ConnectIvity for Predictions of HydRology (DECIPHeR) Framework and Generalized Likelihood Uncertainty Estimation (GLUE). Water, 13(3), 317. https://doi.org/10.3390/w13030317






