A Canopy Transpiration Model Based on Scaling Up Stomatal Conductance and Radiation Interception as Affected by Leaf Area Index
Abstract
1. Introduction
2. Constructing a Theoretical Model of Canopy Conductance
2.1. Defining the Model Structure
2.2. Modelling Transpiration
3. Materials and Methods
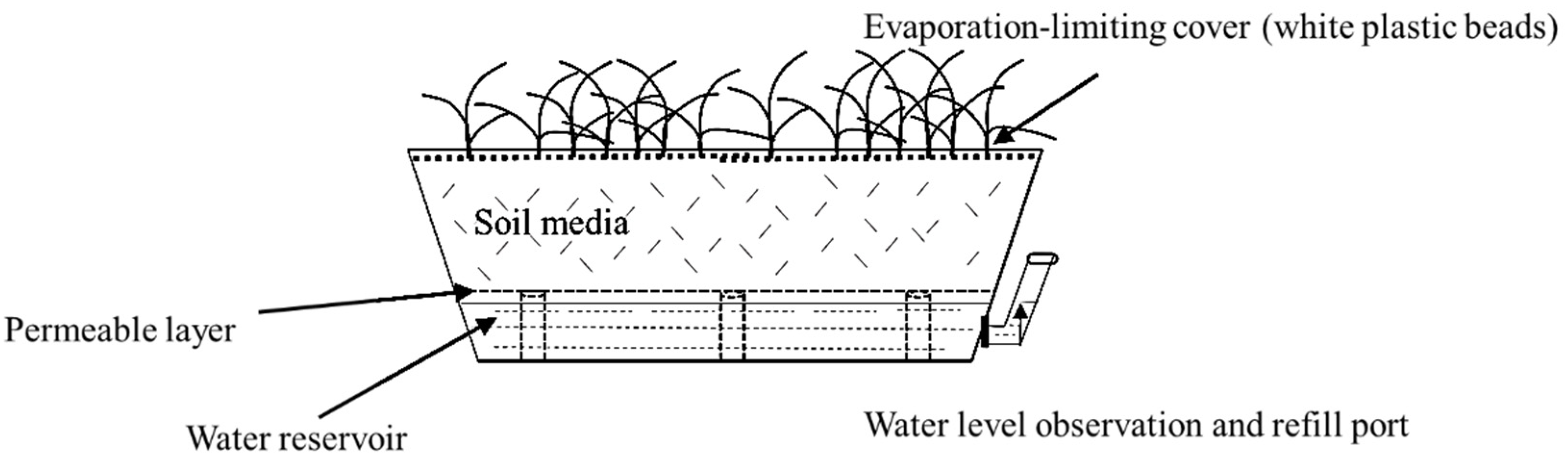
3.1. Establishing and Monitoring the Growing Environment
3.2. Measuring Canopy Transpiration
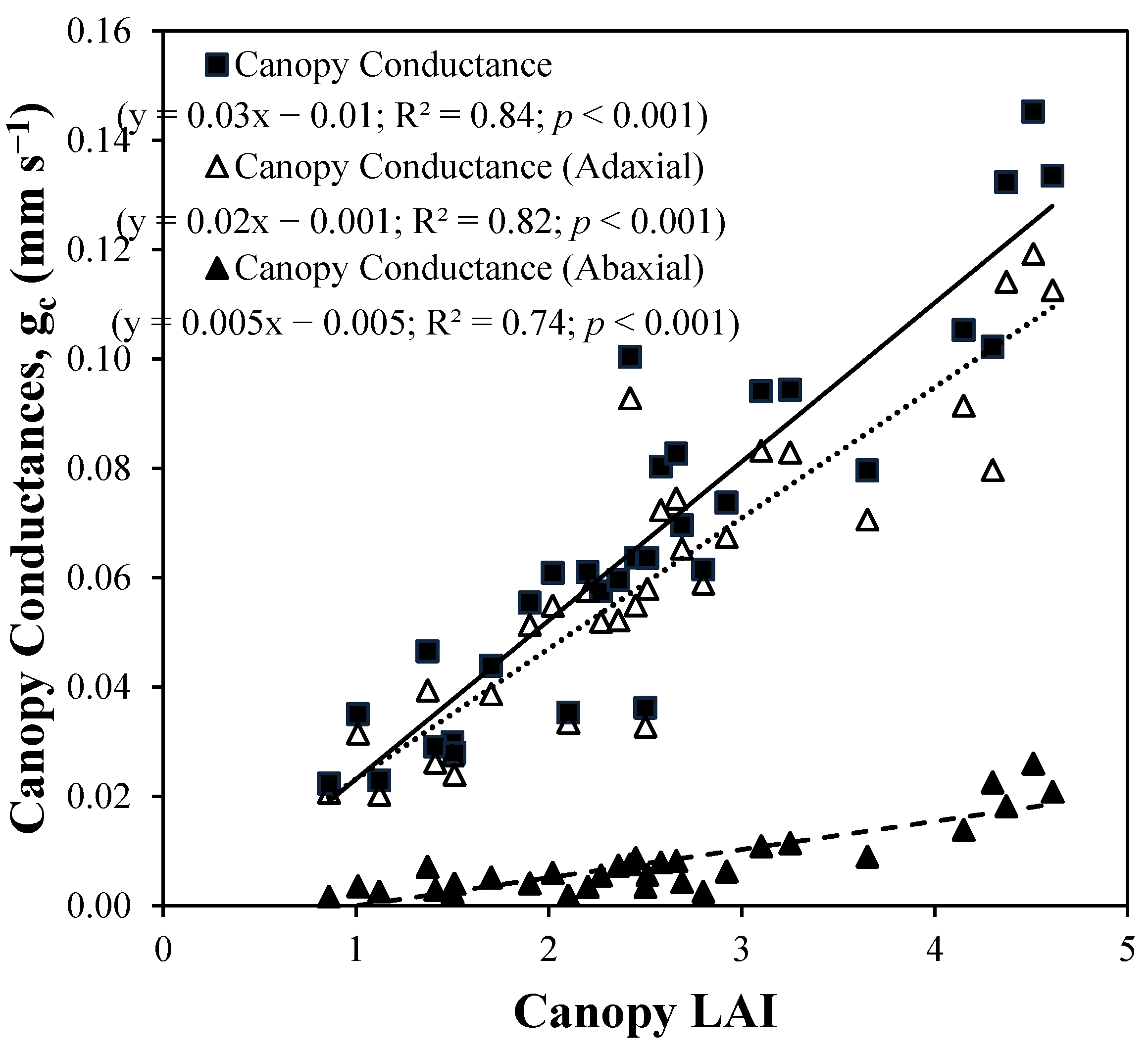
3.3. Measuring Canopy Conductance
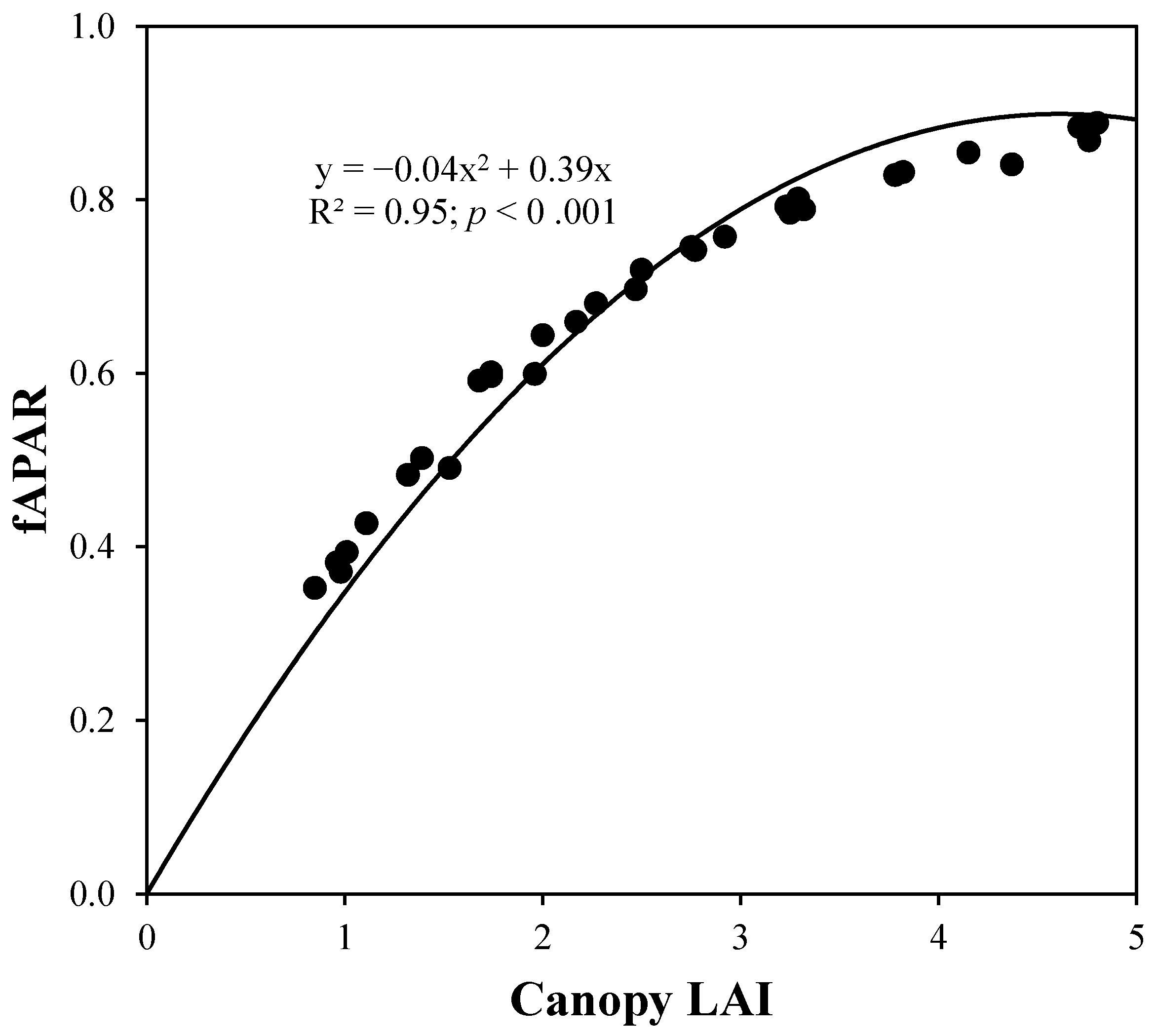
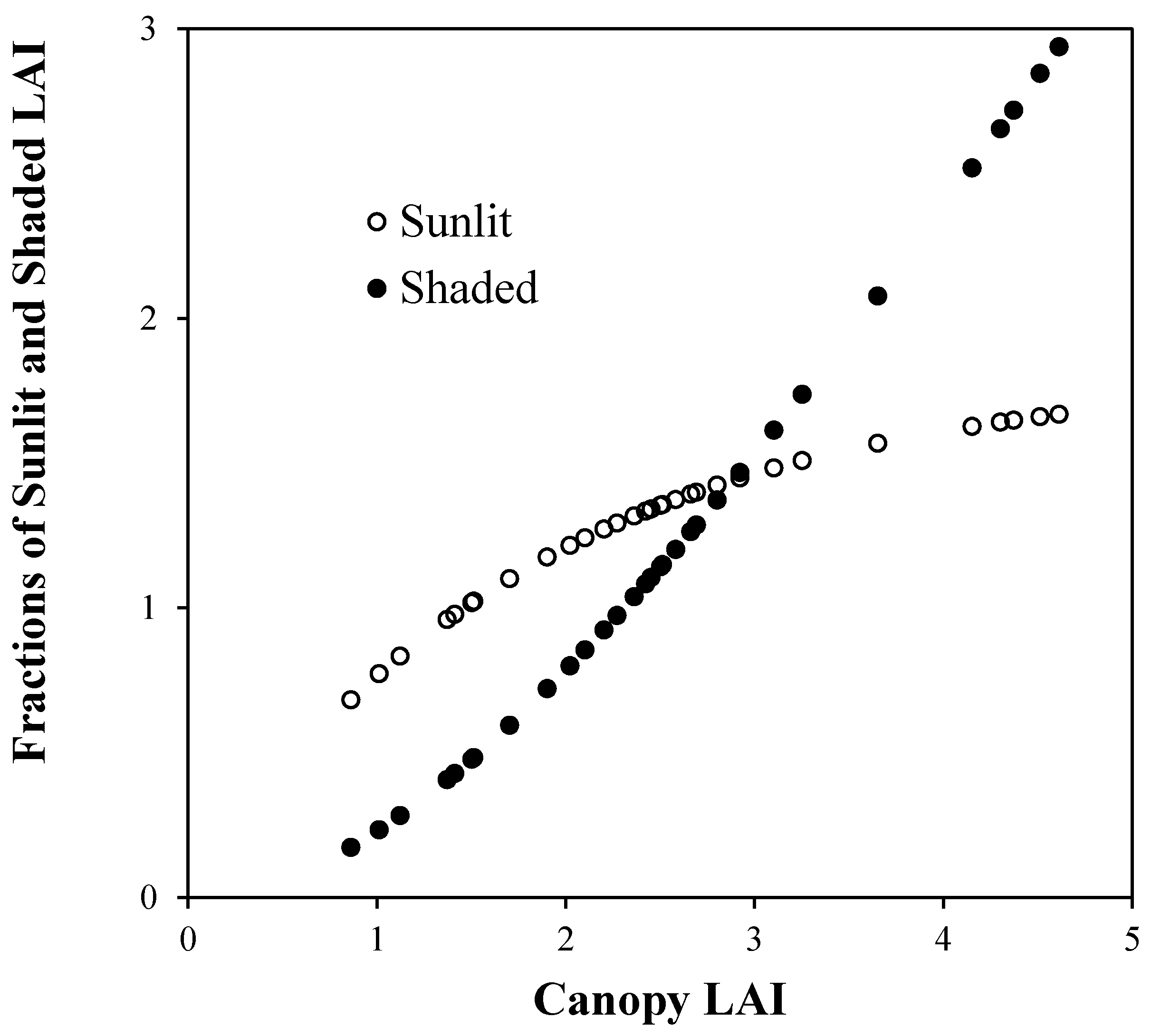
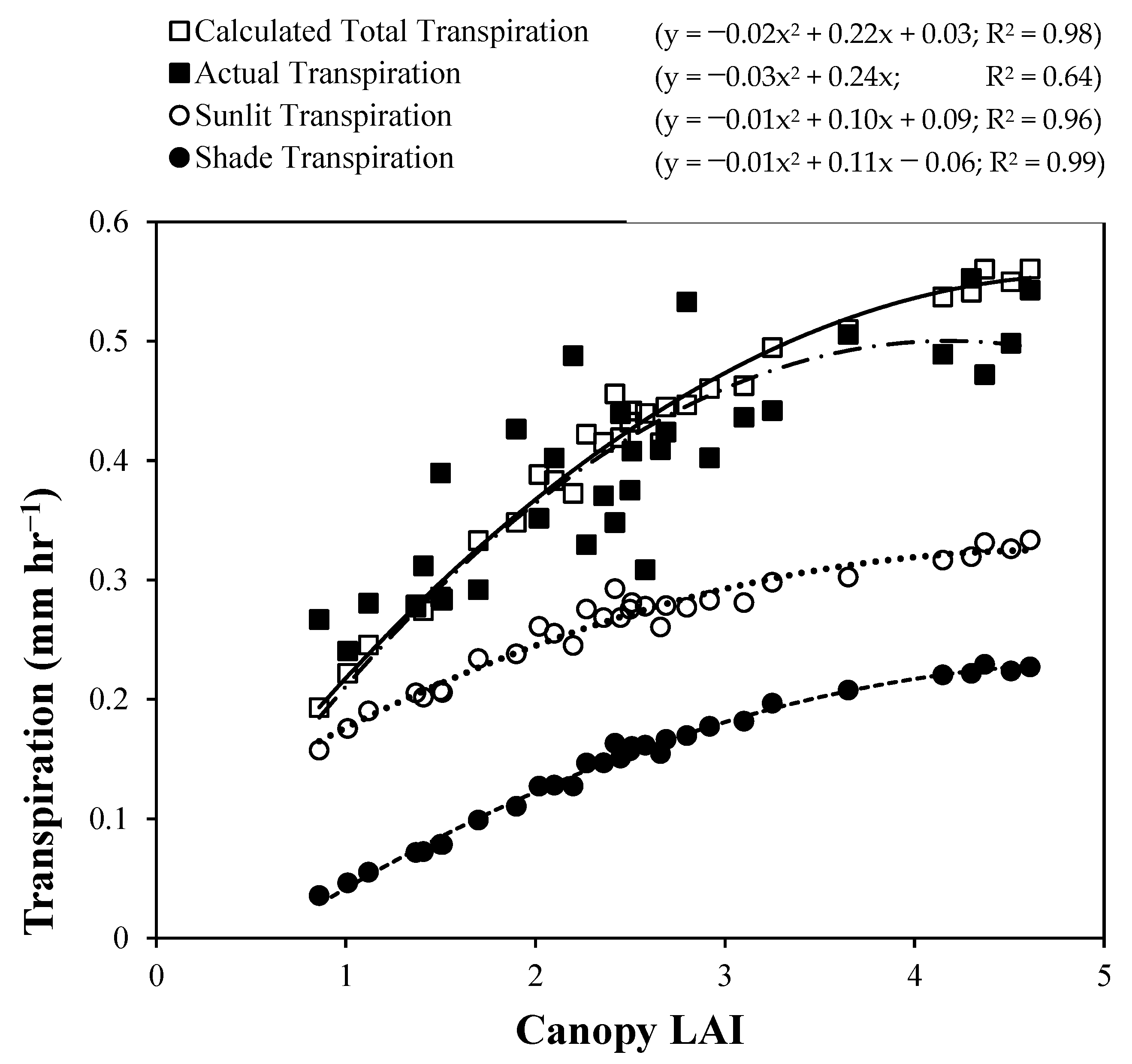
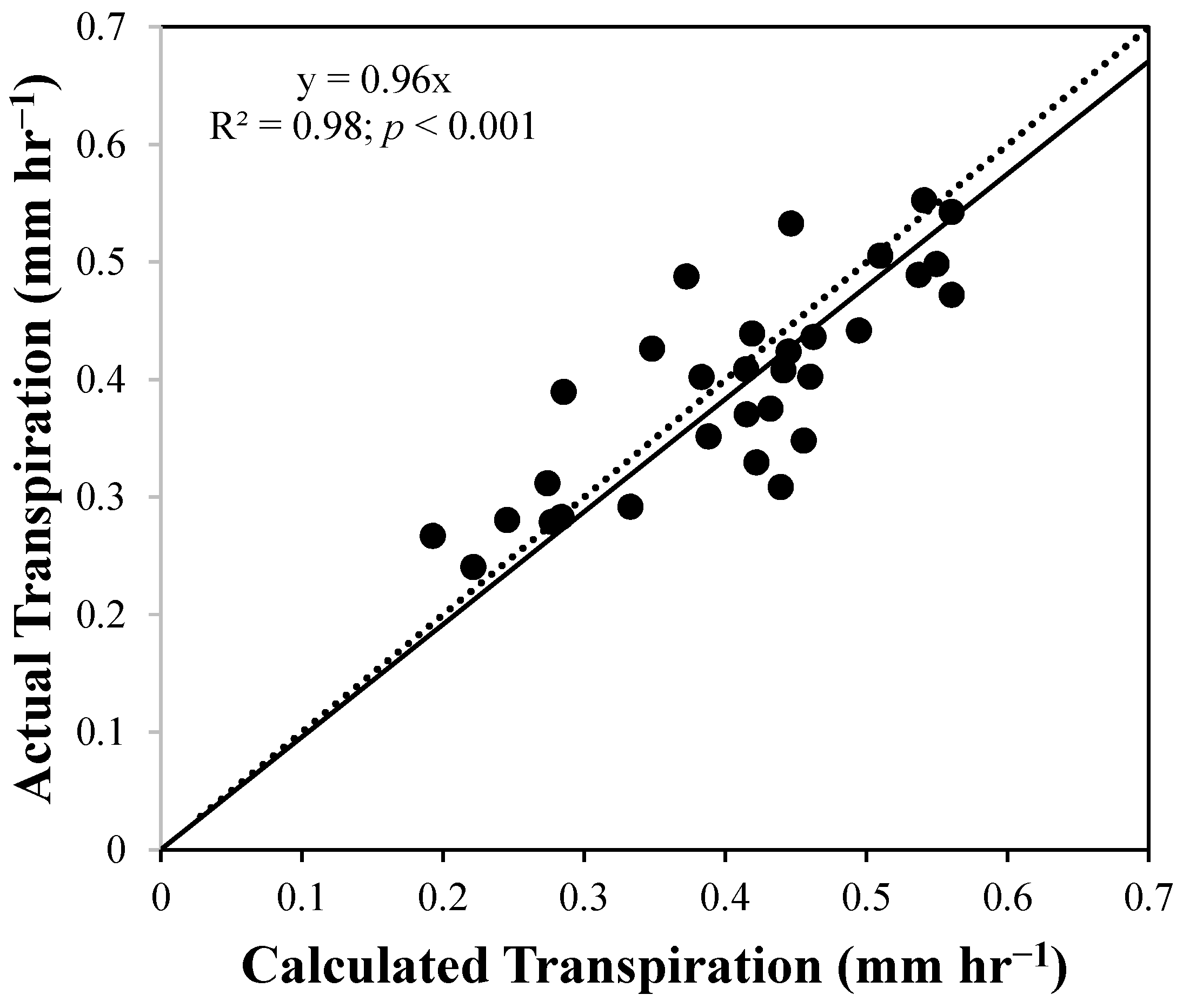
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pieruschka, R.; Huber, G.; Berry, J.A. Control of transpiration by radiation. Proc. Natl. Acad. Sci. USA 2010, 107, 13372–13377. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189, 115–117. [Google Scholar] [CrossRef]
- Jarvis, P.; McNaughton, K. Stomatal Control of Transpiration: Scaling Up from Leaf to Region. In Advances in Ecological Research; Elsevier BV: Amsterdam, The Netherlands, 1986; Volume 15, pp. 1–49. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.; Sauer, T.; Bengal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Du, T.; Hao, X.; Zhang, Y. Scaling Up Stomatal Conductance from Leaf to Canopy Using a Dual-Leaf Model for Estimating Crop Evapotranspiration. PLOS ONE 2014, 9, e95584. [Google Scholar] [CrossRef]
- Dai, Y.; Dickinson, R.E.; Wang, Y.-P. A Two-Big-Leaf Model for Canopy Temperature, Photosynthesis, and Stomatal Conductance. J. Clim. 2004, 17, 2281–2299. [Google Scholar] [CrossRef]
- Gao, Q.; Zhao, P.; Zeng, X.; Cai, X.; Shen, W. A model of stomatal conductance to quantify the relationship between leaf transpiration, microclimate and soil water stress. Plant Cell Environ. 2002, 25, 1373–1381. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Putting the “vap” into evaporation. Hydrol. Earth Syst. Sci. 2007, 11, 210–244. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Testi, L.; Orgaz, F.; García-Tejera, O.; Lopez-Bernal, A.; González-Dugo, M.V.; Ballester-Lurbe, C.; Castel, J.R.; Alarcón-Cabañero, J.J.; Nicolás-Nicolás, E.; et al. Modelling canopy conductance and transpiration of fruit trees in Mediterranean areas: A simplified approach. Agric. For. Meteorol. 2013, 171–172, 93–103. [Google Scholar] [CrossRef]
- Infante, J.; Rambal, S.; Joffre, R. Modelling transpiration in holm-oak savannah: Scaling up from the leaf to the tree scale. Agric. For. Meteorol. 1997, 87, 273–289. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Zhang, K.; Ji, X.; Yang, C.; Sudicky, E.A. Simulating canopy conductance of the Haloxylon ammodendron shrubland in an arid inland river basin of northwest China. Agric. For. Meteorol. 2018, 249, 22–34. [Google Scholar] [CrossRef]
- García-Santos, G.; Bruijnzeel, L.; Dolman, A.J. Modelling canopy conductance under wet and dry conditions in a subtropical cloud forest. Agric. For. Meteorol. 2009, 149, 1565–1572. [Google Scholar] [CrossRef]
- Brisson, N.; Itier, B.; L’Hotel, J.C.; Lorendeau, J.Y. Parameterisation of the Shuttleworth-Wallace model to estimate daily maximum transpiration for use in crop models. Ecol. Model. 1998, 107, 159–169. [Google Scholar] [CrossRef]
- Li, X.; Yang, P.; Ren, S.; Li, Y.; Liu, H.; Du, J.; Li, P.; Wang, C.; Ren, L. Modeling cherry orchard evapotranspiration based on an improved dual-source model. Agric. Water Manag. 2010, 98, 12–18. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D.; Irmak, A.; Arkebauer, T.; Weiss, A.; Martin, D.; Eisenhauer, D. On the scaling up leaf stomatal resistance to canopy resistance using photosynthetic photon flux density. Agric. For. Meteorol. 2008, 148, 1034–1044. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer Nature: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Zhang, B.; Liu, Y.; Xu, D.; Cai, J.; Li, F. Evapotranspiraton estimation based on scaling up from leaf stomatal conductance to canopy conductance. Agric. For. Meteorol. 2011, 151, 1086–1095. [Google Scholar] [CrossRef]
- Idso, S.B.; Reginato, R.J.; Jackson, R.D.; Kimball, B.A.; Nakayama, F.S. The three stages of drying of a field soil. Soil Sci. Soc. Am. J. 1974, 38, 831–837. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 Dual Crop Coefficient Method for Estimating Evaporation from Soil and Application Extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Zotarelli, L.; Dukes, M.; Morgan, K. Interpretation of Soil Moisture Content to Determine soil Field Capacity and Avoid Over-Irrigating Sandy Soils Using Soil Moisture Sensors; University of Florida Cooperation Extension Services: Gainesville, FL, USA, 2010. [Google Scholar]
- Alam, M.S.; Lamb, D.W.; Rahman, M.M. In-situ partitioning of evaporation and transpiration components using a portable evapotranspiration dome—A case study in Tall Fescue (Festuca arundinacea). Agric. Water Manag. 2019, 213, 352–357. [Google Scholar] [CrossRef]
- Alam, M.S.; Lamb, D.W.; Rahman, M.M. A refined method for rapidly determining the relationship between canopy NDVI and the pasture evapotranspiration coefficient. Comput. Electron. Agric. 2018, 147, 12–17. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G.A. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef]
- Al-Kaisi, M.; Brun, L.J.; Enz, J.W. Transpiration and evapotranspiration from maize as related to leaf area index. Agric. For. Meteorol. 1989, 48, 111–116. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Eensalu, E.; Kupper, P.; Sellin, A.; Rahi, M.; Sõber, A.; Kull, O.; Kaurilind, E. Do stomata operate at the same relative opening range along a canopy profile of Betula pendula? Funct. Plant Biol. 2008, 35, 103–110. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage; Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Rothfuss, Y.; Biron, P.; Braud, I.; Canale, L.; Durand, J.-L.; Gaudet, J.-P.; Richard, P.; Vauclin, M.; Bariac, T. Partitioning evapotranspiration fluxes into soil evaporation and plant transpiration using water stable isotopes under controlled conditions. Hydrol. Process. 2010, 24, 3177–3194. [Google Scholar] [CrossRef]
- Katsoulas, N.; Stanghellini, C. Modelling Crop Transpiration in Greenhouses: Different Models for Different Applications. Agronomy 2019, 9, 392. [Google Scholar] [CrossRef]
- Stanghellini, C. Transpiration of greenhouse crops: An aid to climate management. Ph.D. Thesis, The Institute of Agricultural Engineering (IMAG), Wageningen, The Netherlands, 1987. [Google Scholar]
- Prenger, J.J.; Fynn, R.P.; Hansen, R.C. A comparison of four evapotranspiration models in a greenhouse environment. Trans. ASAE 2002, 45, 1779. [Google Scholar] [CrossRef]
- Fynn, R.P.; Al-Shooshan, A.; Short, T.H.; McMahon, R.W. Evapotranspiration measurement and modeling for a potted Chrysanthemum crop. Trans. ASAE 1993, 36, 1907–1913. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Zhang, L.; LeMeur, R. Effect of aerodynamic resistance on energy balance and Penman-Monteith estimates of evapotranspiration in greenhouse conditions. Agric. For. Meteorol. 1992, 58, 209–228. [Google Scholar] [CrossRef]
- Thimijan, R.W.; Heins, R.D. Photometric, radiometric, and quantum light units of measure: A review of procedures for interconversion. HortScience 1983, 18, 818–822. [Google Scholar]
- Delgado-Bonal, A. Entropy of radiation: The unseen side of light. Sci. Rep. 2017, 7, 1642. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, D.; Chen, X.; Zhang, J. A simple method for estimating field crop evapotranspiration from pot experiments. Water 2018, 10, 1823. [Google Scholar] [CrossRef]
- Hagishima, A.; Narita, K.-I.; Tanimoto, J. Field experiment on transpiration from isolated urban plants. Hydrol. Process. 2007, 21, 1217–1222. [Google Scholar] [CrossRef]
- Bell, M. Guide to soil measurements for agronomic and physiological research in small grain cereals. Wheat Spec. Rep. 1993, 18, 40. [Google Scholar]
- Rahman, M.M.; Stanley, J.N.; Lamb, D.W.; Trotter, M.G. Methodology for measuring fAPAR in crops using a combination of active optical and linear irradiance sensors: A case study in Triticale (X Triticosecale Wittmack). Precis. Agric. 2014, 15, 532–542. [Google Scholar] [CrossRef]
- Rahman, M.; Lamb, D.W.; Stanley, J. The impact of solar illumination angle when using active optical sensing of NDVI to infer fAPAR in a pasture canopy. Agric. For. Meteorol. 2015, 202, 39–43. [Google Scholar] [CrossRef]
- Bragg, T.; Webb, N.; Spencer, R.; Wood, J.; Nicholl, C.; Potter, E. User Manual for the Porometer type AP4. Document Code: AP4-UM-3; Delta-T Devices Ltd.: Cambridge, UK, 2004; Volume 4, p. 197. Available online: https://www.delta-t.co.uk/wp-content/uploads/2020/03/AP4-Porometer-User-Manual-A5-v4.pdf (accessed on 2 October 2019).
- Lantinga, E.A.; Nassiri, M.; Kropff, M.J. Modelling and measuring vertical light absorption within grass–clover mixtures. Agric. For. Meteorol. 1999, 96, 71–83. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, Z.; Fan, J.; Zhou, D.; Tang, F. A meta-analysis of the canopy light extinction coefficient in terrestrial ecosystems. Front. Earth Sci. 2014, 8, 599–609. [Google Scholar] [CrossRef]
- Pachepsky, L.; Lu, Z.; Reddy, V. Analysis of abaxial and adaxial stomatal regulation in leaves of Pima cotton (Gossypium barbadense L.) using the 2DLEAF, two-dimensional model of leaf gas exchange. Biotronics 2000, 29, 79–95. [Google Scholar]
- Duchemin, B.; Hadria, R.; Er-Raki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.; Kharrou, M.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Will, R.E.; Wilson, S.M.; Zou, C.B.; Hennessey, T.C. Increased vapor pressure deficit due to higher temperature leads to greater transpiration and faster mortality during drought for tree seedlings common to the forest-grassland ecotone. New Phytol. 2013, 200, 366–374. [Google Scholar] [CrossRef]
- Whitehead, D.; Sheriff, D.; Greer, D. The relationship between stomatal conductance, transpiration rate and tracheid structure in Pinus radiata clones grown at different water vapour saturation deficits. Plant Cell Environ. 1983, 6, 703–710. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.S.; Lamb, D.W.; Warwick, N.W.M. A Canopy Transpiration Model Based on Scaling Up Stomatal Conductance and Radiation Interception as Affected by Leaf Area Index. Water 2021, 13, 252. https://doi.org/10.3390/w13030252
Alam MS, Lamb DW, Warwick NWM. A Canopy Transpiration Model Based on Scaling Up Stomatal Conductance and Radiation Interception as Affected by Leaf Area Index. Water. 2021; 13(3):252. https://doi.org/10.3390/w13030252
Chicago/Turabian StyleAlam, Muhammad Shahinur, David William Lamb, and Nigel W. M. Warwick. 2021. "A Canopy Transpiration Model Based on Scaling Up Stomatal Conductance and Radiation Interception as Affected by Leaf Area Index" Water 13, no. 3: 252. https://doi.org/10.3390/w13030252
APA StyleAlam, M. S., Lamb, D. W., & Warwick, N. W. M. (2021). A Canopy Transpiration Model Based on Scaling Up Stomatal Conductance and Radiation Interception as Affected by Leaf Area Index. Water, 13(3), 252. https://doi.org/10.3390/w13030252





