Quantile-Based Hydrological Modelling
Abstract
:1. Introduction
- Post-processing (two-stage) techniques using stochastic or regression-based methods (including machine learning ones). These techniques model residual errors. Several relevant examples can be found in the literature; see [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and the review by [38], including quantile regression, which is based on the quantile loss function. Further classification of the methods is possible, depending on specific attributes, but this is out of scope here.
- Post-processing approaches: The quantile loss function is directly implemented by the hydrological model. On the other hand, post-processing methods model the residuals of the fitted hydrological model (that have been obtained by implementing a squared error type loss function) at a second stage (i.e., after applying the hydrological models), using a statistical or machine learning method.
- Monte Carlo of Bayesian joint inference approaches: These methods are applied directly to the hydrological model; therefore, there is some resemblance with our approach. In this case, the differences between the two approaches (Bayesian joint inference and our proposed approach) are identical with those identified in the statistical literature regarding the differences between Bayesian statistics and quantile regression modelling. These differences are thoroughly discussed in the Discussion in Section 6.
2. Methods
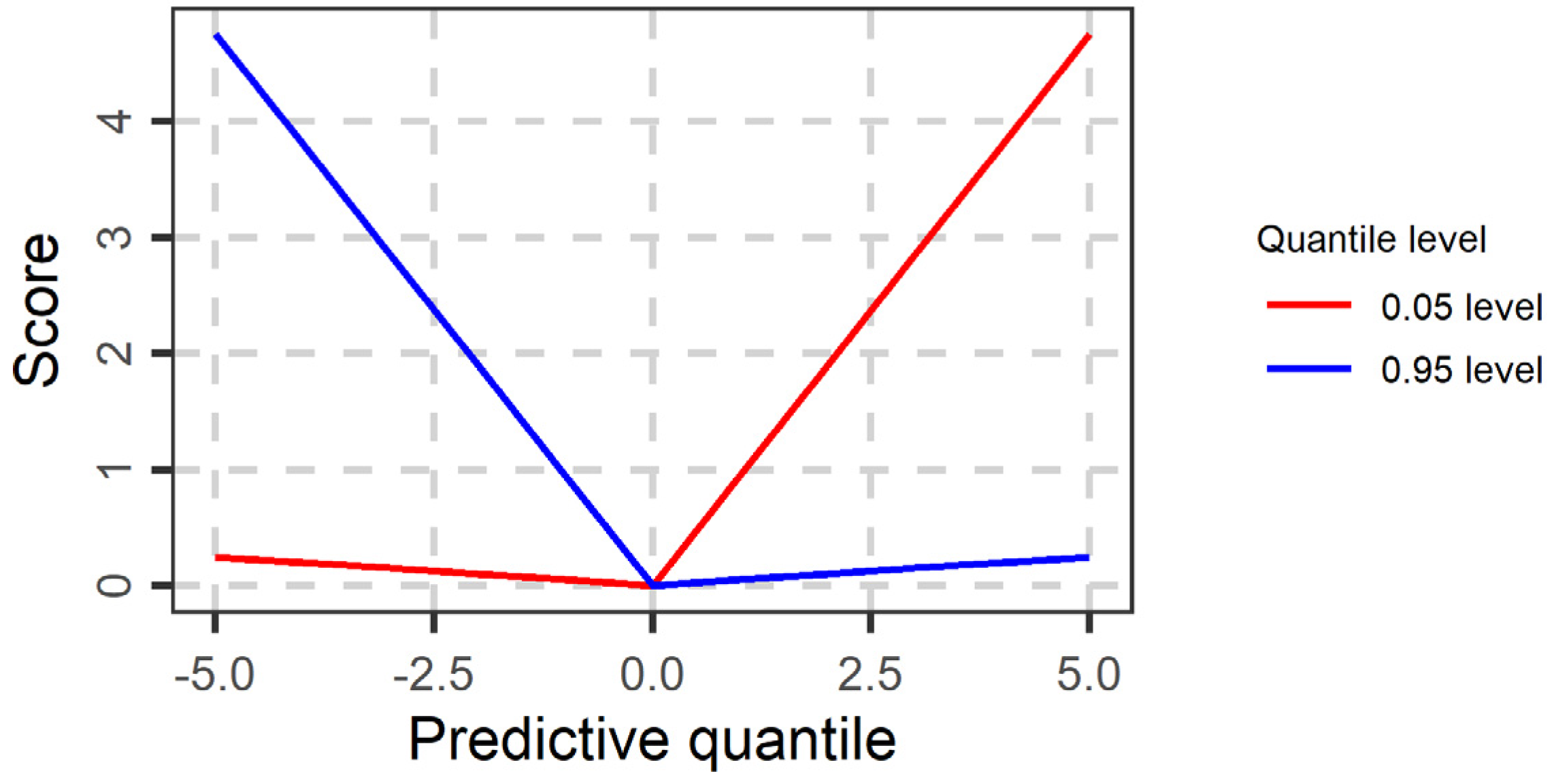
2.1. Quantile Loss Function
2.2. Theoretical Properties of the Quantile Loss Function
2.3. Hydrological Models
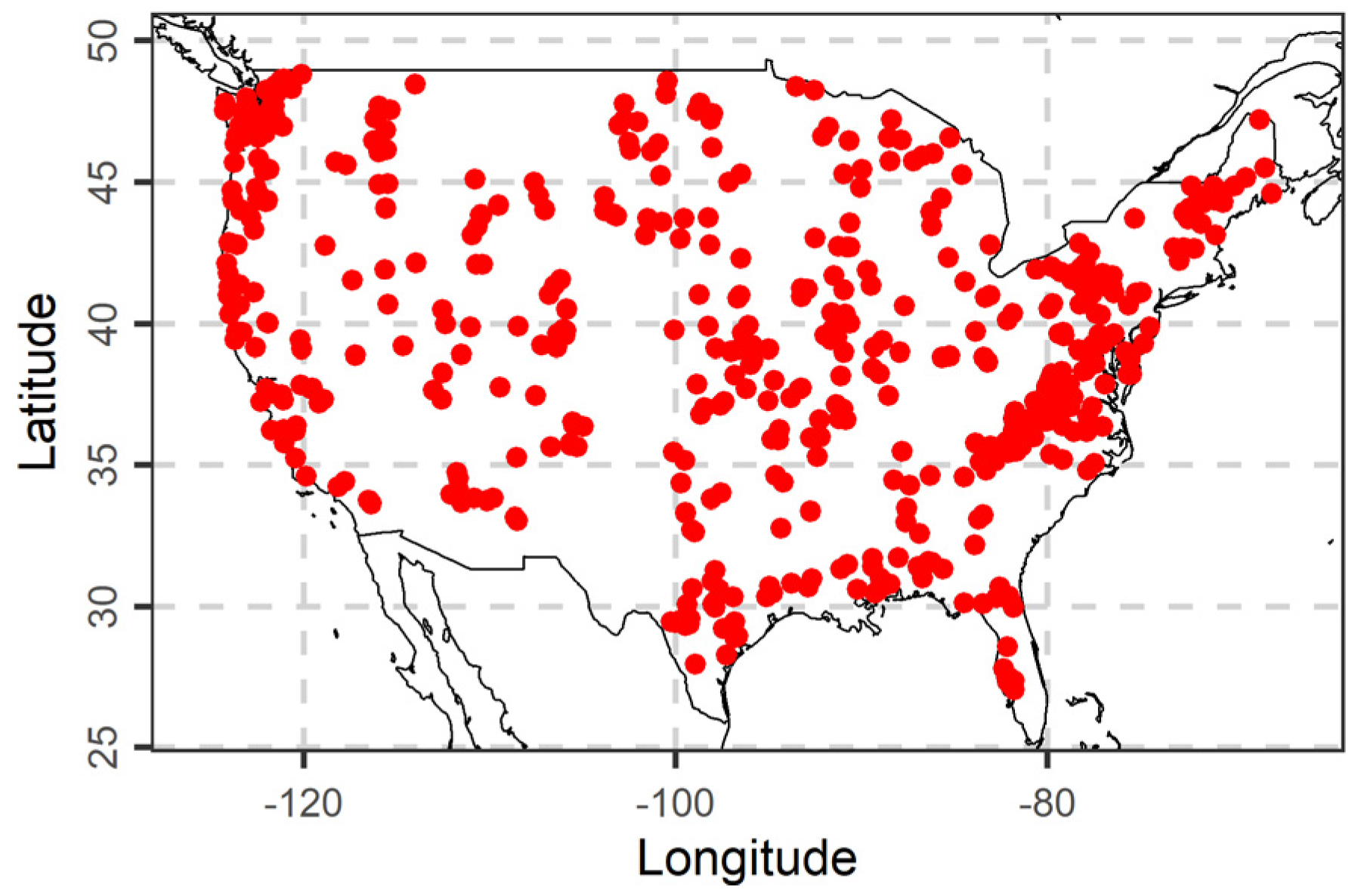
3. Data
4. Implementation and Key Components
- Define the 2-year period 1980–1981 as the warm-up period of the hydrological models.
- Calibrate the hydrological models in the 16-year period 1982–1997 using: (a) the quantile loss function L(r; x, a) at quantile levels a ∈ {0.025, 0.050, 0.100, 0.500, 0.900, 0.950, 0.975}; and (b) the squared error function. That equates to 8 (i.e., 7 + 1; number of loss functions) × 3 (number of hydrological models) = 24 sets of parameters at each river basin. These sets of parameters correspond to different model setups.
- Simulate streamflow in the 16-year period 1998–2013 for each of the 24 model setups.
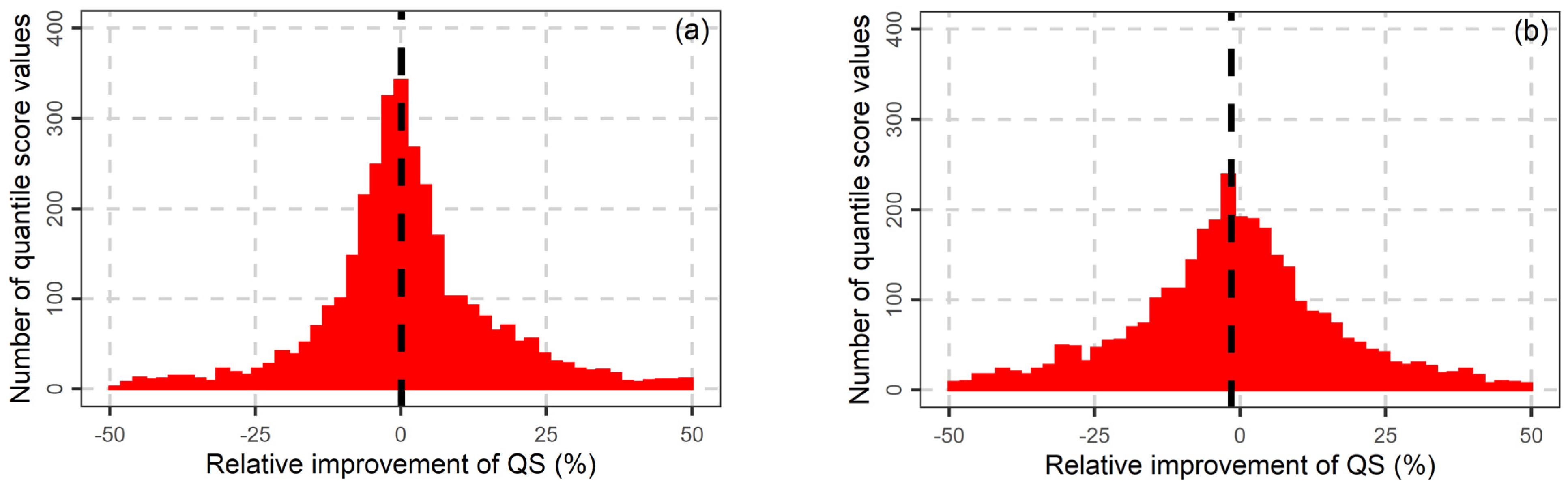
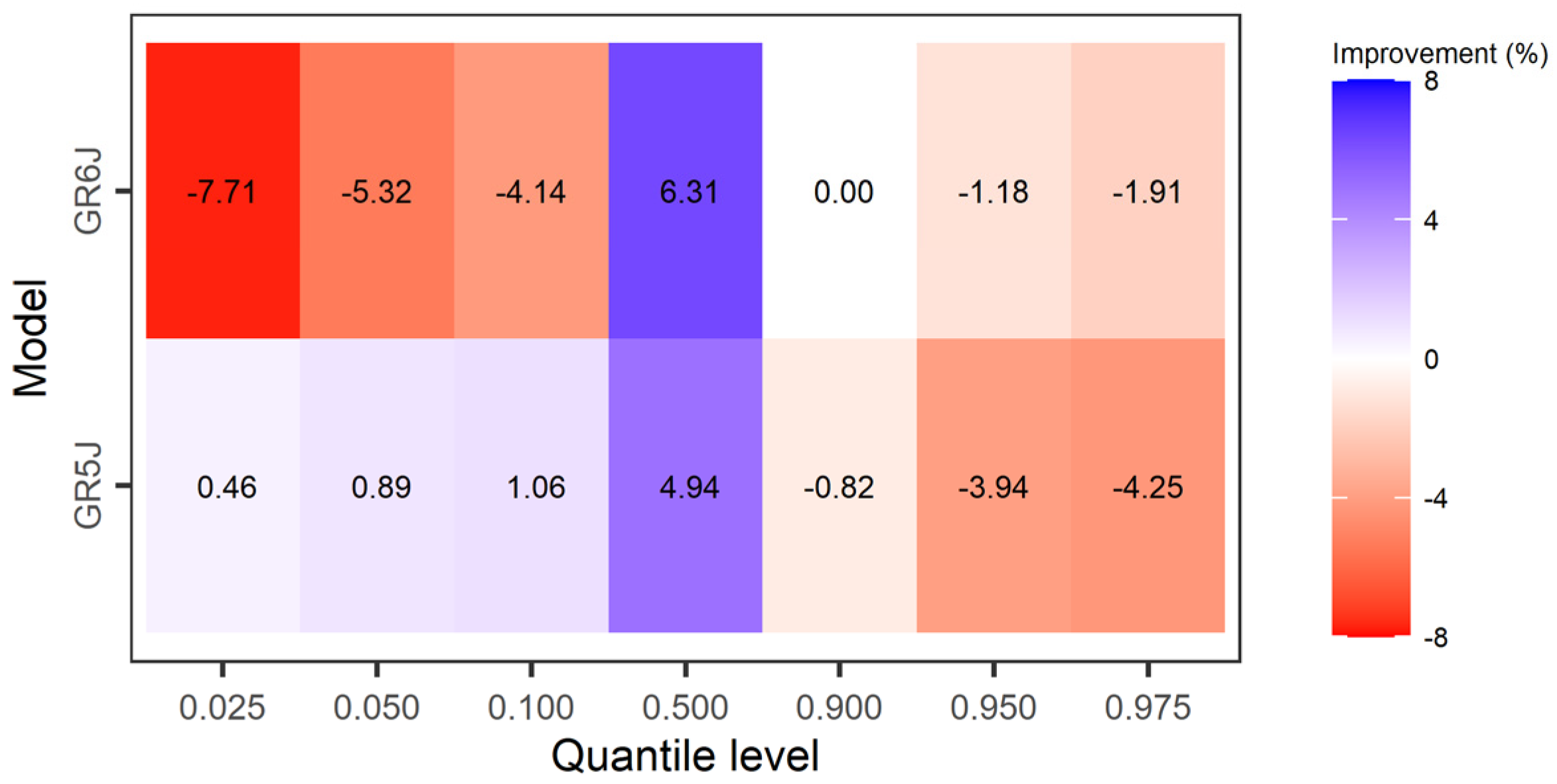
5. Results
6. Discussion
- When one is interested in events at the “limits of probability”.
- When the conditional distribution does not follow a known distribution.
- The possible presence of many outliers of the dependent variable (recall also that median regression is more robust compared to mean regression in the presence of outliers).
- The presence of heteroscedasticity.
- Estimating the parameters of the model is harder compared to Gaussian regression.
- Inference on the parameters (e.g., the computation of confidence intervals) is complicated.
- The possible presence of quantile crossing, i.e., estimated quantiles at higher levels might be lower than respective quantiles at lower levels.
- The full conditional distribution is not available; although, the computation of multiple quantiles can substitute predictive distributions [61]. In this case, a drawback of the method is that it requires the estimation of a high number of sets of model parameters (one set for each quantile).
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Solomatine, D.P.; Wagener, T. 2.16-Hydrological Modeling. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 435–457. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Biondi, D.; Freni, G.; Iacobellis, V.; Mascaro, G.; Montanari, A. Validation of hydrological models: Conceptual basis, methodological approaches and a proposal for a code of practice. Phys. Chem. Earth Parts A/B/C 2012, 42, 70–76. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Todini, E. Hydrological catchment modelling: Past, present and future. Hydrol. Earth Syst. Sci. 2007, 11, 468–482. [Google Scholar] [CrossRef] [Green Version]
- Ju, J.; Dai, H.; Wu, C.; Hu, B.X.; Ye, M.; Chen, X.; Gui, D.; Liu, H.; Zhang, J. Quantifying the uncertainty of the future hydrological impacts of climate change: Comparative analysis of an advanced hierarchical sensitivity in humid and semiarid basins. J. Hydrometeorol. 2021, 22, 601–621. [Google Scholar] [CrossRef]
- Montanari, A. 2.17-Uncertainty of Hydrological Predictions. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 459–478. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three Unsolved Problems in Hydrology (UPH)–A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Biondi, D.; Todini, E. Comparing hydrological postprocessors including ensemble predictions into full predictive probability distribution of streamflow. Water Resour. Res. 2018, 54, 9860–9882. [Google Scholar] [CrossRef] [Green Version]
- Bock, A.R.; Farmer, W.H.; Hay, L.E. Quantifying uncertainty in simulated streamflow and runoff from a continental-scale monthly water balance model. Adv. Water Resour. 2018, 122, 166–175. [Google Scholar] [CrossRef]
- Bogner, K.; Pappenberger, F. Multiscale error analysis, correction, and predictive uncertainty estimation in a flood forecasting system. Water Resour. Res. 2011, 47, W07524. [Google Scholar] [CrossRef] [Green Version]
- Bogner, K.; Pappenberger, F.; Cloke, H.L. Technical note: The normal quantile transformation and its application in a flood forecasting system. Hydrol. Earth Syst. Sci. 2012, 16, 1085–1094. [Google Scholar] [CrossRef] [Green Version]
- Bogner, K.; Liechti, K.; Zappa, M. Post-processing of stream flows in Switzerland with an emphasis on low flows and floods. Water 2016, 8, 115. [Google Scholar] [CrossRef] [Green Version]
- Bogner, K.; Liechti, K.; Zappa, M. Technical note: Combining quantile forecasts and predictive distributions of streamflows. Hydrol. Earth Syst. Sci. 2017, 21, 5493–5502. [Google Scholar] [CrossRef] [Green Version]
- Dogulu, N.; López López, P.; Solomatine, D.P.; Weerts, A.H.; Shrestha, D.L. Estimation of predictive hydrologic uncertainty using the quantile regression and UNEEC methods and their comparison on contrasting catchments. Hydrol. Earth Syst. Sci. 2015, 19, 3181–3201. [Google Scholar] [CrossRef] [Green Version]
- Evin, G.; Thyer, M.; Kavetski, D.; McInerney, D.; Kuczera, G. Comparison of joint versus postprocessor approaches for hydrological uncertainty estimation accounting for error autocorrelation and heteroscedasticity. Water Resour. Res. 2014, 50, 2350–2375. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Markovian forecast processes. J. Am. Stat. Assoc. 1987, 82, 31–37. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Transformation and normalization of variates with specified distributions. J. Hydrol. 1997, 1997, 286–292. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef] [Green Version]
- Krzysztofowicz, R. The case for probabilistic forecasting in hydrology. J. Hydrol. 2001, 249, 2–9. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian system for probabilistic river stage forecasting. J. Hydrol. 2002, 268, 16–40. [Google Scholar] [CrossRef]
- Krzysztofowicz, R.; Kelly, K.S. Hydrologic uncertainty processor for probabilistic river stage forecasting. Water Resour. Res. 2000, 36, 3265–3277. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A.; Zhou, Y. Characterizing distributed hydrological model residual errors using a probabilistic long short-term memory network. J. Hydrol. 2021, 603, 126888. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A.; Zhou, Y. Bayesian LSTM with stochastic variational inference for estimating model uncertainty in process-based hydrological models. Water Resour. Res. 2021, 57, e2021WR029772. [Google Scholar] [CrossRef]
- López López, P.; Verkade, J.S.; Weerts, A.H.; Solomatine, D.P. Alternative configurations of quantile regression for estimating predictive uncertainty in water level forecasts for the upper Severn River: A comparison. Hydrol. Earth Syst. Sci. 2014, 18, 3411–3428. [Google Scholar] [CrossRef] [Green Version]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40, W01106. [Google Scholar] [CrossRef]
- Montanari, A.; Grossi, G. Estimating the uncertainty of hydrological forecasts: A statistical approach. Water Resour. Res. 2008, 44, W00B08. [Google Scholar] [CrossRef] [Green Version]
- Papacharalampous, G.; Tyralis, H.; Langousis, A.; Jayawardena, A.W.; Sivakumar, B.; Mamassis, N.; Montanari, A.; Koutsoyiannis, D. Probabilistic hydrological post-processing at scale: Why and how to apply machine-learning quantile regression algorithms. Water 2019, 11, 2126. [Google Scholar] [CrossRef] [Green Version]
- Papacharalampous, G.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: Methodology development and investigation using toy models. Adv. Water Resour. 2020, 136, 103471. [Google Scholar] [CrossRef] [Green Version]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D.; Montanari, A. Quantification of predictive uncertainty in hydrological modelling by harnessing the wisdom of the crowd: A large-sample experiment at monthly timescale. Adv. Water Resour. 2020, 136, 103470. [Google Scholar] [CrossRef] [Green Version]
- Seo, D.J.; Herr, H.D.; Schaake, J.C. A statistical post-processor for accounting of hydrologic uncertainty in short-range ensemble streamflow prediction. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1987–2035. [Google Scholar] [CrossRef] [Green Version]
- Sikorska-Senoner, A.E.; Quilty, J.M. A novel ensemble-based conceptual-data-driven approach for improved streamflow simulations. Environ. Model. Softw. 2021, 143, 105094. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Burnetas, A.; Langousis, A. Hydrological post-processing using stacked generalization of quantile regression algorithms: Large-scale application over CONUS. J. Hydrol. 2019, 577, 123957. [Google Scholar] [CrossRef]
- Weerts, A.H.; Winsemius, H.C.; Verkade, J.S. Estimation of predictive hydrological uncertainty using quantile regression: Examples from the national flood forecasting system (England and Wales). Hydrol. Earth Syst. Sci. 2011, 15, 255–265. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Liao, G.Y.; Gebremichael, M.; Shedd, R.; Vallee, D.R. Characterizing the uncertainty in river stage forecasts conditional on point forecast values. Water Resour. Res. 2014, 48, W12509. [Google Scholar] [CrossRef]
- Ye, A.; Duan, Q.; Yuan, X.; Wood, E.F.; Schaake, J. Hydrologic post-processing of MOPEX streamflow simulations. J. Hydrol. 2014, 508, 147–156. [Google Scholar] [CrossRef]
- Zhao, L.; Duan, Q.; Schaake, J.; Ye, A.; Xia, J. A hydrologic post-processor for ensemble streamflow predictions. Adv. Geosci. 2011, 29, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Duan, Q.; Miao, C.; Ye, A.; Gong, W.; Di, Z. A review on statistical postprocessing methods for hydrometeorological ensemble forecasting. WIREs Water 2017, 4, e1246. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; Bazame, H.C. Uncertainty quantification for hydrological models based on neural networks: The dropout ensemble. Stoch. Environ. Res. Risk Assess. 2021, 35, 1051–1067. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Montanari, A.; Koutsoyiannis, D. A blueprint for process-based modeling of uncertain hydrological systems. Water Resour. Res. 2012, 48, W09555. [Google Scholar] [CrossRef]
- Hernández-López, M.R.; Francés, F. Bayesian joint inference of hydrological and generalized error models with the enforcement of total laws. Hydrol. Earth Syst. Sci. Discuss. 2017. [Google Scholar] [CrossRef]
- Kuczera, G.; Kavetski, D.; Franks, S.; Thyer, M. Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters. J. Hydrol. 2006, 331, 161–177. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef] [Green Version]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather. Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Reggiani, P.; Weerts, A.H. A Bayesian approach to decision-making under uncertainty: An application to real-time forecasting in the river Rhine. J. Hydrol. 2008, 356, 56–69. [Google Scholar] [CrossRef]
- Todini, E. Paradigmatic changes required in water resources management to benefit from probabilistic forecasts. Water Secur. 2018, 3, 9–17. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Bluecat: A Local Uncertainty Estimator for Deterministic Simulations and Predictions. 2021. Available online: https://doi.org/10.13140/RG.2.2.23863.65445 (accessed on 13 November 2021).
- Sikorska, A.E.; Montanari, A.; Koutsoyiannis, D. Estimating the uncertainty of hydrological predictions through data-driven resampling techniques. J. Hydrol. Eng. 2015, 20, A4014009. [Google Scholar] [CrossRef]
- Robert, C. The Bayesian Choice; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Gneiting, T. Making and evaluating point forecasts. J. Am. Stat. Assoc. 2011, 106, 746–762. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R.W.; Bassett, G., Jr. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.W. Quantile Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Taylor, J.W. A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J. Forecast. 2000, 19, 299–311. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Tyralis, H.; Papacharalampous, G. Boosting algorithms in energy research: A systematic review. Neural Comput. Appl. 2021, 33, 14101–14117. [Google Scholar] [CrossRef]
- Pande, S. Quantile hydrologic model selection and model structure deficiency assessment: 1. Theory. Water Resour. Res. 2013, 49, 5631–5657. [Google Scholar] [CrossRef] [Green Version]
- Pande, S. Quantile hydrologic model selection and model structure deficiency assessment: 2. Applications. Water Resour. Res. 2013, 49, 5658–5673. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Koenker, R.W. Quantile regression: 40 years on. Annu. Rev. Econ. 2017, 9, 155–176. [Google Scholar] [CrossRef] [Green Version]
- Brehmer, J.R.; Gneiting, T. Scoring interval forecasts: Equal-tailed, shortest, and modal interval. Bernoulli 2021, 27, 1993–2010. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Brehmer, J.R.; Gneiting, T. Properization: Constructing proper scoring rules via Bayes acts. Ann. Inst. Stat. Math. 2020, 72, 659–673. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R.W.; D’Orey, V. Computing regression quantiles. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1987, 36, 383–393. [Google Scholar] [CrossRef]
- Koenker, R.W.; D’Orey, V. A remark on algorithm AS 229: Computing dual regression quantiles and regression rank scores. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1994, 43, 410–414. [Google Scholar] [CrossRef]
- Koenker, R.W.; Machado, J.A.F. Goodness of fit and related inference processes for quantile regression. J. Am. Stat. Assoc. 1999, 94, 1296–1310. [Google Scholar] [CrossRef]
- Bentzien, S.; Friederichs, P. Decomposition and graphical portrayal of the quantile score. Q. J. R. Meteorol. Soc. 2014, 140, 1924–1934. [Google Scholar] [CrossRef]
- Nascimento, N.O.; Yang, X.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Linking stream flow to rainfall at the annual time step: The Manabe bucket model revisited. J. Hydrol. 2006, 328, 283–296. [Google Scholar] [CrossRef]
- Michel, C. Hydrologie Appliquée aux Petits Bassins Ruraux; Cemagref: Antony, France, 1991. [Google Scholar]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. Catchment Attributes for Large-Sample Studies; UCAR/NCAR: Boulder, CO, USA, 2017; Available online: https://doi.org/10.5065/D6G73C3Q (accessed on 13 November 2021).
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef] [Green Version]
- Newman, A.J.; Sampson, K.; Clark, M.P.; Bock, A.; Viger, R.J.; Blodgett, D. A Large-Sample Watershed-Scale Hydrometeorological Dataset for the Contiguous USA; UCAR/NCAR: Boulder, CO, USA, 2014; Available online: https://doi.org/10.5065/D6MW2F4D (accessed on 13 November 2021).
- Newman, A.J.; Clark, M.P.; Sampson, K.; Wood, A.; Hay, L.E.; Bock, A.; Viger, R.J.; Blodgett, D.; Brekke, L.; Arnold, J.R.; et al. Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: Data set characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Syst. Sci. 2015, 19, 209–223. [Google Scholar] [CrossRef] [Green Version]
- Newman, A.J.; Mizukami, N.; Clark, M.P.; Wood, A.W.; Nijssen, B.; Nearing, G. Benchmarking of a physically based hydrologic model. J. Hydrometeorol. 2017, 18, 2215–2225. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2; ORNL DAAC: Oak Ridge, TN, USA, 2014; Available online: https://doi.org/10.3334/ORNLDAAC/1219 (accessed on 20 January 2016).
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Dunsmore, I.R. A Bayesian approach to calibration. J. R. Stat. Society Ser. B (Methodol.) 1968, 30, 396–405. [Google Scholar] [CrossRef]
- Waldmann, E. Quantile regression: A short story on how and why. Stat. Model. 2018, 18, 203–218. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Hydrological time series forecasting using simple combinations: Big data testing and investigations on one-year ahead river flow predictability. J. Hydrol. 2020, 590, 125205. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Comparison of stochastic and machine learning methods for multi-step ahead forecasting of hydrological processes. Stoch. Environ. Res. Risk Assess. 2019, 33, 481–514. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Papalexiou, S.M.; Langousis, A.; Khatami, S.; Volpi, E.; Grimaldi, S. Global-scale massive feature extraction from monthly hydroclimatic time series: Statistical characterizations, spatial patterns and hydrological similarity. Sci. Total Environ. 2021, 767, 144612. [Google Scholar] [CrossRef] [PubMed]
- Perrin, C.; Michel, C.; Andréassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Khatami, S.; Peel, M.C.; Peterson, T.J.; Western, A.W. Equifinality and flux mapping: A new approach to model evaluation and process representation under uncertainty. Water Resour. Res. 2019, 55, 8922–8941. [Google Scholar] [CrossRef]
- Khatami, S.; Peterson, T.J.; Peel, M.C.; Western, A.W. Evaluating Catchment Models as Multiple Working Hypotheses: On the Role of Error Metrics, Parameter Sampling, Model Structure, and Data Information Content. 2020. Available online: https://doi.org/10.1002/essoar.10504066.1 (accessed on 13 November 2021).
- Tyralis, H.; Papacharalampous, G.; Tantanee, S. How to explain and predict the shape parameter of the generalized extreme value distribution of streamflow extremes using a big dataset. J. Hydrol. 2019, 574, 628–645. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A.; Papalexiou, S.M. Explanation and probabilistic prediction of hydrological signatures with statistical boosting algorithms. Remote Sens. 2021, 13, 333. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 13 November 2021).
- Coron, L.; Delaigue, O.; Thirel, G.; Dorchies, D.; Perrin, C.; Michel, C. airGR: Suite of GR Hydrological Models for Precipitation-Runoff Modelling. R Package Version 1.6.12. 2021. Available online: https://CRAN.R-project.org/package=airGR (accessed on 13 November 2021).
- Dowle, M.; Srinivasan, A. data.table: Extension of ‘data.frame’. R Package Version 1.14.2. 2021. Available online: https://CRAN.R-project.org/package=data.table (accessed on 13 November 2021).
- Wickham, H.; Hester, J.; Chang, W. devtools: Tools to Make Developing R Packages Easier. R Package Version 2.4.2. 2021. Available online: https://CRAN.R-project.org/package=devtools (accessed on 13 November 2021).
- Warnes, G.R.; Bolker, B.; Gorjanc, G.; Grothendieck, G.; Korosec, A.; Lumley, T.; MacQueen, D.; Magnusson, A.; Rogers, J. Gdata: Various R Programming Tools for Data Manipulation. R Package Version 2.18.0. 2017. Available online: https://CRAN.R-project.org/package=gdata (accessed on 13 November 2021).
- Xie, Y. knitr: A Comprehensive Tool for Reproducible Research in R. In Implementing Reproducible Computational Research; Stodden, V., Leisch, F., Peng, R.D., Eds.; Chapman and Hall/CRC: London, UK, 2014. [Google Scholar]
- Xie, Y. Dynamic Documents with R and Knitr, 2nd ed.; Chapman and Hall/CRC: London, UK, 2015. [Google Scholar]
- Xie, Y. Knitr: A General-Purpose Package for Dynamic Report Generation in R. R Package Version 1.36. 2021. Available online: https://CRAN.R-project.org/package=knitr (accessed on 13 November 2021).
- Allaire, J.J.; Xie, Y.; McPherson, J.; Luraschi, J.; Ushey, K.; Atkins, A.; Wickham, H.; Cheng, J.; Chang, W.; Iannone, R. Rmarkdown: Dynamic Documents for R. R Package Version 2.11. 2021. Available online: https://CRAN.R-project.org/package=rmarkdown (accessed on 13 November 2021).
- Gagolewski, M. Stringi: Character String Processing Facilities. R Package Version 1.7.5. 2021. Available online: https://CRAN.R-project.org/package=stringi (accessed on 13 November 2021).
- Wickham, H. Tidyverse: Easily Install and Load the ‘Tidyverse’. R Package Version 1.3.1. 2021. Available online: https://CRAN.R-project.org/package=tidyverse (accessed on 13 November 2021).
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tyralis, H.; Papacharalampous, G. Quantile-Based Hydrological Modelling. Water 2021, 13, 3420. https://doi.org/10.3390/w13233420
Tyralis H, Papacharalampous G. Quantile-Based Hydrological Modelling. Water. 2021; 13(23):3420. https://doi.org/10.3390/w13233420
Chicago/Turabian StyleTyralis, Hristos, and Georgia Papacharalampous. 2021. "Quantile-Based Hydrological Modelling" Water 13, no. 23: 3420. https://doi.org/10.3390/w13233420
APA StyleTyralis, H., & Papacharalampous, G. (2021). Quantile-Based Hydrological Modelling. Water, 13(23), 3420. https://doi.org/10.3390/w13233420





