Smoothed Particle Hydrodynamics Simulation of a Mariculture Platform under Waves
Abstract
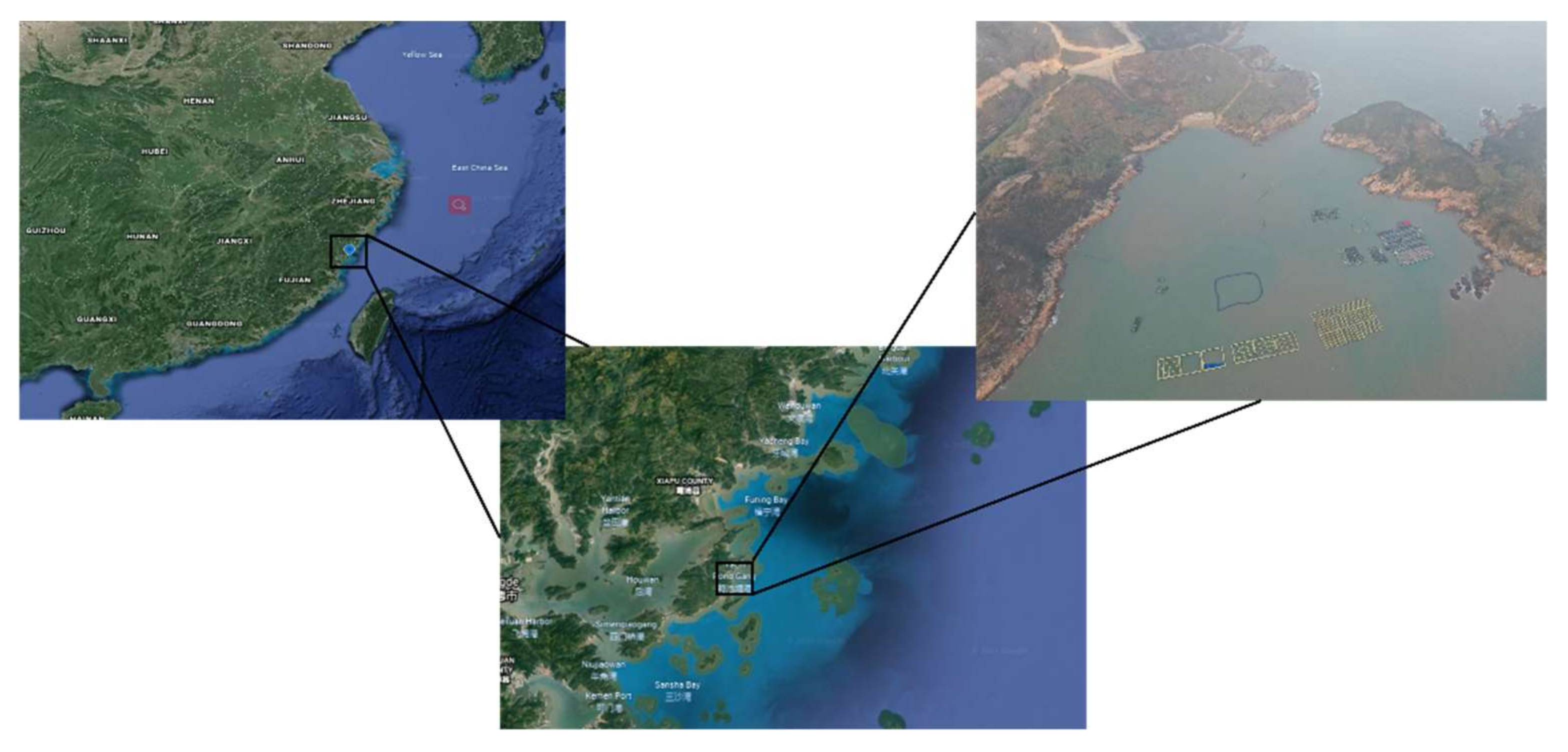
:1. Introduction
2. SPH Model
2.1. SPH Method
2.2. Boundary Conditions
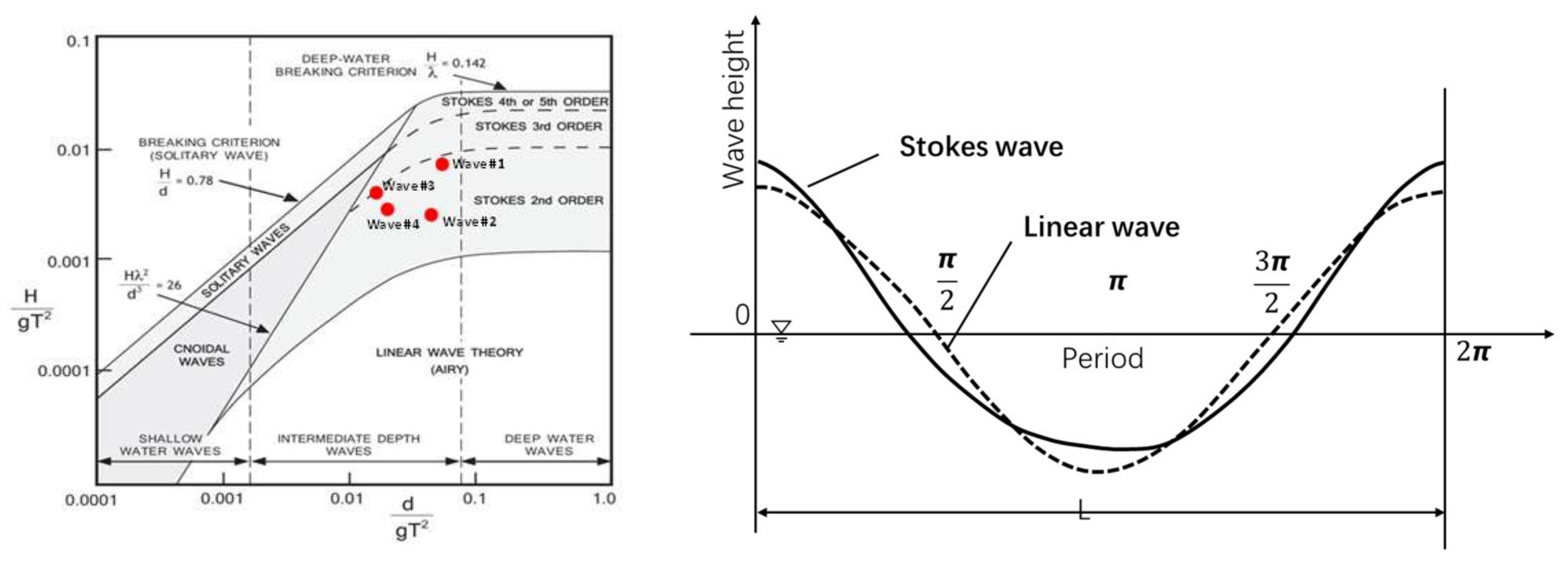
2.3. Wave Generation
2.4. Wave Absorption
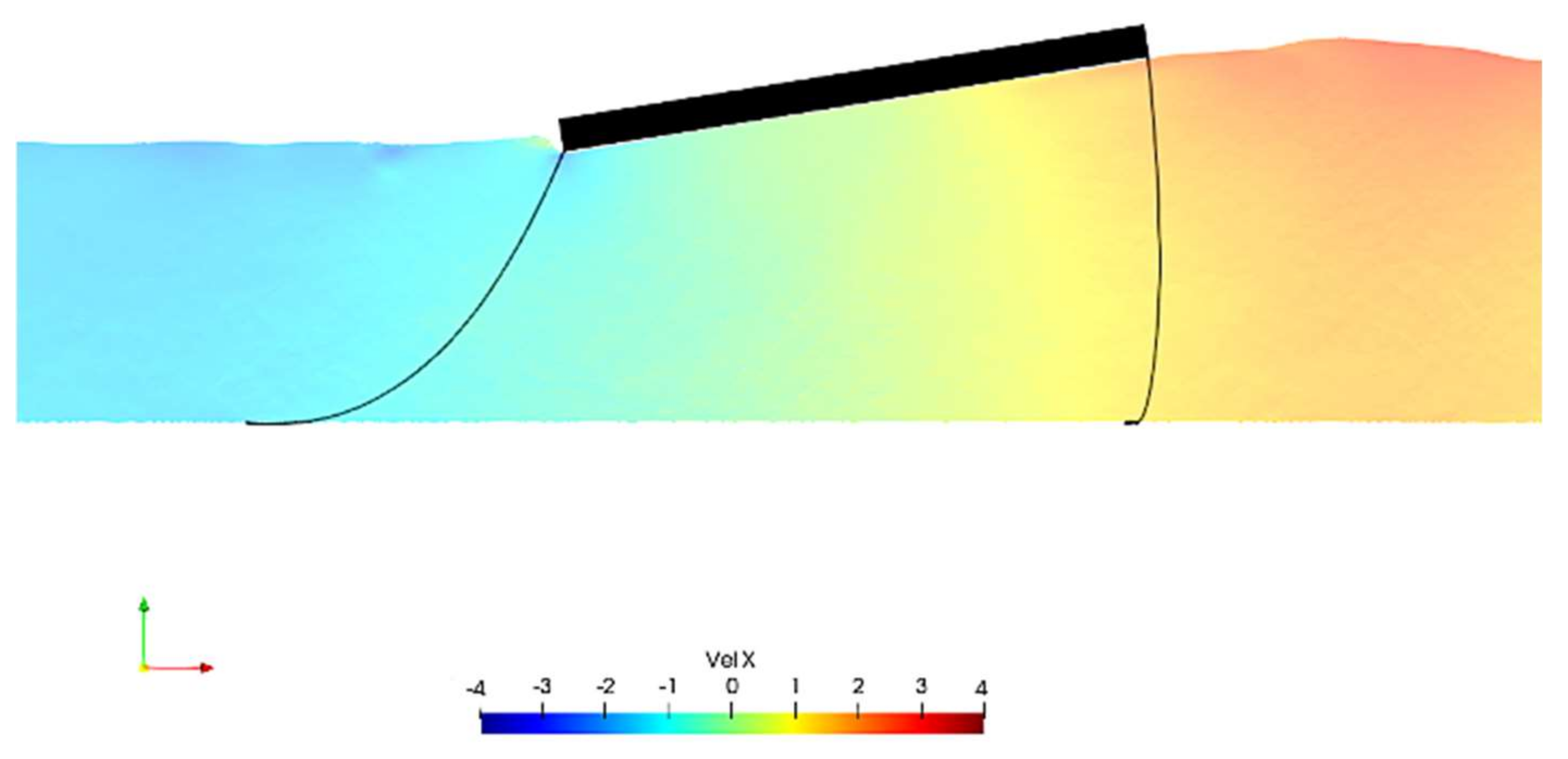
2.5. Fluid-Driven Objects
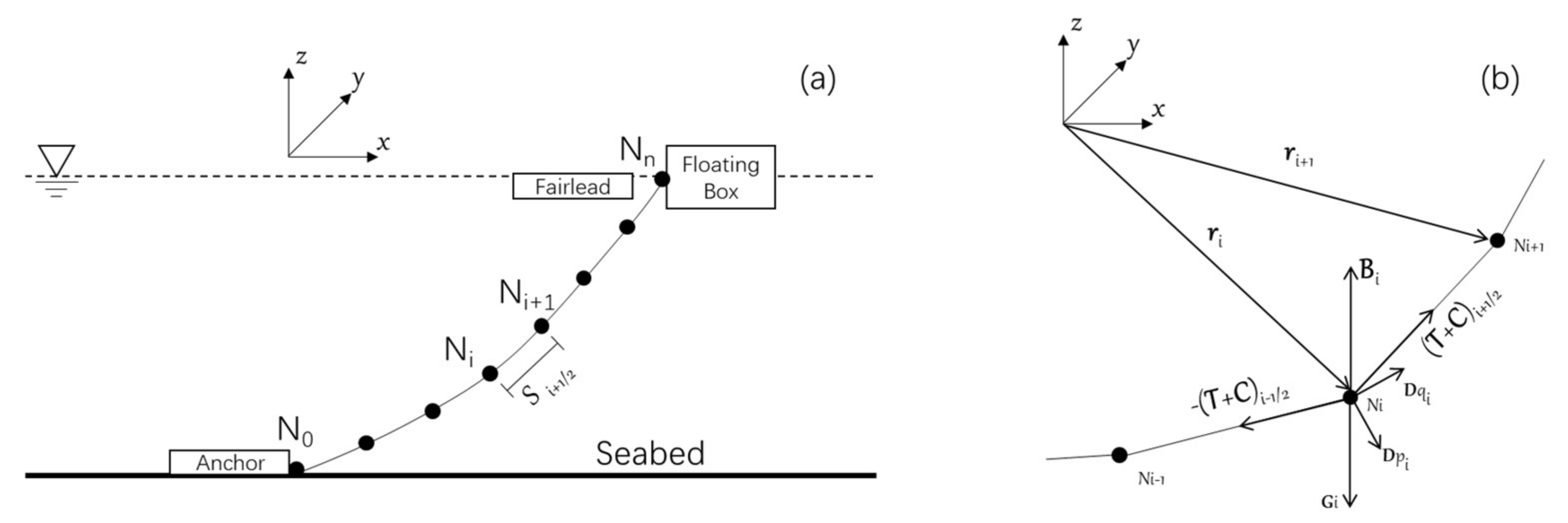
2.6. Moorings
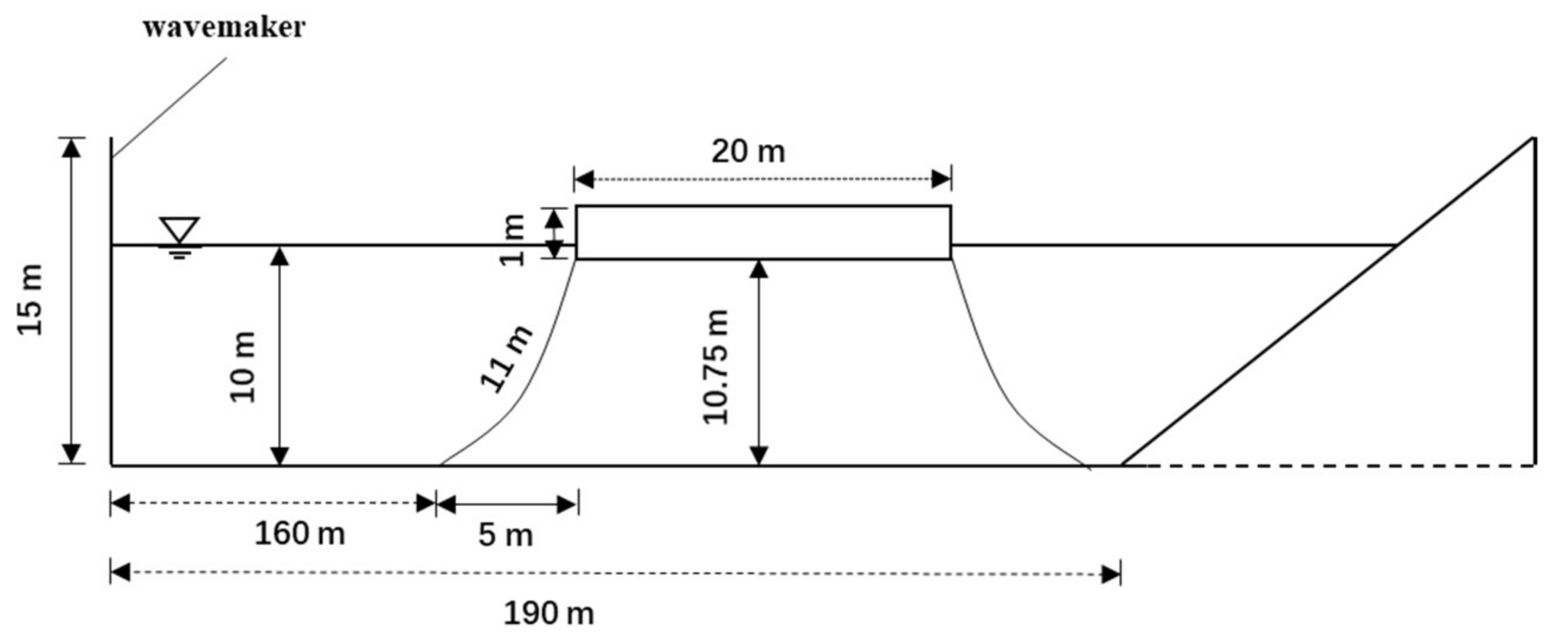
3. Validation and Simulation
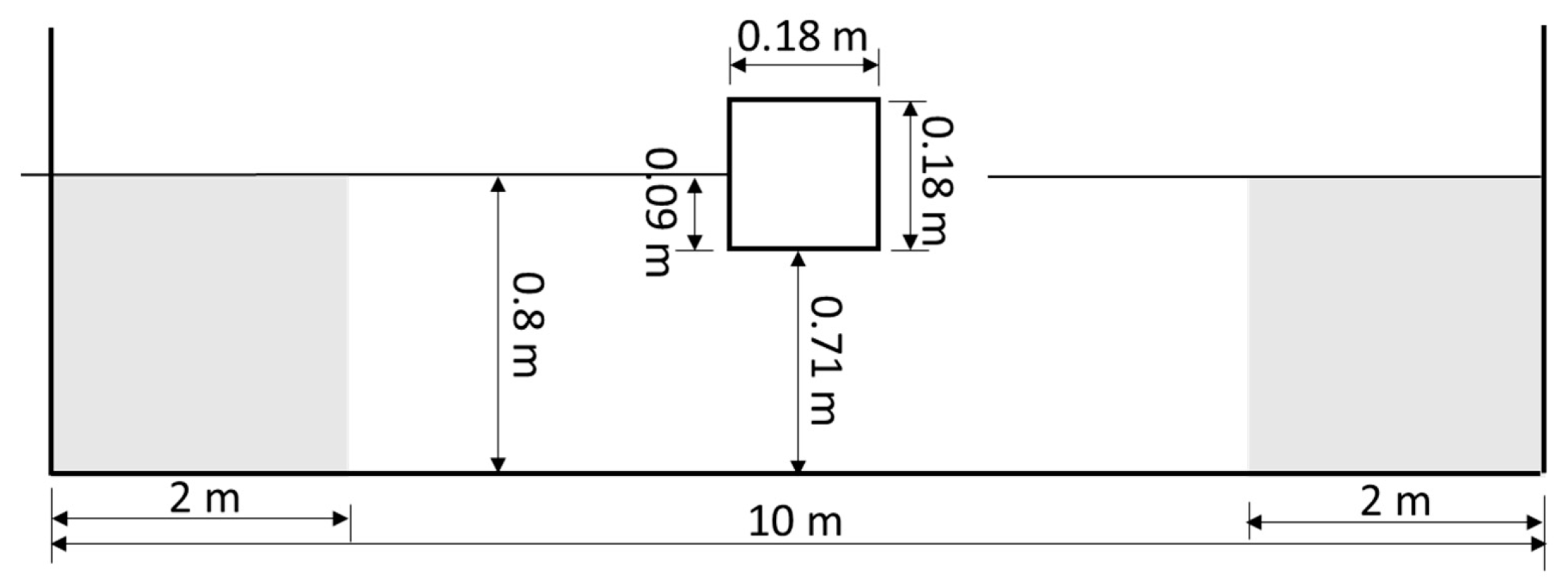
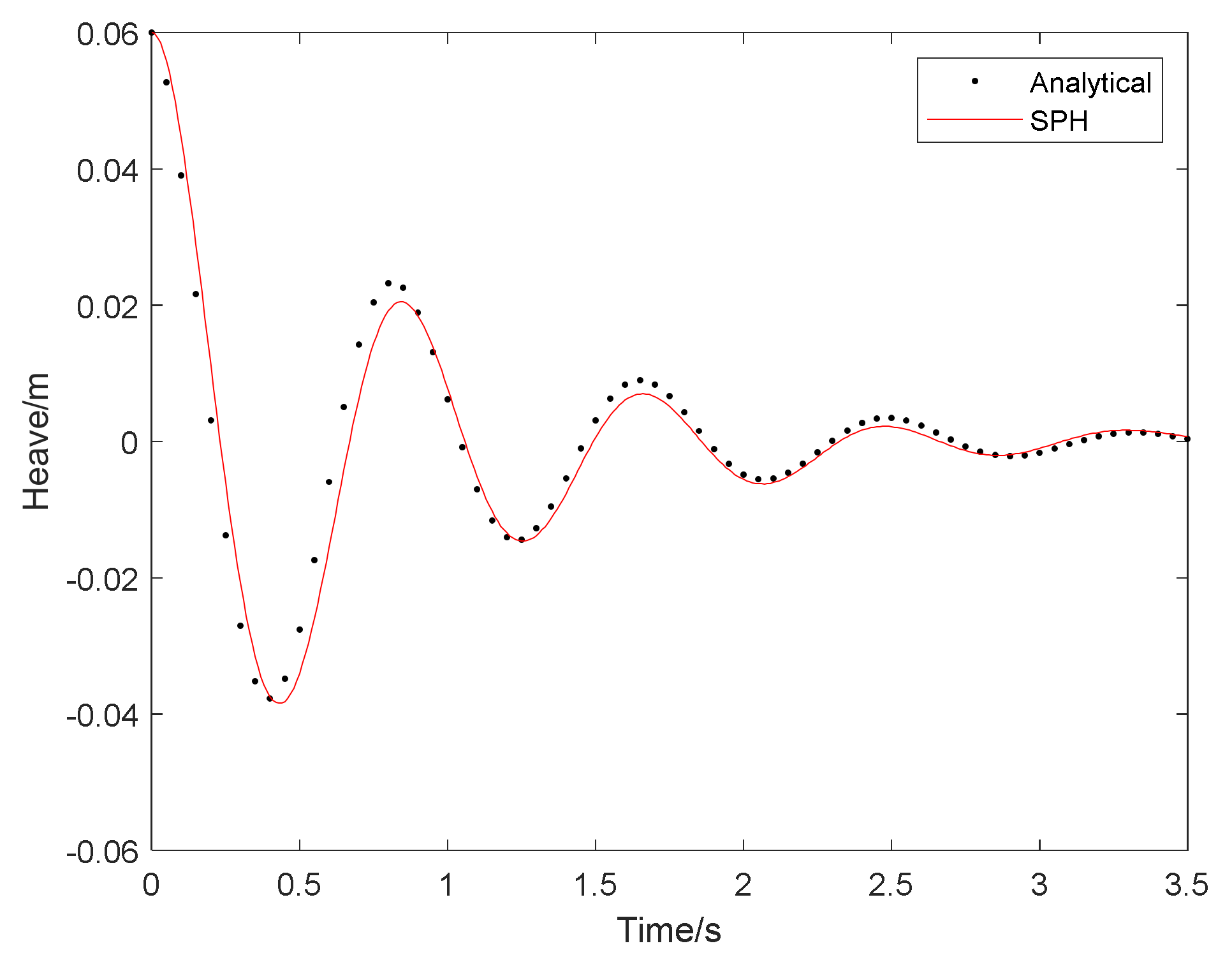
3.1. Decay Test: Theory vs. SPH
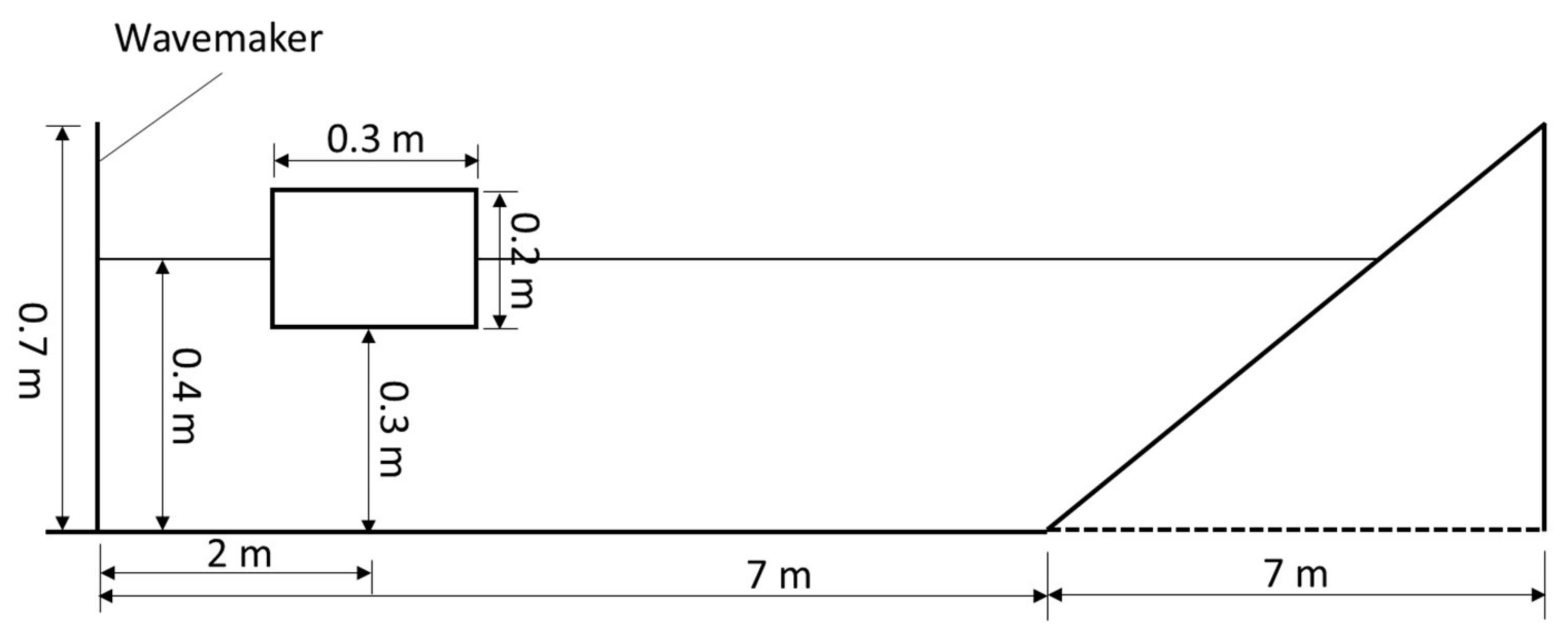
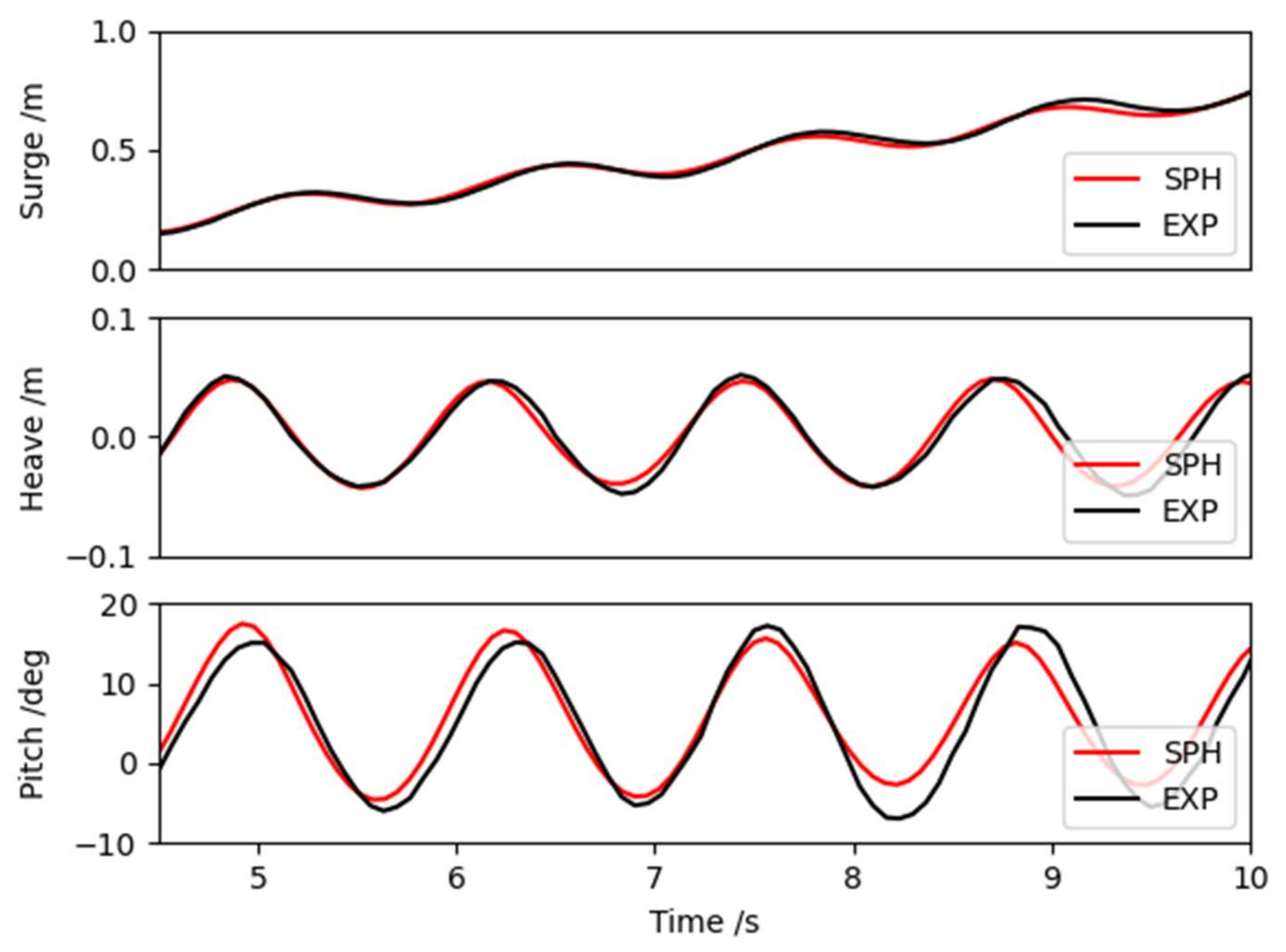
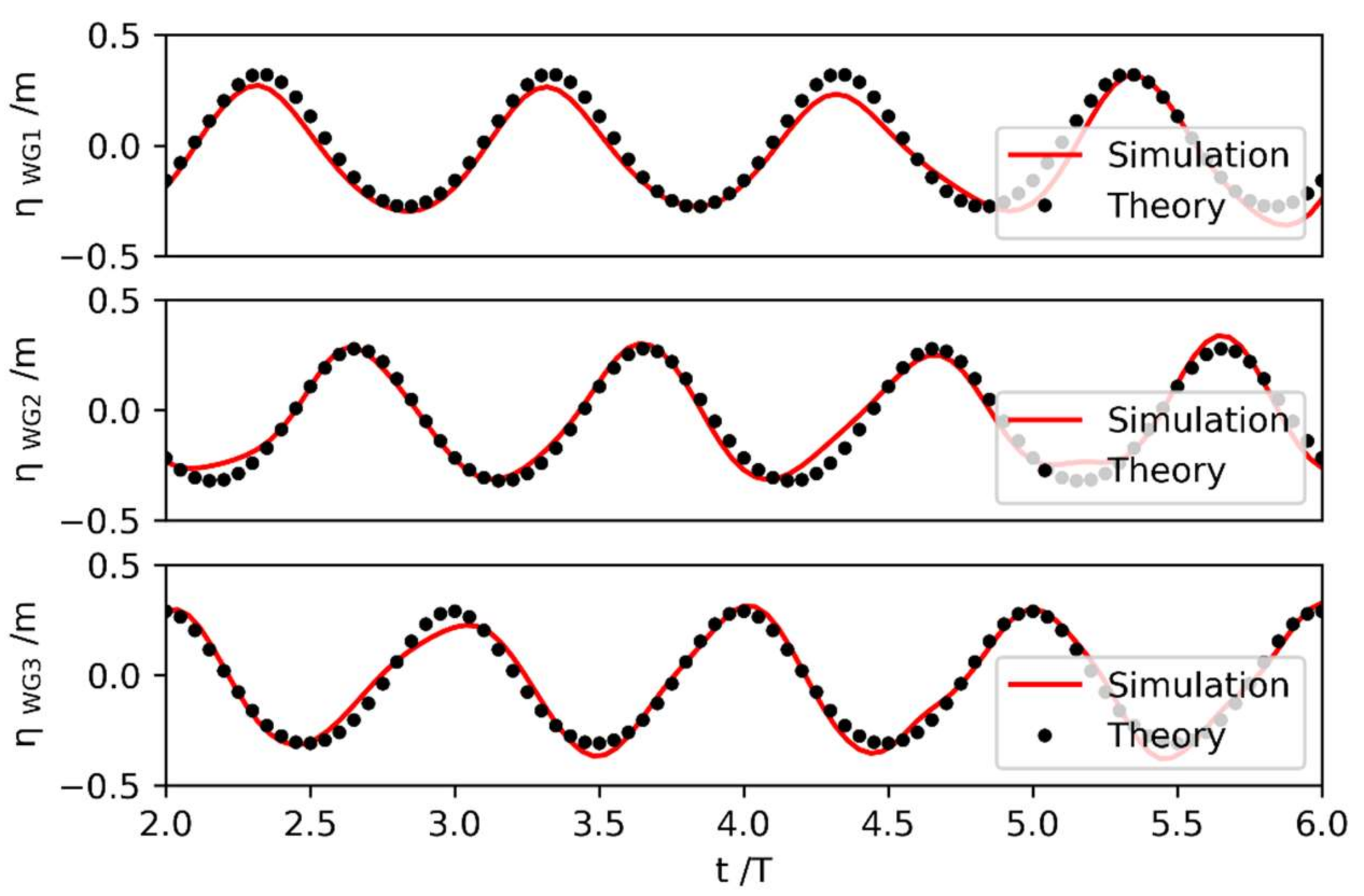
3.2. Floating Body Test: Experiment vs. SPH
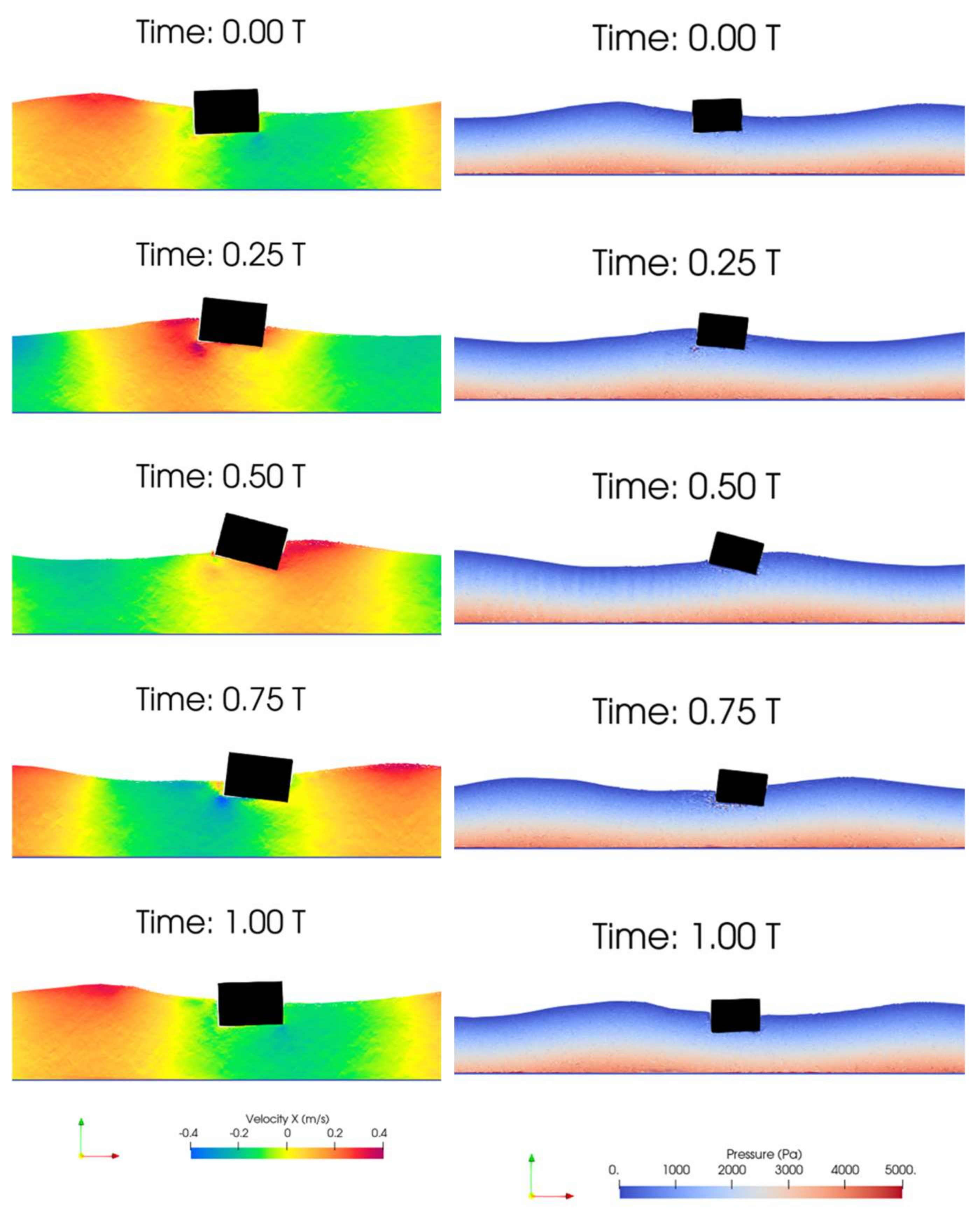
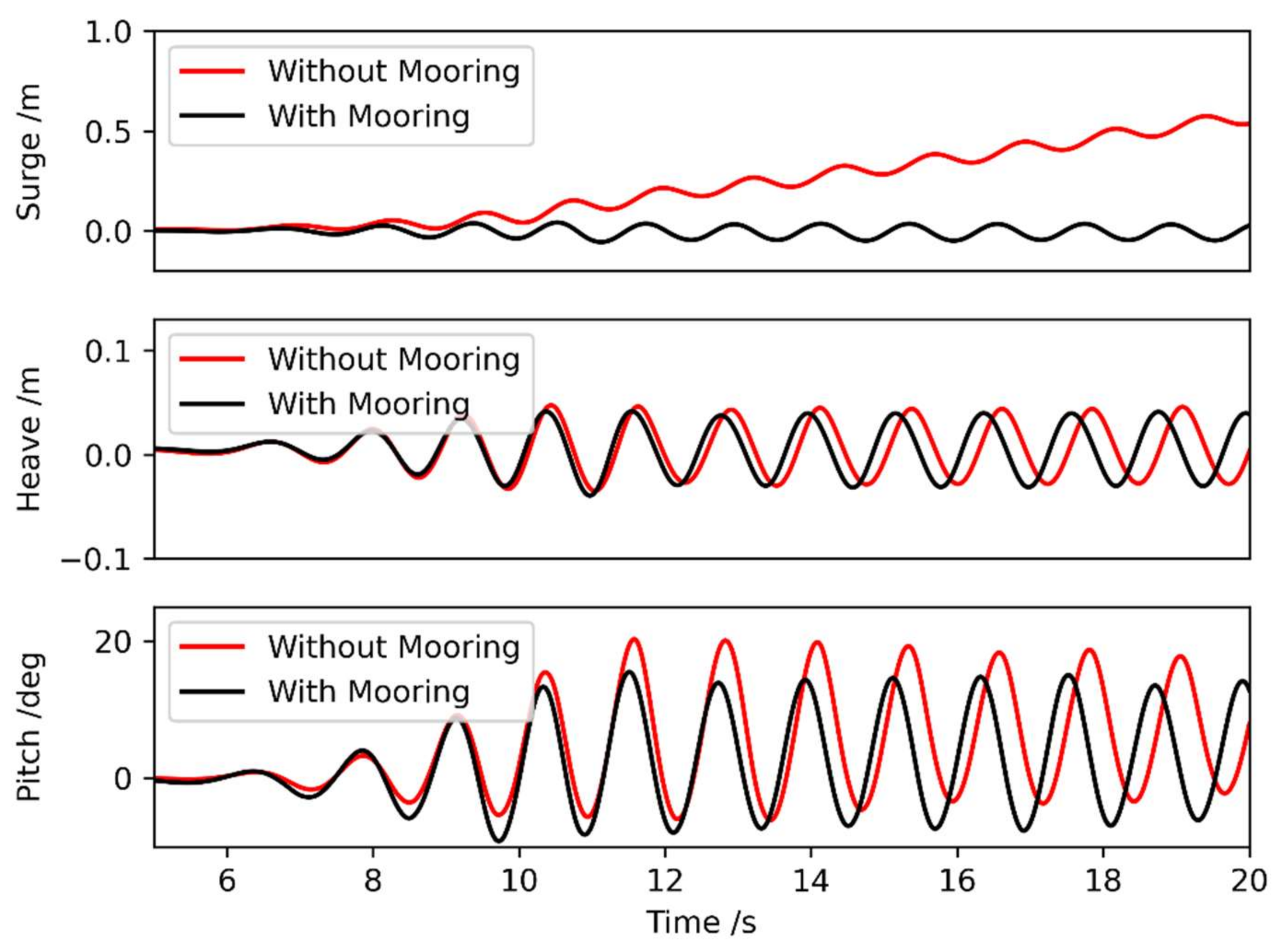
3.3. Floating Body Test: Mooring vs. without Mooring
4. Application
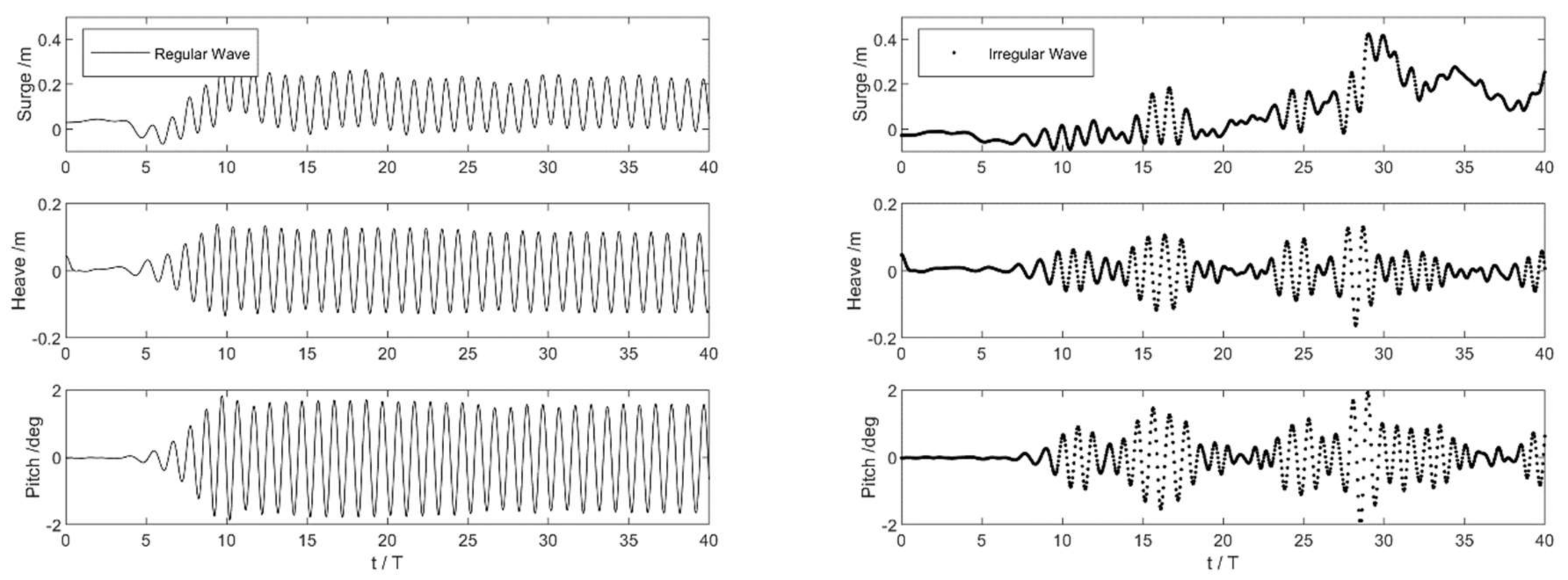
4.1. 3-DoF under a Typical Annual Wave
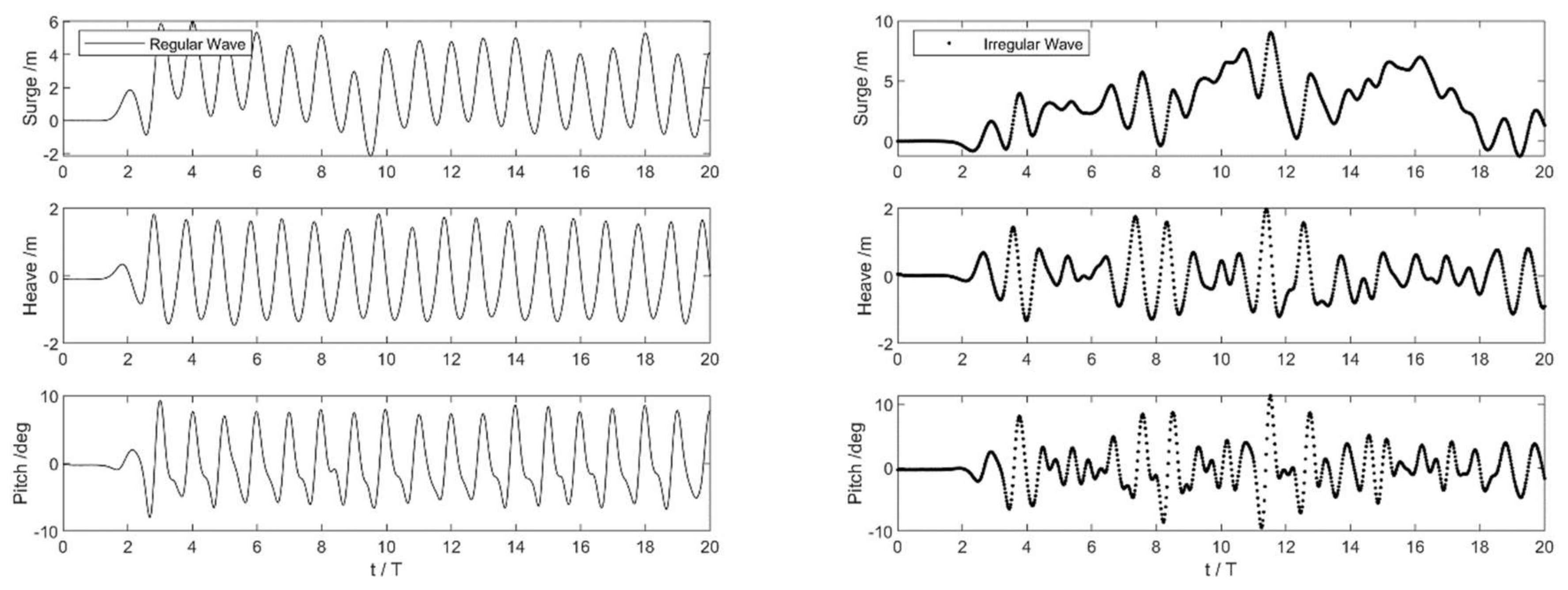
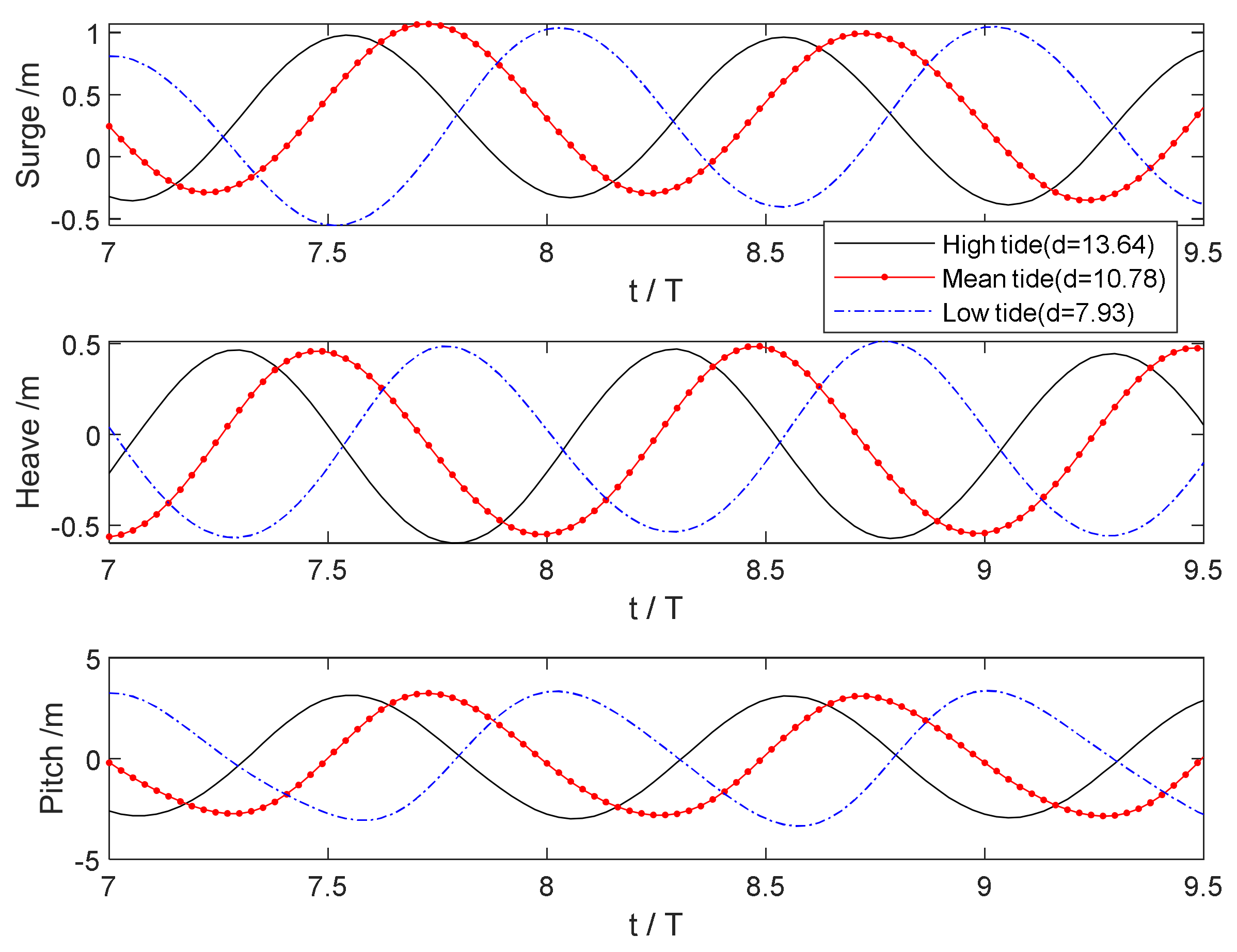
4.2. 3-DoF under Typhoon Dujuan Waves
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gabl, R.; Davey, T.; Nixon, E.; Steynor, J.; Ingram, D.M. Comparison of a floating cylinder with solid and water ballast. Water 2019, 11, 2487. [Google Scholar] [CrossRef] [Green Version]
- Gabl, R.; Davey, T.; Ingram, D.M. Roll motion of a water filled floating cylinder—Additional experimental verification. Water 2020, 12, 2219. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Paredes, G.M. Coupled mooring analysis for floating wave energy converters using CFD: Formulation and validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, C.; Semyonov, D.; Ferrás, L.L.; Nóbrega, J.M. Validation of the CFD-DPM solver DPMFoam in OpenFOAM® through analytical, numerical and experimental comparisons. Granul. Matter 2018, 20, 64. [Google Scholar] [CrossRef]
- Galuppo, W.; Magalhães, A.; Ferrás, L.L.; Nóbrega, J.M.; Fernandes, C. New boundary conditions for simulating the filling stage of the injection molding process. Eng. Comput. 2020, 38, 762–778. [Google Scholar] [CrossRef]
- Gu, H.; Peter, S.; Tim, S. Drag, added mass and radiation damping of oscillating vertical cylindrical bodies in heave and surge in still water. J. Fluids Struct. 2018, 82, 343–356. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Hall, M.; Altomare, C.; Wu, M.; Stratigaki, V.; Troch, P.; Cappietti, L.; Gómez-Gesteira, M. SPH simulation of floating structures with moorings. Coast. Eng. 2019, 153, 103560. [Google Scholar] [CrossRef]
- Gonçalves, N.D.; Ferrás, L.L.; Carneiro, O.S.; Nóbrega, J.M. Using the GPU to design complex profile extrusion dies. Int. Polym. Process. 2015, 30, 442–450. [Google Scholar] [CrossRef] [Green Version]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- St-Germain, P.; Nistor, L.; Townsend, R. Smoothed-particle hydrodynamics numerical modeling of structures impacted by tsunami bores. J. Waterw. Port Coast. Ocean. Eng. 2014, 140, 66–81. [Google Scholar] [CrossRef]
- Zhang, F.; Crespo, A.; Altomare, C. DuaISPHysics: A numerical tool to simulate real breakwaters. J. Hydrodyn. 2018, 30, 95–105. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.C. A smooth particle hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean. Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef] [Green Version]
- Vissio, G.; Passione, B.; Hall, M. Expanding ISWEC modelling with a lumped-mass mooring line model. In Proceedings of the European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Hall, M. Efficient modelling of seabed friction and multi-floater mooring systems in MoorDyn. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Lee, S.C.; Song, S.; Park, S. Platform motions and mooring system coupled solver for a moored floating platform in a wave. Processes 2021, 9, 1393. [Google Scholar] [CrossRef]
- Quartier, N.; Ropero-Giralda, P.; Domínguez, M.J.; Stratigaki, V.; Troch, P. Influence of the drag force on the average absorbed power of heaving wave energy converters using smoothed particle hydrodynamics. Water 2021, 13, 384. [Google Scholar] [CrossRef]
- Pribadi, A.B.K.; Donatini, L.; Lataire, E. Numerical modelling of a mussel line system by means of lumped-mass approach. J. Mar. Sci. Eng. 2019, 7, 309. [Google Scholar] [CrossRef] [Green Version]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver on SPH. Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Valdez-Balderas, D.; Rogers, B.D.; Gómez-Gesteira, M. New multi-GPU implementation for smoothed particle hydrodynamics on heterogeneous clusters. Comput. Phys. Commun. 2013, 184, 1848–1860. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Barreiro, A.; Gómez-Gesteira, M.; Rogers, B.D. GPUs, a new tool of acceleration in CFD: Efficiency and reliability on Smoothed Particle Hydrodynamics methods. PLoS ONE 2011, 6, e20685. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.C.; Rogers, B.D.; Dominguez, J.M.; Gironella, X.; Gómez-Gesteira, M. Numerical modelling of armour block sea breakwater with smoothed particle hydrodynamics. Comput. Struct. 2014, 130, 34–45. [Google Scholar] [CrossRef]
- Altomare, C.; Crespo, A.J.C.; Domínguez, J.M.; Gómez-Gesteira, M.; Suzuki, T.; Verwaest, T. Applicability of smoothed particle hydrodynamics for estimation of sea wave impact on coastal structures. Coast. Eng. 2015, 96, 1–12. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Wendland, H. Piecewiese polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Cas, R.A.F.; Kos, A.M.; Hallworth, M. Gravity currents descending a ramp in a stratified tank. J. Fluid Mech. 1999, 379, 39–70. [Google Scholar] [CrossRef]
- Verlet, L. Computer experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Leimkuhler, B.J.; Reich, S.; Skeel, R.D. Integration methods for molecular dynamics. In Mathematical Approaches to Biomolecular Structure and Dynamics; The IMA Volumes in Mathematics and Its Applications; Mesirov, J.P., Schulten, K., Sumners, D.W., Eds.; Springer: New York, NY, USA, 1996; Volume 82. [Google Scholar]
- Batchelor, G.K. Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Leimkuhler, B.J.; Reich, S.; Skeel, R.D. Integration methods for molecular dynamic. In the IMA Volume in Mathematics and Its Application; Springer: New York, USA, 1996. [Google Scholar]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R. Boundary conditions generated by dynamic particles in SPH Methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Domínguez, J.M.; Crespo, A.J.C.; Cercós-Pita, J.L.; Fourtakas, G.; Rogers, B.D.; Vacondio, R. Evaluation of reliability and efficiency of different boundary conditions in an SPH code. In Proceedings of the 10th SPHERIC International Workshop, Parma, Italy, 9 June 2015. [Google Scholar]
- Biesel, F.; Suquet, F. Etude theorique d’un type d’appareil a la houle. LaHouille Blanche 1951, 2, 157–160. [Google Scholar]
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Schäffer, H.A.; Klopman, G. Review of multidirectional active wave absorption methods. J. Waterw. Port Coast. Ocean. Eng. 2000, 126, 88–97. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Dean, R.G. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991. [Google Scholar]
- Cen, Y. Study on Operating Characteristics of Oscillating-Buoy Wave Energy Converter. Ph.D. Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Ren, B.; He, M.; Dong, P.; Wen, H. Nonlinear simulations of wave-induced motions of a freely floating body using WCSPH method. Appl. Ocean Res 2015, 50, 1–12. [Google Scholar] [CrossRef]
- Mauro, H. The drift of a body floating on waves. J. Ship Res. 1960, 4, 1–10. [Google Scholar]
- National Energy Administration of China. Shallow Sea Mobile Platform Towing and Mooring Safety Specification[S]; National Energy Administration of China: Beijing, China, 2016.
- Xie, G. Conceptual Design of Offshore Wind-Wave Combined Power Generation Platform. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
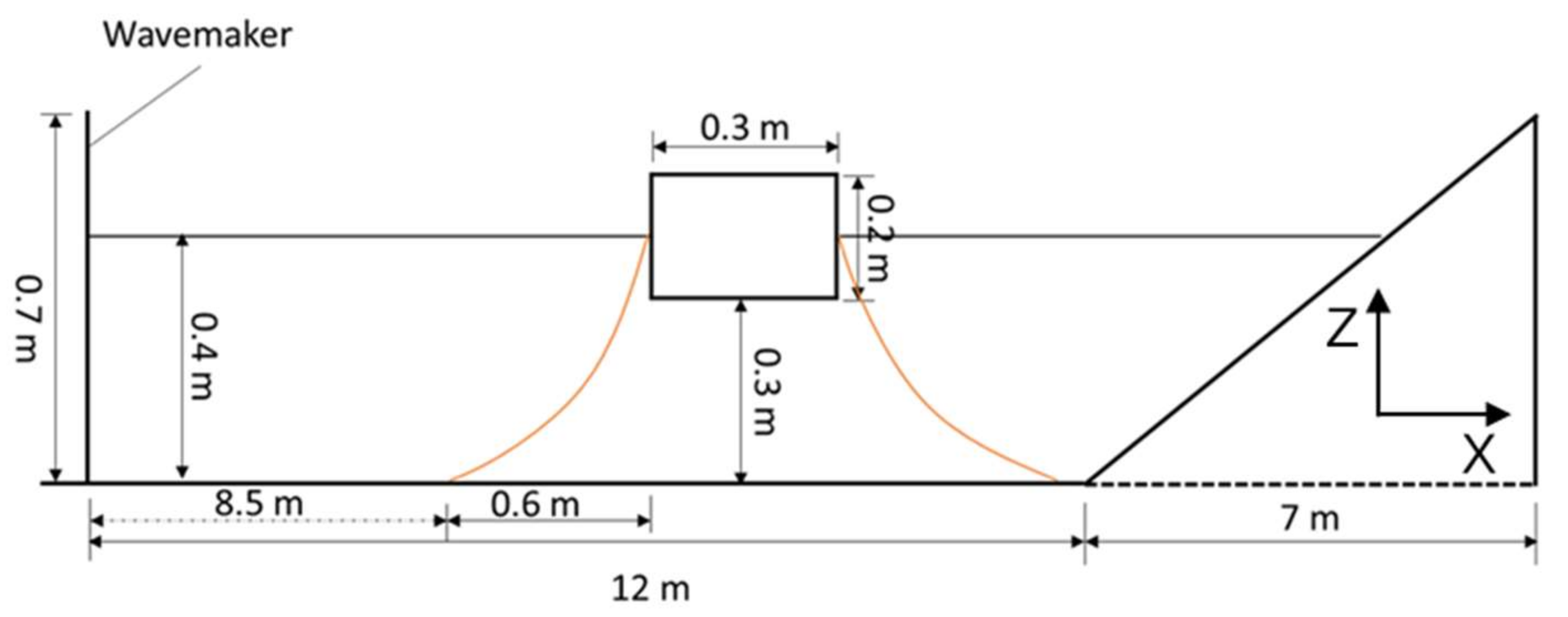
| Time step size | 1 × 10−4 s |
| Segments | 20 |
| Diameter | 0.01 m |
| Mass per unit length | 12 kg/m |
| Cable stiffness | 4 × 105 N/m |
| Points | Coordinates (x, z) |
|---|---|
| Anchor 1 | (8.5, −0.4) |
| Fairlead 1 | (9.1, 0.0) |
| Anchor 2 | (10, −0.4) |
| Fairlead 2 | (9.4, 0.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhang, L.; Xie, Y.; Wang, Z.; Shang, S. Smoothed Particle Hydrodynamics Simulation of a Mariculture Platform under Waves. Water 2021, 13, 2847. https://doi.org/10.3390/w13202847
Zhang F, Zhang L, Xie Y, Wang Z, Shang S. Smoothed Particle Hydrodynamics Simulation of a Mariculture Platform under Waves. Water. 2021; 13(20):2847. https://doi.org/10.3390/w13202847
Chicago/Turabian StyleZhang, Feng, Li Zhang, Yanshuang Xie, Zhiyuan Wang, and Shaoping Shang. 2021. "Smoothed Particle Hydrodynamics Simulation of a Mariculture Platform under Waves" Water 13, no. 20: 2847. https://doi.org/10.3390/w13202847
APA StyleZhang, F., Zhang, L., Xie, Y., Wang, Z., & Shang, S. (2021). Smoothed Particle Hydrodynamics Simulation of a Mariculture Platform under Waves. Water, 13(20), 2847. https://doi.org/10.3390/w13202847






