Discharge Estimation with the Use of Unmanned Aerial Vehicles (UAVs) and Hydraulic Methods in Shallow Rivers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area & Data Used
2.2. UAV Flights and Photogrammetry Software
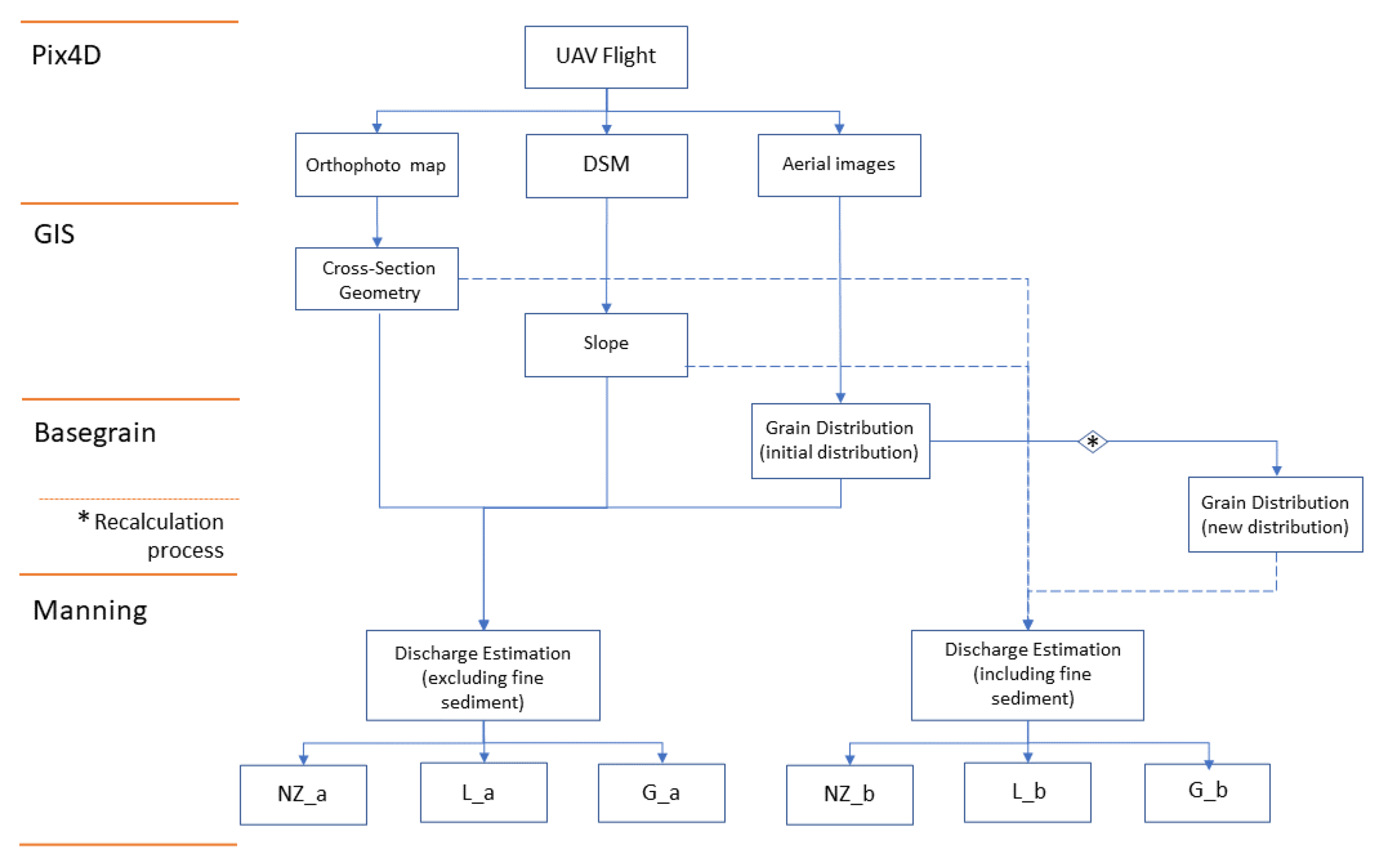
2.3. Methodology
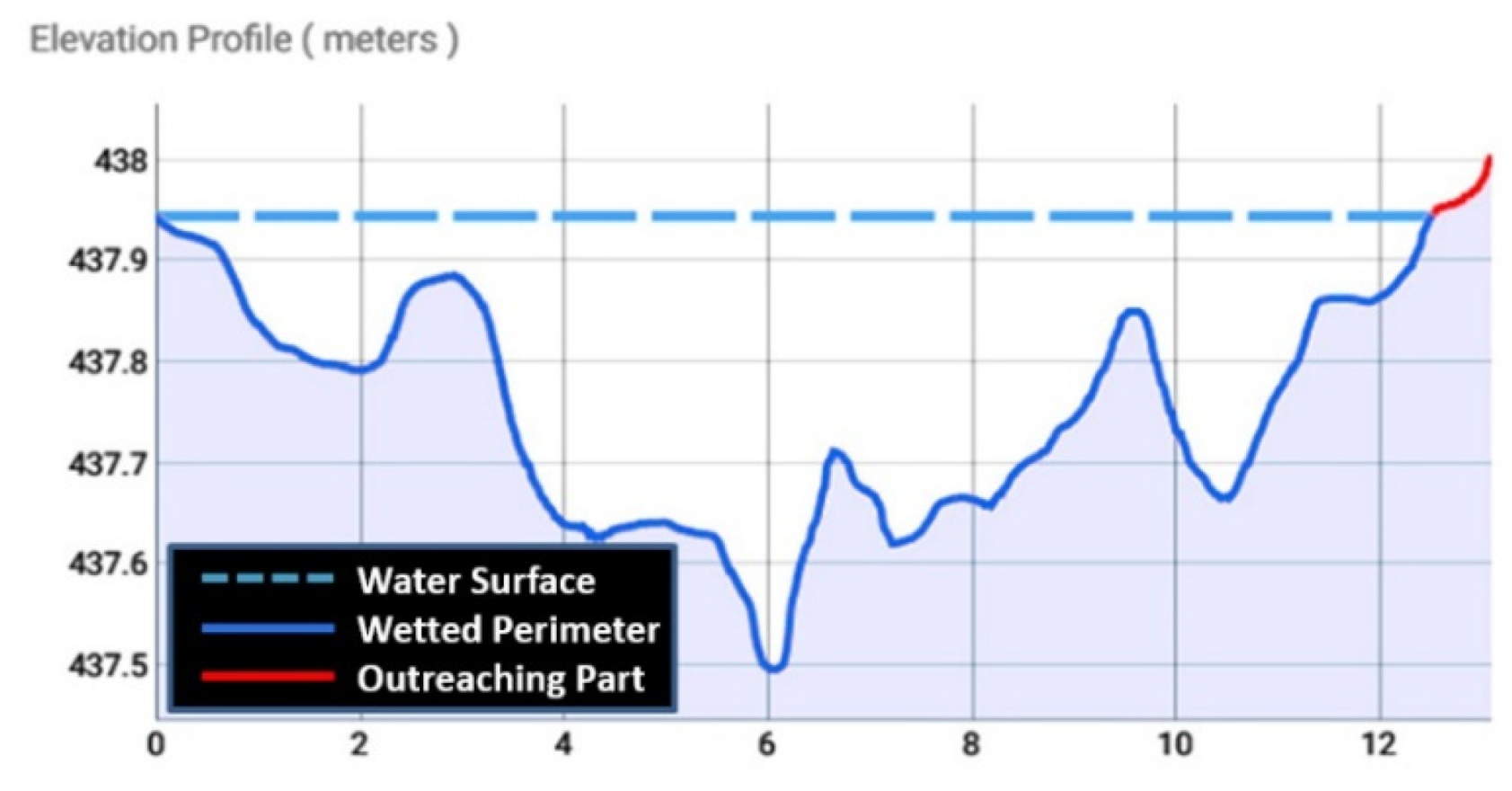
2.3.1. Cross-Section Geometry
2.3.2. Slope
2.3.3. Manning Roughness Coefficient
2.3.4. Riverbed Particle Size Distribution
2.3.5. Discharge Estimation
2.4. Statistical Analysis
3. Results
3.1. Channel Features
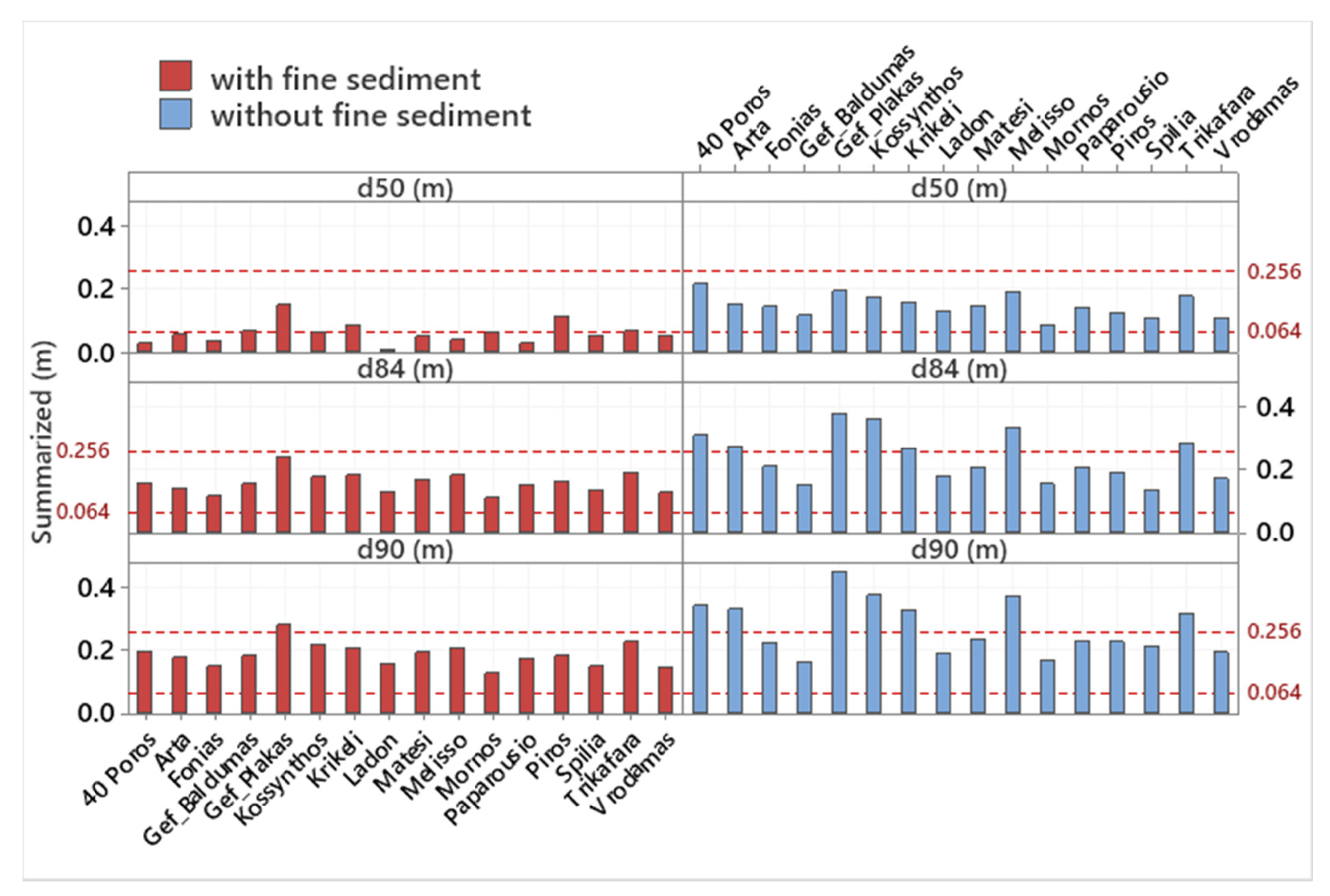
3.2. Particle Size Distribution
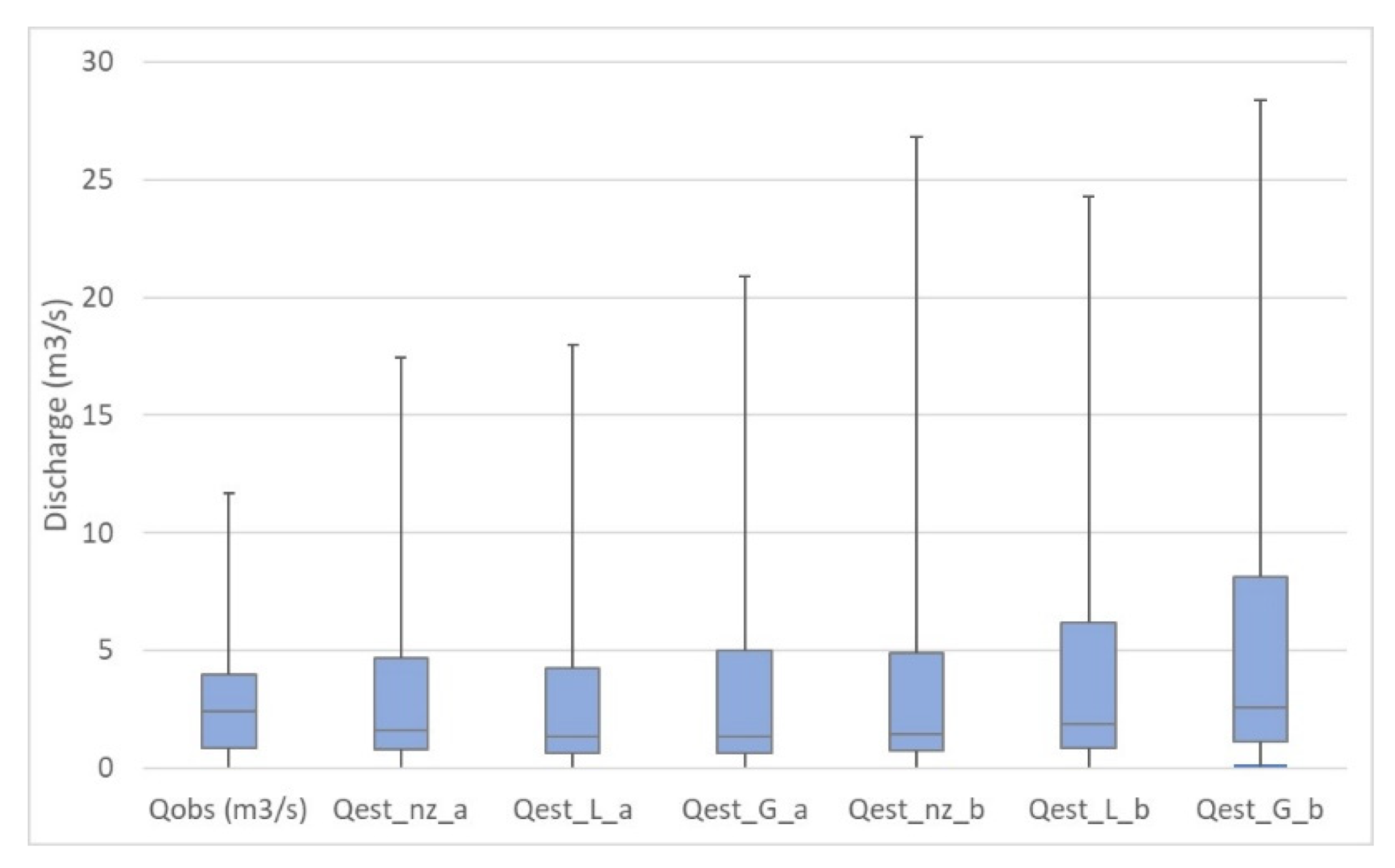
3.3. Discharge Estimation
4. Discussion
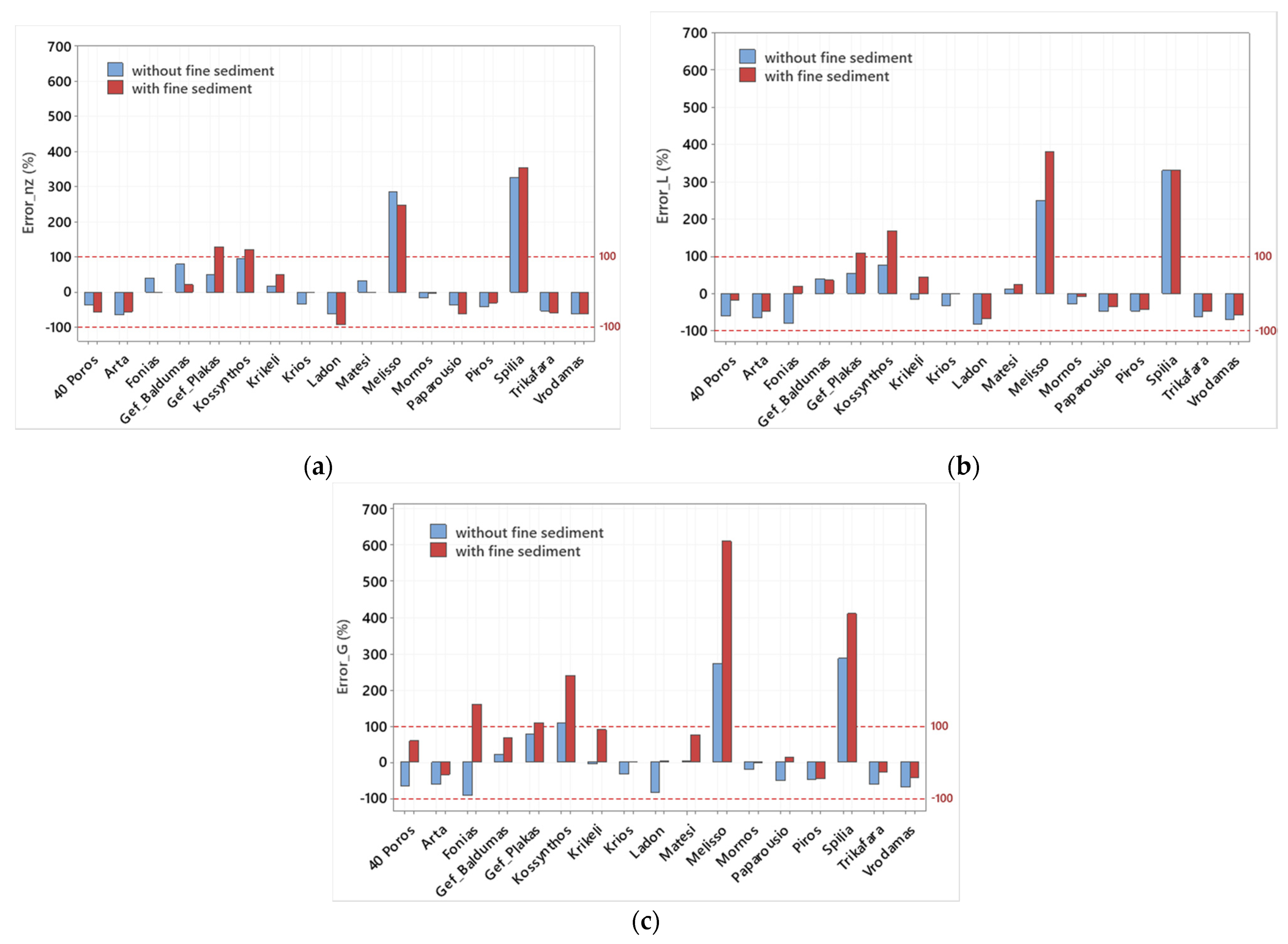
4.1. Discharge Estimation
4.2. Recalculating Particle Size Distribution
4.3. Additional Sources of Error
4.4. Conditions of Applicability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dixon, H.; Hannaford, J.; Fry, M.J. The Effective Management of National Hydrometric Data: Experiences from the United Kingdom. Hydrol. Sci. J. 2013, 58, 1383–1399. [Google Scholar] [CrossRef] [Green Version]
- Irving, K.; Kuemmerlen, M.; Kiesel, J.; Kakouei, K.; Domisch, S.; Jähnig, S.C. A High-Resolution Streamflow and Hydrological Metrics Dataset for Ecological Modeling Using a Regression Model. Sci. Data 2018, 5, 180224. [Google Scholar] [CrossRef]
- Blöschl, G. Predictions in Ungauged Basins—Where Do We Stand? Proc. IAHS 2016, 373, 57–60. [Google Scholar] [CrossRef] [Green Version]
- McGlynn, B.L.; Blöschl, G.; Borga, M.; Bormann, H.; Hurkmans, R.; Komma, J.; Nandagiri, L.; Uijlenhoet, R.; Wagener, T. A Data Acquisition Framework for Prediction of Runoff in Ungauged Basins. In Runoff Prediction in Ungauged Basins, Synthesis across Processes, Places, and Scales; Cambridge University Press: Cambridge, UK; pp. 29–52.
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A Compilation of Data on European Flash Floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Marchi, L.; Borga, M.; Preciso, E.; Gaume, E. Characterisation of Selected Extreme Flash Floods in Europe and Implications for Flood Risk Management. J. Hydrol. 2010, 394, 118–133. [Google Scholar] [CrossRef]
- Mertes, L.A.K. Remote Sensing of Riverine Landscapes: Remote Sensing of Riverine Landscapes. Freshw. Biol. 2002, 47, 799–816. [Google Scholar] [CrossRef]
- Bowen, Z.H.; Waltermire, R.G. Evaluation of Light Detection and Ranging (Lidar) for Measuring River Corridor Topography. J. Am. Water Res. Assoc. 2002, 38, 33–41. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Orfeo, O.; Hardy, R.J.; Kostaschuk, R.; Lane, S.N. Morphology and Flow Fields of Three-Dimensional Dunes, Rio Paraná, Argentina: Results from Simultaneous Multibeam Echo Sounding and Acoustic Doppler Current Profiling: Three-Dimensional Alluvial Dunes, Rio Paraná. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Heritage, G.; Hetherington, D. Towards a Protocol for Laser Scanning in Fluvial Geomorphology. Earth Surf. Process. Landf. 2007, 32, 66–74. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.-A. Satellite Remote Sensing Estimation of River Discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.; Durand, M. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef] [Green Version]
- Lou, H.; Wang, P.; Yang, S.; Hao, F.; Ren, X.; Wang, Y.; Shi, L.; Wang, J.; Gong, T. Combining and Comparing an Unmanned Aerial Vehicle and Multiple Remote Sensing Satellites to Calculate Long-Term River Discharge in an Ungauged Water Source Region on the Tibetan Plateau. Remote Sens. 2020, 12, 2155. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Zeng, C.; Qiao, G.; Li, X.; Hou, A.; Hong, Y. Discharge Estimation in High-Mountain Regions with Improved Methods Using Multisource Remote Sensing: A Case Study of the Upper Brahmaputra River. Remote Sens. Environ. 2018, 219, 115–134. [Google Scholar] [CrossRef]
- Yang, S.; Wang, P.; Lou, H.; Wang, J.; Zhao, C.; Gong, T. Estimating River Discharges in Ungauged Catchments Using the Slope–Area Method and Unmanned Aerial Vehicle. Water 2019, 11, 2361. [Google Scholar] [CrossRef] [Green Version]
- Bandini, F.; Lüthi, B.; Peña-Haro, S.; Borst, C.; Liu, J.; Karagkiolidou, S.; Hu, X.; Lemaire, G.G.; Bjerg, P.L.; Bauer-Gottwein, P. A Drone-Borne Method to Jointly Estimate Discharge and Manning’s Roughness of Natural Streams. Water Res. 2021, 57. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Lawrence Dingman, S.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the Potential for Measuring River Discharge from Space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating Discharge in Rivers Using Remotely Sensed Hydraulic Information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily Discharge Estimation at Ungauged River Sites Using Remote Sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Bonnema, M.G.; Sikder, S.; Hossain, F.; Durand, M.; Gleason, C.J.; Bjerklie, D.M. Benchmarking Wide Swath Altimetry-Based River Discharge Estimation Algorithms for the Ganges River System. Water Resour. Res. 2016, 52, 2439–2461. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.J.; Smith, L.C.; Lee, J. Retrieval of River Discharge Solely from Satellite Imagery and At-Many-Stations Hydraulic Geometry: Sensitivity to River Form and Optimization Parameters. Water Resour. Res. 2014, 50, 9604–9619. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.-L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768–1793. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight Unmanned Aerial Vehicles Will Revolutionize Spatial Ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Vivoni, E.R.; Rango, A.; Anderson, C.A.; Pierini, N.A.; Schreiner-McGraw, A.P.; Saripalli, S.; Laliberte, A.S. Ecohydrology with Unmanned Aerial Vehicles. Ecosphere 2014, 5, 130. [Google Scholar] [CrossRef] [Green Version]
- Vélez-Nicolás, M.; García-López, S.; Barbero, L.; Ruiz-Ortiz, V.; Sánchez-Bellón, Á. Applications of Unmanned Aerial Systems (UASs) in Hydrology: A Review. Remote Sens. 2021, 13, 1359. [Google Scholar] [CrossRef]
- Detert, M.; Johnson, E.D.; Weitbrecht, V. Proof-of-concept for Low-cost and Non-contact Synoptic Airborne River Flow Measurements. Int. J. Remote Sens. 2017, 38, 2780–2807. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Lindroth, E.M.; Rhoads, B.L. Integrating Unmanned Aerial Systems and LSPIV for Rapid, Cost-Effective Stream Gauging. J. Hydrol. 2018, 560, 230–246. [Google Scholar] [CrossRef]
- Zhao, C.S.; Pan, T.L.; Xia, J.; Yang, S.T.; Zhao, J.; Gan, X.J.; Hou, L.P.; Ding, S.Y. Streamflow Calculation for Medium-to-Small Rivers in Data Scarce Inland Areas. Sci. Total Environ. 2019, 693, 133571. [Google Scholar] [CrossRef]
- Kang, B.; Kim, J.G.; Kim, D.; Kang, D.H. Flow Estimation Using Drone Optical Imagery with Non-Uniform Flow Modeling in a Controlled Experimental Channel. KSCE J. Civ. Eng. 2019, 23, 1891–1898. [Google Scholar] [CrossRef]
- Kinzel, P.; Legleiter, C. SUAS-Based Remote Sensing of River Discharge Using Thermal Particle Image Velocimetry and Bathymetric Lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef] [Green Version]
- Fulton, J.W.; Anderson, I.E.; Chiu, C.-L.; Sommer, W.; Adams, J.D.; Moramarco, T.; Bjerklie, D.M.; Fulford, J.M.; Sloan, J.L.; Best, H.R.; et al. QCam: SUAS-Based Doppler Radar for Measuring River Discharge. Remote Sens. 2020, 12, 3317. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J.; Wang, P.; Gong, T.; Liu, H. Low Altitude Unmanned Aerial Vehicles (UAVs) and Satellite Remote Sensing Are Used to Calculated River Discharge Attenuation Coefficients of Ungauged Catchments in Arid Desert. Water 2019, 11, 2633. [Google Scholar] [CrossRef] [Green Version]
- Duró, G.; Crosato, A.; Kleinhans, M.G.; Uijttewaal, W.S.J. Bank Erosion Processes Measured with UAV-SfM along Complex Banklines of a Straight Mid-Sized River Reach. Earth Surf. Dynam. 2018, 6, 933–953. [Google Scholar] [CrossRef] [Green Version]
- Hemmelder, S.; Marra, W.; Markies, H.; De Jong, S.M. Monitoring River Morphology & Bank Erosion Using UAV Imagery—A Case Study of the River Buëch, Hautes-Alpes, France. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 428–437. [Google Scholar] [CrossRef]
- Watanabe, Y.; Kawahara, Y. UAV Photogrammetry for Monitoring Changes in River Topography and Vegetation. Procedia Eng. 2016, 154, 317–325. [Google Scholar] [CrossRef] [Green Version]
- Van Iersel, W.; Straatsma, M.; Middelkoop, H.; Addink, E. Multitemporal Classification of River Floodplain Vegetation Using Time Series of UAV Images. Remote Sens. 2018, 10, 1144. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.S.; Baek, D.; Seo, I.W.; Shin, J. Retrieving Shallow Stream Bathymetry from UAV-Assisted RGB Imagery Using a Geospatial Regression Method. Geomorphology 2019, 341, 102–114. [Google Scholar] [CrossRef]
- Water Framework Directive, Hellenic Centre for Marine Research, 2021. 3D Rivers. Available online: https://wfd.hcmr.gr/category/3drivers/ (accessed on 15 September 2021).
- Dimitriou, E.; Stavroulaki, E. Assessment of Riverine Morphology and Habitat Regime Using Unmanned Aerial Vehicles in a Mediterranean Environment. Pure Appl. Geophys. 2018, 175, 3247–3261. [Google Scholar] [CrossRef]
- Williams, R.D.; Brasington, J.; Vericat, D.; Hicks, D.M. Hyperscale Terrain Modelling of Braided Rivers: Fusing Mobile Terrestrial Laser Scanning and Optical Bathymetric Mapping: Hyperscale Terrain Modelling of Braided Rivers. Earth Surf. Process. Landf. 2014, 39, 167–183. [Google Scholar] [CrossRef]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-Motion Photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Witheridge, G. Background to Rock Sizing Equations; Catchments & Creeks Pty Ltd.: Queensland, Australia, 2011; Available online: https://www.catchmentsandcreeks.com.au/docs/Background-To-Rock-Sizing-Equations.pdf (accessed on 5 October 2021).
- Limerinos. Determination of the Manning Coefficient from Measured Bed Roughness in Natural Channels; Water-Supply Paper 1898; U.S. Geological Survey: Tacoma, WA, USA, 1970. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, G.A. Flow Resistance in Coarse Gravel Bed Rivers. J. Hydraul. Div. 1981, 107, 899–918. [Google Scholar] [CrossRef]
- Soto, A.U.; Madrid-Aris, M. Roughness Coefficient in Mountain Rivers. In Hydraulic Engineering; Cotroneo, G., Rumer, R., Eds.; American Society of Civil Engineering: New York, NY, USA, 2014. [Google Scholar]
- Kim, J.-S. Roughness Coefficient and Its Uncertainty in Gravel-Bed River. Water Sci. Eng. 2010, 3, 217–232. [Google Scholar] [CrossRef]
- McKay, S.K.; Fischenich, J.C.; Engineer Research and Development Center (U.S.); Coastal and Hydraulics Laboratory (U.S.); Coastal Inlets Research Program (U.S.). Robust Prediction of Hydraulic Roughness; Technical Note; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2011. [Google Scholar]
- Carbonneau, P.E.; Lane, S.N.; Bergeron, N.E. Catchment-Scale Mapping of Surface Grain Size in Gravel Bed Rivers Using Airborne Digital Imagery. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Holland, P.G. Manning Formula. In Hydrology and Lakes; Springer: Dordrecht, The Netherlands, 1998; pp. 475–581. [Google Scholar]
- Rantz, S.E. Measurement and Computation of Streamflow: Volume 1, Measurement of Stage and Discharge; Geological Survey Water-Supply Paper- No. 2175; U.S. Government Printing Office: Washington, DC, USA, 1982. [Google Scholar] [CrossRef]
- Eltner, A.; Sardemann, H.; Grundmann, J. Technical Note: Flow Velocity and Discharge Measurement in Rivers Using Terrestrial and Unmanned-Aerial-Vehicle Imagery. Hydrol. Earth Syst. Sci. 2020, 24, 1429–1445. [Google Scholar] [CrossRef] [Green Version]
- Kebede, M.G.; Wang, L.; Li, X.; Hu, Z. Remote Sensing-Based River Discharge Estimation for a Small River Flowing over the High Mountain Regions of the Tibetan Plateau. Int. J. Remote Sens. 2020, 41, 3322–3345. [Google Scholar] [CrossRef]
- Samboko, H.T.; Abas, I.; Luxemburg, W.M.J.; Savenije, H.H.G.; Makurira, H.; Banda, K.; Winsemius, H.C. Evaluation and Improvement of Remote Sensing-Based Methods for River Flow Management. Phys. Chem. Earth Parts A/B/C 2020, 117, 102839. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying Submerged Fluvial Topography Using Hyperspatial Resolution UAS Imagery and Structure from Motion Photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Wigmore, O.; Mark, B. Monitoring Tropical Debris-Covered Glacier Dynamics from High-Resolution Unmanned Aerial Vehicle Photogrammetry, Cordillera Blanca, Peru. Cryosphere 2017, 11, 2463–2480. [Google Scholar] [CrossRef] [Green Version]
- Manfreda, S.; McCabe, M.; Miller, P.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.J.; Lim, G.J.; Cho, J. Drone Flight Scheduling under Uncertainty on Battery Duration and Air Temperature. Comput. Ind. Eng. 2018, 117, 291–302. [Google Scholar] [CrossRef]
- Ure, N.K.; Chowdhary, G.; Toksoz, T.; How, J.P.; Vavrina, M.A.; Vian, J. An Automated Battery Management System to Enable Persistent Missions with Multiple Aerial Vehicles. IEEE/ASME Trans. Mechatron. 2015, 20, 12. [Google Scholar] [CrossRef]
- Jain, K.P.; Tang, J.; Sreenath, K.; Mueller, M.W. Staging Energy Sources to Extend Flight Time of a Multirotor UAV. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); IEEE: Las Vegas, NV, USA, 2020; pp. 1132–1139. [Google Scholar] [CrossRef]
- Lee, D.; Zhou, J.; Lin, W.T. Autonomous Battery Swapping System for Quadcopter. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), IEEE, Denver, CO, USA, 9–12 June 2015; pp. 118–124. [Google Scholar]
- Whitehead, K.; Hugenholtz, C.H. Remote Sensing of the Environment with Small Unmanned Aircraft Systems (UASs), Part 1: A Review of Progress and Challenges. J. Unmanned Veh. Sys. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Annis, A.; Nardi, F.; Petroselli, A.; Apollonio, C.; Arcangeletti, E.; Tauro, F.; Belli, C.; Bianconi, R.; Grimaldi, S. UAV-DEMs for Small-Scale Flood Hazard Mapping. Water 2020, 12, 1717. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications—A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef] [Green Version]
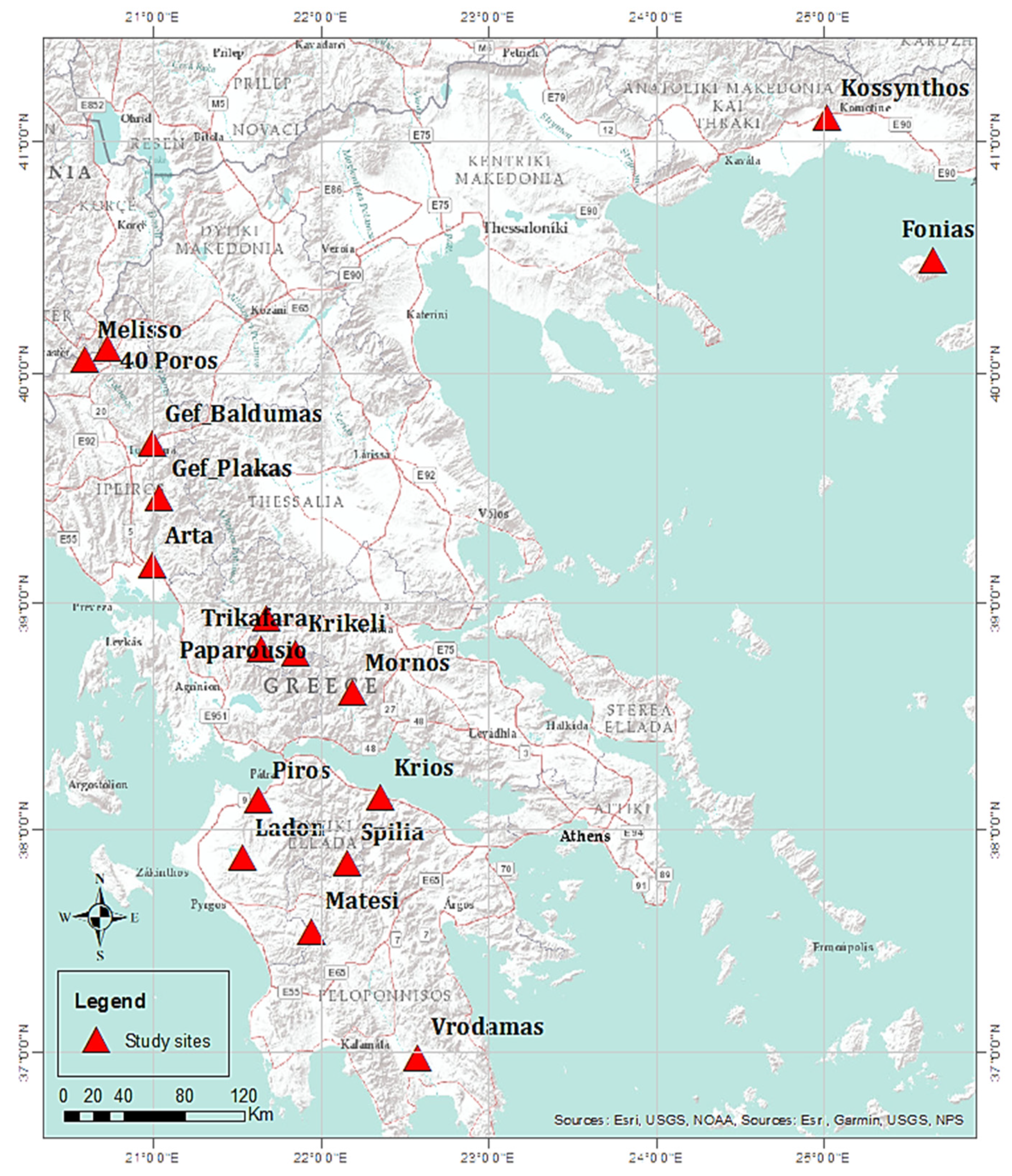

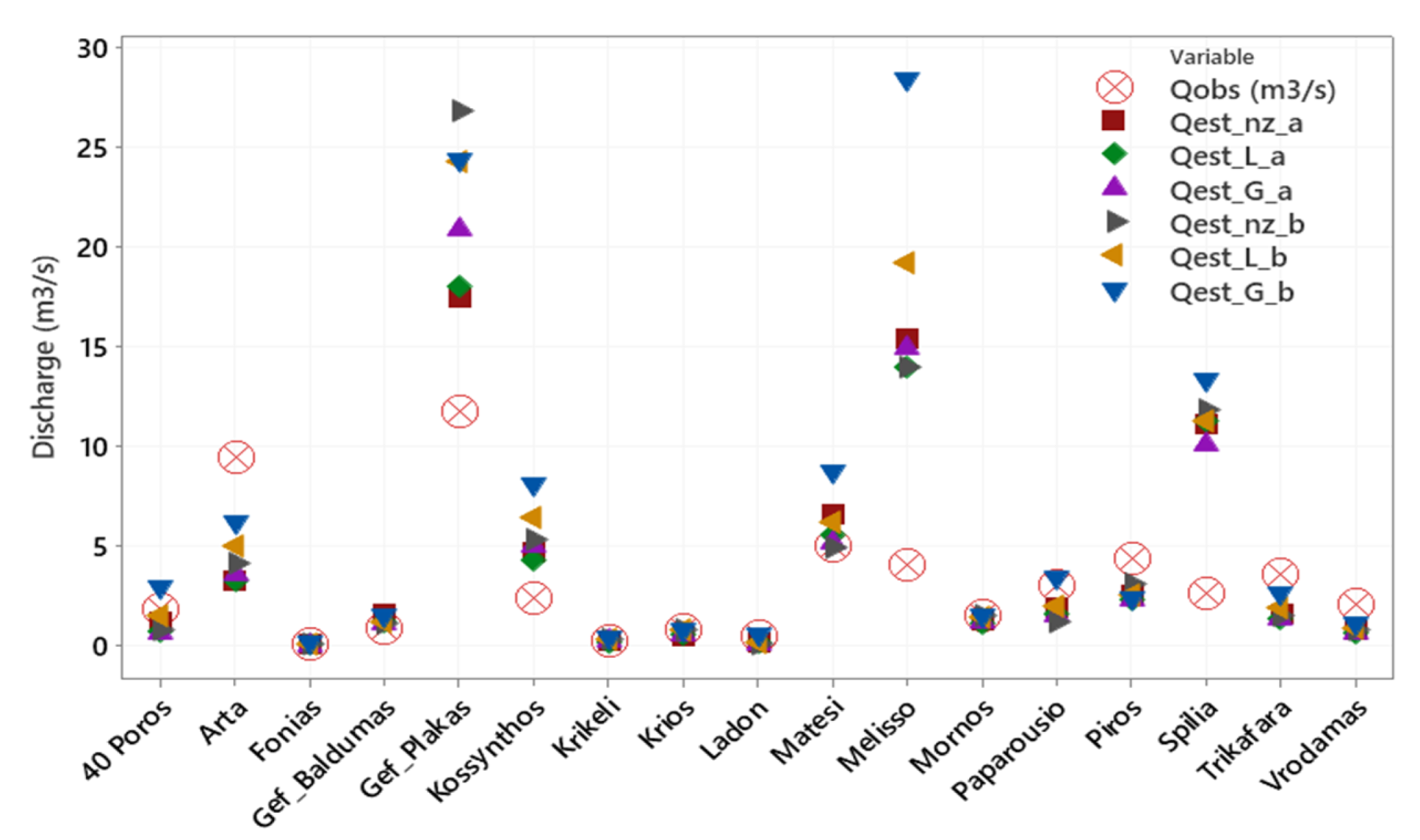
| Study Site Name | River/Stream Name | Latitude | Longitude | Elevation (m) | Discharge (m3/s) | Date of Measurement |
|---|---|---|---|---|---|---|
| 40 Poros | Sarantaporos | 40.11158 | 20.72377 | 416.3 | 1.83 | Jul-2019 |
| Arta | Aracthos | 39.16543 | 20.99305 | 21.1 | 9.4 | Jul-2019 |
| Fonias | Fonias | 40.49137 | 25.65514 | 15.0 | 0.05 | Aug-2018 |
| Gef_Baldumas | Dipotamos | 39.69724 | 20.99341 | 437.9 | 0.87 | Aug-2019 |
| Gef_Plakas | Aracthos | 39.45803 | 21.03130 | 230.3 | 11.76 | Jul-2019 |
| Kossynthos | Kossynthos | 41.10172 | 25.02614 | 21.3 | 2.39 | May-2019 |
| Krikeli | Krikeliotis | 38.77596 | 21.84881 | 827.6 | 0.18 | Jul-2018 |
| Krios | Krios | 38.14006 | 22.35951 | 1.7 | 0.74 | May-2019 |
| Ladon | Pineios (Peloponnese) | 37.87127 | 21.53456 | 64.2 | 0.48 | Jul-2019 |
| Matesi | Alfeios | 37.54373 | 21.94867 | 124.2 | 5.0 | Jul-2019 |
| Melisso | Aoos | 40.06035 | 20.59203 | 359.6 | 4.0 | Jul-2019 |
| Mornos | Mornos | 38.60376 | 22.19012 | 487.5 | 1.5 | Jul-2018 |
| Paparousio | Tavropos | 38.93268 | 21.67211 | 272.1 | 3.0 | Jul-2018 |
| Piros | Piros | 38.12771 | 21.62715 | 7.7 | 4.35 | May-2019 |
| Spilia | Aroanios | 37.84978 | 22.15801 | 418.3 | 2.61 | Jul-2019 |
| Trikfara | Krikeliotis | 38.79830 | 21.64779 | 379.5 | 3.55 | Jul-2018 |
| Vrodamas | Evrotas | 36.97452 | 22.58057 | 136.8 | 2.0 | Jul-2019 |
| Study Site | A (m2) | P (m) | Rh (m) | Slope (m/m) |
|---|---|---|---|---|
| 40 Poros | 1.46 | 9.71 | 0.151 | 0.072 |
| Arta | 5.18 | 21.3 | 0.243 | 0.018 |
| Fonias | 0.18 | 2.95 | 0.063 | 0.067 |
| Gef_Baldumas | 2.48 | 12.75 | 0.195 | 0.008 |
| Gef_Plakas | 16.45 | 46.84 | 0.351 | 0.036 |
| Kossynthos | 2.57 | 6.85 | 0.375 | 0.064 |
| Krikeli | 0.80 | 6.51 | 0.123 | 0.016 |
| Krios | 0.80 | 5.06 | 0.158 | 0.036 |
| Ladon | 0.93 | 10.92 | 0.085 | 0.006 |
| Matesi | 3.08 | 11.58 | 0.267 | 0.08 |
| Melisso | 13.01 | 30.30 | 0.429 | 0.018 |
| Mornos | 1.42 | 10.60 | 0.135 | 0.051 |
| Paparousio | 3.41 | 18.00 | 0.190 | 0.012 |
| Piros | 2.29 | 7.71 | 0.298 | 0.018 |
| Spilia | 3.28 | 7.95 | 0.413 | 0.08 |
| Trikfara | 3.49 | 16.62 | 0.210 | 0.011 |
| Vrodamas | 1.33 | 12.40 | 0.107 | 0.045 |
| Minimum | 0.18 | 2.95 | 0.063 | 0.006 |
| 25th percentile | 1.33 | 7.71 | 0.135 | 0.016 |
| Median | 2.48 | 10.92 | 0.195 | 0.036 |
| 75th percentile | 3.41 | 16.62 | 0.298 | 0.064 |
| Maximum | 16.45 | 46.84 | 0.429 | 0.08 |
| Initial Distribution (Excluding Fine Sediment) | Recalculated Distribution (Including Fine Sediment) | |||||
|---|---|---|---|---|---|---|
| d50 (m) | d84 (m) | d90 (m) | d50 (m) | d84 (m) | d90 (m) | |
| Minimum | 0.088 | 0.137 | 0.164 | 0.010 | 0.112 | 0.129 |
| 25th percentile | 0.122 | 0.179 | 0.208 | 0.039 | 0.135 | 0.157 |
| Median | 0.146 | 0.208 | 0.233 | 0.055 | 0.157 | 0.184 |
| 75th percentile | 0.176 | 0.291 | 0.334 | 0.067 | 0.180 | 0.207 |
| Maximum | 0.215 | 0.377 | 0.451 | 0.151 | 0.242 | 0.282 |
| Range | 0.127 | 0.24 | 0.287 | 0.141 | 0.13 | 0.153 |
| Qobs | Initial Distribution (Excluding Fine Sediment) | Recalculated Distribution (Including Fine Sediment) | |||||
|---|---|---|---|---|---|---|---|
| Estimation method | New_Zealand | Limerinos | Griffiths | New_Zealand | Limerinos | Griffiths | |
| Minimum | 0.05 | 0.07 | 0.01 | 0.00 | 0.04 | 0.06 | 0.13 |
| 25th percentile | 0.87 | 0.78 | 0.62 | 0.61 | 0.75 | 0.83 | 1.12 |
| Median | 2.39 | 1.63 | 1.34 | 1.35 | 1.46 | 1.85 | 2.58 |
| 75th percentile | 4.00 | 4.68 | 4.23 | 5.00 | 4.91 | 6.19 | 8.11 |
| Maximum | 11.70 | 17.43 | 18.00 | 20.89 | 26.81 | 24.31 | 28.39 |
| A (m2) | P (m) | Rh (m) | Slope (m/m) | |
|---|---|---|---|---|
| Average Error (%) | 0.44 | 0.22 | 0.72 | 0.19 |
| NZ_a | L_a | G_a | NZ_b | L_b | G_b | |
|---|---|---|---|---|---|---|
| RMSE_T1 | 4.14 | 3.98 | 4.31 | 5.21 | 5.49 | 7.41 |
| RMSE_T2 | 1.99 | 2.02 | 1.95 | 1.77 | 1.52 | 1.56 |
| Initial Distribution (Excluding Fine Sediment) | Recalculated Distribution (Including Fine Sediment) | |||||
|---|---|---|---|---|---|---|
| New_Zealand | Limerinos | Griffiths | New_Zealand | Limerinos | Griffiths | |
| Minimum | 16.8% | 10.9% | 2.0% | 0.7% | 7.8% | 1.2% |
| 25th percentile | 35.9% | 37.8% | 21.4% | 30.4% | 35.2% | 27.3% |
| Median | 54.2% | 60.6% | 62.2% | 58.7% | 44.9% | 58.4% |
| 75th percentile | 79.5% | 76.6% | 84.6% | 116.4% | 69.4% | 107.1% |
| Maximum | 326.9% | 330.0% | 286.7% | 353.2% | 380.4% | 609.7% |
| A (m2) | P (m) | Rh (m) | Slope (m/m) | Qobs (m3/s) | |
|---|---|---|---|---|---|
| P (m) | 0.948 | ||||
| Rh (m) | 0.653 | 0.456 | |||
| Slope (m/m) | −0.161 | −0.289 | 0.147 | ||
| Qobs (m3/s) | 0.764 | 0.804 | 0.529 | −0.07 | |
| Qest_nz_a (m3/s) | 0.9 | 0.757 | 0.826 | 0.153 | 0.645 |
| Qest_L_a (m3/s) | 0.901 | 0.767 | 0.81 | 0.149 | 0.664 |
| Qest_G_a (m3/s) | 0.932 | 0.812 | 0.779 | 0.108 | 0.696 |
| Qest_nz_b (m3/s) | 0.915 | 0.817 | 0.729 | 0.115 | 0.729 |
| Qest_L_b (m3/s) | 0.943 | 0.82 | 0.784 | 0.095 | 0.695 |
| Qest_G_b (m3/s) | 0.919 | 0.773 | 0.809 | 0.083 | 0.611 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagogiannis, S.; Dimitriou, E. Discharge Estimation with the Use of Unmanned Aerial Vehicles (UAVs) and Hydraulic Methods in Shallow Rivers. Water 2021, 13, 2808. https://doi.org/10.3390/w13202808
Lagogiannis S, Dimitriou E. Discharge Estimation with the Use of Unmanned Aerial Vehicles (UAVs) and Hydraulic Methods in Shallow Rivers. Water. 2021; 13(20):2808. https://doi.org/10.3390/w13202808
Chicago/Turabian StyleLagogiannis, Sergios, and Elias Dimitriou. 2021. "Discharge Estimation with the Use of Unmanned Aerial Vehicles (UAVs) and Hydraulic Methods in Shallow Rivers" Water 13, no. 20: 2808. https://doi.org/10.3390/w13202808
APA StyleLagogiannis, S., & Dimitriou, E. (2021). Discharge Estimation with the Use of Unmanned Aerial Vehicles (UAVs) and Hydraulic Methods in Shallow Rivers. Water, 13(20), 2808. https://doi.org/10.3390/w13202808







