Remote Sensing Methodology for Roughness Estimation in Ungauged Streams for Different Hydraulic/Hydrodynamic Modeling Approaches
Abstract
:1. Introduction
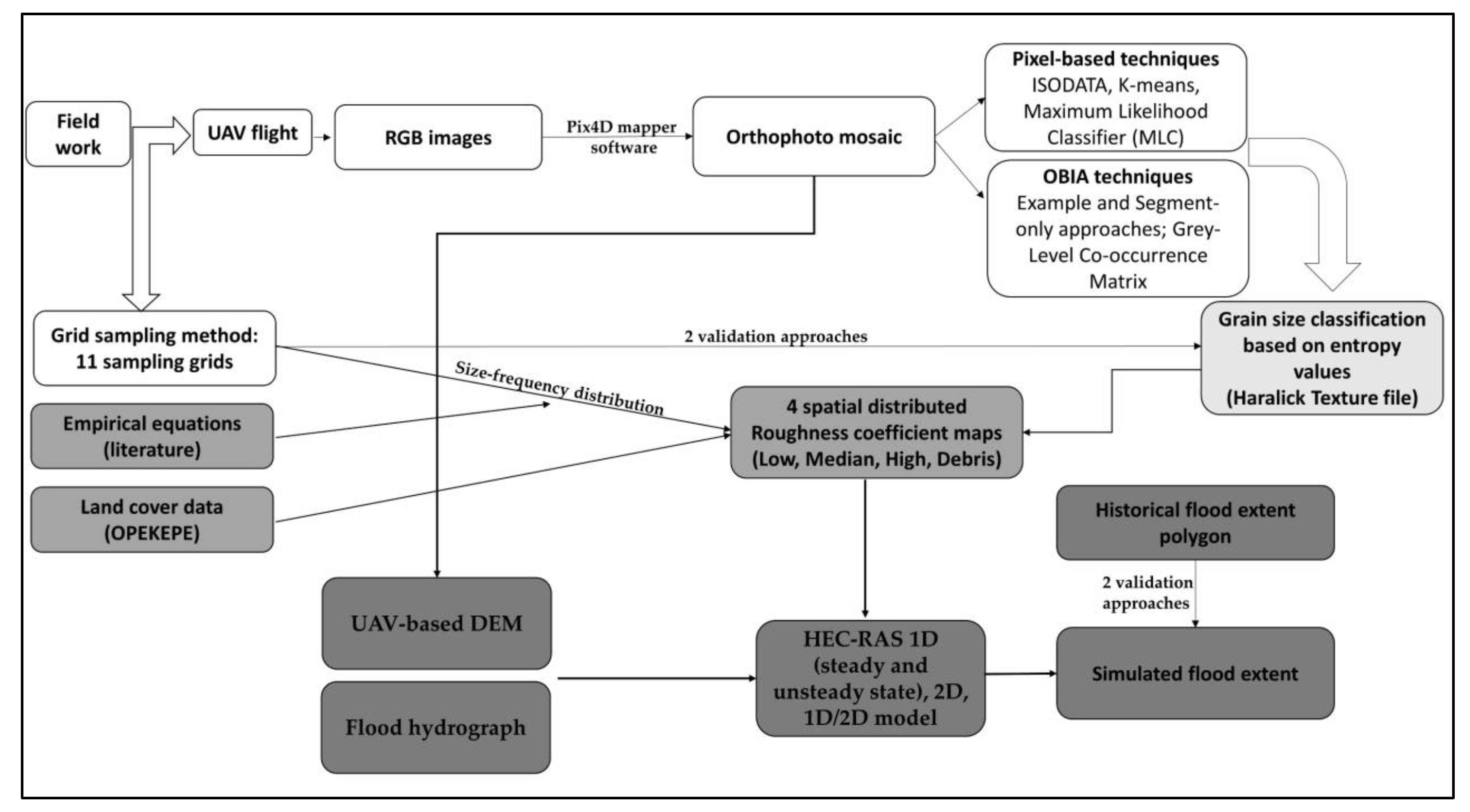
2. Materials and Methods
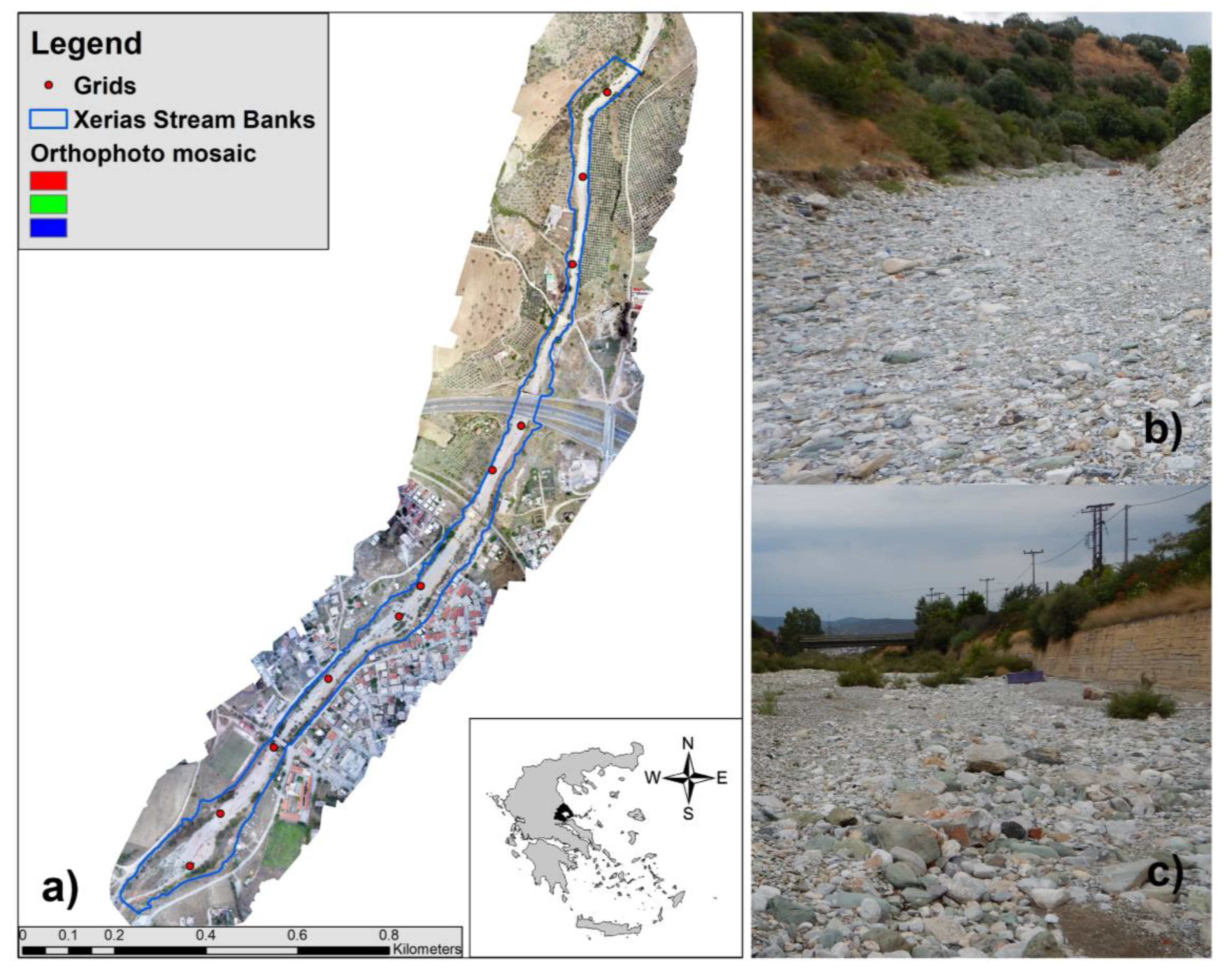
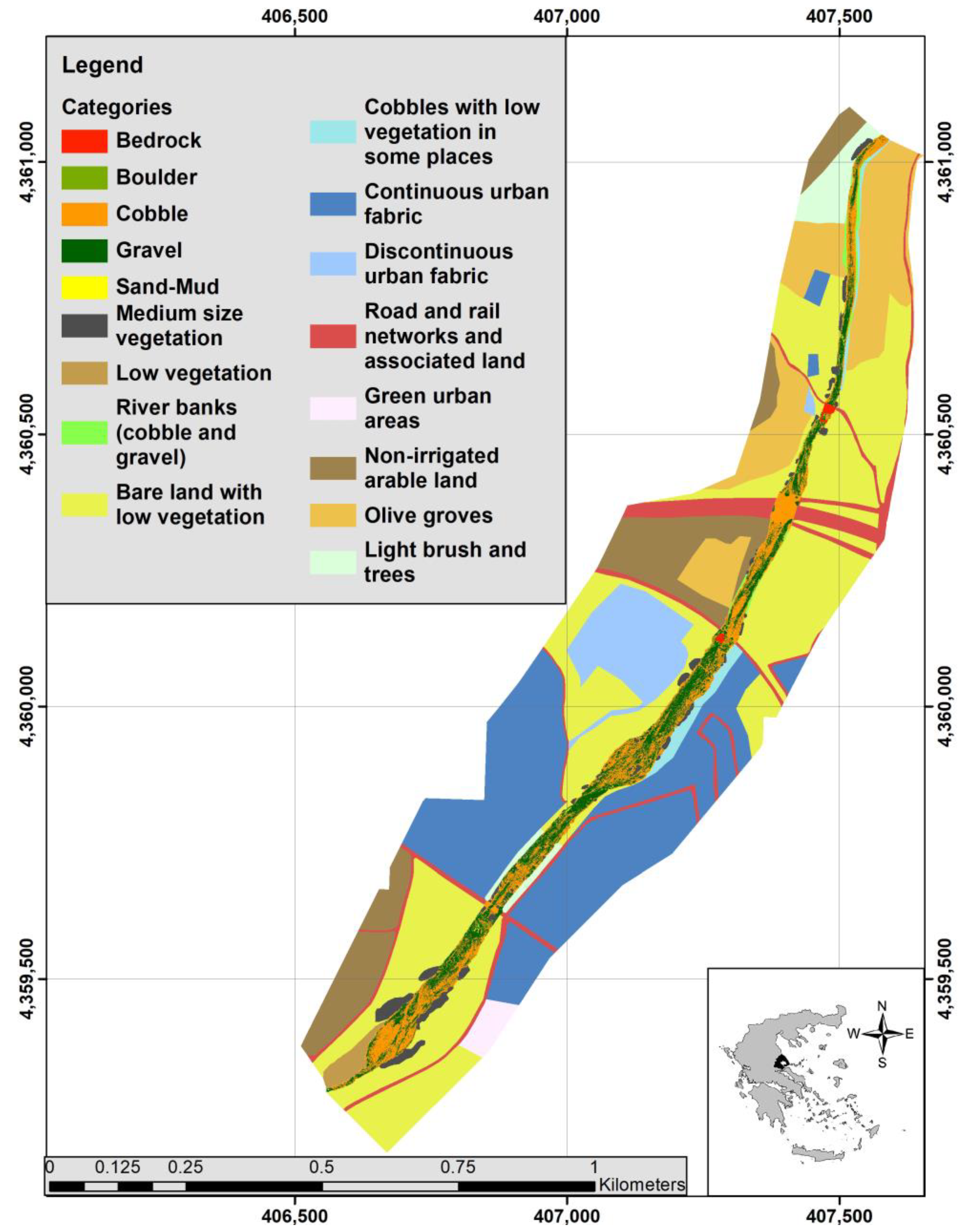
2.1. Study Area
2.2. Data, Ground Truth, and Tools Applied
2.3. Dominant Grain Size Classification via Airborne Image in Streams: Tested Methods
2.4. Manning’s n Roughness Coefficient Estimation Methodology
| A/A | Equation | Reference |
|---|---|---|
| 1 | [56] | |
| 2 | [56] | |
| 3 | [57] | |
| 4 | [57] | |
| 5 | [57] | |
| 6 | [58] | |
| 7 | [58] | |
| 8 | Gravel, n = 0.028–0.035 Cobble, n = 0.03–0.05 Boulder, n = 0.04–0.07 | [59] |
| 9 | [29] | |
| 10 | [60] | |
| 11 | [61] | |
| 12 | [61] | |
| 13 | [61] |
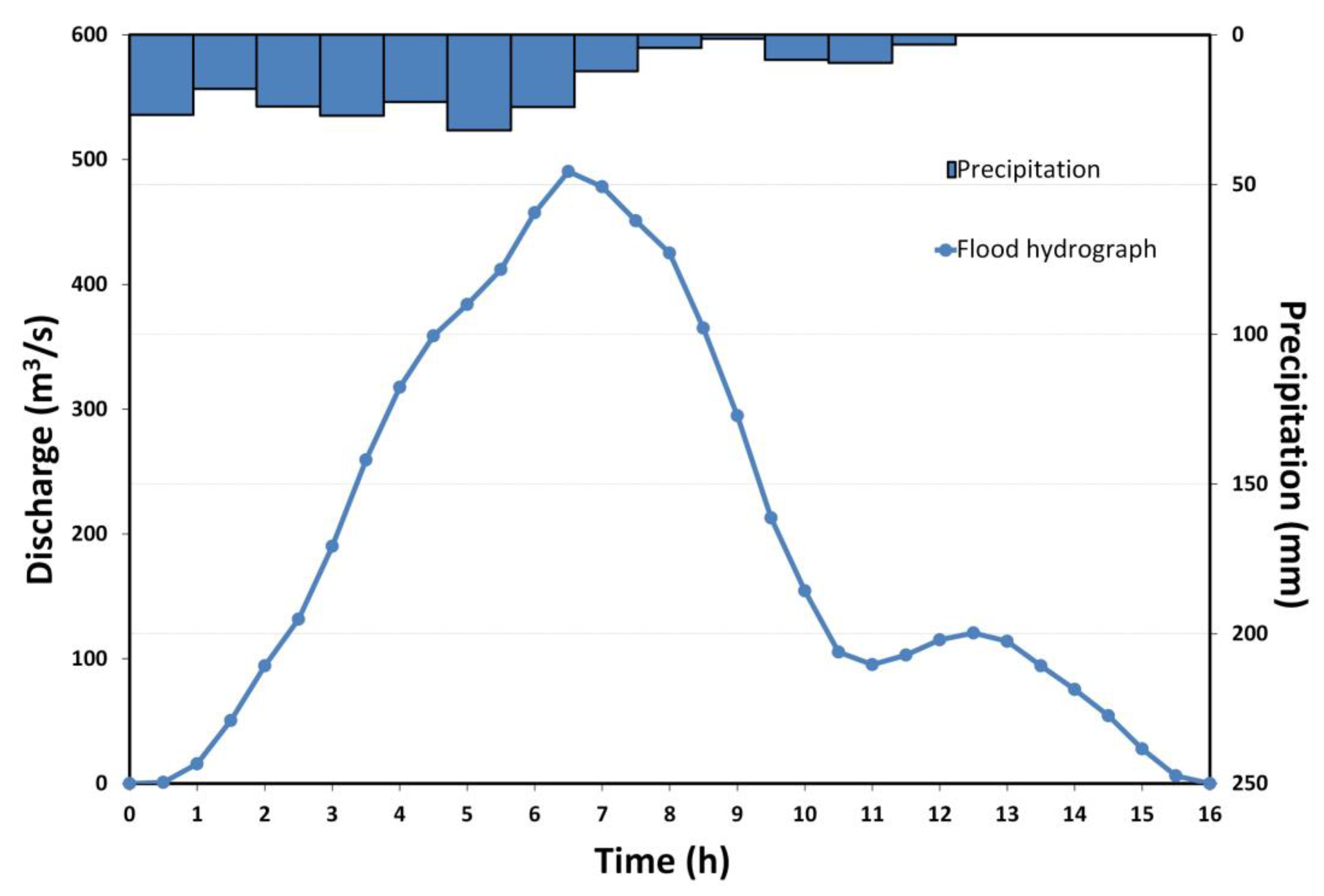
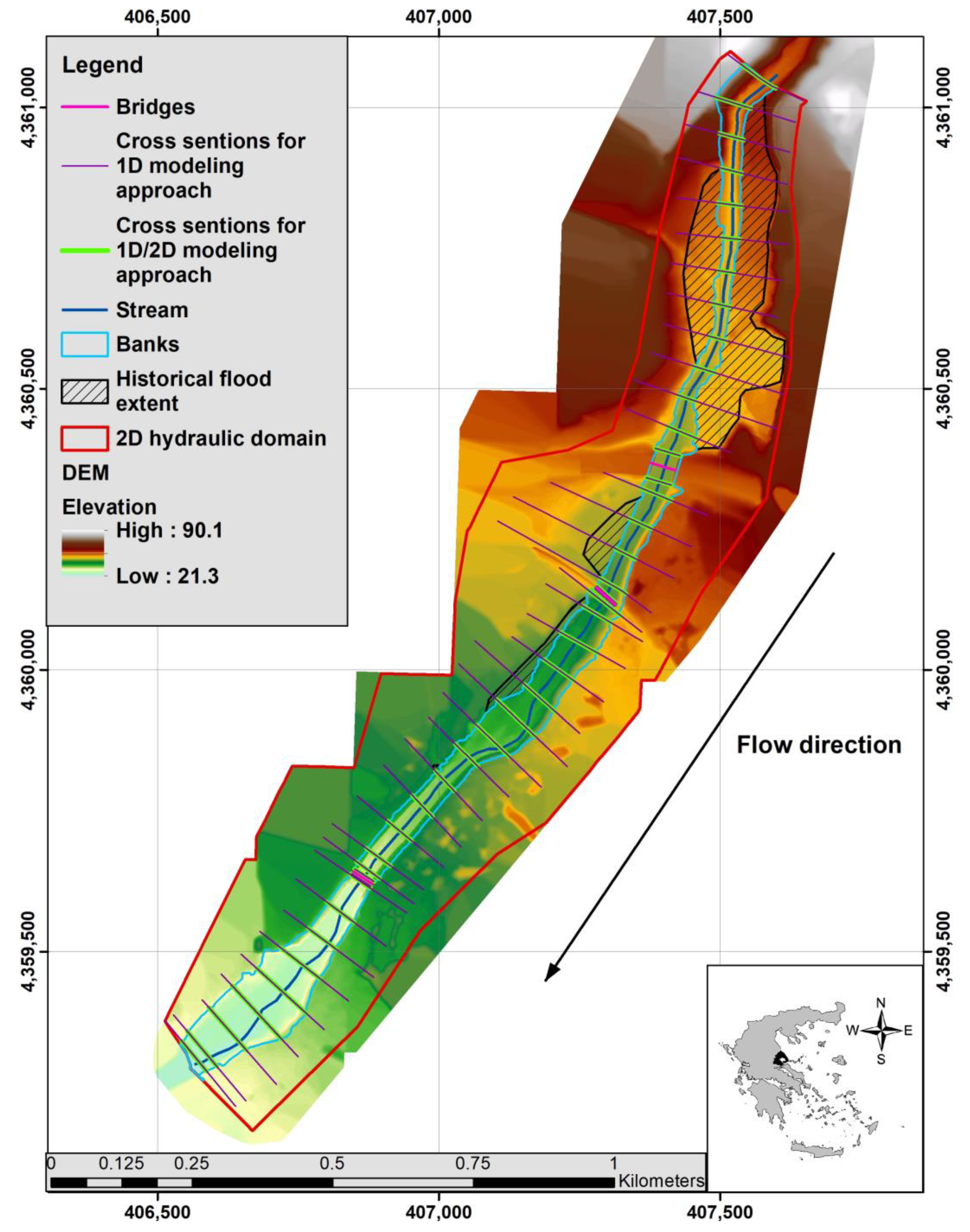
2.5. Hydrodynamic Modeling Configuration
3. Results
3.1. Sediment Grain Size Analysis and Classification
3.1.1. Sediment Grain-Size Distributions (Field Measurements)
3.1.2. Sediment Grain Size Classification via Image Analysis
3.2. Manning’s Roughness Coefficient Estimation
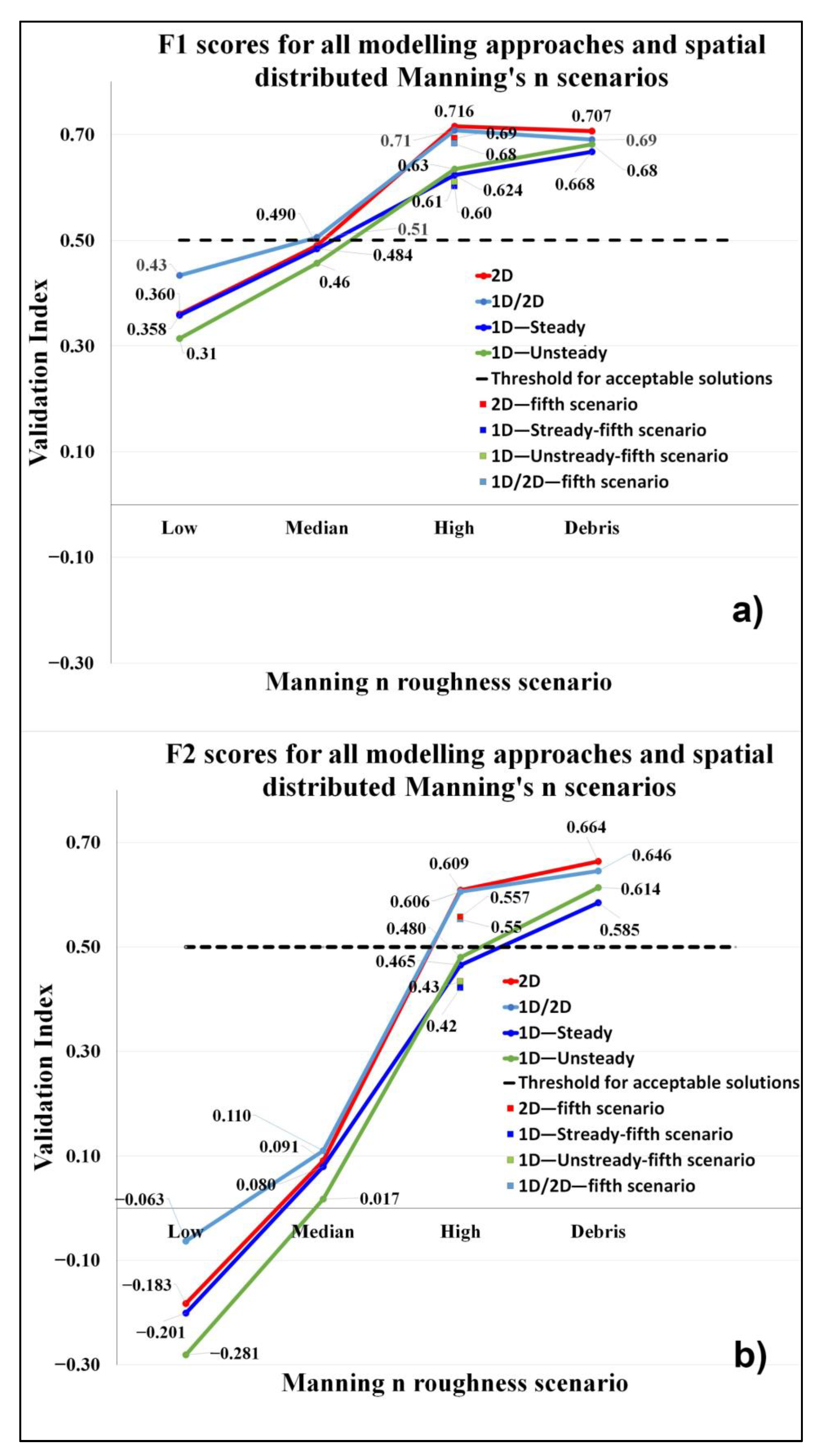
3.3. Hydraulic Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Middleton, G.V.; Southard, J.B. Mechanics of Sediment Movement; SEPM (Society for Sedimentary Geology): Tulsa, OK, USA, 1984; ISBN 978-1-56576-232-9. [Google Scholar]
- Wiberg, P.L.; Dungan Smith, J. Calculations of the Critical Shear Stress for Motion of Uniform and Heterogeneous Sediments. Water Resour. Res. 1987, 23, 1471–1480. [Google Scholar] [CrossRef]
- John, C.K.; Pu, J.H.; Pandey, M.; Hanmaiahgari, P.R. Sediment Deposition within Rainwater: Case Study Comparison of Four Different Sites in Ikorodu, Nigeria. Fluids 2021, 6, 124. [Google Scholar] [CrossRef]
- Clifford, N.J.; Robert, A.; Richards, K.S. Estimation of Flow Resistance I N Gravel-Bedded Rivers: A Physical Explanation of the Multiplier of Roughness Length. Earth Surf. Processes Landf. 1992, 17, 111–126. [Google Scholar] [CrossRef]
- Bray, D.I.; Davar, K.S. Resistance to Flow in Gravel-Bed Rivers. Can. J. Civ. Eng. 1987, 14, 77–86. [Google Scholar] [CrossRef]
- Pu, J.H.; Wallwork, J.T.; Khan, M.A.; Pandey, M.; Pourshahbaz, H.; Satyanaga, A.; Hanmaiahgari, P.R.; Gough, T. Flood Suspended Sediment Transport: Combined Modelling from Dilute to Hyper-Concentrated Flow. Water 2021, 13, 379. [Google Scholar] [CrossRef]
- Rice, S.; Church, M. Grain Size along Two Gravel-Bed Rivers: Statistical Variation, Spatial Pattern and Sedimentary Links. Earth Surf. Processes Landf. 1998, 23, 345–363. [Google Scholar] [CrossRef]
- Bunte, K.; Abt, S.R. Sampling Surface and Subsurface Particle-Size Distributions in Wadable Gravel-and Cobble-Bed Streams for Analyses in Sediment Transport, Hydraulics, and Streambed Monitoring; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2001.
- Wolman, M.G. A Method of Sampling Coarse River-Bed Material. Trans. Am. Geophys. Union 1954, 35, 951. [Google Scholar] [CrossRef]
- Hey, R.D.; Thorne, C.R. Accuracy of Surface Samples from Gravel Bed Material. J. Hydraul. Eng. 1983, 109, 842–851. [Google Scholar] [CrossRef]
- Laronne, J.B.; Shlomi, Y. Depositional Character and Preservation Potential of Coarse-Grained Sediments Deposited by Flood Events in Hyper-Arid Braided Channels in the Rift Valley, Arava, Israel. Sediment. Geol. 2007, 195, 21–37. [Google Scholar] [CrossRef]
- Rice, S.P.; Haschenburger, J.K. A Hybrid Method for Size Characterization of Coarse Subsurface Fluvial Sediments. Earth Surf. Processes Landf. 2004, 29, 373–389. [Google Scholar] [CrossRef]
- Verdu, J.M.; Batalla, R.J.; Martínez-Casasnovas, J.A. High resolution grain-size characterization of gravel bars using image analysis and geo-statistics. Geomorphology 2005, 72, 73–93. [Google Scholar] [CrossRef]
- Arif, M.S.M.; Gülch, E.; Tuhtan, J.A.; Thumser, P.; Haas, C. An Investigation of Image Processing Techniques for Substrate Classification Based on Dominant Grain Size Using RGB Images from UAV. Int. J. Remote Sens. 2017, 38, 2639–2661. [Google Scholar] [CrossRef]
- Chang, F.J.; Chung, C.H. Estimation of Riverbed Grain-Size Distribution Using Image-Processing Techniques. J. Hydrol. 2012, 440–441, 102–112. [Google Scholar] [CrossRef]
- Sime, L.C.; Ferguson, R.I. Information on Grain Sizes in Gravel-Bed Rivers by Automated Image Analysis. J. Sediment. Res. 2003, 73, 630–636. [Google Scholar] [CrossRef]
- Graham, D.J.; Reid, I.; Rice, S.P. Automated Sizing of Coarse-Grained Sediments: Image-Processing Procedures. Math. Geol. 2005, 37, 1–28. [Google Scholar] [CrossRef]
- Graham, D.J.; Rice, S.P.; Reid, I. A Transferable Method for the Automated Grain Sizing of River Gravels. Water Resour. Res. 2005, 41, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Buscombe, D. Estimation of Grain-Size Distributions and Associated Parameters from Digital Images of Sediment. Sediment. Geol. 2008, 210, 1–10. [Google Scholar] [CrossRef]
- Beggan, C.; Hamilton, C.W. New Image Processing Software for Analyzing Object Size-Frequency Distributions, Geometry, Orientation, and Spatial Distribution. Comput. Geosci. 2010, 36, 539–549. [Google Scholar] [CrossRef]
- Sibaruddin, H.I.; Shafri, H.Z.M.; Pradhan, B.; Haron, N.A. Comparison of Pixel-Based and Object-Based Image Classification Techniques in Extracting Information from UAV Imagery Data. In IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing: Bristol, UK, 2018; Volume 169. [Google Scholar]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Conners, R.W.; Trivedi, M.M.; Harlow, C.A. Segmentation of a High.-Resolution Urban. Scene Using Texture Operators. Comput. Vis. Graph. Image Processing 1984, 25, 273–310. [Google Scholar] [CrossRef]
- Hawlick, R.M. Statistical and Structural Approaches to Texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar]
- Carbonneau, P.E.; Lane, S.N.; Bergeron, N.E. Catchment-Scale Mapping of Surface Grain Size in Gravel Bed Rivers Using Airborne Digital Imagery. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. Flood Risk Assessment and Associated Uncertainty. Nat. Hazards Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Papaioannou, G.; Vasiliades, L.; Loukas, A.; Aronica, G.T. Probabilistic Flood Inundation Mapping at Ungauged Streams Due to Roughness Coefficient Uncertainty in Hydraulic Modelling. Adv. Geosci. 2017, 44, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Coon, W. Estimation of Roughness Coefficients for Natural Stream Channels with Vegetated Banks; US Geological Survey: Denver, CO, USA, 1998.
- Marcus, W.A.; Roberts, K.; Harvey, L.; Tackman, G. An Evaluation of Methods for Estimating Manning’s n in Small Mountain Streams. Mt. Res. Dev. 1992, 12, 227. [Google Scholar] [CrossRef]
- Papaioannou, G. Flood Hazard and Risk Modelling Framework for Ungauged Streams and Watersheds; University of Thessaly: Volos, Greece, 2017. [Google Scholar]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the Calibration of Effective Roughness Parameters in HEC-RAS Using Inundation and Downstream Level Observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood Inundation Modelling: A Review of Methods, Recent Advances and Uncertainty Analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Hutanu, E.; Mihu-Pintilie, A.; Urzica, A.; Paveluc, L.E.; Stoleriu, C.C.; Grozavu, A. Using 1D HEC-RAS Modeling and LiDAR Data to Improve Flood Hazard Maps Accuracy: A Case Study from Jijia Floodplain (NE Romania). Water 2020, 12, 1624. [Google Scholar] [CrossRef]
- Albo-Salih, H.; Mays, L. Testing of an Optimization-Simulation Model for Real-Time Flood Operation of River-Reservoir Systems. Water 2021, 13, 1207. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing River Model Set-up for 2-D Dynamic Flood Modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Papaioannou, G.; Vasiliades, L.; Loukas, A.; Alamanos, A.; Efstratiadis, A.; Koukouvinos, A.; Tsoukalas, I.; Kossieris, P. A Flood Inundation Modeling Approach for Urban and Rural Areas in Lake and Large-Scale River Basins. Water 2021, 13, 1264. [Google Scholar] [CrossRef]
- Naeem, B.; Azmat, M.; Tao, H.; Ahmad, S.; Khattak, M.; Haider, S.; Ahmad, S.; Khero, Z.; Goodell, C. Flood Hazard Assessment for the Tori Levee Breach of the Indus River Basin, Pakistan. Water 2021, 13, 604. [Google Scholar] [CrossRef]
- Apel, H.; Aronica, G.T.; Kreibich, H.; Thieken, A.H. Flood Risk Analyses—How Detailed Do We Need to Be? Nat. Hazards 2009, 49, 79–98. [Google Scholar] [CrossRef]
- Liu, Q.; Qin, Y.; Zhang, Y.; Li, Z. A Coupled 1D–2D Hydrodynamic Model for Flood Simulation in Flood Detention Basin. Nat. Hazards 2015, 75, 1303–1325. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative Evaluation of 1D and Quasi-2D Hydraulic Models Based on Benchmark and Real-World Applications for Uncertainty Assessment in Flood Mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood Inundation Mapping Sensitivity to Riverine Spatial Resolution and Modelling Approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Papaioannou, G.; Efstratiadis, A.; Vasiliades, L.; Loukas, A.; Papalexiou, S.; Koukouvinos, A.; Tsoukalas, I.; Kossieris, P. An Operational Method for Flood Directive Implementation in Ungauged Urban Areas. Hydrology 2018, 5, 24. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.H.; Chen, H.; Guo, W.D.; Yeh, S.H.; Chen, W.B.; Liu, C.H.; Lee, S.C. Predicting River Embankment Failure Caused by Toe Scour Considering 1D and 2D Hydraulic Models: A Case Study of Da-An River, Taiwan. Water 2020, 12, 1026. [Google Scholar] [CrossRef] [Green Version]
- Papaioannou, G.; Vasiliades, L.; Loukas, A. Multi-Criteria Analysis Framework for Potential Flood Prone Areas Mapping. Water Resour. Manag. 2015, 29, 399–418. [Google Scholar] [CrossRef]
- Papaioannou, G.; Varlas, G.; Terti, G.; Papadopoulos, A.; Loukas, A.; Panagopoulos, Y.; Dimitriou, E. Flood Inundation Mapping at Ungauged Basins Using Coupled Hydrometeorological-Hydraulic Modelling: The Catastrophic Case of the 2006 Flash Flood in Volos City, Greece. Water 2019, 11, 2328. [Google Scholar] [CrossRef] [Green Version]
- Unger, M.; Pock, T.; Grabner, M.; Klaus, A.; Bischof, H. A Variational Approach to Semiautomatic Generation of Digital Terrain Models. In Proceedings of the Advances in Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Kuno, Y., Wang, J., Pajarola, R., Lindstrom, P., Hinkenjann, A., Encarnação, M.L., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1119–1130. [Google Scholar]
- Küng, O.; Strecha, C.; Beyeler, A.; Zufferey, J.-C.; Floreano, D.; Fua, P.; Gervaix, F. The Accuracy of Automatic Photogrammetric Techniques on Ultra-Light Uav Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-1/C22, 125–130. [Google Scholar] [CrossRef] [Green Version]
- Yuzyk, T.R.; Winkler, T. Procedures for Bed-Material Sampling: Lesson Package No. 28; The Section: Ottawa, ON, Canada, 1999; Volume 4. [Google Scholar]
- Tuceryan, M.; Jain, A.K. Texture Analysis. In Handbook of Pattern Recognition and Computer Vision; World Scientific: Singapore, 1993; pp. 235–276. [Google Scholar]
- Ricard, Y.; Bercovici, D. A Continuum Theory of Grain Size Evolution and Damage. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Markogianni, V.; Dimitriou, E. Landuse and NDVI Change Analysis of Sperchios River Basin (Greece) with Different Spatial Resolution Sensor Data by Landsat/MSS/TM and OLI. Desalination Water Treat. 2016, 57, 29092–29103. [Google Scholar] [CrossRef]
- Chow, W. Open-Channel Hydraulics, 1st ed.; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Brunner, G.W. CEIWR-HEC. HEC-RAS River Analysis System: 2D Modelling User’s Manual Version 6.0; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2021.
- Phillips, J.; Tadayon, S. Selection of Manning’s Roughness Coefficient for Natural and Constructed Vegetated and Non-Vegetated Channels, and Vegetation Maintenance Plan Guidelines for Vegetated Channels in Central Arizona; US Geological Survey: Reston, WV, USA, 2007.
- Hellenic Ministry of Environment and Energy. 1st Update of River Basin Management Plans of the River Basins of Thessaly Water District (EL08). Analysis of the Anthropogenic Pressures and Their Effect on the Surface and Groundwater Waterbodies; Hellenic Ministry of Environment and Energy, Special Secretariat for Water: Athens, Greece, 2017.
- McKay, S.K.; Fischenich, J.C. Robust Prediction of Hydraulic Roughness; U.S. Army Corps of Engineers (USACE), Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2011.
- Javan, M.; McKeogh, E.; Kiely, G. Field Evaluation of Manning’s n in Gravel Rivers. In Channel Flow Resistance: Centennial of Manning’s Formula; Yen, B., Ed.; Water Resources Publications: Littleton, Hongkong, 1992; pp. 318–327. [Google Scholar]
- Ho, C.W.; Huang, H.P. Manning’s Roughness Coefficient of Mountainous Streams in Taiwan. In Channel Flow Resistance: Centennial of Manning’s Formula; Yen, B.C., Ed.; Water Resources Publications: Littleton, Hong Kong, 1992; pp. 299–308. [Google Scholar]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; U.S. G.P.O.: Denver, CO, USA, 1984.
- Romero, M.; Revollo, N.; Molina, J. Flow Resistance in Steep Mountain Rivers in Bolivia. J. Hydrodyn. 2010, 22, 679–684. [Google Scholar] [CrossRef]
- Ugarte, A.S.; Madrid-Aris, M. Roughness Coefficient in Mountain River. In Hydraulic Engineering ’94; Cotroneo, G.V., Rumer, R., Eds.; American Society of Civil Engineers: New York, NY, USA, 1994; Volume 1, pp. 652–656. [Google Scholar]
- Dey, S.; Saksena, S.; Merwade, V. Assessing the Effect of Different Bathymetric Models on Hydraulic Simulation of Rivers in Data Sparse Regions. J. Hydrol. 2019, 575, 838–851. [Google Scholar] [CrossRef]
- Gain, A.K.; Mojtahed, V.; Biscaro, C.; Balbi, S.; Giupponi, C. An Integrated Approach of Flood Risk Assessment in the Eastern Part of Dhaka City. Nat. Hazards 2015, 79, 1499–1530. [Google Scholar] [CrossRef] [Green Version]
- Künzler, M.; Huggel, C.; Ramírez, J.M. A Risk Analysis for Floods and Lahars: Case Study in the Cordillera Central of Colombia. Nat. Hazards 2012, 64, 767–796. [Google Scholar] [CrossRef]
- Kastridis, A.; Stathis, D. Evaluation of Hydrological and Hydraulic Models Applied in Typical Mediterranean Ungauged Watersheds Using Post-Flash-Flood Measurements. Hydrology 2020, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Czuba, J.A.; David, S.R.; Edmonds, D.A.; Ward, A.S. Dynamics of Surface-Water Connectivity in a Low-Gradient Meandering River Floodplain. Water Resour. Res. 2019, 55, 1849–1870. [Google Scholar] [CrossRef]
- Papaioannou, G.; Varlas, G.; Papadopoulos, A.; Loukas, A.; Katsafados, P.; Dimitriou, E. Investigating Sea-State Effects on Flash Flood Hydrograph and Inundation Forecasting. Hydrol. Processes 2021, 35, 1–20. [Google Scholar] [CrossRef]
- Pilotti, M.; Milanesi, L.; Bacchi, V.; Tomirotti, M.; Maranzoni, A. Dam-Break Wave Propagation in Alpine Valley with HEC-RAS 2D: Experimental Cancano Test Case. J. Hydraul. Eng. 2020, 146, 05020003. [Google Scholar] [CrossRef]
- Zhang, K.; Shalehy, M.H.; Ezaz, G.T.; Chakraborty, A.; Mohib, K.M.; Liu, L. An Integrated Flood Risk Assessment Approach Based on Coupled Hydrological-Hydraulic Modeling and Bottom-up Hazard Vulnerability Analysis. Environ. Model. Softw. 2022, 148, 105279. [Google Scholar] [CrossRef]
- Albo-Salih, H.; Mays, L.W.; Che, D. Application of an Optimization/Simulation Model for the Real-Time Flood Operation of River-Reservoir Systems with One-and Two-Dimensional Unsteady Flow Modeling. Water 2022, 14, 87. [Google Scholar] [CrossRef]
- Dasallas, L.; Kim, Y.; An, H. Case Study of HEC-RAS 1D–2D Coupling Simulation: 2002 Baeksan Flood Event in Korea. Water. 2019, 11, 2048. [Google Scholar] [CrossRef] [Green Version]
- Brunner, G.W.; Sanchez, A.; Molls, T.; Parr, D.A. HEC-RAS Verification and Validation Tests; US Army Corps of Engineers–Hydrologic Engineering Center: Davis, CA, USA, 2018; pp. 1–154.
- Brunner, G.W. CEIWR-HEC HEC-RAS River Analysis System: User’s Manual Version 6.0; US Army Corps of Engineers Institute for Water Resources, HEC, January: Davis, CA, USA, 2021.
- Papaioannou, G.; Papadaki, C.; Dimitriou, E. Sensitivity of Habitat Hydraulic Model Outputs to DTM and Computational Mesh Resolution. Ecohydrology 2020, 13, e2182. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Georgiadis, C. The Effect of Riverine Terrain Spatial Resolution on Flood Modeling and Mapping. In First International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2013); Hadjimitsis, D.G., Themistocleous, K., Michaelides, S., Papadavid, G., Eds.; SPIE: Bellingham, DC, USA, 2013; Volume 8795, p. 87951H. [Google Scholar]
- Schumann, G.; Matgen, P.; Cutler, M.E.J.; Black, A.; Hoffmann, L.; Pfister, L. Comparison of Remotely Sensed Water Stages from LiDAR, Topographic Contours and SRTM. ISPRS J. Photogramm. Remote Sens. 2008, 63, 283–296. [Google Scholar] [CrossRef]
- Wang, W.; Yang, X.; Yao, T. Evaluation of ASTER GDEM and SRTM and Their Suitability in Hydraulic Modelling of a Glacial Lake Outburst Flood in Southeast Tibet. Hydrol. Process. 2012, 26, 213–225. [Google Scholar] [CrossRef]
- di Baldassarre, G.; Schumann, G.; Bates, P.D.; Freer, J.E.; Beven, K.J. Flood-Plain Mapping: A Critical Discussion of Deterministic and Probabilistic Approaches. Hydrol. Sci. J. 2010, 55, 364–376. [Google Scholar] [CrossRef]
- Horritt, M.S.; di Baldassarre, G.; Bates, P.D.; Brath, A. Comparing the Performance of a 2-D Finite Element and a 2-D Finite Volume Model of Floodplain Inundation Using Airborne SAR Imagery. Hydrol. Process. 2007, 21, 2745–2759. [Google Scholar] [CrossRef]
- Lim, N.J.; Brandt, S.A. Flood Map Boundary Sensitivity Due to Combined Effects of DEM Resolution and Roughness in Relation to Model Performance. Geomat. Nat. Hazards Risk 2019, 10, 1613–1647. [Google Scholar] [CrossRef] [Green Version]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal, J.C.; Alfieri, L.; Freer, J.E. A High-Resolution Global Flood Hazard Model. Water Resour. Res. 2015, 51, 7358–7381. [Google Scholar] [CrossRef] [Green Version]
- Shastry, A.; Durand, M.; Neal, J.; Fernández, A.; Phang, S.C.; Mohr, B.; Jung, H.C.; Kari, S.; Moritz, M.; Mark, B.G.; et al. Small-Scale Anthropogenic Changes Impact Floodplain Hydraulics: Simulating the Effects of Fish Canals on the Logone Floodplain. J. Hydrol. 2020, 588, 125035. [Google Scholar] [CrossRef]
- Ermilov, A.A.; Baranya, S.; Török, G.T. Image-Based Bed Material Mapping of a Large River. Water 2020, 12, 916. [Google Scholar] [CrossRef] [Green Version]
- Marangoz, A.M.; Oruç, M.; Karakış, S.; Şahin, H. Comparison of Pixel-Based and Object-Oriented Classification Using IKONOS Imagery for Automatic Building Extraction—Safranbolu Testfield. In Proceedings of the 20th ISPRS Congress, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- Laliberte, A.S.; Rango, A.; Havstad, K.M.; Paris, J.F.; Beck, R.F.; McNeely, R.; Gonzalez, A.L. Object-Oriented Image Analysis for Mapping Shrub Encroachment from 1937 to 2003 in Southern New Mexico. Remote Sens. Environ. 2004, 93, 198–210. [Google Scholar] [CrossRef]
- Yu, Q.; Gong, P.; Clinton, N.; Biging, G.; Kelly, M.; Schirokauer, D. Object-Based Detailed Vegetation Classification with Airborne High Spatial Resolution Remote Sensing Imagery. Photogramm. Eng. Remote Sens. 2006, 72, 799–811. [Google Scholar] [CrossRef] [Green Version]
- de Arruda Gomes, M.M.; de Melo Verçosa, L.F.; Cirilo, J.A. Hydrologic Models Coupled with 2D Hydrodynamic Model for High-Resolution Urban Flood Simulation. Nat. Hazards 2021, 108, 3121–3157. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the Effects of Digital Elevation Model Resolution in Urban Fluvial Flood Modelling. J. Hydrol. 2021, 59, 126088. [Google Scholar] [CrossRef]
- Kastridis, A.; Kirkenidis, C.; Sapountzis, M. An Integrated Approach of Flash Flood Analysis in Ungauged Mediterranean Watersheds Using Post-Flood Surveys and Unmanned Aerial Vehicles. Hydrol. Process. 2020, 34, 4920–4939. [Google Scholar] [CrossRef]
- Sharma, V.C.; Regonda, S.K. Two-Dimensional Flood Inundation Modeling in the Godavari River Basin, India—Insights on Model Output Uncertainty. Water 2021, 13, 191. [Google Scholar] [CrossRef]
- Garrote, J.; González-Jiménez, M.; Guardiola-Albert, C.; Díez-Herrero, A. The Manning’s Roughness Coefficient Calibration Method to Improve Flood Hazard Analysis in the Absence of River Bathymetric Data: Application to the Urban Historical Zamora City Centre in Spain. Appl. Sci. 2021, 11, 9267. [Google Scholar] [CrossRef]

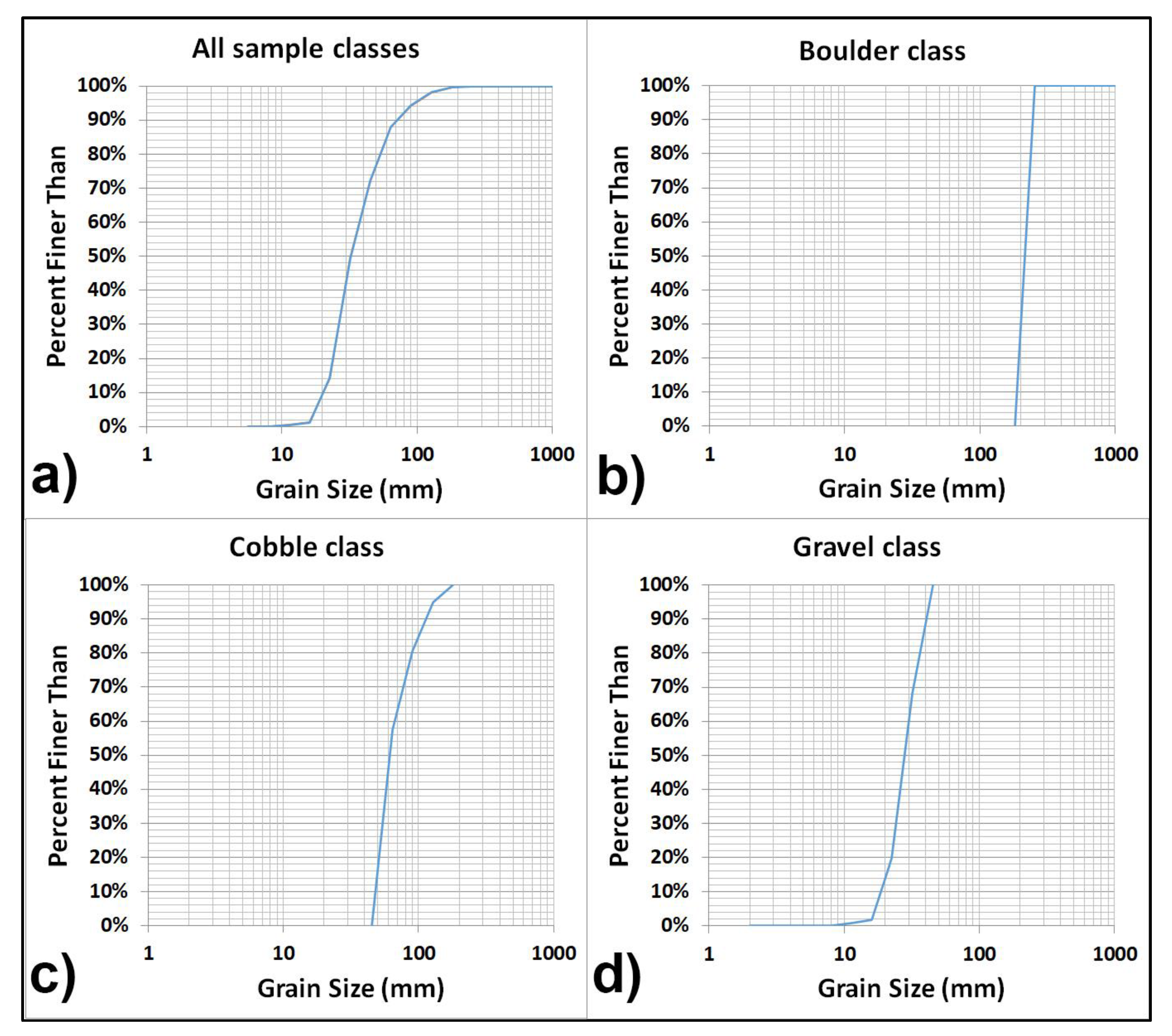

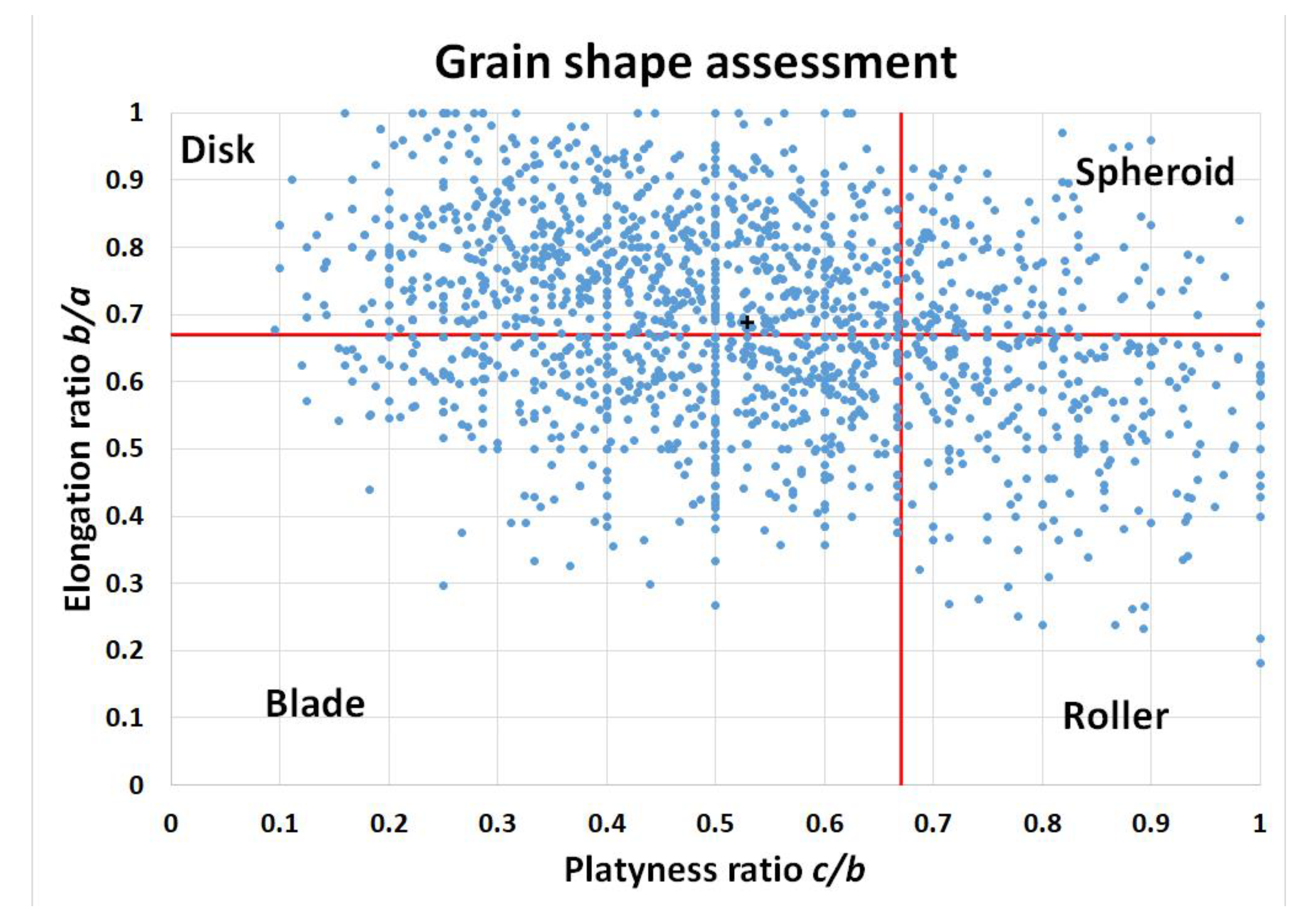
| Substrate Type | Size (cm) |
|---|---|
| Sand-mud | 0.0062–0.2 |
| Gravel | 0.2–6.4 |
| Cobble | 6.4–25.6 |
| Boulder | 25.6–409.6 |
| Bedrock | >409.6 |
| Approach | Method | Tool | Anticipated Result |
|---|---|---|---|
| Pixel-based image analysis | Supervised/Unsupervised classification | ISODATA, K-means, Maximum Likelihood Classifier (MLC) | Pixel-based classification map |
| Object-based image analysis (OBIA) | ENVI feature extraction module (ENVI v.5.5) | Example and Segment-only approaches | Object-based classification map |
| Local image texture analysis (QGIS v.3.18) | Grey-Level Co-occurrence Matrix (GLCM) | Reclassified entropy values (Band 2) interpreting grain size classes |
| Predefined Diameters | ds, (m) | Predefined Diameters | ds, (m) | Predefined Diameters | ds, (m) | |||
|---|---|---|---|---|---|---|---|---|
| Gravel | D50 | 0.028 | Cobble | D50 | 0.062 | Boulder | D50 | 0.219 |
| D65 | 0.031 | D65 | 0.073 | D65 | 0.230 | |||
| D84 | 0.039 | D84 | 0.100 | D84 | 0.244 | |||
| D90 | 0.041 | D90 | 0.115 | D90 | 0.249 |
| Approach/Method | Bands | Results and Set Parameters |
|---|---|---|
| Pixel-based image analysis/ Maximum Likelihood Classifier | RGB | Riparian vegetation and the vegetation detected in the middle of the stream-bed |
| Boulders and Bedrock classes | ||
| Object-based analysis (OBIA)/ ENVI feature extraction module | RGB | Boulders (full lambda; 35 scale value; 50 merge value; SVM) |
| Cobbles (polynomial kernel type/ radial basis function) | ||
| Red and Intensity | Gravels (SVM; radial or polynomial kernel type) | |
| Object-based analysis (OBIA)/GLCM | Haralick Texture file (Entropy band) | Cobbles, Gravels, and Sand-mud |
| CODE | Classification Category | Manning’s n Scenarios | |||
|---|---|---|---|---|---|
| Low | Median | High | Debris | ||
| 1 | * Bedrock | 0.013 | 0.013 | 0.013 | 0.013 |
| 2 | Boulder | 0.0301 | 0.0414 | 0.082 | 0.0984 |
| 3 | Cobble | 0.0265 | 0.035 | 0.073 | 0.0876 |
| 4 | Gravel | 0.0223 | 0.0297 | 0.068 | 0.0816 |
| 5 | Sand-Mud | 0.026 | 0.0305 | 0.035 | 0.042 |
| 6 | Medium size vegetation | 0.04 | 0.06 | 0.08 | 0.096 |
| 7 | Low vegetation | 0.025 | 0.0375 | 0.05 | 0.06 |
| 8 | River banks (cobble and gravel) | 0.0223 | 0.0341 | 0.0731 | 0.08772 |
| 9 | Bare land with low vegetation | 0.03 | 0.035 | 0.05 | 0.06 |
| 10 | Cobble with low vegetation in some places | 0.0318 | 0.042 | 0.0878 | 0.10536 |
| 11 | * Continuous urban fabric | 0.06 | 0.09 | 0.12 | 0.12 |
| 12 | Discontinuous urban fabric | 0.03 | 0.04 | 0.05 | 0.06 |
| 13 | * Road and rail networks and associated land | 0.013 | 0.013 | 0.013 | 0.013 |
| 14 | Green urban areas | 0.017 | 0.025 | 0.033 | 0.0396 |
| 15 | Non-irrigated arable land | 0.025 | 0.035 | 0.045 | 0.054 |
| 16 | * Olive groves | 0.06 | 0.08 | 0.1 | 0.1 |
| 17 | Light brush and trees | 0.035 | 0.05 | 0.06 | 0.072 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papaioannou, G.; Markogianni, V.; Loukas, A.; Dimitriou, E. Remote Sensing Methodology for Roughness Estimation in Ungauged Streams for Different Hydraulic/Hydrodynamic Modeling Approaches. Water 2022, 14, 1076. https://doi.org/10.3390/w14071076
Papaioannou G, Markogianni V, Loukas A, Dimitriou E. Remote Sensing Methodology for Roughness Estimation in Ungauged Streams for Different Hydraulic/Hydrodynamic Modeling Approaches. Water. 2022; 14(7):1076. https://doi.org/10.3390/w14071076
Chicago/Turabian StylePapaioannou, George, Vassiliki Markogianni, Athanasios Loukas, and Elias Dimitriou. 2022. "Remote Sensing Methodology for Roughness Estimation in Ungauged Streams for Different Hydraulic/Hydrodynamic Modeling Approaches" Water 14, no. 7: 1076. https://doi.org/10.3390/w14071076
APA StylePapaioannou, G., Markogianni, V., Loukas, A., & Dimitriou, E. (2022). Remote Sensing Methodology for Roughness Estimation in Ungauged Streams for Different Hydraulic/Hydrodynamic Modeling Approaches. Water, 14(7), 1076. https://doi.org/10.3390/w14071076









