Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method
Abstract
1. Introduction
2. Reference Evapotranspiration
3. Materials and Methods
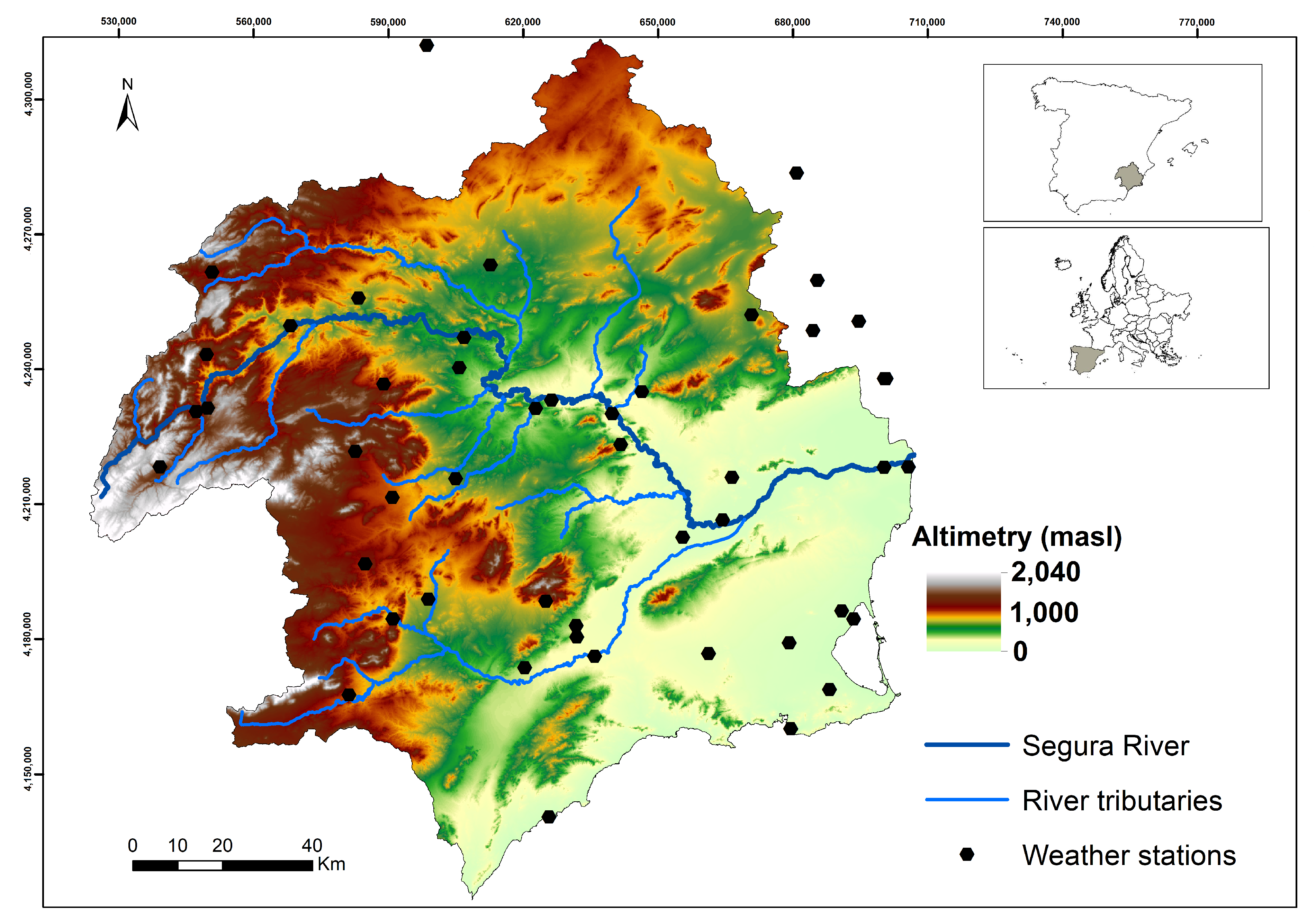
3.1. Study Area
3.2. Data Sources
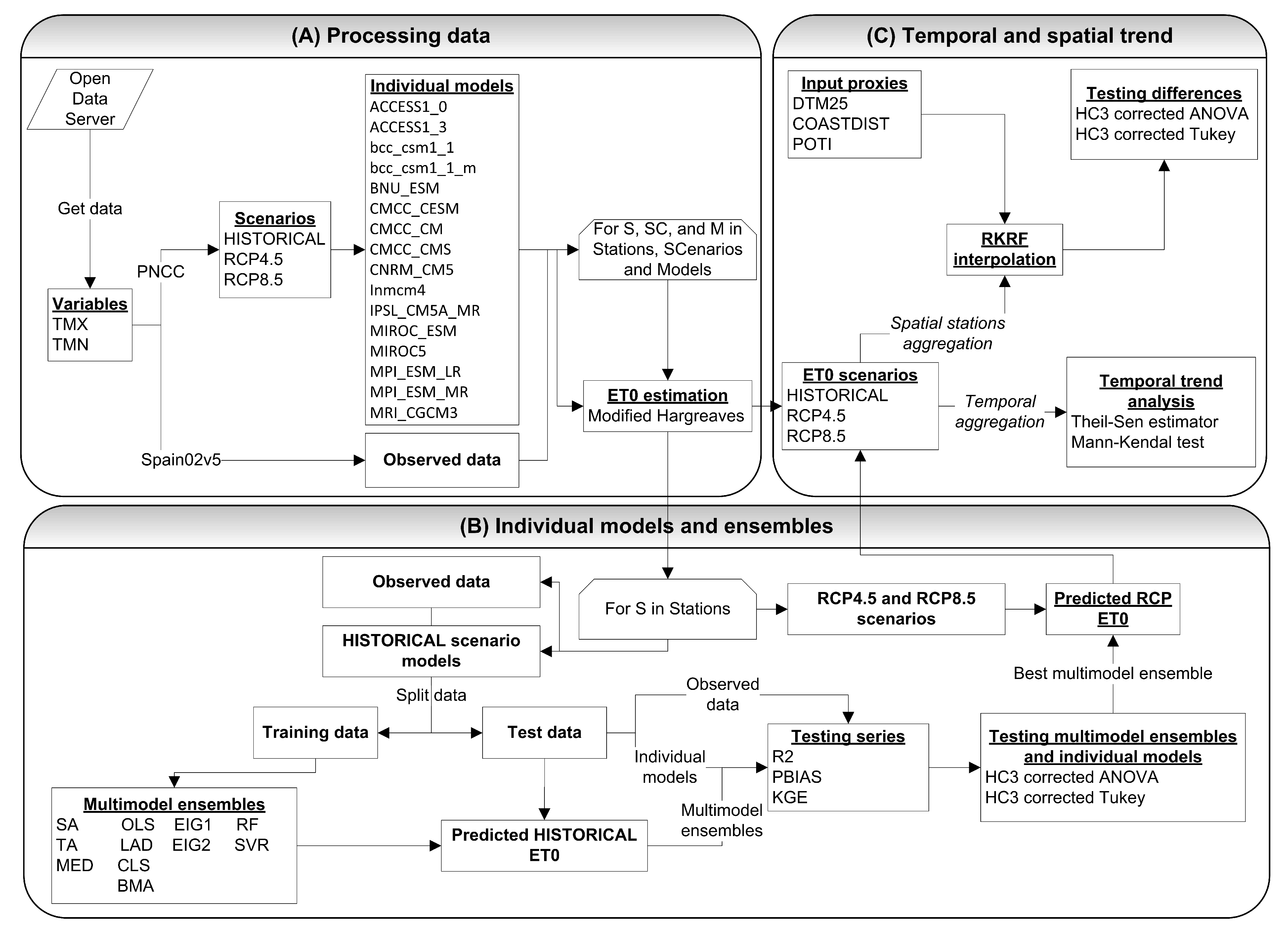
3.3. Multi-Model Ensemble
3.4. Evaluation and Comparison of Individual Regional Models and Multi-Model Ensembles
- ANOVA 1. Its objective is to evaluate performance between the different series and forecast methods (Series factor). This variable factor consists of classes (16 regionalized models, 3 simple ensembles, 2 geometric-based ensembles, 4 regression-based ensembles, and 2 machine learning ensembles) and stations observations.
- ANOVA 2. In addition, to better interpret the results, a second analysis was designed, with the same data but grouping the series according to their type (regionalized models, simple ensembles, regression-based ensembles, geometric ensembles, and machine learning ensembles).
3.5. Temporal and Spatial Patterns of ET
3.6. Summarized Workflow
4. Results and Discussion
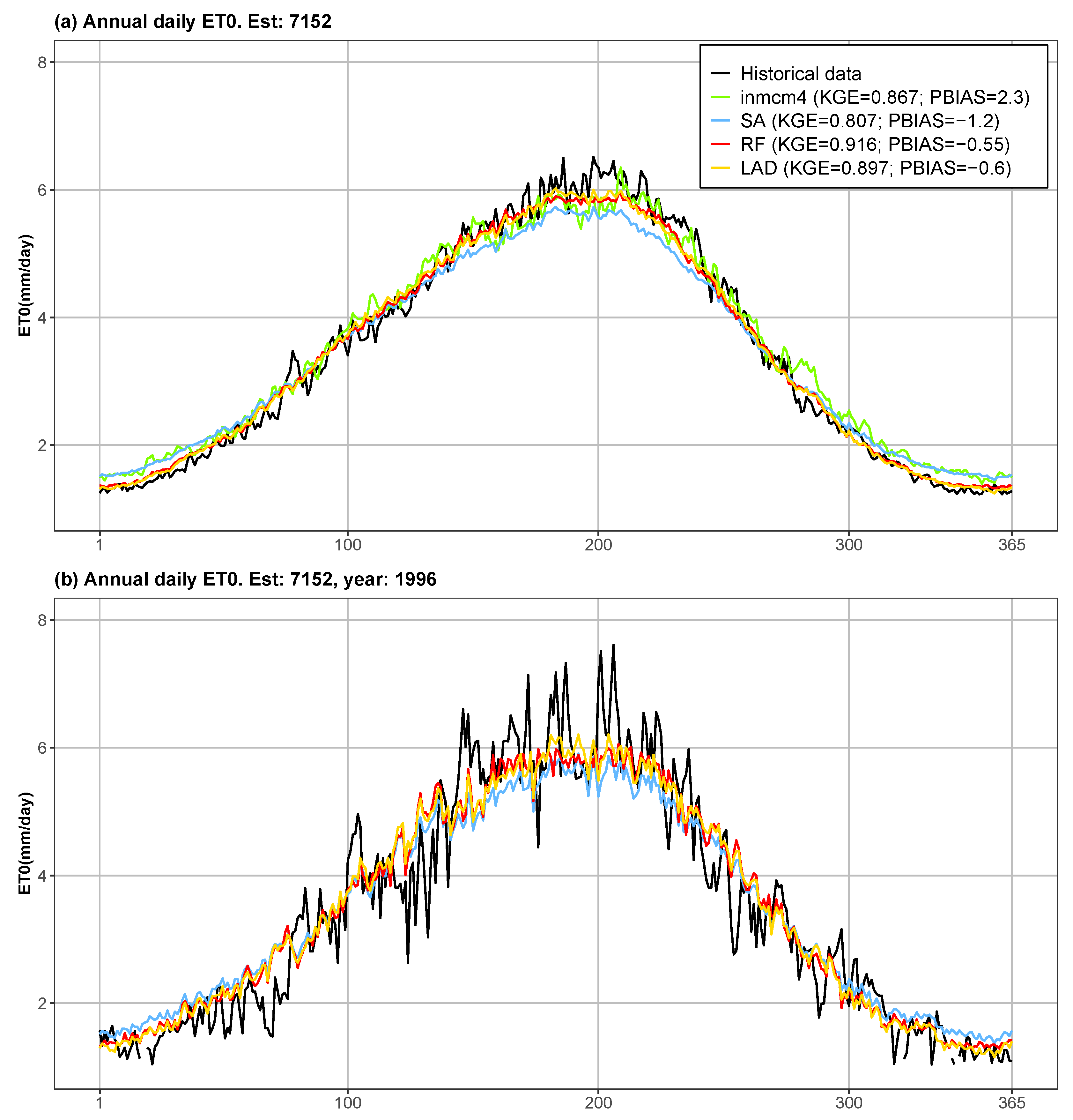
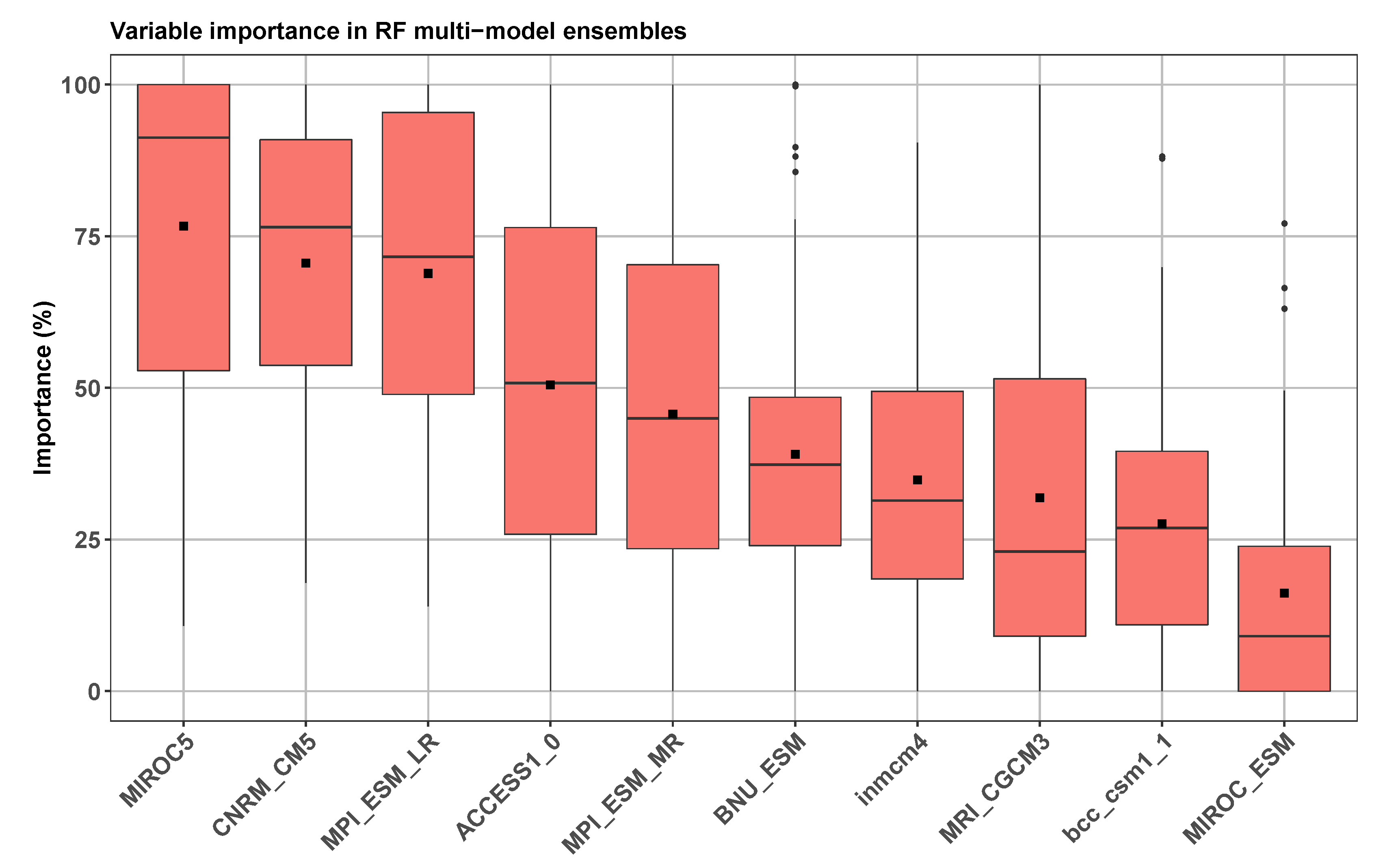
4.1. Performance of Individual Models and Multi-Model Ensembles
4.2. Temporal and Spatial Trend of Climate Change Scenarios
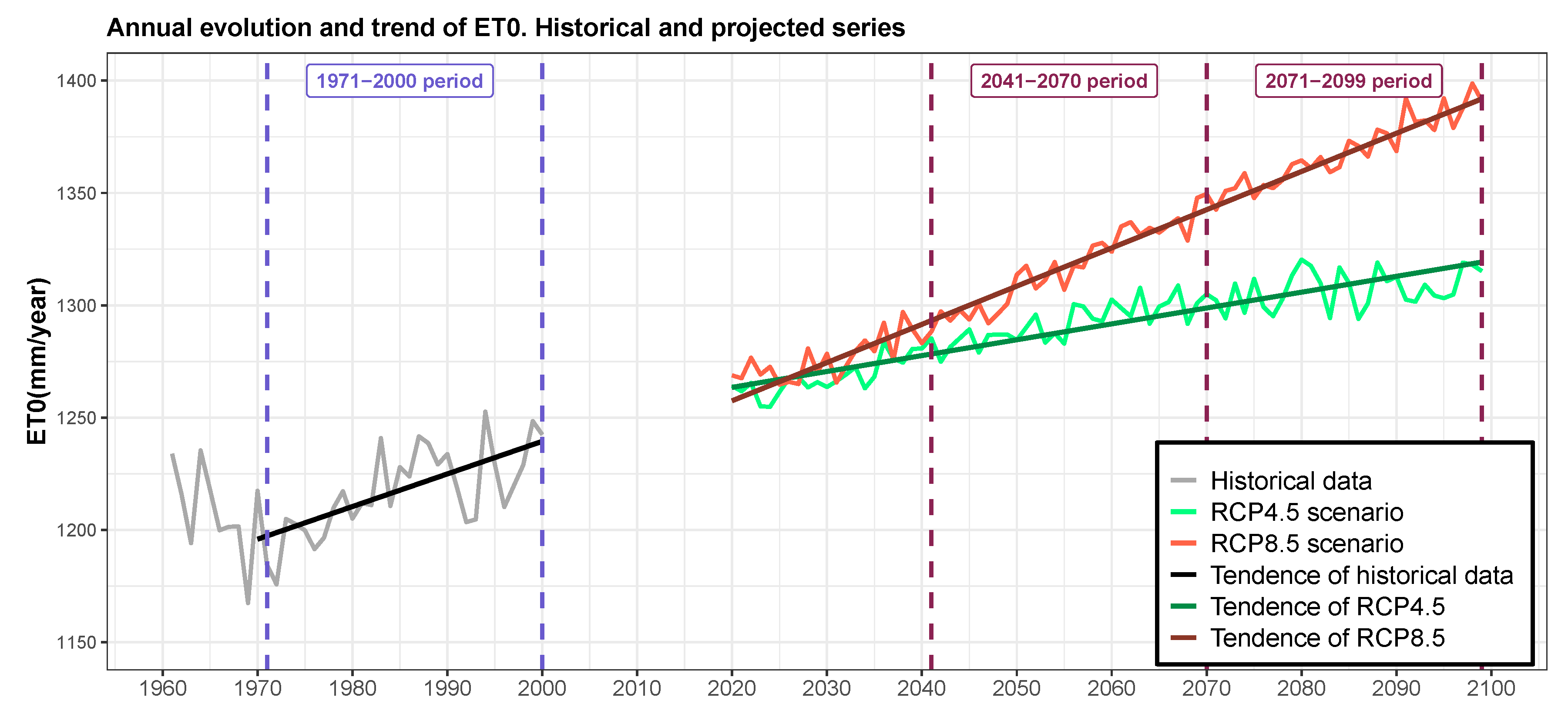
4.2.1. Temporal Trend of Anual ET
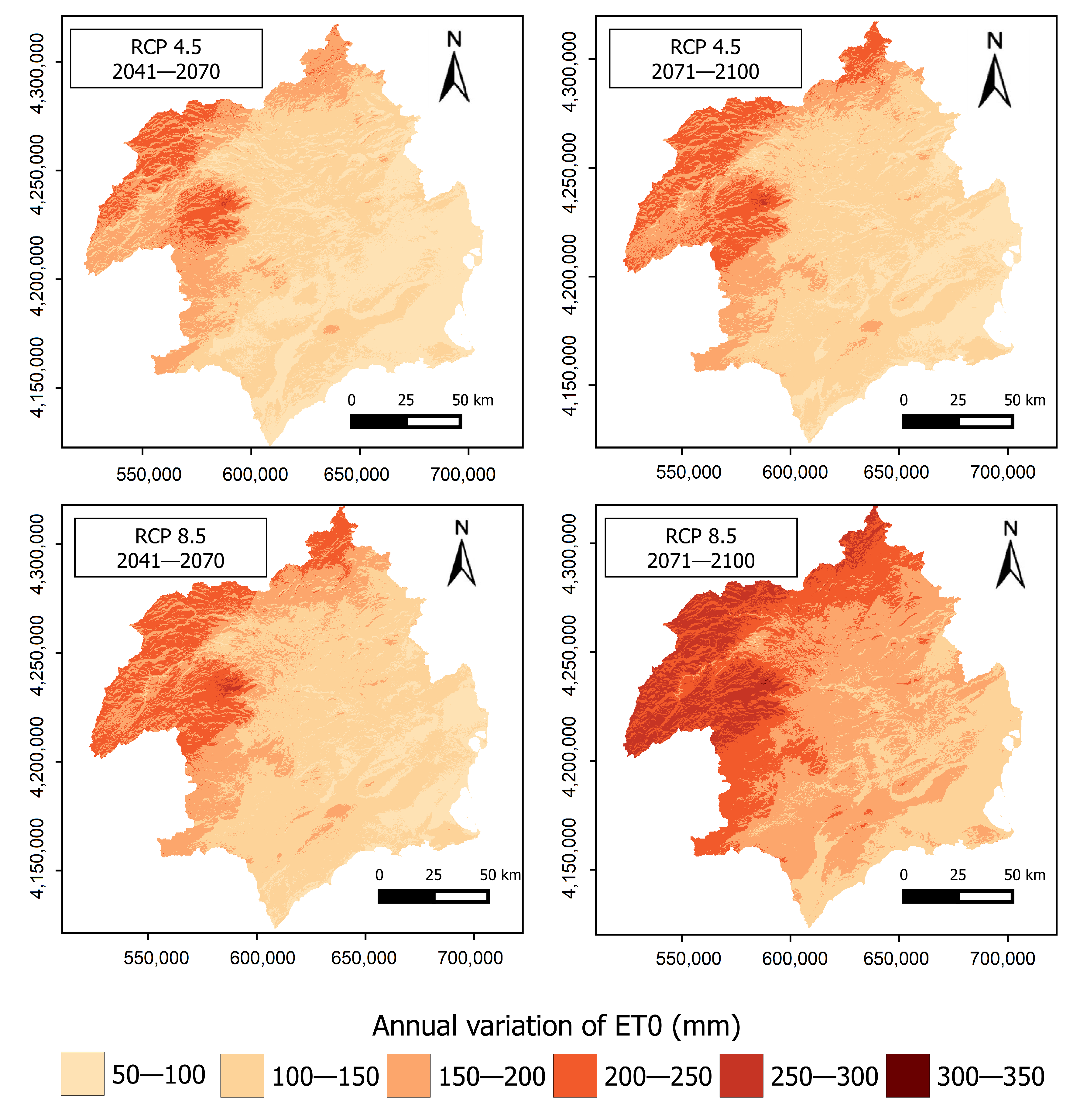
4.2.2. Spatial Distribution of Annual Variation in ET
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Type of Serie | Series Class | R | sd | se | PBIAS (abs.) | sd | se | KGE | sd | se |
|---|---|---|---|---|---|---|---|---|---|---|
| Regionalized individual model | ACCESS1_0 | 0.779 | 0.041 | 0.006 | 6.22 | 5.23 | 0.76 | 0.803 | 0.078 | 0.011 |
| ACCESS1_3 | 0.795 | 0.043 | 0.006 | 4.83 | 5.10 | 0.74 | 0.802 | 0.076 | 0.011 | |
| bcc_csm1_1 | 0.757 | 0.046 | 0.007 | 6.79 | 5.24 | 0.76 | 0.784 | 0.075 | 0.011 | |
| bcc_csm1_1_m | 0.785 | 0.044 | 0.006 | 5.56 | 5.24 | 0.76 | 0.839 | 0.067 | 0.010 | |
| BNU_ESM | 0.774 | 0.051 | 0.007 | 5.05 | 5.16 | 0.74 | 0.827 | 0.071 | 0.010 | |
| CMCC_CESM | 0.762 | 0.049 | 0.007 | 6.05 | 5.47 | 0.79 | 0.816 | 0.073 | 0.010 | |
| CMCC_CM | 0.779 | 0.039 | 0.006 | 7.13 | 5.28 | 0.76 | 0.813 | 0.070 | 0.010 | |
| CMCC_CMS | 0.762 | 0.042 | 0.006 | 6.28 | 5.32 | 0.77 | 0.816 | 0.072 | 0.010 | |
| CNRM_CM5 | 0.775 | 0.046 | 0.007 | 7.99 | 5.53 | 0.80 | 0.784 | 0.078 | 0.011 | |
| inmcm4 | 0.783 | 0.042 | 0.006 | 5.08 | 5.17 | 0.75 | 0.833 | 0.070 | 0.010 | |
| IPSL_CM5A_MR | 0.784 | 0.043 | 0.006 | 6.89 | 5.53 | 0.80 | 0.791 | 0.074 | 0.011 | |
| MIROC_ESM | 0.762 | 0.051 | 0.007 | 6.58 | 5.51 | 0.80 | 0.786 | 0.082 | 0.012 | |
| MIROC5 | 0.788 | 0.042 | 0.006 | 8.81 | 5.40 | 0.78 | 0.789 | 0.077 | 0.011 | |
| MPI_ESM_LR | 0.769 | 0.046 | 0.007 | 7.45 | 5.54 | 0.80 | 0.799 | 0.076 | 0.011 | |
| MPI_ESM_MR | 0.763 | 0.048 | 0.007 | 7.59 | 5.47 | 0.79 | 0.794 | 0.075 | 0.011 | |
| MRI_CGCM3 | 0.733 | 0.047 | 0.007 | 9.74 | 5.71 | 0.82 | 0.731 | 0.079 | 0.011 | |
| Geometric based ensemble | EIG1 | 0.871 | 0.027 | 0.004 | 6.88 | 5.36 | 0.77 | 0.784 | 0.084 | 0.012 |
| EIG2 | 0.871 | 0.027 | 0.004 | 0.00 | 0.00 | 0.00 | 0.798 | 0.073 | 0.010 | |
| Machine learning based ensemble | RF | 0.974 | 0.005 | 0.001 | 1.12 | 0.41 | 0.06 | 0.957 | 0.010 | 0.001 |
| SVR | 0.904 | 0.022 | 0.003 | 0.38 | 0.24 | 0.03 | 0.926 | 0.019 | 0.003 | |
| Regression based ensemble | BMA | 0.872 | 0.027 | 0.004 | 0.00 | 0.00 | 0.00 | 0.906 | 0.020 | 0.003 |
| CLS | 0.864 | 0.031 | 0.004 | 5.00 | 4.66 | 0.67 | 0.815 | 0.072 | 0.010 | |
| LAD | 0.872 | 0.027 | 0.004 | 0.61 | 0.49 | 0.07 | 0.906 | 0.023 | 0.003 | |
| OLS | 0.872 | 0.027 | 0.004 | 0.00 | 0.00 | 0.00 | 0.907 | 0.020 | 0.003 | |
| Simple ensemble | MED | 0.867 | 0.027 | 0.004 | 6.51 | 5.22 | 0.75 | 0.789 | 0.082 | 0.012 |
| SA | 0.871 | 0.027 | 0.004 | 6.71 | 5.34 | 0.77 | 0.787 | 0.083 | 0.012 | |
| TA | 0.871 | 0.027 | 0.004 | 6.53 | 5.22 | 0.75 | 0.788 | 0.082 | 0.012 |
| Type of Serie | Series Class | R | sd | se | PBIAS (abs.) | sd | se | KGE | sd | se |
|---|---|---|---|---|---|---|---|---|---|---|
| Regionalized model | ACCESS1_0 | 0.794 | 0.043 | 0.006 | 7.61 | 5.58 | 0.81 | 0.785 | 0.079 | 0.011 |
| ACCESS1_3 | 0.803 | 0.046 | 0.007 | 6.34 | 5.06 | 0.73 | 0.798 | 0.075 | 0.011 | |
| bcc_csm1_1 | 0.768 | 0.050 | 0.007 | 6.45 | 5.27 | 0.76 | 0.802 | 0.071 | 0.010 | |
| bcc_csm1_1_m | 0.779 | 0.051 | 0.007 | 5.78 | 5.29 | 0.76 | 0.822 | 0.066 | 0.010 | |
| BNU_ESM | 0.779 | 0.059 | 0.009 | 5.93 | 5.36 | 0.77 | 0.819 | 0.072 | 0.010 | |
| CMCC_CESM | 0.764 | 0.053 | 0.008 | 7.36 | 5.11 | 0.74 | 0.800 | 0.068 | 0.010 | |
| CMCC_CM | 0.717 | 0.044 | 0.006 | 9.51 | 5.99 | 0.86 | 0.786 | 0.063 | 0.009 | |
| CMCC_CMS | 0.755 | 0.049 | 0.007 | 7.36 | 5.38 | 0.78 | 0.794 | 0.069 | 0.010 | |
| CNRM_CM5 | 0.783 | 0.049 | 0.007 | 8.38 | 5.79 | 0.84 | 0.770 | 0.077 | 0.011 | |
| inmcm4 | 0.788 | 0.046 | 0.007 | 5.85 | 5.14 | 0.74 | 0.826 | 0.068 | 0.010 | |
| IPSL_CM5A_MR | 0.796 | 0.049 | 0.007 | 7.45 | 5.34 | 0.77 | 0.791 | 0.071 | 0.010 | |
| MIROC_ESM | 0.754 | 0.053 | 0.008 | 7.30 | 5.56 | 0.80 | 0.777 | 0.075 | 0.011 | |
| MIROC5 | 0.799 | 0.046 | 0.007 | 9.34 | 6.06 | 0.87 | 0.786 | 0.077 | 0.011 | |
| MPI_ESM_LR | 0.775 | 0.050 | 0.007 | 8.20 | 5.60 | 0.81 | 0.785 | 0.072 | 0.010 | |
| MPI_ESM_MR | 0.762 | 0.051 | 0.007 | 8.59 | 5.70 | 0.82 | 0.778 | 0.070 | 0.010 | |
| MRI_CGCM3 | 0.736 | 0.048 | 0.007 | 11.07 | 6.40 | 0.92 | 0.716 | 0.083 | 0.012 | |
| Geometric based ensemble | EIG1 | 0.877 | 0.033 | 0.005 | 7.70 | 5.56 | 0.80 | 0.775 | 0.082 | 0.012 |
| EIG2 | 0.877 | 0.033 | 0.005 | 3.30 | 2.92 | 0.42 | 0.787 | 0.069 | 0.010 | |
| Machine learning based ensemble | RF | 0.881 | 0.032 | 0.005 | 3.09 | 3.00 | 0.43 | 0.915 | 0.031 | 0.004 |
| SVR | 0.875 | 0.033 | 0.005 | 3.25 | 2.97 | 0.43 | 0.891 | 0.032 | 0.005 | |
| Regression based ensemble | BMA | 0.878 | 0.033 | 0.005 | 3.28 | 2.93 | 0.42 | 0.890 | 0.033 | 0.005 |
| CLS | 0.870 | 0.035 | 0.005 | 6.18 | 5.01 | 0.72 | 0.803 | 0.071 | 0.010 | |
| LAD | 0.878 | 0.033 | 0.005 | 3.20 | 2.98 | 0.43 | 0.891 | 0.035 | 0.005 | |
| OLS | 0.878 | 0.033 | 0.005 | 3.28 | 2.92 | 0.42 | 0.890 | 0.033 | 0.005 | |
| Simple ensemble | MED | 0.873 | 0.033 | 0.005 | 7.41 | 5.48 | 0.79 | 0.779 | 0.080 | 0.012 |
| SA | 0.877 | 0.033 | 0.005 | 7.56 | 5.52 | 0.80 | 0.777 | 0.082 | 0.012 | |
| TA | 0.877 | 0.033 | 0.005 | 7.41 | 5.46 | 0.79 | 0.778 | 0.080 | 0.012 |
| Regionalized Individual Model | Importance (%) | sd | se |
|---|---|---|---|
| MIROC5 | 76.67 | 29.21 | 4.22 |
| CNRM_CM5 | 70.57 | 24.83 | 3.58 |
| MPI_ESM_LR | 68.86 | 27.28 | 3.94 |
| ACCESS1_0 | 50.47 | 30.41 | 4.39 |
| MPI_ESM_MR | 45.69 | 30.57 | 4.41 |
| BNU_ESM | 39.04 | 26.95 | 3.89 |
| inmcm4 | 34.81 | 23.74 | 3.43 |
| MRI_CGCM3 | 31.91 | 27.98 | 4.04 |
| bcc_csm1_1 | 27.63 | 22.56 | 3.26 |
| MIROC_ESM | 16.16 | 20.33 | 2.94 |
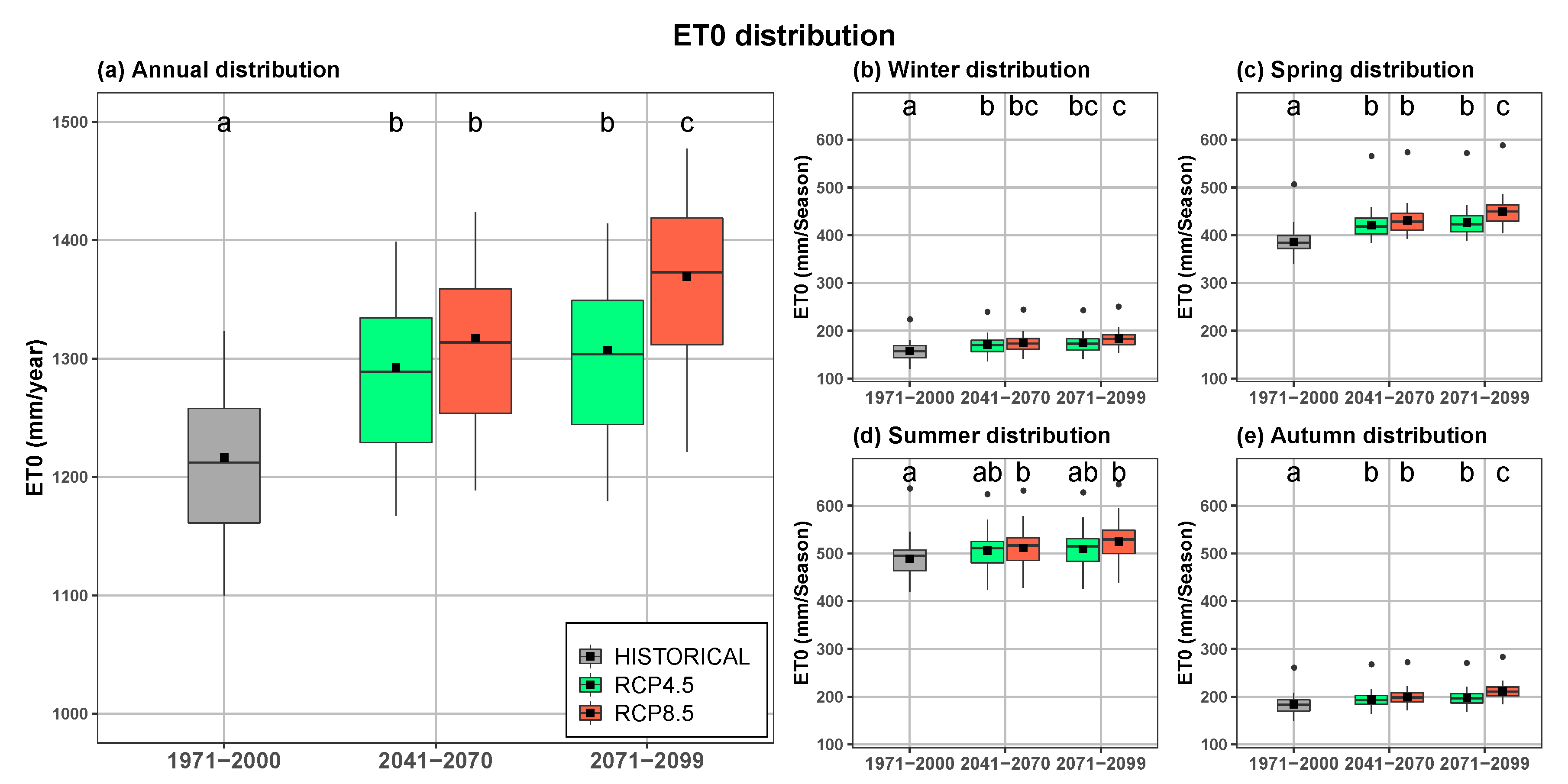
| Period | Scenario | ET0 (mm) | sd | se | |
|---|---|---|---|---|---|
| Annual | 1971–2000 | HISTORICAL | 1216.32 | 85.44 | 12.33 |
| 2041–2070 | RCP4.5 | 1292.36 | 85.08 | 12.28 | |
| 2041–2070 | RCP8.5 | 1317.32 | 86.10 | 12.43 | |
| 2071–2099 | RCP4.5 | 1307.21 | 85.76 | 12.38 | |
| 2071–2099 | RCP8.5 | 1369.13 | 88.57 | 12.78 | |
| Autumn | 1971–2000 | HISTORICAL | 184.24 | 18.76 | 2.71 |
| 2041–2070 | RCP4.5 | 194.20 | 16.99 | 2.45 | |
| 2041–2070 | RCP8.5 | 199.71 | 16.78 | 2.42 | |
| 2071–2099 | RCP4.5 | 197.49 | 16.98 | 2.45 | |
| 2071–2099 | RCP8.5 | 211.13 | 16.52 | 2.39 | |
| Spring | 1971–2000 | HISTORICAL | 385.87 | 27.26 | 3.93 |
| 2041–2070 | RCP4.5 | 421.51 | 29.21 | 4.22 | |
| 2041–2070 | RCP8.5 | 430.92 | 29.20 | 4.21 | |
| 2071–2099 | RCP4.5 | 426.63 | 29.37 | 4.24 | |
| 2071–2099 | RCP8.5 | 449.52 | 29.54 | 4.26 | |
| Summer | 1971–2000 | HISTORICAL | 488.43 | 35.83 | 5.17 |
| 2041–2070 | RCP4.5 | 505.66 | 37.46 | 5.41 | |
| 2041–2070 | RCP8.5 | 511.65 | 38.50 | 5.56 | |
| 2071–2099 | RCP4.5 | 509.03 | 37.95 | 5.48 | |
| 2071–2099 | RCP8.5 | 524.97 | 40.42 | 5.83 | |
| Winter | 1971–2000 | HISTORICAL | 157.79 | 18.34 | 2.65 |
| 2041–2070 | RCP4.5 | 170.99 | 18.36 | 2.65 | |
| 2041–2070 | RCP8.5 | 175.04 | 18.17 | 2.62 | |
| 2071–2099 | RCP4.5 | 174.07 | 18.19 | 2.63 | |
| 2071–2099 | RCP8.5 | 183.51 | 17.30 | 2.50 |
References
- IPCC. Climate Change 2013-The Physical Science Basis: Summary for Policymakers; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2013. [Google Scholar]
- World Climate Research Programme. CORDEX: Coordinated Regional Climate Downscaling Experiment; World Climate Research Programme’s Working Group: Norrköping, Sweden, 2020. [Google Scholar]
- Van der Linden, P.; Mitchell, J. ENSEMBLES: Climate Change and Its Impacts: Summary of Research and Results from the ENSEMBLES Project; Technical Report; Met Office Hadley Centre: Exeter, UK, 2009. [Google Scholar]
- Gutiérrez, J.; Brands, S.; Herrera, S.; Gaitán, E.; San-Martín, D.; Sordo, C.; Tuni, M.; Manzanas, R. Proyecto esTcena: Programa Coordinado Para la Generación de Escenarios Regionalizados de Cambio Climático: Regionalización Estadística; Cantabria University, Spanish National Research Council and Spanish Meteorological Agency: Santander, Spain, 2013. [Google Scholar]
- Amblar Francés, P.; Casado Calle, M.; Pastor Saavedra, A.; Ramos Calzado, P.; Rodríguez Camino, E. Guía de Escenarios Regionalizados de Cambio Climático Sobre España a Partir de los Resultados del IPCC-AR5; AEMET: Madrid, Spain, 2017; p. 102. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2016; p. 1535. [Google Scholar]
- AEMET. Proyecciones Climáticas Para el Siglo XXI. Plan Nacional de Adaptación al Cambio Climático (PNACC); AEMET: Madrid, Spain, 2020. [Google Scholar]
- Mitchell, T.D.; Hulme, M. Predicting regional climate change: Living with uncertainty. Prog. Phys. Geogr. Earth Environ. 1999, 23, 57–78. [Google Scholar] [CrossRef]
- Devineni, N.; Sankarasubramanian, A.; Ghosh, S. Multimodel ensembles of streamflow forecasts: Role of predictor state in developing optimal combinations. Water Resour. Res. 2008, 44, W09404. [Google Scholar] [CrossRef] [PubMed]
- Hagedorn, R.; Doblas-Reyes, F.J.; Palmer, T. The rationale behind the success of multi-model ensembles in seasonal forecasting — I. Basic concept. Tellus A Dyn. Meteorol. Oceanogr. 2005, 57, 219–233. [Google Scholar] [CrossRef]
- Oviedo Torres, B.E.; León Aristizábal, G. Guía de Procedimiento Para la Generación de Escenarios de Cambio Climático Regional y Local a Partir de los Modelos Globales; Instituto de Hidrología, Meteorología y Estudios Ambientales: Bogotá, Colombia, 2010; p. 89. [Google Scholar]
- Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, X.; Giorgi, F. Upgrades to the reliability ensemble averaging method for producing probabilistic climate-change projections. Clim. Res. 2010, 41, 61–81. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, Z.; Li, L. Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs. J. Clim. 2011, 24, 4741–4756. [Google Scholar] [CrossRef]
- Giménez, P.O.; Galiano, S.G.; Giraldo-Osorio, J. Identifying a robust method to build RCMs ensemble as climate forcing for hydrological impact models. Atmos. Res. 2016, 174, 31–40. [Google Scholar] [CrossRef]
- Min, S.K.; Hense, A.; Paeth, H.; Kwon, W.T. A Bayesian decision method for climate change signal analysis. Meteorol. Z. 2004, 13, 421–436. [Google Scholar] [CrossRef]
- Min, S.K.; Hense, A. A Bayesian approach to climate model evaluation and multi-model averaging with an application to global mean surface temperatures from IPCC AR4 coupled climate models. Geophys. Res. Lett. 2006, 33, 1–15. [Google Scholar] [CrossRef]
- Huntingford, C.; Jeffers, E.S.; Bonsall, M.B.; Christensen, H.M.; Lees, T.; Yang, H. Machine learning and artificial intelligence to aid climate change research and preparedness. Environ. Res. Lett. 2019, 14, 124007. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zheng, L.; Liu, D.L.; Ji, F.; Clark, A.; Yu, Q. Using multi-model ensembles of CMIP5 global climate models to reproduce observed monthly rainfall and temperature with machine learning methods in Australia. Int. J. Climatol. 2018, 38, 4891–4902. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.; Shahid, S.; Iqbal, Z.; Nawaz, N.; Khan, N. Multi-model ensemble predictions of precipitation and temperature using machine learning algorithms. Atmos. Res. 2020, 236, 104806. [Google Scholar] [CrossRef]
- Kumar, A.; Mitra, A.; Bohra, A.; Iyengar, G.; Durai, V. Multi-model ensemble (MME) prediction of rainfall using neural networks during monsoon season in India. Meteorol. Appl. 2012, 19, 161–169. [Google Scholar] [CrossRef]
- Acharya, N.; Shrivastava, N.A.; Panigrahi, B.; Mohanty, U. Development of an artificial neural network based multi-model ensemble to estimate the northeast monsoon rainfall over south peninsular India: An application of extreme learning machine. Clim. Dyn. 2014, 43, 1303–1310. [Google Scholar] [CrossRef]
- CHS. Plan Hidrológico de la Demarcación Hidrográfica del Segura 2015/21; Ministerio de Agricultura, Alimentación y Medio Ambiente; Confederación Hidrográfica del Segura: Murcia, Spain, 2015. [Google Scholar]
- Giménez, P.; García-Galiano, S. Assessing regional climate models (RCMs) ensemble-driven reference evapotranspiration over Spain. Water 2018, 10, 1181. [Google Scholar] [CrossRef]
- Gomariz-Castillo, F.; Alonso-Sarría, F.; Cabezas-Calvo-Rubio, F. Calibration and spatial modelling of daily ET0 in semiarid areas using Hargreaves equation. Earth Sci. Inform. 2018, 11, 325–340. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Number 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.L.; Liu, W.Z. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its projected changes during 2011–2099 on the Loess Plateau of China. Agric. For. Meteorol. 2012, 154, 147–155. [Google Scholar] [CrossRef]
- Tao, X.E.; Chen, H.; Xu, C.Y.; Hou, Y.K.; Jie, M.X. Analysis and prediction of reference evapotranspiration with climate change in Xiangjiang River Basin, China. Water Sci. Eng. 2015, 8, 273–281. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Izquierdo-Miñano, C.; Gomariz-Castillo, F.; Jiménez-Guerrero, P. Regionalización de la temperatura, precipitación y humedad diaria en la Cuenca del Segura a partir de variables ambientales y Random Forest. In Miradas Confluyentes: Aportaciones de los Jóvenes Investigadores; Lozano-Reina, G., Planes-Muñoz, D., Ponce, A.I., Madrid-Valero, J.J., Eds.; Servicio de Publicaciones de la Universidad de Murcia: Murcia, Spain, 2020; Chapter 5; pp. 96–127. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Di Stefano, C.; Ferro, V. Estimation of evapotranspiration by Hargreaves formula and remotely sensed data in semi-arid Mediterranean areas. J. Agric. Eng. Res. 1997, 68, 189–199. [Google Scholar] [CrossRef]
- López-Urrea, R.; de Santa Olalla, F.M.; Fabeiro, C.; Moratalla, A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.C.; Allen, R.G. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Gomariz-Castillo, F. Estimación de Variables y Parámetros Hidrológicos y Análisis de su Influencia Sobre la Modelización Hidrológica: Aplicación a los Modelos de Témez y Swat. Ph.D. Thesis, Universidad de Murcia, Murcia, Spain, 2016. [Google Scholar]
- Hargreaves, G. Simplified Coefficients for Estimating Monthly Solar Radiation in North America and Europe; Departmental Paper; Utah State University: Logan, UT, USA, 1994. [Google Scholar]
- Allen, R. Evaluation of Procedures for Estimating Mean Monthly Solar Radiation from Air Temperature; Report Prepared for FAO, Water Resources Development and Management Service; FAO: Rome, Italy, 1995; p. 120. [Google Scholar]
- Samani, Z.A. Estimating Solar Radiation and Evapotranspiration Using Minimum Climatological Data. J. Irrig. Drain. Eng. 2000, 126, 265–267. [Google Scholar] [CrossRef]
- Terink, W.; Immerzeel, W.W.; Droogers, P. Climate change projections of precipitation and reference evapotranspiration for the Middle East and Northern Africa until 2050. Int. J. Climatol. 2013, 33, 3055–3072. [Google Scholar] [CrossRef]
- Wang, W.; Xing, W.; Shao, Q.; Yu, Z.; Peng, S.; Yang, T.; Yong, B.; Taylor, J.; Singh, V.P. Changes in reference evapotranspiration across the Tibetan Plateau: Observations and future projections based on statistical downscaling. J. Geophys. Res. Atmos. 2013, 118, 4049–4068. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Peng, S.; Yu, Z.; Yong, B.; Taylor, J. Changes of reference evapotranspiration in the Haihe River Basin: Present observations and future projection from climatic variables through multi-model ensemble. Glob. Planet. Chang. 2014, 115, 1–15. [Google Scholar] [CrossRef]
- CEDEX. Evaluación del Impacto del Cambio Climático en los Recursos Hídricos y Sequías en España; Centro de Estudios y Experimentación de Obras Públicas, Ministerio de Fomento y Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente: Madrid, Spain, 2017. [Google Scholar]
- Kidron, G.J.; Zohar, M. Spatial evaporation patterns within a small drainage basin in the Negev Desert. J. Hydrol. 2010, 380, 376–385. [Google Scholar] [CrossRef]
- Mardikis, M.; Kalivas, D.; Kollias, V. Comparison of interpolation methods for the prediction of reference evapotranspiration—An application in Greece. Water Resour. Manag. 2005, 19, 251–278. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Lanjeri, S.; López-Moreno, J.I. Comparison of different procedures to map reference evapotranspiration using geographical information systems and regression-based techniques. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 1103–1118. [Google Scholar] [CrossRef]
- Conesa García, C. Las Formas del Relieve; Editum: Murcia, Spain, 2006; pp. 47–94. [Google Scholar]
- Colino Sueiras, J.; Martínez-Carrasco Pleite, F.; Martínez Paz, J. El Impacto de la PAC Renovada Sobre el Sector Agrario de la Región de Murcia; Consejo Económico y Social de la Región de Murcia: Murcia, Spain, 2014. [Google Scholar]
- Calvo García-Tornel, F. Sureste español: Regadío, tecnologías hidráulicas y cambios territoriales. Scr. Nova Rev. Electrónica Geogr. Y Cienc. Soc. 2006, 10, 1–35. [Google Scholar]
- Morales Gil, A.; Rico Amorós, A.; Hernández Hernández, M. El trasvase Tajo-Segura. Obs. Medioambient. 2005, 8, 73–110. [Google Scholar]
- García Aróstegui, J.; Senent Alonso, M.; Martínez Vicente, D.; Aragón Rueda, R. La Sobreexplotación de Acuíferos; Instituto Euromediterráneo del Agua: Murcia, Spain, 2014; pp. 63–132. [Google Scholar]
- López Bermudez, F.; Quiñonero Rubio, J.; García Marín, R.; Martín de Balmaseda, E.; Sánchez Fuster, M.; Chocano Vañó, C.; Guerrero García, F. Fuentes y manantiales de la Cuenca del Segura; Instituto Euromediterráneo del Agua y Confederación Hidrogárfica del Segura: Murcia, Spain, 2014. [Google Scholar]
- Pellicer-Martínez, F.; Martínez-Paz, J.M. Climate change effects on the hydrology of the headwaters of the Tagus River: Implications for the management of the Tagus–Segura transfer. Hydrol. Earth Syst. Sci. 2018, 22, 6473–6491. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Bi, D.; Dix, M.; Marsland, S.; O’Farrell, S.; Rashid, H.; Uotila, P.; Hirst, A.; Kowalczyk, E.; Golebiewski, M.; Sullivan, A.; et al. The ACCESS coupled model: Description, control climate and evaluation. Aust. Meteorol. Oceanogr. J. 2013, 63, 41–64. [Google Scholar] [CrossRef]
- Wu, T.; Li, W.; Ji, J.; Xin, X.; Li, L.; Wang, Z.; Zhang, Y.; Li, J.; Zhang, F.; Wei, M.; et al. Global carbon budgets simulated by the Beijing Climate Center Climate System Model for the last century. J. Geophys. Res. Atmos. 2013, 118, 4326–4347. [Google Scholar] [CrossRef]
- Ji, D.; Wang, L.; Feng, J.; Wu, Q.; Cheng, H.; Zhang, Q.; Yang, J.; Dong, W.; Dai, Y.; Gong, D.; et al. Description and basic evaluation of Beijing Normal University Earth System Model (BNU-ESM) version 1. Geosci. Model Dev. 2014, 7, 2039–2064. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Holland, M.M.; Gent, P.R.; Ghan, S.; Kay, J.E.; Kushner, P.J.; Lamarque, J.F.; Large, W.G.; Lawrence, D.; Lindsay, K.; et al. The Community Earth System Model: A Framework for Collaborative Research. Bull. Am. Meteorol. Soc. 2013, 94, 1339–1360. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Sanna, A.; Giuseppe Fogli, P.; Manzini, E.; Vichi, M.; Oddo, P.; Navarra, A. Effects of Tropical Cyclones on Ocean Heat Transport in a High-Resolution Coupled General Circulation Model. J. Clim. 2011, 24, 4368–4384. [Google Scholar] [CrossRef]
- Weare, B.C.; Cagnazzo, C.; Fogli, P.G.; Manzini, E.; Navarra, A. Madden-Julian Oscillation in a climate model with a well-resolved stratosphere. J. Geophys. Res. Atmos. 2012, 117, 1–11. [Google Scholar] [CrossRef]
- Voldoire, A.; Sanchez-Gomez, E.; Salas y Mélia, D.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef]
- Volodin, E.M.; Dianskii, N.A.; Gusev, A.V. Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izv. Atmos. Ocean. Phys. 2010, 46, 414–431. [Google Scholar] [CrossRef]
- Dufresne, J.L.; Foujols, M.A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef]
- Watanabe, S.; Hajima, T.; Sudo, K.; Nagashima, T.; Takemura, T.; Okajima, H.; Nozawa, T.; Kawase, H.; Abe, M.; Yokohata, T.; et al. MIROC-ESM 2010: Model description and basic results of CMIP5-20c3m experiments. Geosci. Model Dev. 2011, 4, 845–872. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Jungclaus, J.; Reick, C.H.; Legutke, S.; Bader, J.; Böttinger, M.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K.; et al. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J. Adv. Model. Earth Syst. 2013, 5, 572–597. [Google Scholar] [CrossRef]
- Yukimoto, S.; Adachi, Y.; Hosaka, M.; Sakami, T.; Yoshimura, H.; Hirabara, M.; Tanaka, T.Y.; Shindo, E.; Tsujino, H.; Deushi, M.; et al. A New Global Climate Model of the Meteorological Research Institute: MRI-CGCM3—Model Description and Basic Performance—. J. Meteorol. Soc. Jpn. 2012, 90A, 23–64. [Google Scholar] [CrossRef]
- Herrera, S.; Cardoso, R.M.; Soares, P.M.; Espírito-Santo, F.; Viterbo, P.; Gutiérrez, J.M. Iberia01: A new gridded dataset of daily precipitation and temperatures over Iberia. Earth Syst. Sci. Data 2019, 11, 1947–1956. [Google Scholar] [CrossRef]
- Weiss, C.E.; Roetzer, G.R. GeomComb: (Geometric) Forecast Combination Methods. R Package Version 1.0. 2016. Available online: https://CRAN.R-project.org/package=GeomComb.
- Zeugner, S.; Feldkircher, M. Bayesian Model Averaging Employing Fixed and Flexible Priors: The BMS Package for R. J. Stat. Softw. 2015, 68. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab-An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Timmermann, A. Chapter 4 Forecast Combinations. In Handbook of Economic Forecasting; Elsevier: Amsterdam, The Netherlands, 2006; Volume 1, pp. 135–196. [Google Scholar] [CrossRef]
- Armstrong, J.S. Combining Forecasts. In Principles of Forecasting: A Handbook for Researchers and Practitioners; Armstrong, J.S., Ed.; Springer: Boston, MA, USA, 2001; pp. 417–439. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Ramanathan, R. Improved methods of combining forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Elliott, G.; Timmermann, A. Optimal forecast combinations under general loss functions and forecast error distributions. J. Econom. 2004, 122, 47–79. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Graefe, A.; Küchenhoff, H.; Stierle, V.; Riedl, B. Limitations of Ensemble Bayesian Model Averaging for forecasting social science problems. Int. J. Forecast. 2015, 31, 943–951. [Google Scholar] [CrossRef]
- Hinne, M.; Gronau, Q.F.; van den Bergh, D.; Wagenmakers, E.J. A Conceptual Introduction to Bayesian Model Averaging. Adv. Methods Pract. Psychol. Sci. 2020, 3, 200–215. [Google Scholar] [CrossRef]
- Hsiao, C.; Wan, S.K. Is there an optimal forecast combination? J. Econom. 2014, 178, 294–309. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; p. 745. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Caputo, B.; Sim, K.; Furesjo, F.; Smola, A. Appearance–Based Object Recognition Using SVMs: Which Kernel Should I Use? In Proceedings of the NIPS Workshop on Statistical Methods for Computational Experiments in Visual Processing and Computer Vision, Whistler, BC, Canada, 12–14 December 2002; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Levene, H. Robust tests for equality of variances. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Olkin, I., Hotelling, H., Eds.; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Long, J.S.; Ervin, L.H. Using Heteroscedasticity Consistent Standard Errors in the Linear Regression Model. Am. Stat. 2000, 54, 217–224. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Cannarozzo, M.; Noto, L.; Viola, F. Spatial distribution of rainfall trends in Sicily (1921–2000). Phys. Chem. Earth Parts A/B/C 2006, 31, 1201–1211. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- IGN. Modelo Digital del Terreno con Paso de Malla de 25 m; Centro Nacional de Información Geográfica: Madrid, Spain, 2015. [Google Scholar]
- Hofierka, J.; Suri, M. The solar radiation model for Open source GIS: Implementation and applications. In Proceedings of the Open Source GIS-GRASS Users Conference, Trento, Italy, 11–13 September 2002; Volume 2002, pp. 51–70. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin: Boston, MA, USA, 2005; Volume 5. [Google Scholar]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2053–2075. [Google Scholar] [CrossRef] [PubMed]
- Nowotarski, J.; Raviv, E.; Trück, S.; Weron, R. An empirical comparison of alternative schemes for combining electricity spot price forecasts. Energy Econ. 2014, 46, 395–412. [Google Scholar] [CrossRef]
- Palm, F.C.; Zellner, A. To combine or not to combine? issues of combining forecasts. J. Forecast. 1992, 11, 687–701. [Google Scholar] [CrossRef]
- Blanc, S.M.; Setzer, T. When to choose the simple average in forecast combination. J. Bus. Res. 2016, 69, 3951–3962. [Google Scholar] [CrossRef]
- Körner, S.; Holzäpfel, F.; Sölch, I. Probabilistic Multimodel Ensemble Wake-Vortex Prediction Employing Bayesian Model Averaging. J. Aircr. 2019, 56, 695–706. [Google Scholar] [CrossRef]
- Tegegne, G.; Melesse, A.M.; Worqlul, A.W. Development of multi-model ensemble approach for enhanced assessment of impacts of climate change on climate extremes. Sci. Total Environ. 2020, 704, 135357. [Google Scholar] [CrossRef]
- Tomas-Burguera, M.; Beguería, S.; Vicente-Serrano, S.M. Climatology and trends of reference evapotranspiration in Spain. Int. J. Climatol. 2020, 1–15. [Google Scholar] [CrossRef]

| Regionalized Model | HISTORICAL Scenario | RCP4.5 Scenario | RCP8.5 Scenario | Model Used for Ensemble |
|---|---|---|---|---|
| ACCESS1_0 [57] | x | x | x | x |
| ACCESS1_3 [57] | x | x | ||
| bcc_csm1_1 [58] | x | x | x | x |
| bcc_csm1_1_m [58] | x | x | ||
| BNU_ESM [59] | x | x | x | x |
| CMCC_CESM [60] | x | x | ||
| CMCC_CM [61] | x | x | ||
| CMCC_CMS [62] | x | |||
| CNRM_CM5 [63] | x | x | x | x |
| inmcm4 [64] | x | x | x | x |
| IPSL_CM5A_MR [65] | x | x | ||
| MIROC_ESM [66] | x | x | x | x |
| MIROC5 [66] | x | x | x | x |
| MPI_ESM_LR [67] | x | x | x | x |
| MPI_ESM_MR [67] | x | x | x | x |
| MRI_CGCM3 [68] | x | x | x | x |
| TOTAL | 16 | 12 | 13 | 10 |
| Scenarios | S | Z | p-Value | (mm year) | (mm year) |
|---|---|---|---|---|---|
| HISTORICAL | 223 | 3.773 | 0.0002 | 1194.467 | 1.45 |
| RCP4.5 | 2370 | 9.842 | >0.0001 | 1262.78 | 0.71 |
| RCP8.5 | 2870 | 11.920 | >0.0001 | 1255.79 | 1.70 |
| CEDEX | This Study | |||
|---|---|---|---|---|
| Scenario/Impact Period | 2041–2070 | 2071–2100 | 2041–2070 | 2071–2100 |
| RCP4.5 | 6 | 8 | 10.7 | 11.2 |
| RCP8.5 | 9 | 15 | 11.8 | 15.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Aĺvarez, M.; Gomariz-Castillo, F.; Alonso-Sarría, F. Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method. Water 2021, 13, 222. https://doi.org/10.3390/w13020222
Ruiz-Aĺvarez M, Gomariz-Castillo F, Alonso-Sarría F. Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method. Water. 2021; 13(2):222. https://doi.org/10.3390/w13020222
Chicago/Turabian StyleRuiz-Aĺvarez, Marcos, Francisco Gomariz-Castillo, and Francisco Alonso-Sarría. 2021. "Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method" Water 13, no. 2: 222. https://doi.org/10.3390/w13020222
APA StyleRuiz-Aĺvarez, M., Gomariz-Castillo, F., & Alonso-Sarría, F. (2021). Evapotranspiration Response to Climate Change in Semi-Arid Areas: Using Random Forest as Multi-Model Ensemble Method. Water, 13(2), 222. https://doi.org/10.3390/w13020222







