On Dam Failure Induced Seismic Signals Using Laboratory Tests and on Breach Morphology due to Overtopping by Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Configuration
2.2. Seismic Signal Processing by Hilbert–Huang Transform (HHT)
2.3. Dam Breach Model—Overtopping
3. Results and Discussions
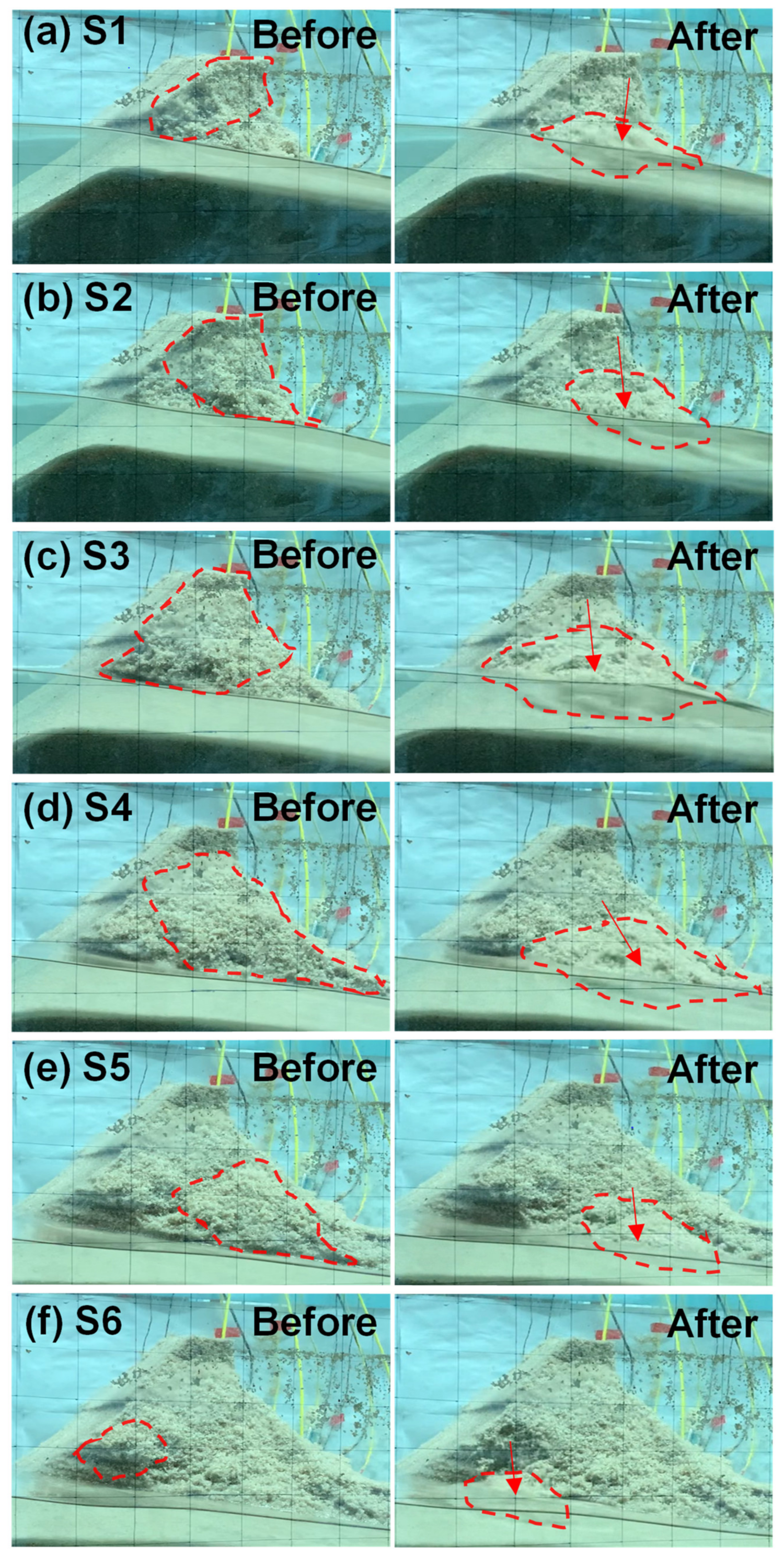
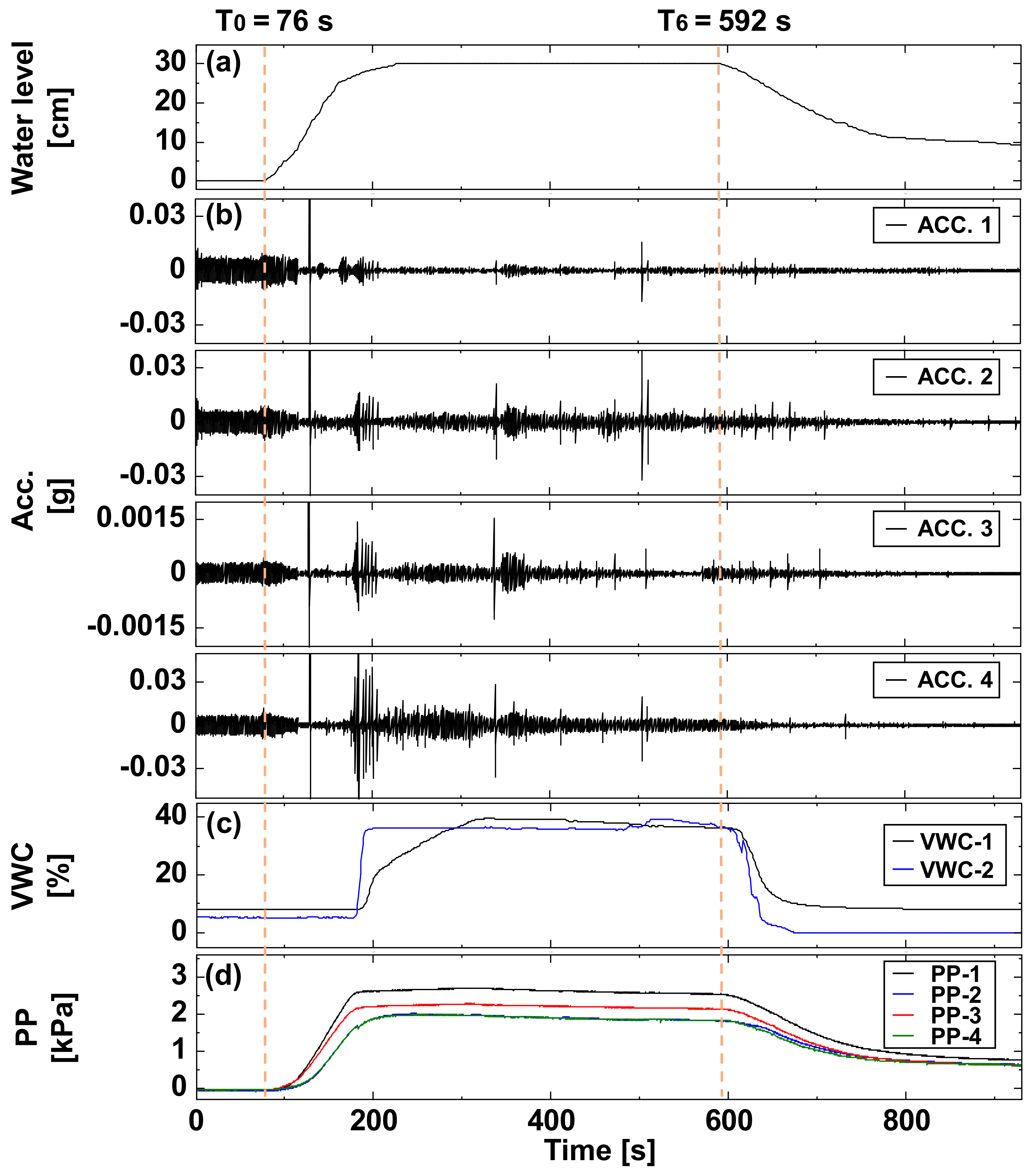
3.1. Measurements of the Test
3.2. Seismic Signals Due to Retrogressive Erosion before Overtopping
- (1)
- A single slide—Event 3: A single slide is defined as a rapid one-time sliding that displaces a large volume of mass [54]. Strong seismic energy is often released. Event 3 was a single slide that occurred immediately after the precursor Events 1 and 2 during 184 s (T2) to 185.6 s. The seismic signal, time–frequency spectrum, and the front and top view of Event 3 are shown in Figure 8. The amplitudes and spectral traces were larger and stronger than other events in this test due to a larger displaced mass and displacement. The duration of Event 3 was also longer than other events. It is noted that the average frequency of the seismic signal of Event 3 was 375 Hz.
- (2)
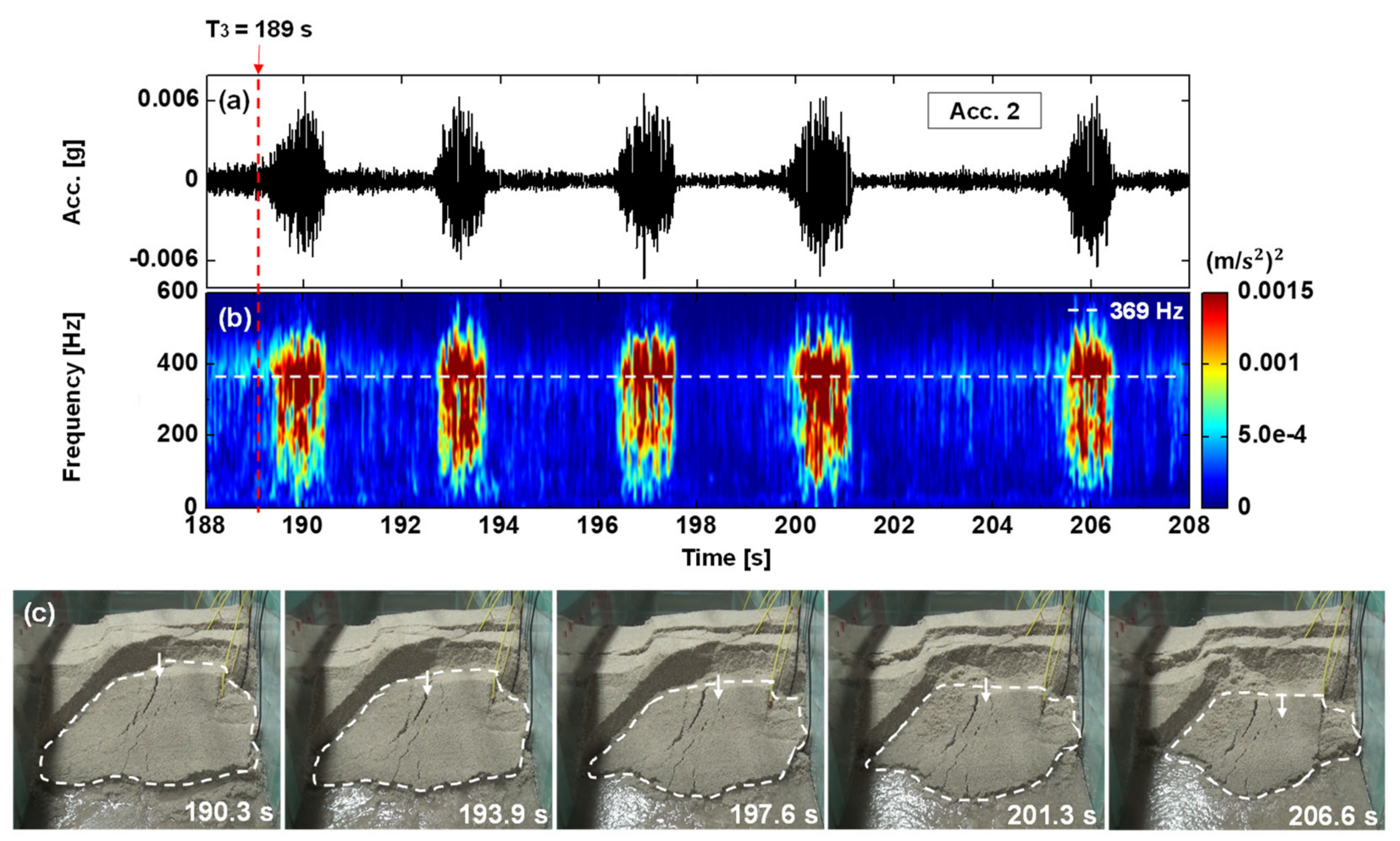
- An intermittent slide—Event 4: An intermittent slide is defined as the same mass sliding down multiple times on the same rupture surface [54]. An intermittent slide usually generates nearly periodic seismic signals. Event 4, an intermittent slide, occurred during 189 s (T3) ~ 207 s, which was about 3 s after Event 3. The displaced mass of the first two movements was the same mass in Event 3 and moved short distances on the same rupture surface, while another deeper rupture surface developed and part of the displaced mass of the third–fifth movements slid on it (see Supplementary Materials Video S3 for Event 4). The corresponding seismic signal, spectrum, and images of Event 4 are presented in Figure 9. For every 2–5 s there was a movement in this event. The nearly periodic seismic signals and spectral traces can easily be identified.
- (3)
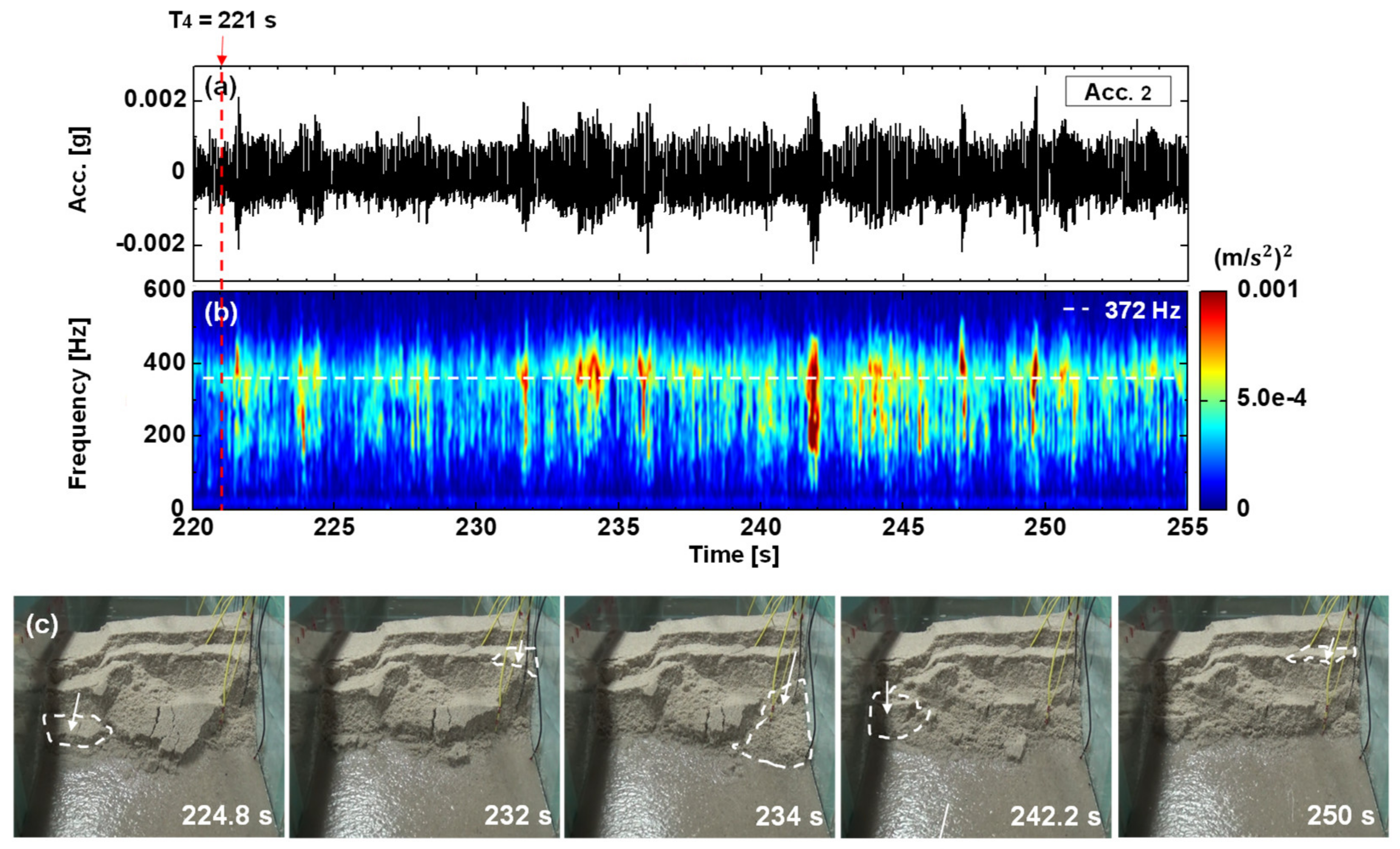
- A successive slide—Event 5: A successive slide is defined as the many irregularly and randomly occurrences of sliding on multiple rupture surfaces and the displaced masses are from many different locations [54]. A successive slide usually generates aperiodic or random seismic signals. Event 5, a successive slide, occurred during 221 s (T4) ~ 251 s. In Figure 10, the signal shown was induced by random sliding of many different masses from place to place. The seismic signal was much more irregular without a pattern and the intervals between slides were random.
- (4)
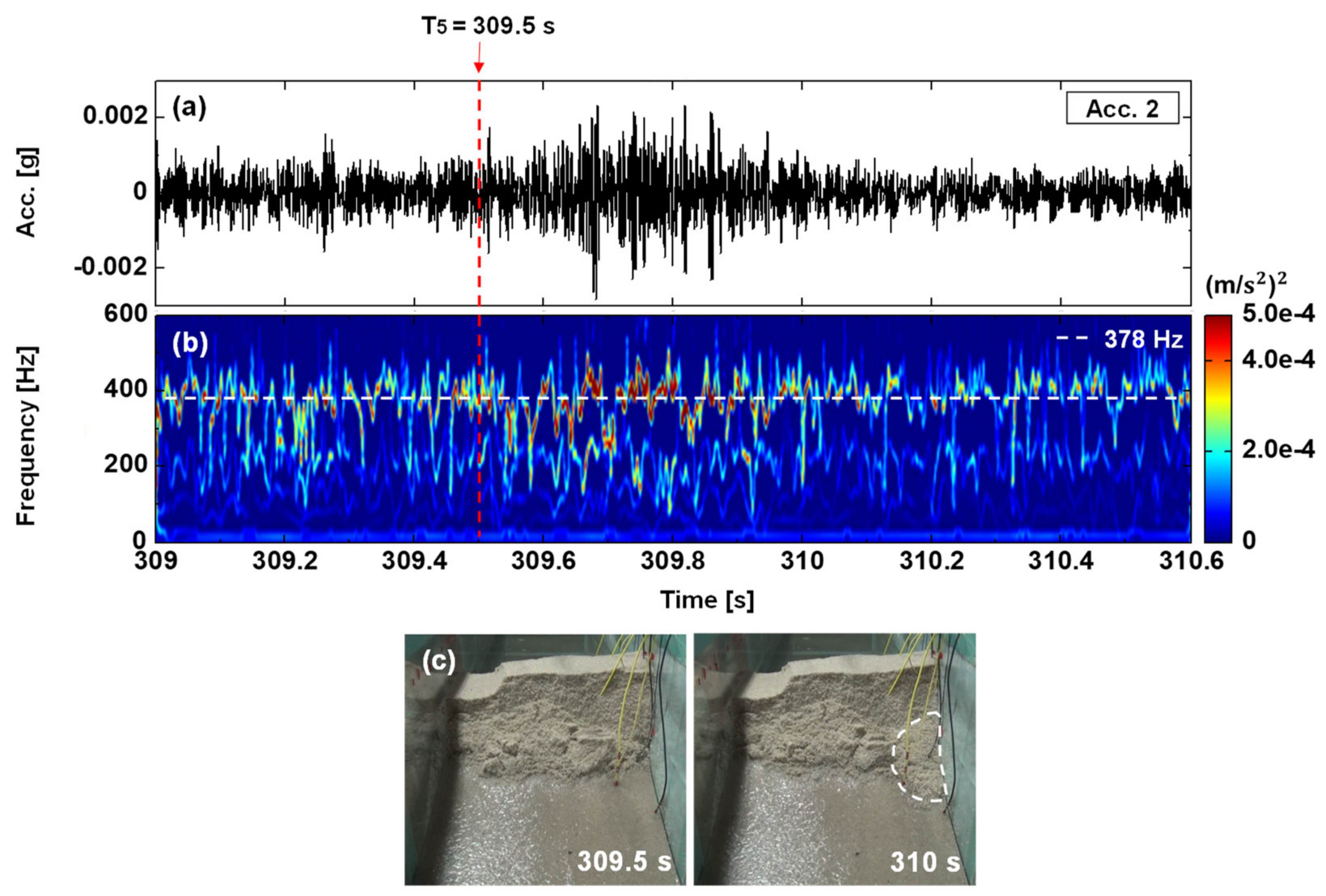
- A fall—Event 6: A fall is that mass falls down through the air and falls almost vertically. Figure 11 shows the fall, Event 6, which occurred at 309.5 s (T5). The duration of Event 6 was short. The amplitudes of the signal were small and the energy traces in the spectrum were also weak owing to the fact that only a small mass fell in Event 6.

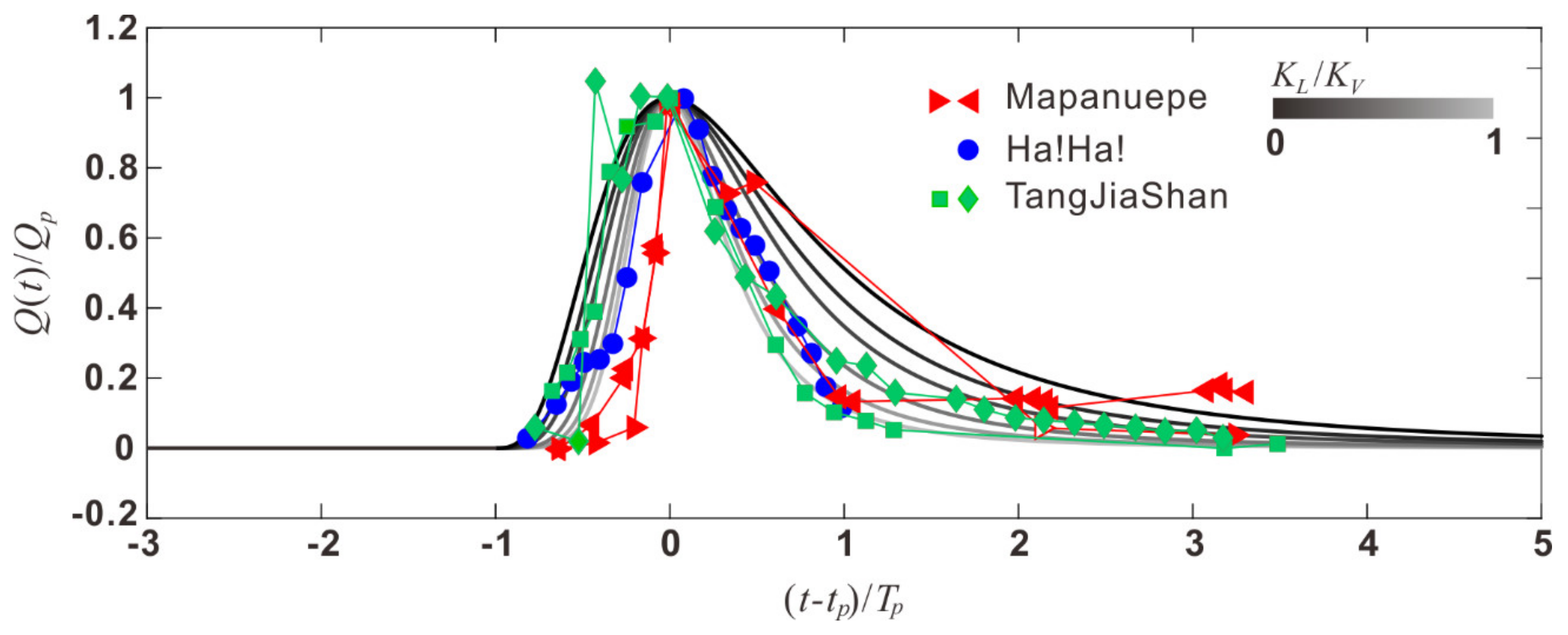
3.3. Comparison of the Dam Breach Model Result with the Breach Events from Literature
3.4. Comparision of the Dam Breach Model Result with the Test Result after Overtopping (Event 7)

4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of symbols
| elevation of the breach channel () | |
| streamwise direction () | |
| breach channel width ( | |
| initial breach channel width () | |
| time (s) | |
| sediment flux () | |
| water level (elevation) of the lake () | |
| dam initial elevation (before overtopping) ( | |
| dam breach crest elevation () | |
| streamwise position of dam breach crest () | |
| lake area () | |
| erosion volume of breach crest () | |
| drop of the dam elevation to the breach crest elevation:() | |
| flow depth of the breach crest: () | |
| downstream slope of the dam (initial) (-) | |
| upstream slope of the dam (initial) (-) | |
| dimensionless sediment transport coefficient (-) | |
| breach channel local gradient (-) | |
| scaled dimensionless sediment transport coefficient (-) | |
| scaled dimensionless sediment transport coefficient in vertical direction (-) | |
| scaled dimensionless sediment transport coefficient in lateral direction (-) | |
| local discharge () | |
| peak discharge ( | |
| estimated test discharge () | |
| dimensionless discharge coefficient (-) | |
| defined operation time (accumulated discharge) () | |
| dimensionless scaling constant, related to the shape of the dam (-) |
References
- Costa, J.E.; Schuster, R.L. The formation and failure of natural dams. Geol. Soc. Am. Bull. 1988, 100, 1054–1068. [Google Scholar] [CrossRef]
- Fan, X.M.; Dufresne, A.; Subramanian, S.S.; Strom, A.; Hermanns, R.; Stefanelli, C.T.; Hewitt, K.; Yunus, A.P.; Dunning, S.; Capra, L.; et al. The formation and impact of landslide dams—State of the art. Earth Sci. Rev. 2020, 203, 103116. [Google Scholar] [CrossRef]
- Chen, S.-C.; Hsu, C.-L.; Wu, T.; Chou, H.-T.; Cui, P. Landslide dams induced by typhoon Morakot and risk assessment. In Proceedings of the 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, Padua, Italy, 14–17 June 2011; pp. 653–660. [Google Scholar]
- Tsou, C.-Y.; Feng, Z.-Y.; Chigira, M. Catastrophic landslide induced by typhoon Morakot, Shiaolin, Taiwan. Geomorphology 2011, 127, 166–178. [Google Scholar] [CrossRef]
- Wu, C.-H.; Chen, S.-C.; Feng, Z.-Y. Formation, failure, and consequences of the Xiaolin landslide dam, triggered by extreme rainfall from Typhoon Morakot. Taiwan. Landslides 2014, 11, 357–367. [Google Scholar] [CrossRef]
- Feng, Z.-Y. The seismic signatures of the surge wave from the 2009 Xiaolin landslide—Dam breach in Taiwan. Hydrol. Process. 2011, 26, 1342–1351. [Google Scholar] [CrossRef]
- Chen, R.-F.; Chang, K.-J.; Angelier, J.; Chan, Y.-C.; Deffontaines, B.; Lee, C.-T.; Lin, M.-L. Topographical changes revealed by high-resolution airborne LiDAR data: The 1999 Tsaoling landslide induced by the Chi–Chi earthquake. Eng. Geol. 2006, 88, 160–172. [Google Scholar] [CrossRef]
- Chigira, M.; Wang, W.-N.; Furuya, T.; Kamai, T. Geological causes and geomorphological precursors of the Tsaoling landslide triggered by the 1999 Chi-Chi earthquake, Taiwan. Eng. Geol. 2003, 68, 259–273. [Google Scholar] [CrossRef]
- Li, M.-H.; Hsu, M.-H.; Hsieh, L.-S.; Teng, W.-H. Inundation Potentials Analysis for Tsao-Ling Landslide Lake Formed by Chi-Chi Earthquake in Taiwan. Nat. Hazards 2002, 25, 289–303. [Google Scholar] [CrossRef]
- Hsu, Y.-S.; Hsu, Y.-H. Impact of earthquake-induced dammed lakes on channel evolution and bed mobility: Case study of the Tsaoling landslide dammed lake. J. Hydrol. 2009, 374, 43–55. [Google Scholar] [CrossRef]
- Cui, P.; Zhou, G.G.D.; Zhu, X.H.; Zhang, J.Q. Scale amplification of natural debris flows caused by cascading landslide dam failures. Geomorphology 2013, 182, 173–189. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Cui, P.; Zhu, X.; Tang, J.; Chen, H.; Sun, Q. A preliminary study of the failure mechanisms of cascading landslide dams. Int. J. Sediment Res. 2015, 30, 223–234. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, X.; Peng, A.; Wang, X.; Fan, Z. Flood Risk Analysis for Cascade Dam Systems: A Case Study in the Dadu River Basin in China. Water 2019, 11, 1365. [Google Scholar] [CrossRef]
- Říha, J.; Kotaška, S.; Petrula, L. Dam Break Modeling in a Cascade of Small Earthen Dams: Case Study of the Čižina River in the Czech Republic. Water 2020, 12, 2309. [Google Scholar] [CrossRef]
- Shrestha, B.B.; Nakagawa, H. Hazard assessment of the formation and failure of the Sunkoshi landslide dam in Nepal. Nat. Hazards 2016, 82, 2029–2049. [Google Scholar] [CrossRef]
- Suriñach, E.; Vilajosana, I.; Khazaradze, G.; Biescas, B.; Furdada, G.; Vilaplana, J.M. Seismic detection and characterization of landslides and other mass movements. Nat. Hazards Earth Syst. Sci. 2005, 5, 791–798. [Google Scholar] [CrossRef]
- Suwa, H.; Mizuno, T.; Ishii, T. Prediction of a landslide and analysis of slide motion with reference to the 2004 Ohto slide in Nara, Japan. Geomorphology 2010, 124, 157–163. [Google Scholar] [CrossRef]
- Yamada, M.; Matsushi, Y.; Chigira, M.; Mori, J. Seismic recordings of landslides caused by Typhoon Talas (2011), Japan. Geophys. Res. Lett. 2012, 39, 13301. [Google Scholar] [CrossRef]
- Provost, F.; Malet, J.-P.; Hibert, C.; Helmstetter, A.; Radiguet, M.; Amitrano, D.; Langet, N.; Larose, E.; Abancó, C.; Hürlimann, M.; et al. Towards a standard typology of endogenous landslide seismic sources. Earth Surf. Dyn. 2018, 6, 1059–1088. [Google Scholar] [CrossRef]
- Yan, Y.; Cui, Y.F.; Liu, D.Z.; Tang, H.; Li, Y.J.; Tian, X.; Zhang, L.; Hu, S. Seismic signal characteristics and interpretation of the 2020 “6.17” Danba landslide dam failure hazard chain process. Landslides 2021, 18, 1–18. [Google Scholar] [CrossRef]
- Yan, Y.; Cui, Y.; Guo, J.; Hu, S.; Wang, Z.; Yin, S. Landslide reconstruction using seismic signal characteristics and numerical simulations: Case study of the 2017 “6.24” Xinmo landslide. Eng. Geol. 2020, 270, 105582. [Google Scholar] [CrossRef]
- Feng, Z.-Y.; Lo, C.-M.; Lin, Q.-F. The characteristics of the seismic signals induced by landslides using a coupling of discrete element and finite difference methods. Landslides 2017, 14, 661–674. [Google Scholar] [CrossRef]
- Yan, Y.; Cui, P.; Chen, S.-C.; Chen, X.-Q.; Chen, H.-Y.; Chien, Y.-L. Characteristics and interpretation of the seismic signal of a field-scale landslide dam failure experiment. J. Mt. Sci. 2017, 14, 219–236. [Google Scholar] [CrossRef]
- Feng, Z.-Y.; Huang, H.-Y.; Chen, S.-C. Analysis of the characteristics of seismic and acoustic signals produced by a dam failure and slope erosion test. Landslides 2020, 17, 1605–1618. [Google Scholar] [CrossRef]
- Jiang, X.G.; Wei, Y.W.; Wu, L.; Lei, Y. Experimental investigation of failure modes and breaching characteristics of natural dams. Geomat. Nat. Hazards Risk 2018, 9, 33–48. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, J.; Wei, Y.; Niu, Z.; Chen, F.; Zou, Z.; Zhu, Z. The influence of materials on the breaching process of natural dams. Landslides 2018, 15, 243–255. [Google Scholar]
- Nian, T.-K.; Wu, H.; Li, D.-Y.; Zhao, W.; Takara, K.; Zheng, D.-F. Experimental investigation on the formation process of landslide dams and a criterion of river blockage. Landslides 2020, 17, 2547–2562. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, B.; Peng, J.; Zhang, Z.; Zhuang, J.; Huang, W.; Leng, Y.; Duan, Z. Experimental study on the longitudinal evolution of the overtopping breaching of noncohesive landslide dams. Eng. Geol. 2021, 288, 106137. [Google Scholar] [CrossRef]
- Hu, W.; Scaringi, G.; Xu, Q.; Huang, R.Q. Acoustic Emissions and Microseismicity in Granular Slopes Prior to Failure and Flow-Like Motion: The Potential for Early Warning. Geophys. Res. Lett. 2018, 45, 10406–10415. [Google Scholar] [CrossRef]
- Poli, P. Creep and slip: Seismic precursors to the Nuugaatsiaq landslide (Greenland). Geophys. Res. Lett. 2017, 44, 8832–8836. [Google Scholar] [CrossRef]
- Butler, R. Seismic precursors to a 2017 Nuugaatsiaq, Greenland, earthquake–landslide–tsunami event. Nat. Hazards 2019, 96, 961–973. [Google Scholar] [CrossRef]
- Feng, Z.-Y.; Hsu, C.-M.; Chen, S.-H. Discussion on the Characteristics of Seismic Signals Due to Riverbank Landslides from Laboratory Tests. Water 2019, 12, 83. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.C.; Shih, H.H.; Zheng, Q.N.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Takayama, S.; Miyata, S.; Fujimoto, M.; Satofuka, Y. Numerical simulation method for predicting a flood hydrograph due to progressive failure of a landslide dam. Landslides 2021. [Google Scholar] [CrossRef]
- Wu, W. Simplified physically based model of earthen embankment breaching. J. Hydraul. Eng. 2011, 137, 1549–1564. [Google Scholar] [CrossRef]
- Alhasan, Z.; Jandora, J.; Říha, J. Study of dam-break due to overtopping of four small dams in the Czech Republic. Acta Univ. Agric. Silvic. Mendel. Brun. 2015, 63, 717–729. [Google Scholar] [CrossRef]
- Tian, S.; Dai, X.; Wang, G.; Lu, Y.; Chen, J. Formation and evolution characteristics of dam breach and tailings flow from dam failure: An experimental study. Nat. Hazards 2021, 107, 1–18. [Google Scholar] [CrossRef]
- Capart, H. Analytical solutions for gradual dam breaching and downstream river flooding. Water Resour. Res. 2013, 49, 1968–1987. [Google Scholar] [CrossRef]
- Capart, H.; Hsu, J.P.C.; Lai, S.Y.J.; Hsieh, M.-L. Formation and decay of a tributary-dammed lake, Laonong River, Taiwan. Water Resour. Res. 2010, 46, W11522. [Google Scholar] [CrossRef]
- Lane, E.W. The importance of fluvial morphology in hydraulic engineering. Proc. Am. Soc. Civ. Eng. 1955, 81, 1–17. [Google Scholar]
- Alhasan, Z.; Jandora, J.; Říha, J. Comparison of specific sediment transport rates obtained from empirical formulae and dam breaching experiments. Environ. Fluid Mech. 2016, 16, 997–1019. [Google Scholar] [CrossRef]
- AnCAD, Inc. Visual Signal Reference Guide, Version1.6. Available online: http://www.ancad.com.tw/VisualSignal/doc/1.6/RefGuide.html (accessed on 15 July 2021). (In Chinese).
- Paola, C.; Voller, V.R. A generalized Exner equation for sediment mass balance. J. Geophys. Res. Earth Surf. 2005, 110, F04014. [Google Scholar] [CrossRef]
- Visser, P.J. Application of sediment transport formulae to sand-dike breach erosion. Oceanogr. Lit. Rev. 1996, 43, 954. [Google Scholar]
- Haddadchi, A.; Omid, M.H.; Dehghani, A.A. Bedload equation analysis using bed load-material grain size. J. Hydrol. Hydromech. 2013, 61, 241–249. [Google Scholar] [CrossRef][Green Version]
- Cao, Z.; Yue, Z.; Pender, G. Landslide dam failure and flood hydraulics. Part II: Coupled mathematical modelling. Nat. Hazards 2011, 59, 1021–1045. [Google Scholar] [CrossRef]
- Capart, H.; Bellal, M.; Young, D.-L. Self-similar evolution of semi-infinite alluvial channels with moving boundaries. J. Sediment. Res. 2007, 77, 13–22. [Google Scholar] [CrossRef]
- Hsu, J.P.C.; Capart, H. Onset and growth of tributary-dammed lakes. Water Resour. Res. 2008, 44, W11201. [Google Scholar] [CrossRef]
- Voller, V.R.; Swenson, J.B.; Paola, C. An analytical solution for a Stefan problem with variable latent heat. Int. J. Heat Mass Transf. 2004, 47, 5387–5390. [Google Scholar] [CrossRef]
- Lai, S.Y.J.; Capart, H. Two-diffusion description of hyperpycnal deltas. J. Geophys. Res. Space Phys. 2007, 112, F03005. [Google Scholar] [CrossRef]
- Lai, S.Y.J.; Capart, H. Reservoir infill by hyperpycnal deltas over bedrock. Geophys. Res. Lett. 2009, 36, L08402. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Henderson, F.M. Open Channel Flow; Macmillan: New York, NY, USA, 1966. [Google Scholar]
- Feng, Z.-Y.; Chen, S.-H. Discussions on landslide types and seismic signals produced by the soil rupture due to seepage and retrogressive erosion. Landslides 2021, 18, 2265–2279. [Google Scholar] [CrossRef]
- Liu, N.; Chen, Z.; Zhang, J.; Lin, W.; Chen, W.; Xu, W. Draining the Tangjiashan barrier lake. J. Hydraul. Eng. 2010, 136, 914–923. [Google Scholar] [CrossRef]
- Capart, H.; Spinewine, B.; Young, D.; Zech, Y.; Brooks, G.R.; Leclerc, M.; Secretan, Y. The 1996 Lake Ha! Ha! breakout flood, Québec: Test data for geomorphic flood routing methods. J. Hydraul. Res. 2007, 45 (Suppl. 1), 97–109. [Google Scholar] [CrossRef]
- Umbal, J.V.; Rodolfo, K.S. The 1991 Lahars of Southwestern Mount Pinatubo and Evolution of the Lahar-Dammed Mapanuepe Lake. In Fire and Mud: Eruptions and Lahars of Mount Pinatubo, Philippines; Newhall, C.G., Punongbayan, R.S., Eds.; University of Washington Press: Washington, DC, USA, 1996; pp. 951–970. [Google Scholar]
- Pařílková, J.; Říha, J.; Zachoval, Z. The influence of roughness on the discharge coefficient of a broad-crested weir. J. Hydrol. Hydromech. 2012, 60, 101–114. [Google Scholar] [CrossRef][Green Version]
- Imanian, H.; Mohammadian, A.; Hoshyar, P. Experimental and numerical study of flow over a broad-crested weir under different hydraulic head ratios. Flow Meas. Instrum. 2021, 80, 102004. [Google Scholar] [CrossRef]
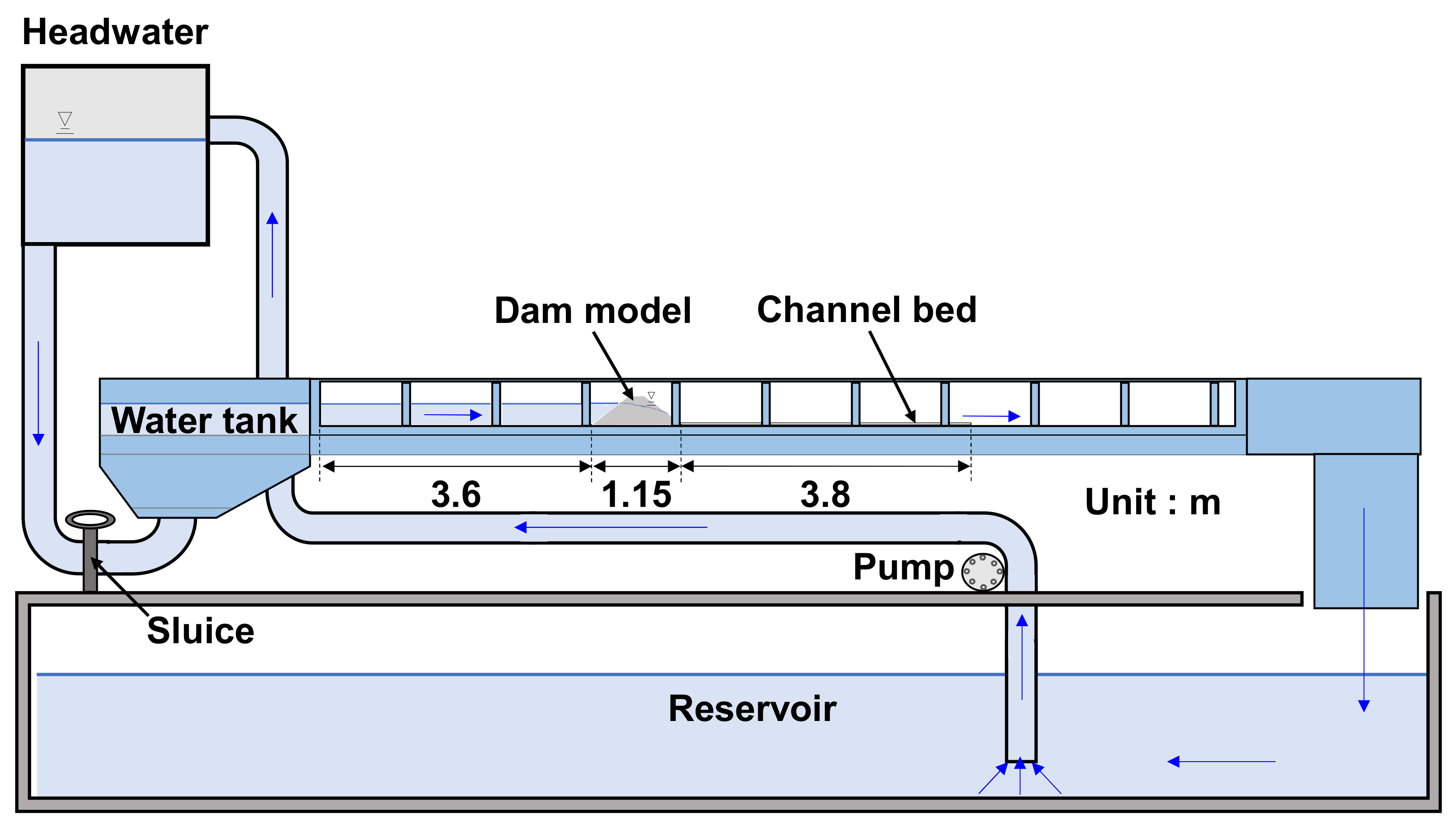

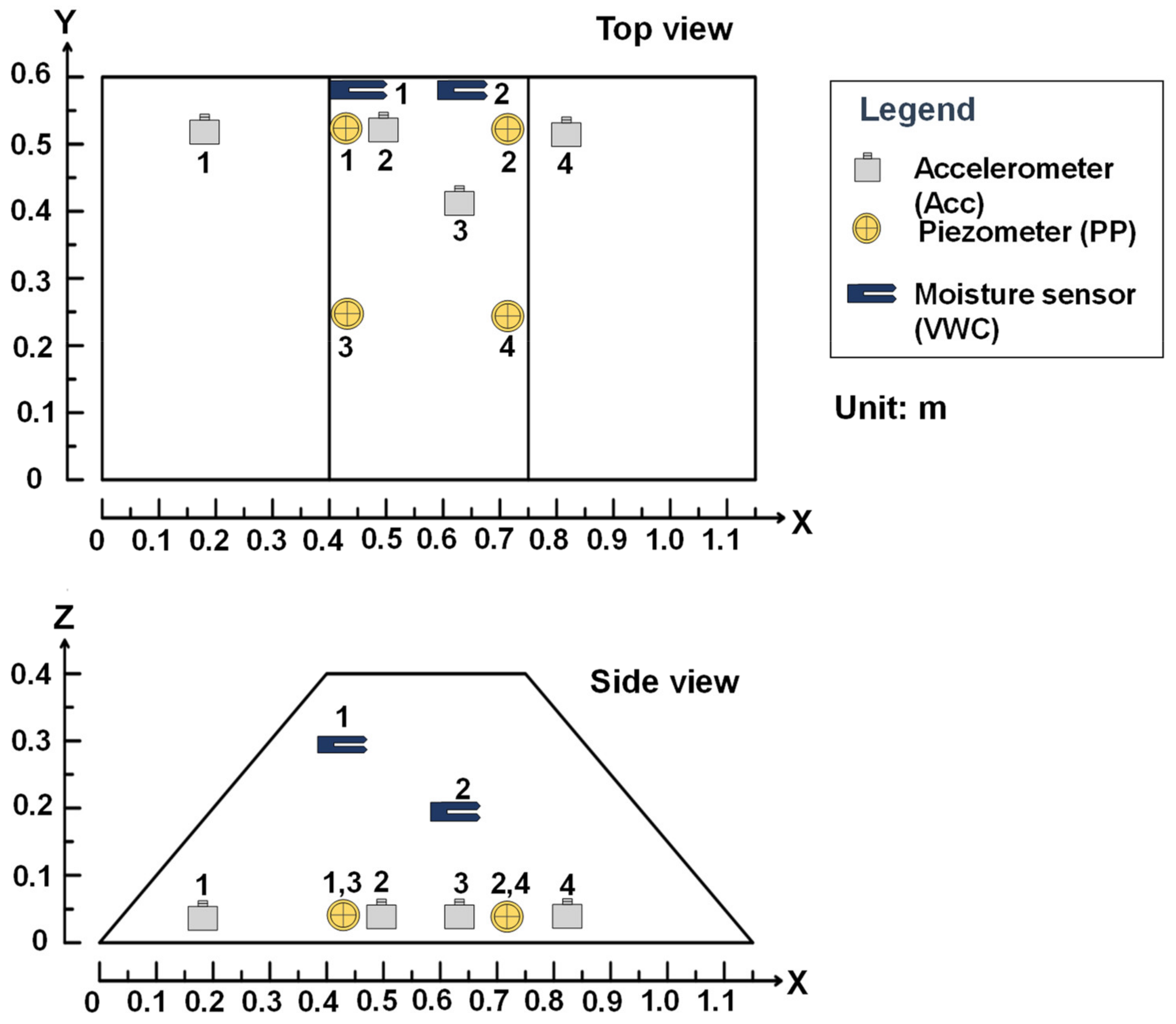
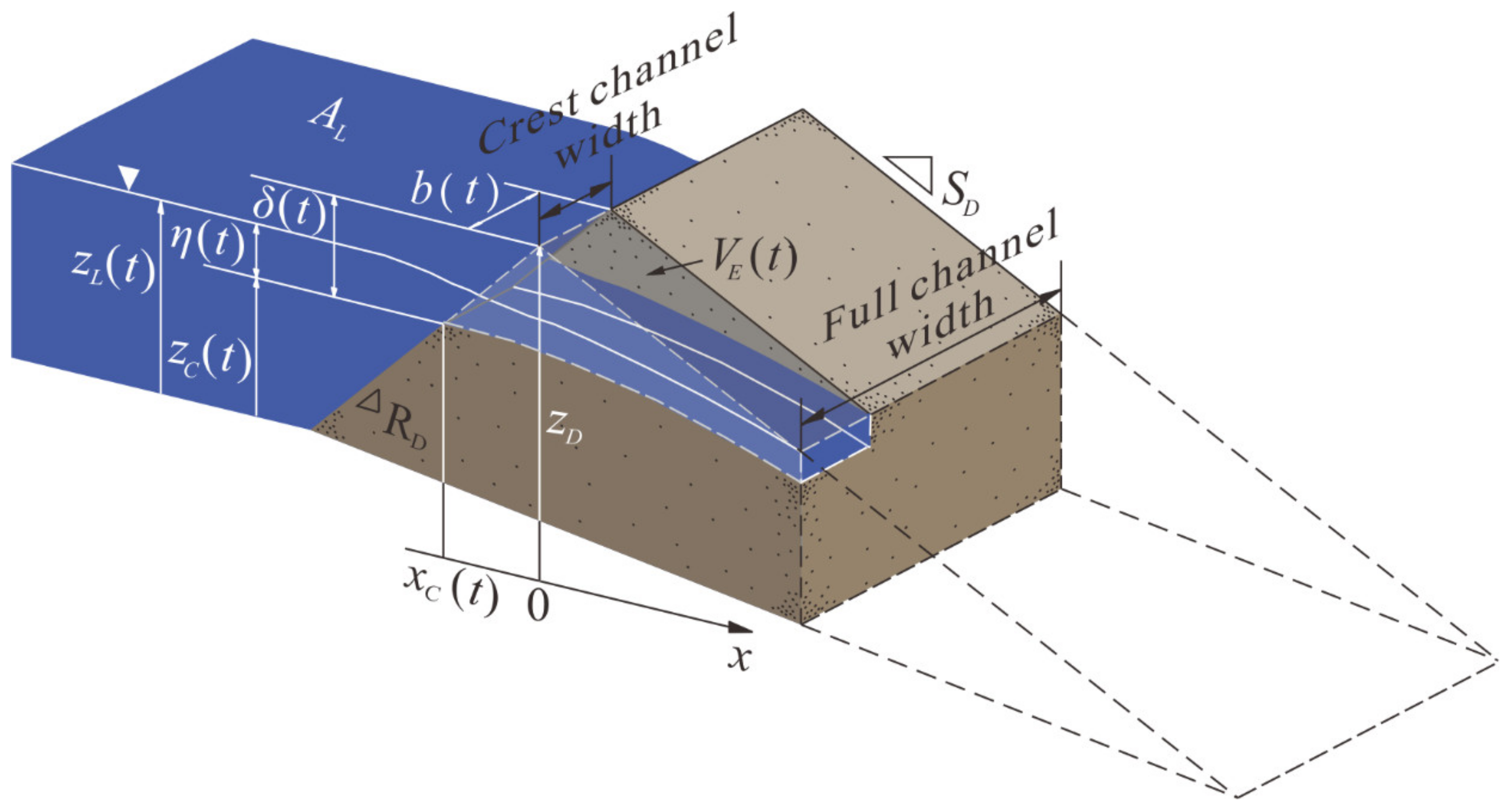

| Slope (°) | Height (m) | Crest Width (m) | Bottom Length (m) | Channel Width (m) | Maximum Water Level (m) |
|---|---|---|---|---|---|
| 45 | 0.4 | 0.35 | 1.15 | 0.6 | 0.3 |
| Time, s | Event | Variation of the Seismic Signals |
|---|---|---|
| 0–116 | The flow pump was opened and the sluice was opened. | Frequency of the flow pump: 106 Hz, 227 Hz |
| 76 | T0 = 76 s when water reached the upstream toe of the dam model; the water continued to fill the tank up to 0.3 cm. | - |
| 116 | The flow pump was closed; the sluice remained opened. | Frequency of the environment: 101 Hz; |
| 130 | A tapping was made to leave a time marker. | Amplitudes of the signals at 130 s were very high. |
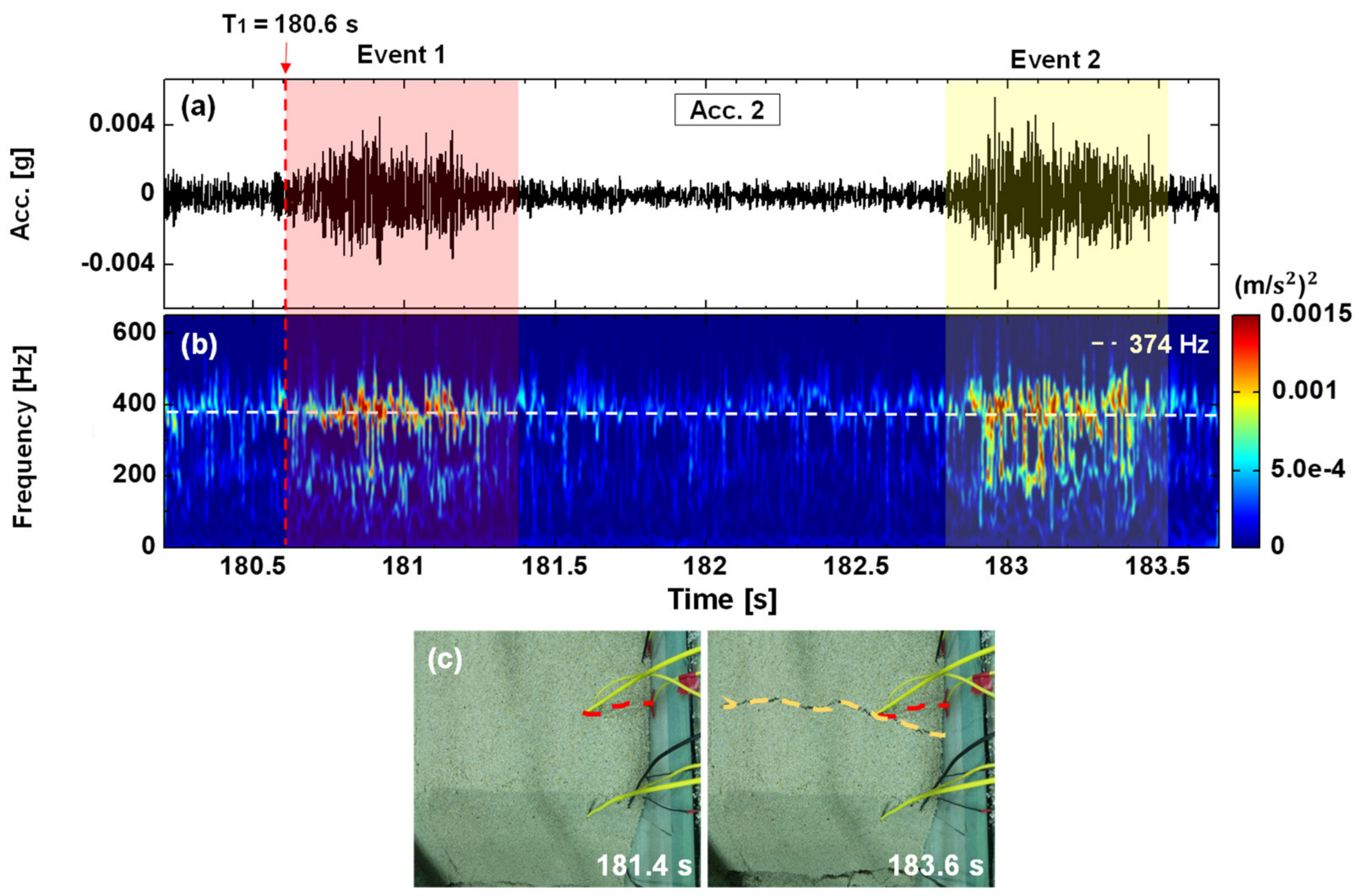
| 180.6–183.5 | T1 =180.6 s; Event 1 and 2 precursor signals; one smaller crack and one larger crack developed prior to a slide (see Supplementary Materials Video S1) | Two precursor seismic signals occurred prior to a slide; the 1st with lower energy; the 2nd with higher energy. |
| 184–185.6 | T2 = 184 s; a single slide (Event 3) occurred (see Supplementary Materials Video S2) | Seismic signals significantly increased |
| 189–207 | T3 = 189 s; an intermittent slide (Event 4) occurred (see Supplementary Materials Video S3); retrogressive erosion | Seismic signals significantly increased nearly periodically in about 2 to 5 s. |
| 221–251 | T4 = 221 s; a successive slide (Event 5) occurred (see Supplementary Materials Video S4); retrogressive erosion | Seismic signals significantly increased aperiodically. |
| 309.5–310 | T5 = 309.5 s; a fall (or collapse) (Event 6) occurred (see Supplementary Materials Video S5) | Seismic signals suddenly increased and the duration was very short. |
| 412–510 | Many single slides with different magnitudes occurred; retrogressive erosion | Seismic signals significantly increased with different corresponding amplitudes |
| 592–930 | T6 = 592 s; Overtopping process (Event 7) (see Supplementary Materials Videos S6 and S7); the sluice was then closed; six lateral slides occurred. | Seismic signals significantly increased when the six lateral slides occurred. Strong spectral traces appear around 220–420 Hz in the time–frequency spectrum due to the overtopping water flow. |
| 930 | The end of the test |
| Dam/Lake | Date | AL | b (m) | Qp | Source |
|---|---|---|---|---|---|
| Mapanuepe | 25–27 August 1991 | 6.7 | 70 | 0.65 | Umbal and Rodolfo (1996) [57] |
| 12–16 October 1991 | 6.7 | 70 | 0.39 | ||
| Ha!Ha! | 19–22 July 1996 | 6 | 90 | 0.85 | Capart et al. (2007) [56] |
| Tangjiashan | 10–11 June 2008 | 6.4 | 110 | 6.5 | Liu et al. (2010) [55] |
| Parameters/Unit | Value | Source |
|---|---|---|
| [m] | 0.3 | Measured from the initial dimensions of the test dam |
| [m] | 0.3 | |
| [m] | 0.3 | |
| [m] | 0.015 | |
| [m2] | 2.22 | |
| dt [s] | 0.005 | Numerical calculation time step |
| 1.875 | Calibrated from the test result | |
| 0.1375 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-Y.; Tseng, I.-F.; Chen, S.-C.; Feng, Z.-Y. On Dam Failure Induced Seismic Signals Using Laboratory Tests and on Breach Morphology due to Overtopping by Modeling. Water 2021, 13, 2757. https://doi.org/10.3390/w13192757
Hung C-Y, Tseng I-F, Chen S-C, Feng Z-Y. On Dam Failure Induced Seismic Signals Using Laboratory Tests and on Breach Morphology due to Overtopping by Modeling. Water. 2021; 13(19):2757. https://doi.org/10.3390/w13192757
Chicago/Turabian StyleHung, Chi-Yao, I-Fan Tseng, Su-Chin Chen, and Zheng-Yi Feng. 2021. "On Dam Failure Induced Seismic Signals Using Laboratory Tests and on Breach Morphology due to Overtopping by Modeling" Water 13, no. 19: 2757. https://doi.org/10.3390/w13192757
APA StyleHung, C.-Y., Tseng, I.-F., Chen, S.-C., & Feng, Z.-Y. (2021). On Dam Failure Induced Seismic Signals Using Laboratory Tests and on Breach Morphology due to Overtopping by Modeling. Water, 13(19), 2757. https://doi.org/10.3390/w13192757








