Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment
Abstract
1. Introduction
2. Material and Methods
2.1. Location of the Conventional Facultative Lagoon
2.2. Experimental Tracer Studies
2.3. Experimental Suspended Solid Concentrations
2.4. Validation of Data from Research
3. CFD Model Specifications
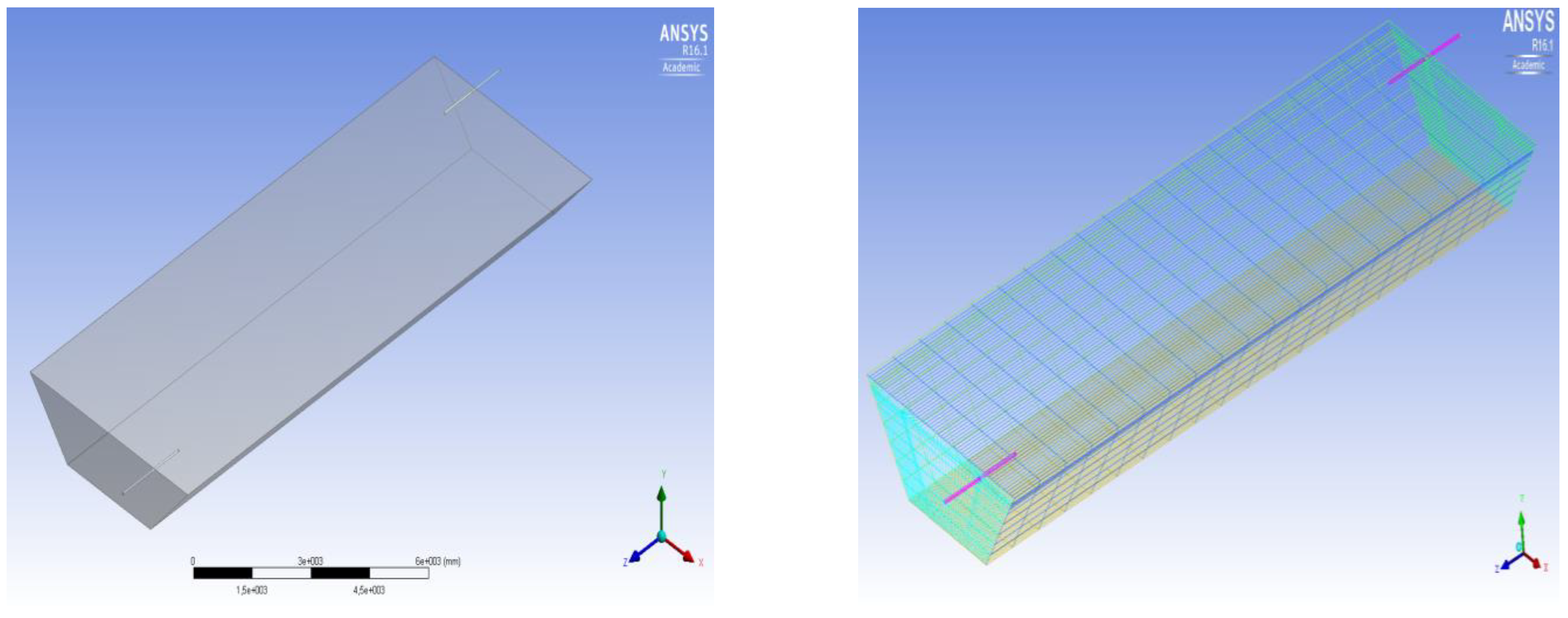
3.1. Geometry and Discretization
3.2. Boundary Conditions
3.3. Drag and Slip Forces Models
3.4. Properties of the Materials
3.5. Governing Equations
- Continuity equation
- Equation for momentum
- Turbulence model
3.6. Mesh Independence Test
4. Results and Discussion
4.1. Mesh Independence Test
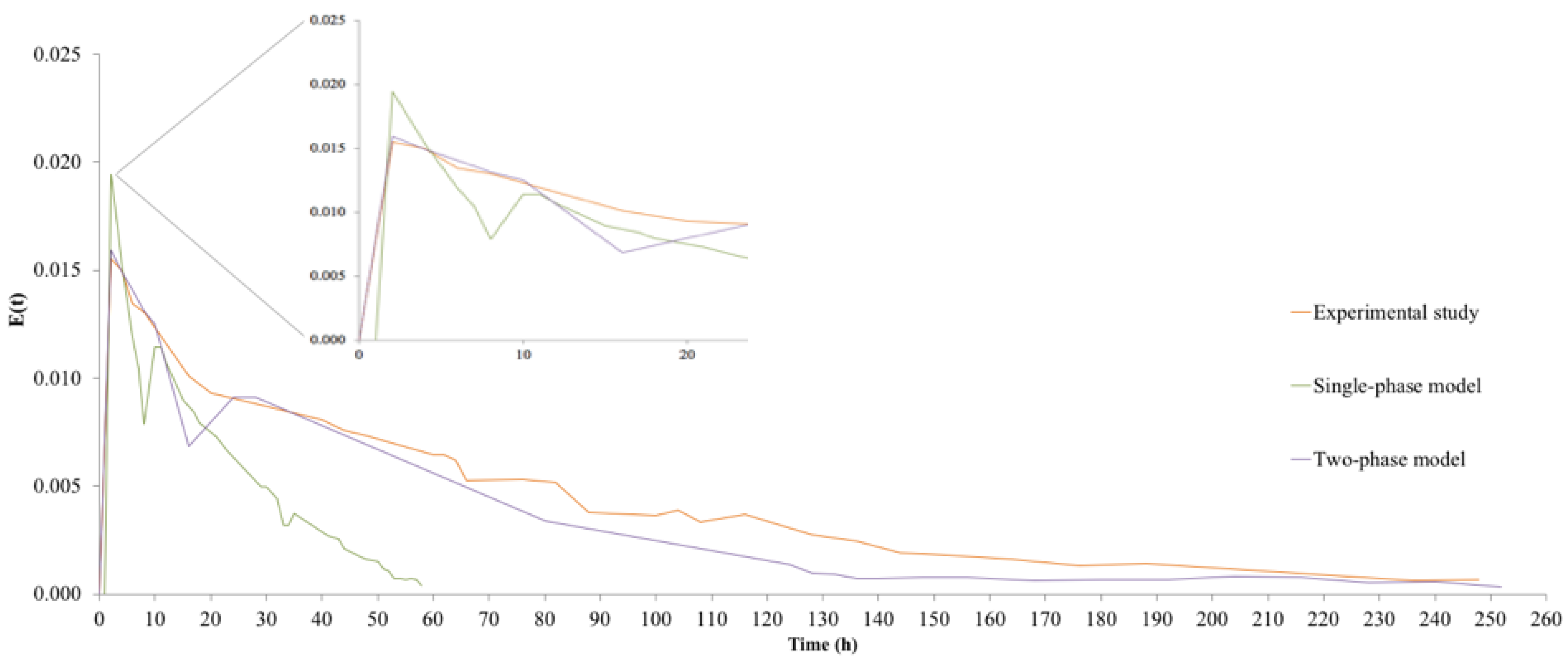
4.2. Tracer Studies: CFD Models vs. Experimental Results
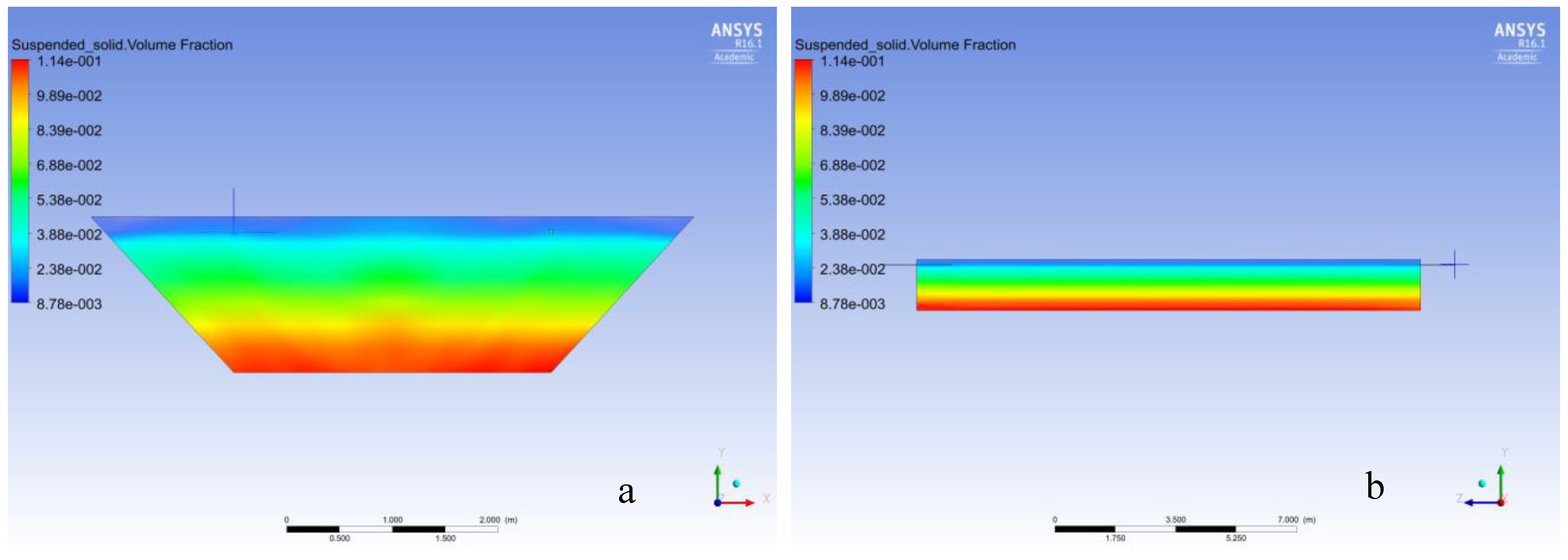
4.3. Single-Phase CFD Model vs. Two-Phase CFD Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Butler, E.; Hung, Y.T.; Al Ahmad, M.S.; Yeh, R.Y.L.; Liu, R.L.H.; Fu, Y.P. Oxidation pond for municipal wastewater treatment. Appl. Water Sci. 2015, 7, 1–21. [Google Scholar] [CrossRef]
- Rao, S. A review of the technological feasibility of aquacultures for municipal wastewater treatment. Int. J. Environ. Stud. 2007, 27, 219–223. [Google Scholar] [CrossRef]
- Olukanni, D.; Ducoste, J. Optimization of waste stabilization pond design for developing nations using computational fluid dynamics. Ecol. Eng. 2011, 37, 1878–1888. [Google Scholar] [CrossRef]
- Zapata, A.; Peña, M. CFD model to characterize the transport of the flame retardant BDE 99 in a secondary facultative lagoon. Tech. J. Eng. Fac. 2020, 43, 41–48. [Google Scholar] [CrossRef]
- Pham, D.; Everaert, G.; Janssens, N.; Alvarado, A.; Nopens, I.; Goethalsa, L. Algal community analysis in a waste stabilisation pond. Ecol. Eng. 2014, 73, 302–306. [Google Scholar] [CrossRef]
- Vendramelli, R.; Vijay, S.; Yuan, Q. Phosphorus Removal Mechanisms in a Facultative Wastewater Stabilization Pond. Water Air Soil Pollut. 2016, 227, 1–10. [Google Scholar] [CrossRef]
- Katia, N.; Iolanda, C.; Bernadete, M.; Varesche, S. Diversity of anoxygenic phototrophic bacteria in anaerobic lagoons and facultative stabilization pond used in treatment of sewage. Int. J. Aquat. Biol. 2020, 8, 9–17. [Google Scholar] [CrossRef]
- Fukami, K.; Nishijima, T.; Ishida, Y. Stimulative and inhibitory effects of bacteria on the growth of microalgae. Hydrobiologia 1997, 358, 185–191. [Google Scholar] [CrossRef]
- Nameche, T.; Vasel, J. Hydrodynamic studies and modelization for aerated lagoons and waste stabilization ponds. Water Res. 1998, 32, 3039–3045. [Google Scholar] [CrossRef]
- Persson, J. The hydraulic performance of ponds of various layouts. Urban Water 2000, 2, 243–250. [Google Scholar] [CrossRef]
- Alvarado, A.; Vesvikar, M.; Cisneros, J.; Maere, T.; Goethals, P.; Nopens, I. CFD study to determine the optimal configuration of aerators in a full-scale waste stabilization pond. Water Res. 2013, 47, 4528–4537. [Google Scholar] [CrossRef] [PubMed]
- Coggins, L.; Sounness, J.; Zheng, L.; Ghisalberti, M.; Ghandouani, A. Impact of hydrodynamic reconfiguration with baffles on treatment performance in waste stabilisation ponds: A full-scale experiment. Water 2018, 10, 109. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Lemckert, C.; Roiko, A.; Stration, H. On the hydrodynamics and treatment efficiency of waste stabilisation ponds: From a literature review to a strategic evaluation framework. J. Clean. Prod. 2018, 183, 495–514. [Google Scholar] [CrossRef]
- Alvarado, A.; Sánchez, E.; Durazno, G.; Vesvikar, M.; Nopens, I. CFD analysis of sludge accumulation and hydraulic performance of a waste stabilization pond. Water Sci. Technol. 2012, 66, 2370–2377. [Google Scholar] [CrossRef] [PubMed]
- Ouedraogo, F.; Zhang, J.; Cornejo, P.; Zhang, Q.; Mihelcic, J.; Tejada-Martinez, A. Impact of sludge layer geometry on the hydraulic performance of a waste stabilization pond. Water Res. 2016, 99, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Pougatch, K.; Salcudean, M.; Gartshore, I.; Pagoria, P. Computational modelling of large aerated lagoon hydraulics. Water Res. 2007, 41, 2109–2116. [Google Scholar] [CrossRef] [PubMed]
- Broughton, A.; Shilton, A. Tracer studies on an aerated lagoon. CEUR Workshop Proc. 2012, 1542, 33–36. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Tejada-Martínez, A.; Zhang, Q. Developments in computational fluid dynamics-based modeling for disinfection technologies over the last two decades: A review. Environ. Model. Softw. 2014, 58, 71–85. [Google Scholar] [CrossRef]
- Sah, L.; Rousseau, D.; Hooijmans, C. Numerical Modelling of Waste Stabilization Ponds: Where Do We Stand? Water Air Soil Pollut. 2012, 223, 3155–3171. [Google Scholar] [CrossRef]
- Norvill, Z.; Shilton, A.; Guieysse, B. Emerging contaminant degradation and removal in algal wastewater treatment ponds: Identifying the research gaps. J. Hazard. Mater. 2016, 313, 291–309. [Google Scholar] [CrossRef]
- Zapata, A.; Peña, M. CFD Model to characterize the physical processes of energy transfer in a secondary facultative lagoon. Water Sci. Technol. 2020, 82, 1193–1204. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Chen, H. Using the Köppen classification to quantify climate variation and change: An example for 1901–2010. Environ. Dev. 2013, 6, 69–79. [Google Scholar] [CrossRef]
- ANSYS®. ANSYS Fluent Theory Guide, Release 16.1; Ansys, Inc.: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Patziger, M.; Kiss, K. Analysis of suspended solids transport processes in primary settling tanks. Water Sci. Technol. 2015, 72, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kinyua, A.; Maureen, N.; Zhang, J.; Camacho-Céspedes, F.; Tejada-Martinez, A.; Ergas, S. Use of Physical and Biological Process Models to Understand the Performance of Tubular Anaerobic Digesters. Biochem. Eng. J. 2016, 107, 35–44. [Google Scholar] [CrossRef]
- Pérez, J.; Aldana, G.; Arguello, G. Axial Dispersion Model for Continuous Flow Systems Adjusted Boundary Conditions. Inf. Tecnol. 2016, 27, 169–180. [Google Scholar] [CrossRef][Green Version]
- Environmental Protection Agency. Waste Water Collection, Treatment and Storage; USEPA: Washington, DC, USA, 1995. Available online: https://www3.epa.gov/ttnchie1/ap42/ch04/final/c4s03.pdf (accessed on 25 August 2021).
- Huggins, D.; Piedrahita, R.; Rumsey, T. Analysis of sediment transport modeling using computational fluid dynamics (CFD) for aquaculture raceways. Aquac. Eng. 2004, 31, 277–293. [Google Scholar] [CrossRef]
- Pevere, A.; Guibaud, G.; van Hullebusch, E.; Lens, P.; Baudu, M. Viscosity evolution of anaerobic granular sludge. Biochem. Eng. J. 2006, 27, 315–322. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Longman Group Ltd.: New York, NY, USA, 1995. [Google Scholar]
- Wadnerkar, D.; Ranjeet, P.; Moses, O.; Vishnu, K. CFD simulation of solid-liquid stirred tanks. Adv. Powder Technol. J. 2012, 23, 445–453. [Google Scholar] [CrossRef]
- Wood, M.; Greenfield, P.; Howes, T.; Johns, M.; Keller, J. Computational fluid dynamic modelling of wastewater ponds to improve design. Water Sci. Technol. 1995, 31, 111–118. [Google Scholar] [CrossRef]
- Sah, L.; Diederik, P.; Hooijmans, C.; Piet, N. 3D model for a secondary facultative pond. Ecol. Model. 2011, 222, 1592–1603. [Google Scholar] [CrossRef]
- Hernández, R.; Fernández, C.; Baptista, P. Research Methodology, 5th ed.; Mc Graw Hill: Mexico City, Mexico, 2010. [Google Scholar]
- Shilton, A.; Harrison, J. Development of guidlines for improved hydraulic design of waste stabilisation ponds. Water Sci. Technol. 2003, 48, 173–180. [Google Scholar] [CrossRef] [PubMed]

| Zone | Boundary | Value | Units | Observations |
|---|---|---|---|---|
| Inlet | Velocity inlet | 0.115 | m·s−1 | Turbulence Intensity = 5.29% Dh = 0.0546 m Re = 5822 I = 0.053% k = 5.78 × 10−5 J·kg−1 ε = 8.00 × 10−6 m2·s−3 Conc.: 0.041% w/v, UDF |
| Outlet | Outflow | 1.0 Fraction | N.A | Turbulence Intensity = 7.3% Re = 506 I = 0.073 (%) k = 8.00 × 10−7 J·kg−1 ε = 1.00 × 10−8 m2·s−3 |
| Walls | Stationary Wall | --- | N.A | Polyethylene of low density |
| Surface | Free surface | 0.81 | m·s−1 | The prevailing direction of the wind was used with an average speed of 0.81 m·s−1 and northeast (NE) direction. |
| Mesh No. | Mesh Cell Size (m) | Velocity of Fluid (m·s−1) | Suspended Solids Concentration (% w/v) |
|---|---|---|---|
| 1 | 0.500 | 0.01340 | 0.2930 |
| 2 | 0.050 | 0.01120 | 0.2240 |
| 3 | 0.025 | 0.01123 | 0.2221 |
| Parameter | Study 1 | Single-Phase CFD Model | Two-Phase CFD Model |
|---|---|---|---|
| Experimental retention time (h) | 75 | 62 | 70 |
| Theoretical retention time (h) | 95.76 | 95.76 | 95.76 |
| Error (%) | 22 | 35 | 26 |
| Variance (σ2) | 4602 | 3057 | 4607 |
| Dispersion number (δ) | 0.436 | 0.478 | 0.403 |
| Depth (m) | PL/2 | PL/2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Average Concentration | UDF “Define Profile” | |||||||
| Concentration (% w/v) | ||||||||
| Exp. | SD | Sim. | SD | %E | Sim. | SD | %E | |
| 0.05 | 0.017 | 0.0023 | 0.026 | 0.0014 | 48 | 0.019 | 0.0010 | 12 |
| 0.45 | 0.016 | 0.0032 | 0.053 | 0.0037 | 230 | 0.019 | 0.0017 | 18 |
| 1.40 | 0.097 | 0.0023 | 0.094 | 0.0016 | 3 | 0.099 | 0.0009 | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapata Rivera, A.M.; Ducoste, J.; Peña, M.R.; Portapila, M. Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment. Water 2021, 13, 2356. https://doi.org/10.3390/w13172356
Zapata Rivera AM, Ducoste J, Peña MR, Portapila M. Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment. Water. 2021; 13(17):2356. https://doi.org/10.3390/w13172356
Chicago/Turabian StyleZapata Rivera, Andres Mauricio, Joel Ducoste, Miguel Ricardo Peña, and Margarita Portapila. 2021. "Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment" Water 13, no. 17: 2356. https://doi.org/10.3390/w13172356
APA StyleZapata Rivera, A. M., Ducoste, J., Peña, M. R., & Portapila, M. (2021). Computational Fluid Dynamics Simulation of Suspended Solids Transport in a Secondary Facultative Lagoon Used for Wastewater Treatment. Water, 13(17), 2356. https://doi.org/10.3390/w13172356







