Droplet Evaporation in a Gas-Droplet Mist Dilute Turbulent Flow behind a Backward-Facing Step
Abstract
:1. Introduction
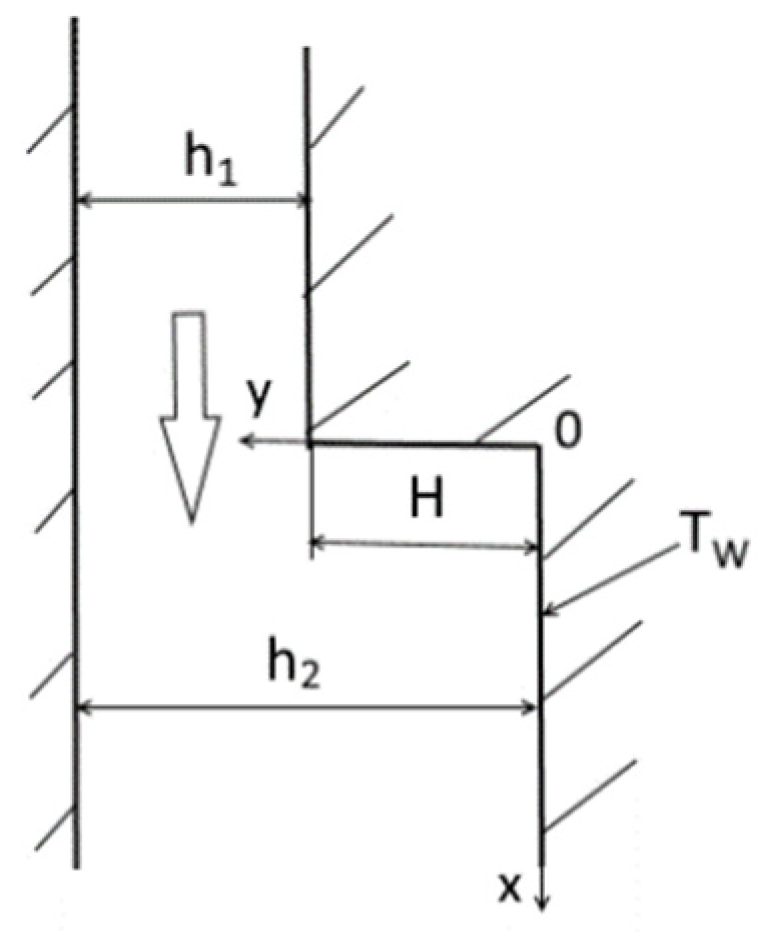
2. Mathematical Model and Method of Numerical Realization
3. Numerical Procedures and Validation
4. The Numerical Results and Discussion
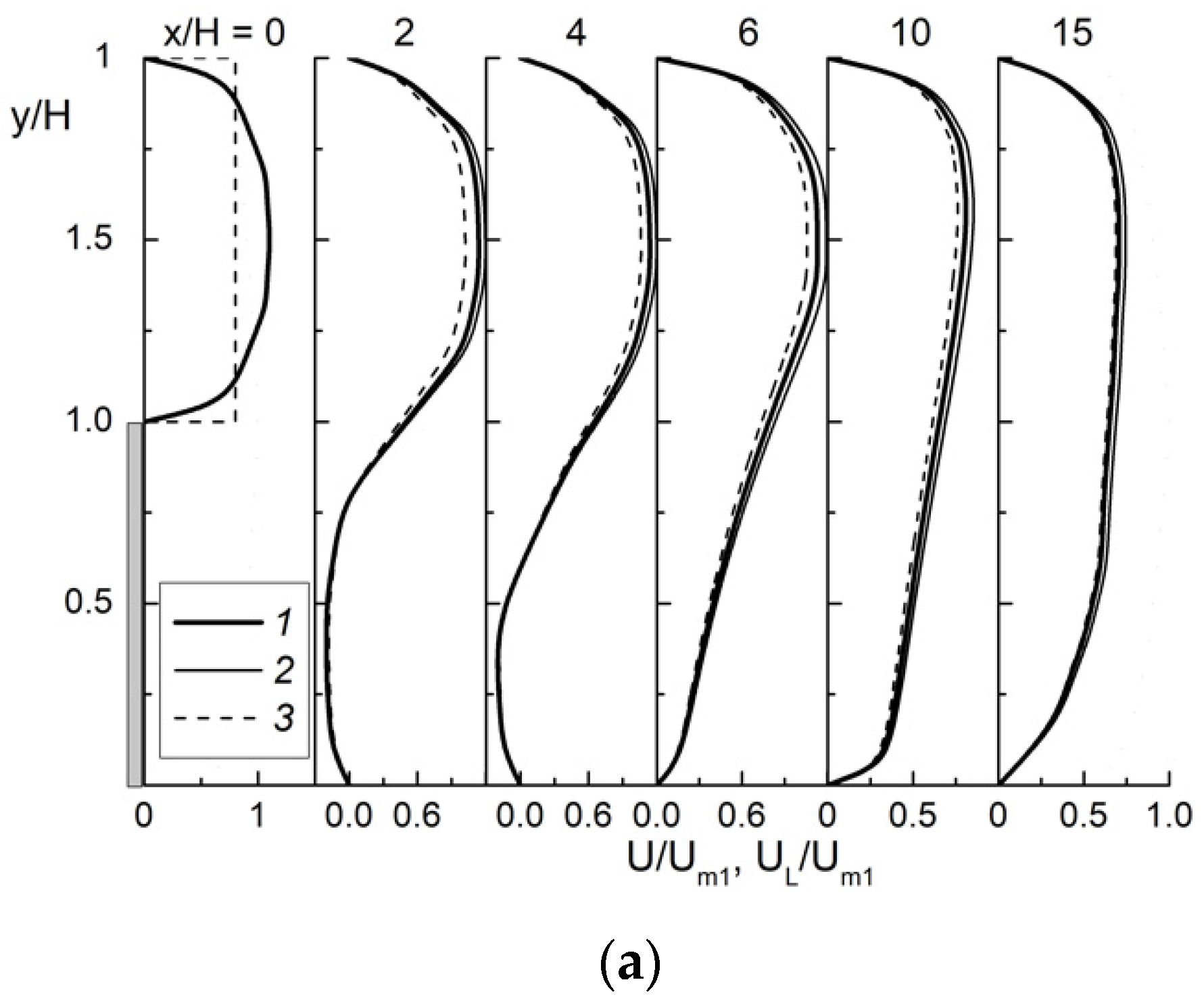
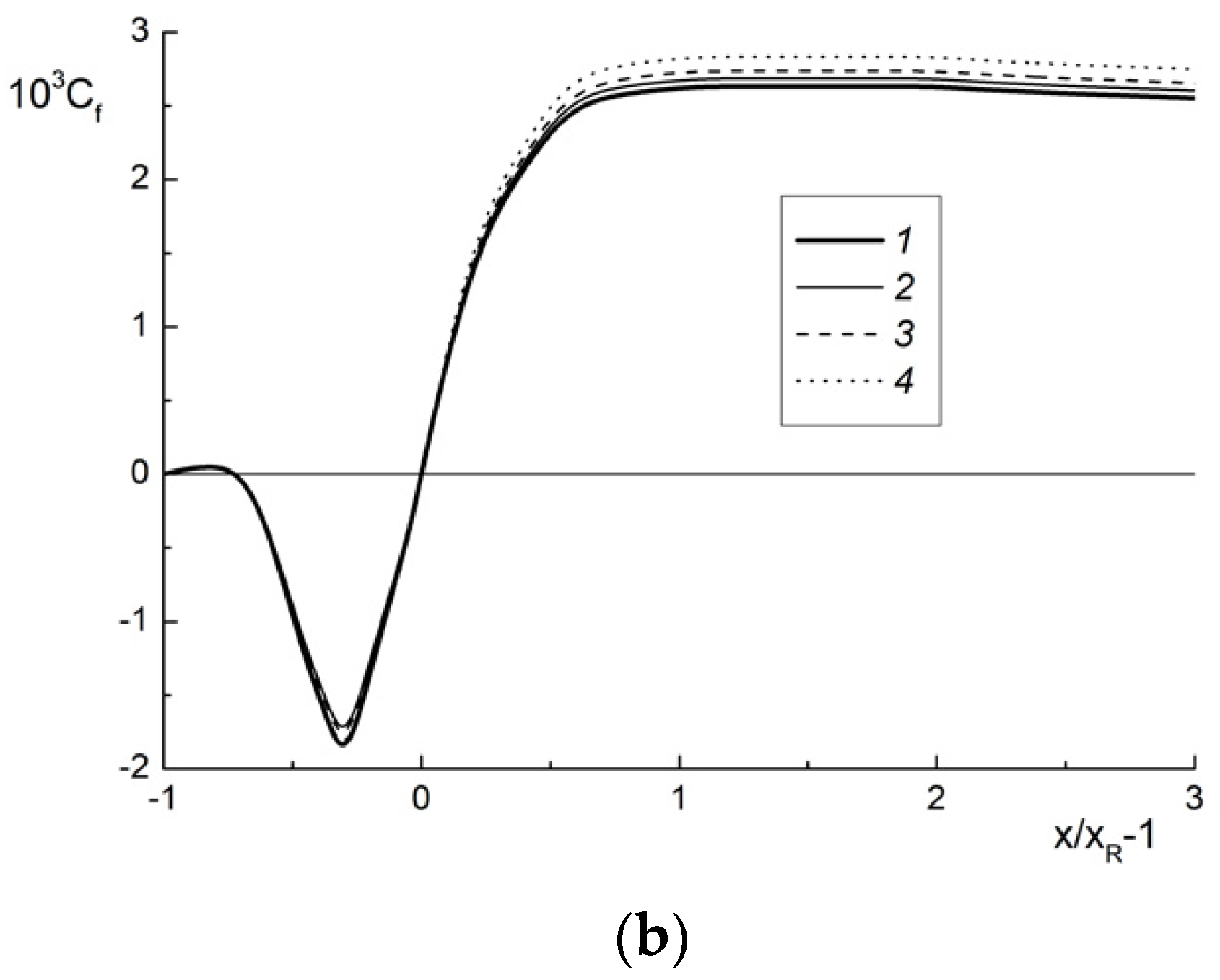
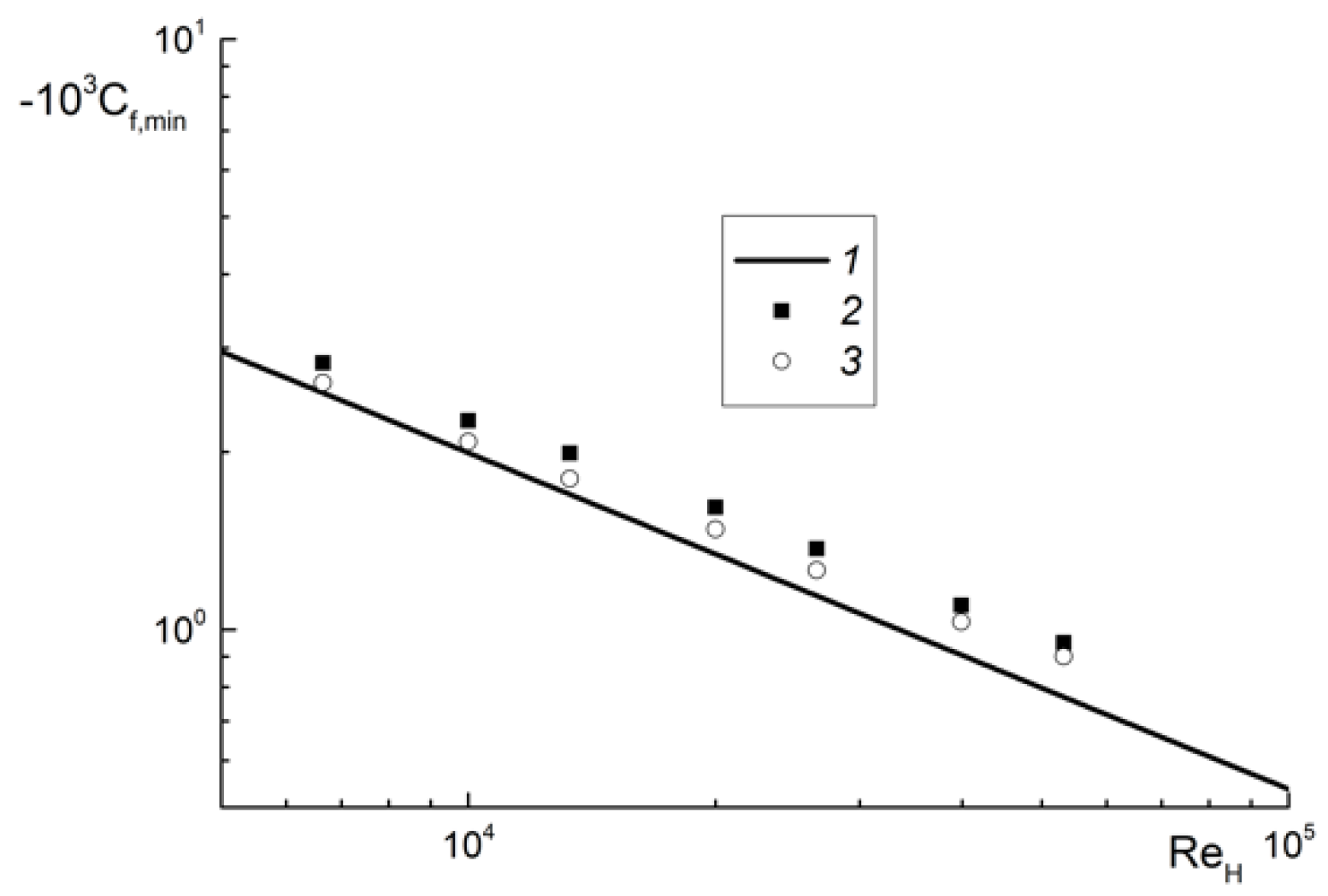
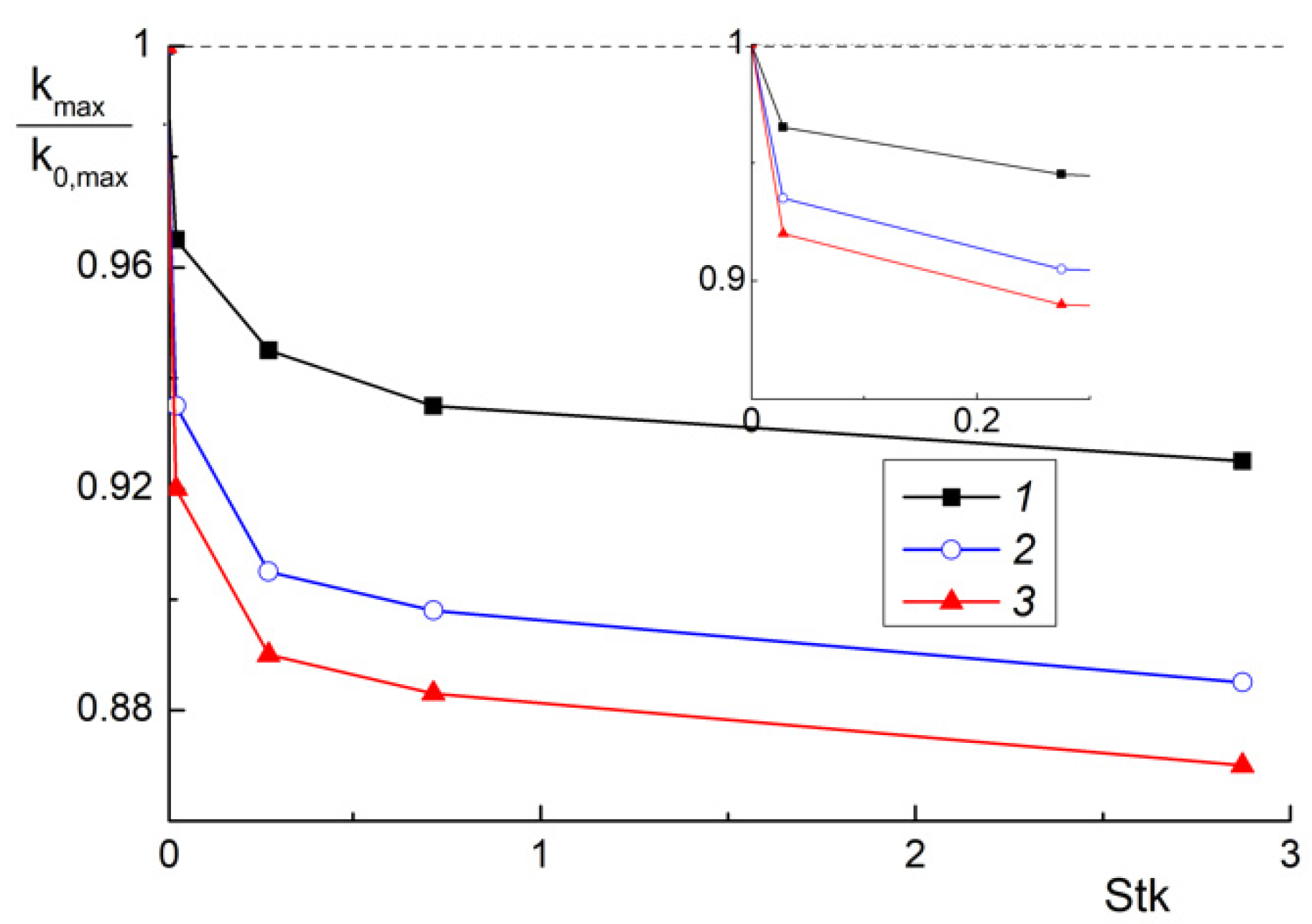
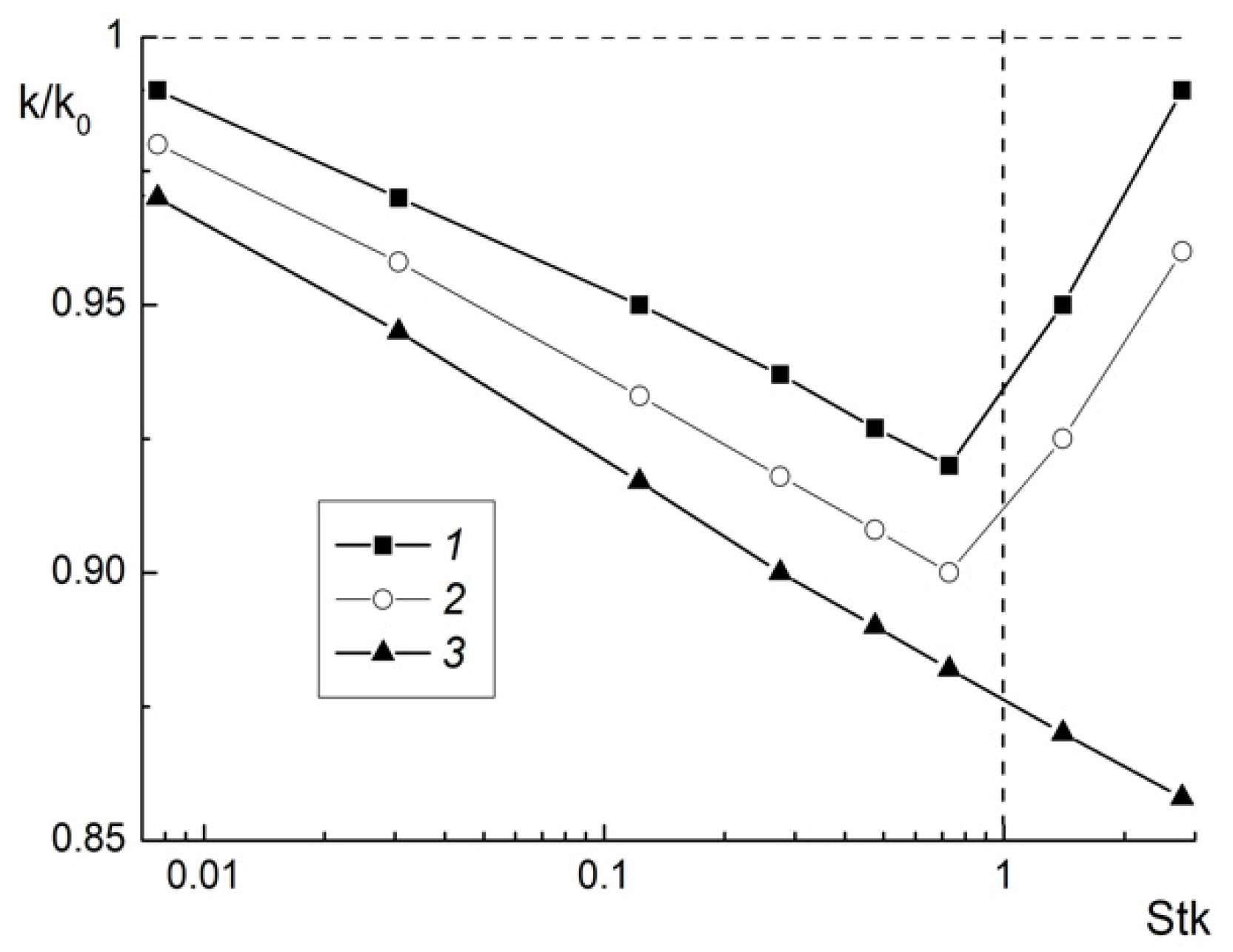
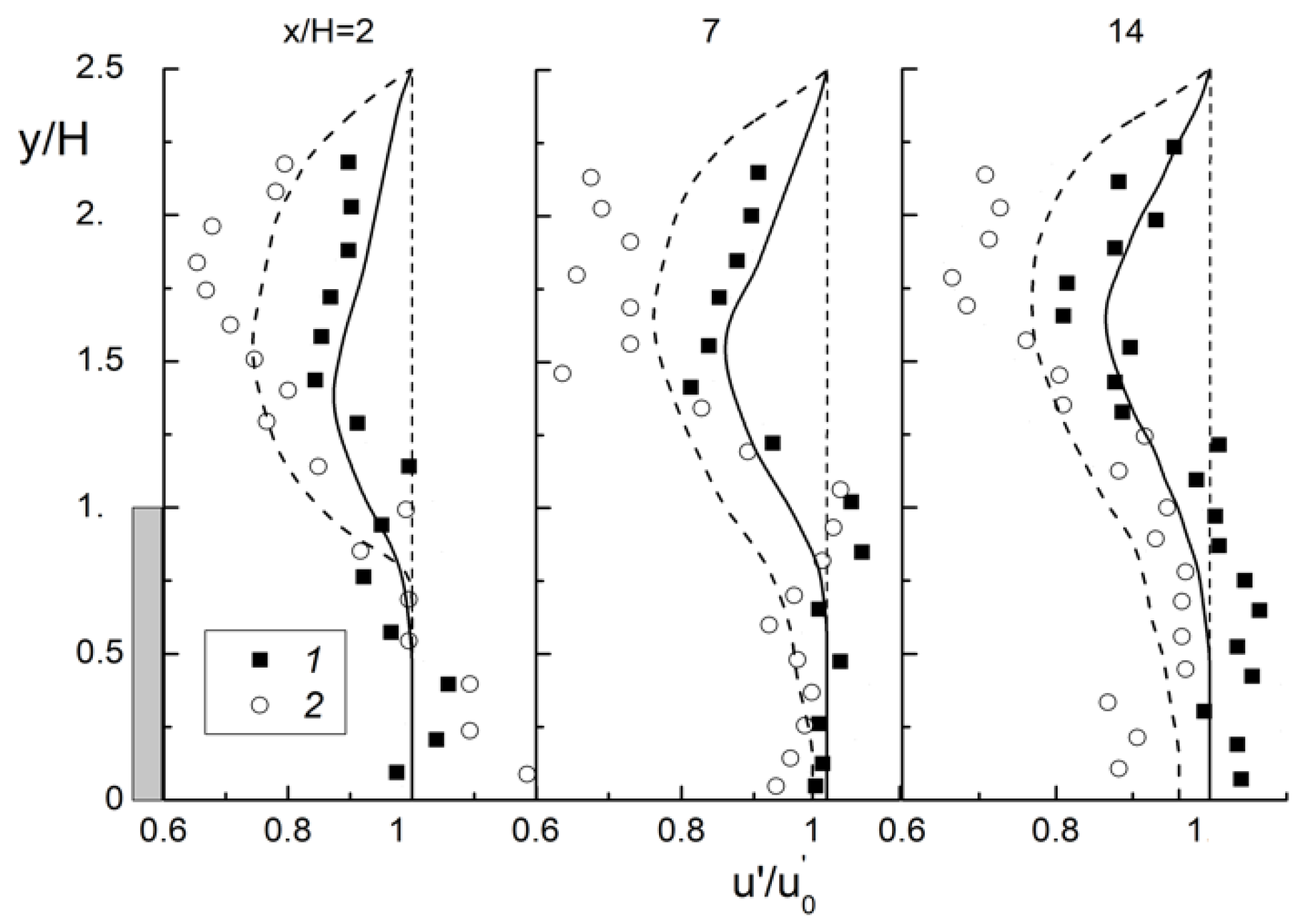
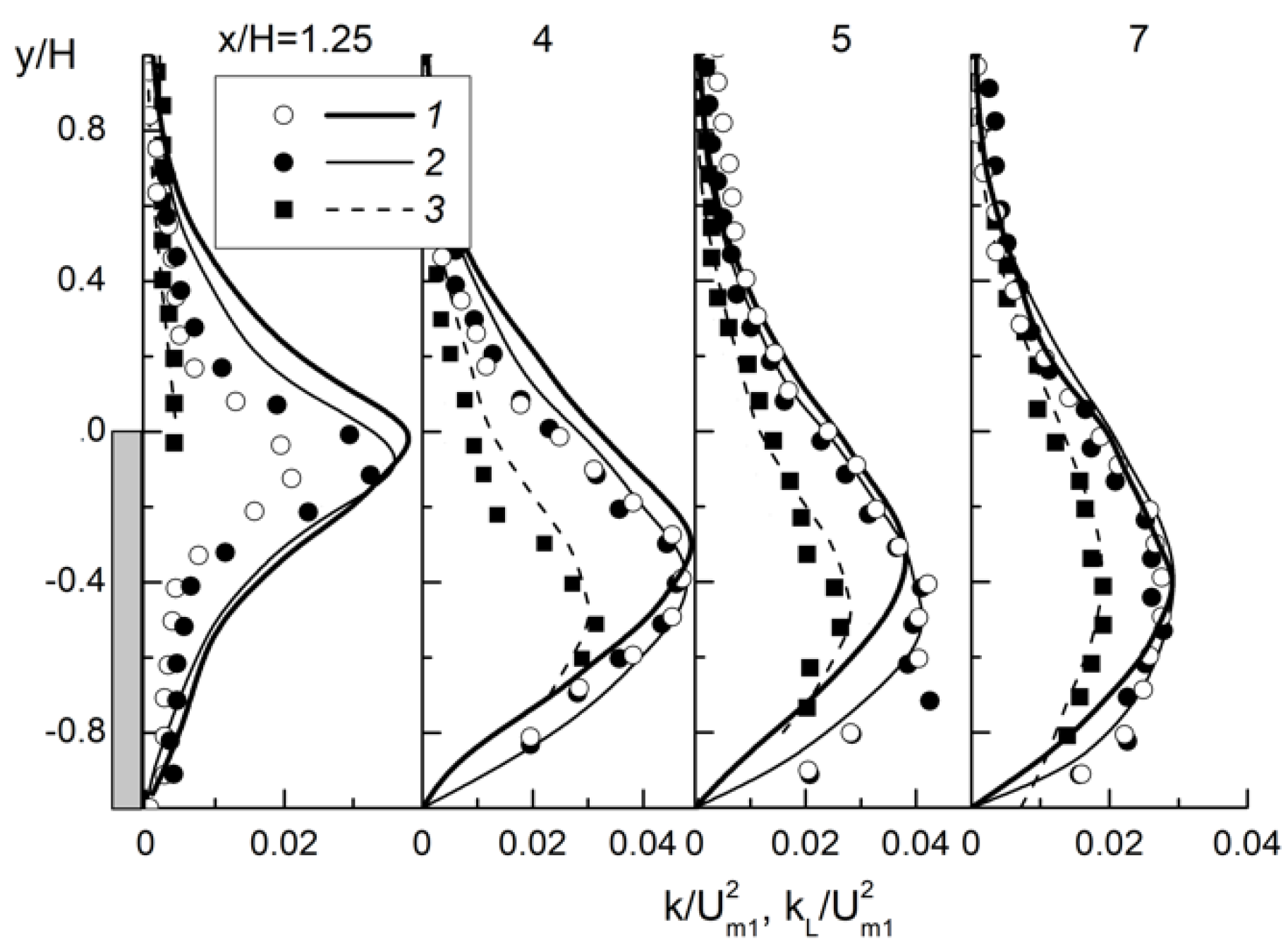
4.1. Flow Structure, Wall Friction and Turbulence Quantities
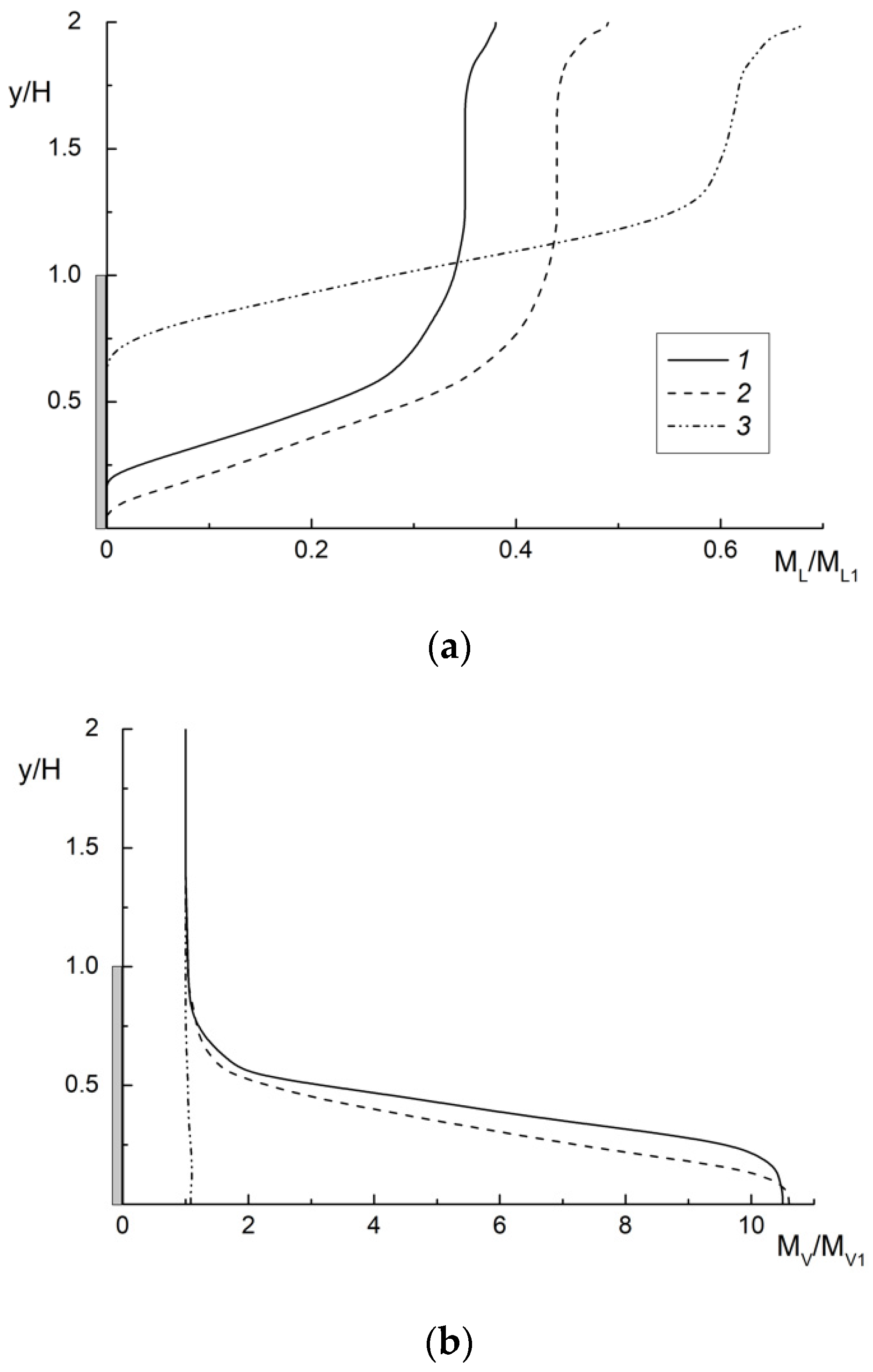
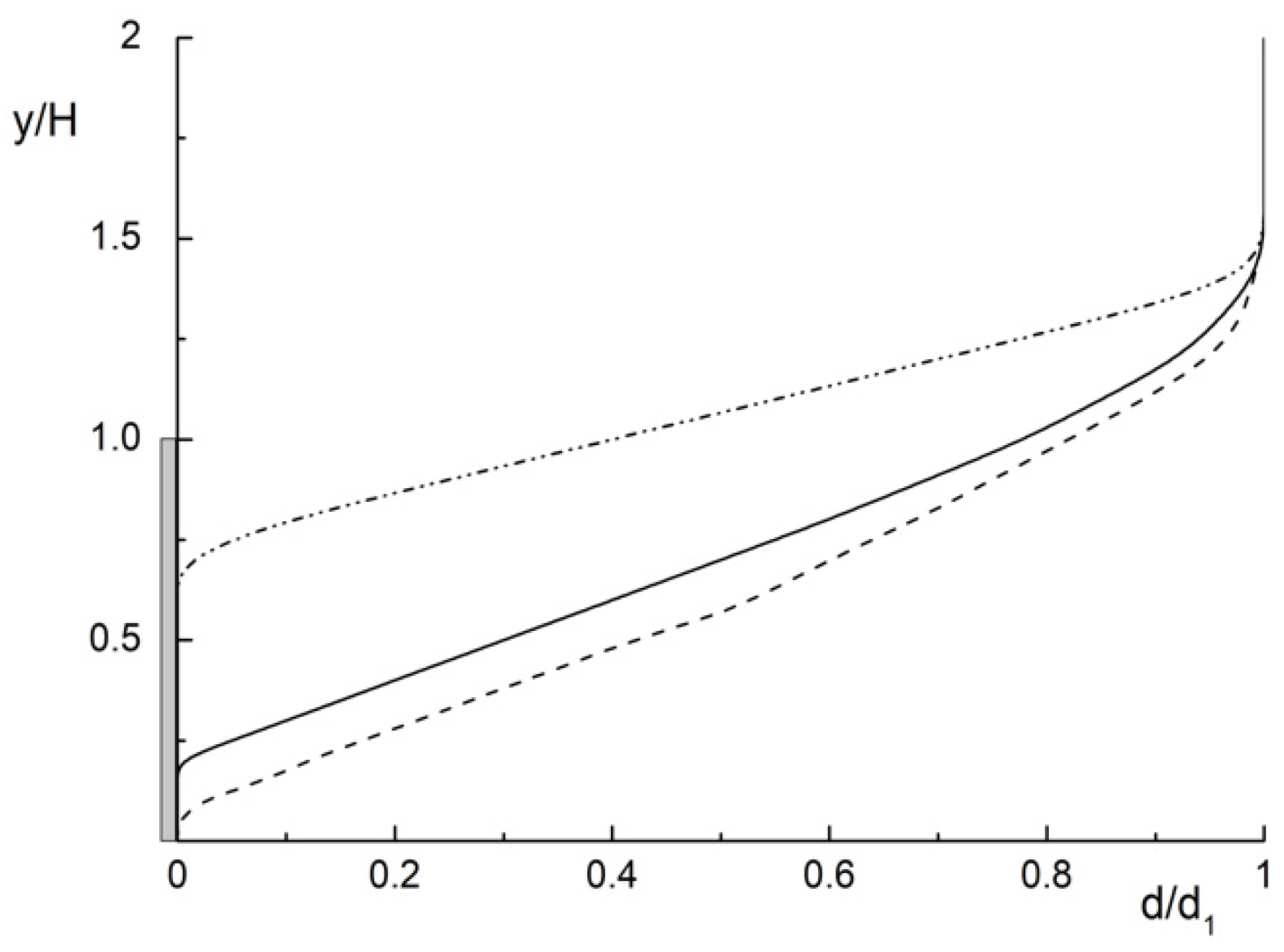
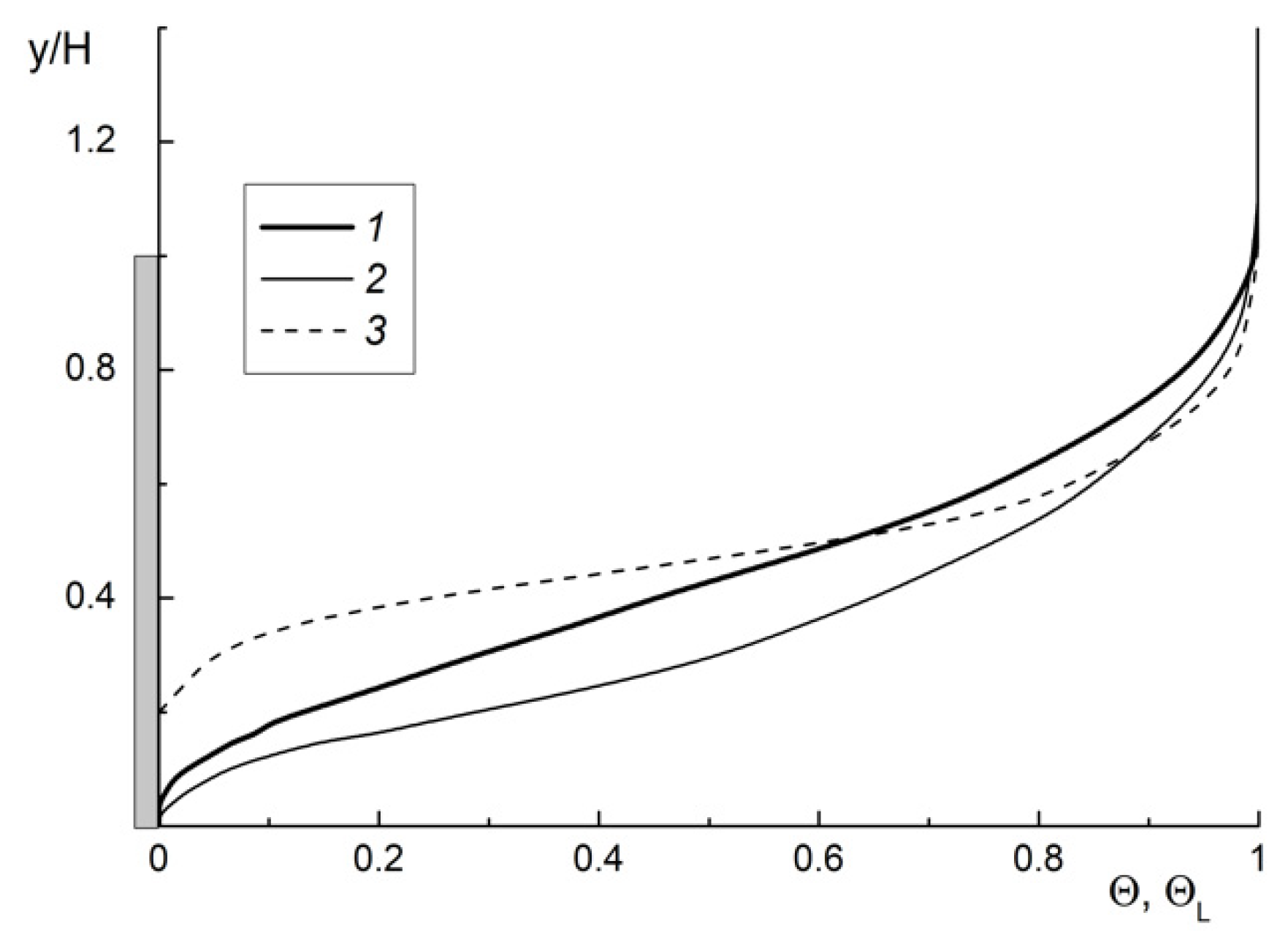
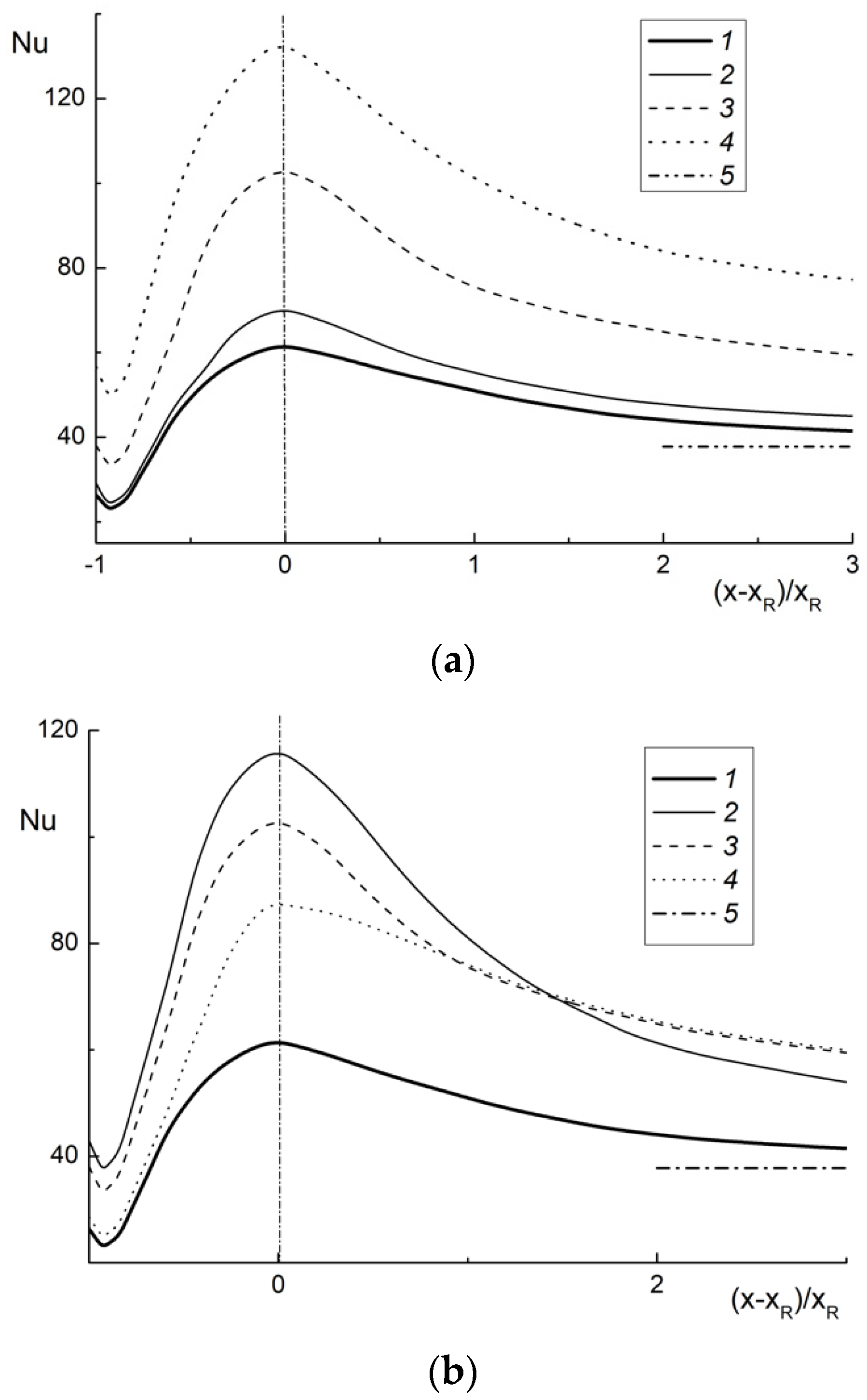
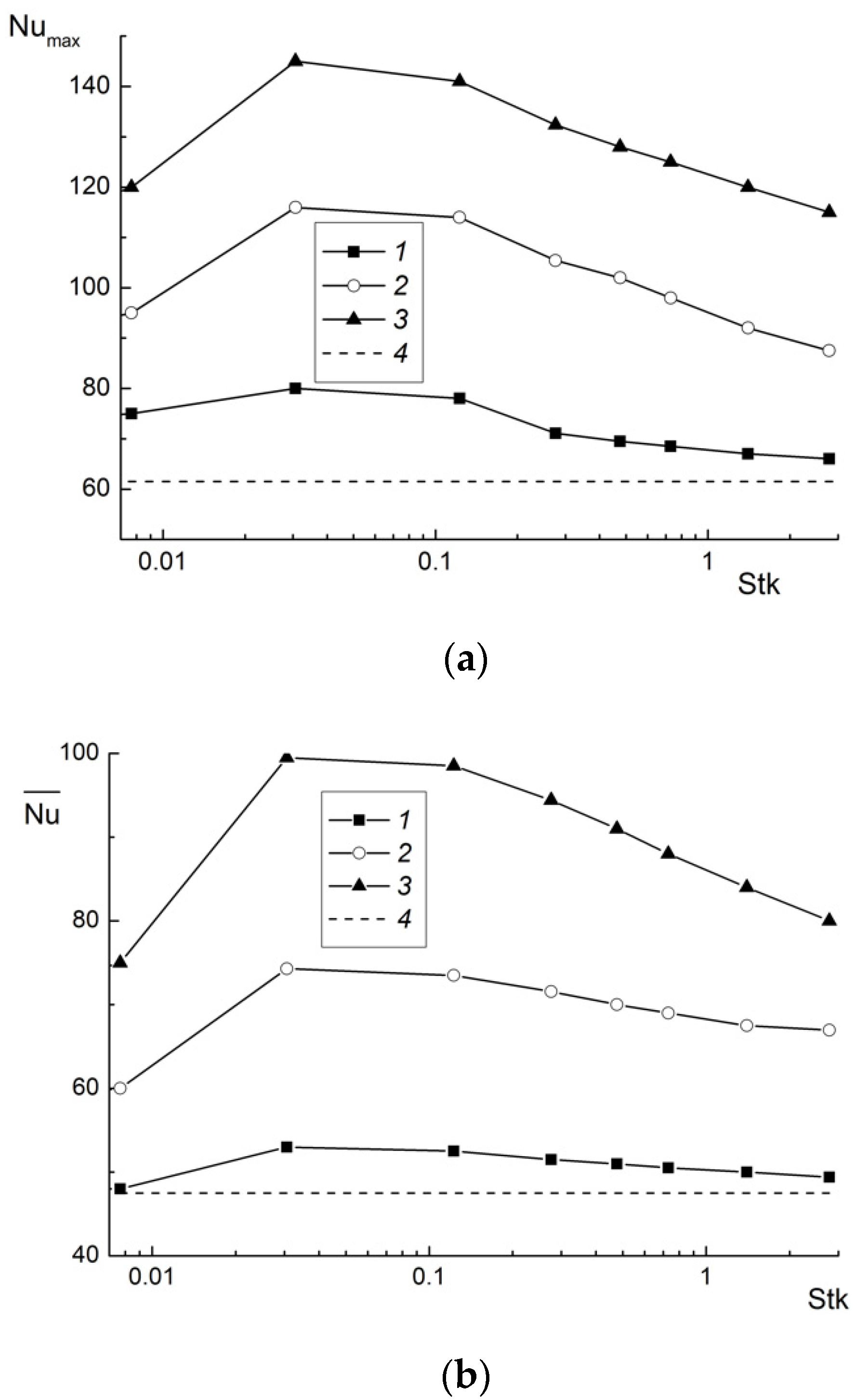
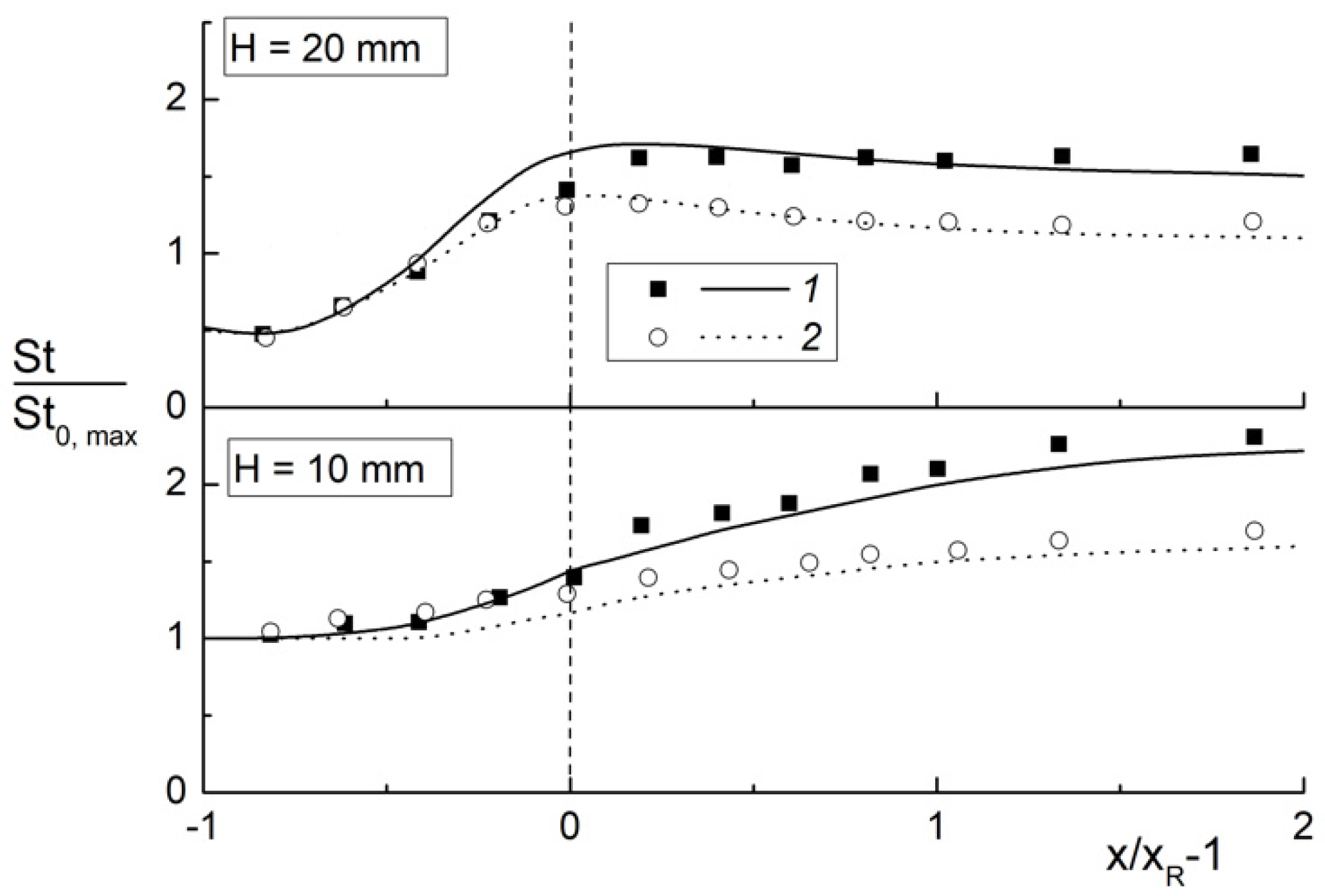
4.2. Heat Transfer
5. Comparison with the Results Obtained for Gas-Dispersed and Droplet-Laden Flows in a Backward-Facing Step
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| wall friction coefficient | |
| CP | heat capacity |
| d | droplet diameter |
| ER = (H + h1)/h1 | expansion ratio |
| h1 | height of the duct before the sudden expansion |
| h2 | height of the duct after the sudden expansion |
| H | step height |
| turbulent kinetic energy | |
| L | duct length |
| ML | mass fraction |
| Nusslet number | |
| ReH = Um1H/ν | the Reynolds number, based on the step height |
| Stk = τ/τf | the mean Stokes number |
| T | temperature |
| UL | the mean droplet velocity |
| Um1 | mean-mass flow velocity |
| US | the fluid (gas) velocity seen by the droplet |
| U* | friction velocity |
| the Weber number | |
| x | streamwise coordinate |
| xR | position of the flow reattachment point |
| xNu_max | position of the peak of heat transfer rate |
| y | distance normal from the wall |
| Subscripts | |
| 0 | single-phase fluid (air) flow |
| 1 | initial condition |
| W | wall |
| L | liquid |
| m | mean-mass |
| Greek | |
| Φ | volume fraction |
| ε | dissipation of the turbulent kinetic energy |
| λ | thermal conductivity |
| ρ | density |
| μ | the dynamic viscosity |
| ν | kinematic viscosity |
| τ | the particle relaxation time |
| τW | wall shear stress |
| Acronym | |
| BFS | backward-facing step |
| CV | control volume |
| RANS | Reynolds-averaged Navier-Stokes |
| SMC | second moment closure |
| TKE | turbulent kinetic energy |
References
- Eaton, J.K.; Johnston, J.P. A review of research on subsonic turbulent flow reattachment. AIAA J. 1981, 19, 1093–1100. [Google Scholar] [CrossRef]
- Simpson, R.L. Aspects of turbulent boundary-layer separation. Prog. Aerosp. Sci. 1996, 32, 457–521. [Google Scholar] [CrossRef]
- Ota, T. A survey of heat transfer in separated and reattached flows. Appl. Mech. Rev. 2000, 53, 219–235. [Google Scholar] [CrossRef]
- Terekhov, V.I.; Bogatko, T.V.; Dyachenko, A.Y.; Smulsky, Y.I.; Yarygina, N.I. Heat Transfer in Subsonic Separated Flows; Novosibirsk State Technical University Publishing House: Novosibirsk, Russia, 2016. (In Russian) [Google Scholar]
- Chen, L.; Asai, K.; Nonomura, T.; Xi, G.N.; Liu, T.S. A review of backward-facing step (BFS) flow mechanisms, heat transfer and control. Therm. Sci. Eng. Prog. 2018, 6, 194–216. [Google Scholar] [CrossRef]
- Ruck, B.; Makiola, B. Particle dispersion in a single-sided backward-facing step flow. Int. J. Multiph. Flow 1988, 14, 787–800. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 314, 97–117. [Google Scholar] [CrossRef]
- Chan, C.K.; Zhang, H.Q.; Lau, K.S. Numerical simulation of gas-particle flows behind a backward-facing step using an improved stochastic separated flow model. J. Comp. Mech. 2001, 27, 412–417. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Kozelev, M.V.; Pershukov, V.A. Prediction of turbulent gas-dispersed channel flow with recirculation zones. Fluid Dyn. 1994, 29, 65–75. [Google Scholar] [CrossRef]
- Mohanarangam, K.; Tu, J.Y. Two-fluid model for particle-turbulence interaction in a backward-facing step. AIChE J. 2007, 53, 2254–2264. [Google Scholar] [CrossRef]
- Benavides, A.; Van Vachem, B. Eulerian–Eulerian prediction of dilute turbulent gas-particle flow in a backward-facing step. Int. J. Heat Fluid Flow 2009, 30, 452–461. [Google Scholar] [CrossRef]
- Mukin, R.V.; Zaichik, L.I. Nonlinear algebraic Reynolds stress model for two-phase turbulent flows laden with small heavy particles. Int. J. Heat Fluid Flow 2012, 33, 81–91. [Google Scholar] [CrossRef]
- Riella, M.; Kahraman, R.; Tabor, G.R. Reynolds-averaged two-fluid model prediction of moderately dilute fluid-particle flow over a backward-facing step. Int. J. Multiph. Flow 2018, 106, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Sazhin, S.S. Modelling of fuel droplet heating and evaporation: Recent results and unsolved problems. Fuel 2017, 196, 69–101. [Google Scholar] [CrossRef]
- Abu Talib, A.R.; Hilo, A.K. Fluid flow and heat transfer over corrugated backward facing step channel. Case Stud. Therm. Eng. 2021, 24, 100862. [Google Scholar] [CrossRef]
- Hishida, K.; Nagayasu, T.; Maeda, M. Augmentation of convective heat transfer by an effective utilization of droplet inertia. Int. J. Heat Mass Transfer 1995, 38, 1773–1785. [Google Scholar] [CrossRef]
- Elgobashi, S. On predicting particle-laden turbulent flows. Appl. Scient. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M. A statistical model for predicting the fluid displaced/added mass and displaced heat capacity effects on transport and heat transfer of arbitrary density particles in turbulent flows. Int. J. Heat Mass Transf. 2011, 54, 4247–4265. [Google Scholar] [CrossRef]
- Miyafuji, Y.; Senaha, I.; Oyakawa, K.; Hiwada, M. Enhancement of Heat Transfer at Downstream of a Backward-Facing Step by Mist Flow. In Proceedings of the 2nd International Conference on Jets, Wakes and Separated Flows ICJWSF-2008, Berlin, Germany, 16–18 September 2008. [Google Scholar]
- Wang, B.; Zhang, H.Q.; Wang, X.L. Large eddy simulation of particle response to turbulence along its trajectory in a backward-facing step turbulent flow. Int. J. Heat Mass Transf. 2006, 49, 415–420. [Google Scholar] [CrossRef]
- Fadai-Ghotbi, A.; Manceau, R.; Boree, J. Revisiting URANS computations of the backward-facing step flow using second moment closures. Influence of the numerics. Flow Turbul. Combust. 2008, 81, 395–410. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Second moment closure modelling of flow, turbulence and heat transfer in droplet-laden mist flow in a vertical pipe with sudden expansion. Int. J. Heat Mass Transf. 2013, 66, 210–222. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. The effect of droplets evaporation on turbulence modification and heat transfer enhancement in a two-phase mist flow downstream of a pipe sudden expansion. Flow Turbul. Combust. 2017, 98, 341–354. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical modeling of two-phase flow. Ann. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A 1991, 3, 446–456. [Google Scholar] [CrossRef]
- Derevich, I.V.; Zaichik, L.I. Particle deposition from a turbulent flow. Fluid Dyn. 1988, 23, 722–729. [Google Scholar] [CrossRef]
- Zaichik, L.I. A statistical model of particle transport and heat transfer in turbulent shear flows. Phys. Fluids 1999, 11, 1521–1534. [Google Scholar] [CrossRef]
- Elgobashi, S. An Updated Classification Map of Particle-Laden Turbulent Flows. In Proceedings of the IUTAM Symposium on Computational Approaches to Multiphase Flow, Fluid Mechanics and Its Applications, Argonne National Laboratory, Lemont, IL, USA, 4–7 October 2004; Volume 81, pp. 3–10. [Google Scholar]
- Gore, R.A.; Crowe, C.T. The effect of particle size on modulating turbulent intensity. Int. J. Multiph. Flow 1989, 15, 279–285. [Google Scholar] [CrossRef]
- Lin, S.P.; Reitz, R.D. Drop and spray formation from a liquid jet. Ann. Rev. Fluid Mech. 1998, 30, 85–105. [Google Scholar] [CrossRef]
- Snegirev, A.Y. Transient temperature gradient in a single-component vaporizing droplet. Int. J. Heat Mass Transf. 2013, 65, 80–94. [Google Scholar] [CrossRef]
- Derevich, I.V. Statistical modelling of mass transfer in turbulent two-phase dispersed flows. 1. Model development. Int. J. Heat Mass Transf. 2000, 43, 3709–3723. [Google Scholar] [CrossRef]
- Wang, H.G.; Zhang, C.G.; Xiong, H.B. Growth and collapse dynamics of a vapor bubble near or at a wall. Water 2021, 13, 12. [Google Scholar] [CrossRef]
- Hanjalic, K.; Jakirlic, S. Contribution towards the second-moment closure modelling of separating turbulent flows. Comput. Fluids 1998, 27, 137–156. [Google Scholar] [CrossRef]
- Kasagi, N.; Matsunaga, A. Three-dimensional particle-tracking velocimetry measurement of turbulence statistics and energy budget in a backward-facing step flow. Int. J. Heat Fluid Flow 1995, 16, 477–485. [Google Scholar] [CrossRef]
- Vogel, J.C.; Eaton, J.K. Combined heat transfer and fluid dynamics measurements downstream of a backward facing step. ASME J. Heat Transf. 1985, 107, 922–929. [Google Scholar] [CrossRef]
- Tihon, J.; Legrand, J.; Legentilhomme, P. Near-wall investigation of backward-facing step flows. Exp. Fluids 2001, 31, 484–493. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomov, M.A.; Terekhov, V.I. Droplet Evaporation in a Gas-Droplet Mist Dilute Turbulent Flow behind a Backward-Facing Step. Water 2021, 13, 2333. https://doi.org/10.3390/w13172333
Pakhomov MA, Terekhov VI. Droplet Evaporation in a Gas-Droplet Mist Dilute Turbulent Flow behind a Backward-Facing Step. Water. 2021; 13(17):2333. https://doi.org/10.3390/w13172333
Chicago/Turabian StylePakhomov, Maksim A., and Viktor I. Terekhov. 2021. "Droplet Evaporation in a Gas-Droplet Mist Dilute Turbulent Flow behind a Backward-Facing Step" Water 13, no. 17: 2333. https://doi.org/10.3390/w13172333
APA StylePakhomov, M. A., & Terekhov, V. I. (2021). Droplet Evaporation in a Gas-Droplet Mist Dilute Turbulent Flow behind a Backward-Facing Step. Water, 13(17), 2333. https://doi.org/10.3390/w13172333





