Differences in the Ice Particle Shattering Impact on the CIP Measurements in the Stratiform Cloud Region and the Embedded Convection Region
Abstract
:1. Introduction
2. Instrument and Data
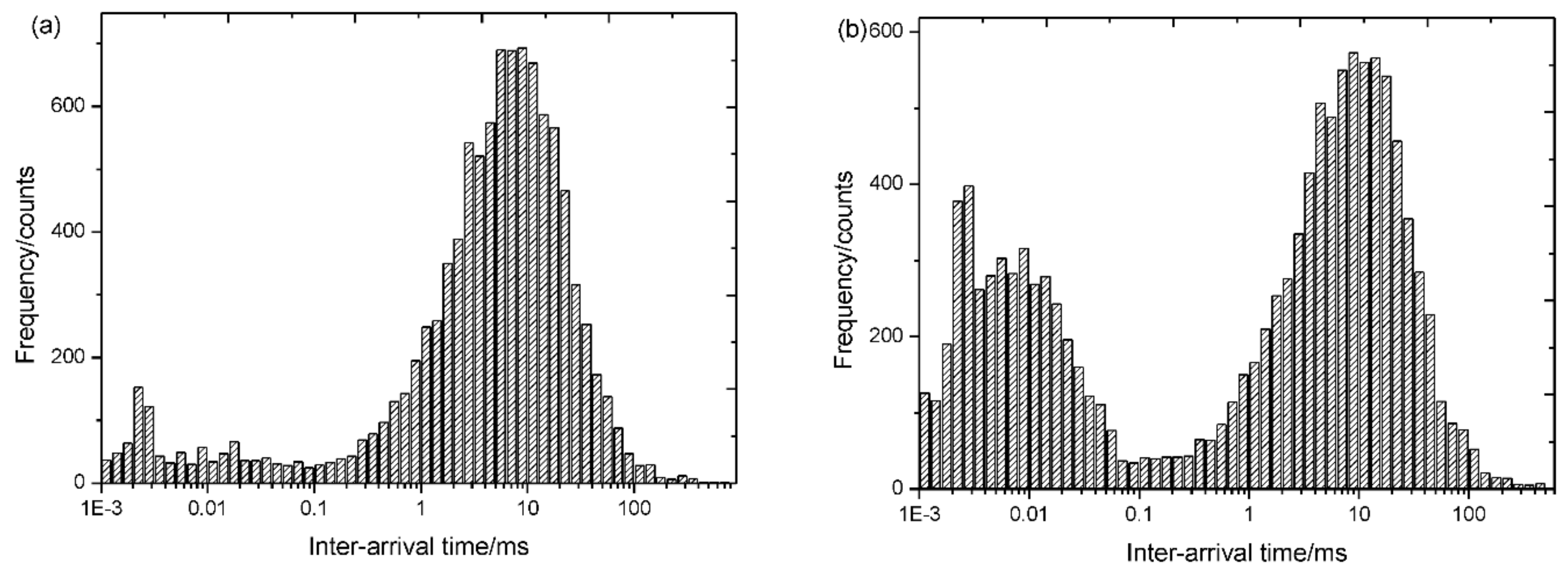
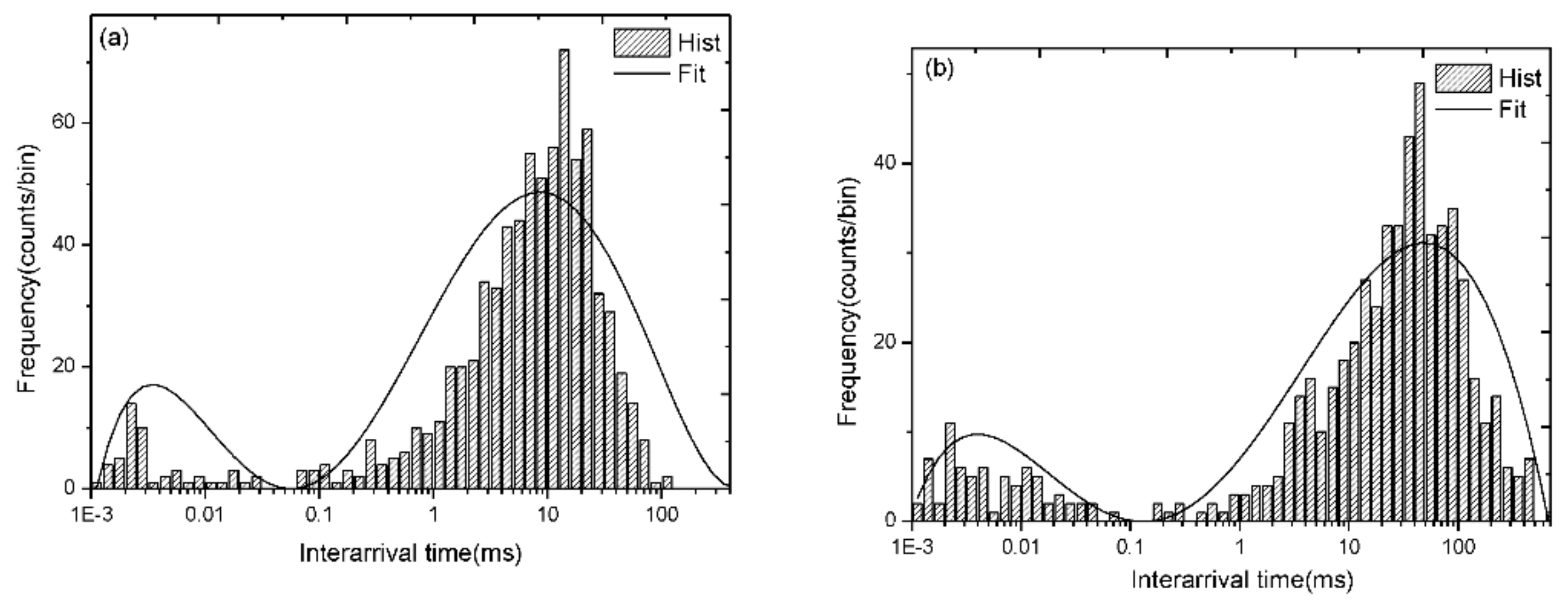
3. Time-Variant Interarrival Time Threshold Method
- The data for analysis are read and the arrival time of the particle is extracted.
- Taking 10 s as a statistical period and on the premise that the number of particles meets the statistical requirements, the interarrival time of the particles is counted in the form of histogram statistics.
- The distribution of the particles’ interarrival time is fitted using a polynomial fitting method.
- If the fitted mode is consistent with a double mode, the threshold of the interarrival time can be determined as twice the peak value in the short mode.
- Then, the shattered fragments in the statistical period can be identified using the determined threshold.
4. Shattering Effects on the Cloud Microphysical Parameters Measurement
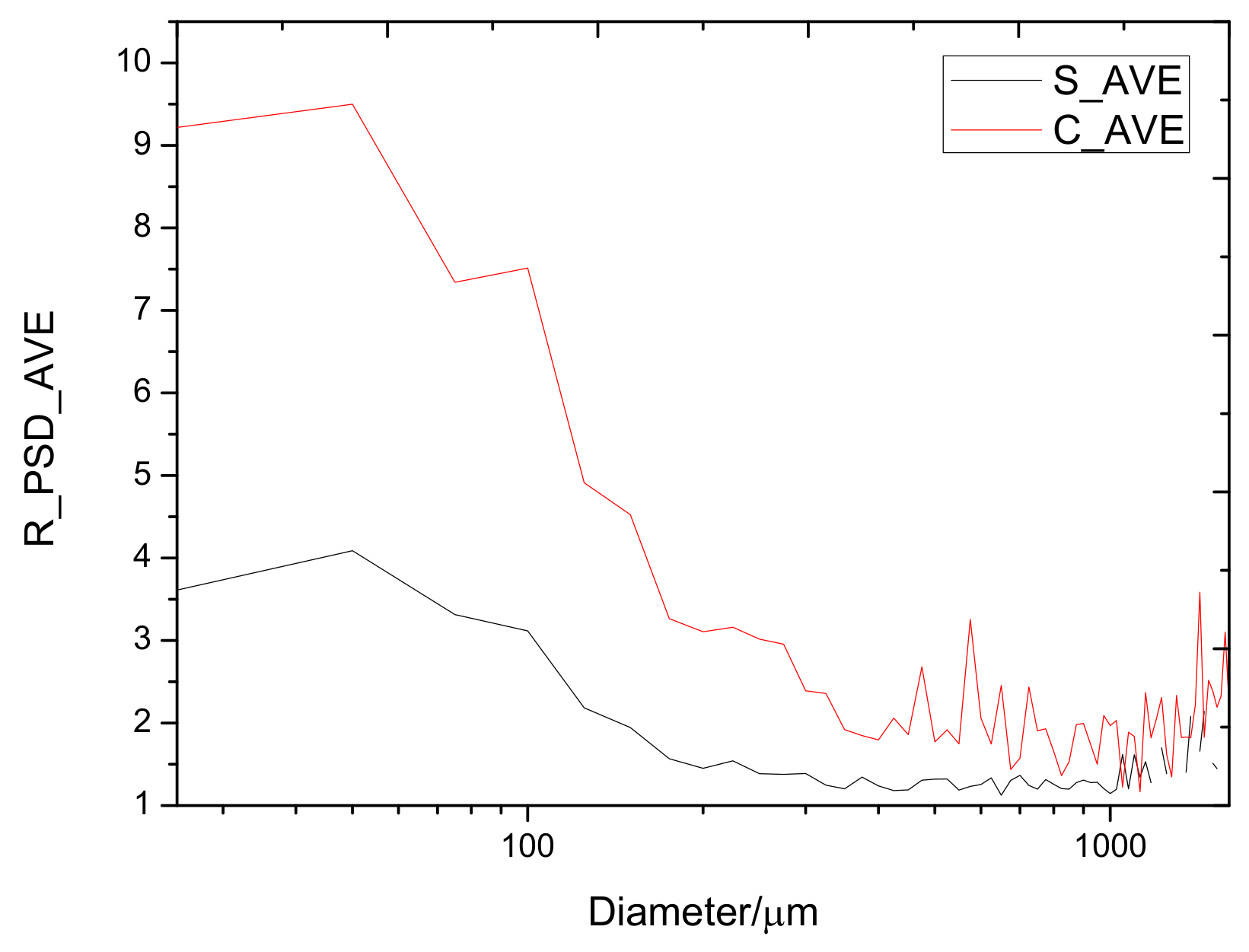
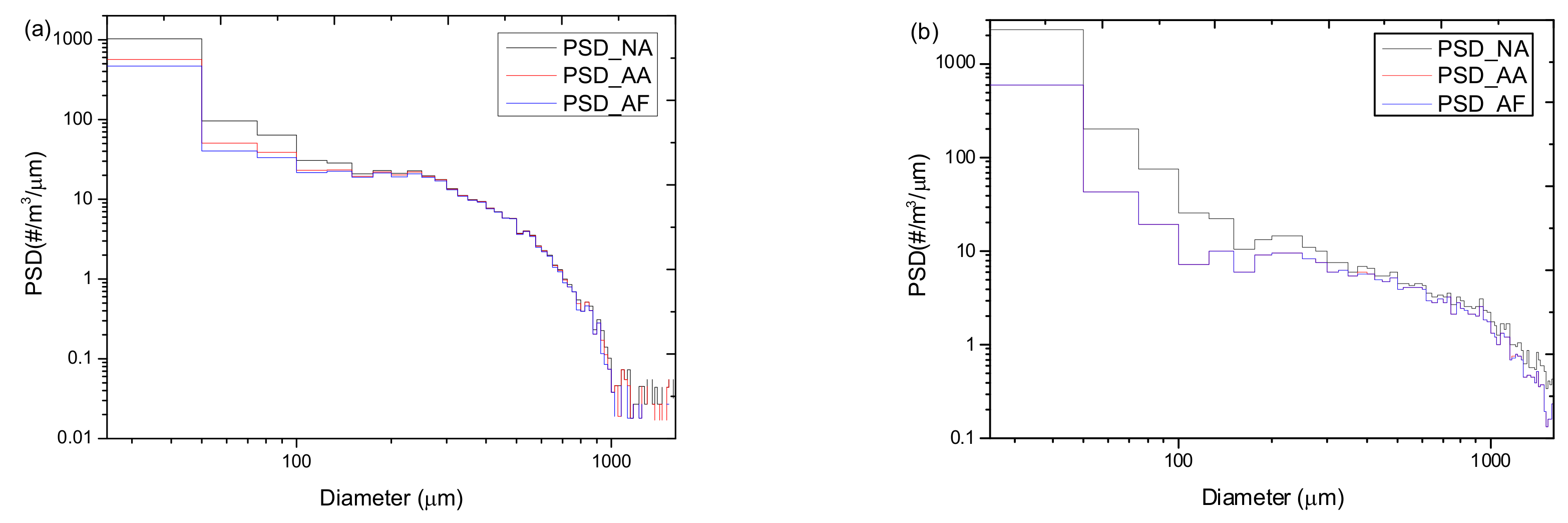
4.1. Effects on Cloud Particle Size Distribution
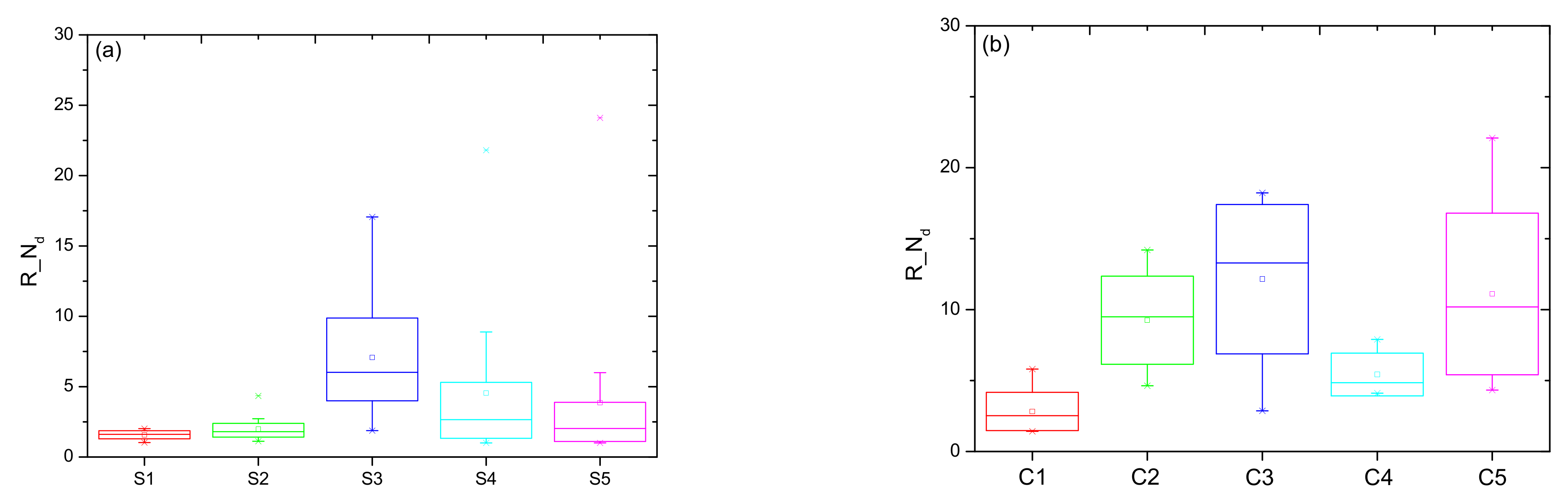
4.2. Effects on the Particle Number Concentration
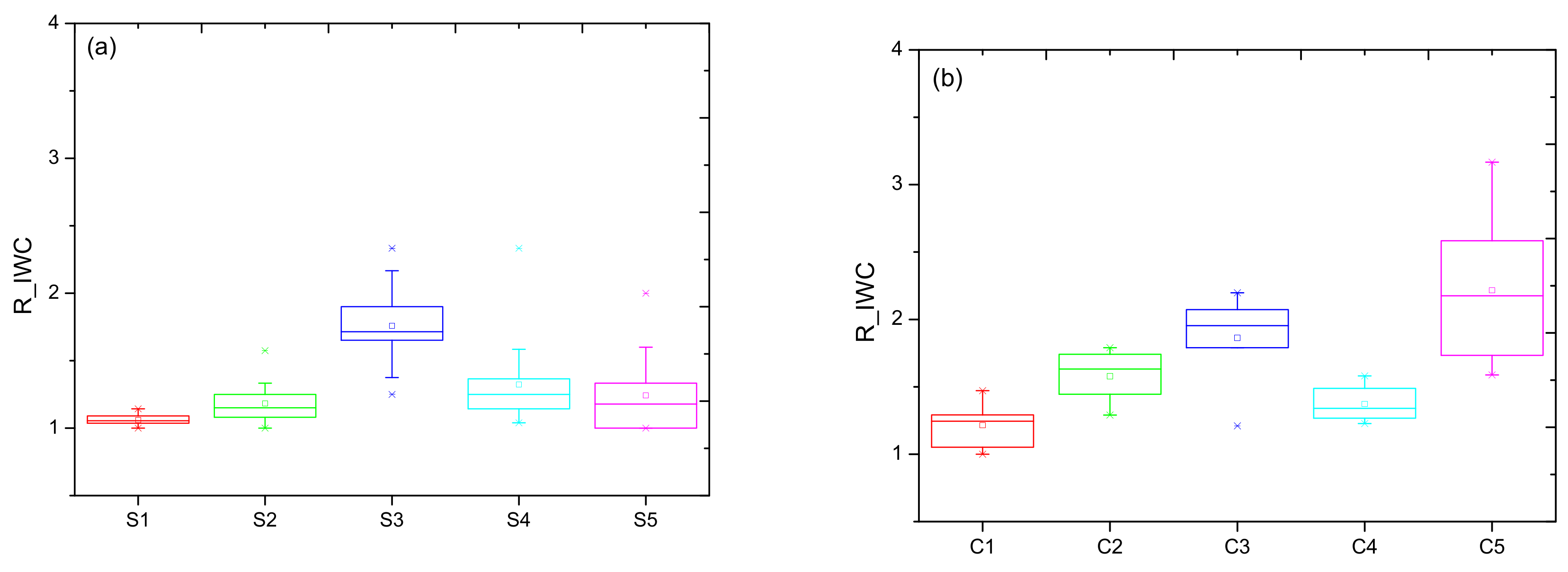
4.3. Effects on the Ice Water Content
5. Discussion
5.1. The Interarrival Time Threshold
5.2. Small Ice Particles
6. Conclusions
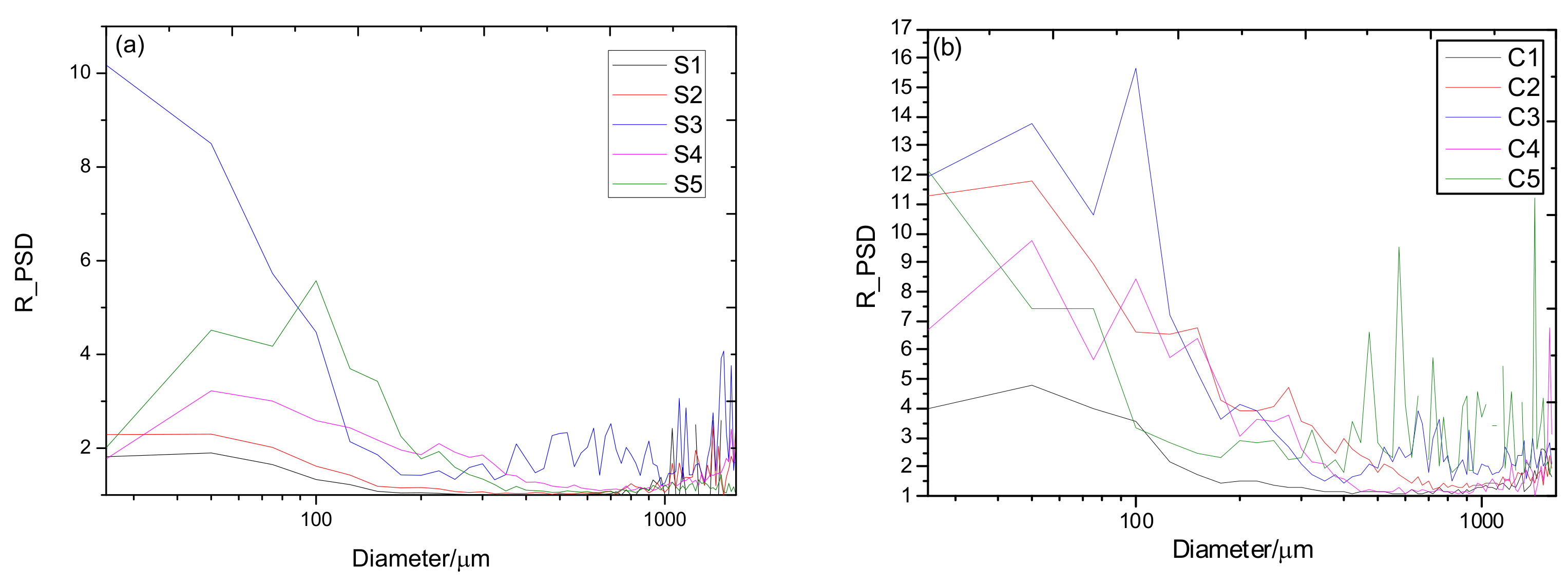
- The effect of shattering on particle size distribution decreases with the increasing size below 400 μm, fluctuates between 400 μm and 1000 μm and slightly increases with the increasing size of larger than 1000 μm. However, the average ratio of the convective clouds is larger than that of the stratiform regions in the whole size, and nearly twice that in the size of less than 1000 μm.
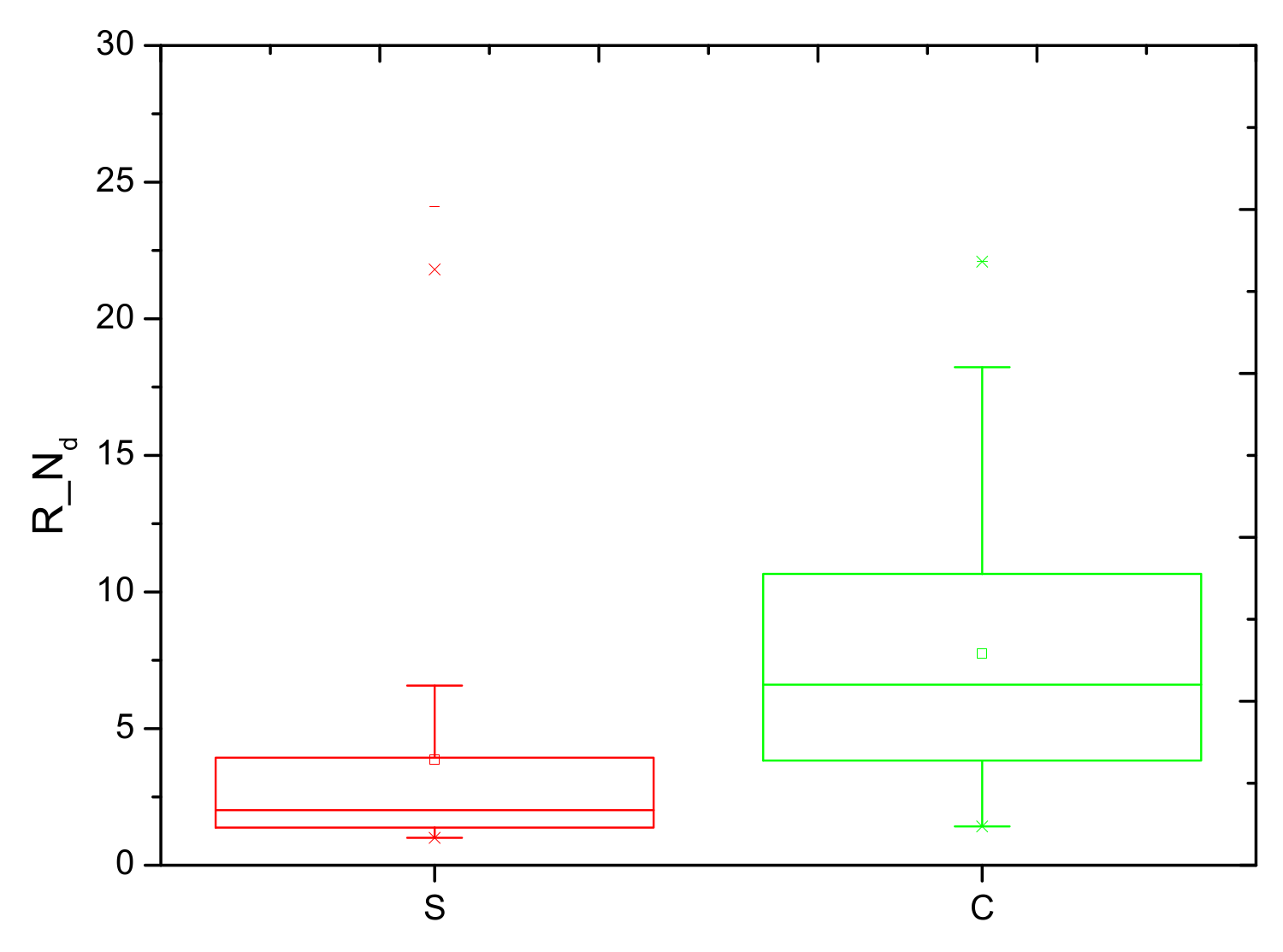
- Shattered fragments may increase the measured particle number concentration by up to one or two orders of magnitude. In terms of stratiform and convective regions, the influence of shattering events on the particle number concentration in a convective cloud region is greater than that in a stratiform region. On average, the influence on the number concentration measurement in a convective region is 1.5 times that in a stratiform cloud region, and the median difference is even larger: the influence in a convective region is nearly three times that in a stratiform cloud region.
- In terms of the effect of shattering on the ice water content measurement, the influence of shattering events on the ice water measurement in a convective cloud region is greater than that in a stratiform region. On average, the contribution of shattering on the CIP IWC measurement in a convective region is 1.2 times that in a stratiform cloud region.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yanchao, H. The numerical simulation on study of convective and stratiform mixed clouds, part(I)─The model and paramterization of microphysical processes. Acta Meteorol. Sin. 1996, 5, 54544–54557. (In Chinese) [Google Scholar]
- Huang, M.Y.; Hong, Y.C.; Xu, H.Y. The effects of the existence of stratiform cloud on the development of cumulus cloud and its precipitation. Acta Meteorol. Sin. 1987, 45, 72–77. (In Chinese) [Google Scholar]
- Evans, A.G.; Locatelli, J.D.; Stoelinga, M.T.; Hobbs, P.V. The IMPROVE-1 storm of 1–2 February 2001. Part II:Cloud structures and the growth of precipitation. J. Atmos. Sci. 2005, 62, 3456–3473. [Google Scholar] [CrossRef]
- Shichao, Z.; Xueliang, G.; Guangxian, L.; Lijun, G. Ice crystal habits and growth processes in stratiform clouds with embedded convection examined through Aircraft Observation in Northern China. J. Atmos. Sci. 2015, 72, 2011–2032. [Google Scholar]
- Hallett, J. Production of secondary ice particles during the riming process. Nature 1974, 249, 26–28. [Google Scholar] [CrossRef]
- Rangno, A.L.; Hobbs, P.V. Microstructures and precipitation development in cumulus and small cumulonimbus clouds over the warm pool of the tropical Pacific Ocean. Q. J. R. Meteorol. Soc. 2005, 131, 639–673. [Google Scholar] [CrossRef]
- Morrison, H.; McCoy, R.B.; Klein, S.A.; Xie, S.C.; Luo, Y.L.; Avramv, A.; Chen, M.X.; Cole, J.N.S.; Falk, M.; Foster, M.J.; et al. Intercomparison of model simulations of mixed-phaseclouds observed during the ARM mixed-phase arctic cloud experiment. II: Multilayer cloud. Q. J. R. Meteorol. Soc. 2009, 135, 1003–1019. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, Y.; Wang, H.; Zheng, Y.; Morrison, H. Modeling convective-stratiform precipitation processes on a Mei-Yu front with the Weather Research and Forecasting model: Comparison with observations and sensitivity to cloud microphysics parameterizations. J. Geophys. Res. 2010, 115, D18117. [Google Scholar] [CrossRef] [Green Version]
- Hou, T.J.; Lei, H.C.; Hu, Z.X.; Yang, J.F.; Li, X.Y. Simulations of microphysics and precipitation in a stratiform cloud case over northern China: Comparison of two microphysics schemes. Adv. Atmos. Sci. 2020, 37, 117–129. [Google Scholar] [CrossRef]
- Padmakumari, B.; Maheskumar, R.S.; Morwal, S.B.; Harikishan, G.; Konwar, M.; Kulkarni, J.R.; Goswami, B.N. Aircraft observations of elevated pollution layers near the foothills of the Himalayas duringCAIPEEX-2009. Q. J. R. Meteorol. Soc. 2013, 139, 625–638. [Google Scholar] [CrossRef]
- Padmakumari, B.; Maheskumar, R.S.; Harikishan, G.; Kulkarni, J.R.; Goswami, B.N. Comparative study of aircraft- and satellite-derived aerosol and cloudmicrophysical parameters during CAIPEEX-2009 over the Indian region. Int. J. Remote Sens. 2013, 34, 358–373. [Google Scholar] [CrossRef]
- Min, Q.; Joseph, E.; Lin, Y.; Min, L.; Yin, B.; Daum, P.H.; Kleinman, L.I.; Wang, J.; Lee, Y.-N. Comparison of MODIS cloud microphysical propertieswith in-situ measurements over the Southeast Pacific. Atmos. Chem. Phys. 2012, 12, 11261–11273. [Google Scholar] [CrossRef] [Green Version]
- Korolev, A.V.; Isaac, G.A. Shattering during sampling by OAPs and HVPS. Part 1: Snow particles. J. Atmos. Ocean. Technol. 2005, 22, 528–542. [Google Scholar] [CrossRef]
- Korolev, A.V.; Emery, E.F.; Strapp, J.W.; Cober, S.G.; Isaac, G.A.; Wasey, M.; Marcotte, D. Small ice particles in tropospheric clouds: Fact or artifact? Airborne icing instrumentation evaluation experiment. Bull. Am. Meteor. Soc. 2011, 92, 967–973. [Google Scholar] [CrossRef] [Green Version]
- Gultepe, I.; Isaac, G.A.; Cober, S.G. Ice crystal number concentration versus temperature for climate studies. Int. J. Climatol. 2001, 21, 1281–1302. [Google Scholar] [CrossRef]
- Field, P.R.; Heymsfield, A.J.; Bansemer, A. Shattering and Particle Interarrival Times Measured by Optical Array Probes in Ice Cloud. J. Atmos. Ocean. Technol. 2006, 23, 1357–1371. [Google Scholar] [CrossRef] [Green Version]
- Korolev, A.V.; Emery, E.F.; Creelman, K. Modification and tests of particle probe tips to mitigate effects of ice shattering. J. Atmos. Ocean. Technol. 2013, 30, 690–708. [Google Scholar] [CrossRef]
- Korolev, A.V.; Emery, E.F.; Strapp, J.W.; Cober, S.G.; Isaac, G.A. Quantification of the Effects of Shattering on Airborne Ice Particle Measurements. J. Atmos. Ocean. Technol. 2013, 30, 2527–2553. [Google Scholar] [CrossRef]
- Jackson, R.C.; McFarquhar, G.M.; Stith, J.; Beals, M.; Shaw, R.A.; Jensen, J.; Fugal, J.; Korolev, A. An assessment of the Impact of antishattering tips and artifact removal techniques on cloud ice size distributions measured by the 2DC Cloud Probe. J. Atmos. Ocean. Technol. 2014, 31, 2567–2590. [Google Scholar] [CrossRef]
- Jackson, R.C.; Mcfarquhar, G.M. An assessment of the Impact of antishattering tips and artifact removal techniques on bulk cloud ice microphysical and optical properties measured by the 2DC Cloud Probe. J. Atmos. Ocean. Technol. 2014, 31, 2131–2144. [Google Scholar] [CrossRef]
- Minsong, H.; Hengchi, L.; Jiatian, C.; Xiaoqing, Z. Cloud particle shattering during sampling by airborne optical array probes. Chin. J. Atmos. Sci. 2016, 40, 647–656. [Google Scholar]
- Zhao, Z.; Lei, H. Observed microphysical structure of nimbostratus innortheast cold vortex over China. Atmos.Res. 2014, 142, 91–99. [Google Scholar] [CrossRef]
- Zhao, Z.; Lei, H. Aircraft observations of liquid and ice in mid-latitudemixed-phase clouds. Adv. Atmos. Sci. 2014, 31, 604–610. [Google Scholar] [CrossRef]
- Jiefan, Y.; Hengchi, L.E.I.; Hou, T. Observational Evidence of High Ice Concentration in a Shallow Convective Cloud Embedded in Stratiform Cloud over North China. Adv. Atmos. Sci. 2017, 34, 509–520. [Google Scholar]
- Hobbs, P.V.; Rangno, A.L. Rapid development of high ice particle concentrations in small polar maritime cumuliform clouds. J. Atmos. Sci. 1990, 47, 2710–2722. [Google Scholar] [CrossRef] [Green Version]
- Hobbs, P.V.; Locatelli, J.D. Rainbands, precipitation cores and generating cells in a cyclonic storm. J. Atmos. Sci. 1978, 35, 230–241. [Google Scholar]
- Lu, G.X.; Guo, X.L. Distribution and origin of aerosol and its transform relationship with CCN derived from the spring multi-aircraft measurements of Beijing Cloud Experiment (BCE). Chin. Sci. Bull. 2012, 57, 2460–2469. [Google Scholar] [CrossRef] [Green Version]
- McFarquhar, G.M.; Baumgardner, D.; Bansemer, A.; Abel, S.J.; Crosier, J.; French, J.; Rosenberg, P.; Korolev, A.; Schwarzoenboeck, A.; Leroy, D.; et al. Processing of Ice Cloud In-Situ Data Collected by Bulk Water, Scattering, and Imaging Probes: Fundamentals, Uncertainties and Effortstowards Consistency. Meteor. Monogr. 2017, 58, 11.1–11.33. [Google Scholar] [CrossRef]
- Grosvenor, D.P.; Choularton, T.W.; Lachlan-Cope, T.; Gallagher, M.W.; Crosier, J.; Bower, K.N.; Ladkin, R.S.; Dorsey, J.R. In-situ aircraft observations of ice concentrations withinclouds over the Antarctic Peninsula and Larsen Ice Shelf. Atmos. Chem. Phys. 2012, 12, 11275–11294. [Google Scholar] [CrossRef] [Green Version]
- Heymsfield, A.J.; Schmitt, C.; Bansemer, A. Ice cloud particle size distributions and pressure-dependent terminal velocities from in situ observations at temperatures from 0 to −86 °C. J. Atmos. Sci. 2013, 70, 4123–4154. [Google Scholar] [CrossRef]
- Huang, M.S.; Lei, H.C.; Jin, L. Pseudo Particle Identification in the image data from the Airborne Cloud and Precipitation Particle Image Probe. Chin. J. Atmos. Sci. 2017, 41, 1113–1124. [Google Scholar]
- Heymsfield, A.J.; Parrish, J.L. A computational technique for increasing the effective sampling volume of the PMS two-dimensional particle size spectrometer. J. Appl. Meteor. 1978, 17, 1566–1572. [Google Scholar] [CrossRef]
- Huang, M.S.; Lei, H.C. Processing method for the partial particles and its influence on the cloud microphysical parameters measured by the airborne cloud and precipitation image probe. Acta Phys. Sin. 2018, 67, 249202. [Google Scholar]
- Gultepe, I.; Heymsfield, A.J.; Field, P.R.; Axisa, D. Ice-phase precipitation. Meteor. Monogr. 2017, 58, 16.1–16.36. [Google Scholar] [CrossRef]
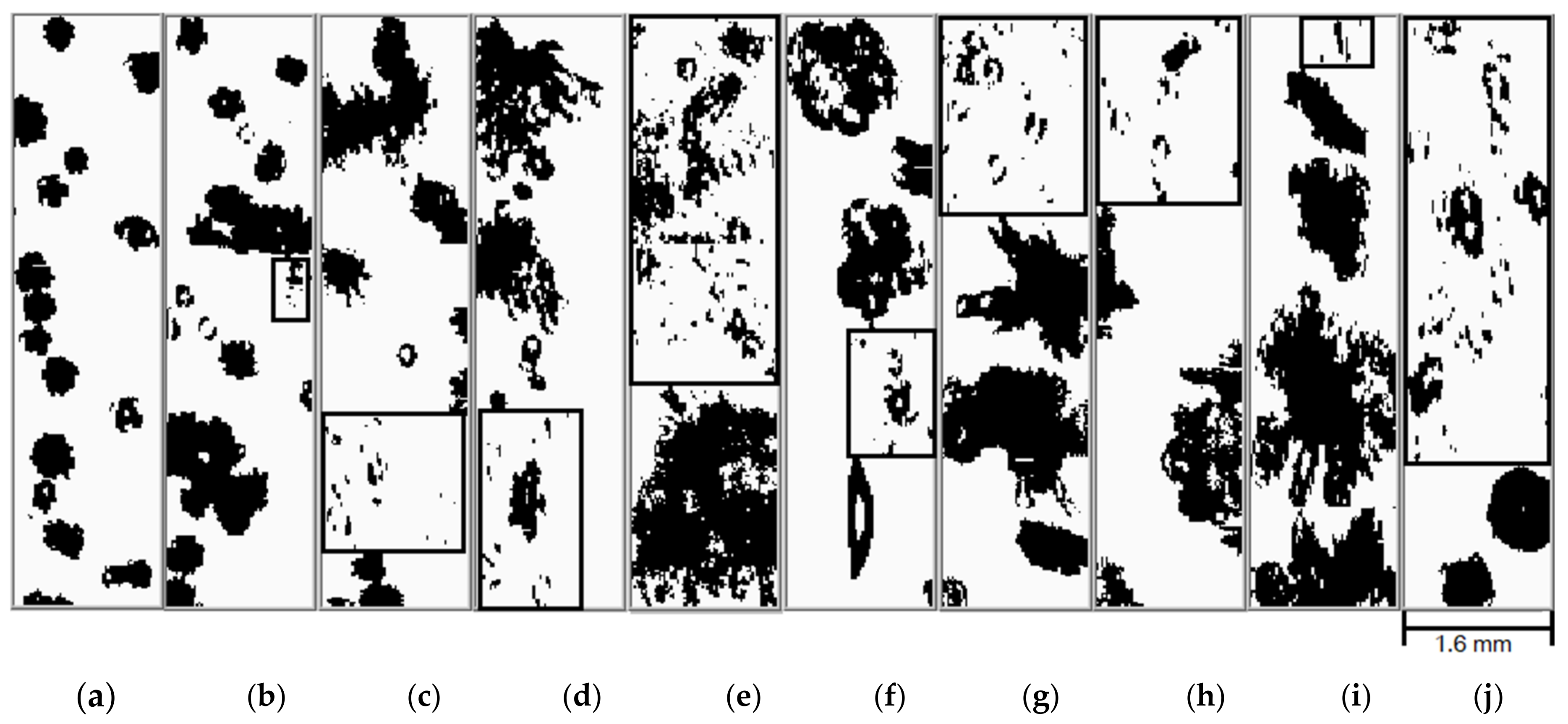

| Flight | Time (BT 1) | Cloud | Code |
|---|---|---|---|
| 20090418 | 17:44:30–17:46:30 | Stratiform | S1 |
| 20090418 | 17:48:00–17:50:00 | Convective | C1 |
| 20090418 | 17:51:00–17:54:00 | Stratiform | S2 |
| 20090501 | 09:23:00–09:25:00 | Stratiform | S3 |
| 20090501 | 09:30:00–09:32:00 | Convective | C2 |
| 20090501 | 09:46:00–09:51:00 | Stratiform | S4 |
| 20090501 | 09:38:00–09:39:00 | Convective | C3 |
| 20090501 | 09:51:00–09:52:00 | Convective | C4 |
| 20090501 | 10:17:00–10:22:30 | Stratiform | S5 |
| 20090501 | 10:25:00–10:26:30 | Convective | C5 |
| Cloud | Mean | Q1 | Minimum | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| Stratiform | 3.86 | 1.38 | 1.00 | 2.02 | 3.94 | 24.10 |
| Convective | 7.75 | 3.83 | 1.42 | 6.61 | 10.66 | 22.09 |
| Cloud | Mean | Q1 | Minimum | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|
| Stratiform | 1.29 | 1.08 | 1.00 | 1.20 | 1.36 | 2.33 |
| Convective | 1.61 | 1.28 | 1.00 | 1.49 | 1.79 | 3.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M. Differences in the Ice Particle Shattering Impact on the CIP Measurements in the Stratiform Cloud Region and the Embedded Convection Region. Water 2021, 13, 2322. https://doi.org/10.3390/w13172322
Huang M. Differences in the Ice Particle Shattering Impact on the CIP Measurements in the Stratiform Cloud Region and the Embedded Convection Region. Water. 2021; 13(17):2322. https://doi.org/10.3390/w13172322
Chicago/Turabian StyleHuang, Minsong. 2021. "Differences in the Ice Particle Shattering Impact on the CIP Measurements in the Stratiform Cloud Region and the Embedded Convection Region" Water 13, no. 17: 2322. https://doi.org/10.3390/w13172322
APA StyleHuang, M. (2021). Differences in the Ice Particle Shattering Impact on the CIP Measurements in the Stratiform Cloud Region and the Embedded Convection Region. Water, 13(17), 2322. https://doi.org/10.3390/w13172322





