1. Introduction
In rainfall-runoff modeling, loss parameter is one of the most important parameters, which refers to amount of rainfall that does not appear at the stream directly, which mainly consists of infiltration, evapotranspiration, interception, depression storage, and transmission losses. Several loss models have been proposed for use with event-based rainfall-runoff models, such as the initial loss-continuing loss (IL-CL) model, the Soil Conservation Service (SCS) Curve Number model and probability-distributed model (PDM) [
1]. More sophisticated loss models exist that can simulate evaporation and movement of water within the soil profile and in the groundwater layers, such as the Xinanjiang model [
2] and soil moisture accounting model [
3]. In many cases however (particularly in poorly gauged catchments), the simplest loss models such as IL-CL model can produce reasonably accurate design flood estimates. However, a key limitation of event-based loss models is the lack of knowledge about the antecedent moisture condition of the catchment [
4,
5]. Given the importance of antecedent moisture conditions in flood estimation [
6], several methods have been suggested to overcome this limitation [
7,
8,
9,
10,
11]. In addition, joint probability approaches [
12] are often used to incorporate the natural variability of antecedent moisture conditions in a catchment. This has been considered in several studies based on various loss models including the SCS Curve Number method [
8,
13,
14], PDM [
15] and the Green–Ampt infiltration equation [
16]. Stochastic loss modeling is becoming popular in rainfall-runoff modeling to account for its inherent variability [
17,
18,
19]. Here losses are assumed to be a random variable and is generally specified by a probability distribution.
In many Australian catchments, simplistic loss models are often found to provide reasonable approximations of runoff generation; with the lumped conceptual IL-CL model being widely adopted [
20,
21]. The initial loss is based on the antecedent moisture prior to an event and is specifically defined as the amount of rainfall occurring before the effective start of runoff. In calculating initial loss, a surface runoff threshold value (such as 0.01 mm/h) is generally used following the approach of Rahman et al. [
12] where it is assumed that surface runoff starts when this surface runoff threshold is exceeded. The initial loss can be estimated by examining the continuous rainfall and runoff data of the given catchment. The continuing loss is a combination of other losses but is mostly based on the infiltration rate across the catchment and is defined as a ‘constant loss rate’ throughout the remainder of the storm under consideration. Continuing losses are dependent on catchment characteristics and is generally considered to be a ‘fixed input’ in a given catchment, except for changes over time due to change of catchment soil profile, plantation, and other similar factors. Although variability in the continuing loss has been studied in the past [
22], this variability is most likely due to uncertainties (both epistemic and aleatoric) and not the inherent random nature of the parameter itself. In contrast, the initial loss is a measure of the antecedent catchment wetness of a given storm event. Given the stochastic nature of meteorological factors involved, primarily wetting and drying processes, initial loss should ideally be treated as a random variable in rainfall-runoff modeling. In the use of Monte Carlo simulation methods, the joint probabilities of key inputs, such as initial loss, are needed for rainfall-runoff modeling [
12,
17].
Due to complex spatial and temporal variability of hydro-meteorological processes, losses cannot be measured in field studies very accurately rather it needs to be estimated from calibration of historic rainfall-runoff records. Historic records (such as streamflow and rainfall), however, are limited in many countries, including Australia. Data are further limited using only the most extreme rainfall-runoff events in rainfall-runoff modeling (rather than records in their entirety) and gauge recording issues (such as rating curve extrapolation) during these extreme events. These data limitations make it difficult to identify the underlying probability distribution for initial loss. There have been few studies that have examined the stochastic nature of initial loss and identified suitable initial loss probability distributions with a reasonable degree of accuracy, as noted below.
Regionalization of losses is needed to apply rainfall-runoff models for ungauged catchments. Regionalization refers to characterization of regional behavior of a variable of interest (such as flood quantile or parameters of a probability distribution) over a given region so that the variable can be estimated at any arbitrary ungauged location within the study area. One of the most common regionalization approaches is regional flood frequency analysis (RFFA) where a prediction equation is developed for a flood quantile (e.g., 100-year flood) or for parameters of a probability distribution as a function of climatic and catchment characteristics [
23,
24,
25,
26]. The regionalization of initial loss refers to identification of the regional mean or median initial loss value (in simplistic form) or regional values of a probability distribution function that can specify regional initial loss values.
Rahman et al. [
12] examined the sensitivities of design flood estimates to uncertainties in the initial loss distributions. The authors found the Beta distribution to be a reasonable fit with respect to descriptive statistics of the observed and simulated initial loss data. However, the authors did not apply any goodness-of-fit tests in selecting an appropriate probability distribution for initial loss. Design flood estimates were found to be most sensitive to the variance and upper limits when specifying model parameters. The study by Rahman et al. [
12] was limited to ten catchments in a relatively mild climatic region of Victoria, Australia, therefore, Tularam and Ilahee [
22] extended the analysis to 15 catchments in tropical Queensland. The Beta distribution originally suggested by Rahman et al. [
12] for Victorian catchments was found be appropriate for the initial loss data in tropical Queensland.
Previous studies [
12,
22] adopted crude goodness-of-fit tests, which are problematic as parameters were estimated from the same dataset that the model fit was derived. Gamage et al. [
27] overcame this limitation by adopting a more robust method of distributional model fitting. In this regard, Gamage et al. [
27] were able to assess the probability density model most suited to the true (unknown) initial loss distribution and for the six South Australian catchments, the Gamma distribution was found to reasonably represent initial loss data. Several other Australian studies have also derived and applied initial loss distributions within a Monte Carlo simulation framework [
17,
28,
29,
30]; each study found either the Beta or Gamma distributions to be the most representative of the true underlying distribution for initial loss.
The principal objective of the paper is to identify a probability distribution that is better suited to represent the initial loss data for a range of catchment and climatic characteristics in Australia. The probability-distributed losses are becoming more common in Australian applications as Australian Rainfall and Runoff has recommended Monte Carlo simulation in rainfall and runoff modeling [
20,
31]. In this regard, five probability distributions (four parametric and one nonparametric model) are assessed using a bootstrap-based goodness-of-fit method, given three distance measures based on the empirical density function (EDF). Secondly, the impact of the relative accuracy of parameters of the underlying initial loss distributions on design flood estimates is evaluated. Given the lack of knowledge regarding the true underlying distribution, different functional forms are examined along with possible errors in the descriptive statistics (mean and variance) of the initial loss data. The investigation is then extended to the effect of regionalization of model parameters and distributions to evaluate the impact of uncertainties in initial losses on design flood estimates.
2. Bootstrap-Based Goodness-of-Fit Procedure
2.1. Probability Distributions
Previous studies commonly found the Gamma and Beta distributions to be representative of the initial loss data in Australia. Both distributions were included in this study, along with the Normal and Weibull distributions for comparative purposes. Parameters of a probability distribution can be estimated from an observed sample using several techniques, both numerical and graphical, which produce notably different parameter estimates and confidence limits. More commonly used techniques for estimating distributional parameters include the method of moments (MOM), method of maximum likelihood (ML) and probability weighted moments. In this study, the distributional parameters are estimated using the ML method, which maximizes the conditional probability of generating the observed data to select the parameters.
These parametric distributions rely on the assumption that the population (which the observed data sample belongs to) has an underlying parent distribution. This results in the observed data being fitted to a probability density function with a known theoretical distribution. Nonparametric approaches, however, make no prior assumption about the form of the underlying probability distribution. This method, however, relies heavily on the observed data and its empirical grouping into bins. This study, therefore, compared both parametric and nonparametric distributions for describing initial losses. The most widely used nonparametric method is the kernel density estimate (KDE) [
32].
For a given data sample
and kernel function
, the probability density can be estimated by:
where
is a smoothing factor known as the bandwidth and
is the Gaussian kernel, specified as
The bandwidth is the most important characteristic of a KDE, with a strong influence on the shape of the density function. It is, therefore, necessary to implement a reliable method to estimate the optimal bandwidth [
33,
34,
35]. The optimal bandwidth can be estimated using the so-called rule of thumb methods [
36], as in Equation (2), which is based on minimizing the asymptotic mean squared error (AMISE) for a kernel density estimate.
where
is the inter-quartile range and
is the sample standard deviation. Jones et al. [
37] found the estimator to be “close enough to be reasonably representative” as compared to the best estimate.
2.2. Model Selection
The model selection methods are used to infer the model that best fits the observed data. These are commonly measures of distance between the parent and hypothetical distributions. Three of the most commonly used goodness-of-fit tests based on the EDF are adopted in this study. Each of these may be defined regarding the corresponding order statistics (for brevity ), as follows:
Kolmogorov Smirnov (K-S) test statistic:
Cramér–von Mises (C–vM) test statistic:
Anderson-Darling (A-D) test statistic:
These classical methods, however, estimate the parameters and fit the model to the available dataset, leading to the failure of such techniques in many cases [
38]. Bootstrap resampling techniques [
39,
40] overcome these limitations and have been shown to be effective in wide range of scenarios [
41].
The bootstrap resampling technique adopted here is the parametric bootstrap, which undertakes Monte Carlo simulations from a parametric model of the data. This procedure allows for more reliable critical values to be derived (irrespective of parameter values), along with an approximation of the p-values. The procedure can be formalized as follows: For an observed dataset from unknown distribution , the most suited hypothetical distribution can be assessed for each probability distribution:
Estimate the model parameters () from and construct the cumulative density function (CDF)
Evaluate , and (Equations (4)–(6)), where
Generate bootstrap samples of size from , denoted as given
Estimate from and construct the CDF
Evaluate , and (Equations (1)–(3)), where
For a given test statistic (), the critical value is the empirical quantile of order of . The p-value can also be approximated as . The null hypothesis ( versus ) can be rejected if , and for comparative purposes if . Given the hypothetical models (being the Gamma, Beta, Weibull, Normal or KDE models) where the null hypothesis is not rejected, the most suited distribution for the observed data is the model with the smallest test statistic , indicating the model closest to .
It should be noted here that the study area (eastern NSW) was considered to be a homogeneous region to regionalize the distribution of initial loss. The classical homogeneity test, such as Hosking and Wallis [
42] was not applied as our objective was to regionalize the parameters of the assumed probability distributions for the initial loss. However, three goodness-of-fit tests were applied to assess whether the hypothesized distribution adequately fits the observed initial loss data as discussed above.
3. Rainfall-Runoff Modeling
The principal focus of this study is to evaluate the effect of probability-distributed initial losses on design flood estimates when used within a Monte Carlo simulation framework. The nature of Monte Carlo framework is the incorporation of an expected degree of variability into the process/system. To assess the variability in initial loss data alone, while still allowing for a Monte Carlo framework, random seeds for all other input variables of the rainfall-runoff model are kept fixed to allow for reproducible variability in each of these input variables.
3.1. Rainfall-Runoff Model
The rainfall-runoff model adopted in this study is a conceptual semi-distributed model called RORB [
43]. It is an event-based model that is here run at an hourly time step. The catchment river system is represented in the model by a network of model storages. Runoff generation is modeled here using the initial loss-continuing loss model; however, the initial loss-proportional loss model is also available for use. In RORB, non-linear storage routing is used to transform direct runoff and simple river routing is employed where flows are simply lagged in time. This model is adopted due to its simplicity, which lends itself to fast computations (beneficial for large data sets), its flexibility, which allows for ease-of-use in joint probability approaches, and its ability to approximate catchment response [
44].
Baseflow is not modeled in RORB therefore it was calculated externally using a recursive digital filter, which was later added to the surface runoff hydrograph. Input precipitation depth was estimated using intensity frequency duration (IFD) calculator (Australian Bureau of Meteorology). The areal average precipitation over the catchment was estimated using areal reduction factor based on the catchment area, burst duration and return period [
45]. Catchments were spatially divided into several subareas and stream reaches to account for the spatial heterogeneity of catchment and rainfall characteristics. Precipitation was estimated as spatial averages for each subarea using natural neighbors interpolation based on several surrounding rainfall gauges. The temporal pattern data were obtained from Australian Rainfall and Runoff data hub [
27].
3.2. Model Calibration
The calibration of each RORB model is undertaken using several observed rainfall-runoff events. Three model parameters are calibrated in this study: specifically, the routing parameter, and the initial loss and continuing loss for the runoff generation model. Calibration of the parameter set involved optimizing four key statistics; being the absolute differences in the peak flow, time to peak flow, and 72 h runoff volume representative of biases in magnitude, timing and mass respectively, and the average absolute ordinate error (being the average absolute error between modeled and gauged flows at each time step) representative of the overall shape of the flood hydrograph.
3.3. Stochastic Design Storms
A statistical storm approach, based on depth-duration-frequency (DDF) data, is employed in this study. In Australia, a revision of DDF data was completed in 2016 as part of Australian Rainfall and Runoff, which provides regionalized burst DDF data for a 0.025° resolution grid across Australia [
31]. The data are provided for standard durations between 1 min and 168 h, ranging in frequency from 63.2% to 1% annual exceedance probability (AEP) (equal to return periods of 1 year to 100 years).
DDF data represents design rainfall at a point, therefore to estimate rainfall across an entire catchment, areal reduction factors are used to provide estimates of areal precipitation. Areal reduction factors have been calculated specifically for Australian conditions [
45] and are therefore adopted in this study. Both short duration (less than 18 h) and long duration (equal to or longer than 18 h) values have been derived based on catchment area, rainfall duration, and rainfall frequency.
The temporal distribution of rainfall throughout the event needs to be specified. In Australia, storm temporal patterns from historic events have been regionalized as part of the revision of Australian Rainfall and Runoff [
46]. These storm patterns are identified by their critical burst duration (being the duration of the rarest burst within the storm period), as opposed to the total storm duration. Recorded events are regionalized using a region-of-influence approach, based on the similarity of source event characteristics (original event from the source pluviograph) to target event characteristics (design event at the target location). Patterns are available for standard burst durations between 5 min and 168 h, and burst frequencies rarer than the 63.2% AEP (above a return period of 1 year). These regionalized historic temporal patterns allow for ensembles of patterns to be generated for each rainfall duration and frequency.
The DDF data discussed earlier is based on burst events (as in the rarest burst within a storm for a given duration); however, in this study we adopt a storm event approach. For this reason, design burst depths need to be transformed into design storm depths. Here, the design burst depth is transformed using the storm to burst rainfall ratio (being the ratio of the total depth to the critical burst depth for the specified historic temporal pattern) to scale the burst depth up to a storm depth. This method is limited in that the pre- and post-burst periods are assumed to scale at the same rate as the critical burst, while this assumption is reasonable in current conditions, it could prove problematic in climate change scenarios where bursts have been seen to scale faster.
3.4. Design Flood Estimation
A classical approach to design flood estimation first assumes the peak flow and causative rainfall are probability neutral (as in having equal AEPs). Second, several storm durations (around the time of concentration, considering the catchment size) are simulated, then the design flood becomes the hydrograph that produces the highest peak across all durations. One of the key limitations of this approach is the use of a single design storm and parameter set for each given duration. Here, this classical approach has been modified to incorporate the joint probability of key flood producing inputs using Monte Carlo simulation. Crude Monte Carlo sampling techniques are computationally expensive, therefore, to improve the efficiency of the Monte Carlo simulations a stratified sampling approach is adopted with 50 bins and 50 runs per bin.
The depth, frequency and temporal distribution of rainfall in the design storm event were treated as random variables (as outlined in
Section 3.3). The initial loss was also treated as a random variable specified by a probability distribution. However, remaining inputs were fixed, including the burst rainfall duration of the design storm, spatial distribution of rainfall across the catchment, routing parameter for modeling catchment response and continuing loss for calculating rainfall excess. Rainfall was assumed to be spatially uniform across the catchment; this should have minimal impact given the relatively small catchment sizes and general homogeneity of design rainfall depths throughout each catchment.
The regional design floods at a given site were estimated by a RORB model where regional initial loss value (specified by a probability distribution) was adopted as the input value along with other regional/at-site input data). To assess the relative accuracy of the regional design flood estimates, these were compared with the observed design floods, which were estimated by an at-site flood frequency analysis assuming a GEV distribution. Here, the parameters of the GEV distribution were evaluated using the maximum likelihood estimation method.
To determine the impact of a single variable (the initial loss) within a Monte Carlo framework an entirely stochastic modeling approach cannot be adopted due to the inherent variability between Monte Carlo sets. A pseudo-random approach is therefore applied, where the random seed of each variable is specified to ensure predictability between Monte Carlo sets while accounting for the joint probability of key inputs.
5. Results
In this section, first the probability distribution better suited to initial loss data from several historic studies is presented. Thereafter, the variability of peak flow estimates caused due to the differences of initial loss probability distributions where uncertainties exist is investigated; specifically, the impact of assuming a probability density function, uncertainties in the descriptive statistics of observed datasets and unknowns when regionalizing distributions of initial losses are discussed.
5.1. Probability-Distributed Initial Losses
The first objective was to evaluate the functional form of initial losses for a wide range of catchments throughout Australia. For this purpose, a bootstrap-based goodness-of-fit procedure was employed, as explained in
Section 2, using previously calibrated initial loss data sets, according to
Section 4.1. The null hypothesis was evaluated for all 92 catchments and five probability distributions, using three goodness-of-fit tests at a significance level 10%. It should be noted that 5% or 1% significance levels can also be adopted; however, use of 10% level is commonly accepted in statistical hydrology [
12,
27]. The quality of the goodness-of-fit test statistics is dependent on the unknown underlying distribution, on the distribution parameters and on the sample size. Although these tests can be quite powerful in some situations, they may produce erroneous statistics in others. With this in mind, here we will highlight some of the more interesting findings that can be drawn from the bootstrap procedure.
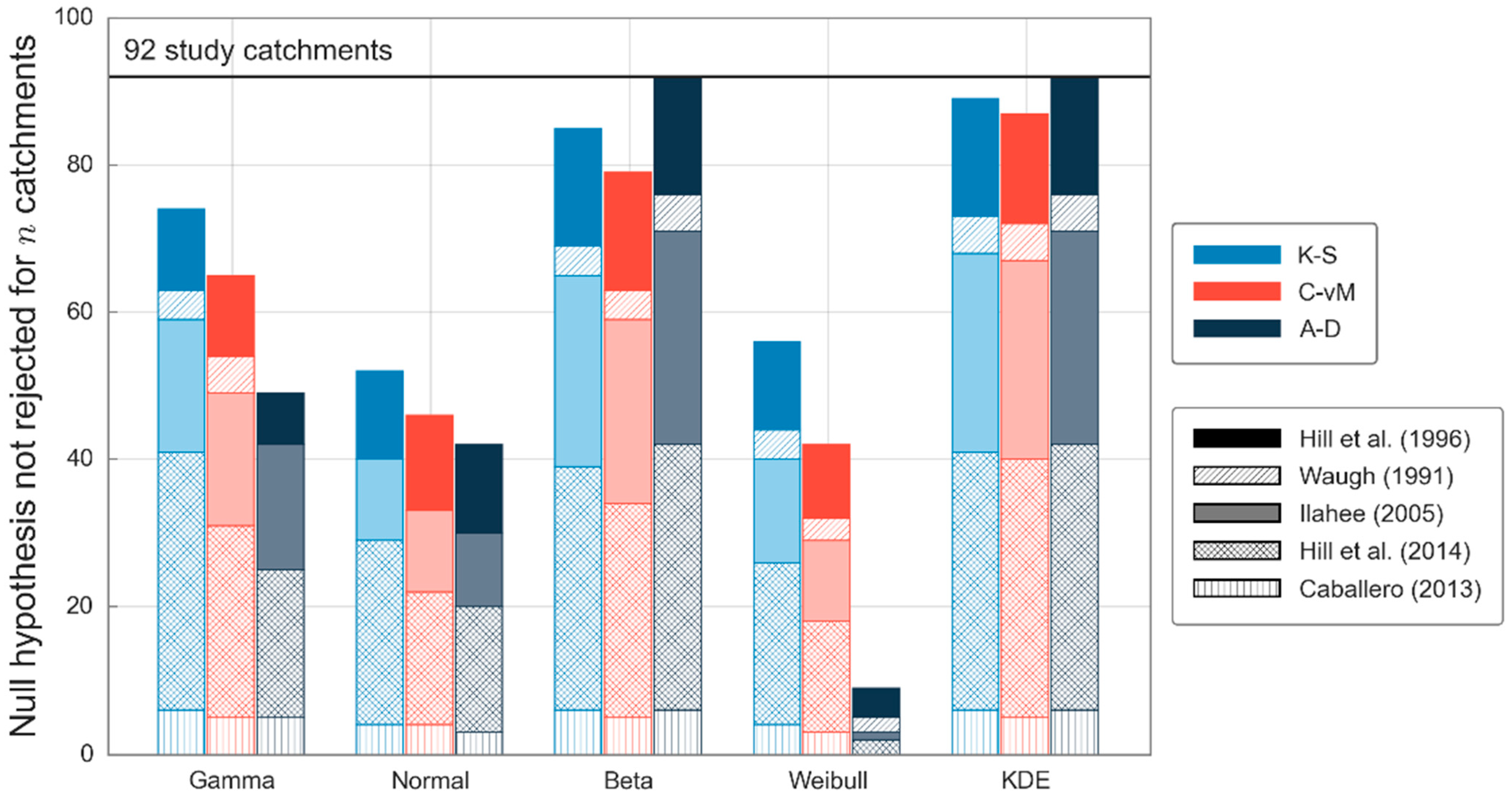
The three goodness-of-fit tests are separately applied to each of the catchment data sets and a count of the number of catchments in which the null hypothesis is not rejected is reported for each study (see
Figure 1). The first interesting result is that the goodness-of-fit tests appear to be of similar magnitudes, except for the A-D test for the Weibull distribution. Apart from this one anomaly, we cannot reject the fit to the remaining candidate distributions for a large proportion (typically more than half) of the 92 study catchments. In particular, it is noted that most catchments could not be rejected when using the Beta and KDE distributions. However, this is to be expected given that both distributions have the largest parameter sets. Application of the Weibull distribution at this point, appears to be questionable for the initial loss data.
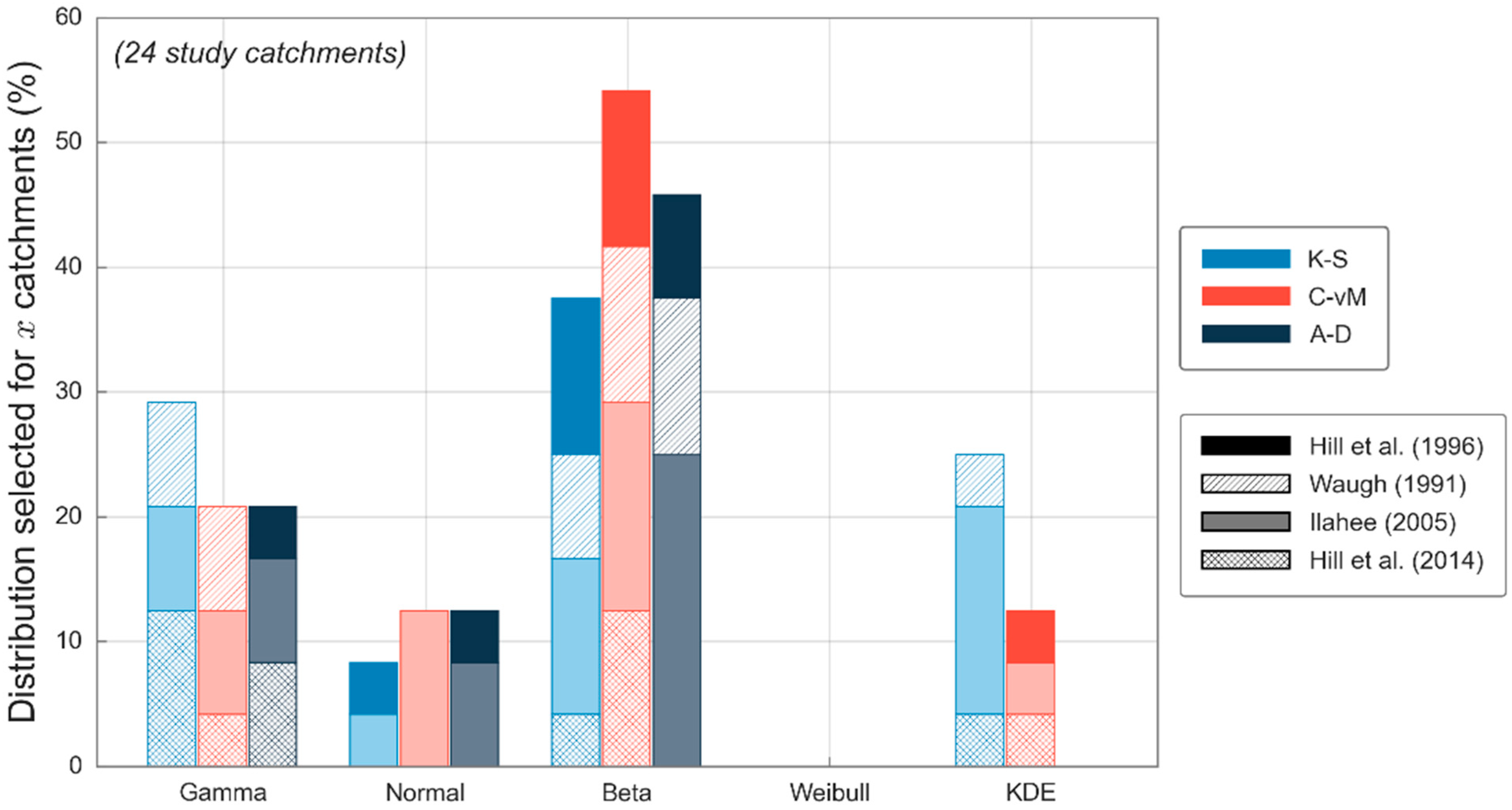
Following on from this, the percentage of cases for which each candidate distribution is selected as the most representative distribution (see
Section 2.2) for each goodness-of-fit test is reported for each study (see
Figure 3). Here it can be seen that three candidate distributions (Gamma, Normal and Beta) were selected for a rather large percentage of catchments across all three goodness-of-fit tests, which demonstrates their potential suitability for representing the underlying initial loss distribution. The KDE distribution; however, returned mixed results across the three goodness-of-fit tests, with the distribution not being selected at all using the A-D test, but then being selected for 50% of catchments using the K-S test.
It was stated earlier that while not ideal, sample sizes of ten or more were included in this analysis. Realistically, a sample size of 25 to 30 is required to accurately derive probability distributions, any less than this could result in overfitting of the data. For this reason, a comparison of results using sample sizes greater than 10 and 30 was employed. A total of 24 study catchments were found to have sample sizes above 30 across four studies, resulting in less variability in geographic and meteorological characteristics. The number of catchments in which the null hypothesis is not rejected (see
Figure 2) remained relatively similar using the two sample size thresholds (in terms of percentages). However, results from the selection of a single distribution that better fits the observed data changed markedly (see
Figure 3 for a threshold of ten and see
Figure 4 for a threshold of 30). Similar biases are noted for the KDE distribution; however, where the smaller threshold resulted in similar results across the Gamma, Normal, and Beta distributions, a larger threshold results in the Beta distribution becoming dominant. The Gamma and Normal distributions are still selected as better fit for rather large percentages but are relatively small in comparison to the Beta distribution.
Although none of the distributions can be universally chosen as the best, some recommendations can still be made. Among the five distributions, the Beta and Gamma distributions are considered most suitable for rainfall-runoff modeling within a Monte Carlo environment.
5.2. Effect of Functional Form of Initial Losses on Flood Estimates
After the initial selection of probability distributions most suited to flood modeling, design floods are estimated (as described in
Section 3) using all five candidate distributions successively for the eight study catchments (outlined in
Section 4.2). Each candidate distribution is used to model the calibrated initial loss data for each catchment (sample sizes listed in
Table 1), with parameters estimated using the MLE method. Design flood estimates resulting from each successive candidate distribution are compared using relative errors of the peak flows:
where
Q is the recorded/actual peak flow and
is the predicted peak flow. Here the simulated peak flow represents the results from each successive candidate distribution and given the actual peak flow is unknown, here it is taken as the average value across all candidate distributions:
where
i the ith candidate initial loss distribution given {
i = 1, ⋯,
m}.
The results are shown as boxplots, which demonstrate the relative errors across the eight study catchments for each of the five quantiles and candidate distributions (see
Figure 5); where the boxes represent the IQR, the red horizontal line signifies the median value, and the red circle marker indicates the mean value. Please note that the more frequent events tend to result in greater variability; this phenomenon is expected as initial losses represent a much greater proportion of total rainfall depths in frequent events as compared to rare events. The main result here is the similarity of design floods resulting from different candidate distributions, with most peak flows only deviating from the mean by about ±3%.
5.3. Effect of Statistical Uncertainties in Initial Losses on Flood Estimates
Distribution assumptions as we have discovered have little impact on design floods; however, issues may also arise from uncertainties in the sample dataset due to limited sample sizes, measurement uncertainty of data used in calibration and model structural uncertainty, among others. Here design floods are estimated using six shifted distributions for the eight study catchments; the distribution is shifted by ±10%, ±25% and ±50% of the mean value in each succession. Relative errors of the design floods are calculated according to Equation (7), where the actual peak flow is taken to be the design floods resulting from the original candidate distribution and the predicted peak flow is the design flood estimated using the shifted distributions.
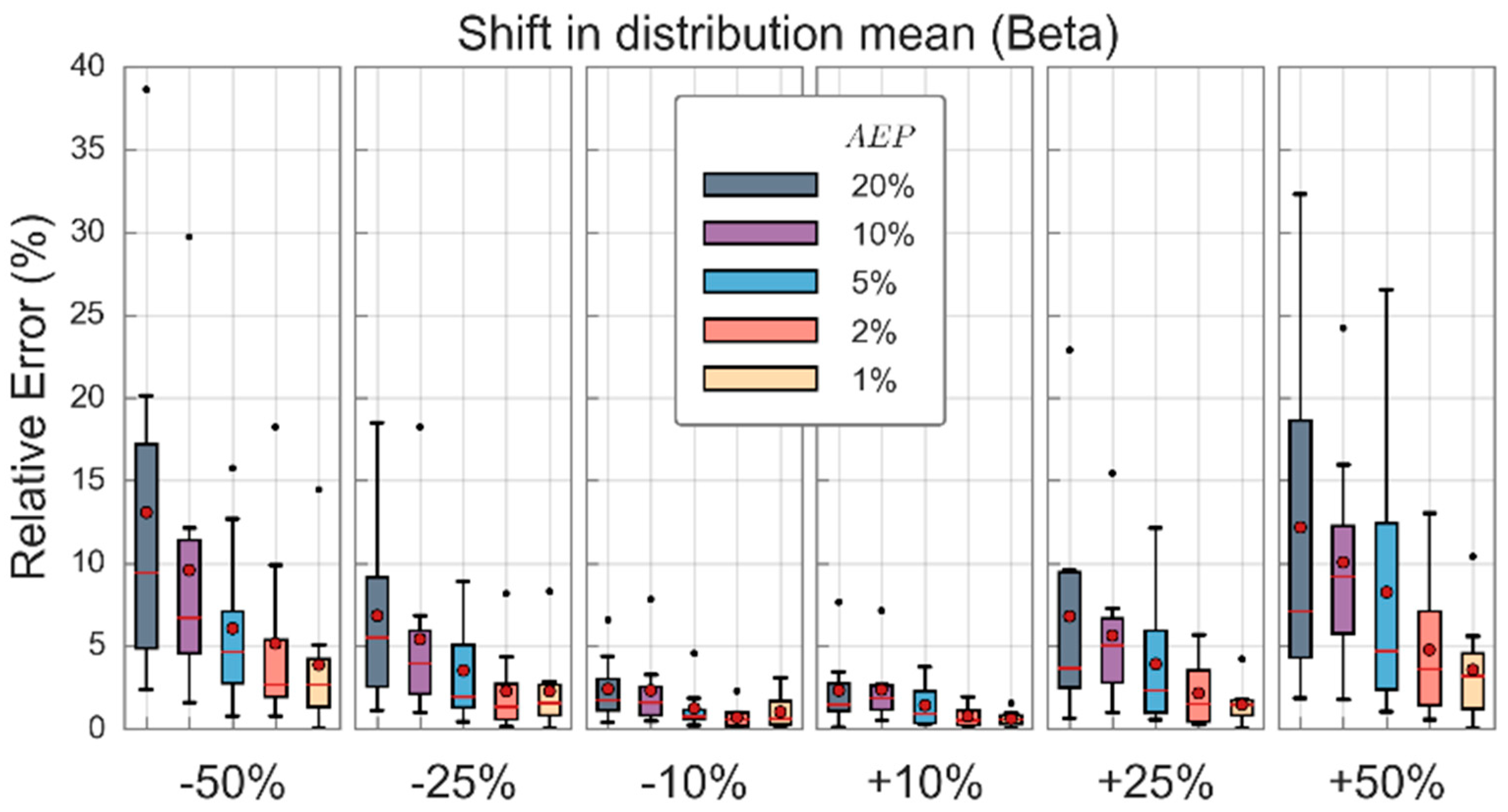
Design floods using shifted distributions were estimated for all five candidate distributions; however, given the similarity in results between distributions only the results for the Beta distribution is presented (see
Figure 6). Uncertainties in the mean initial loss value tended to result in less than two fifths of the uncertainty in design floods; i.e., peak flow estimates were within ±4% of actual peak flows when the mean initial loss shifted by ±10%, similarly peak flow errors were within ±10% and 20% when the mean shifted by ±25% and ±50%, respectively. Uncertainties of up to 10% in the mean initial loss value have negligible effect on design flood estimates. Similarly, for applications where events rarer than the 1% AEP are of interest, uncertainties of up to 50% in the mean value have minor impacts on design flood estimates. Additionally, of interest, for applications where events rarer than the 1% AEP are of interest, the mean initial loss value has minimal effect on design floods for up to ±50% uncertainty in mean values.
Similarly, the variance of each candidate distribution was varied to determine the significance of the distribution tails on peak flow estimates. The variance of each distribution was altered by ±10%, ±25% and ±50% while keeping the mean of the initial loss distribution fixed. Relative errors were typically found to be within ±3%, indicating that the distribution tails are insignificant in calculating the peak flow values.
5.4. Effect of Regionalization of Initial Loss on Flood Estimates
So far, one of the key assumptions made is the availability of rainfall-runoff records for the calibration of initial loss data; in many cases; however, catchments are either poorly gauged or ungauged. A brief assessment is therefore made as to the potential effect on design floods estimated using either partially or fully regionalized data sets. Given the use of both parametric and nonparametric probability distributions, two distinct regionalization techniques are adopted.
The regionalization of parametric distributions consists of three main themes; first we assume enough data are available to characterize the first two statistical moments (mean and variance), then the following two techniques assume no data are available at the site of interest, as follows:
Regionalization of the probability distribution (dist): each candidate distribution is assumed to be the true underlying distribution at the site of interest, the first two statistical moments are derived from observed data and then the distribution parameters are estimated using the MoM.
Regionalization of distribution parameters (param): candidate distributions are assumed to be the true underlying distribution and parameters are estimated as the average within a hydrologically similar region (where individual catchment parameters were estimated using the MLE).
Regionalization of statistical moments (stat): the candidate distribution is assumed to be representative of the true underlying distribution, the first two statistical moments are regionalized within a hydrologically similar region and then the distribution parameters are estimated using the MoM.
Design floods are estimated using the three regionalization techniques for the eight study catchments. Resulting design floods from the three successive regionalization methods are compared using relative errors of the peak flows (Equation (7)), where the actual peak flow is taken as the design flood, estimated using a GEV distribution where parameters are estimated with the MLE and the observed annual maximum flood dataset. Results are presented in
Figure 7. Regionalizing the distribution alone results in minor uncertainties. Regionalizing initial losses for catchments without data (either through the distribution parameters or data statistics) results in up to ±15% uncertainty in design flood estimates. Most of this error is most likely due to uncertainties in the mean value, with observed mean values being significantly higher than the regionalized mean values. The uncertainty in design flood estimates by our study is smaller as compared to similar previous studies. For example, the variation of mean initial loss value by 50% resulted in design flood estimates to vary in the range of 16% to 41% by Caballero and Rahman [
28] for three study catchments in south-east Australia. In another study, based on eastern Australian data, a difference of up to 30% was noted between design flood estimates obtained by at-site flood frequency analysis and probability-distributed initial loss/Monte Carlo simulation approach [
20,
49].
Given the freedom of nonparametric distributions to take on any functional form, the parametric regionalization methods could not be adopted. Rather, for nonparametric models two main themes were adopted; first assuming enough data are available to characterize the median value and the second assuming no data are available, as follows:
Regionalization of the probability distribution (dist): a standardized KDE distribution is assumed to be representative of the underlying distribution and the median value is derived from the observed data; the standardized KDE distribution is derived from individual KDE distributions within a hydrologically similar region, each distribution is normalized by the median value and the average distribution is determined.
Regionalization of the probability distribution and median value (dist + median): a standardized KDE distribution is assumed to be the true underlying distribution and the median value is estimated from within a hydrologically similar region.
Overall, relative errors in the design flood estimates using the nonparametric model appear to be higher than the equivalent for parametric models, both for catchments where sufficient data are available to characterize key statistics and where no data are available (see
Figure 8).
The design flood estimates obtained in this study using regionalized initial loos values are compared with regional design flood estimates by the recommended RFFA method in the Australian Rainfall and Runoff (ARR), the national guideline. It has been found that our method provides design flood estimates that are well within the confidence limits recommended by ARR RFFE model. The absolute median relative error values considering all our eight study catchments range 17% to 22% with a standard deviation of 6% to 11%. It should be noted that due to high rainfall variability in Australia, design flood estimates at ungauged catchments are associated with a high degree of uncertainty (generally in the range of 30 to 50%) as reported in the ARR.
5.5. Conclusions
Several hypothetical probability distributions have been compared with regards to their suitability in representing the true underlying initial loss distribution. Further to this, the impact of uncertainties in probability-distributed initial losses on design flood estimates has been evaluated. Design floods were estimated using a Monte Carlo simulation technique with stratified sampling, using stochastic rainfall depths, temporal patterns, and initial losses. The main results of this study can be summarized as follows:
The functional form of the initial loss data in Australia can be approximated using the Beta and Gamma models. These results are in line with differing outcomes in previous studies, for instance Rahman et al. [
12] recommend the use of the Beta distribution to represent initial losses, while Caballero and Rahman [
28] determine the Gamma distribution to be most appropriate for initial loss data.
By setting differing thresholds for the minimum sample size of initial loss data used to derive probability distributions, mixed results were found. This highlights the importance of sample size in deriving probability distributions of initial losses.
Design flood estimates from successive candidate distributions showed relative errors typically within ±3%, similarly by shifting the distribution mean relative errors within approximately ±20% and a change in the distribution variance also resulted in relative errors within ±3%. These results lead us to conclude that knowledge of the central tendency of distributed initial losses is more important than knowledge of the true functional form of the initial loss data.
Larger parameter sets generally present issues in regionalization; however, the comparison of the 4-parameter Beta and 2-parameter Gamma distributions showed that this was not the case in this study. Under the assumption that the catchments were ungauged, the relative errors of the design floods using the two distributions were comparable, with the Beta model producing slightly less uncertainty.
Regionalization of the initial loss distributions led to design floods being estimated to within ±15% accuracy, with the largest uncertainty coming from errors in regionalization of the central tendency of initial loss data. This leads us to conclude that initial loss distributions can be regionalized relatively easily; however, difficulties lie in accurate estimation of the central tendency of the distribution.
Although this study investigated the significance of the tails of the initial loss distribution (i.e., variance) on peak flow estimates, it is noted that further investigation into the impact of these tails on confidence limits where these are derived should be a topic of future research. The distribution tails would be expected to have a more substantial impact on the confidence limits rather than the peak flow estimates. Although the initial loss-continuing loss model has been adopted for runoff generation in this study, we feel that given the initial loss is simply a measure of the antecedent moisture condition these results are typical of what might be found with similar models of this type. However, more research is required to test this approach on similar models.
The current study sought to determine the feasibility of regionalizing probability-distributed initial losses and the potential effect of this regionalized initial loss data on design flood estimates. More comprehensive regionalization schemes, such as regional equations based on geographic or meteorological characteristics, are left to future research efforts.
It should be noted that due to absence of recorded streamflow data (with good quality and adequate length), no catchment was selected from interior/arid regions of Australia. Hence, the findings of this study are not applicable to these arid regions. However, most of the population and development projects in Australia are concentrated to coastal regions; the outcomes of this study, are applicable to these coastal regions, in particular eastern NSW. When good quality streamflow data are available in the arid regions, this study should be repeated with the enhanced dataset.
Only four theoretical distribution functions are adopted to regionalize initial loss data in the study area. More distributions could have been adopted; however, use of these four distributions has demonstrated that it is feasible to regionalize initial loss data in the study area. In future studies, other theoretical distribution functions should be tested.