Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading
Abstract
1. Origin of the Issue
2. Birth and Application History of Influence Radius
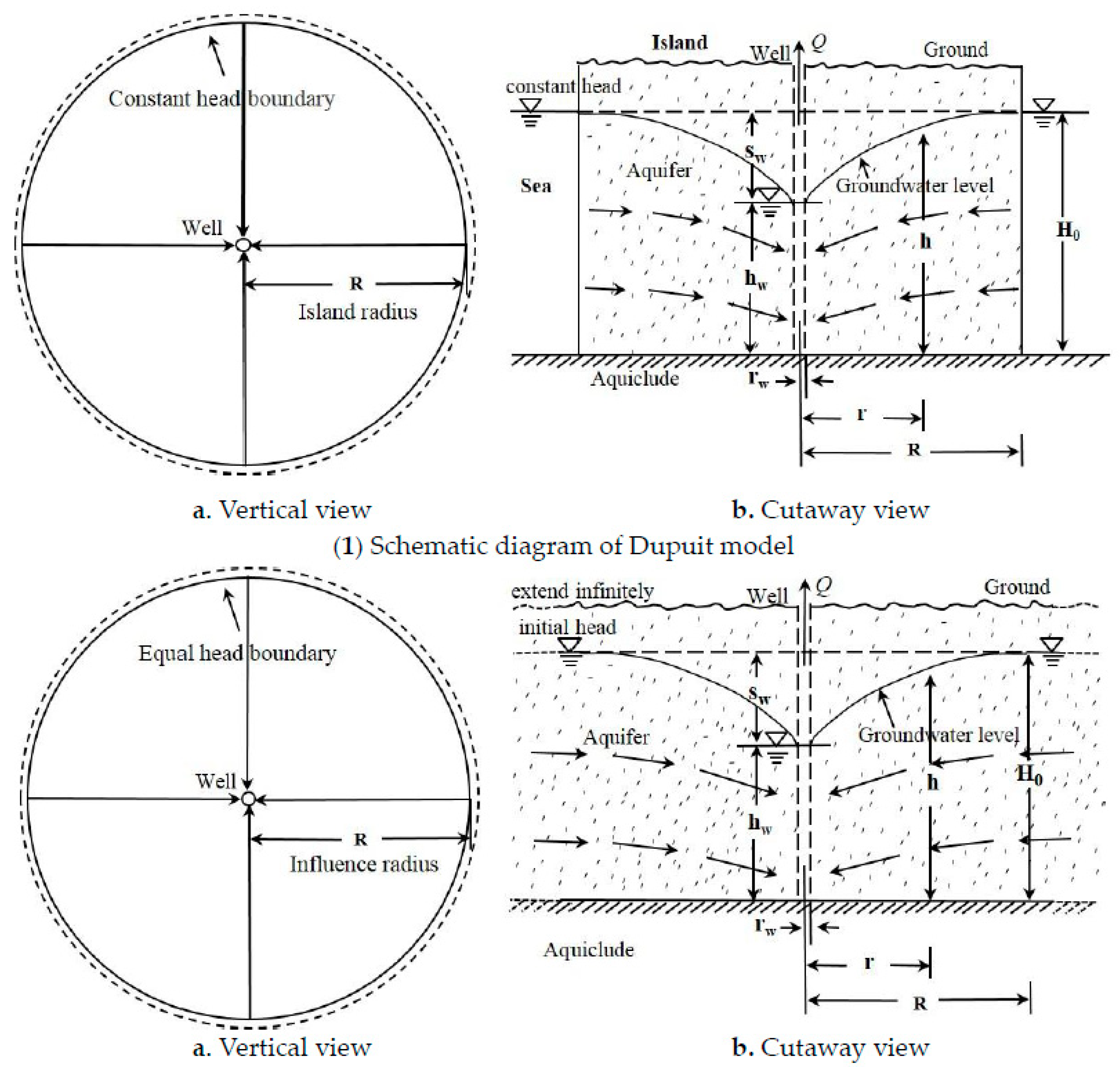
2.1. Birth: A Misunderstanding
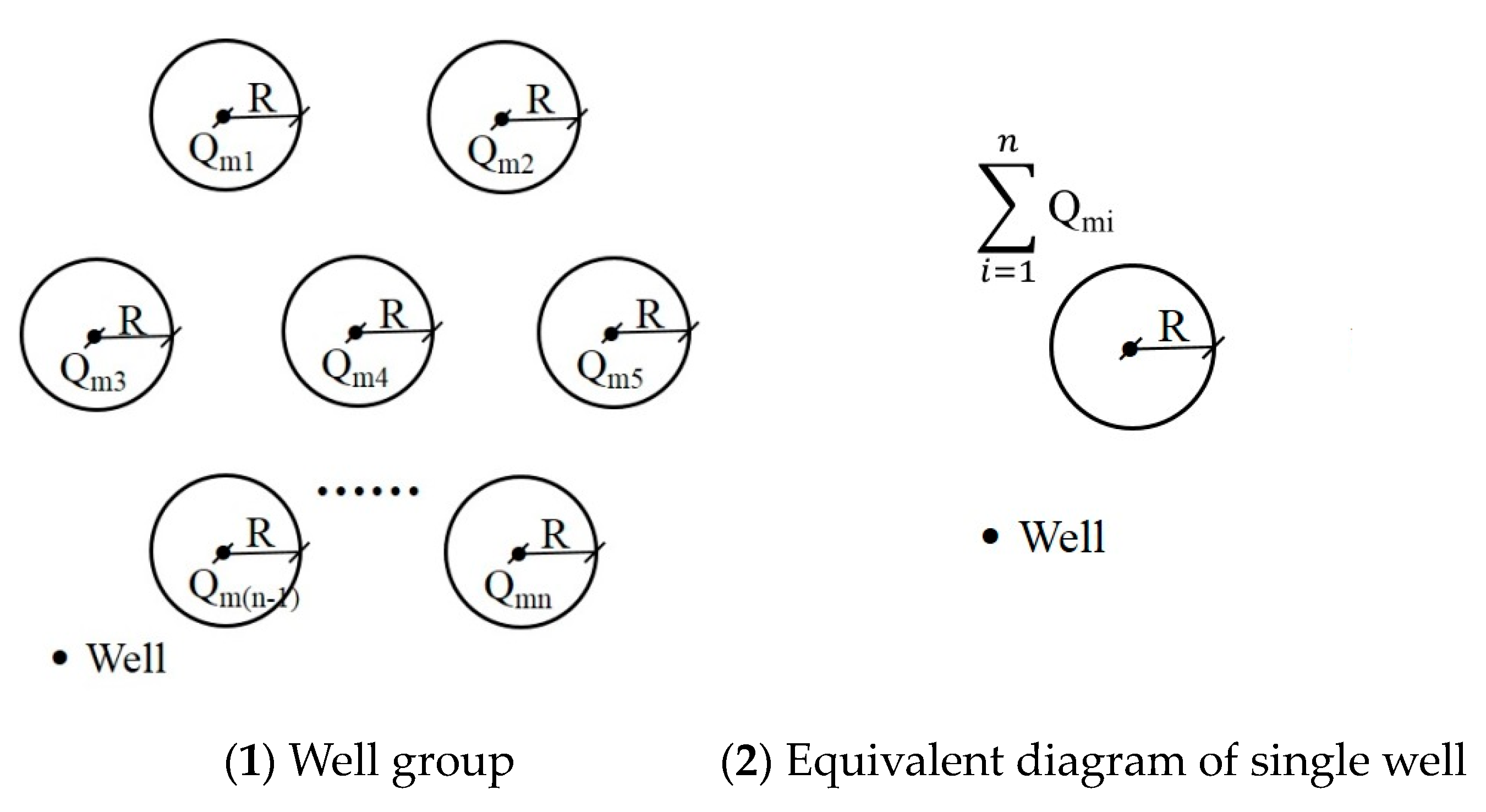
2.2. Application: Crude Simplification
3. Gap between Theory and Practice
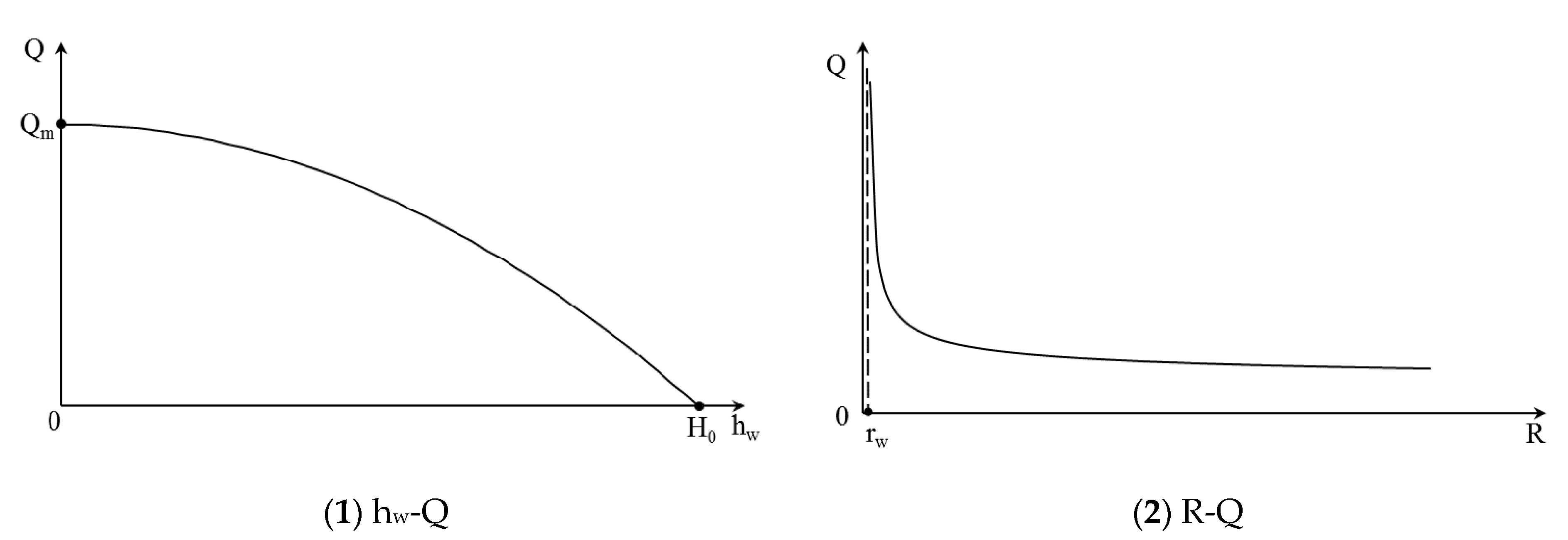
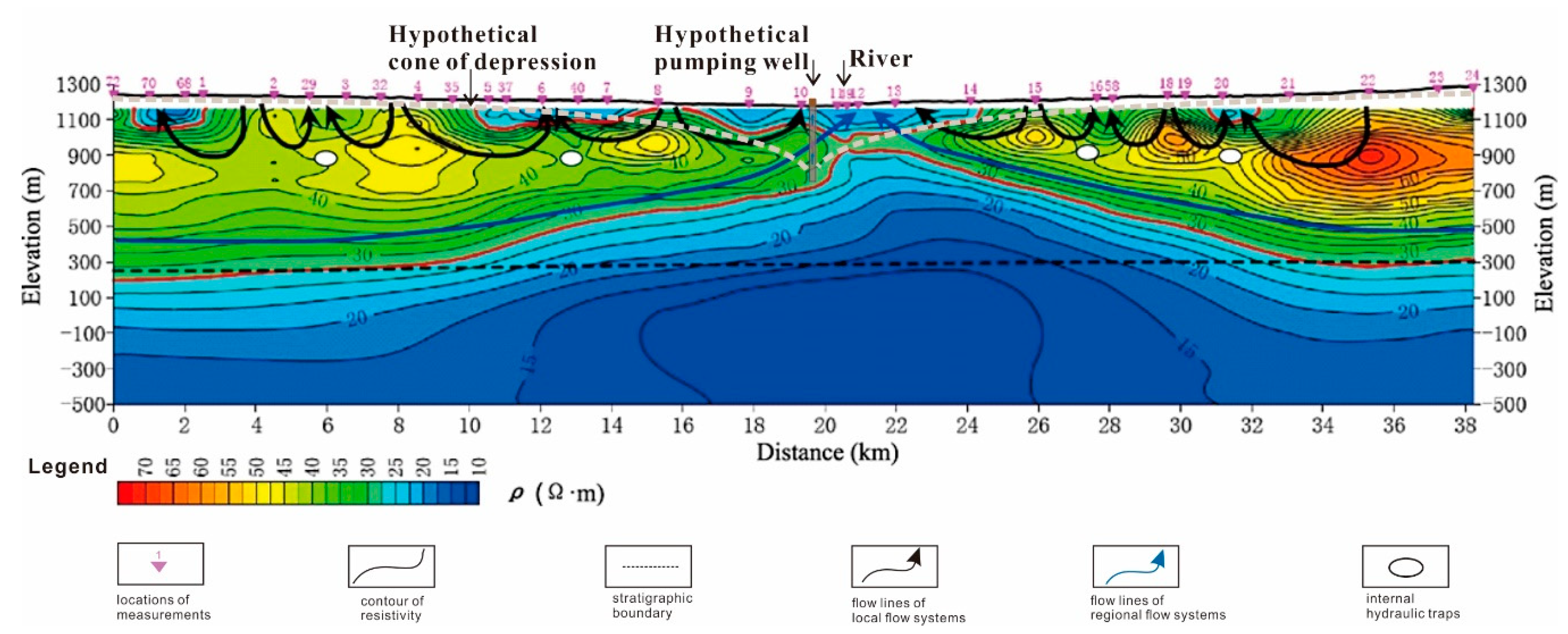
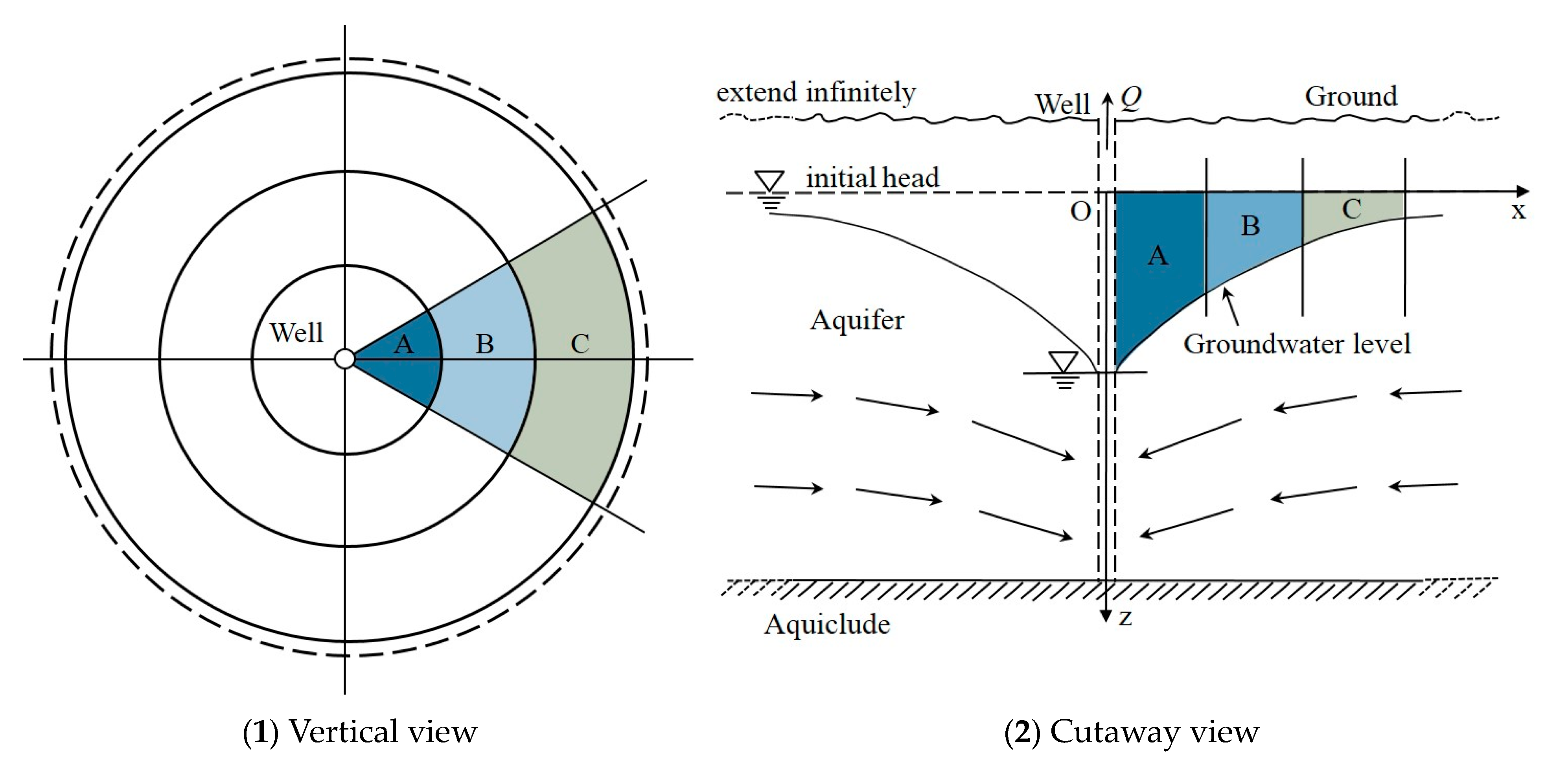
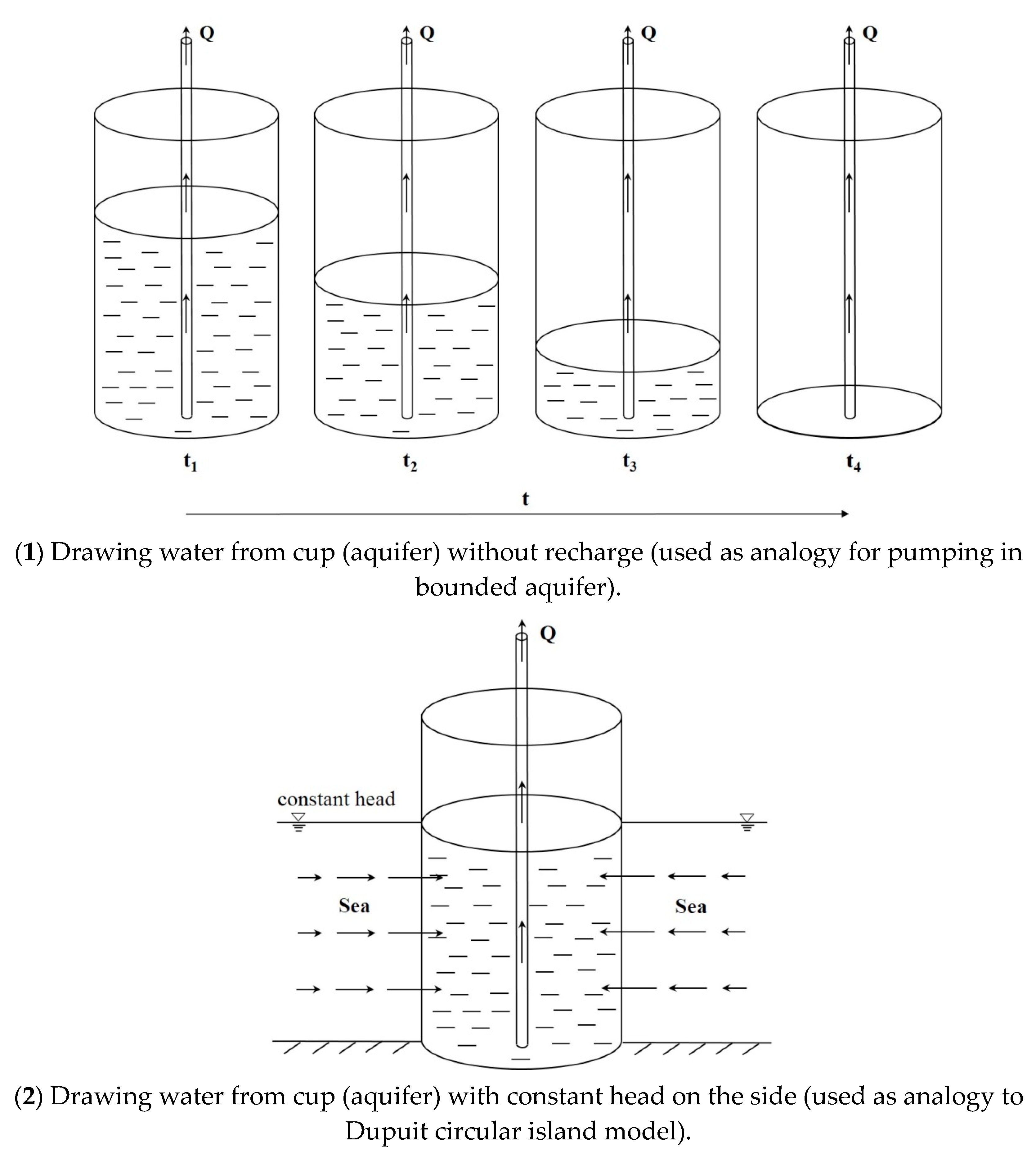
3.1. Substance of Influence Radius: Distance
3.2. The Continuity Principle of Fluids Reverses the Rationality of the Influence Radius
3.3. Essential Difference between Theory and Practice
4. The Dilemma of Practice
4.1. Misleading the Management of Sustainable Groundwater Development
4.2. Misleading the Safeguarding of Groundwater Quality
5. Summary and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description | Dimension |
| R | Influence radius | L |
| K | Hydraulic conductivity | LT−1 |
| H0 | Thickness of aquifer | L |
| sw | Drawdown of pumping well | L |
| Q | Water yield of pumping well | L3T−1 |
| rw | Radius of pumping well | L |
| T | Transmissibility coefficient of aquifer | L2T−1 |
| t | Time from beginning of pumping to formation of stable cone of depression of groundwater level | T |
| μ | Specific yield | / |
| I | Hydraulic gradient of groundwater level | / |
| r | Distance between pumping well and observation well | L |
| h | Groundwater level at distance r from pumping well | L |
| hw | Water level of pumping well | L |
| e | Empirical coefficient | / |
| Q0 | Water yield of single pumping well | L3T−1 |
| B | Width of aquifer | L |
| Qm | Maximum water yield of pumping well | L3T−1 |
| S | Distance in physics | L |
| v | Seepage velocity | LT−1 |
| n | Porosity of porous media (aquifer) | / |
References
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon [The Public Fountains of the City of Dijon]; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Dupuit, J. Etudes Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et à Travers les Terrains Perméables [Theoretical and Practical Studies on the Movement of Water in Open Channels and Permeable Ground]; Dunod: Paris, France, 1863. [Google Scholar]
- Thiem, G.A. Hydrologische Methoden; Gebhardt: Leipzig, Germany, 1906. [Google Scholar]
- Chen, Y.S.; Yao, D.S.; Hua, R.R. Try to discuss the influence radius. Geotech. Invest. Survey 1976, 6, 5–33. (In Chinese) [Google Scholar]
- Todd, D.K. Ground Water Hydrology; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Wang, J.H.; Wang, F. Discussion on the range of groundwater depression cone, radius of influence and scope of environmental impacts during pumping. J. Hydraul. Eng. 2020, 51, 827–834, (In Chinese with English abstract). [Google Scholar]
- Wang, X.M.; Wang, X.H.; Wen, W.; Li, G.Y. Model analysis of Dupuit’s steady well flow formula. Coal. Geol. Explor. 2014, 6, 73–75, (In Chinese with English abstract). [Google Scholar]
- Chen, C.X.; Lin, M.; Cheng, J.M. Groundwater Dynamics, 5th ed.; Geological Publishing House: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Chen, C.X. Stable well flow model of influence radius and sustainable yield: Differences of a basic theoretical problem in Groundwater Dynamics—Discuss with academician Xue Yuqun. J. Hydraul. Eng. 2010, 41, 1003–1008. (In Chinese) [Google Scholar]
- Xue, Y.Q. Discussion on the stable well flow model and Dupuit formula—Reply to professor Chen Chongxi’s article “Discussion”. J. Hydraul. Eng. 2011, 39, 1252–1256. (In Chinese) [Google Scholar]
- Chen, C.X. Rediscuss on stable well flow model of influence radius and sustainable yield: Differences of a basic theoretical problem in Groundwater Dynamics—Reply to academician Xue Yuqun’s discussion. J. Hydraul. Eng. 2014, 45, 117–121. (In Chinese) [Google Scholar]
- Xue, Y.Q.; Wu, J.C. Groundwater Dynamics, 3rd ed.; Geological Publishing House: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Wu, C.M.; Yeh, T.C.J.; Zhu, J.; Lee, T.H.; Hsu, N.S.; Chen, C.H.; Sancho, A.F. Traditional analysis of aquifer tests: Comparing apples to oranges? Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Eos Trans. AGU 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill, Inc.: New York, NY, USA, 1979. [Google Scholar]
- China Geological Survey. Handbook of Hydrogeology, 2nd ed.; Geological Publishing House: Beijing, China, 2012. (In Chinese)
- Zhang, H.R. The steady state of groundwater movement. Hydrogeol. Eng. Geol. 1986, 6, 18–21. (In Chinese) [Google Scholar]
- Zhu, D.T. Discussion on Dupuit formula and Forchheimer formula. J. Hydraul. Eng. 2012, 43, 502–504. (In Chinese) [Google Scholar]
- Zhang, H.R. A couple of interesting inference of Theis’s equation. Hydrogeol. Eng. Geol. 1985, 5, 30–32. (In Chinese) [Google Scholar]
- Chang, P.Y.; Hsu, S.Y.; Chen, Y.W.; Liang, C.; Wen, F.; Lu, H.Y. Using the resistivity imaging method to monitor the dynamic effects on the vadose zone during pumping tests at the Pengtsuo site in Pingtung, Taiwan. Terr. Atmos. Ocean. Sci. 2016, 27, 059. [Google Scholar] [CrossRef][Green Version]
- Chang, P.Y.; Chang, L.C.; Hsu, S.Y.; Tsai, J.P.; Chen, W.F. Estimating the hydrogeological parameters of an unconfined aquifer with the time-lapse resistivity-imaging method during pumping tests: Case studies at the Pengtsuo and Dajou sites. Taiwan. J. Appl. Geophys. 2017, 144, 134–143. [Google Scholar] [CrossRef]
- Craik, A.D.D. “Continuity and change”: Representing mass conservation in fluid mechanics. Arch. Hist. Exact Sci. 2013, 67, 43–80. [Google Scholar] [CrossRef]
- Tóth, J. A theoretical analysis of groundwater flow in small drainage basin. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]
- Tóth, J. Cross-formation gravity flow of groundwater: A mechanism of the transport and accumulation of petroleum (The generalized hydraulic theory of petroleum migration). AAPG Stud. Geol. 1980, 10, 121–167. [Google Scholar]
- Mádl-Szónyi. From the Artesian Paradigm to Basin Hydraulics: The Contribution of József Tóth to Hungarian Hydrogeology; Publishing Company of Budapest University of Technology and Economics: Budapest, Hungary, 2008. [Google Scholar]
- Zhang, R.Q.; Liang, X.; Jin, M.G.; Wan, L.; Yu, Q.C. Fundamentals of Hydrogeology, 7th ed.; Geological Publishing House: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Jiang, X.W.; Wan, L.; Wang, J.Z.; Yin, B.X.; Fu, W.X.; Lin, C.H. Field identification of groundwater flow systems and hydraulic traps in drainage basins using a geophysical method. Geophys. Res. Lett. 2014, 41, 2812–2819. [Google Scholar] [CrossRef]
- Zha, Y.Y.; Shi, L.S.; Liang, Y.; Tso, C.H.M.; Zeng, W.Z.; Zhang, Y.G. Analytical sensitivity map of head observations on heterogeneous hydraulic parameters via the sensitivity equation method. J. Hydrol. 2020, 591, 125282. [Google Scholar] [CrossRef]
- Liu, Y.P.; Yamanaka, T.; Zhou, X.; Tian, F.Q.; Ma, W.C. Combined use of tracer approach and numerical simulation to estimate groundwater recharge in an alluvial aquifer system: A case study of Nasunogahara area, central Japan. J. Hydrol. 2014, 519, 833–847. [Google Scholar] [CrossRef]
- Yuan, R.Q.; Song, X.F.; Han, D.M.; Zhang, L.; Wang, S.Q. Upward recharge through groundwater depression cone in piedmont plain of North China Plain. J. Hydrol. 2013, 500, 1–11. [Google Scholar] [CrossRef]
- Chen, C.X. Improvement of Dupuit model: With infiltration recharge. Hydrogeol. Eng. Geol. 2020, 47, 1–4, (In Chinese with English abstract). [Google Scholar]
- Zhu, Y.G.; Zhai, Y.Z.; Du, Q.Q.; Teng, Y.G.; Wang, J.S.; Yang, G. The impact of well drawdowns on the mixing process of river water and groundwater and water quality in a riverside well field, Northeast China. Hydrol. Process. 2019, 33, 945–961. [Google Scholar] [CrossRef]
- Wood, W.W. Groundwater “durability” not “sustainability”? Groundwater 2020. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Demirel, M.C.; Nawaz, N.; Khan, N. The changing characteristics of groundwater sustainability in Pakistan from 2002 to 2016. Hydrogeol. J. 2019, 27, 2485–2496. [Google Scholar] [CrossRef]
- Jia, X.Y.; Hou, D.Y.; Wang, L.W.; O’Connor, D.; Luo, J. The development of groundwater research in the past 40 years: A burgeoning trend in groundwater depletion and sustainable management. J. Hydrol. 2020, 587, 125006. [Google Scholar] [CrossRef]
- White, E.K.; Costelloe, J.; Peterson, T.J.; Western, A.W.; Carrara, E. Do groundwater management plans work? Modelling the effectiveness of groundwater management scenarios. Hydrogeol. J. 2019, 27, 1–24. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Giordano, M. Global groundwater? Issues and solutions. Ann. Rev. Environ. Resour. 2009, 34, 153–178. [Google Scholar] [CrossRef]
- Konikow, L.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Erban, L.E.; Gorelick, S.M.; Zebker, H.A.; Fendorf, S. Release of arsenic to deep groundwater in the Mekong Delta, Vietnam, linked to pumping-induced land subsidence. Proc. Natl. Acad. Sci. USA 2013, 110, 13751–13756. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Gleeson, T.; Alley, W.M.; Allen, D.M.; Sophocleous, M.A.; Zhou, Y.X.; Taniguchi, M.; VanderSteen, J. Towards sustainable groundwater use: Setting long-term goals, backcasting, and managing adaptively. Groundwater 2012, 50, 19–26. [Google Scholar] [CrossRef]
- Qian, H.; Chen, J.; Howard, K.W.F. Assessing groundwater pollution and potential remediation processes in a multi-layer aquifer system. Environ. Pollut. 2020, 263, 114669. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, B.R.; Reedy, R.C.; Gates, J.B.; Gowda, P.H. Impact of agroecosystems on groundwater resources in the Central High Plains, USA. Agric. Ecosyst. Environ. 2010, 139, 700–713. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Hakan, A. Application of multivariate statistical techniques in the assessment of groundwater quality in seawater intrusion area in Bafra Plain. Turkey 2013, 185, 2439. [Google Scholar]
- Jia, Y.F.; Xi, B.D.; Jiang, Y.H.; Guo, H.M.; Yang, Y.; Lian, X.Y.; Han, S.B. Distribution, formation and human-induced evolution of geogenic contaminated groundwater in China: A review. Sci. Total Environ. 2018, 643, 967–993. [Google Scholar] [CrossRef] [PubMed]
- Lei, S.; Jiao, J.J. Seawater intrusion and coastal aquifer management in China: A review. Environ. Earth Sci. 2014, 72, 2811–2819. [Google Scholar]
- Narasimhan, T.N. Hydrogeology in North America: Past and future. Hydrogeol. J. 2005, 13, 7–24. [Google Scholar] [CrossRef]
- Chinese Academy of Science. Development Strategy of Chinese Subjects: Groundwater Science; Science Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Zhang, F.G.; Huang, G.X.; Hou, Q.X.; Liu, C.Y.; Zhang, Y.; Zhang, Q. Groundwater quality in the Pearl River Delta after the rapid expansion of industrialization and urbanization: Distributions, main impact indicators, and driving forces. J. Hydrol. 2019, 577, 124004. [Google Scholar] [CrossRef]
- Kurwadkar, S. Emerging trends in groundwater pollution and quality. Water Environ. Res. 2014, 86, 1677–1691. [Google Scholar] [CrossRef]
- Zhang, B.; Song, X.; Zhang, Y.; Han, D.; Tang, C.; Yu, Y.; Ma, Y. Hydrochemical characteristics and water quality assessment of surface water and groundwater in Songnen plain, Northeast China. Water Res. 2012, 46, 2737–2748. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Khu, S.T.; Xi, B.; Su, J.; Hao, F.; Wu, J.; Huo, S. Status and challenges of water pollution problems in China: Learning from the European experience. Environ. Earth Sci. 2014, 72, 1243–1254. [Google Scholar] [CrossRef]
- Datta, B.; Prakash, O.; Cassou, P.; Valetaud, M. Optimal unknown pollution source characterization in a contaminated groundwater aquifer—evaluation of a developed dedicated software tool. J. Geosci. Environ. Prot. 2014, 2, 41–51. [Google Scholar] [CrossRef]
- Ayvaz, M.T. A linked simulation—optimization model for solving the unknown groundwater pollution source identification problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef] [PubMed]
- Sun, A.Y.; Painter, S.L.; Wittmeyer, G.W. A constrained robust least squares approach for contaminant release history identification. Water Resour. Res. 2006, 42, 263–269. [Google Scholar] [CrossRef]
- Mirghani, B.Y.; Mahinthakumar, K.G.; Tryby, M.E.; Ranjithan, R.S.; Zechman, E.M. A parallel evolutionary strategy based simulation—optimization approach for solving groundwater source identification problems. Adv. Water Resour. 2009, 32, 1373–1385. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B.; Jain, A. Identification of unknown groundwater pollution sources using artificial neural networks. J. Water Res. Plan. Manag. 2004, 130, 506–514. [Google Scholar] [CrossRef]
- Singh, R.M.; Datta, B. Identification of groundwater pollution sources using GA-based linked simulation optimization model. J. Hydrol. Eng. 2006, 11, 101–109. [Google Scholar] [CrossRef]
- Hintze, S.; Gaétan, G.; Hunkeler, D. Influence of surface water-groundwater interactions on the spatial distribution of pesticide metabolites in groundwater. Sci. Total Environ. 2020, 733, 139109. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.W.; Wan, L.; Ke, S.; Liu, S.A.; Han, G.L.; Guo, H.M.; Dong, A.G. Fractionation of Mg isotopes by clay formation and calcite precipitation in groundwater with long residence times in a sandstone aquifer, Ordos Basin, China. Geochim. Cosmochim. Acta 2018, 237, 261–274. [Google Scholar] [CrossRef]
- Kim, J.W. Optimal pumping time for a pump-and-treat determined from radial convergent tracer tests. Geosci. J. 2014, 18, 69–80. [Google Scholar] [CrossRef]
- Bortone, I.; Erto, A.; Nardo, A.D.; Santonastaso, G.F.; Chianese, s.; Musmarra, D. Pump-and-treat configurations with vertical and horizontal wells to remediate an aquifer contaminated by hexavalent chromium. J. Contam. Hydrol. 2020, 235, 103725. [Google Scholar] [CrossRef]
- Cecconet, D.; Sabba, F.; Devecseri, M.; Callegari, A.; Capodaglio, A.G. In situ groundwater remediation with bioelectrochemical systems: A critical review and future perspectives. Environ. Int. 2020, 137C, 105550. [Google Scholar] [CrossRef]
- Margalef-Marti, R.; Carrey, R.; Vilades, M.; Carrey, R.; Viladés, M.; Jubany, I.; Vilanova, E.; Grau, R.; Soler, A.; Otero, N. Use of nitrogen and oxygen isotopes of dissolved nitrate to trace field-scale induced denitrification efficiency throughout an in-situ groundwater remediation strategy. Sci. Total Environ. 2019, 686, 709–718. [Google Scholar] [CrossRef] [PubMed]
- Gierczak, R.F.D.; Devlin, J.F.; Rudolph, D.L. Field test of a cross-injection scheme for stimulating in situ denitrification near a municipal water supply well. J. Contam. Hydrol. 2007, 89, 48–70. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Environmental Protection, the People’s Republic of China. Technical Guideline for Delineating Source Water Protection Areas (HJ 338-2018); China Environment Press: Beijing, China, 2018. (In Chinese)
- Zhou, Y. Sources of water, travel times and protection areas for wells in semi-confined aquifers. Hydrogeol. J. 2011, 19, 1285–1291. [Google Scholar] [CrossRef]
- Ameli, A.A.; Craig, J.R. Semi-analytical 3D solution for assessing radial collector well pumping impacts on groundwater–surface water interaction. Hydrol. Res. 2017, 49, 17–26. [Google Scholar] [CrossRef]
- Valois, R.; Cousquer, Y.; Schmutz, M.; Pryet, A.; Delbart, C.; Dupuy, A. Characterizing stream-aquifer exchanges with self-potential measurements. Groundwater 2018, 56, 437–450. [Google Scholar] [CrossRef]
- Zhu, Y.G.; Zhai, Y.Z.; Teng, Y.G.; Wang, G.Q.; Du, Q.Q.; Wang, J.S.; Yang, G. Water supply safety of riverbank filtration wells under the impact of surface water-groundwater interaction: Evidence from long-term field pumping tests. Sci. Total Environ. 2020, 711, 135141. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Zheng, X.L.; Fan, X.F. Numerical modeling of steady state 3-D groundwater flow beneath an incomplete river caused by riverside pumping. J. Hydraul. Eng 1999, 30, 32–37, (In Chinese with English abstract). [Google Scholar]
- Liu, S.; Zhou, Y.; Tang, C.; McClain, M.; Wang, X.S. Assessment of alternative groundwater flow models for Beijing Plain, China. J. Hydrol. 2021, 596, 126065. [Google Scholar] [CrossRef]
| Equation Name | Equation | Application Condition | Author, Year | Parameter |
|---|---|---|---|---|
| Weber equation | Unconfined aquifer | Schultze, 1924 | R: influence radius, [L]; K: hydraulic conductivity, [LT−1]; H0: thickness of aquifer, [L]; t: time from beginning of pumping to formation of stable cone of depression of groundwater level, [T]; μ: specific yield; sw: drawdown of pumping well, [L]; Q: water yield of pumping well, [L3T−1]; I: hydraulic gradient of groundwater level | |
| Kusakin equation | Unconfined or confined aquifer | Chertousov, 1949 | ||
| Unconfined aquifer | Aravin and Numerov, 1953 | |||
| Siechardt equation | Preliminary stage of pumping in unconfined or confined aquifer | Chertousov, 1962 | ||
| Wilbur equation | Unconfined aquifer | Chen, 1976 | ||
| Kelgay equation | Completely penetrating well in unconfined aquifer | Chen, 1976 |
| Model/Equation Name | Equations Group | Application Condition | Author, Year | Parameter |
|---|---|---|---|---|
| Forward model/equation | R: influence radius, [L]; K: hydraulic conductivity, [LT−1]; H0: thickness of aquifer, [L]; t: time from beginning of pumping to formation of stable cone of depression of groundwater level, [T]; μ: specific yield; sw: drawdown of pumping well, [L]; Q: water yield of pumping well, [L3T−1]; I: hydraulic gradient of groundwater level. | |||
| Plotnikov equation | Well group pumping | Chen et al., 1976 | ||
| Dupuit–Forchheimer equation | Unconfined aquifer | Poehls and Smith, 2009 | ||
| sw-calculate equation | Confined aquifer | China Geological Survey, 2012 | ||
| Inversion model/equation | ||||
| Siechardt equation | Confined aquifer | China Geological Survey, 2012 | ||
| Wilbur equation | Unconfined aquifer | |||
| K (m/d) | R (m) |
|---|---|
| 0.5–1 | 25–50 |
| 1–5 | 50–100 |
| 5–20 | 100–300 |
| 20–50 | 300–400 |
| 50–100 | 400–500 |
| 75–150 | 500–600 |
| 100–200 | 600–1500 |
| 200–500 | 1500–3000 |
| Viewpoint | Reference |
|---|---|
| (1) Dupuit’s R is an abstract parameter that reflects the well supply conditions and is recommended as a reference recharge radius. (2) There is still a considerable amount of drawdown beyond the range that we used to think of as R. | [4] |
| R should be interpreted as a parameter indicating the distance beyond which the drawdown is negligible or unobservable. | [15] |
| R does not exist in an infinite aquifer. | [17] |
| (1) In theory, R does not exist in a confined aquifer that extends indefinitely without overcurrent recharge. (2) In practice, R should be considered as the horizontal distance from the pumping well to the point where the water level cannot actually be observed to drop and can be used as the basis for designing reasonable distances between wells. | [12] |
| (1) Dupuit’s R is different from Thiem’s R. (2) Confusion between them has led to theoretical errors and incorrect methods of groundwater resource evaluation. | [8] |
| (1) The magnitude of R has assumed properties making it essentially the same as unsteady flow. (2) The Kusakin equation with a time factor should be applied to the calculation of R. | [18] |
| (1) Dupuit’s R is different from Thiem’s R. (2) Dupuit’s R is simply the radius of the round island, while Thiem’s R is a variable related to the cone of depression of the groundwater level. | [7] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, Y.; Cao, X.; Jiang, Y.; Sun, K.; Hu, L.; Teng, Y.; Wang, J.; Li, J. Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading. Water 2021, 13, 2050. https://doi.org/10.3390/w13152050
Zhai Y, Cao X, Jiang Y, Sun K, Hu L, Teng Y, Wang J, Li J. Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading. Water. 2021; 13(15):2050. https://doi.org/10.3390/w13152050
Chicago/Turabian StyleZhai, Yuanzheng, Xinyi Cao, Ya Jiang, Kangning Sun, Litang Hu, Yanguo Teng, Jinsheng Wang, and Jie Li. 2021. "Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading" Water 13, no. 15: 2050. https://doi.org/10.3390/w13152050
APA StyleZhai, Y., Cao, X., Jiang, Y., Sun, K., Hu, L., Teng, Y., Wang, J., & Li, J. (2021). Further Discussion on the Influence Radius of a Pumping Well: A Parameter with Little Scientific and Practical Significance That Can Easily Be Misleading. Water, 13(15), 2050. https://doi.org/10.3390/w13152050










