Simulating Diurnal Variations of Water Temperature and Dissolved Oxygen in Shallow Minnesota Lakes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Daily Year-Round Water Temperature Model
2.2. Daily Dissolved Oxygen Model
2.3. Sediment Temperature Simulation
2.4. Modifications to the Daily Model
2.5. Modeled Shallow Lakes
3. Modeling Results
3.1. Model Calibration
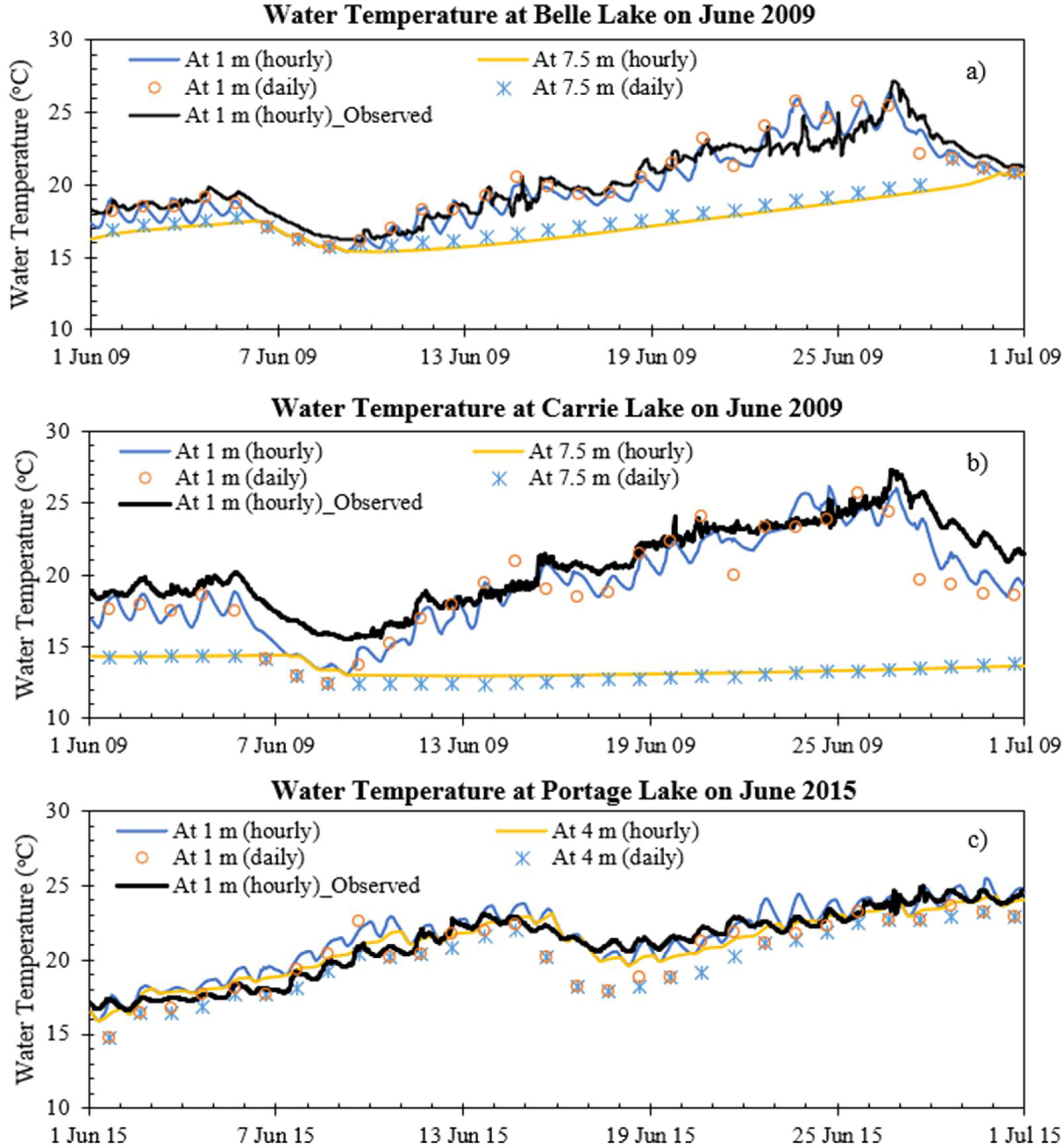
3.2. Diurnal Variations
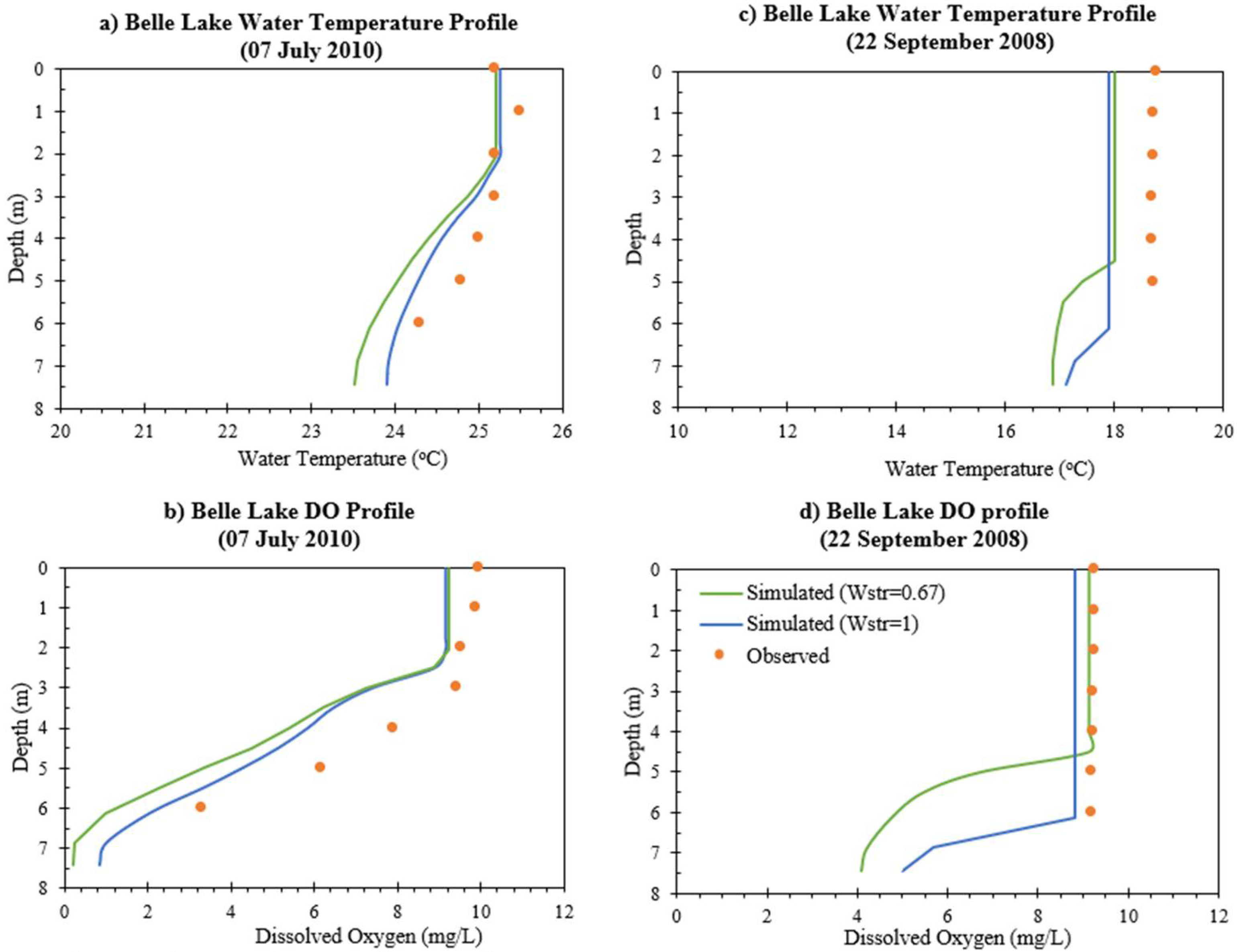
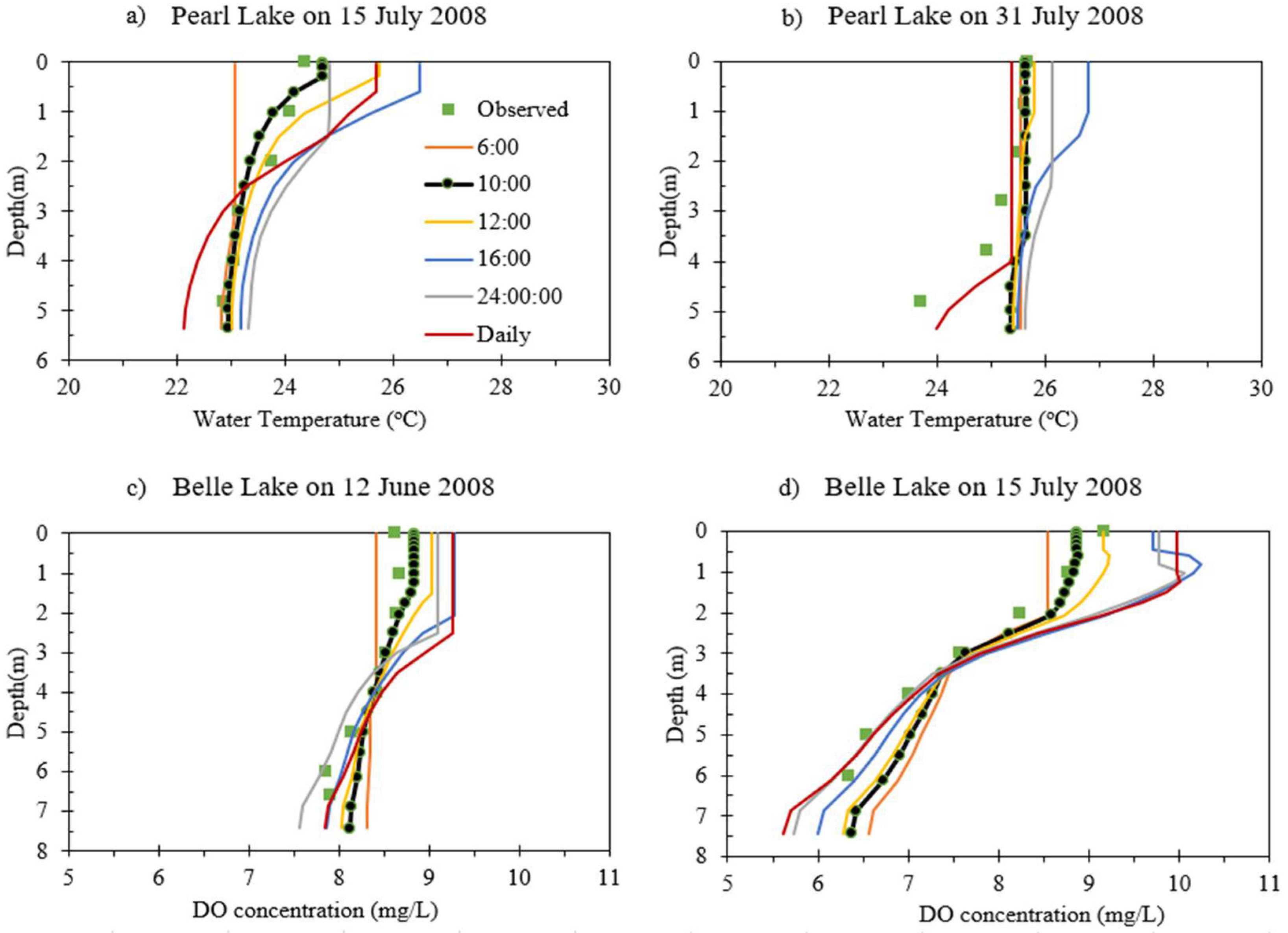
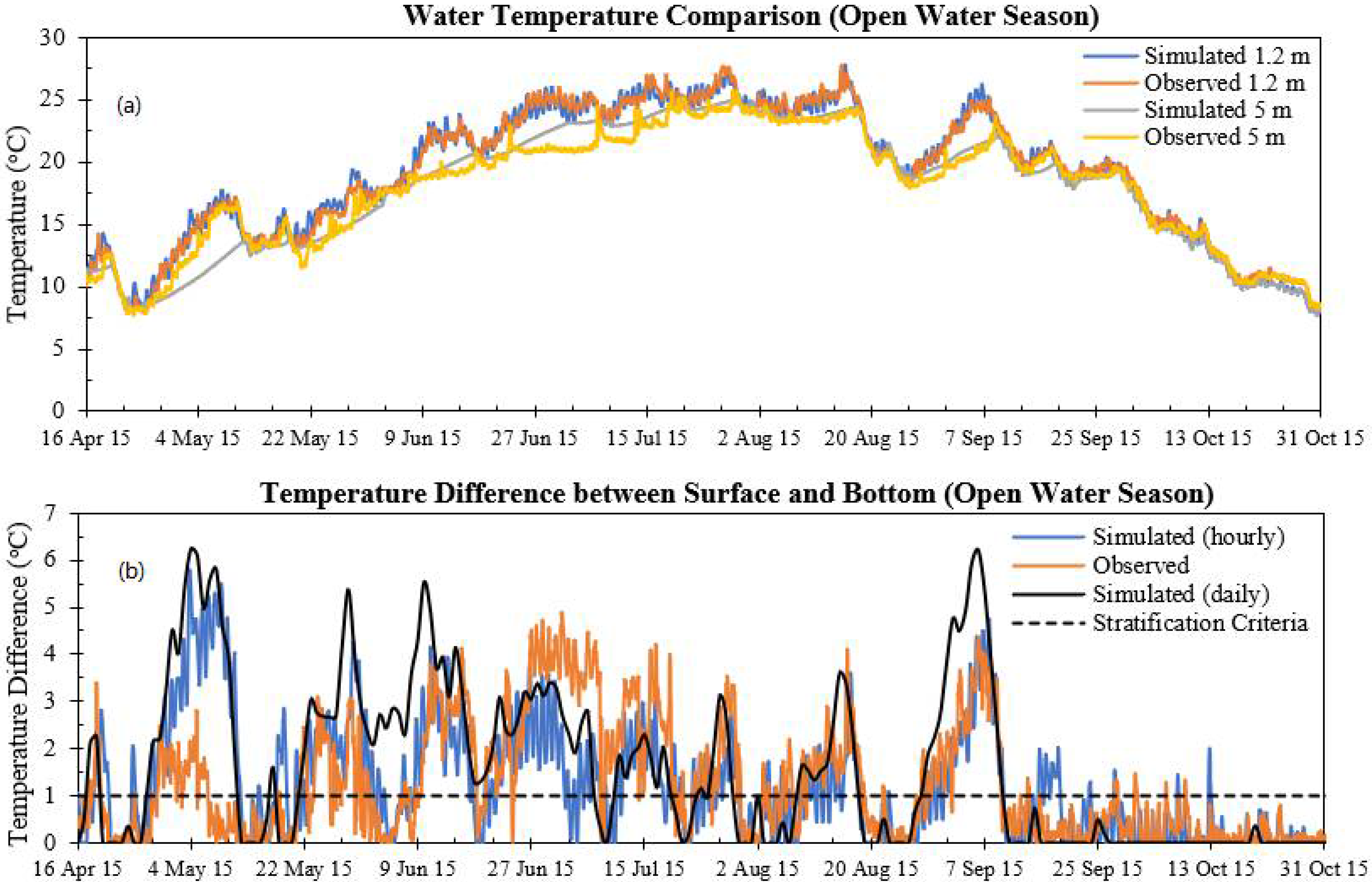
3.3. Profile Comparison
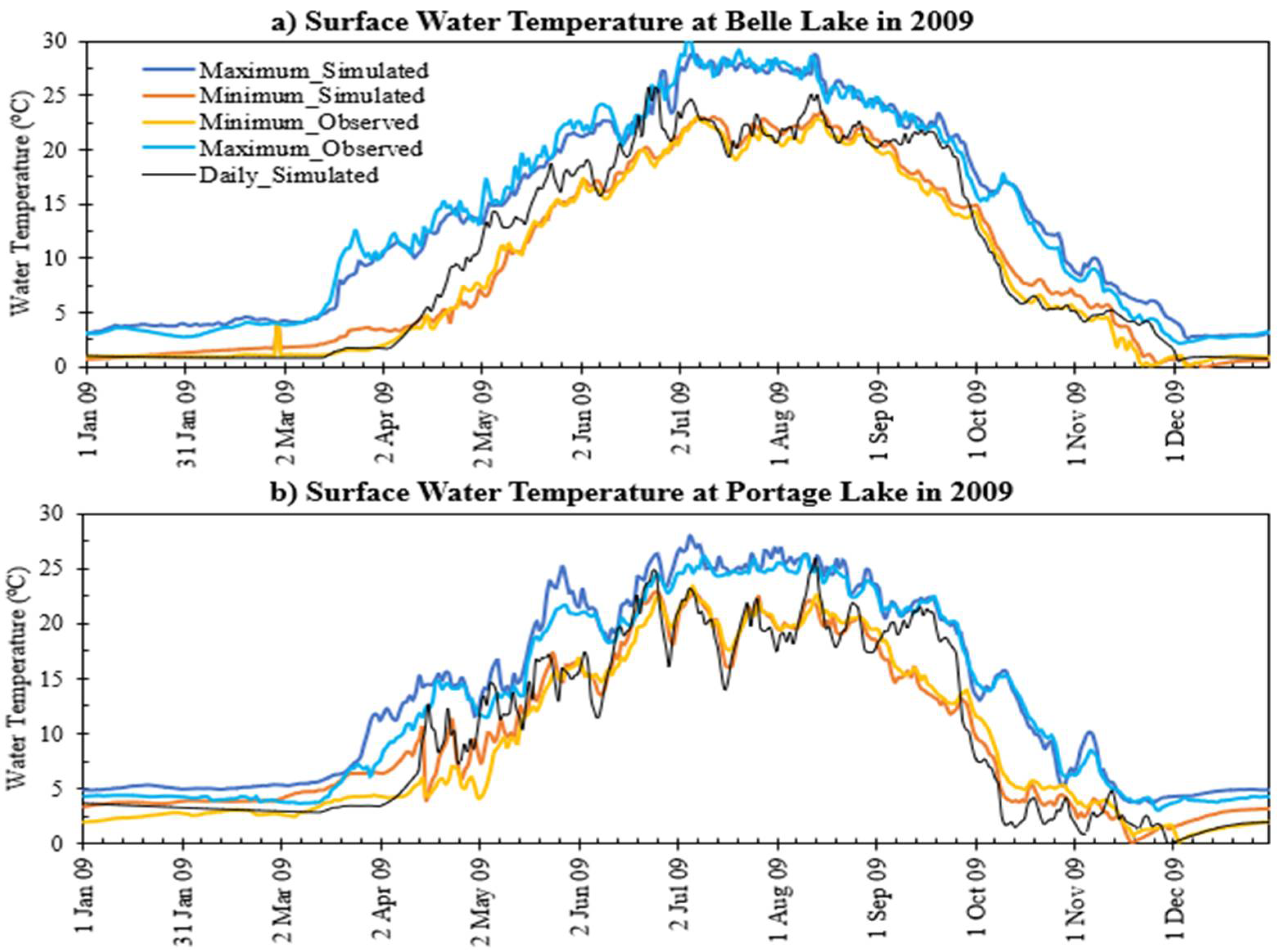
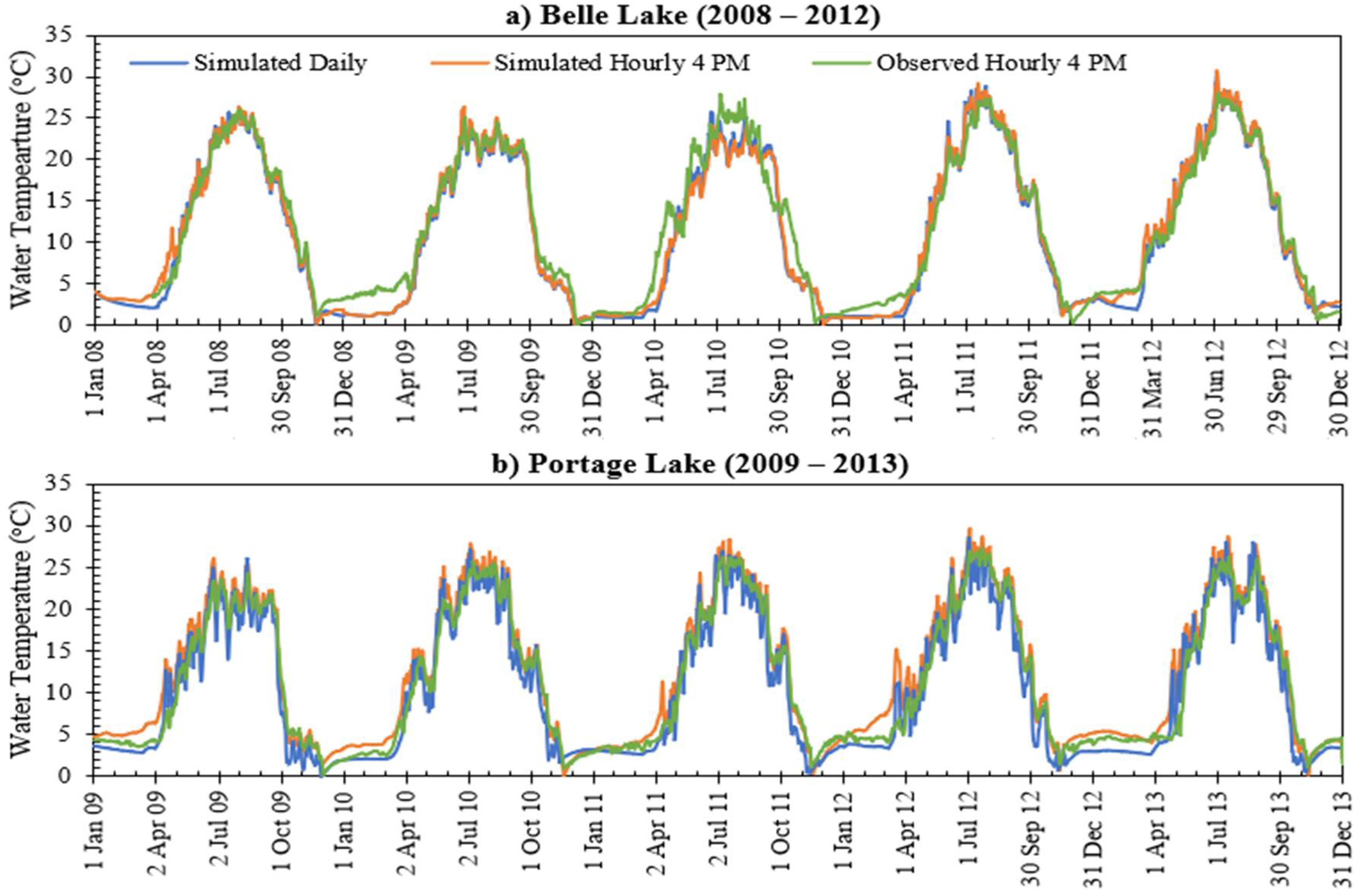
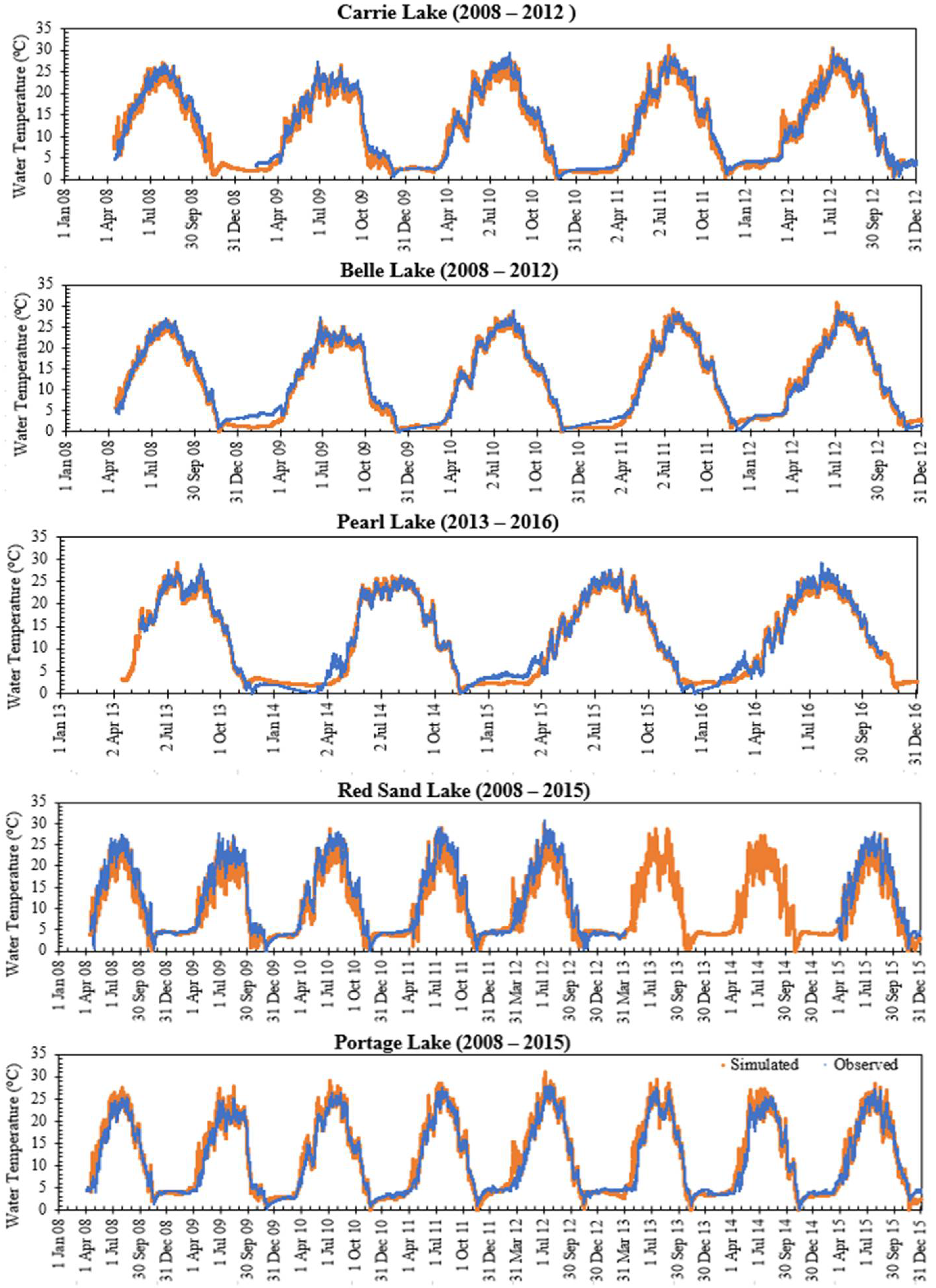
3.4. Comparison of Long-Term Surface Temperature Simulation
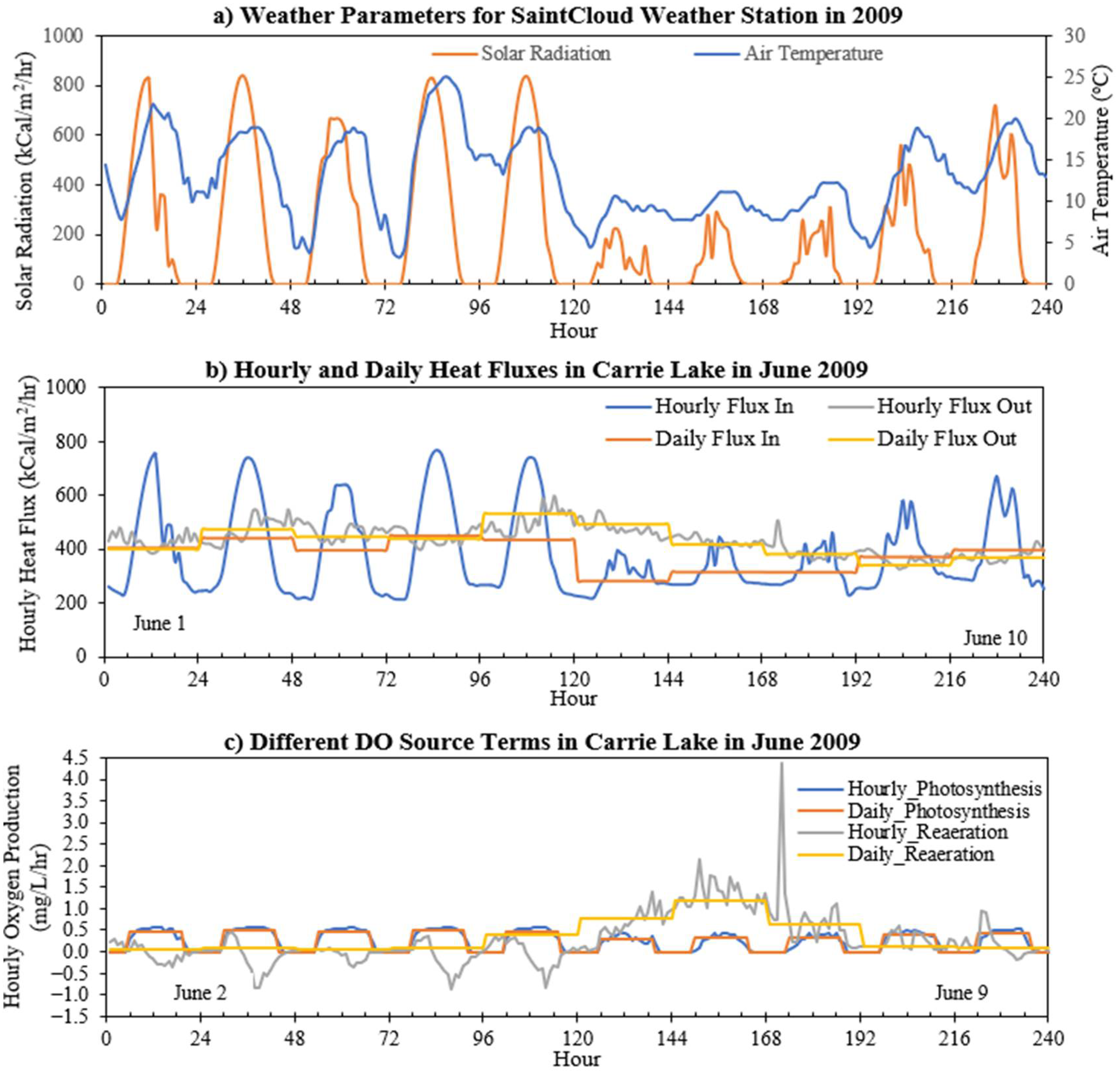
3.5. Comparison of Heat Flux, DO Production and Reaeration
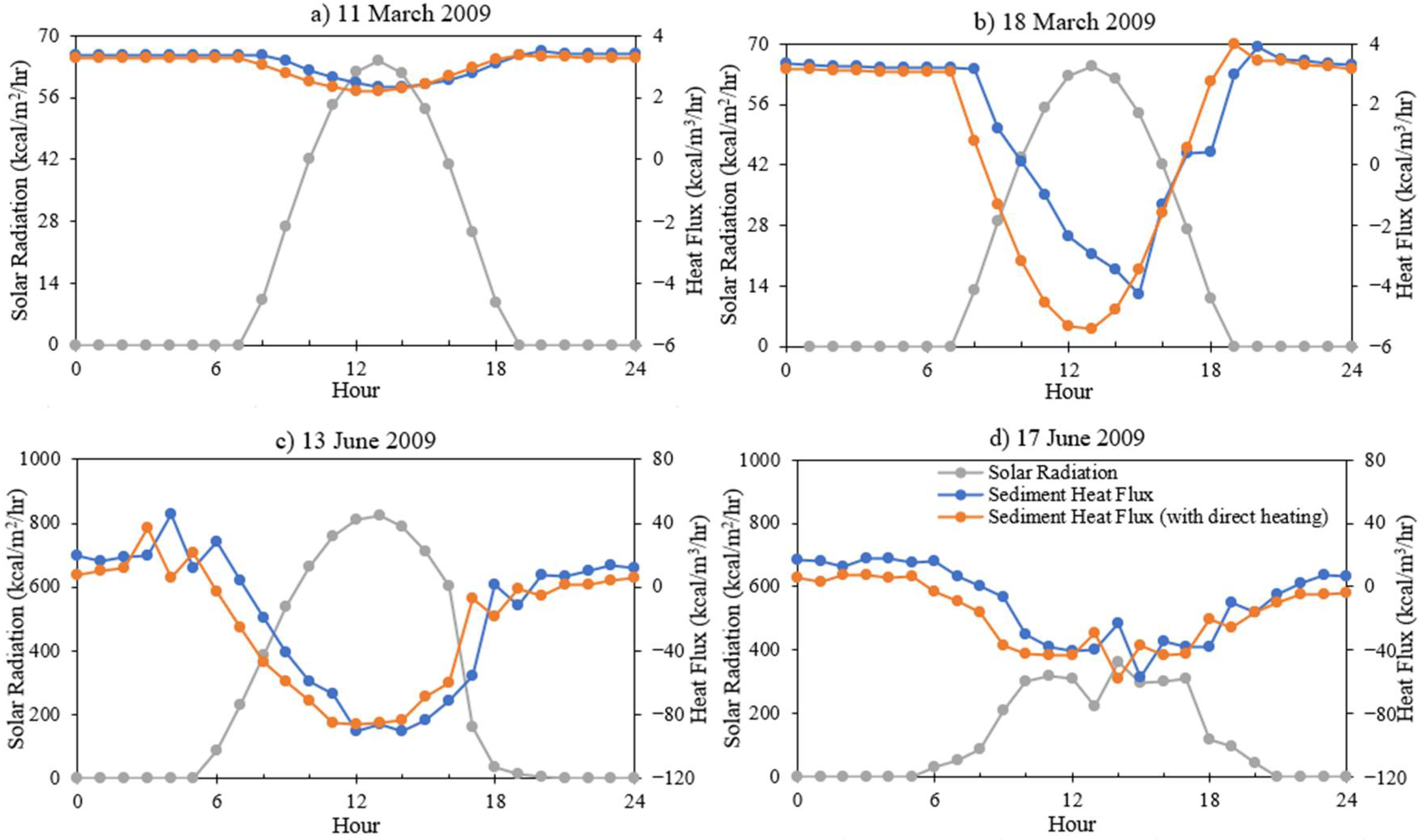
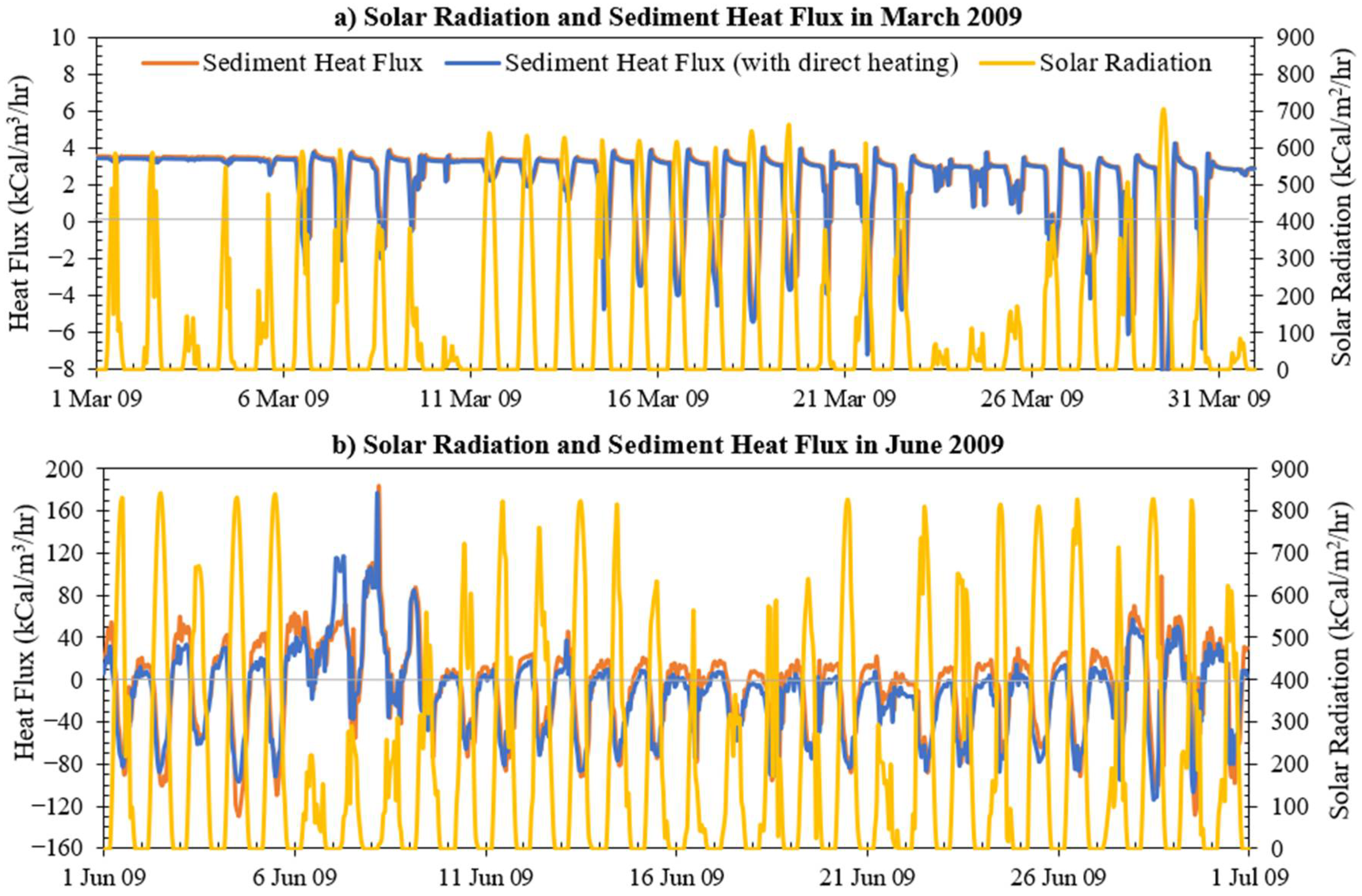
3.6. Impact of Direct Solar Radiation Heating on Sediment Bed
4. Discussion
4.1. Short-Term Mixing Prediction
4.2. Stratification Prediction
4.3. Application in Lake Management
4.4. Future Studies
5. Conclusions
- MINLAKE2018 was calibrated against measured profiles in five shallow Minnesota lakes (Table 4) with an average standard error of 1.48 °C for temperature and 2.02 mg/L for DO. With the help of available surface water temperature hourly data, the average RMSE of long-term water temperature simulation was 1.50 °C with a standard deviation of 0.32 °C. For Pearl Lake, the average RMSE for water temperature simulation at six different depths is 1.30 °C with a standard deviation of 0.15 °C.
- When compared with the daily MINLAKE2012 model, for Pearl Lake (Hmax = 5.6 m), the hourly model calculated 12% and 13% more temperature stratification for ice cover period and open water season, respectively (Table 6). Similarly, for DO, stratification increases were 14% and 20% for ice cover period and open water season, respectively. For other lakes, hourly model simulation also resulted in increased stratification percentages for water temperature and DO. The hourly model can capture diurnal changes and mixing events that lasted a few hours within a day, which the daily model ignores. Moreover, it was observed that the daily model could not predict most of the weak stratifications of shallow lakes in the fall season (Figure 12). As a result, to ensure desired water quality for aquatic organisms and fish habitat, the hourly model is suitable for shallow lakes all year round.
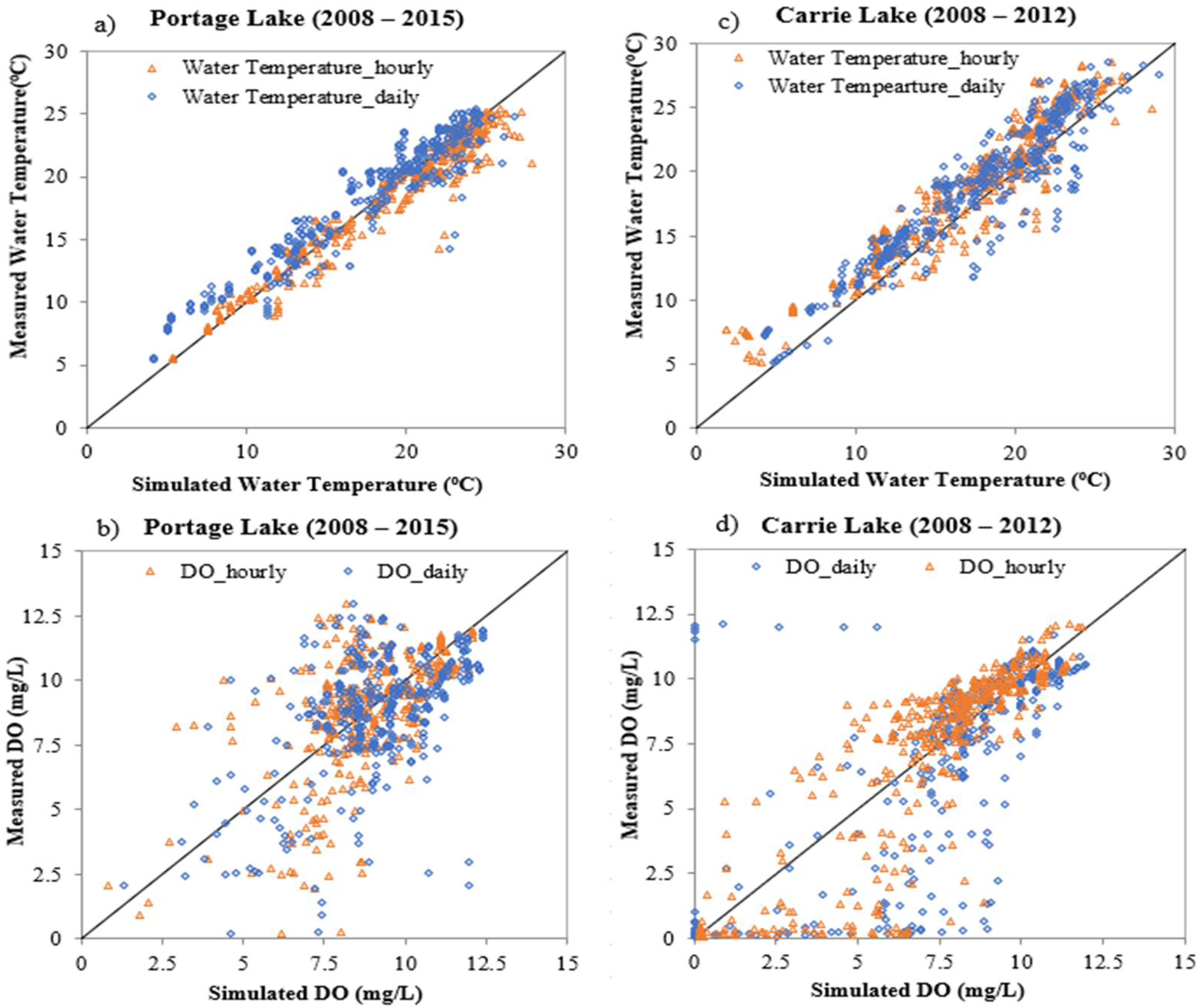
- The hourly model MINLAKE2018 performs better than the daily model MINLAKE2012 in water temperature and DO profile simulation (Figure 2). The RMSEs of temperature and DO from MINLAKE2018 decreased by 17.3% and 18.2%, respectively, and Nash-Sutcliffe efficiency increased by 10.3% and 66.7%, respectively, in comparison to MINLAKE2012.
- Sediment heating subroutine was modified to include direct heating of sediment from solar radiation for all sediment layers. After modification, the sediment heat flux pattern became coincident with the solar radiation pattern eliminating the lag time between the change in solar radiation and the change in heat flux to appear. The magnitude of sediment heat flux was reduced for both cases (heat flux going from water to sediment or sediment to water) after the sediment subroutine was modified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coutant, C.C. Striped bass, temperature, and dissolved oxygen: A speculative hypothesis for environmental risk. Trans. Am. Fish. Soc. 1985, 14, 31–61. [Google Scholar] [CrossRef]
- USACE. CE-QUAL-R1: A Numerical One-Dimensional Model of Reservoir Water Quality; User’s Manual; U.S. Army Corps of Engineers Waterways Experiment Station: Vicksburg, MS, USA, 1995.
- Chapra, S.C. Surface Water-Quality Modeling; Waveland Press: Salem, WI, USA, 2008. [Google Scholar]
- Fang, X.; Jiang, L.; Jacobson, P.C.; Fang, N.Z. Simulation and validation of cisco habitat in Minnesota lakes using the lethal-niche-boundary curve. Br. J. Environ. Clim. Chang. 2014, 4, 444–470. [Google Scholar] [CrossRef]
- Riley, M.J.; Stefan, H.G. MINLAKE: A dynamic lake water quality simulation model. Ecol. Model. 1988, 43, 155–182. [Google Scholar] [CrossRef]
- Fang, X.; Alam, S.R.; Stefan, H.G.; Jiang, L.; Jacobson, P.C.; Pereira, D.L. Simulations of water quality and oxythermal cisco habitat in Minnesota lakes under past and future climate scenarios. Water Qual. Res. J. Can. 2012, 47, 375–388. [Google Scholar] [CrossRef]
- Riley, M.J.; Stefan, H.G. Dynamic Lake Water Quality Simulation Model “MINLAKE"; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1987; 140p. [Google Scholar]
- Fang, X.; Stefan, H.G. Modeling of Dissolved Oxygen Stratification Dynamics in Minnesota Lakes under Different Climate Scenarios; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1994; 260p. [Google Scholar]
- Hondzo, M.; Stefan, H.G. Regional water temperature characteristics of lakes subjected to climate change. Clim. Chang. 1993, 24, 187–211. [Google Scholar] [CrossRef]
- Stefan, H.G.; Fang, X. Dissolved oxygen model for regional lake analysis. Ecol. Model. 1994, 71, 37–68. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Temperature and Dissolved Oxygen Simulations for a Lake with Ice Cover; Project Report 356; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1994. [Google Scholar]
- Fang, X.; Stefan, H.G. Dynamics of heat exchange between sediment and water in a lake. Water Resour. Res. 1996, 32, 1719–1727. [Google Scholar] [CrossRef]
- Fang, X.; Ellis, C.R.; Stefan, H.G. Simulation and observation of ice formation (freeze-over) in a lake. Cold Reg. Sci. Technol. 1996, 24, 129–145. [Google Scholar] [CrossRef]
- Fang, X.; Alam, S.R.; Jacobson, P.; Pereira, D.; Stefan, H.G. Simulations of Water Quality in Cisco Lakes in Minnesota; St. Anthony Falls Laboratory: Minneapolis, MN, USA, 2010. [Google Scholar]
- Xu, Z.; Xu, Y.J. A deterministic model for predicting hourly dissolved oxygen change: Development and application to a shallow eutrophic lake. Water 2016, 8, 41. [Google Scholar] [CrossRef]
- Martin, J.L. Hydro-Environmental Analysis: Freshwater Environments; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Heddam, S. Modeling hourly dissolved oxygen concentration (DO) using two different adaptive neuro-fuzzy inference systems (ANFIS): A comparative study. Environ. Monit. Assess. 2013, 186, 597–619. [Google Scholar] [CrossRef]
- Kisi, O.; Alizamir, M.; Gorgij, A.D. Dissolved oxygen prediction using a new ensemble method. Environ. Sci. Pollut. Res. 2020, 27, 9589–9603. [Google Scholar] [CrossRef] [PubMed]
- Granger, R.J.; Hedstrom, N. Modelling hourly rates of evaporation from small lakes. Hydrol. Earth Syst. Sci. 2011, 15, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Hondzo, M.; Stefan, H.G. Lake water temperature simulation model. J. Hydraul. Eng. 1993, 119, 1251–1273. [Google Scholar] [CrossRef]
- Jamily, J.A. Developing an Hourly Water Quality Model to Simulate Diurnal Water Temperature and Dissovled Oxygen Variations in Shallow Lakes; Auburn University: Auburn, AL, USA, 2018. [Google Scholar]
- Gu, R.; Stefan, H.G. Year-round temperature simulation of cold climate lakes. Cold Reg. Sci. Technol. 1990, 18, 147–160. [Google Scholar] [CrossRef]
- Ji, Z.-G. Hydrodynamics and Water Quality: Modeling Rivers, Lakes, and Estuaries; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Megard, R.O.; Tonkyn, D.W.; Senft, W.H. Kinetics of oxygenic photosynthesis in planktonic algae. J. Plankton Res. 1984, 6, 325–337. [Google Scholar] [CrossRef]
- Holley, E. Oxygen transfer at the air-water interface. Transp. Process. Lakes Ocean. 1977, 7, 117. [Google Scholar]
- Thomann, R.V.; Mueller, J.A. Principles of Surface Water Quality Modeling and Control; Harper Collins Publishers Inc.: New York, NY, USA, 1987; p. xii. [Google Scholar]
- Utley, B.C.; Vellidis, G.; Lowrance, R.; Smith, M.C. Factors affecting sediment oxygen demand dynamics in blackwater streams of Georgia’s coastal plain. J. Am. Water Resour. Assoc. 2008, 44, 742–753. [Google Scholar] [CrossRef]
- Truax, D.D.; Shindala, A.; Sartain, H. Comparison of two sediment oxygen demand measurement techniques. J. Environ. Eng. 1995, 121, 619–624. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Long-term lake water temperature and ice cover simulations/measurements. Cold Reg. Sci. Technol. 1996, 24, 289–304. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Temperature variability in the lake sediments. Water Resour. Res. 1998, 34, 717–729. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G.; Davis, M.B. Status of Climate Change Effect Simulations for Mirror Lake, New Hampshire; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1993; 52p. [Google Scholar]
- Walters, R.A.; Carey, G.F.; Winter, D.F. Temperature computation for temperate lakes. Appl. Math. Mod. 1978, 2, 41–48. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Ma, W.; Su, Z. Physical control on half-hourly, daily and monthly turbulent flux and energy budget over a high-altitude small lake on the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 2289–2303. [Google Scholar] [CrossRef]
- NAS; NAE. Water Quality Criteria 1972—A Report of the Committee on Water Quality Criteria; Environmental Protection Agency: Washington, DC, USA, 1973.
- Fang, X.; Stefan, H.G. Chapter 16 Impacts of Climatic Changes on Water Quality and Fish Habitat in Aquatic Systems. In Handbook of Climate Change Mitigation; Chen, W.-Y., Seiner, J.M., Suzuki, T., Lackner, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 1, pp. 531–570. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Buzzelli, C.P.; Powers, S.P.; Luettich, R.A., Jr.; McNinch, J.E.; Peterson, C.H.; Pinckey, J.L.; Paerl, H.W. Estimating the spatial extent of bottom water hypoxia and benthic fishery habitat degradation in the Neuse River Estuary, NC. Mar. Ecol. Prog. Ser. 2002, 230, 103–112. [Google Scholar] [CrossRef]
- Waldhauer, R.; Draxler, A.F.J.; McMillan, D.G.; Zetlin, C.A.; Leftwich, S.; Matte, A.; O’Reilly, J.E. Biological, physical and chemical dynamics along a New York Bight transect and their relation to hypoxia. Estuaries 1985, 8, 129. [Google Scholar]
- Yin, K.; Lin, Z.; Ke, Z. Temporal and spatial distribution of dissolved oxygen in the Pearl River Estuary and adjacent coastal waters. Cont. Shelf Res. 2004, 24, 1935–1948. [Google Scholar] [CrossRef] [Green Version]
- Pena, M.A.; Katsev, S.; Oguz, T.; Gilbert, D. Modeling dissolved oxygen dynamics and hypoxia. Biogeosciences 2010, 7, 933–957. [Google Scholar] [CrossRef] [Green Version]
- Levin, L.A.; Ekau, W.; Gooday, A.J.; Jorissen, F.; Middelburg, J.; Naqvi, J.; Neira, S.W.A.; Rabalais, N.N.; Zhang, F. Effects of natural and human-induced hypoxia on coastal benthos. Biogeosciences 2009, 6, 2063–2098. [Google Scholar] [CrossRef] [Green Version]
- Ekau, W.; Auel, H.; Portner, H.O.; Gilbert, D. Impacts of hypoxia on the structure and processes in the pelagic community (zooplankton, macro-invertebrates and fish). Biogeosciences 2009, 6, 5073–5144. [Google Scholar]
- D’ Avanzo, C.; Kremer, J.N. Diel oxygen dynamics and anoxic events in an eutrophic estuary of Waquoit Bay, Massachusetts. Estuaries 1994, 171, 131–139. [Google Scholar] [CrossRef]
- Shen, J.; Wang, T.; Herman, J.; Masson, P.; Arnold, G.L. Hypoxia in a coastal embayment of the Chesapeake Bay: A model diagnostic study of oxygen dynamics. Estuaries Coasts 2008, 31, 652–663. [Google Scholar] [CrossRef]
- Marsden, M.W. Lake restoration by reducing external phosphorus loading; the influence of sediment phosphorus release. Freshw. Biol. 1989, 21, 139–162. [Google Scholar] [CrossRef]
- Sondergaard, M.; Jeppesen, E.; Jensen, J.P.; Amsinck, S.L. Water framework directive: Ecological classification of Danish lakes. J. Appl. Ecol. 2005, 42, 616–629. [Google Scholar] [CrossRef]
- Philips, G.; Kelly, A.; Pitt, J.A.; Sanderson, R.; Taylor, E. The recovery of a very shallow eutrophic lake, 20 years after the control of effluent derived phosphorus. Freshw. Biol. 2005, 50, 1628–1638. [Google Scholar] [CrossRef]
- Jeppesen, E.; Sondergaard, M.; Jensen, J.P.; Havens, K.E.; Anneville, O.; Carvalho, L.; Coveney, M.F.; Deneke, R.; Dokulil, M.T.; Foy, B.; et al. Lake responses to reduced nutrient loading: An analysis of contemporary long-term data from 35 case studies. Freshw. Biol. 2005, 50, 1747–1771. [Google Scholar] [CrossRef]
- Welch, E.B.; Cooke, G.D. Internal phosphorus loading in shallow lakes: Importance and control. Lake Reserv. Manag. 2009, 21, 209–217. [Google Scholar] [CrossRef] [Green Version]

| Lake | Surface Area, As, (km2) | Max. Depth Hmax, (m) | Geometry Ratio 1 (m)0.5 | Mean Chl-a (μg/L) | Trophic Status | Simulation Years | Number of Days with Profile Data |
|---|---|---|---|---|---|---|---|
| Carrie | 0.37 | 7.90 | 3.12 | 6.71 | Mesotrophic | 2008–2012 | 50 |
| Belle | 3.71 | 7.60 | 5.77 | 27.10 | Eutrophic | 2008–2012 | 73 |
| Pearl | 3.05 | 5.55 | 7.53 | 16.91 | Eutrophic | 2008–2012 | 36 |
| Portage | 1.54 | 4.57 | 7.71 | 15.98 | Eutrophic | 2008–2015 | 86 |
| Red Sand | 2.11 | 4.57 | 8.34 | 4.43 | Mesotrophic | 2008–2015 | 87 |
| Calibration Parameter | Effect on Model Results | Description of the Parameter |
|---|---|---|
| Wstr | Temperature and DO profiles | Wind sheltering coefficient |
| BOD | DO Profiles | Biochemical oxygen demand depending on lake trophic status |
| Sb20 | DO Profiles | Sediment oxygen demand, lake tropic dependent |
| EMCOE(1) | Temperature and DO Profiles | Multiplier for diffusion coefficient in the metalimnion |
| EMCOE(2) | DO Profiles | Multiplier for SOD below the mixed layer |
| Pmax | DO Profiles | Maximum photosynthesis rate for oxygen production |
| Parameter/Lakes | Red Sand Lake | Portage Lake | Carrie Lake | Pearl Lake | Belle Lake |
|---|---|---|---|---|---|
| Wstr | 0.47 (0.47) | 0.37 (0.37) | 1 (1.0) | 0.6 (0.4) | 0.67 (1.0) |
| BOD | 0.75 (0.75) | 1.5 (1.5) | 1 (0.75) | 0.75 (1.5) | 1.5 (1.0) |
| Sb20 | 0.75 (0.75) | 1.5 (1.5) | 1.5 (0.75) | 0.75 (1.5) | 1.5 (1.8) |
| EMCOE(1) | 1 (7) | 1 (3) | 1 (3) | 1 (0.8) | 1 (4) |
| EMCOE(2) | 1 (3) | 1.1 (1) | 0.82 (1.2) | 1 (0.7) | 1 (0.5) |
| Pmax | 9.6 (16.8) | 9.6 (8.5) | 9.6 (9.6) | 9.6 (8.5) | 9.6 (7.7) |
| Lake Name | Hourly Model (MINLAKE2018) | |||||
|---|---|---|---|---|---|---|
| Water Temperature | Dissolved Oxygen | |||||
| RMSE 1 (°C) | NSE 2 | Slope 3 | RMSE (mg/L) | NSE | Slope | |
| Carrie Lake | 2.21 | 0.85 | 1.04 | 1.69 | 0.78 | 0.96 |
| Pearl Lake | 1.03 | 0.98 | 0.98 | 2.23 | 0.35 | 1.00 |
| Belle Lake | 1.03 | 0.96 | 1.03 | 1.53 | 0.69 | 1.00 |
| Red Sand Lake | 1.86 | 0.94 | 0.97 | 2.77 | 0.36 | 0.99 |
| Portage Lake | 1.41 | 0.97 | 0.98 | 1.91 | 0.31 | 0.99 |
| Average ± STD 4 | 1.48 ± 0.32 | 0.96 ± 0.02 | 0.98 ± 0.01 | 2.02 ± 0.49 | 0.50 ± 0.22 | 0.99 ± 0.02 |
| Lake Name | Daily Model (MINLAKE2012) | |||||
| Carrie Lake | 2.47 | 0.77 | 1.08 | 2.76 | 0.42 | 0.92 |
| Pearl Lake | 1.04 | 0.97 | 0.98 | 2.58 | 0.13 | 0.98 |
| Belle Lake | 1.14 | 0.96 | 1.01 | 2.09 | 0.43 | 0.94 |
| Red Sand Lake | 2.48 | 0.79 | 0.97 | 2.90 | 0.29 | 0.98 |
| Portage Lake | 1.82 | 0.86 | 1.03 | 2.03 | 0.22 | 0.96 |
| Average ± STD | 1.79 ± 0.69 | 0.87 ± 0.09 | 1 ± 0.03 | 2.47 ± 0.39 | 0.30 ± 0.13 | 0.96 ± 0.03 |
| Surface Depths | Carrie Lake | Pearl Lake | Belle Lake | Red Sand Lake | Portage |
|---|---|---|---|---|---|
| RMSE | 1.82 | 1.22 | 1.19 | 1.95 | 1.33 |
| NSE | 0.95 | 0.98 | 0.98 | 0.94 | 0.99 |
| Slope | 0.98 | 0.98 | 0.99 | 0.97 | 0.99 |
| Pearl Lake | 1.7 m | 2.4 m | 3.4 m | 4.4 m | 5.0 m |
| RMSE | 1.08 | 1.18 | 1.47 | 1.47 | 1.42 |
| NSE | 0.98 | 0.98 | 0.97 | 0.96 | 0.97 |
| Slope | 0.98 | 0.99 | 0.98 | 0.97 | 0.98 |
| Lake Name | Geometry Ratio (Secchi Depth) | % Hours or Days of Temperature Stratification | |||
| Ice Cover Period | Open Water Season | ||||
| Hourly Model | Daily Model | Hourly Model | Daily Model | ||
| Carrie | 3.12 (1.48 m) | 89 | 89 | 65 | 64 |
| Belle | 5.77 (1.46 m) | 86 | 80 | 37 | 35 |
| Pearl | 7.53 (1.85 m) | 93 | 81 | 80 | 67 |
| Portage | 7.71 (2.00 m) | 89 | 83 | 26 | 25 |
| Red Sand | 8.34 (3.04 m) | 90 | 89 | 32 | 16 |
| Lake Name | Geometry Ratio (Secchi Depth) | % Hours or Days of DO Stratification | |||
| Ice Cover Period | Open Water Season | ||||
| Hourly Model | Daily Model | Hourly Model | Daily Model | ||
| Carrie | 3.12 (1.48 m) | 75 | 66 | 58 | 71 |
| Belle | 5.77 (1.46 m) | 88 | 76 | 56 | 52 |
| Pearl | 7.53 (1.85 m) | 93 | 79 | 67 | 47 |
| Portage | 7.71 (2.00 m) | 89 | 67 | 48 | 38 |
| Red Sand | 8.34 (3.04 m) | 90 | 87 | 37 | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasnim, B.; Jamily, J.A.; Fang, X.; Zhou, Y.; Hayworth, J.S. Simulating Diurnal Variations of Water Temperature and Dissolved Oxygen in Shallow Minnesota Lakes. Water 2021, 13, 1980. https://doi.org/10.3390/w13141980
Tasnim B, Jamily JA, Fang X, Zhou Y, Hayworth JS. Simulating Diurnal Variations of Water Temperature and Dissolved Oxygen in Shallow Minnesota Lakes. Water. 2021; 13(14):1980. https://doi.org/10.3390/w13141980
Chicago/Turabian StyleTasnim, Bushra, Jalil A. Jamily, Xing Fang, Yangen Zhou, and Joel S. Hayworth. 2021. "Simulating Diurnal Variations of Water Temperature and Dissolved Oxygen in Shallow Minnesota Lakes" Water 13, no. 14: 1980. https://doi.org/10.3390/w13141980
APA StyleTasnim, B., Jamily, J. A., Fang, X., Zhou, Y., & Hayworth, J. S. (2021). Simulating Diurnal Variations of Water Temperature and Dissolved Oxygen in Shallow Minnesota Lakes. Water, 13(14), 1980. https://doi.org/10.3390/w13141980







