Abstract
Due to eutrophication, many lakes require periodic management and restoration, which becomes unpredictable due to internal nutrient loading. To provide better lake management and restoration strategies, a deterministic, one-dimensional water quality model MINLAKE2020 was modified from daily MINLAKE2012 by incorporating chlorophyll-a, nutrients, and biochemical oxygen demand models into the regional year-around temperature and dissolved oxygen (DO) model. MINLAKE2020 was applied to six lakes (varying depth and trophic status) in Minnesota focusing on studying the internal nutrient dynamics. The average root-mean-square errors (RMSEs) of simulated water temperature and DO in six lakes are 1.51 °C and 2.33 mg/L, respectively, when compared with profile data over 2–4 years. The average RMSE of DO simulation decreased by 24.2% when compared to the MINLAKE2012 model. The internal nutrient dynamics was studied by analyzing time series of phosphorus, chlorophyll-a, and DO over several years and by performing a sensitivity analysis of model parameters. A long-term simulation (20 years) of Lake Elmo shows that the simulated phosphorus release from sediment under the anoxic condition results in surface phosphorus increase, which matches with the observed trends. An average internal phosphorus loading increase of 92.3 kg/year increased the average daily phosphorus concentration by 0.0087 mg/L.
1. Introduction
Eutrophication has been a threat to waterbodies since the beginning of the twentieth century in industrialized countries [1,2,3,4]. A large proportion of the anthropogenic increase in nitrogen and phosphorus flux due to industrialization is delivered to ground or surface waters through direct runoff, human and animal wastes, and atmospheric deposition. Over time, excess nutrients are transported to waterbodies [5,6]. When a waterbody undergoes any human-influenced ecosystem changes such as nutrient loading, extreme weather events, or invasive organisms; algal species (cyanobacteria) can form dense overgrowths known as algal blooms. Since these blooms can produce toxins that are harmful to people and wildlife they are often referred to as harmful algal blooms (HAB). HABs cause undesirable changes in aquatic resources such as reduced water clarity, hypoxia, fish kills, loss of biodiversity, and an increase in nuisance species [7,8]. Oxygen is consumed by both living and dead algae which results in low oxygen concentration in lakes typically known as hypoxia (below 2–4 mg/L of dissolved oxygen (DO)). Eutrophication also has a detrimental effect on human health through increased exposure to cyanobacteria toxins [9,10], nitrites, and nitrates [7,8] in drinking water. Since most cities use surface water as the drinking water source, HABs can cause serious problems of off-flavor odor and taste (sometimes described as earthy or musty). In some cases, drinking water no longer remains safe to drink and complete remediation is needed. For example, the state of Ohio committed to spending USD 172 million to clean up Lake Erie as HABs were causing severe drinking water problems [11]. Furthermore, the economic costs of eutrophication, for restoring the ecosystem services (e.g., housing amenity value, recreation opportunities, freshwater provisioning, and food and fiber production) are high [12,13,14]. Eutrophication can have serious effects on the social health of a community causing decreases in the activity that are dependent on aquatic or seafood harvests or tourism, resulting in disruption of social, and cultural practices.
In North America, more than 41% of lakes are eutrophic; the proportions for the Asia Pacific, Europe, Africa, and South America are 53%, 28%, 48%, and 41%, respectively [15]. Management and restoration solutions to control eutrophication require predicting the lake’s nutrient concentration, understanding interactions between nutrients and water quality variables, and quantifying algal growth and decay. Since the 1970s, numerical modeling has shown to be an effective tool to quantify nutrient concentrations [16,17]. Several promising lake models (MINLAKE, PCLake, LAKE2K, CE-QUAL-W2, EFDC, and ELCOM-CAEDYM) have been developed over the past decades. The key state variables of these models are nutrients, principally phosphorus (P), nitrogen (N), and sometimes silica (Si) [18,19] since these nutrients link to primary production.
The Minnesota Lake Water Quality Management Model (MINLAKE) is a one-dimensional (along depth direction), deterministic water quality model with a time step of one day. MINLAKE was developed in 1988 to support lake eutrophication studies and was capable of simulating water temperature, chlorophyll a (Chla), phosphorus, nitrogen, biochemical oxygen demand (BOD), dissolved oxygen (DO) for lakes during the open water season [20]. MINLAKE1988 was further developed to include ice-cover period simulation [21], simplified regional DO model [22], modified year-round nutrient model [23], and hourly water temperature and DO model [24]. MINLAKE nutrient model (MINLAKE98) was applied to three lakes but did not perform well for multiple-year simulation [23]; hence, the model was not used further. The most recent version of MINLAKE with daily simulation, MINLAKE2012 was capable of simulating water temperature and DO in different types of lakes with good agreement with observations [25] but lacks a nutrient model. LAKE2K is also a one-dimensional lake water quality model which simulates carbon, nitrogen, oxygen, phosphorus, silica concentrations, and phytoplankton and zooplankton biomass using water balance, heat balance, and mass balance for the epilimnion, metalimnion, and hypolimnion (three layers) of a lake [26]. A two-dimensional hydrodynamic and water quality model, CE-QUAL-W2 (originally developed in 1990s) can be used in rivers, lakes, reservoirs, estuaries, and even a combination of river segments and multiple reservoirs but is more suitable for relatively long and narrow water bodies [27]. PCLake (1990) is a process-based model to simulate water quality in shallow, non-stratifying lakes in temperate climate zones with a uniform daily time-step for processes. The recent version of PCLake, PCLake+ simulates basic stratification in temperature using mixing depth and two layers: the epilimnion and hypolimnion only [28]. EFDC is a state-of-the-art, versatile model that can simulate one-, two- or three-dimensional flow, transport, and biogeochemical processes in surface water systems such as rivers, lakes, estuaries, and reservoirs. ELCOM is a three-dimensional hydrodynamic model which is often integrated with a water quality model CAEDYM [29] and this coupled model has been used to simulate water quality and algal bloom scenarios [30,31]. Though EFDC and ELCOM-CAEDYM are very flexible and support a variety of conditions, the complexity of these models makes them difficult to apply when data are scarce. Each of these models has some limitations such as modeling for a certain type of waterbody (PCLake), only modeling certain water quality constituents (MINLAKE2012), neglecting some physical processes (CE-QUAL-W2 and Lake2K), or problems due to model complexity (EFDC and ELCOM-CAEDYM). Apart from these models, during the last two decades, new manifestations of eutrophication have emerged [1,32,33]. In order to improve operational control of algal blooms and management applications, models are often integrated into warning systems to predict short-term phytoplankton blooms [34]. For example, the EcoTaihu model has been integrated into a Windows software platform to predict algal blooms in Lake Taihu [35]. Elliott [36] used PROTECH model to study the effect of an increase in water temperature and phosphorus loading on phytoplankton in Lake Windermere.
High phosphorus release from lake sediments is frequently reported as an important mechanism delaying lake recovery after external loading of phosphorus has been reduced [37,38,39]. A study of 78 stormwater ponds revealed that more than one-third of the sampled ponds may experience internal loading of phosphorus although these ponds are shallow and had short periods of anoxic condition [40]. A long-term survey of 35 lakes in Europe and North America concluded that internal release of phosphorus typically continues for 10–15 years after the external loading reduction [41] but in some lakes, the internal release may last longer than 20 years [38]. In shallow lakes, it is common to observe the negligible change in phosphorus concentrations in lake water even after external load diversion [42]. For example, Lake Trummen in Sweden remained hypereutrophic even after 11 years of sewage (primary source of external loading) diversion. Eventually, internal phosphorus loading was reduced dramatically by removing 1 m of high phosphorus sediment [42].
Since internal loading adds uncertainty to lake restoration processes, a reliable lake water quality tool which (a) focuses on the internal nutrient dynamics, (b) considers all physical processes (ice cover, sediment heat transfer, etc.), (c) can be applied to different types of lakes, and (d) is capable of multiple year simulation, is necessary and very useful. A simple, one-dimensional lake water quality model, which can predict chlorophyll-a, phosphorus, DO in various types of lakes (shallow to deep, small to large surface area, and oligotrophic to eutrophic) for short-term and long-term simulations, is needed for lake management and restoration purpose. Since MINLAKE2012 was capable of simulating water temperature and DO in all lake types with good performance [25], it was selected for further enhancement. The more general daily lake water quality model MINLAKE2020 was developed by including phytoplankton, zooplankton, nutrients, and BOD sub-models into the existing temperature and DO model of MINLAKE2012. To verify the performance of the model, it was applied to six Minnesota lakes having varying depths and trophic status and having 15–70 days of profile data for model calibration/validation over different time spans (2–20 years). The objective of this study was to use MINLAKE2020 to understand the internal nutrient dynamics and explore the interaction/connection among nutrients, phytoplankton dynamics, and stratification/mixing dynamics in lakes. Thus, the inflow sub model developed for MINLAKE2020 was disabled to provide a better understanding of the nutrient dynamics within the lakes.
2. Materials and Methods
Section 2.1, Section 2.2, Section 2.3, Section 2.4, Section 2.5 and Section 2.6 provide descriptions and governing equations for MINLAKE2020 to simulate unsteady phytoplankton (quantified using chlorophyll-a concentration), zooplankton, and nutrients for both the open water season and the ice cover periods. Since this study focuses on the nutrients/phytoplankton internal dynamics/cycles, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 for water quality variables modelled by MINLAKE2020 do not include inflow and outflow as a part of mass balance processes.
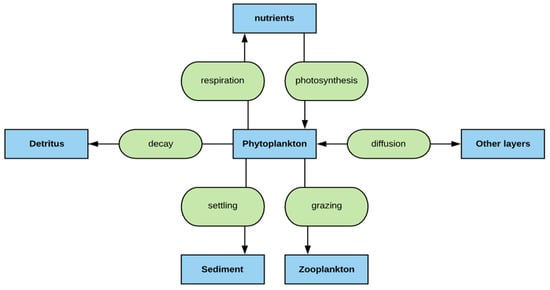
Figure 1.
Schematic diagram of phytoplankton (Chlorophyll-a) cycle modeled by MINLAKE2020.
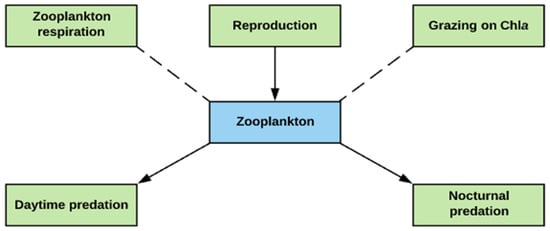
Figure 2.
Schematic diagram of zooplankton cycle modeled by MINLAKE2020.
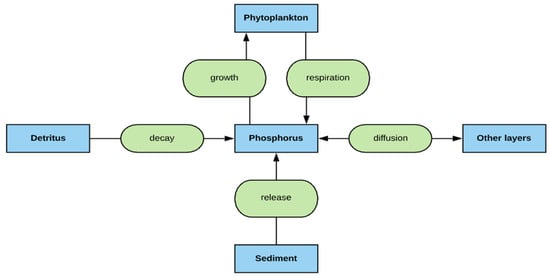
Figure 3.
Schematic diagram of phosphorus cycle modeled by MINLAKE2020.
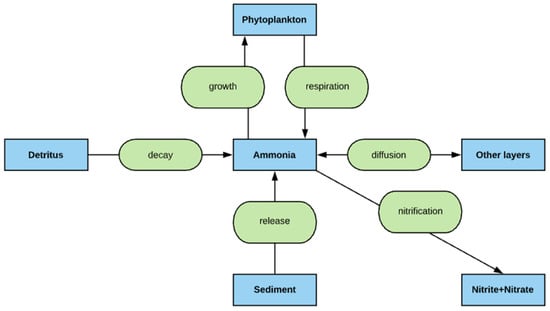
Figure 4.
Schematic diagram of ammonia cycle modeled by MINLAKE2020.
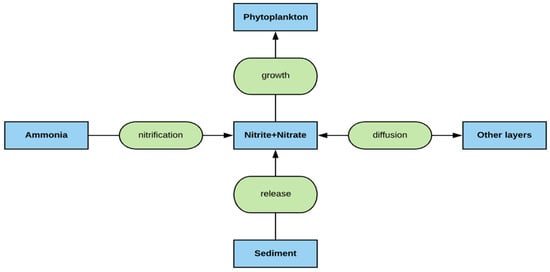
Figure 5.
Schematic diagram of nitrate-nitrite cycle modeled by MINLAKE2020.
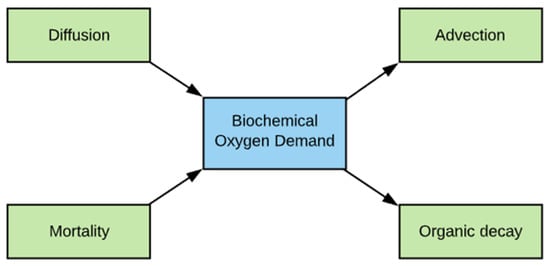
Figure 6.
Schematic diagram of BOD cycle modeled by MINLAKE2020.
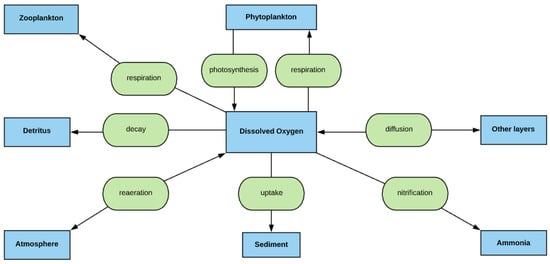
Figure 7.
Schematic diagram of DO cycle modeled by MINLAKE2020.
2.1. MINLAKE Overview
MINLAKE models use the basic one-dimensional advection-diffusion equation to simulate the dynamic variations of state variables in horizontal layers of a lake.
where C is the concentration of a state variable, v is the vertical settling velocity of the particulate form of some of the state variables (v = 0 for dissolved); z is the vertical coordinate measured positively downward; Kz is the vertical turbulent diffusion coefficient; and A horizontal area of the control volume. The one-dimensional vertical advection-diffusion equation is solved using a series of layers characterized by depth from the water surface, thickness, layer volume, and horizontal areas. The MINLAKE model developed by Riley and Stefan [43] (called MINLAKE88 in this paper) was capable of simulating water temperature and DO profiles with three levels of complexity for phytoplankton. The first and simplest form is a single algal group model with productivity distributed in the mixed layer [43]. The second level of complexity has the algal growth term unique to each layer using Michaelis-Menten equation for a single algal group. The level three considers up to three groups of algae, phosphorus, nitrogen, BOD for lakes during the open water season. MINLAKE88 is not widely used because of its inability to perform multiple-year simulations. Due to a lack of available data, the nutrient model could not be developed further. Gu and Stefan [21] included an ice-cover period simulation in MINLAKE88 to model snow thickness, ice cover thickness, and water temperature but no other state variables. In 1991, Hondzo and Stefan introduced a more general water temperature simulation model for MINLAKE which can be applied to a wide variety of lakes and regions [44]. An important modification of MINLAKE was accomplished in 1994 when Fang [45] developed the regional dissolved oxygen model and combined it with MINLAKE to study the impact of global climate warming on lake water quality and fish habitat in Minnesota lakes. The regional lake model was developed to model different types (categorizing by stratification strength and eutrophication) of lakes by maximum depths (shallow, medium-depth, and deep), surface area (small, medium area, and large), and trophic status (eutrophic, mesotrophic, and oligotrophic). The regional DO model is a simplified version of the DO model that did not simulate daily nutrients and Chla concentrations but used the annual mean Chlorophyll-a concentration with seasonal variation patterns [22] to specify daily Chla for DO simulation. Separate sub-models for winter conditions were developed and integrated with MINLAKE96 to simulate water temperature and DO year-round over many years as long as daily weather data are available [46]. The MINLAKE96 model was further modified and refined as it was used in a study in 2010, to simulate water quality conditions in cisco lakes, which are typically deep mesotrophic or oligotrophic lakes [47]. The MINLAKE96 model was further modified by West-Mack to simulate phosphorus, nitrogen, and chlorophyll-a simulation in 1998 [23,48] and the updated model is called MINLAKE98 here. The mass balance equations for chlorophyll-a, phosphorus, nitrogen, and DO were modified from those of MINLAKE88. The model was tested on three lakes and produced satisfactory results but due to lack of observed data and inability of the model to run for multiple years, the nutrient model was not further developed. The source code of MINLAKE98 was also lost and no longer available for further improvement.
MINLAKE96 was further modified in 2018 to calculate the hourly water temperature and DO using hourly weather conditions [24,49]. MINLAKE2012 is the most recent version of the daily MINLAKE model and can simulate year-round water temperature and DO in various lakes of different regions, using an Excel spreadsheet as the user interface. For all MINLAKE model variants, water temperature is simulated first by solving the following heat transport equation.
where Tw (z, t) is the water temperature in °C, which is a function of depth (z in m) and time (t in d); A(z) (m2) is the horizontal area for each layer of water as a function of the depth; Kz (m2/day) is the vertical turbulent heat diffusion coefficient which is a function of depth and time; Cp (J/m3-°C) represents the heat capacity of water per unit volume; Hw (J/m3-day) is the heat source and/or sink term per unit volume of water. Determination of the turbulent diffusion coefficient is discussed in detail by Fang [45]. In the regional daily MINLAKE model, the vertical heat diffusion coefficient Kz for epilimnion and hypolimnion is calculated using the following equation:
where Kz is the vertical diffusion coefficient in cm2/s (1 cm2/s = 8.64 m2/day = 0.36 m2/h), As is the surface area of the lake (km2) and N2 is the Brunt-Vaisala stability frequency of the stratification (s−2). In the epilimnion, N2 was set at a minimum value of 0.000075 [42]. Equations (1) and (2) are solved numerically using an implicit finite difference scheme and a Gaussian elimination method with time steps of one day.
2.2. Phytoplankton Simulation
In MINLAKE2020, the chlorophyll-a model was modified to overcome many of the limitations of previous MINLAKE models. The model can simulate up to three algal groups (diatoms, green algae, and blue-green algae) and the shift from diatoms early in the season to green and then blue-green algae during the summer. The algal groups are distinguished by different rates of photosynthesis, respiration, settling, zooplankton grazing, and different nutrient requirements. A schematic diagram of the phytoplankton cycle applicable to all algal groups is presented in Figure 1.
Phytoplankton growth depends on the maximum growth rate of the algae (Gmax), half-saturation coefficients for nutrients, water temperature, solar irradiance, external nutrient concentrations, and the current Chla concentration. The maximum growth rate of algae varies for different classes of algae. The algal growth limitation by nutrients is modeled using a Michaelis-Menten equation [50]:
where f(S) is dimensionless, S is the concentration of the nutrient (P, N, or Si) in water (mg/L), and KS is the half-saturation constant for the nutrient (mg/L). Algal growth dependence on water temperature is modeled by equations given by Lehman et al. [51]:
T is the water temperature (°C). The maximum growth occurs at an optimal temperature, Topt (°C), and the growth rate decreases both above and below Topt. Tmin (°C) is a low temperature at which phytoplankton growth is reduced to 90% from the optimum. Tmax (°C) is the high temperature at which growth is reduced by 90%. Phytoplankton growth is usually limited by available light, which is a function of the depth and the light attenuation coefficients due to water (Kw) and algae (Kc). The Haldane equation [52] is used in MINLAKE2020 to calculate the light limitation for algal growth, which was also used in MINLAKE88, MINLAKE98, and the regional DO model:
where f(L) is the light limitation coefficient (dimensionless), I(z) is the photosynthetically active radiation (PAR) as a function of depth, TD is the photoperiod (h) as a function of Julian day, RAD is daily solar radiation, and K1 and K2 are the light limitation and inhibition coefficients [53], respectively. The units for I(z), K1, and K2 are in µE/m2/s. In MINLAKE88 and MINLAKE98, light limitation and inhibition coefficients were specified by the user. In MINLAKE2020, light limitation and inhibition coefficients are calculated using the same equations as in the regional DO model [23].
Phytoplankton populations are removed from a water column by four processes: respiration, mortality, settling, and zooplankton grazing (Figure 1). Each phytoplankton population is assigned a fixed or calibrated respiration rate, mortality rate, and settling rate. Respiration affects the available phosphorus and DO immediately whereas mortality contributes with a time lag through detrital decay. In MINLAKE2020, a single class of zooplankton is simulated. To simulate the Chla lost by grazing of zooplankton, the zooplankton population (ZP(t), #/m3) is simulated in a separate subroutine on daily basis. Grazing is assumed to take place in the evening when zooplankton rises to the upper layers and is dependent on the temperature and Chla concentration. The Michaelis-Menten equation is used to simulate the effect of Chla concentration on grazing. It is assumed that no grazing occurs below a threshold Chla concentration (Chlamin in Equation (9)):
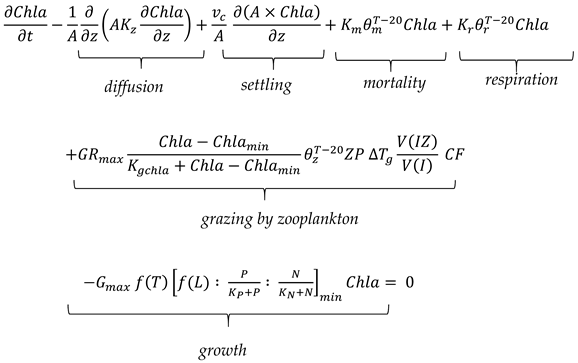 where Chla is the chlorophyll-a concentration (mg/L), vc is the phytoplankton settling velocity (m/d), Km, Kr, θm, and θr are mortality and respiration rates (d−1) and corresponding temperature adjustment coefficients (dimensionless), respectively. Gmax is the maximum growth rate of phytoplankton (d−1), GRmax is maximum grazing rate (mg Chla/individual zooplankton per d), Chlamin is minimum chlorophyll concentration for grazing to occur (mg/L), Kgchla is half-saturation constant for grazing (mg/L), KP and KN are the half-saturation constants for phosphorus and nitrogen (mg/L), respectively; P and N are the available concentration of phosphorus and nitrogen (mg/L), respectively; ZP is the zooplankton density (#/m3), ΔTg (<1 d) is time that zooplankton spends in a layer during the night to graze (d), V(IZ)/V(I) is the day depth (layer IZ) and the layer I volume ratio, and CF is the unit conversion from L to m3 (=0.001).
where Chla is the chlorophyll-a concentration (mg/L), vc is the phytoplankton settling velocity (m/d), Km, Kr, θm, and θr are mortality and respiration rates (d−1) and corresponding temperature adjustment coefficients (dimensionless), respectively. Gmax is the maximum growth rate of phytoplankton (d−1), GRmax is maximum grazing rate (mg Chla/individual zooplankton per d), Chlamin is minimum chlorophyll concentration for grazing to occur (mg/L), Kgchla is half-saturation constant for grazing (mg/L), KP and KN are the half-saturation constants for phosphorus and nitrogen (mg/L), respectively; P and N are the available concentration of phosphorus and nitrogen (mg/L), respectively; ZP is the zooplankton density (#/m3), ΔTg (<1 d) is time that zooplankton spends in a layer during the night to graze (d), V(IZ)/V(I) is the day depth (layer IZ) and the layer I volume ratio, and CF is the unit conversion from L to m3 (=0.001).

Zooplankton grazing is only simulated to represent the dynamics of algae. Zooplankton grazing rates vary with different classes of algae. For example, zooplankton is more likely to feed on green algae than blue-green algae [23].
where ΔTg(I) is the time of grazing for layer I (d), TD is the photoperiod (h) from sunrise to sunset, Chla(k, I) is the chlorophyll-a concentration of phytoplankton group k in layer I, and IZ is the day-depth layer, where DO ≥ 0.5 mg/L. Zooplankton grazing of phytoplankton (Chla) occurs during nocturnal migration at the day depth. The nocturnal grazing rate is calculated for each layer (I = 1, …, IZ) between the day depth and the surface using the volume day depth/layer ratio Vr = V(IZ)/V(I) [43].
2.3. Zooplankton Simulation
MINLAKE2020 includes a zooplankton model to simulate (1) Chla lost by zooplankton grazing and (2) DO consumed by zooplankton respiration. A single class of zooplankton is simulated in the lake environment each day. During the day, zooplankton retreats to deeper water seeking refuge from visual predators. They begin to rise to the surface at dusk while grazing and return to deeper layers at dawn (Figure 2). Zooplankton activity of these two periods is treated separately in the model.
Zooplankton is assumed to have a constant reproduction rate and a time-varying predation rate for determining the zooplankton population ZP(t) as a function of time (t, day). The day depth, light level at the day depth, and predation on zooplankton are calculated as the first step in zooplankton simulation. The day depth of zooplankton is identified as the deepest layer in which the DO concentration is greater than 0.5 mg/L and therefore changes with time depending on DO vertical depth distribution. Below the day depth, the grazing is zero. In MINLAKE2020, dual effects of seasonal predation and light limitation are included to simulate biomanipulation techniques related to methods of increasing the zooplankton population [54]. The dominant zooplankton predators are assumed to be visual predators and zooplankton predation only occurs in the daytime. The light limitation assumes a linear variation of predation between two light levels [55].
where PDd is the daytime predation rate (d−1) and Pd is the daily predation rate (d−1) calculated using Equation (12). XI is the light intensity at the day depth (µE/m2/s), XImin is the light intensity at which no predation occurs (µE/m2/s) and XImax is light intensity above which predation is not light inhibited (µE/m2/s). When the light intensity XI is less than XImin or larger than XImax, the ratio in Equation (11) is reset to zero or one, respectively.
Both daytime and nocturnal predation are calculated in MINLAKE2020. Daytime predation combines light limitation with a time-varying maximum predation rate. A linear function is used to calculate the time-varying daytime predation rate Pd given in Equation (12) when Julian day DY is between DYmin and DYmax.
where Pmin and Pmax are minimum and maximum predation rates (d−1), respectively. DYmin is Julian day of the last day of minimum predation rate and DYmax is Julian day of the beginning of maximum predation rate: Pd = Pmin when DY < DYmin and Pd = Pmax when DY > DYmax. For example, for Elmo Lake, West and Stefan [23] set Pmin, Pmax, DYmin, and DYmax as 0.05 d−1, 0.7 d−1, 110 (20 April), and 140 (20 May); it means Pmin occur on and before 20 April and Pmax occur on and after 20 May.
Zooplankton density in the daytime is determined using Equation (13) including first-order reproduction and daytime predation:
where Repro is the reproduction rate (dimensionless) and ZP(t − 1) is the zooplankton density in the previous day.
Nocturnal predation occurs during nocturnal migration at the day depth. The nocturnal predation rate is calculated for each layer between the day depth and the surface.
where PD(t, I) is the nocturnal predation rate in layer I during migration (#/m3) and PDn is the nocturnal predation rate (d−1) as a constant input parameter. ZP(t) is the zooplankton population in the day depth layer calculated using Equation (13), and ZPmin is the minimum concentration of zooplankton for predation to occur (#/m3). V(IZ) and V(I) are the volumes of the day depth layer and layer I (m3), respectively. ΔTg(I) is the time that zooplankton spent in layer I during the night (d). The daytime ZP(t) minus PD(t, I) gives the zooplankton population for the next day.
The second part of zooplankton simulation is the simulation of phytoplankton grazing by zooplankton which begins with a vertical rise in the evening. Temperature and Chla concentration affect grazing in the water layer (see Equation (9)). A Michaelis-Menten ratio is used to express the effect of Chla concentration on grazing with a refugium effect for no grazing below a threshold Chla concentration (Chlamin in Equation (9)).
2.4. Phosphorus Simulation
In most cases, phosphorus is known to be the primary nutrient controlling the trophic state of lakes in the Upper Midwest USA and Canada [56]. Phytoplankton can only use the soluble reactive phosphorus (SRP) which is composed of orthophosphate and polyphosphate ions. The model only simulates the readily accessible phosphorus and indirectly models organic phosphorus as detritus. Phytoplankton growth removes SRP from the water. Respiration releases phosphorus into the water column. Mortality does not directly release phosphorus to the water column but contributes to the detrital mass (BOD); phosphorus is released from the detrital mass through decay. Though diffusion of phosphorus occurs between layers, phosphorus is also transported indirectly between layers by phytoplankton and detritus settling. Figure 3 graphically represents/summarizes the SRP fate and transport modeled by MINLAKE2020.
Phosphorus, accumulated from the detrital biomass, sediment release (zero-order kinetics), and respiration, are used by the phytoplankton, in the presence of sunlight, for growth. Algae need both nitrogen and phosphorus for growth. However, phosphorus is particularly important for algal growth as it is usually in short supply compared to other nutrients. If it is assumed that nitrogen is in abundant supply, phosphorus becomes the only limiting nutrient for algal growth (green and blue-green algae), which is modeled in the application of MINLAKE2020. Uptake depends on the maximum growth rate, light limitation, nutrient limitation, Chla concentration at that time, and the yield ratio of P to Chla as shown in Equation (15).
The differential equation representing SRP fate and transport in a layer is given as Equation (15):
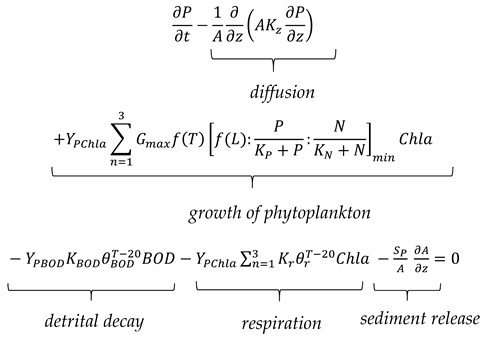 where KBOD and θr are decay rate (d−1) and corresponding temperature adjustment coefficient, respectively; SP is the rate of phosphorus released at the water-sediment interface (g P/m2/d) at anoxic condition and it is calibrated against available phosphorus/Chla/DO profiles, YPChla is mass yield ratio of phosphorus to chlorophyll, and YPBOD is mass yield ratio of phosphorus to BOD.
where KBOD and θr are decay rate (d−1) and corresponding temperature adjustment coefficient, respectively; SP is the rate of phosphorus released at the water-sediment interface (g P/m2/d) at anoxic condition and it is calibrated against available phosphorus/Chla/DO profiles, YPChla is mass yield ratio of phosphorus to chlorophyll, and YPBOD is mass yield ratio of phosphorus to BOD.

A phosphorus/chlorophyll yield coefficient (YPChla) is used to determine the amount of phosphorus consumed during photosynthesis as well as the amount of phosphorus released during algal respiration. In MINLAKE98, the value of YPChla was derived from the mass yield coefficient of phosphorus to BOD divided by the mass yield coefficient of chlorophyll to BOD [23]. This value is 1.1 mg P/mg Chla for YPChla, which was assumed to be constant in MINLAKE98, and is close to that presented by Thomann and Mueller [57] of 1.0 µg P/µg Chla. In MINLAKE2020, YPchla is set to 1.1 mg P/mg Chla for all simulated lakes. However, the phytoplankton biomass does not depend on phosphorus solely, it also depends on the nitrogen concentration.
There are three source terms for phosphorus: detrital decay (death of phytoplankton), sediment release, and phytoplankton respiration. For many lakes which have a history of progressive eutrophication, the lake sediments have now become the primary source of phosphorus to the water. If the sediment-water interface is anoxic, phosphate ions go to the water at an increased rate, depending upon the concentration difference between porewaters and the overlying water [58]. MINLAKE2020 simulates SRP release back to water when the DO concentration becomes zero.
The daily zero-order internal phosphorus release (same as Equation (15)) was included in MINLAKE88 [20] and MINLAKE98 [46] before. CE-QUAL-W2 [59] includes the zero-order and first-order phosphorus release from sediment. EFDC model [60] has a governing equation for total phosphate including a sediment-water exchange flux of phosphate (g P/m2/d) for the control volume at the bottom. ELCOM-CAEDYM [29] simulates phosphorus release from sediment as a function of temperature, DO and pH. There are some empirical models that quantified long-term internal phosphorus release for the whole lake (not for mass balance equation for a water layer or control volume), for example, Nurnberg [61] determined the internal phosphorus release per year after analyzing the data from various lakes. Stigebrandt et al. [62] and Stigebrandt and Andersson [63] developed a two-layer DIP (dissolved inorganic phosphorus) model including two mass balance equations for the Baltic proper and having a time step of one year. Stigebrandt and Andersson [63] used 47 years (1968–2014) of observational data to derive the phosphorus flux from anoxic bottoms, which is about 1.22 tons P/km2/year (or 1.22 g P/m2/year) for the Baltic proper. Stigebrandt et al. [62] used a load-response model to explain the evolution of TP in the surface (0–60m) and bottom layers (60 m to bottom) from 1980 to 2005 and suggested that the average specific DIP flux from anoxic bottoms in the Baltic proper is about 2.3 g P/m2/year. If the average anoxic period of the Baltic proper is 100–150 days per year, then the phosphorus flux would be 0.01–0.02 g P/m2/d.
2.5. Nitrogen Simulation
When phosphorus is in excess (e.g., P >> Kp), nitrogen can become the limiting nutrient for algae growth, which is not a usual scenario in many lakes. Nitrogen is available in two forms (ammonium NH4, and nitrite plus nitrate, represented as NO2-3 in this paper). MINLAKE2020 models both ammonia and NO2-3 separately. Schematic diagrams of the NH4 and NO2-3 sub models are given in Figure 4 and Figure 5, respectively. Nitrogen N in Equations (9), (15), and (19) is the sum of NH4 and NO2-3 concentrations (in mg N/L).
Diffusion of ammonia and NO2-3 occurs between layers. Nitrification is the biological oxidation process (assuming DO) of ammonia to nitrite followed by the faster oxidation of the nitrite to nitrate so that nitrite and nitrate are often modeled as one variable. The uptake of ammonia and nitrate due to phytoplankton growth is calculated as a zero-order sink term with a preference in the uptake of ammonium over the uptake of nitrate. It directly links to the growth of phytoplankton. Respiration of phytoplankton releases ammonia (Equation (16)) but not nitrate. Mortality of phytoplankton does not directly release ammonia or nitrate to the water but contributes to the detrital mass (BOD), and then ammonia is released through the decay of the detrital mass, as shown in Equation (16). Therefore, ammonia is also transported indirectly between layers by phytoplankton (Equation (9)) and detritus settling (Equation (18)). Ammonia and nitrite releases from the sediment are also modeled when DO is low (depending on the DO concentration of the overlying water). The model does not consider the atmospheric deposition of ammonia or NO2-3 and denitrification (the reduction of nitrate to nitrogen gas, N2).
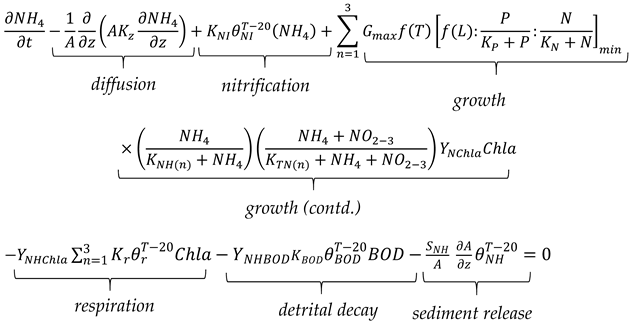



Equations (16) and (17) provide the governing equations to model NH4 and NO2-3 in each water layer. KNI and θNI are the first-order nitrification rate (d−1) and the temperature adjustment coefficient, respectively; KNH(n) and KTN(n) are the half-saturation constants for preferential uptake of ammonia over nitrate and nitrogen uptake for each algae class, respectively; SNH, SNO, θNH, and θNO are ammonia and nitrite release rates from sediment (g N/m2/d) and corresponding temperature adjustment coefficients, respectively; YNHBOD, YNHChla, and YNOChla are the mass yield ratios of ammonia to BOD, ammonia to chlorophyll, and nitrate to chlorophyll, respectively; and KBOD and θBOD are the first-order BOD or detritus decay rate (d−1) and the temperature adjustment coefficient, respectively.
In MINLAKE2020 phytoplankton growth is simulated by external nutrient limitation and the model does not allow for nitrogen fixation (storage of excess nitrogen for later use) as MINLAKE88 did [49]. MINLAKE2020 simulates the release of ammonia from dead algae indirectly through detrital decay. In the normal range of ammonia concentration, when KNH(n) is small, the Michaelis-Menten ratio for ammonia in Equation (16) will be close to 1.0, and in Equation (17) one minus the Michaelis-Menten ratio will be small; therefore, it has preferential uptake of ammonia over nitrate.
2.6. BOD Simulation
BOD is an important parameter in the DO, phosphorus, and nitrogen cycles. The microbial decay or decomposition of organic matter, which is detritus from the mortality of phytoplankton in MINLAKE2020, consumes oxygen, and therefore, the amount of organic matter is represented as BOD, an oxygen equivalent. However, DO directly affects biological decay processes and phosphorus release under anoxic conditions. In the regional DO model [22], a constant rate for BOD was used for each simulation lake depending on the lake’s trophic state. For the year-round lake water quality model [46], different constant rates of BOD for the open water seasons and winter ice cover periods were used over multiple years. However, BOD is an important parameter for nutrient cycles and DO cycle and is affected by mortality, organic decay, diffusion, and advection (Figure 6) and simulated separately in MINLAKE2020.
The differential equation representing BOD in a layer is given as Equation (18):
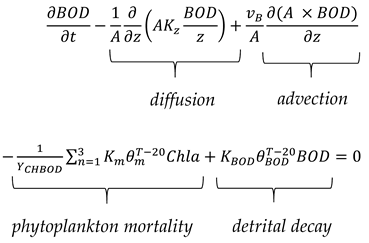 where vB and YCHBOD represent detritus settling velocity (m/d) and the mass yield ratio of Chla to BOD, respectively. In the model, BOD is increased from two sources (Figure 6). First, detritus travels to adjacent layers via diffusion. Secondly, the mortality of the phytoplankton adds to the detritus concentration. BOD has two sink terms (Figure 6): advection (settling in the vertical direction) and organic decay. Detritus falls from the concerning layers and goes to another layer or the sediment. The microbial decay of organic matter is a function of the detrital mass expressed in oxygen equivalents (BOD). The mortality of cells and a fraction of the grazed phytoplankton are converted from Chla concentrations to oxygen equivalents using the constant carbon/Chla ratio and stoichiometric relationships. The result is a one-to-one correspondence between detrital decay and the utilization of oxygen. This cycle is very important for nutrient calculation as it directly adds to the nutrient load through detrital decay.
where vB and YCHBOD represent detritus settling velocity (m/d) and the mass yield ratio of Chla to BOD, respectively. In the model, BOD is increased from two sources (Figure 6). First, detritus travels to adjacent layers via diffusion. Secondly, the mortality of the phytoplankton adds to the detritus concentration. BOD has two sink terms (Figure 6): advection (settling in the vertical direction) and organic decay. Detritus falls from the concerning layers and goes to another layer or the sediment. The microbial decay of organic matter is a function of the detrital mass expressed in oxygen equivalents (BOD). The mortality of cells and a fraction of the grazed phytoplankton are converted from Chla concentrations to oxygen equivalents using the constant carbon/Chla ratio and stoichiometric relationships. The result is a one-to-one correspondence between detrital decay and the utilization of oxygen. This cycle is very important for nutrient calculation as it directly adds to the nutrient load through detrital decay.

2.7. DO Simulation
DO is one of the vital parameters of lake water quality simulation. Aquatic organisms and fish depend on the availability of DO in the waterbody [64]. A schematic diagram of the processes contributing to the DO concentration is given in Figure 7. It shows that DO is added to a water layer through diffusion and photosynthesis; and is removed by respiration of algae and zooplankton, detrital decay (BOD), sediment oxygen demand (SOD), and nitrification. The surface reaeration can add or remove DO depending on whether surface DO is less or greater than saturated DO (a function of surface temperature and lake elevation). Phytoplankton (modeled as Chla) growth can add DO to the water layer through photosynthesis to the point where water could be supersaturated with DO in some cases. These dynamic processes can happen over time scales of less than one day (the time step of the MINLAKE2020 simulation). Therefore, the model outputs DO profiles as an integration of different physical (e.g., mixing), chemical, and biological processes over the day. DO removal from the water layer through phytoplankton respiration is simulated to occur at a constant rate throughout the day while photosynthesis occurs only during the hours with solar radiation. In MINLAKE2020, the adjustments for low DO levels on SOD, BOD, and algal respiration follow Edwards and Owens’s [65] formula. SOD is calculated for each layer, and it is treated as a sink term in the one-dimensional (vertical) transport equation [22,57]. Oxygen uptake of the sediment depends on the area and composition of bottom materials in contact with the water [22,66].
The differential equation representing DO dynamics in a layer is given as Equation (19):
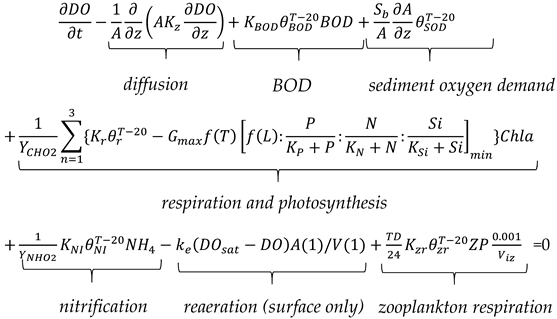 where Kzr and θzr are the zooplankton respiration rate (d−1) and the temperature adjustment coefficient, respectively; KNH(n) and KTN(n) are the half-saturation constant for preferential uptake of ammonia over nitrate and for nitrogen uptake for each algae class, respectively; Sb and θSOD are sediment oxygen demand of sediment (g O/m2/d) and corresponding temperature adjustment coefficient, respectively; ke is the surface oxygen transfer coefficient (m/d), A(1) and V(1) are horizontal area (m2) and lake volume (m3) for the first or surface layer; YNHO2 and YCHO2 are the mass yield ratios of ammonia to oxygen and chlorophyll to oxygen, respectively. Calibration of the sediment oxygen demand is very important for simulating DO in the hypolimnion.
where Kzr and θzr are the zooplankton respiration rate (d−1) and the temperature adjustment coefficient, respectively; KNH(n) and KTN(n) are the half-saturation constant for preferential uptake of ammonia over nitrate and for nitrogen uptake for each algae class, respectively; Sb and θSOD are sediment oxygen demand of sediment (g O/m2/d) and corresponding temperature adjustment coefficient, respectively; ke is the surface oxygen transfer coefficient (m/d), A(1) and V(1) are horizontal area (m2) and lake volume (m3) for the first or surface layer; YNHO2 and YCHO2 are the mass yield ratios of ammonia to oxygen and chlorophyll to oxygen, respectively. Calibration of the sediment oxygen demand is very important for simulating DO in the hypolimnion.
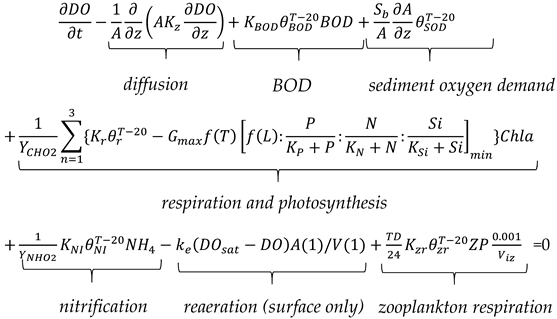
2.8. Interaction and Connection among Modeling Variables
This study is focused on the internal nutrient dynamics and its interaction/connection to the phytoplankton, BOD and DO dynamics in the lakes; therefore, the inflow and outflow sub-model was disabled. The MINLAKE2020 DO model is different from that of MINLAKE2012, where daily Chla and BOD were specified as model input based on lake trophic status. For MINLAKE2020, several modifications were made to simulate phosphorus, nitrogen, Chla, and BOD concentrations and zooplankton activity in the DO simulation. The photosynthetic oxygen production calculation was modified, and the nitrification and zooplankton respiration were added to the DO model while the rest of the terms were the same as in MINLAKE2012. In MINLAKE 2020, photosynthetic oxygen production is dependent on the simulated daily Chla concentration rather than the data driven Chla pattern and annual mean concentration used in MINLAKE2012.
The diffusion of DO occurs between the water layers in the metalimnion and hypolimnion. The spring and fall overturn periods for temperate lakes completely mix water columns and make all modeling variables distributed uniformly along with the depth. Since zooplankton usually spend the largest amount of their time in the day depth layer, zooplankton respiration is simulated at the day depth only. BOD removes oxygen from the water layer through the decay of detritus which is accumulated from phytoplankton mortality and removed by settling (Figure 6). Nitrification removes oxygen from the water layer through the conversion of ammonia to nitrite then to nitrate. Nitrification is applied to the DO model only if nitrogen is simulated.
From Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and from Equations (9)–(19), one can see the complex interactions and connections among modeling variables. For example, when the settling velocity of the phytoplankton group is increased, it reduces Chla concentration and in turn, affects detritus (BOD) and phosphorus, but phosphorus goes back to affect phytoplankton growth. Additionally, DO concentrations in different water layers connect/integrate changes in water temperature, nutrients, and phytoplankton dynamics (Figure 1). The sediment oxygen demand is an important factor for DO mass balance and results in the anoxic condition in the hypolimnion that leads to phosphorus release from sediment. Therefore, exploring/understanding the internal cycles/dynamics of nutrients/phytoplankton and their interactions in different lakes helps us to gain insights of lake ecosystem and then develop appropriate restoration strategies.
2.9. Model Coefficients and Parameters
MINLAKE2020 model was designed to simulate small lakes (As < 25 km2) provided that the user specifies the input data and calibration parameters accordingly. Variation in lake characteristics is reflected in model input data/parameters. Lake bathymetry and weather data (depending on lake geographic location) need to be supplied to the model. For many lakes in Minnesota, depth or elevation contour lines can be downloaded from the Minnesota Department of Natural Resources (MN DNR) LakeFinder website (https://www.dnr.state.mn.us/lakefind/index.html, , accessed on 5 June 2019), from which horizontal areas at different elevations/depths can be determined. The weather data include daily air temperature (°F), dew point temperature (°F), wind speed (mph), solar radiation (Langley), sunshine percentage, and precipitation including rainfall (cm) and snowfall (mm). To facilitate the comparison of DO simulation results, in MINLAKE2020, the user can run the DO simulation in two ways: (1) using MINLAKE 2012 regional DO model, i.e., nutrients and Chla are not simulated (called the RegDO model); (2) using MINLAKE2020 (called the NCDO model). This model first simulates nutrients and Chla and then DO [67]. Table 1 lists nutrient, Chla, and DO calibration parameters in MINLAKE2020 and includes descriptions and effects on specific model results.

Table 1.
Nutrient, Chla, and DO calibration parameters for MINLAKE2020.
The number of algal classes and the light attenuation coefficient are important input parameters for the simulation. Moreover, the snow and ice model require various coefficients (e.g., snow and ice density, specific heat, thermal conductivity, etc.) as input parameters, which has been well tested in the previous studies [68]. The temperature adjustment coefficients for BOD, photosynthesis, respiration, and sediment oxygen demand were set to 1.047 [69], 1.066 [57], 1.047 [20], 1.065 [70], respectively. Mass ratios of Chla to oxygen, phosphorus to oxygen, and phosphorus to chlorophyll-a are 0.0083, 0.0091, and 1.1, respectively. The inclusion of phytoplankton and zooplankton simulation in MINLAKE2020 calls for many additional input parameters or model coefficients. Most of the zooplankton-related coefficients were taken from West and Stefan’s study [23]. Zooplankton respiration rate was set to 0.002 d−1 and the reproduction rate was 0.02 d−1. Minimum light intensity for zooplankton predation, light intensity for maximum zooplankton predation, Julian day for the end of low predation period, and Julian day for the beginning of maximum predation were set to 0 µE (m2s)−1, 0.1 µE (m2s)−1, 110 (20 April), and 140 (20 May), respectively. Minimum seasonal day time predation rate, maximum seasonal day time predation rate, and overnight predation rate were set to 0.05 d−1, 0.7 d−1, and 0.03 d−1, respectively. For any lake, these parameters were kept constant whereas some of the model parameters were updated/calibrated based on the comparison of simulation results with observed data. The first four parameters were used in the regional DO model, but the respiration rate Kr was not calibrated (constant).
3. Lakes Simulated
In this study, six lakes (Table 2) were selected for the model calibration, the sensitivity analysis of model parameters/coefficients, and understanding the interaction/connection among seasonal variations of nutrients and chlorophyll-a: two shallow lakes (Pearl and Carrie), two medium-depth lakes (Riley and Thrush), and two deep lakes (Carlos and Elmo). The maximum depths range from 5.6 to 50.0 m. All six lakes are located in northeastern Minnesota since they have the necessary data for the study. The nearest weather station to the lake was selected for providing weather data: St. Cloud Regional Airport for Pearl, Carrie, and Carlos lakes; Duluth International Airport for Thrush and Riley lakes; and Minneapolis/St. Paul International Airport for Elmo Lake. The geometry ratio (GR = As0.25/Hmax, As in m2, and Hmax in m being the surface area and the maximum depth of the lake) is a very important characteristic parameter of a lake that is related to stratification, lake habitat, etc. [71]. The lake geometry ratio is between 0.75 and 7.53. The lower the geometry ratio, the stronger the lake stratification. Two medium-depth (6 m < Hmax ≤ 20 m, [72]) and two deep lakes (Hmax > 20 m, [72]) selected for the study are strongly stratified (geometry ratio less than 3), one medium-depth and one shallow lake are weakly stratified (geometry ratio between 3 and 10). Based on observed Chla concentration, Pearl, Carrie, and Riley lakes are eutrophic (mean Chla > 10 µg/L [73]), Elmo and Carlos are mesotrophic lakes (mean Chla between 4 and 10 µg/L [73]), and Thrush is an oligotrophic lake. The nutrient model was calibrated and validated based on available measured water temperature, chlorophyll-a, phosphorus and DO profile data on particular days, downloaded from the LakeFinder website.

Table 2.
Characteristics of six study lakes in Minnesota.
4. Result and Discussion
4.1. Model Calibration
For MINLAKE 2020 model application to the six study lakes, the temperature model was calibrated first and then the nutrient model was calibrated. Temperature model calibration ensured that thermal and mixing dynamics were modeled accurately because water temperature and mixing dynamics directly affect nutrients, Chla, and zooplankton processes (Equations (9)–(19)). The wind sheltering coefficient and the multiplier for diffusion coefficient in metalimnion are the main calibration parameters for temperature modeling. Although MINLAKE2020 has an integrated nitrogen model, for this study, only phosphorus was simulated since phosphorus is the limiting nutrient in these six lakes. Green algae and blue-green algae were simulated separately and then combined to represent the total chlorophyll-a concentration. The MINLAKE2020 development also included the inflow and outflow subroutines from MINLAKE88, which were tested/verified to ensure they function properly; however, the inflow/outflow function was not activated for the simulation of the six study lakes (Table 2). Certain inflow and outflow were reported for Carrie, Pearl, and Carlos Lake [74,75,76] whereas inflows in the other three lakes were minor, and the inflow quality (nutrients and phytoplankton) data were scarce. These approximations are appropriate since the study objective is to examine/understand the internal dynamics and cycles of nutrients over multiple years in six lakes with different stratification and trophic characteristics.
Figure 8 shows an example of the calibration results of water temperature and DO time series at two depths (1 and 7 m) at Lake Carrie including measured data. During 2008–2010, Lake Carrie had measured water temperature and DO profile data for 36 days or 342 data points in total. MINLAKE2020 simulated water temperature and DO with a root mean square error of 1.75 °C and 1.95 mg/L, respectively. Corresponding regression coefficients of measured versus simulated (R2) are 0.99 and 0.93, respectively. The statistical results summarized in Table 3 show that for the six lakes, MINLAKE2020 model performed better than MINLAKE2012, especially for DO simulations, when simulated profiles were compared with observed profiles. The main reason for this improvement is the simulation of Chla concentration on daily time step rather than using the specified pattern of observed data. Table 3 shows the model performance improved significantly with the NCDO model in Carlos and Thrush lakes. The average root-mean-square error (RMSE) of DO simulations in six lakes from MINLAKE2020 decreased by 24.2%, and average Nash-Sutcliffe efficiency (NSE) [77] also increased with respect to MINLAKE2012. Chlorophyll concentration affects the solar radiation attenuation in the water column (Equation (8)) and then affects water temperature simulation as shown in Table 3 even though the average RMSE, NSE, and R2 for temperature (regression coefficient of measured versus simulated) from the two models are almost the same.
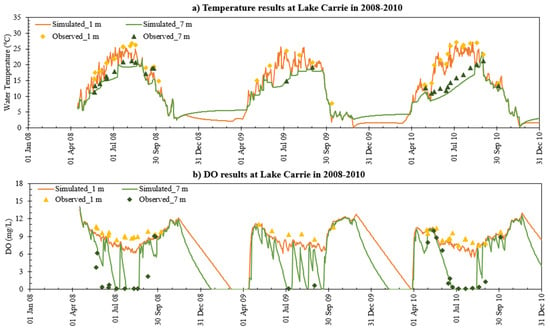
Figure 8.
Time series of simulated (a) water temperature and (b) DO at two depths in Lake Carrie in 2008–2010.

Table 3.
Statistical parameters for six lakes when simulated profiles were compared with observed.
For Chla simulation of six lakes, RMSE ranges from 0.0006 to 0.0276 mg/L. Figure 9 shows an example comparison between simulated Chla of MINLAKE2020 (NCDO model) and specified Chla from MINLAKE2012 (RegDO model) for Lake Elmo. From 1980 to 2018, there were 74 days in 10 years with measured temperature and DO profiles (1506 data points) for model calibration but no profile data in 2007 and 2009. The average chlorophyll concentration was 0.0075 mg/L in 74 days but 0.0036 mg/L over 10 days in 2008. Even though there were no profile data in 2009, we identified some Chla data in 2009 as shown in Figure 9. MINLAKE2012 uses the annual mean Chla concentration and seasonal variation patterns [22] (depending on trophic status) to specify daily Chla for DO simulation. Therefore, the RegDO model had higher Chla in 2007 and 2009 due to the lack of available profile data in these two years whereas the NCDO model predicts the Chla reasonably well in 2008 and 2009 when comparing with data.
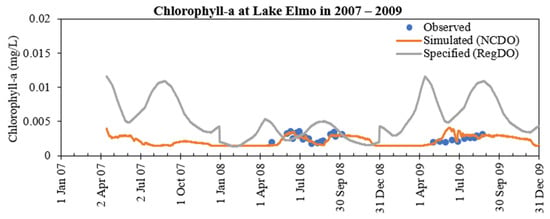
Figure 9.
Simulated (NCDO model), specified (RegDO model), and observed chlorophyll-a near the surface in Lake Elmo in 2007–2009.
Some lakes, such as Lake Elmo and Carrie Lake (Table 3), do not exhibit a noticeable change in simulated DO concentrations based on the model used for simulation. Some lakes, e.g., Pearl Lake, exhibit a noticeable change in simulated DO concentration depending on the model (RegDO or NCDO model). Figure 10a,b show the time series of DO concentrations simulated by the NCDO model and RegDO model including observed DO at the surface (1 m) and near the bottom (5 m) of Pearl Lake in 2010–2012, respectively. The RegDO model somewhat overpredicts surface DO concentration but the NCDO model underpredicts DO. For the bottom DO, the NCDO model does a better job while the RegDO model overpredicts DO. When BOD is simulated, the winter DO decreases, predicted by MINLAKE2020, are smaller than those predicted by MINLAKE2012 when BOD is specified as a part of the model inputs. There are very limited data for P comparison between simulated and observed, and RMSE ranges from 0.005 to 0.036 mg/L. DO simulation is an overall model performance indication (Table 3).
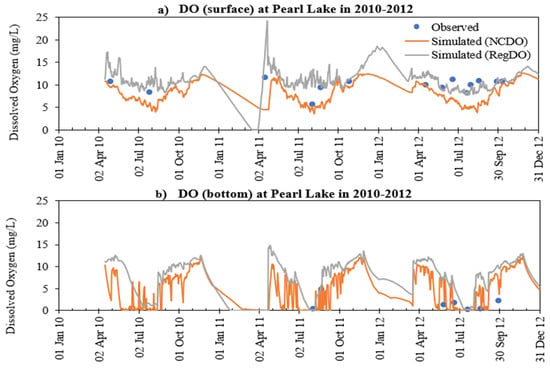
Figure 10.
Simulated and observed dissolved oxygen near (a) the surface (1 m) and (b) bottom (5 m) in Pearl Lake in 2010–2012, respectively.
4.2. Chla and Phosphorus Profiles
Lake Elmo was extensively monitored in 1988 by the Metropolitan Council [65] and had measured phosphorus concentration data at five depths (0, 8, 16, 24, and 32 m) and DO data at 31 depths for open water season. The comparison between simulated and observed concentrations for Chla, phosphorus, and DO on three days in 1988 is presented in Figure 11. Since Elmo is a deep lake and solar radiation cannot penetrate below the euphotic zone, the Chla concentration becomes zero in the deep layers. On 11 April 1988, the lake is more or less well mixed and phosphorus concentration did not vary much throughout the depth but DO concentration gradually declined along with depth due to the contribution of more sink terms (Equation (18)) but for the profile plot, the slope was not steep. The Chla concentration is highest at the surface and did not vary much throughout the depth. On 18 May 1988, the stratification increases and the simulated DO at the bottom is near zero. The Chla concentration is not maximum at the surface, but at 8 m depth from the surface. The phosphorus concentration is higher at the deeper layers because of detrital decay and phytoplankton respiration. On 19 October 1988, the phosphorus near the surface layer is being used by the phytoplankton for growth, the lake became strongly stratified and the bottom layers of the lake become anoxic so that the phosphorus release from sediment contributed to the higher phosphorus concentration at the deeper depths, which increased along with depth from metalimnion and hypolimnion.
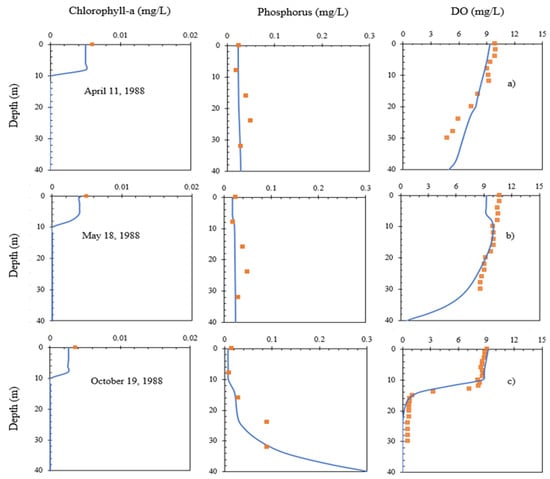
Figure 11.
Simulated (line) and observed (dots) chlorophyll-a, phosphorus, and dissolved oxygen profiles for Lake Elmo on (a) 11 April, (b) 18 May, and (c) 19 October 1988.
Thrush Lake has measured Chla data at both the epilimnion and hypolimnion. The comparison between simulated and observed concentrations for Chla and DO on three days in 1986 is plotted in Figure 12. Thrush is an oligotrophic lake with lower oxygen demands (low BOD and SOD); therefore, the simulated and observed bottom DO is greater than zero, and there is no phosphorus release from sediment in all three days (Figure 12). Since no phosphorus data were available, only simulated phosphorus was plotted and has no increase in the hypolimnion. Due to lower light attenuation coefficients, solar radiation can penetrate through the deepest layers of the lake. The calculated euphotic depth (at 1% surface solar radiation) is equal to or greater than the maximum depth (14.6 m) for all of the three selected dates; therefore, the simulated Chla is not zero near the bottom but increases below the mixed layer, especially on 17 June 1986. On 13 May 1986, the Chla and phosphorus concentration did not vary much throughout the depth. The DO concentration gradually decreased below the mixed layer on 13 May and 17 June 1996, due to the contribution of more sink terms. On 14 October 1986, the lake became well mixed due to the fall overturn and had uniform distribution for simulated Chla, phosphorus, and DO. The model underpredicts the mixed layer depth on 13 May and then overpredicts DO at the hypolimnion.
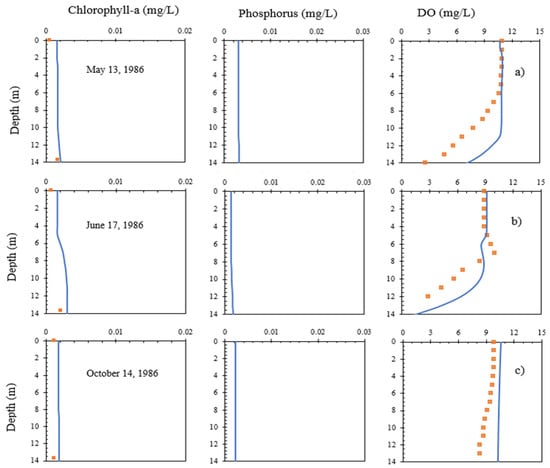
Figure 12.
Simulated (line) and observed (dots) chlorophyll-a, phosphorus, and dissolved oxygen profiles for Thrush Lake on (a) 13 May, (b) 17 June, and (c) 14 October 1986.
4.3. Chlorophyll-a and Phosphorus Interaction
Figure 13 and Figure 14 show examples of simulated time series of P, Chla, and DO with observed data for a deep lake (Elmo) and a shallow lake (Carrie), respectively. Figure 13 shows simulated and observed Chla and phosphorus (P) at three depths (at 1 m, 20 m, 40 m from the surface) of Elmo Lake from 16 April 2007 to 31 December 2009. This is a continuous year-round simulation including two open-water seasons and two ice cover periods, which was not done before using MINLAKE models for Chla and P simulation. The first year of simulation is considered as model warm-up period and the results may have more uncertainties due to the assumed initial conditions, for example, phosphorus concentration from the water surface to 20 m was low during the open water season (Figure 13a,b). The simulated ice cover was from 5 December 2007 to 16 April 2008, 7 December 2008 to 10 April 2009 for Elmo Lake, which is marked by blue shaded regions.
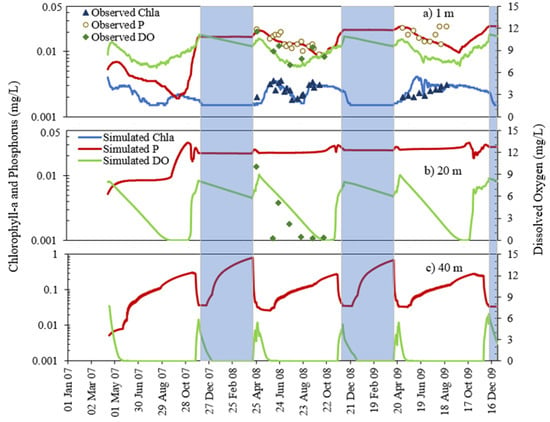
Figure 13.
Simulated and observed chlorophyll-a, phosphorus, and dissolved oxygen concentration at (a) 1 m, (b) 20 m, (c) 40 m depth from the surface at Elmo Lake in 2007–2009 (blue shaded area represents the ice cover period). The scale for the major y axis in (c) is larger than one in (a,b).
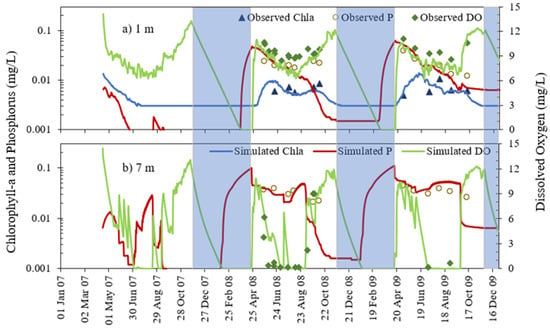
Figure 14.
Simulated and observed chlorophyll-a, phosphorus, and dissolved oxygen concentration at (a) 1 m and (b) 7 m depth from the surface at Carrie Lake in 2007–2009 (blue shaded area represents the ice cover period).
Near the water surface (1 m), DO concentrations are near saturation as a function of temperature (lowest DO in the middle of summer) and range from 6.69–11.13 mg/L. From late October to late November, before the ice starts to form at the surface of the lake, phosphorus at the surface and other surface layers start to increase due to more mixing and fall overturns. This increase is more evident in 2007 when phosphorus was low in the summer. During the ice cover period, the phosphorus concentration becomes stable at 1 m and 20 m as the organic processes (photosynthesis) become slow due to the near-zero water temperature and/or low light (attenuated by snow cover). After the ice melts out in late spring, the simulated phosphorus concentrations at 1 m increase for a brief period due to spring overturn and then, start to decrease as a result of the phosphorus uptake by phytoplankton. During the early summer (May) of 2008 and 2009, simulated Chla concentration increases gradually from 0.0016 mg/L to a maximum of 0.0033 mg/L (observed on 15 June).
At the deep layers (e.g., 20 and 40 m), DO becomes anoxic during the summer at deep hypolimnion since Elmo Lake is strongly stratified. Anoxic periods at 20 m and 40 m were on average 12 days and 210 days per year from 2007 to 2009, respectively. In the deeper layers, in addition to detrital decay and phytoplankton respiration, sediment release could add up to the available phosphorus. Since there is a long period of anoxic condition at 40 m during the summer, early fall, and some part of the ice cover period, phosphorus release from sediment contributes to a major portion of phosphorus increase. Phosphorus peaks in deepest layers were simulated to occur just after the anoxic condition ends and before the fall or spring mixing/overturns. These overturns sharply reduce phosphorus in very deep layers (e.g., 40 m) and increases phosphorus in other shallower layers. The calculated euphotic depth is 9 m for the simulation period; therefore, there is no photosynthesis below this depth and simulated Chla is zero at 20 m and 40 m. Chla is typically measured near the surface; therefore, there is no measured Chla at the deep depths to compare with simulated values.
Figure 14 shows simulated and observed P, Chla, and DO at two depths (at 1 m, 7 m from the surface) of Carrie Lake from 16 April 2007 to 31 December 2009. The calculated euphotic depth ranges from 3.75 m to 4.23 m from the surface; therefore, the Chla is zero at the bottom layers (e.g., 7 m). Phosphorus release from sediments due to anoxic conditions under the ice cover periods for both 2008 and 2009 winter was not only at 7 m but also at 1 m (does not happen in deep lakes such as Elmo Lake) and triggered algal bloom at 1 m in early summer of 2008 and 2009 (after ice melting). During the summer of 2008 and 2009, the concentration of DO gradually increases at the surface, and sediment phosphorus release decreases which results in a gradual decrease in phosphorus concentration. The DO concentration decreases with depth because of no photosynthesis in the deeper layers (below the euphotic zone) plus sedimentary oxygen demands. Simulated DO at 7 m has some fluctuations in the summer of 2008 and 2009 due to short period strong mixing and results in anoxic conditions only in a few days. The simulated high phosphorus concentrations directly correspond to the simulated anoxic DO conditions in the 2008 and 2009 winters (Figure 14b).
4.4. Sensitivity Analysis
MINLAKE2020 model is sensitive to several calibration parameters. The model was first calibrated with a regression coefficient (R2 for measured versus modeled profile data) of 0.8972 for DO simulation; then, only one model parameter was changed at a time and the regression coefficient for each new run of DO simulation was determined. Table 4 lists the calibration parameters with the calibrated and uncalibrated values and the regression coefficients of DO simulations with uncalibrated values for Lake Elmo in 2007–2009. In Figure 15 and Figure 16, sensitivity analysis graphs are plotted for five parameters: maximum photosynthesis rate Gmax (used in Equations (9), (15)–(17) and (19)), sediment phosphorus release rate SP (used in Equation (9)), half-saturation coefficient of phosphorus KP (used in Equations (9), (15)–(17) and (19)), minimum Chla for grazing Chlamin (used in Equation (9)), and settling velocities of algae (vc) and BOD (vB) (used in Equations (9) and (18)) for Elmo and Pearl Lake, respectively. Units of these model parameters are given in Table 4, and the below corresponding equations.

Table 4.
Calibration parameters used in MINLAKE2020 for Lake Elmo with regression coefficients of the DO simulation.
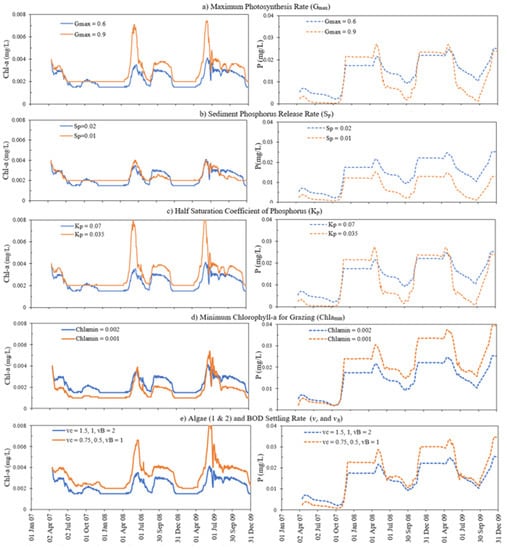
Figure 15.
Sensitivity analysis of Chla (left panels) and phosphorus (right panels) on (a) maximum photosynthesis rate Gmax, (b) sediment phosphorus release rate SP, (c) half saturation coefficient of phosphorus KP, (d) minimum Chla for grazing Chlamin, and (e) algae and BOD settling rates vc, and vB for simulation of Elmo Lake in 2007–2009.
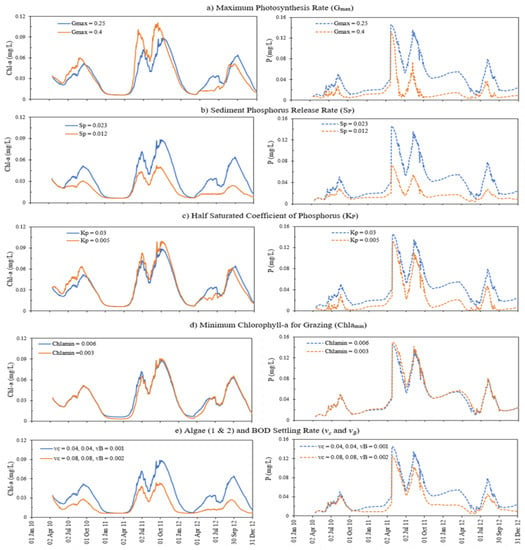
Figure 16.
Sensitivity analysis of Chla (left panels) and phosphorus (right panels) on (a) maximum photosynthesis rate Gmax, (b) sediment phosphorus release rate SP, (c) half saturation coefficient of phosphorus KP, (d) minimum Chla for grazing Chlamin, and (e) algae and BOD settling rates vc, and vB for simulation of Pearl Lake in 2010–2012.
In Figure 15 and Figure 16, the blue line corresponds to simulation results using the calibrated value of the parameter which has produced satisfactory results. The calibrated maximum photosynthesis rate Gmax is 0.6 for Lake Elmo. When Gmax is increased to 0.9, the Chla concentration increases throughout the simulation period on average by 30 percent; the phosphorus concentration increases in the ice cover period because of the detrital decay of increased algae. Higher Gmax corresponds to higher phytoplankton growth which uses more nutrients (phosphorus) except the slow growth period under ice cover. This results in an average 32% decrease in phosphorus concentration in open water season.
When the sediment phosphorus release rate SP was decreased from 0.02 to 0.01, the phosphorus concentration decreased by 55% (on average). The phosphorus starts to decrease during the ice cover period in December 2007 as the sediment phosphorus release start contributing to the phosphorus concentration in anoxic condition. After ice melting, as the algae begin to grow and use up phosphorus, the phosphorus concentration decreases even further in summer. The half saturation coefficient of phosphorus is decreased from 0.07 mg/L to 0.035 mg/L. Since the surface layer is not limited by light, the decrease in the half saturation coefficient results in greater phosphorus limitation which results in increased algal growth. The phosphorus concentration decreases except for the ice cover period which is governed by the sediment phosphorus release in anoxic condition. The increase in the minimum chlorophyll-a threshold for grazing results in less grazing of zooplankton and a subsequent increase in Chla. The settling velocity of algae (both green algae and blue-green algae) is a very sensitive parameter for phytoplankton and BOD simulation. In Figure 15e, as the settling velocity of green algae, blue-green algae, and detritus was decreased to 0.75, 0.5, and 1.0, respectively, the phytoplankton concentration increased due to less loss of phytoplankton from the simulating layer from settling. The phosphorus concentration increases due to the release of phosphorus through respiration of the increased algal population.
For a shallow lake such as Pearl, the effect of maximum photosynthesis rate (Figure 16a) is not as straightforward as for a deep stratified lake such as Elmo Lake (Figure 15a). In addition to the predicted increase, the Chla concentration decreases in spring of 2011 and 2012, early summer and fall of 2012 as a result of the spring and fall overturn when Gmax is increased from 0.25 to 0.4. The Chla is not very sensitive to the half-saturation coefficient (KP) and the minimum Chla threshold for zooplankton grazing (Chlamin). However, the phosphorus concentration decreased by an average of 60% when KP is decreased from 0.03 to 0.005 mg/L (Figure 16c). As KP decreases, the Chla increases throughout the time period except for a portion of summer and fall of 2012. This happens due to the increased respiration of algae which also causes a greater reduction is phosphorus. The zooplankton grazing, being negligible for Pearl Lake, does not affect the phosphorus concentration much. Hence, phosphorus is not sensitive of zooplankton grazing in Pearl Lake.
4.5. Long-Term Simulations Using MINLAKE2020
West and Stefan [23] performed a multiple-year simulation (same calibration parameters) using MINLAKE98 for Lake Riley and Elmo. For Lake Riley, a different set of calibration parameters was needed for different years whereas, for Lake Elmo, the model could simulate successfully for 1985–1990 with the regression coefficient for temperature and DO as 0.91 and 0.79, respectively. For a simulation of 1985–1990 using the MINLAKE2020 NCDO model, the regression coefficient for temperature and DO are 0.9944 and 0.9715 against 146 profile data points, respectively. Simulated phosphorus and Chla concentrations at different depths are satisfactory as well. MINLAKE2020 performed well for multiple-year simulation allowing the user to simulate 20 consecutive years with the same calibration parameters (Figure 17). For a 20-year simulation (1989–2009) using the MINLAKE2020 NCDO model, the regression coefficients for temperature and DO are 0.9888 and 0.9419 against 864 profile data points, respectively. The simulated Chla and phosphorus match reasonably well with observed values with the same trend. Moreover, the phosphorus and Chla concentration at five simulation depths (1 m, 8 m, 12 m, 20 m, and 30 m) match well with the available observed data [54].
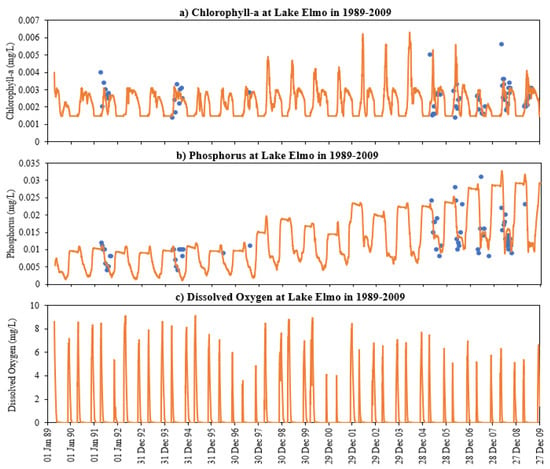
Figure 17.
Simulated (line) and observed (dots) surface (1 m) (a) chlorophyll-a, (b) phosphorus, and (c) dissolved oxygen for long-term simulation of Lake Elmo from 1989 to 2009.
From 1989 to 1996, both phosphorus and chlorophyll-a seasonal variations were reasonably stable. Phosphorus started to increase from 1997 and matched with observed data from 2004 to 2007. The average daily phosphorus was 0.0071 mg/L from 1990 to 1996 and 0.0158 mg/L from 1997 to 2009. Comparing these two periods, the average daily phosphorus increased by 0.0087 mg/L. As phosphorus increased, it resulted in some higher peaks in spring algal blooms as shown in Figure 17a. The phosphorus increase trend is caused by the increase in phosphorus release from the lake sediment which is related to the anoxic condition in lakes. Therefore, the phosphorus release for each layer (the last term in Equation (15) times the layer volume) and then each day (sum for all layers) was outputted and added together for the annual phosphorus release amount. From 1990 (excluding 1989 for the initial condition effect) to 1996, the average yearly sediment phosphorus release is 151.8 kg (21.27 kg of standard deviation) but from 1997 to 2009 average yearly sediment phosphorus release is 244.1 kg (53.28 kg of standard deviation). The average annual phosphorus release increases by 60.8%. Figure 17c shows the time series of the simulated DO at 41 m (1 m above the deepest lake bottom) from 1989 to 2009 and clearly shows many anoxic days in the open water seasons and the ice cover periods, which result in phosphorus release from sediment. From 1990 to 1996, the average anoxic days is 228 but from 1997 to 2009 average anoxic days is 253 (34 days of standard deviation). An average of 25 days more of the anoxic condition is one of the causes of the phosphorus increase trend. From DO simulation it was observed that the anoxia started at a lower depth in the water column (16 m) from 1999 to 2009 compared to earlier simulation years. As a result, the anoxia had a greater horizontal-area coverage. Since the sediment release is a function of the bottom area (Equation (15)), the increased bottom area resulted in the increased sediment phosphorus release.
5. Conclusions
A one-dimensional daily water quality model MINLAKE2020 was developed from the daily temperature and DO MINLAKE2012 model by incorporating phytoplankton, zooplankton, nutrient, and BOD simulation into the model. The inflow-outflow submodel of MINLAKE2020 was disabled for this study to focus on the internal nutrient dynamics inside the lake. The model was applied to six Minnesota lakes with varying characteristics in terms of depth (two shallow lakes, two medium-depth lakes, and two deep lakes) and trophic status (two eutrophic, two mesotrophic, and two oligotrophic lakes). The simulated water temperature, DO, Chla, and phosphorus time series and profiles were compared with available observed data in 15–36 days for two to four years. The model was also applied to long-term simulation over 20 years (1989–2009) for Lake Elmo. Simulation results from the MINLAKE2020 model provide the following conclusions:
- MINLAKE2020 was calibrated against measured profiles in six Minnesota lakes (Table 4) for the short term (2–4 years) with an average standard error of 1.51 °C for temperature and 2.33 mg/L for DO. The average standard error for DO simulation of these lakes decreased by 24.2% from the original MINLAKE2012 model, which indicates better model performance. DO results reflect/integrate reasonably simulated phosphorus, Chla, and BOD results at different layers (see Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 and Figure 17).
- The addition of phosphorus and Chla simulation in MINLAKE2020 improved model performance in comparison to MINLAKE2012 where Chla was specified input. It greatly affects the DO concentration in some lakes such as Pearl Lake (Figure 10). Thrush Lake and Carlos Lake also showed significant improvement in DO simulation with MINLAKE2020. The standard error decreased by 2.12 mg/L and 1.76 mg/L for Thrush and Carlos Lake, respectively.
- The deep lakes exhibit a certain trend for phosphorus and Chla simulation year by year whereas the shallow lakes might show a significant change in phosphorus and Chla concentration year by year due to two overturn periods (complete mixing) and the complex interactions/connections among phosphorus, Chla, and DO (Figure 13 and Figure 14), which are evident through governing Equations (9) and (15)–(19) and processes simulated (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).
- DO concentration is a primary control of internal loading via anoxic release of phosphorus from the lake sediment. MINLAKE2020 was applied to Lake Elmo for a 20-year (1989 to 2009) continuous simulation with a single set of calibration parameters with regression coefficients of 0.99 and 0.94 for temperature and DO profiles, respectively. An increasing trend of surface phosphorus was simulated from 1997 to 2009 which matches well with the observed condition and is directly related to sediment phosphorus release. The average yearly sediment phosphorus release increased from 151.8 kg during the period 1990–1996 to 244.1 kg during the period 1997–2009. This increase is caused by the average 25-day increase in the anoxic condition at the bottom depth (41 m) and the increase in the anoxic horizontal area (as a result of anoxia at lower depths) in later years.
MINLAKE2020 explains the internal link between phosphorus, Chla, and DO. This model can help in choosing/testing effective ways of lake restoration and management. For example, since Lake Elmo experiences internal loading of phosphorus, removing the external nutrient source might not be an effective restoration technique for this lake. Though MINLAKE2020 has simulated six lakes with good correlation to the observed data, more lakes need to be simulated to verify the model in different scenarios before using it professionally for evaluating lake restoration measures. Since the nutrient model is complex and requires a number of calibration parameters, incorporating automatic calibration (by programming software) will make the model more efficient and user-friendly in the future.
Author Contributions
B.T. developed the final version of the MINLAKE2020 program, conducted the simulations, analyzed the result, and prepared the manuscript draft and revisions. X.F. supervised model development, simulation runs, data analysis, and revised the manuscript. J.S.H. supervised the writing and revised the manuscript. D.T. secured research funds and revised the manuscript. All authors made contributions to the study and writing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study is partially supported by funding from Auburn University for the PAIR project “A prototype framework of climate services for decision making.” Di Tian is PI, Xing Fang and others are six Co-PIs. This study is also partially supported by funding from the OUC-AU Joint Center for Aquaculture and Environmental Science for the project “Identifying potential bioaccumulation hotspots of heavy metals in dynamic estuarine systems in Alabama, USA and China.” Matthew N. Waters is PI, Xing Fang and Joel Hayworth are Co-PIs at Auburn University; Jinfen Pan is PI, Min Wang is Co-PI from OUC (Ocean University of China).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Some or all data, models, or code generated or used during the study are proprietary or confidential and may only be provided with restrictions. The model input and output data are specifically designed for a research numerical model. They are available upon request but are not useful for the general public.
Conflicts of Interest
The authors declare no conflict of interest.
List of Symbols, Corresponding Description and Units
| Symbols | Description and Units |
| A | Area (m2) |
| BOD | Biochemical oxygen demand (mg/L) |
| Chla | Chlorophyll concentration (mg/L) |
| Chlamin | Minimum chlorophyll concentration for grazing to occur (mg/L) |
| DO | Dissolved Oxygen concentration (mg/L) |
| DOsat | Saturated oxygen concentration (mg/L) |
| f(L) | Light limiting growth factor (between 0 and 1) |
| f(S) | Michalis-Menten growth limiting factor [-] |
| f(T) | Temperature function for growth [-] |
| Gmax | Maximum growth rate (d−1) |
| GRmax | Grazing maximum (mg Chla/ind. zooplankton/d) |
| Kgchla | Half-saturation constant for grazing (mg/L) |
| I(z) | Intensity of photosynthetically active radiation (µE/m2/h) |
| K1 | Light limitation coefficient (µE/m2/h) |
| K2 | Light inhibition coefficient (µE/m2/h) |
| KBOD | Organic decomposition rate (d−1) |
| Ke | Surface oxygen gas exchange (transfer) coefficient (m/d) |
| Km | Mortality rate (d−1) |
| KN | Half-saturation constant for nitrogen (mg/L) |
| KNI | Nitrification rate (d−1) |
| KNH(n) | Half-saturation constant for preferential uptake of ammonia over nitrate [-] |
| KTN(n) | Half-saturation constant of nitrogen for each algal class (mg/L) |
| KP | Half-saturation constant for phosphorus (mg/L) |
| Kr | Respiration rate (d−1) |
| Kzr | Zooplankton respiration rate (d−1) |
| Kz | Eddy diffusivity (cm2/s) |
| N | Nitrogen concentration |
| NH4 | Ammonia concentration (mg N/L) |
| NO3 | Nitrate concentration (mg N/L) |
| NO2 | Nitrite concentration (mg N/L) |
| NO2-3 | Nitrite + Nitrate concentration (mg N/L) |
| n | Phytoplankton species [-] |
| P | SRP or soluble reactive phosphorus concentration (mg/L) |
| θBOD | Temperature adjustment coefficient for BOD [-] |
| θSOD | Temperature adjustment coefficient for SOD [-] |
| θm | Temperature adjustment coefficient for mortality [-] |
| θr | Temperature adjustment coefficient for respiration [-] |
| θzr | Temperature adjustment coefficient for zooplankton grazing [-] |
| θNH | Temperature adjustment coefficient for ammonia [-] |
| θNO | Temperature adjustment coefficient for nitrate [-] |
| θNI | Temperature adjustment coefficient for nitrification [-] |
| RAD | Solar radiation (cal/cm2/d) |
| Sb | Sedimentary oxygen demand rate at 20°C (g O/m2/d) |
| SNH | Ammonia release rate from sediment (g N/m2/d) |
| SNO | Nitrite release rate from sediment (g N/m2/d) |
| SP | Phosphorus release rate from sediment (g P/m2/d) |
| t | Time (d) |
| T | Air temperature (°C) |
| TD | Length of day light (h) |
| Tmax | Maximum temperature at which phytoplankton growth is reduced 90 percent (°C) |
| Tmin | Minimum temperature at which phytoplankton growth is reduced 90 percent (°C) |
| Topt | Optimal temperature at which maximum phytoplankton growth occurs (°C) |
| TP | Total phosphorus (mg/L) |
| vc | Phytoplankton settling velocity (m/d) |
| vB | Detritus settling velocity (m/d) |
| Viz | Volume of day depth (m3) |
| Vr | Volume day depth/layer ratio [-] |
| YCHO2 | Mass yield ratio of chlorophyll to oxygen |
| YNChla | Mass yield ratio of Nitrogen to Chlorophyll-a |
| YNHBOD | Mass yield ratio of ammonia to BOD [-] |
| YPBOD | Mass yield ratio of ammonia to BOD [-] |
| YPCHLA | Mass yield ratio of ammonia to BOD [-] |
| z | Depth (m) |
| ZP | Zooplankton concentration (#/m3) |
| ZPmin | Minimum concentration of zooplankton for predation to occur (#/m3) |
| PDd | Daytime predation rate (d−1) |
| Pd | Daily predation rate (d−1) |
| XI | Light intensity at the day depth (µE/m2/s) |
| XImax | Light intensity at which no predation occurs (µE/m2/s) |
| XImin | Light intensity at which no predation occurs (µE/m2/s) |
| Pmax | Maximum predation rate (d−1) |
| DY | Julian day of last day of minimum predation rate [-] |
| DYmin | Julian day of last day of minimum predation rate [-] |
| DYmax | Julian day of beginning of maximum predation rate [-] |
| PD(t,I) | Nocturnal predation rate in layer I (#/m3) |
| PDn | Nocturnal predation rate (d−1) |
| ΔTg(I) | Time that zooplankton spent in a layer I during the night (d) |
References
- Le Moal, M.; Gascuel-Odoux, C.; Menesguen, A.; Souchon, Y.; Etrillard, C.; Levain, A.; Moatar, F.; Pannard, A.; Souchu, P.; Lefebvre, A.; et al. Eutrophication: A new wine in an old bottle? Sci. Total Environ. 2019, 651, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moss, B. Cogs in the endless machine: Lakes, climate change and nutrient cycles: A review. Sci. Total Environ. 2011, 434, 130–142. [Google Scholar] [CrossRef] [PubMed]
- Takolander, A.; Cabeza, M.; Leskinen, E. Climate change can cause complex responses in Baltic Sea macroalgae: A systematic review. J. Sea Res. 2017, 123, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Zhang, Y.; Zhang, L.; Zhou, Y. A bibliometric review of nitrogen research in eutrophic lakes and reservoirs. J. Environ. Sci. 2017, 66, 274–285. [Google Scholar] [CrossRef]
- Liu, Y.; Villalba, G.; Ayres, R.U.; Schroder, H. Global phosphorus flows and environmental impacts from a consumption perspective. J. Ind. Ecol. 2008, 12, 229–247. [Google Scholar] [CrossRef]
- Turner, R.E. Linking landscape and water quality in the Mississippi river basin for 200 years. Bioscience 2003, 53, 563–572. [Google Scholar] [CrossRef]
- Wolfe, A.H.; Patz, J.A. Reactive nitrogen and human health: Acute and longterm implications. AMBIO J. Hum. Environ. 2002, 31, 120–125. [Google Scholar] [CrossRef]
- Townsend, A.R.; Howarth, R.W.; Bazzaz, F.A.; Booth, M.S.; Cleveland, C.C.; Collinge, S.K.; Dobson, A.P.; Epstein, P.R.; Holland, E.A.; Keeney, D.R.; et al. Human health effects of a changing global nitrogen cycle. Front. Ecol. Environ. 2003, 1, 240–246. [Google Scholar] [CrossRef]
- Hudnell, H.K.; Dortch, Q. Cyanobacterial Harmful Algal Blooms: Chapter 2: A Synopsis of Research Needs Identified at the Interagency, International Symposium on Cyanobacterial Harmful Algal Blooms (ISOC-HAB); US Environmental Protection Agency: Washington, DC, USA, 2008; Volume 38, pp. 17–43.
- Hudnell, H.K. The state of U.S. freshwater harmful algal blooms assessments, policy and legislation. Toxicon 2010, 55, 1024–1034. [Google Scholar] [CrossRef] [PubMed]
- Seewer, J. Ohio wants to put Lake Erie on a new, strict pollution diet. AP News, 15 February 2020. [Google Scholar]
- Moomaw, W.R.; Birch, M.B. Cascading costs: An economic nitrogen cycle. Sci. China Ser. C Life Sci. 2005, 48, 678–696. [Google Scholar]
- Pretty, J.N.; Mason, C.F.; Nedwell, D.B.; Hine, R.E.; Leaf, S.; Dils, R. Environmental Costs of Freshwater Eutrophication in England and Wales. Environ. Sci. Technol. Libr. 2003, 37, 201–208. [Google Scholar] [CrossRef] [Green Version]
- Dodds, W.K.; Bouska, W.W.; Eitzmann, J.L.; Pilger, T.J.; Pitts, K.L.; Riley, A.J.; Schloesser, J.T.; Thornbrugh, D.J. Eutrophication of U.S. freshwaters: Analysis of potential economic damages. Environ. Sci. Technol. 2008, 43, 12–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bartram, J.; Chorus, I. Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management; World Health Organization: London, UK, 1999; p. 400. [Google Scholar]
- Imboden, D.M. Phosphorus model of lake eutrophication. Limnol. Oceanogr. 1974, 19, 297–304. [Google Scholar] [CrossRef] [Green Version]
- Vollenweider, R.A.; Kerekes, J. Eutrophication of Waters. Monitoring, Assessment and Control; OECD Cooperative Programme on Monitoring of Inland Waters; Organization for Economic Co-Operation and Development (OECD): Paris, France, 1982; Volume 156. [Google Scholar]
- De Senerpont Domis, L.N.; Van de Waal, D.B.; Helmsing, N.R.; Donk, E.V.; Mooij, W.M. Community stoichiometry in a changing world: Combined effects of warming and eutrophication on phytoplankton dynamics. Ecology 2014, 95, 1485–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reynolds, C.S.; Irish, A.E.; Elliott, J.A. The ecological basis for simulating phytoplankton responses to environmental change (PROTECH). Ecol. Model. 2001, 140, 271–291. [Google Scholar] [CrossRef]
- Riley, M.J.; Stefan, H.G. MINLAKE: A dynamic lake water quality simulation model. Ecol. Model. 1988, 43, 155–182. [Google Scholar] [CrossRef]
- Gu, R.; Stefan, H.G. Year-round temperature simulation of cold climate lakes. Cold Reg. Sci. Technol. 1990, 18, 147–160. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Modeling of Dissolved Oxygen Stratification Dynamics in Minnesota Lakes under Different Climate Scenarios; St Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1994; Volume 55414, p. 260. [Google Scholar]
- West, D.; Stefan, H.G. Simulation of Lake Water Quality Using a One-Dimensional Model with Watershed Input. In Model Description and Application to Lake Riley and Lake Elmo; Project Report No.430; St. Anthony Falls Laboratory, University of Minnesota: Minneapolis, MN, USA, 1998. [Google Scholar]
- Jamily, J.A. Developing an Hourly Water Quality Model to Simulate Diurnal Water Temperature and Dissolved Oxygen Variations in Shallow Lakes. Master’s Thesis, Auburn University, Auburn, AL, USA, 2018. [Google Scholar]
- Batick, B.M. Modeling Temperature and Dissolved Oxygen in the Cheatham Reservoir with CE-QUAL-W2; Vanderbilt University: Nashville, TN, USA, 2011. [Google Scholar]
- Chapra, S.C.; Martin, J.L. LAKE2K, a Modeling Framework for Simulating Lake Water Quality (Version 1.2): Documentation and users Manual; Civil and Environmental Engineering Department, Tufts University: Medford, MA, USA, 2004. [Google Scholar]
- Cole, T.M.; Buchak, E.M. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 2.0. User Manual; DTIC Document; DTIC: Fort Belvoir, VA, USA, 1995. [Google Scholar]
- Janssen, A.B.G.; Teurlincx, S.; Beusen, A.H.W.; Huijbregts, M.A.J.; Rost, J.; Schipper, A.M.; Seelen, L.M.S.; Mooij, W.M.; Janse, J.H. PCLake+: A process-based ecological model to assess the trophic state of stratified and non-stratified freshwater lakes worldwide. Ecol. Model. 2019, 396, 23–32. [Google Scholar] [CrossRef]
- Hipsey, M.R.; Romero, J.R.; Antenucci, J.P.; Hamilton, D. Computational Aquatic Ecosystem Dynamics Model: CAEDYM v2; Contract Research Group, Centre for Water Research, University of Western Australia: Crawley, WA, Australia, 2005; p. 102. [Google Scholar]
- Hannoun, I.; List, E.J.; Kavanagh, K.B.; Chiang, W.-L.; Ding, L.; Preston, A.; Karafa, D.; Rachkley, I. Use of ELCOM and CAEDYM for Water Quality Simulation in Boulder Basin; Water Environment Federation: Alexandria, VA, USA, 2006. [Google Scholar]
- Carraro, E.; Guyennon, N.; Hamilton, D.; Valsecchi, L.; Manfredi, E.C.; Viviano, G.; Salerno, F.; Tratari, G.; Copetti, D. Coupling high-resolution measurements to a three dimensional lake model to assess the spatial and temporal dynamics of the cyanobacterium Planktothrix rubescens in a medium-sized lake. Hydrobiologia 2012, 698, 77–95. [Google Scholar] [CrossRef]
- Pomati, F.; Matthews, B.; Seehausen, O.; Ibelings, B.W. Eutrophication and climate warming alter spatial (depth) co-occurrence patterns of lake phytoplankton assemblages. Hydrobiologia 2017, 787, 375–385. [Google Scholar] [CrossRef]
- Anderson, D.M.; Cembella, A.D.; Hallegraeff, G.M. Progress in Understanding Harmful Algal Blooms: Paradigm shifts and new technologies for research, monitoring, and management. Annu. Rev. Mar. Sci. 2012, 4, 143–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shimoda, Y.; Arhonditsis, G.B. Phytoplankton functional type modelling: Running before we can walk? A critical evaluation of the current state of knowledge. Ecol. Model. 2016, 320, 29–43. [Google Scholar] [CrossRef]
- Zhang, X.; Recknagel, F.; Chen, Q.; Cao, H.; Li, R. Spatially-explicit modelling and forecasting of cyanobacteria growth in Lake Taihu by evolutionary computation. Ecol. Model. 2015, 306, 216–225. [Google Scholar] [CrossRef]
- Elliott, A.H. Predicting the impact of changing nutrient load and temperature on the phytoplankton of England’s largest lake, Windermere. Freshw. Biol. 2011, 57, 400–413. [Google Scholar] [CrossRef] [Green Version]
- Marsden, M.W. Lake restoration by reducing external phosphorus loading: The influence of sediment phosphorus release. Freshw. Biol. 1989, 21, 139–162. [Google Scholar] [CrossRef]
- Sondergaard, M.; Jeppesen, E.; Jensen, J.P.; Amsinck, S.L. Water framework directive: Ecological classification of Danish lakes. J. Appl. Ecol. 2005, 42, 616–629. [Google Scholar] [CrossRef]
- Philips, G.; Kelly, A.; Pitt, J.A.; Sanderson, R.; Taylor, E. The recovery of a very shallow eutrophic lake, 20 years after the control of effluent derived phosphorus. Freshw. Biol. 2005, 50, 1628–1638. [Google Scholar] [CrossRef]
- Taguchi, V.J.; Olsen, T.A.; Janke, B.D.; Gulliver, J.S.; Finlay, J.C.; Stefan, H.G. Internal loading in stormwater ponds as a phosphorus source to downstream waters. Limnol. Oceanogr. Lett. 2020, 5, 322–330. [Google Scholar] [CrossRef]
- Jeppesen, E.; Sondergaard, M.; Jensen, J.P.; Havens, K.E.; Anneville, O.; Carvalho, L.; Coveney, M.F.; Deneke, R.; Dokulil, M.T.; Foy, B.; et al. Lake responses to reduced nutrient loading: An analysis of contemporary long-term data from 35 case studies. Freshw. Biol. 2005, 50, 1747–1771. [Google Scholar] [CrossRef]
- Welch, E.B.; Cooke, G.D. Internal phosphorus loading in shallow lakes: Importance and control. Lake Reserv. Manag. 2009, 21, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Riley, M.J.; Stefan, H.G. Dynamic Lake Water Quality Simulation Model “MINLAKE”; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1987; Volume 55414, p. 140. [Google Scholar]
- Hondzo, M.; Stefan, H.G. Lake water temperature simulation model. J. Hydraul. Eng. 1993, 119, 1251–1273. [Google Scholar] [CrossRef]
- Fang, X.; Stefan, H.G. Modeling of dissolved oxygen stratification dynamics in Minnesota lakes under different climate scenarios. Ecol. Model. 1994, 71, 37–68. [Google Scholar]
- Fang, X.; Stefan, H.G. Temperature and Dissolved Oxygen Simulations for a Lake with Ice Cover; Project Report 356; St. Anthony Falls Hydraulic Laboratory, University of Minnesota: Minneapolis, MN, USA, 1994. [Google Scholar]
- Fang, X.; Alam, S.R.; Jacobson, P.; Pereira, D.; Stefan, H.G. Simulations of Water Quality in Cisco Lakes in Minnesota; St. Anthony Falls Laboratory, University of Minnesota: Minneapolis, MN, USA, 2010. [Google Scholar]
- West, D.; Stefan, H.G. Simulation of Water Quality and Primary Productivity Control Strategies for Lake McCarrons; Project Report No.426; St. Anthony Falls Laboratory, University of Minnesota: Minneapolis, MN, USA, 2000. [Google Scholar]
- Tasnim, B.; Jamily, J.A.; Fang, X.; Zhou, Y.; Hayworth, J.S. Simulating diurnal variations of water temperature and dissolved oxygen in shallow Minnesota lakes. Water 2021, 13, 1980. [Google Scholar] [CrossRef]
- Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef] [Green Version]
- Lehman, J.T.; Botkins, D.B.; Likens, G.E. The assumptions and rationales of a computer model of phytoplankton population dynamics. Limnol. Oceanogr. 1975, 20, 343–364. [Google Scholar] [CrossRef]
- Megard, R.O.; Tonkyn, D.W.; Senft, W.H. Kinetics of oxygenic photosynthesis in planktonic algae. J. Plankton Res. 1984, 6, 325–337. [Google Scholar] [CrossRef]
- Megard, R.O.; Combs, W.S.; Smith, P.D.; Knoll, A.S. Attenuation of light and daily integral rates of photosynthesis attained by planktonic algae1. Limnol. Oceanogr. 1979, 24, 1038–1050. [Google Scholar] [CrossRef]
- Shapiro, J.; Forsberg, B.; Lamarra, V.; Lindmark, G.; Lynch, M.; Smeltzer, E.; Zoto, G. Experiments and Experiences in Biomanipulation; Interim Report No. 19; Limnological Research Center, University of Minnesota: Minneapolis, MN, USA, 1982. [Google Scholar]
- Wright, D.; O’Brien, W.J.; Vinyard, G.L. Adaptive value of vertical migration: A simulation model argument for the predation hypothesis, Evolution and Ecology of Zooplankton Communities. In Evolution and Ecology of Zooplankton Communities; Kerfoot, C.W., Ed.; University Press of New England: Lebanon, NH, USA, 1980; pp. 138–147. [Google Scholar]
- Dillon, P.J.; Rigler, F.H. The phosphorus-chlorophyll relationship in lakes: Phosphorus-chlorophyll relationship. Limnol. Oceanogr. 1974, 19, 767–773. [Google Scholar] [CrossRef]
- Thomann, R.V.; Mueller, J.A. Principles of Surface Water Quality Modeling and Control; Harper Collins Publishers Inc: New York, NY, USA, 1987; p. 644. [Google Scholar]
- Goldman, C.R.; Horne, A.J. Limnology; McGraw-Hill: New York, NY, USA, 1983. [Google Scholar]
- Cole, T.M.; Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 3.72 User Manual; Department of Civil and Environmental Engineering, Portland State University: Portland, OR, USA, 2015. [Google Scholar]
- Hamrick, M.J. The Environmental Fluid Dynamics Code Theory and Computation Volume 3: Water Quality Module; Tetra Tech, Inc.: Fairfax, VA, USA, 2007; p. 90. [Google Scholar]
- Nürnberg, G.K. The prediction of internal phosphorus load in lakes with anoxic hypolimnia. Limnol. Oceanogr. 1984, 29, 111–124. [Google Scholar] [CrossRef]
- Stigebrandt, A.; Rahm, L.; Viktorsson, L.; Ödalen, M.; Hall, P.O.J.; Liljebladh, B. A new phosphorus paradigm for the Baltic proper. Ambio 2014, 43, 634–643. [Google Scholar] [CrossRef] [Green Version]
- Stigebrandt, A.; Andersson, A. The eutrophication of the Baltic Sea has been boosted and perpetuated by a major internal phosphorus source. Front. Mar. Sci. 2020, 7, 572994. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, X. Simulations and validation of cisco lethal conditions in Minnesota lakes under past and future climate scenarios using constant survival limits. Water 2016, 8, 279. [Google Scholar] [CrossRef] [Green Version]
- Edwards, R.; Owens, M. The oxygen balance of streams. Ecol. Ind. Soc. 1965, 6, 149–172. [Google Scholar]
- Henderson-Sellers, B. Engineering Limnology; Pitman Advanced Pub. Program: Boston, MA, USA, 1984; p. 356. [Google Scholar]
- Tasnim, B. Enhancement and Redevelopment of the Regional Lake Water Quality Model with Applications. Master’s Thesis, Auburn University, Auburn, AL, USA, 2020. [Google Scholar]
- Fang, X.; Stefan, H.G. Long-term lake water temperature and ice cover simulations/measurements. Cold Reg. Sci. Technol. 1996, 24, 289–304. [Google Scholar] [CrossRef]
- Brown, L.C.; Barnwell, T.O. The Enhanced Stream Water Quality Models QUAL2E and QUAL2W-UNCAS: Documentation and User Manual; U.S. Environmental Protection Agency: Athens, GA, USA, 1987.
- Zison, S.W.; Mills, W.B.; Diemer, D.; Chen, C.W. Rates, Constants and Kinetic Formulations in Surface Water Quality Modeling; Tetra Tech, Inc., for USEPA, ORD: Athens, GA, USA, 1978; p. 317. [Google Scholar]
- Stefan, H.G.; Hondzo, M.; Fang, X.; Eaton, J.G.; McCormick, J.H. Simulated long-term temperature and dissolved oxygen characteristics of lakes in the north-central United States and associated fish habitat limits. Limnol. Oceanogr. 1996, 41, 1124–1135. [Google Scholar] [CrossRef]
- Stefan, H.G.; Fang, X. Dissolved oxygen model for regional lake analysis. Ecol. Model. 1994, 71, 37–68. [Google Scholar] [CrossRef]
- NAS and NAE. Water Quality Criteria 1972—A Report of the Committee on Water Quality Criteria; Environmental Protection Agency: Washington, DC, USA, 1973.
- Barr Engineering. Pearl Lake and Mill Creek Bacterial Total Maximum Daily Load Report; Barr Engineering: Minneapolis, MN, USA, 2012. [Google Scholar]
- Engel, L.; Valley, R.; Beck, D.; Anderson, J. Sentinel Lake Assessment Report Lake Carlos (21-0057) Douglas County, Minnesota; Minnesota Pollution Control Agency & MN Minnesota Department of Natural Resources: St. Paul, MN, USA, 2010.
- Engel, L.; Heiskary, S.; Valley, R.; Tollefson, D. Sentinel Lake Assessment Report Carrie Lake (34-0032) Kandiyohi County, Minnesota; Minnesota Pollution Control Agency & Minnesota Department of Natural Resources: St. Paul, MN, USA, 2012.
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).