Hydroenergy Harvesting Assessment: The Case Study of Alviela River
Abstract
:1. Introduction
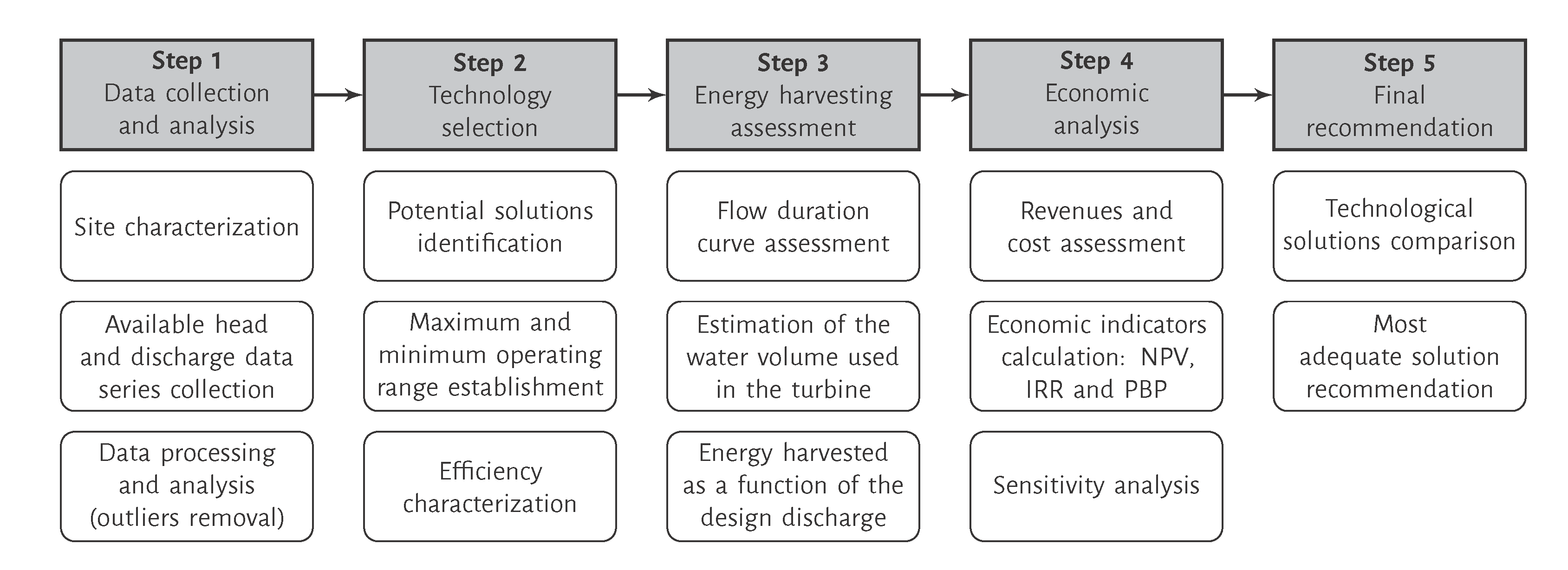
2. Methodology
- Step 1
- consists of identifying the primary purpose of the water supply or collectors system, its main characteristics and the potential locations for energy harvesting, which must combine excessive head, large discharges and sufficient available space to install the powerhouse and the turbine. For the identified locations, available head and discharge data must be collected and should include, at least, three consecutive years representative of the system operation. If necessary, it should be identified, the derived discharge that cannot be turbined. Above all, the construction of MHP cannot compromise the primary purpose of the system, which can be the water supply or the wastewater drainage or treatment.
- Step 2
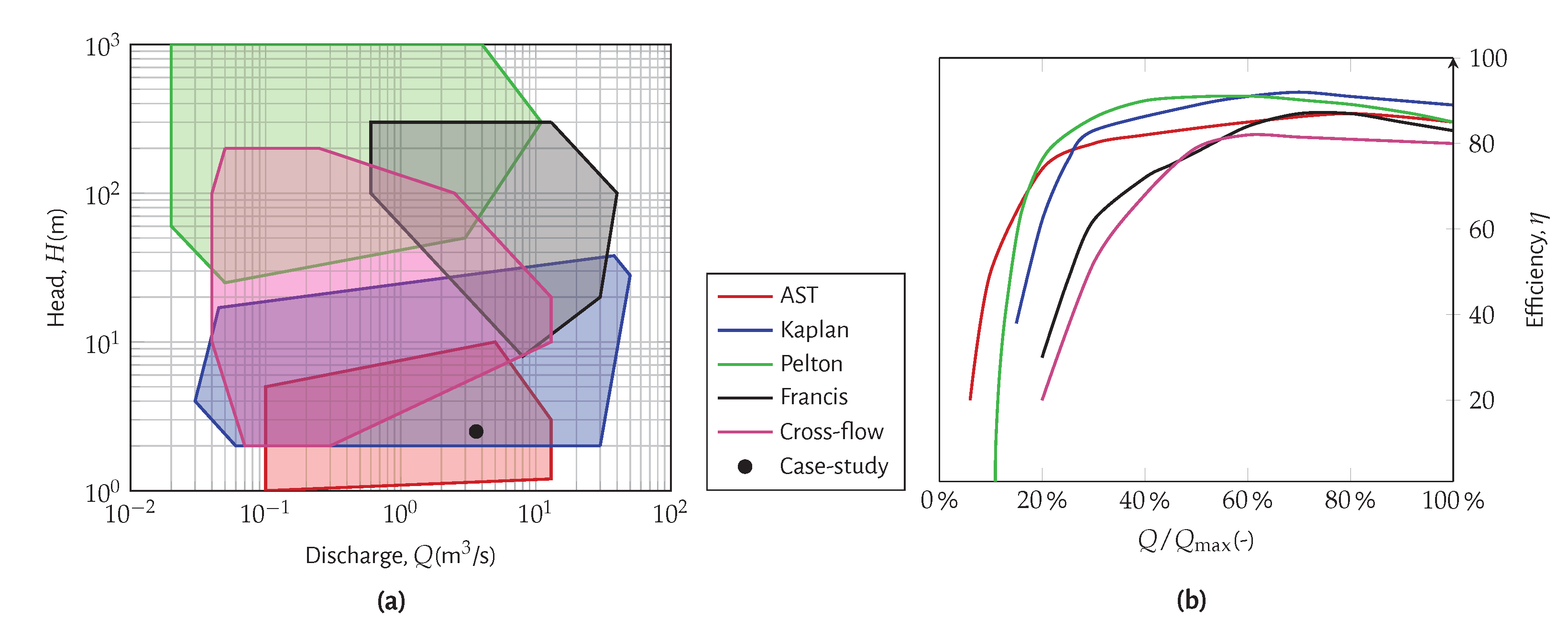
- focuses on the selection of possible technological solutions based on the available head and discharges range and the technical features of each solution. For this purpose, Figure 2a), which presents performance characteristics of possible solutions, can be used. Usually, the best solutions are: the AST, Kaplan, PAT, Cross-flow and waterwheel turbines for low-heads (1–20 m) [29]; PAT, Francis and Cross-flow turbines for medium heads (20–100 m); and Francis and Pelton turbines for high heads (>100 m). For each solution, the maximum and minimum operating ranges of heads and discharges as well as the efficiency curve versus discharge should be defined. Figure 2b) presents the variation of the turbine efficiency with the maximum discharge percentage for several turbines.
- Step 3
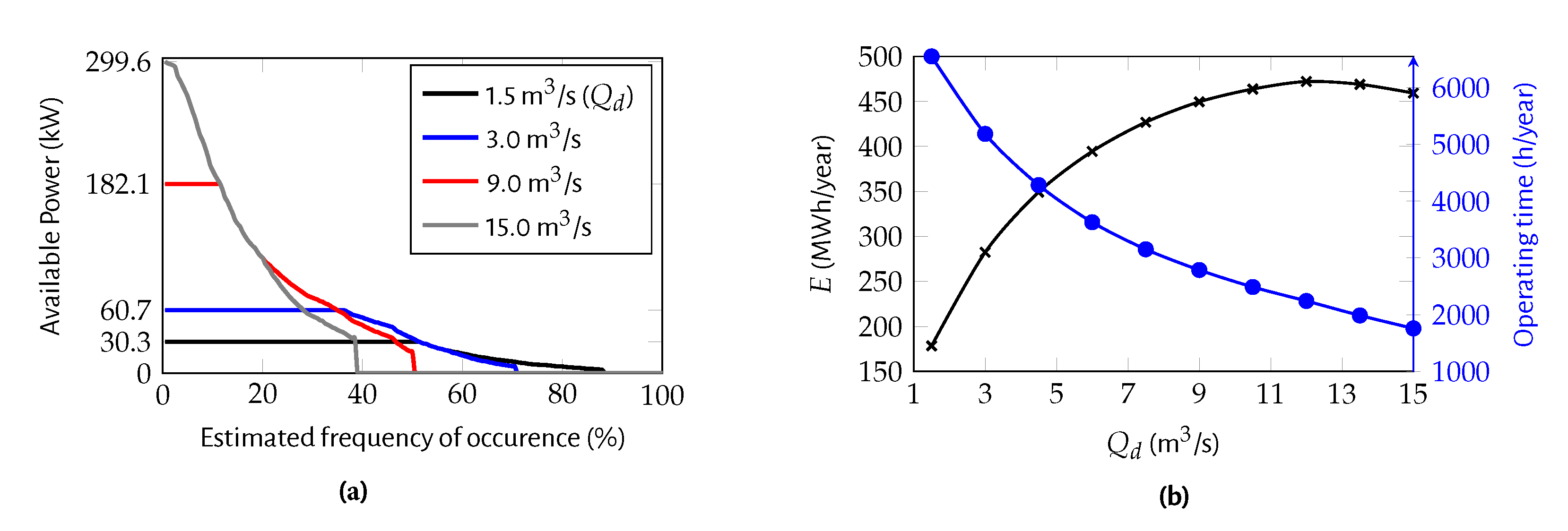
- consists of the simulation of the energy harvesting over one year for each energy recovery solution, considering the head and discharge data and different values of design discharge. The proposed method requires the following input data: the pressure head and discharge data over at least three consecutive years with a time-stamp that can vary between 15 min, in systems highly demand dependent (e.g., networks), and 1–5 days, in systems with high seasonal variation (e.g., transmission systems, storage tanks); the interval of acceptable design discharges; and the discharge range of operation of the turbine (Figure 2a).Initially, the discharge probability of occurrence curve is calculated over the assessment period (e.g., three years) based on discharge time history, and used to define the range of design discharges, . The annual energy harvesting is calculated for each design discharge, , taking into account the probability of occurrence curve.The turbined discharge at simulated time step is determined considering the following rules: (i) if the available discharge, , is higher than the maximum for the considered design discharged, than the turbine will only operate with and the remaining discharge will be derived through a bypass; (ii) if the available discharge, , is within the operating range of the turbine, , the turbine will use for energy production; and (iii) if the available discharge is lower than the minimum, the turbine will not operate.The annual harvested energy, E (kWh), for each design discharge, , is calculated by the time integration of the product of the available power, , by the respective efficiency for each discharge over one year:being the specific weight of water (9800 N/m), Q the turbined discharge (m/s), H the available net head (m), the efficiency of the turbine for the turbined discharge. The installed power, P(kW), is calculated as a function of the design discharge, , and design net head, :where is the efficiency for the design discharge and design net head.The annual volume used by the turbine, the annual harvested energy and the total power are calculated for each design discharge.
- Step 4
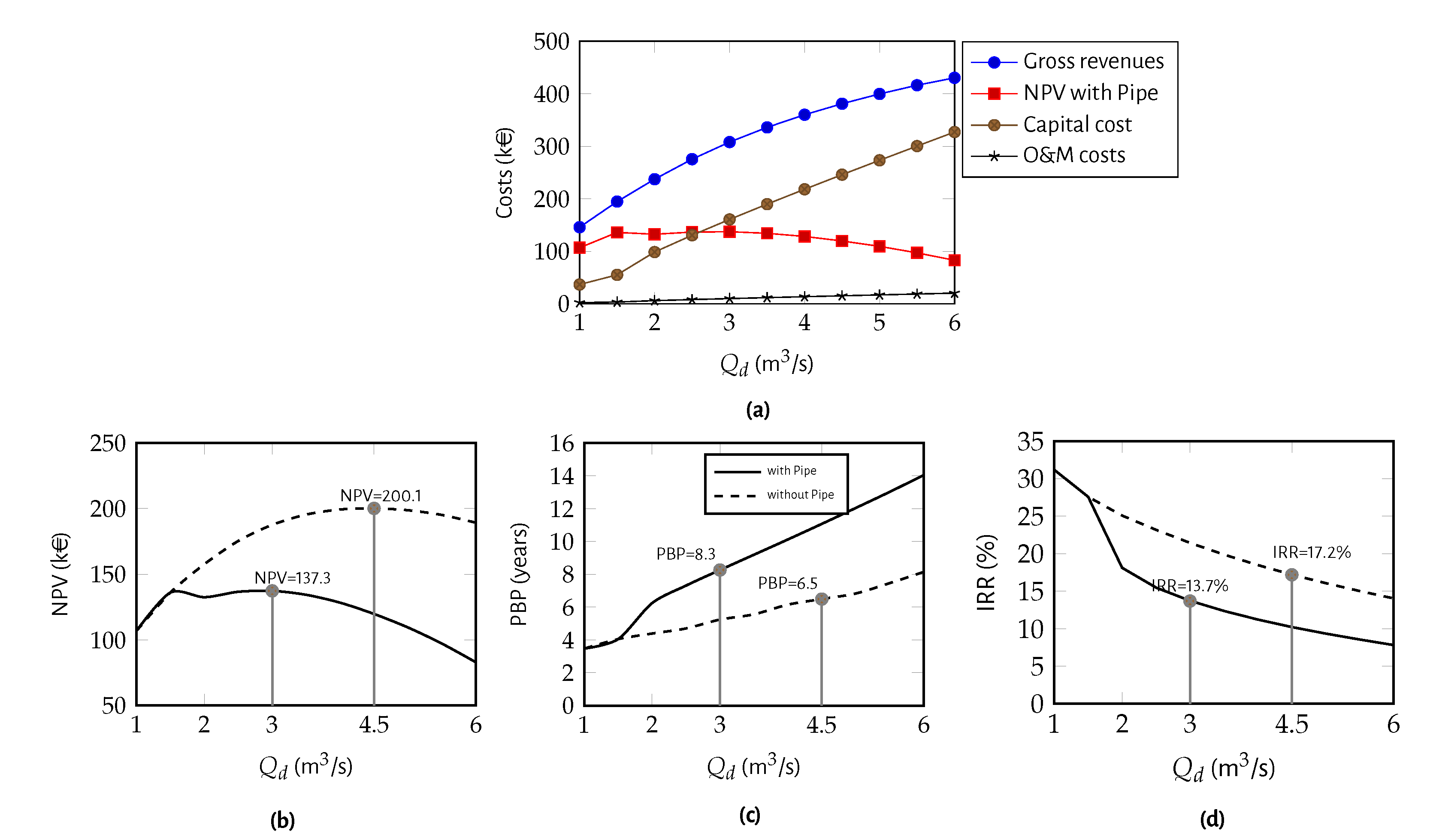
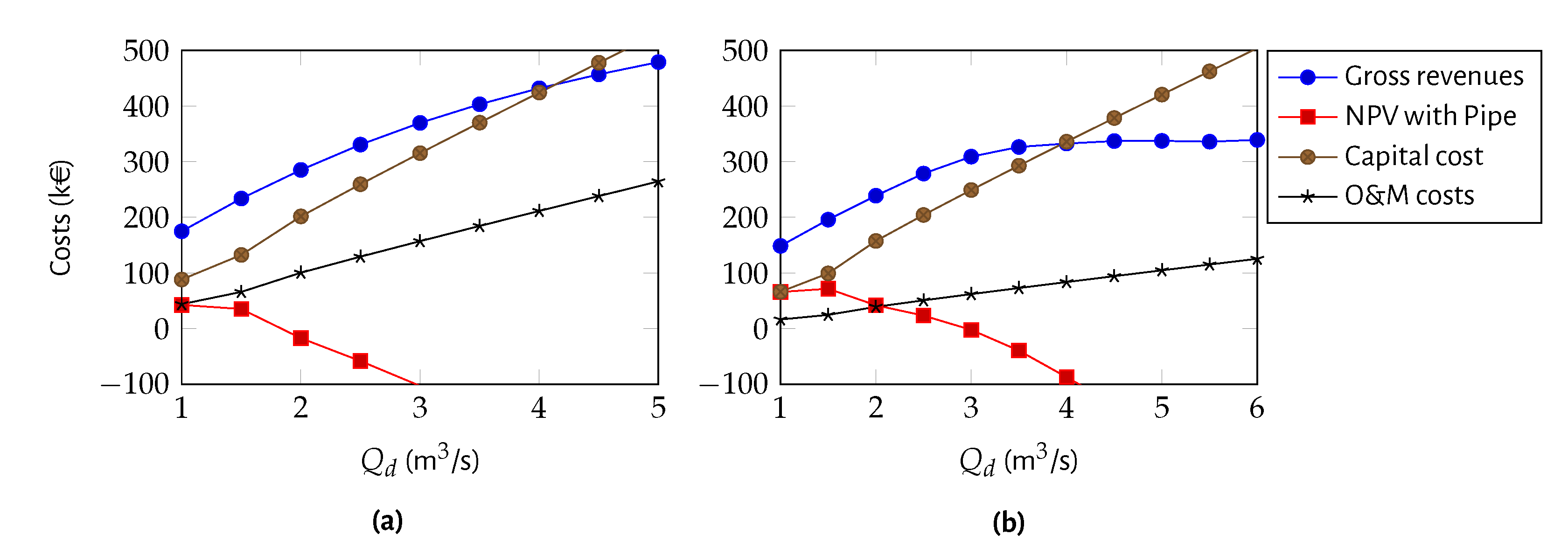
- consists of the economic analysis of the project based on the annual harvested energy for each design discharge. Capital costs, operation and maintenance (O&M) costs and gross and net revenues are calculated. Three economic indicators are typically used to evaluate the feasibility of the project: the net present value (NPV), the payback period (PBP) and the internal rate of return (IRR). These are calculated for each design discharge and for each selected turbine. The additional input data to calculate these indicators are: the discount rate, ; the project lifetime, n (years); the energy cost unit, (€/kWh); the capital cost (CC); and the annual O&M costs described as a percentage of CC. The CC includes the equipment control, management, civil works and turbine generator setup. The civil works and equipment costs can be estimated by using empirical equations for the initial costs [31] or cost estimations based on similar projects [32]. When only the turbine cost is known, the civil works’ cost can be estimated based on its weight on the total cost of the project and, then, estimated the CC [33]. The CC, net revenue, accumulated revenues over the period of analysis and the referred economic indicators are calculated for each design discharge and for each technological solution. These indicators will contribute to finding the best solution which corresponds to the maximum NPV of the project. Finally, a sensitivity analysis to the main uncertain parameters, such as the capital cost, the O&M costs and the discount rate, should be carried to assess their impact on the final decision.
- Step 5
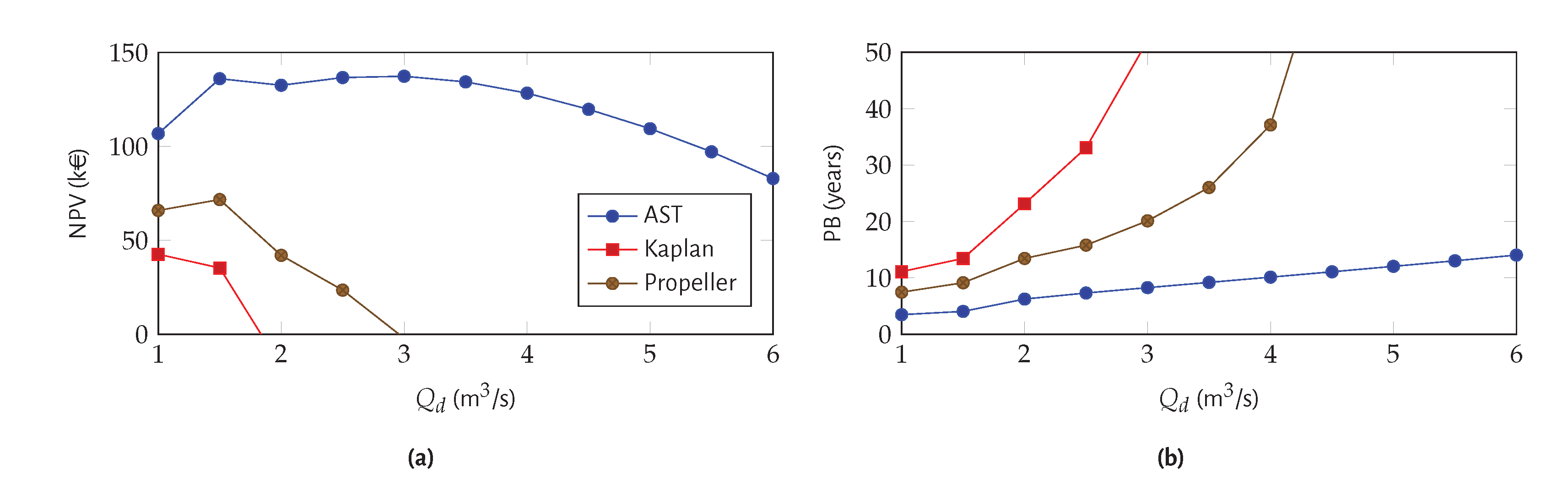
- consists of the comparison of analysed technological solutions to select the best technical and economical option for energy harvesting in the analysed water system. The main parameters to be compared for each design discharge scenario are harvested energy, CC, PBP, NPV and IRR. The final solution is the one that leads to the highest NPV with an acceptable IRR (>10%) and an adequate payback period ideally lower than 10 years [34]. The project is only feasible, if the NPV is higher than zero, which means that the investment is recovered within the project lifetime. If the NPV is equal to zero, the investment cost is retrieved and the minimum rate of return of capital is achieved, so the profitability of the project is doubtful. If the NPV is negative, the project is financially impractical.It should be highlighted that the project design discharge depends not only on the energy harvested but also on the economic analysis, since higher discharges not only lead to higher revenues but also to higher capital and O&M costs.A computational tool has been implemented in MATLAB for carrying out the described simulations.
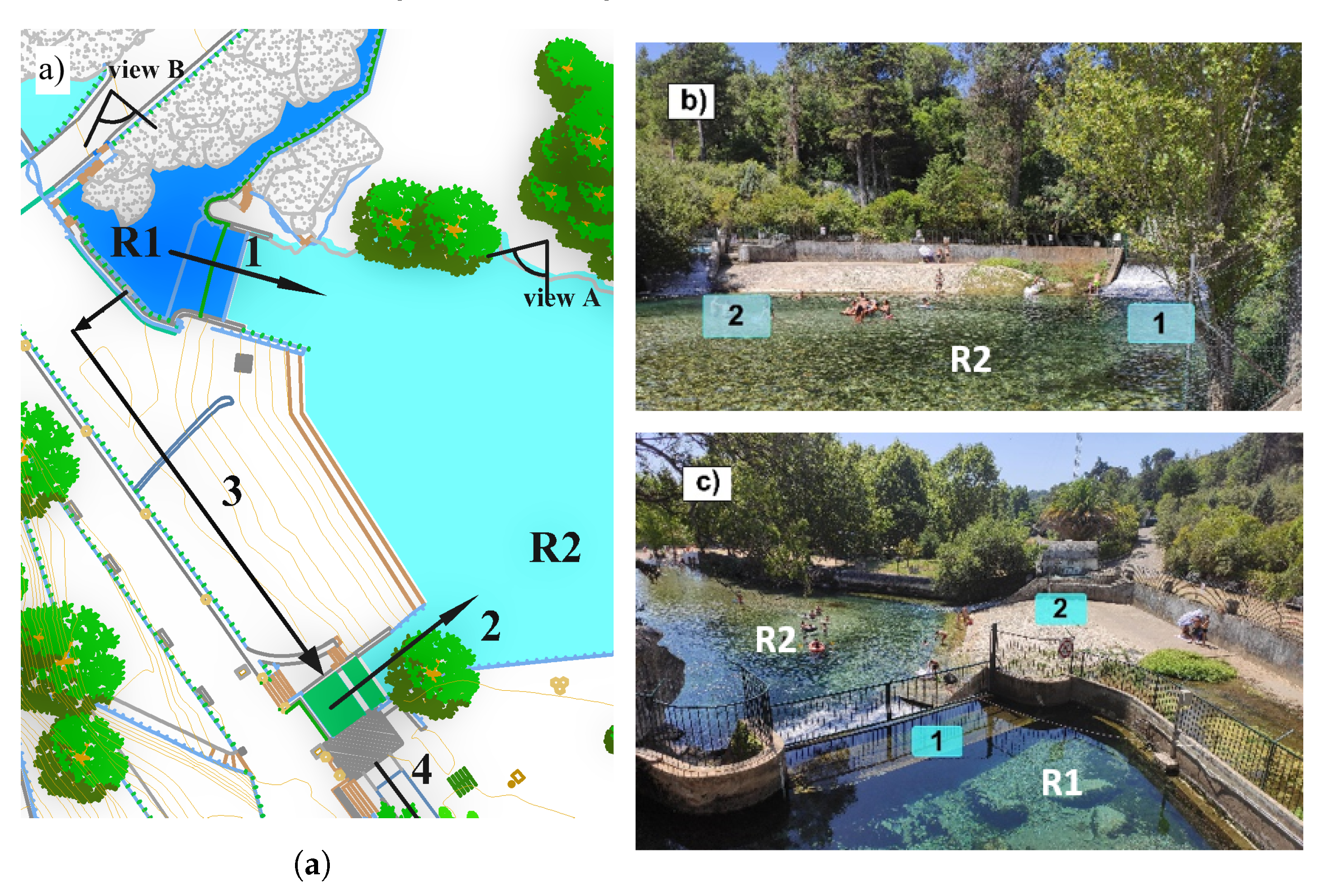
3. Case Study: Alviela River Source
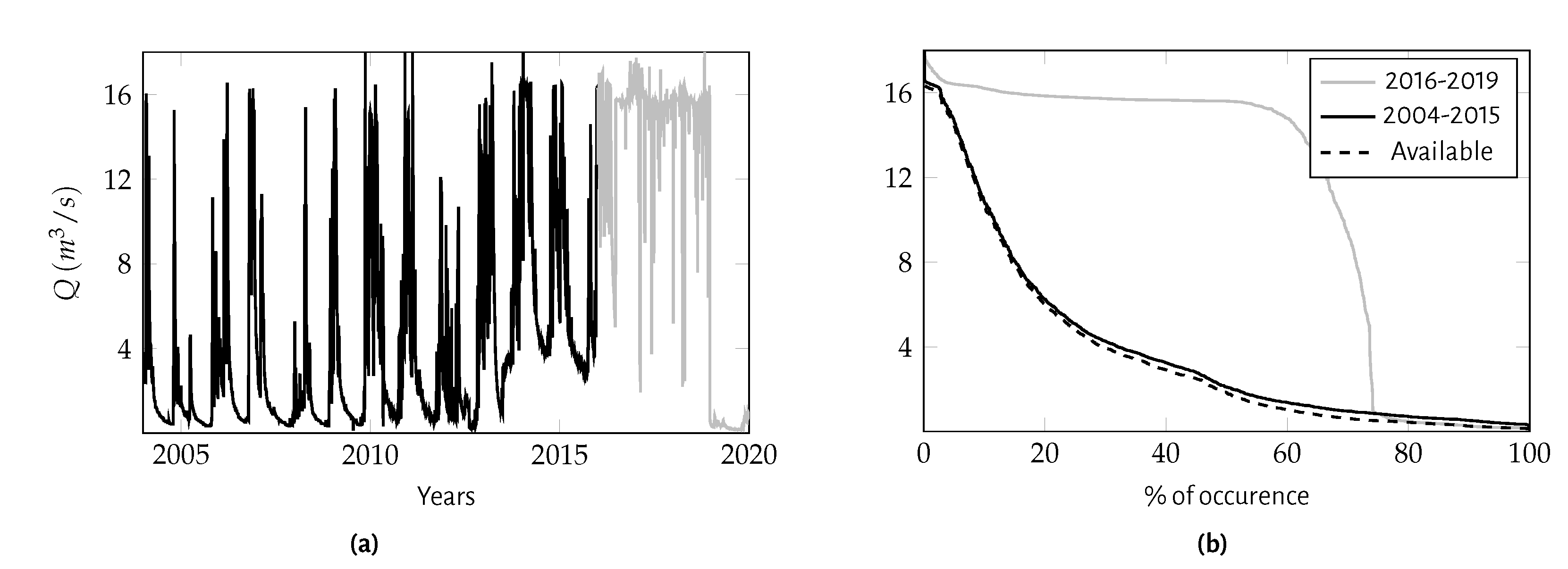
3.1. Data Collection and Analysis
3.2. Technology Selection
3.3. Energy Harvesting Assessment
3.4. Economic Analysis
3.5. Final Recommendation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Panguluri, S.; Grayman, W.M.; Clark, R.M. Water Distribution System Analysis: Field Studies, Modeling and Management: A Reference Guide for Utilities; Report; U. S. Environmental Protection Agency: Washington, DC, USA, 2005.
- Coelho, B.; Andrade-Campos, A. Efficiency achievement in water supply systems—A review. Renew. Sustain. Energy Rev. 2014, 30, 59–84. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M.; Mello, M.; Rodriguez-Diaz, J.A.; Morillo, J.G.; Adeyeye, K.; Coughlan, P.; Gallagher, J.; McNabola, A. Reducing the Energy Dependency of Water Networks in Irrigation, Public Drinking Water, and Process Industry: REDAWN Project. Proceedings 2018, 2, 681. [Google Scholar] [CrossRef] [Green Version]
- Blinco, L.J.; Simpson, A.R.; Lambert, M.F.; Marchi, A. Comparison of pumping regimes for Water Distribution Systems to minimize cost and greenhouse gases. J. Water Resour. Plan. Manag. 2016. [Google Scholar] [CrossRef] [Green Version]
- Vieira, F.; Ramos, H.M. Hybrid solution and pump-storage optimization in water supply system efficiency: A case study. Energy Policy 2008, 36, 4142–4148. [Google Scholar] [CrossRef]
- Musz-Pomorska, A.; Widomski, M.K. Modelling Studies of Water Chlorination Efficiency in Municipal Water Supply Network. Ecol. Chem. Eng. A 2020, 27, 1–13. [Google Scholar] [CrossRef]
- Samaras, K.; Zouboulis, A.; Karapantsios, T.; Kostoglou, M. A CFD-based simulation study of a large scale flocculation tank for potable water treatment. Chem. Eng. J. 2010, 162, 208–216. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R. Accounting for Greenhouse Gas Emissions in Multiobjective Genetic Algorithm Optimization of Water Distribution Systems. J. Water Resour. Plan. Manag. 2010, 136, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Ramos, H.M.; McNabola, A.; López-Jiménez, P.A.; Pérez-Sánchez, M. Smart Water Management towards Future Water Sustainable Networks. Water 2019, 12, 58. [Google Scholar] [CrossRef] [Green Version]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. A comprehensive and well tested energy balance for water supply systems. Urban Water J. 2017, 14, 853–861. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. Top-Down and Bottom-Up Approaches for Water-Energy Balance in Portuguese Supply Systems. Water 2018, 10, 577. [Google Scholar] [CrossRef] [Green Version]
- Mitrovic, D.; Chacón, M.C.; García, A.M.; Morillo, J.G.; Diaz, J.A.R.; Ramos, H.M.; Adeyeye, K.; Carravetta, A.; McNabola, A. Multi-Country Scale Assessment of Available Energy Recovery Potential Using Micro-Hydropower in Drinking, Pressurised Irrigation and Wastewater Networks, Covering Part of the EU. Water 2021, 13, 899. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; Ramos, H.; López-Jiménez, P. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef] [Green Version]
- McNabola, A.; Coughlan, P.; Williams, A.P. Energy recovery in the water industry: An assessment of the potential of micro-hydropower. Water Environ. 2014, 294–304. [Google Scholar] [CrossRef]
- Mérida García, A.; Rodríguez Díaz, J.; García Morillo, J.; McNabola, A. Energy Recovery Potential in Industrial and Municipal Wastewater Networks Using Micro-Hydropower in Spain. Water 2021, 13, 691. [Google Scholar] [CrossRef]
- Monteiro, L.; Delgado, J.; Covas, D. Improved Assessment of Energy Recovery Potential in Water Supply Systems with High Demand Variation. Water 2018, 10, 773. [Google Scholar] [CrossRef] [Green Version]
- Power, C.; Coughlan, P.; McNabola, A. Microhydropower Energy Recovery at Wastewater-Treatment Plants: Turbine Selection and Optimization. J. Hydraul. Eng. ASCE 2016. [Google Scholar] [CrossRef]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe inline installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower Potential in Water Distribution Networks: Pressure Control by PATs. Water Resour. Manag. 2014, 29, 699–714. [Google Scholar] [CrossRef]
- Carravetta, A.; Houreh, S.D.; Ramos, H.M. Pumps as Turbines—Fundamentals and Applications; Springer: Berlin, Germany, 2018. [Google Scholar]
- Crespo Chacón, M.; Rodríguez Díaz, J.A.; García Morillo, J.; McNabola, A. Hydropower energy recovery in irrigation networks: Validation of a methodology for flow prediction and pump as turbine selection. Renew. Energy 2020, 147, 1728–1738. [Google Scholar] [CrossRef]
- Delgado, J.; Ferreira, J.P.; Covas, D.I.C.; Avellan, F. Variable speed operation of centrifugal pumps running as turbines. experimental investigation. Renew. Energy 2019. [Google Scholar] [CrossRef]
- Delgado, J.; Andolfattoa, L.; Covas, D.I.C.; Avellan, F. Hill chart modelling using the Hermite polynomial chaos expansion for the performance prediction of pumps running as turbines. Energy Convers. Manag. 2019, 187, 578–592. [Google Scholar] [CrossRef]
- Elbatran, A.; Yaakob, O.; Ahmed, Y.M.; Shabara, H. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 40–50. [Google Scholar] [CrossRef]
- Bousquet, C.; Samora, I.; Manso, P.; Rossi, L.; Heller, P.; Schleiss, A.J. Assessment of hydropower potential in wastewater systems and application to Switzerland. Renew. Energy 2017, 113, 64–73. [Google Scholar] [CrossRef]
- Kaunda, C.S.; Kimambo, C.Z.; Nielsen, T.K. A technical discussion on microhydropower technology and its turbines. Renew. Sustain. Energy Rev. 2014, 35, 445–459. [Google Scholar] [CrossRef]
- Simmons, S.; Dellinger, G.; Lyons, M.; Terfous, A.; Ghenaim, A.; Lubitz, W.D. Effects of Inclination Angle on Archimedes Screw Generator Power Production with Constant Head. J. Hydraul. Eng. 2021, 147. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability 2020, 12, 7352. [Google Scholar] [CrossRef]
- Loots, I.; Dijk, M.V.; Barta, B.; Vuuren, S.V.; Bhagwan, J. A review of low head hydropower technologies and applications in a South African context. Renew. Sustain. Energy Rev. 2015, 50, 1254–1268. [Google Scholar] [CrossRef] [Green Version]
- Waters, S.; Aggidis, G.A. Over 2000 years in review: Revival of the Archimedes Screw from Pump to Turbine. Renew. Sustain. Energy Rev. 2015, 51, 497–505. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, S.S.; Kansal, M.L. Risk based initial cost assessment while planning a hydropower project. Energy Strategy Rev. 2020, 31. [Google Scholar] [CrossRef]
- Intralawan, A.; Smajgl, A.; McConnell, W.; Ahlquist, D.B.; Ward, J.; Kramer, D.B. Reviewing benefits and costs of hydropower development evidence from the Lower Mekong River Basin. Wiley Interdiscip. Rev. Water 2019. [Google Scholar] [CrossRef]
- Ramos, H. Guidelines for Design of Small Hydropower Plants; WREAN (Western Regional Energy Agency & Network) and DED (Department of Economic Development): Belfast, North Ireland, 2000; p. 210. [Google Scholar]
- Castro, R. Uma Introdução às Energias Renováveis: Eólica, Fotovoltaica e Minihídrica, 3rd ed.; IST Press: Palo Alto, CA, USA, 2018. (In Portuguese) [Google Scholar]
- Lashofer, A.; Hawle, W.; Kaltenberger, F.; Pelikan, B. Die Wasserkraftschnecke—Praxis, Prüfstand und Potenzial. Österreichische Wasser-und Abfallwirtschaft 2013, 65, 339–347. [Google Scholar] [CrossRef]
- Ogayar, B.; Vidal, P.G. Cost determination of the electro-mechanical equipment of a small hydro-power plant. Renew. Energy 2009, 34, 6–13. [Google Scholar] [CrossRef]

| Turbine | Qd (m3/s) | P (kW) | E (MWh/year) | Operation (h/year) | V (hm3) | Pipe (k€) | CC (k€) | O&M (k€/year) | Net Revenue (k€/year) | NPV (k€) | PBP (years) | IRR (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AST | 3 | 55 | 282 | 5183 | 55.98 | 50.4 | 160.7 | 0.8 | 23.9 | 137.3 | 8.3 | 13.7 |
| Kaplan | 1 | 22 | 160 | 7326 | 26.37 | 0 | 88.3 | 3.5 | 10.5 | 42.6 | 11.1 | 10.2 |
| Propeller | 1.5 | 33 | 179 | 5479 | 29.58 | 0 | 99.3 | 2.0 | 13.7 | 71.7 | 9.13 | 12.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, P.F.G.; Martins, N.M.C.; Fontes, P.; Covas, D. Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water 2021, 13, 1764. https://doi.org/10.3390/w13131764
Oliveira PFG, Martins NMC, Fontes P, Covas D. Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water. 2021; 13(13):1764. https://doi.org/10.3390/w13131764
Chicago/Turabian StyleOliveira, Pedro F. G., Nuno M. C. Martins, Pedro Fontes, and Dídia Covas. 2021. "Hydroenergy Harvesting Assessment: The Case Study of Alviela River" Water 13, no. 13: 1764. https://doi.org/10.3390/w13131764
APA StyleOliveira, P. F. G., Martins, N. M. C., Fontes, P., & Covas, D. (2021). Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water, 13(13), 1764. https://doi.org/10.3390/w13131764






