PATs Behavior in Pressurized Irrigation Hydrants towards Sustainability
Abstract
1. Introduction
2. Methodology
2.1. Analytical Concept for Irrigation Hydrant
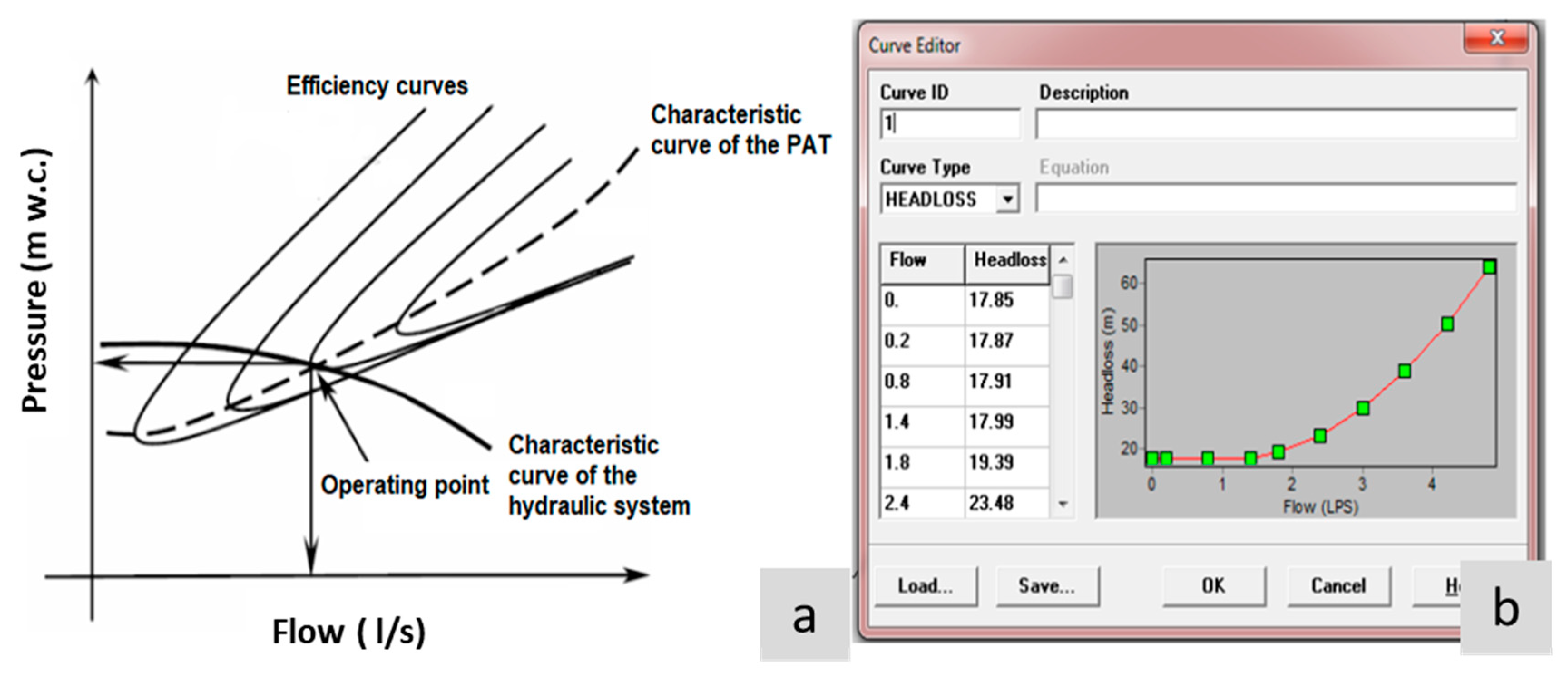
2.2. Mathematical Modeling
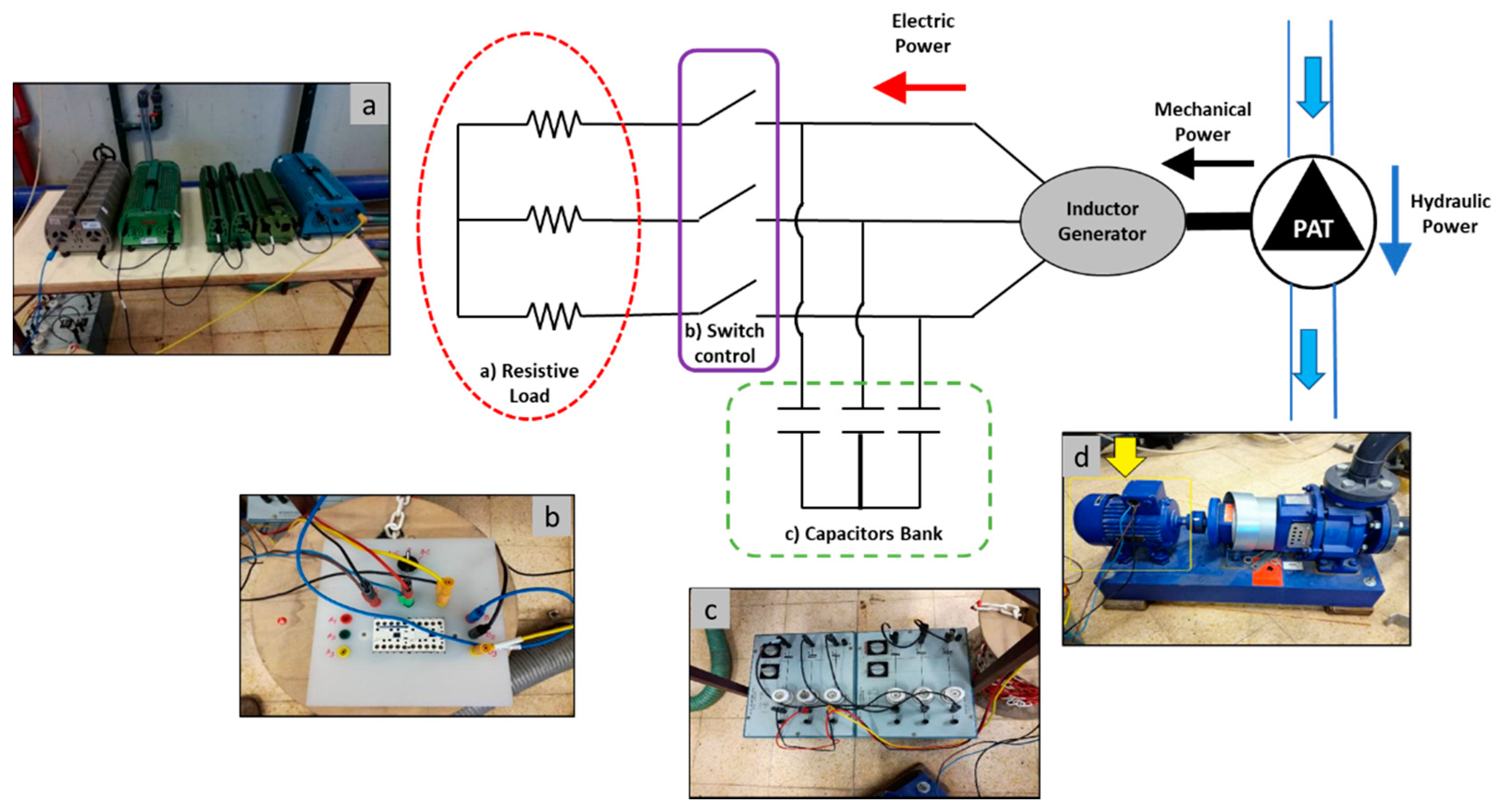
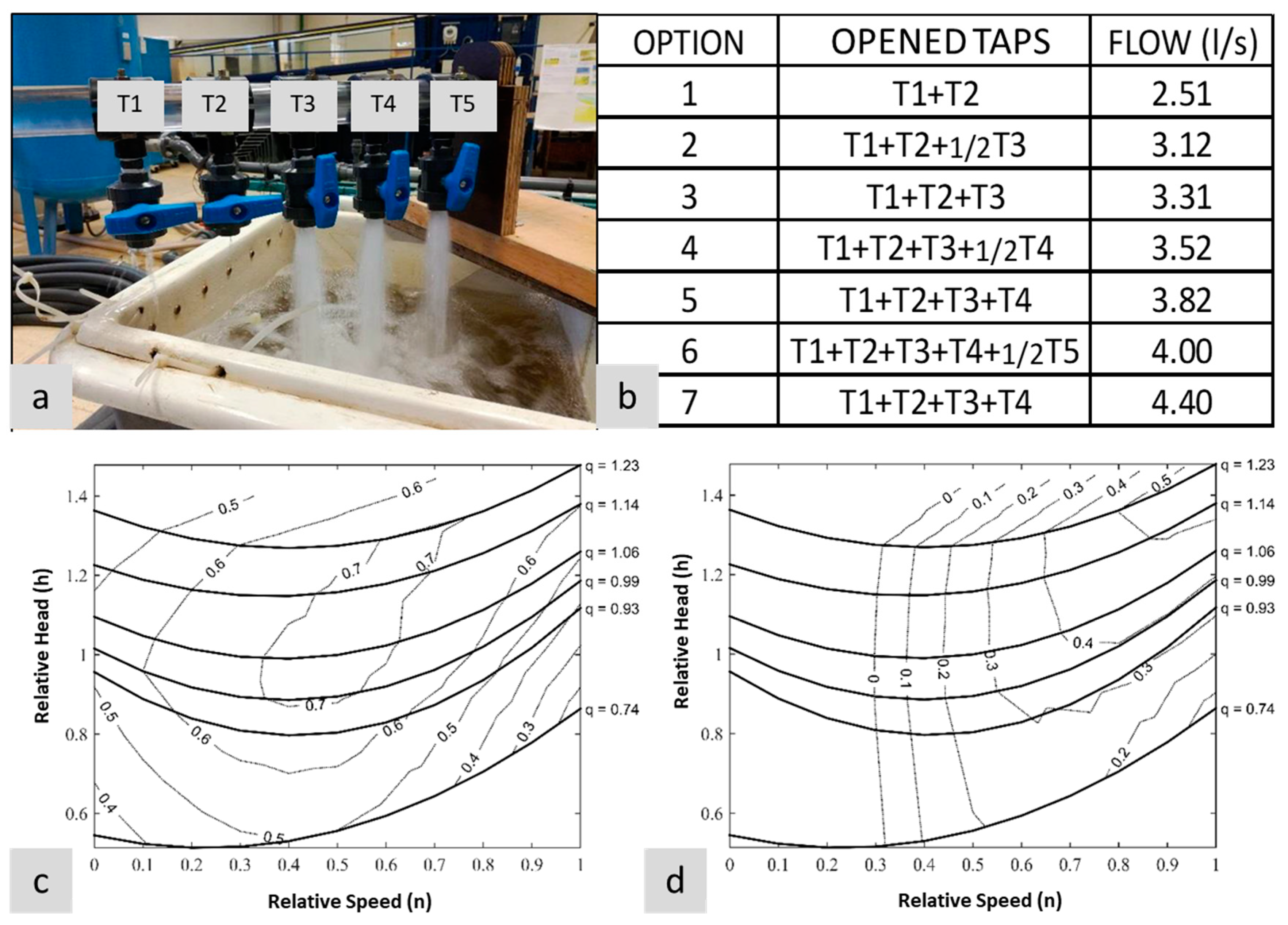
2.3. Experimental Model
2.4. Unsteady Flow Characterization
3. Results and Discussion of the Case Study
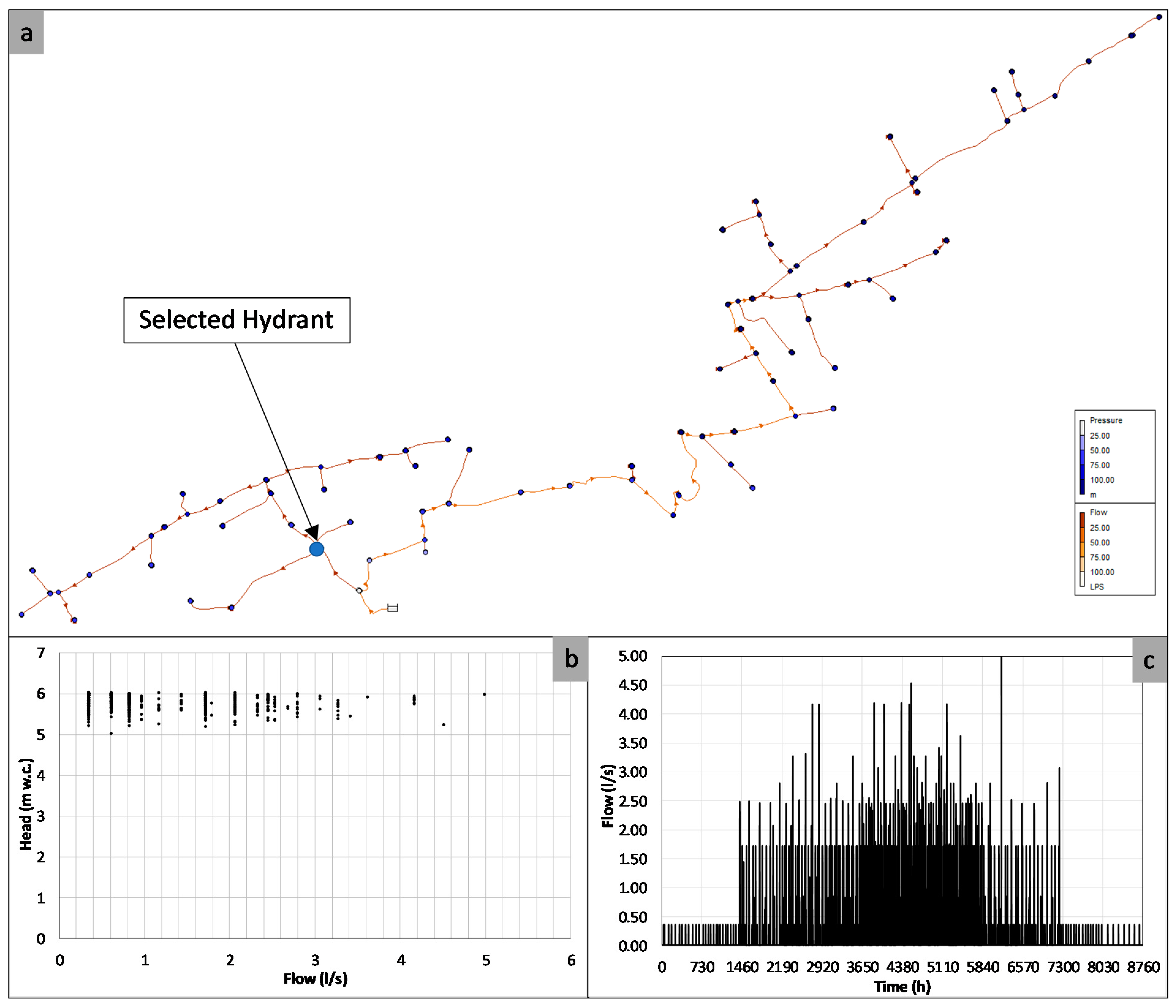
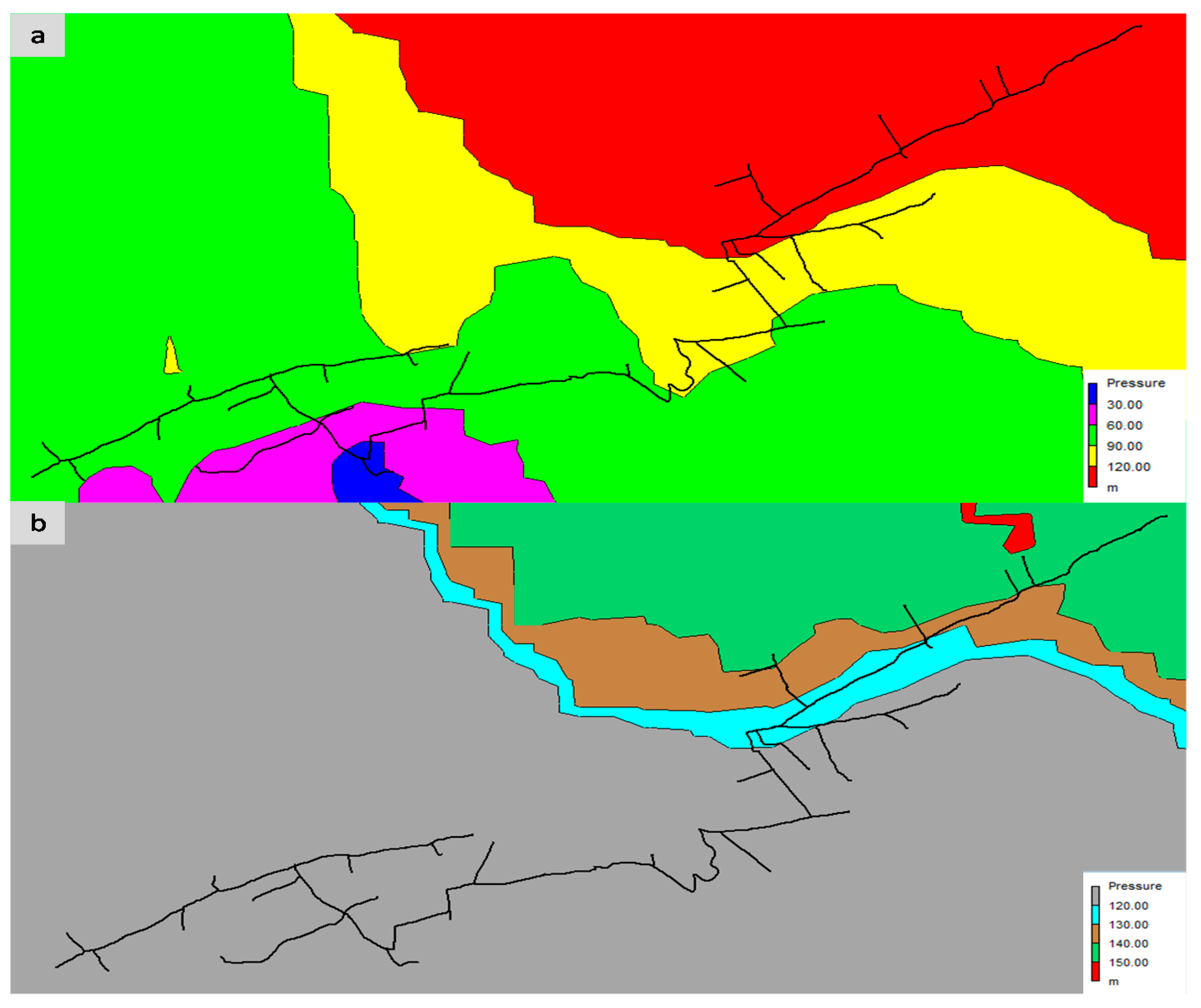
3.1. Irrigation Network and Selected Hydrant
3.2. Model Simulation
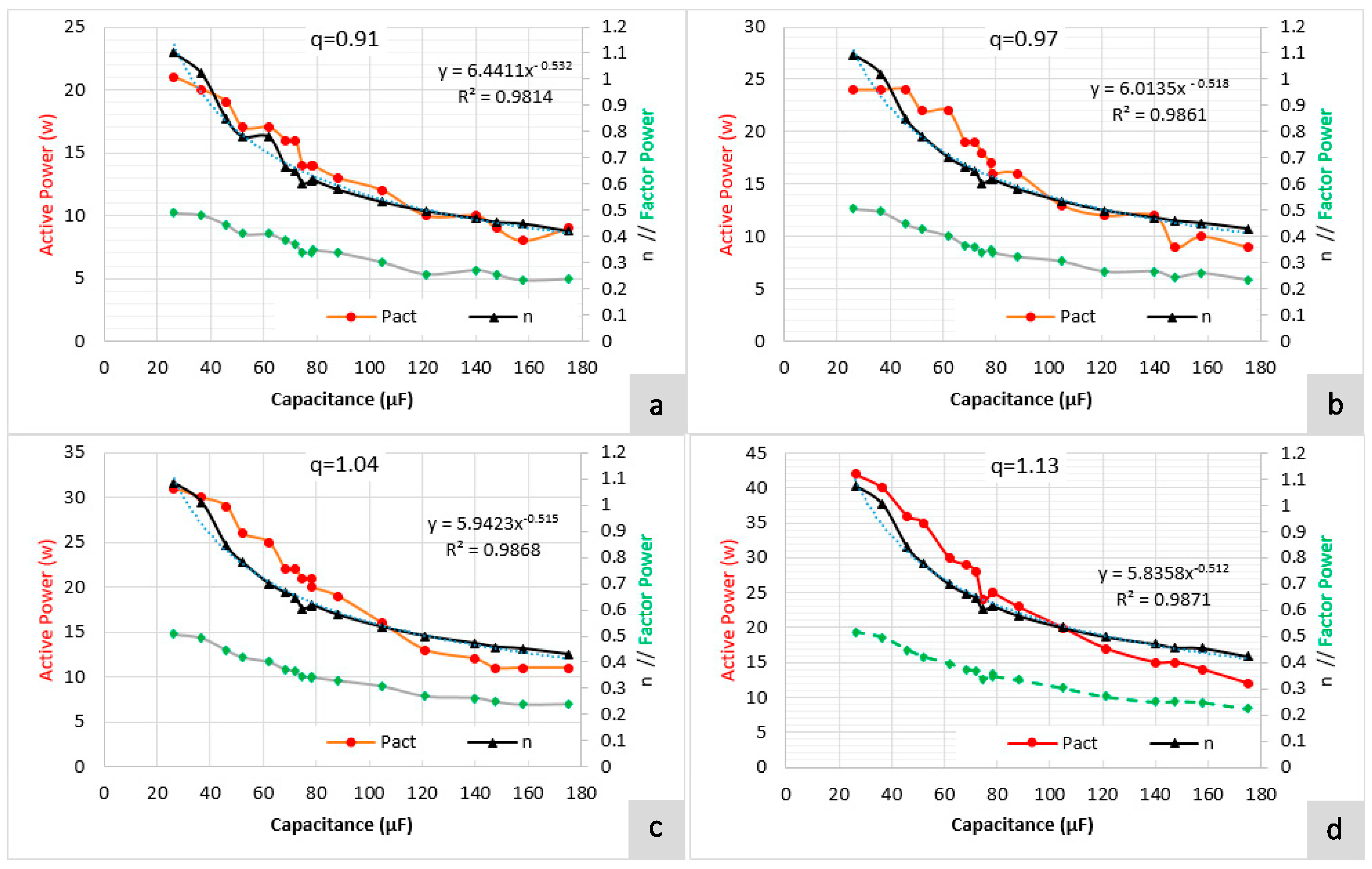
3.3. PAT Pilot Station: Experimental Tests
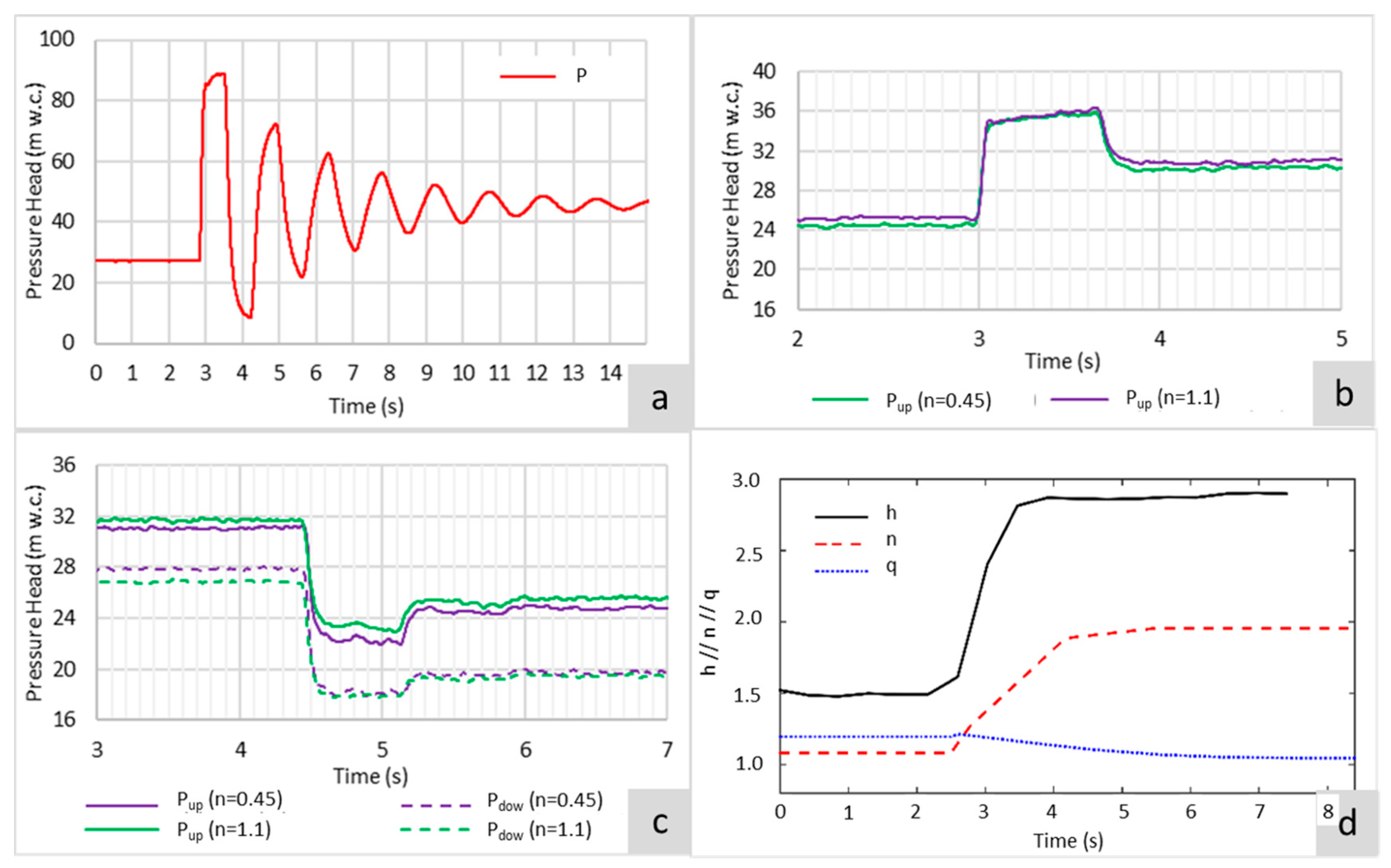
3.4. PAT Pilot Station: Unsteady Experimental Tests
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernard, L. 2020 Statistical Review of World Energy, 69th ed.; BP: London, UK, 2020. [Google Scholar]
- Corcoran, L.; Mcnabola, A.; Coughlan, P. Optimization of Water Distribution Networks for Combined Hydropower Energy Recovery and Leakage Reduction. J. Water Resour. Plan. Manag. 2015, 142, 1–8. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; López-Jiménez, P.; Ramos, H. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Paish, O. Micro-hydropower: Status and prospects. Proc. Inst. Mech. Eng. Part A J. Power Energy 2005, 216, 31–40. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, S.K.; Khatod, D.K. Optimal installation of small hydropower plant—A review. Renew. Sustain. Energy Rev. 2011, 15, 3862–3869. [Google Scholar] [CrossRef]
- Arriaga, M. Pump as turbine—A pico-hydro alternative in Lao People’s Democratic Republic. Renew. Energy 2010, 35, 1109–1115. [Google Scholar] [CrossRef]
- Ahlborg, H.; Sjöstedt, M. Small-scale hydropower in Africa: Socio-technical designs for renewable energy in Tanzanian villages. Energy Res. Soc. Sci. 2015, 5, 20–33. [Google Scholar] [CrossRef]
- Qadir, M.; Boers, T.M.; Schubert, S.; Ghafoor, A.; Murtaza, G. Agricultural water management in water-starved countries: Challenges and opportunities. Agric. Water Manag. 2003, 62, 165–185. [Google Scholar] [CrossRef]
- García Morillo, J.; McNabola, A.; Camacho, E.; Montesinos, P.; Rodríguez Díaz, J.A. Hydro-power energy recovery in pressurized irrigation networks: A case study of an Irrigation District in the South of Spain. Agric. Water Manag. 2018, 204, 17–27. [Google Scholar] [CrossRef]
- García-López, J.; García-Ruiz, R.; Domínguez, J.; Lorite, I.J. Improving the sustainability of farming systems under semi-arid conditions by enhancing crop management. Agric. Water Manag. 2019, 223, 105718. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Postacchini, M.; Darvini, G.; Finizio, F.; Pelagalli, L.; Soldini, L.; Di Giuseppe, E. Hydropower Generation Through Pump as Turbine: Experimental Study and Potential Application to Small-Scale WDN. Water 2020, 12, 958. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; di Nardo, A.; Carravetta, A.; Ramos, H.M.; Adeyeye, K. Zero-net energy management for the monitoring and control of dynamically-partitioned smart water systems. J. Clean. Prod. 2020, 252, 119745. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Experimental characterization of two Pumps As Turbines for hydropower generation. Renew. Energy 2016, 99, 180–187. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Corcoran, L.; Power, C.; Williams, A.P.; Harris, L.; Gallagher, J.; Styles, D. Energy recovery in the water industry using micro-hydropower: An opportunity to improve sustainability. Water Policy 2014, 16, 168–183. [Google Scholar] [CrossRef]
- Capelo, B.; Pérez-Sánchez, M.; Fernandes, J.F.P.; Ramos, H.M.; López-Jiménez, P.A.; Branco, P.J.C. Electrical behaviour of the pump working as turbine in off grid operation. Appl. Energy 2017, 208, 302–311. [Google Scholar] [CrossRef]
- Mirafzal, B.; Skibinski, G.L.; Tallam, R.M. Determination of parameters in the universal induction motor model. IEEE Trans. Ind. Appl. 2009, 45, 142–151. [Google Scholar] [CrossRef]
- Fu, H.Z.; Wang, M.H.; Ho, Y.S. Mapping of drinking water research: A bibliometric analysis of research output during 1992–2011. Sci. Total Environ. 2013, 443, 757–765. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, H.; Robinson, Z.P.; Wang, X.; Wu, J.; Li, X.; Xu, J.; Li, F. Environmental footprint assessment of green campus from a food-water-energy nexus perspective. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2018; Volume 152, pp. 240–246. [Google Scholar] [CrossRef]
- Samora, I.; Franca, M.; Schleiss, A.; Ramos, H. Simulated Annealing in Optimization of Energy Production in a Water Supply Network. Water Resour. Manag. 2016, 30, 1533–1547. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; Ramos, H.; López-Jiménez, P. Modeling Irrigation Networks for the Quantification of Potential Energy Recovering: A Case Study. Water 2016, 8, 234. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M. Methodology for energy efficiency analysis in pressurized irrigation networks: Practical application. Water 2017, 9, 799. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 6th ed.; McGrau-Hill: New York, NY, USA, 2008. [Google Scholar]
- Ramos, H. Simulation and Control of Hydrotransients at Small Hydroelectric Power Plants. Ph.D. Thesis, IST Portugal, Lisboa, Portugal, 1995. [Google Scholar]
- Ramos, H.M.; Borga, A.; Simão, M. Surge damping analysis in pipe systems: Modelling and experiments. J. Hydraul. Res. 2004, 42, 413–425. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. PATs operating in water networks under unsteady flow conditions: Control valve manoeuvre and overspeed effect. Water 2018, 10, 529. [Google Scholar] [CrossRef]
- Lin, T.; Zhu, Z.; Li, X.; Li, J.; Lin, Y. Theoretical, experimental, and numerical methods to predict the best efficiency point of centrifugal pump as turbine. Renew. Energy 2021, 168, 31–44. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Riasi, A.; Kandi, A. Selection optimization of variable speed pump as turbine (PAT) for energy recovery and pressure management. Energy Convers. Manag. 2021, 227, 113586. [Google Scholar] [CrossRef]
- Gallagher, J.; Harris, I.M.; Packwood, A.J.; McNabola, A.; Williams, A.P. A strategic assessment of micro-hydropower in the UK and Irish water industry: Identifying technical and economic constraints. Renew. Energy 2015, 81, 808–815. [Google Scholar] [CrossRef]
- Bousquet, C.; Samora, I.; Manso, P.; Rossi, L.; Heller, P.; Schleiss, A.J. Assessment of hydropower potential in wastewater systems and application to Switzerland. Renew. Energy 2017, 113, 64–73. [Google Scholar] [CrossRef]
- Obaid, W.; Hamid, A.K.; Ghenai, C. Solar/wind pumping system with forecasting in Sharjah, United Arab Emirates. Int. J. Electr. Comput. Eng. 2021, 11, 2088–8708. [Google Scholar]
- Nikolić, M.; Mršević, D.; Ristić, L.; Čantrak, Đ.; Janković, N. Induction Machine Driven Pump Applied as Turbine in Micro-hydro Power Plants. In Proceedings of the 2021 6th International Symposium on Environment-Friendly Energies and Applications (EFEA), Sofia, Bulgaria, 24–26 March 2021; IEEE: Piscataway Township, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Mitrovic, D.; Chacón, M.C.; García, A.M.; Morillo, J.G.; Diaz, J.A.R.; Ramos, H.M.; McNabola, A. Multi-Country Scale Assessment of Available Energy Recovery Potential Using Micro-Hydropower in Drinking, Pressurised Irrigation and Wastewater Networks, Covering Part of the EU. Water 2021, 13, 899. [Google Scholar] [CrossRef]
- Duan, H.-F.; Ghidaoui, M.; Pedro, J.; Lee, Y.-K.T. Unsteady friction and visco-elasticity in pipe fluid transients. J. Hydraul. Res. 2010, 48, 354–362. [Google Scholar] [CrossRef]



| HYDRANT | ERT | HYDRANT | ERT | HYDRANT | ERT | HYDRANT | ERT |
|---|---|---|---|---|---|---|---|
| MWh/year | MWh/year | MWh/year | MWh/year | ||||
| H024 | 1.99 | H044 | 5.6 | H066 | 0.13 | H086 | 0.48 |
| H025 | 1.56 | H045 | 16.12 | H067 | 0.22 | H087 | 0.27 |
| H026 | 0.48 | H046 | 5.14 | H070 | 1.4 | H088 | 0.51 |
| H027 | 1.92 | H047 | 5.03 | H071 | 0.4 | H089 | 0.73 |
| H028 | 0.12 | H048 | 13.37 | H072 | 0.28 | H090 | 0.59 |
| H029 | 2.27 | H049 | 0.26 | H073 | 0.22 | H100 | 0.89 |
| H030 | 0.77 | H050 | 1.93 | H074 | 0.64 | H101 | 1.05 |
| H031 | 1.36 | H051 | 2.67 | H075 | 0.31 | H123 | 1.78 |
| H032 | 3.94 | H052 | 0.86 | H076 | 1.34 | H126 * | 0.13 |
| H033 | 4.19 | H053 | 11.05 | H077 | 0.52 | H140 | 0.73 |
| H035 | 3.57 | H055 | 0.04 | H078 | 3.68 | H148 | 0.32 |
| H036 | 2.5 | H056 | 0.01 | H079 | 0.76 | H152 | 2.47 |
| H037 | 1.12 | H057 | 0.55 | H080 | 1.41 | H188 | 2.81 |
| H038 | 3.54 | H058 | 0.99 | H081 | 0.4 | H200 | 1.35 |
| H039 | 0.64 | H059 | 0.46 | H082 | 1.28 | H201 | 1.58 |
| H040 | 3.57 | H062 | 2.32 | H083 | 0.87 | H202 | 2.08 |
| H042 | 33.73 | H064 | 0.22 | H084 | 0.8 | - | - |
| H043 | 9.13 | H065 | 0.8 | H085 | 1.5 | - | - |
| n | Resistive Load (Ω) | |||
|---|---|---|---|---|
| 120 | 150 | 200 | 600 | |
| 0.5 | 241.06 | 190.90 | 149.44 | 127.02 |
| 0.6 | 167.40 | 130.01 | 103.08 | 86.55 |
| 0.7 | 122.99 | 93.95 | 75.30 | 62.58 |
| 0.8 | 94.16 | 70.91 | 57.37 | 47.25 |
| 0.9 | 74.40 | 55.33 | 45.13 | 36.88 |
| 1.0 | 60.27 | 44.31 | 36.41 | 29.55 |
| 1.1 | 49.81 | 36.25 | 29.99 | 24.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Sánchez, M.; Fernandes, J.F.P.; Branco, P.J.C.; López-Jiménez, P.A.; Ramos, H.M. PATs Behavior in Pressurized Irrigation Hydrants towards Sustainability. Water 2021, 13, 1359. https://doi.org/10.3390/w13101359
Pérez-Sánchez M, Fernandes JFP, Branco PJC, López-Jiménez PA, Ramos HM. PATs Behavior in Pressurized Irrigation Hydrants towards Sustainability. Water. 2021; 13(10):1359. https://doi.org/10.3390/w13101359
Chicago/Turabian StylePérez-Sánchez, Modesto, João F. P. Fernandes, P. J. Costa Branco, P. Amparo López-Jiménez, and Helena M. Ramos. 2021. "PATs Behavior in Pressurized Irrigation Hydrants towards Sustainability" Water 13, no. 10: 1359. https://doi.org/10.3390/w13101359
APA StylePérez-Sánchez, M., Fernandes, J. F. P., Branco, P. J. C., López-Jiménez, P. A., & Ramos, H. M. (2021). PATs Behavior in Pressurized Irrigation Hydrants towards Sustainability. Water, 13(10), 1359. https://doi.org/10.3390/w13101359










