Numerical Model of Leachate Recirculation in Bioreactor Landfills with High Kitchen Waste Content
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hydro–Biochem–Mechanical-Coupled Model
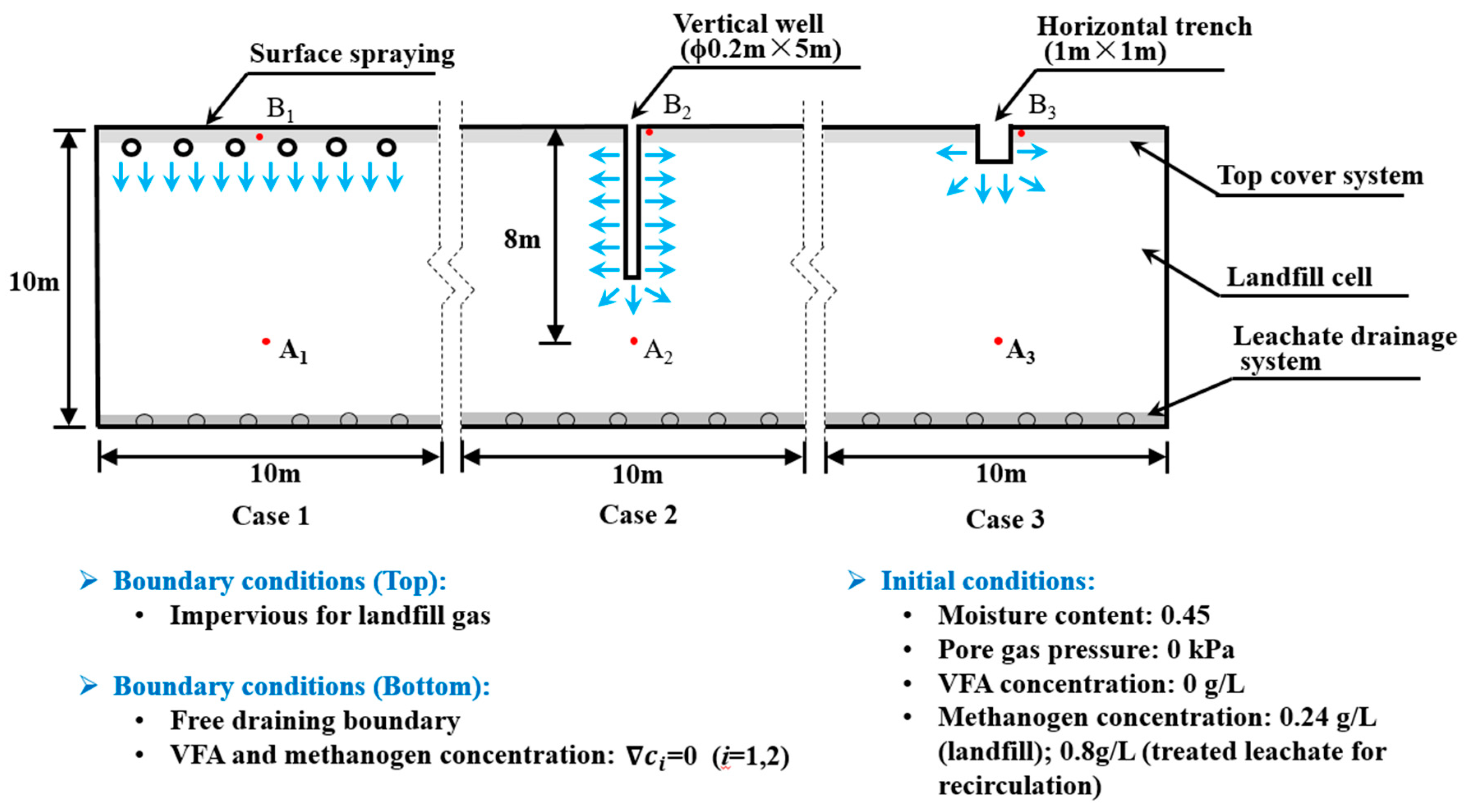
2.2. Numerical Cases of Leachate Recirculation in a Typical Kitchen-Waste-Rich Bioreactor Landfill Cell
3. Results and Discussion
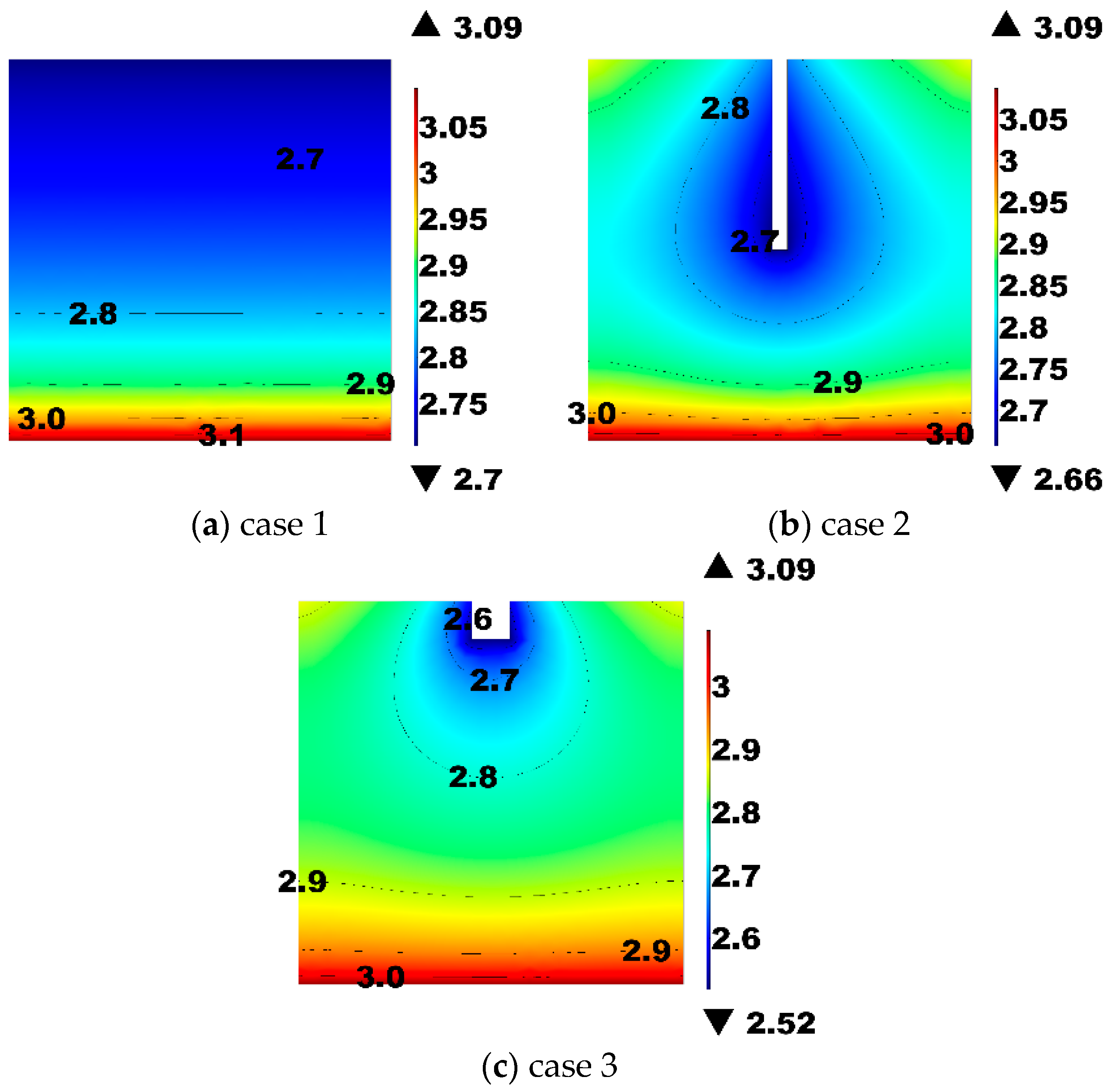
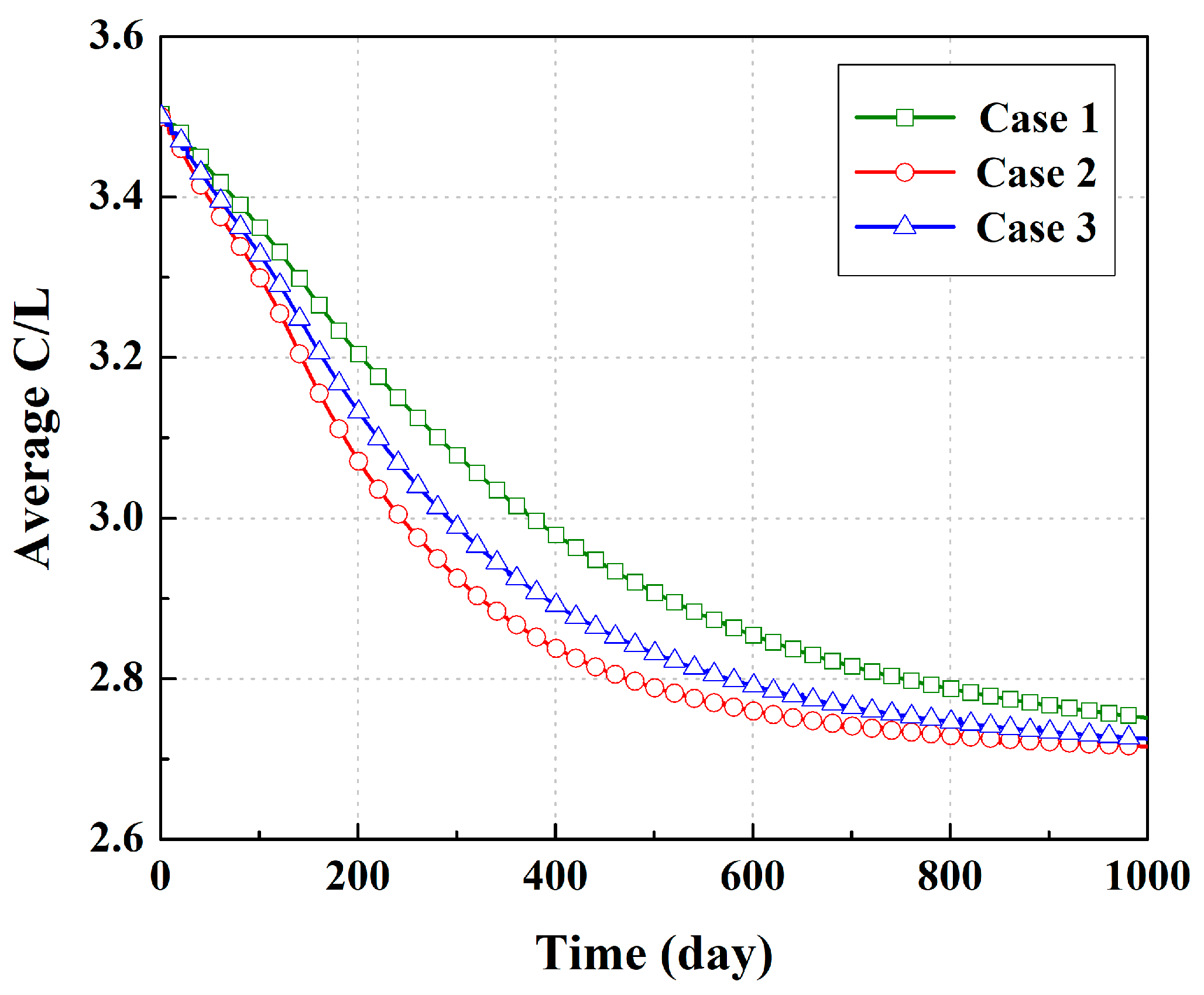
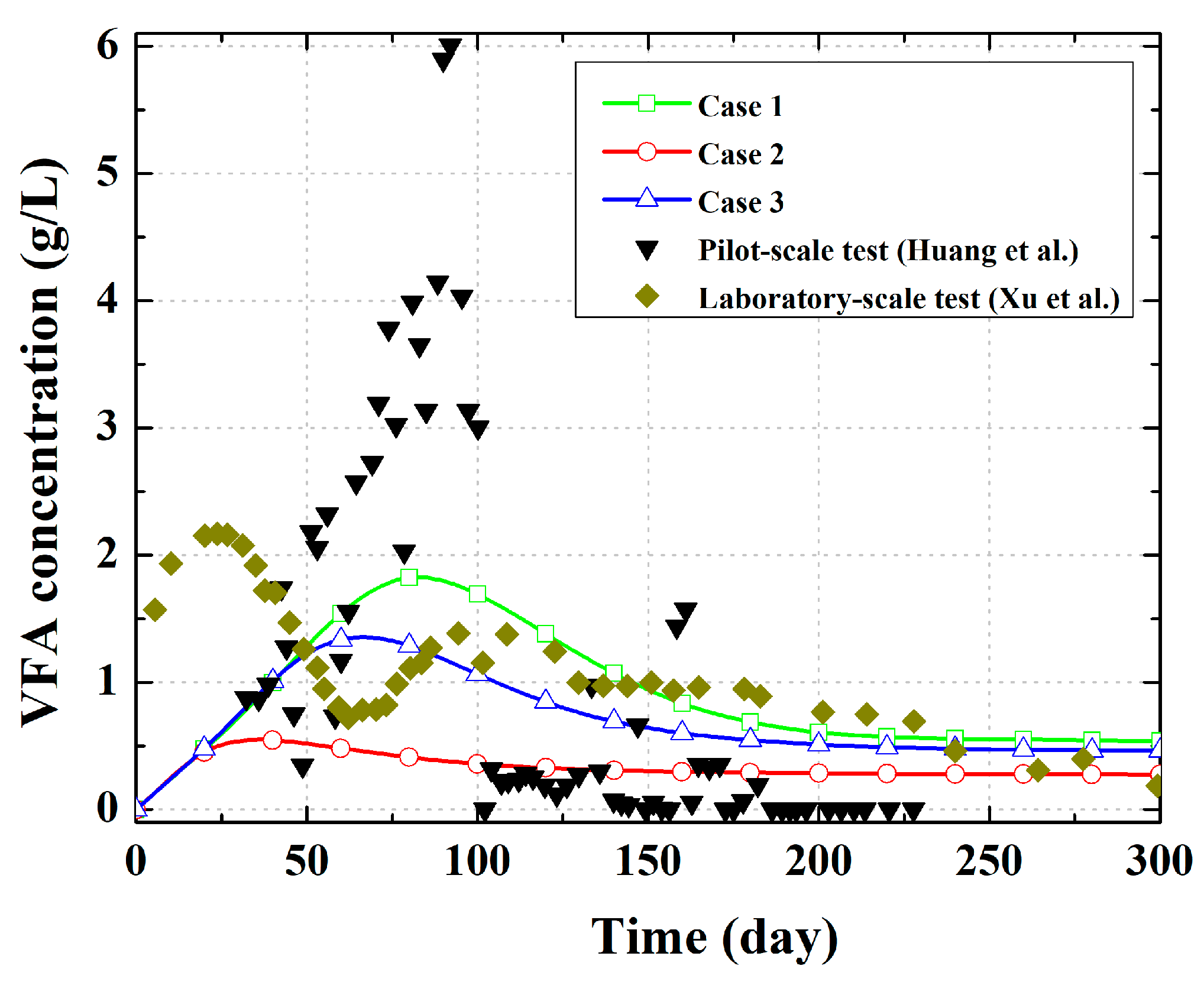
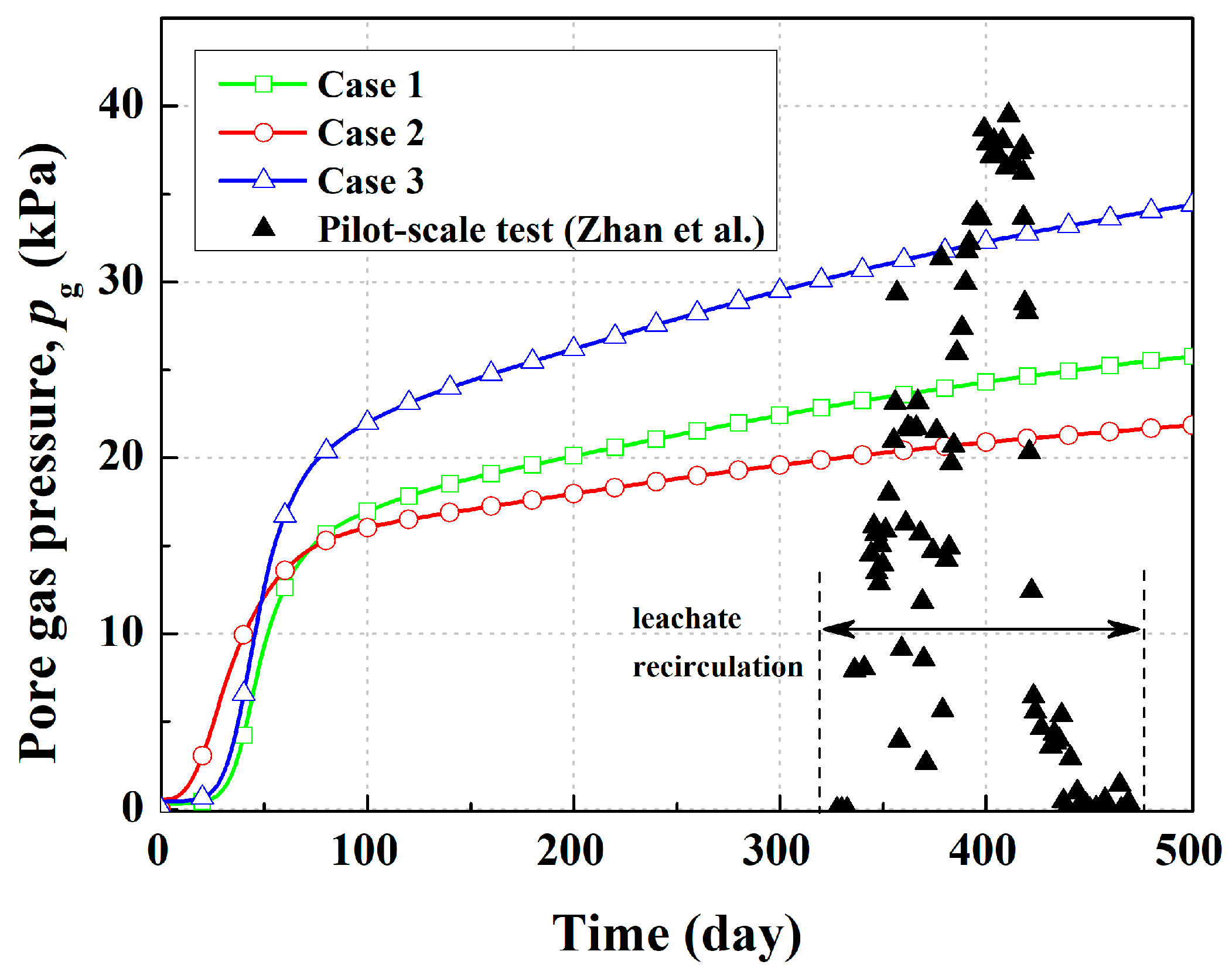
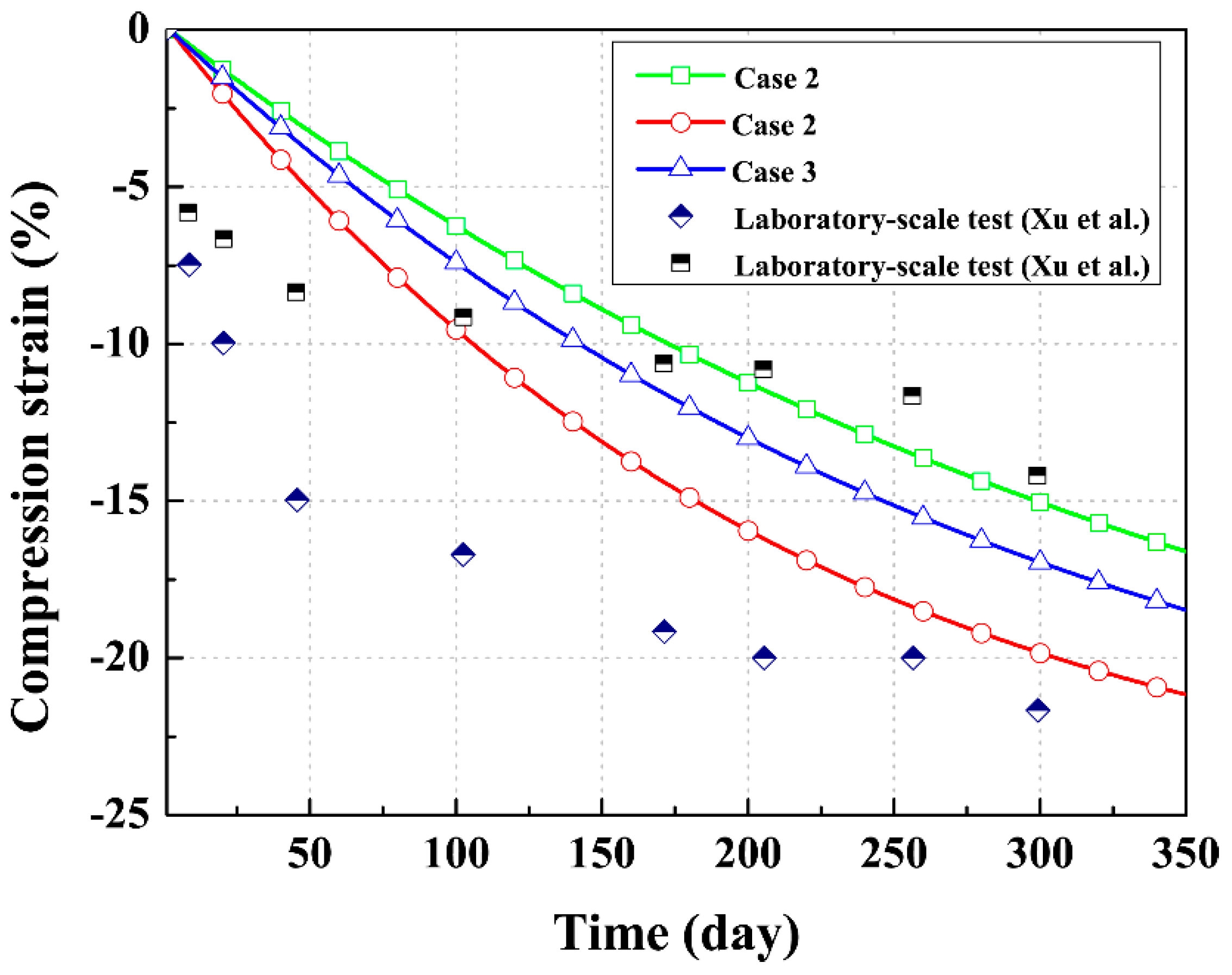
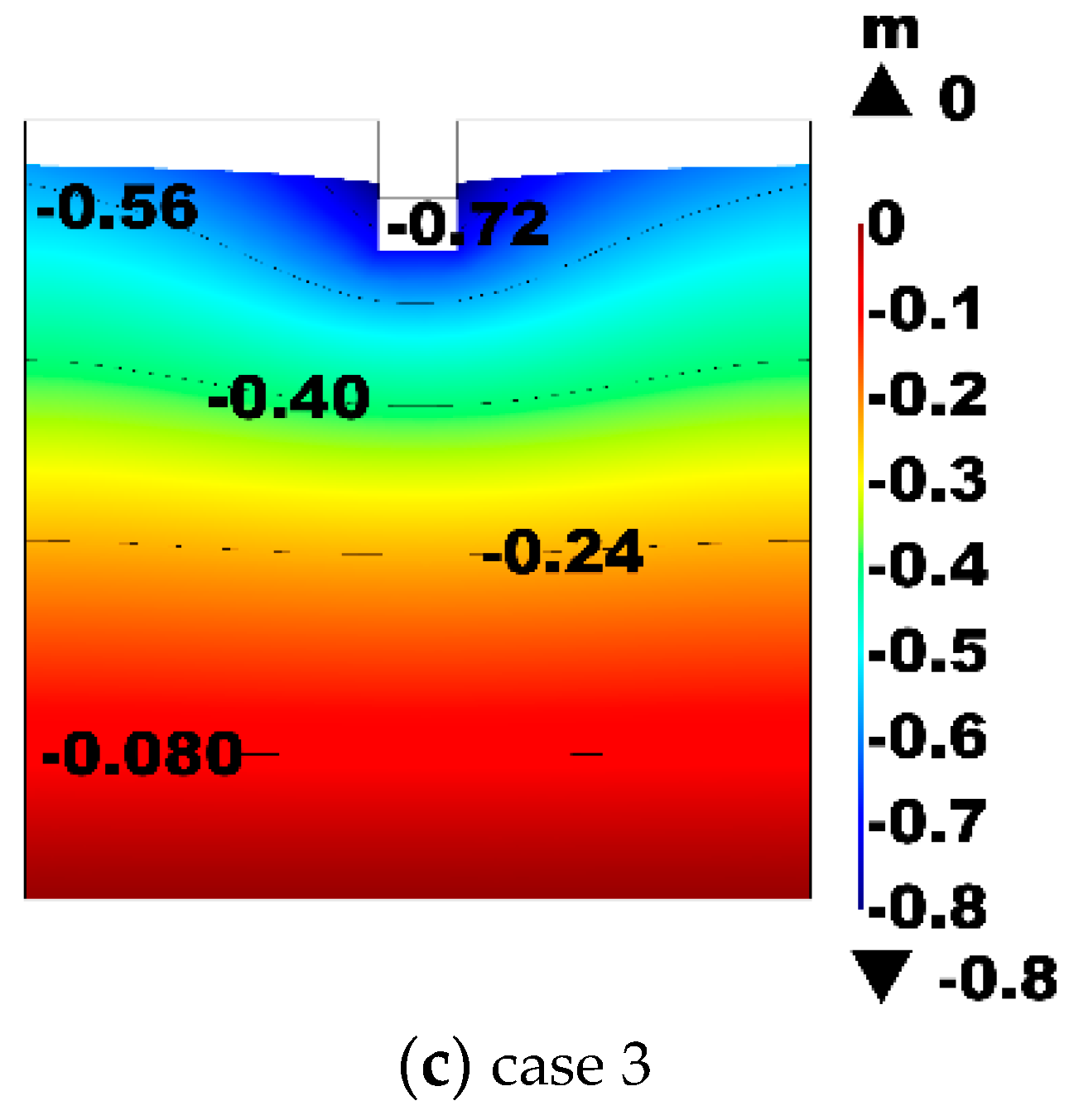
3.1. Acceleration of Landfill Stabilization Process
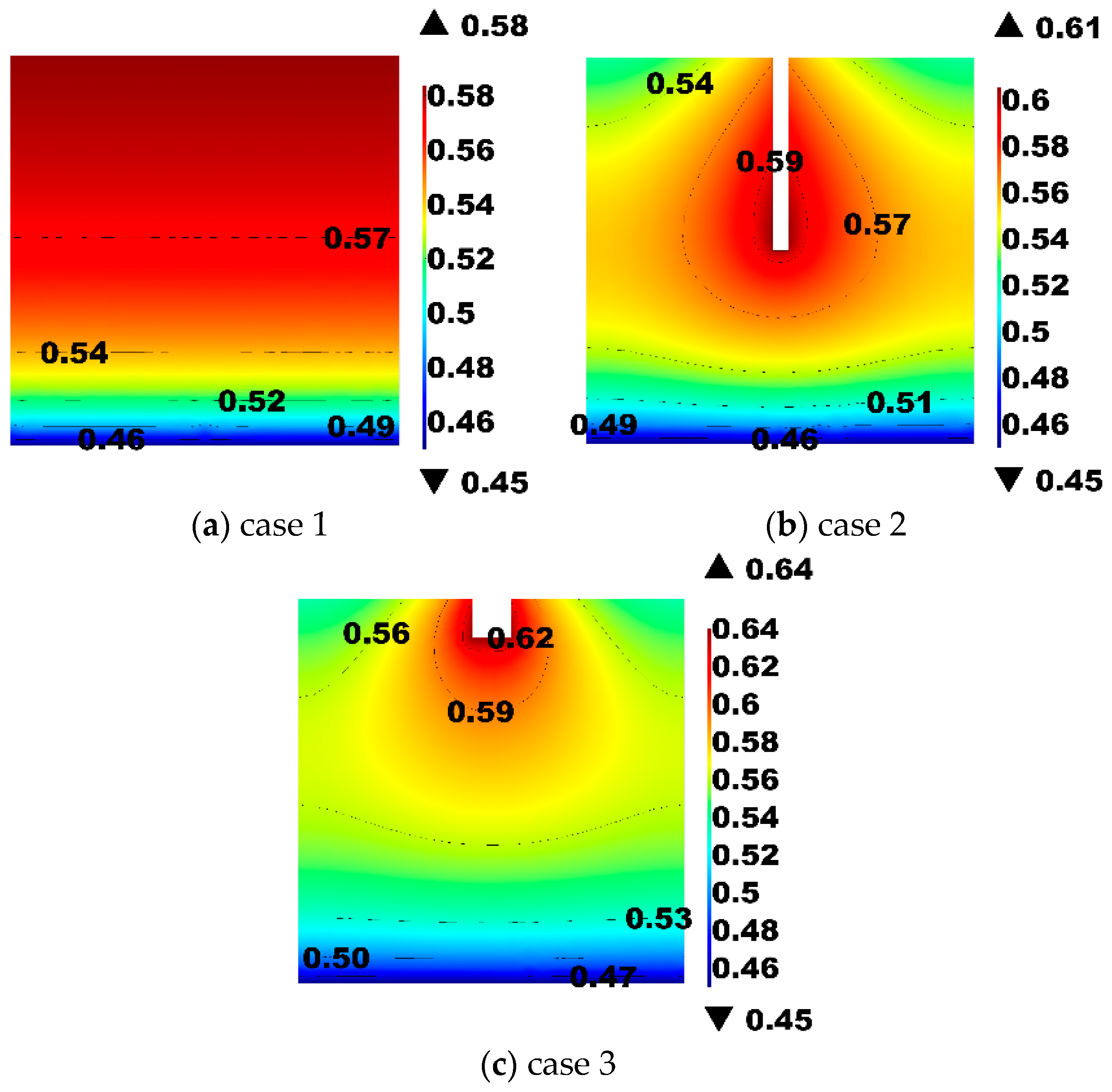
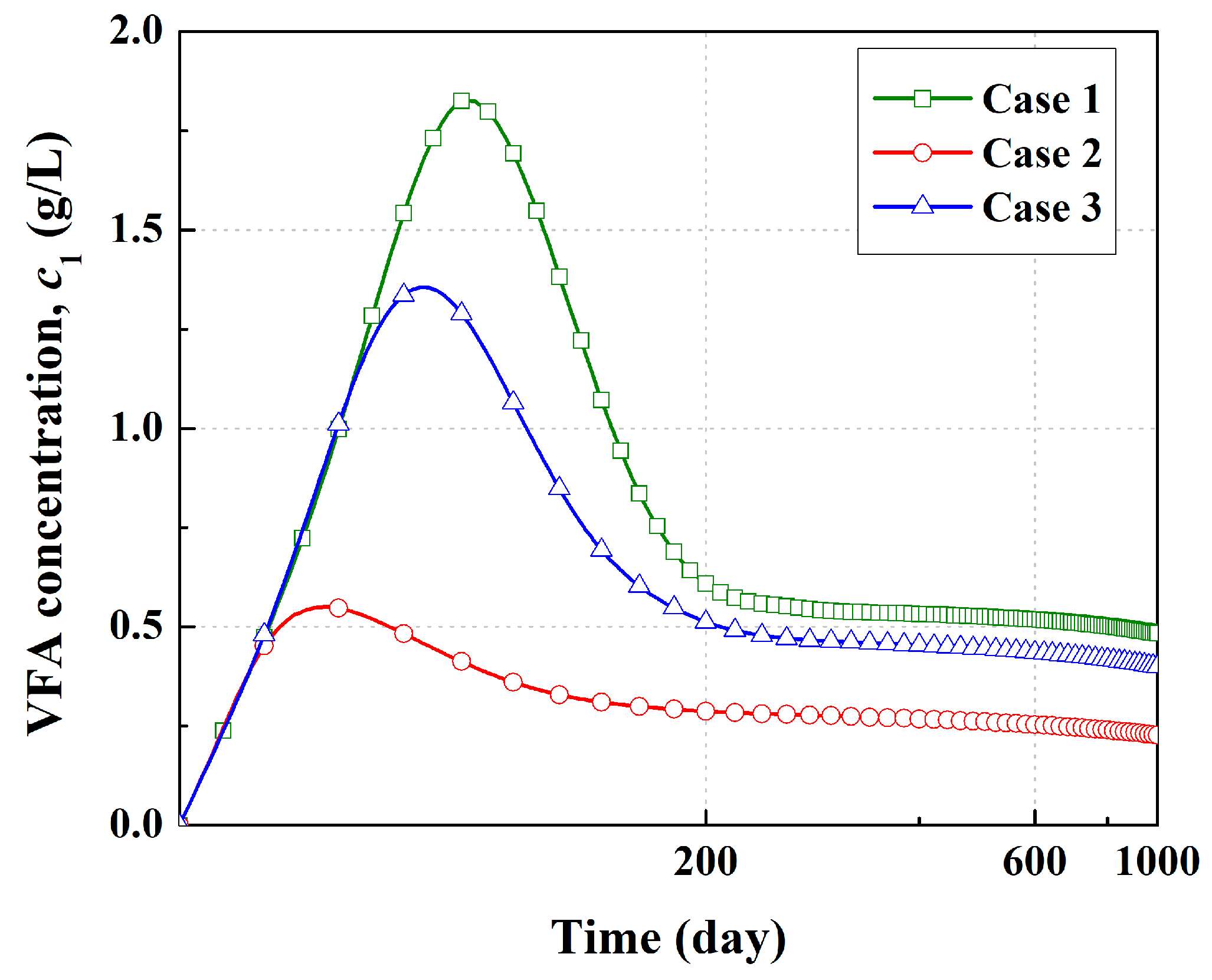
3.2. Moisture Distribution in Landfill Cell and Removal of VFA in Leachate
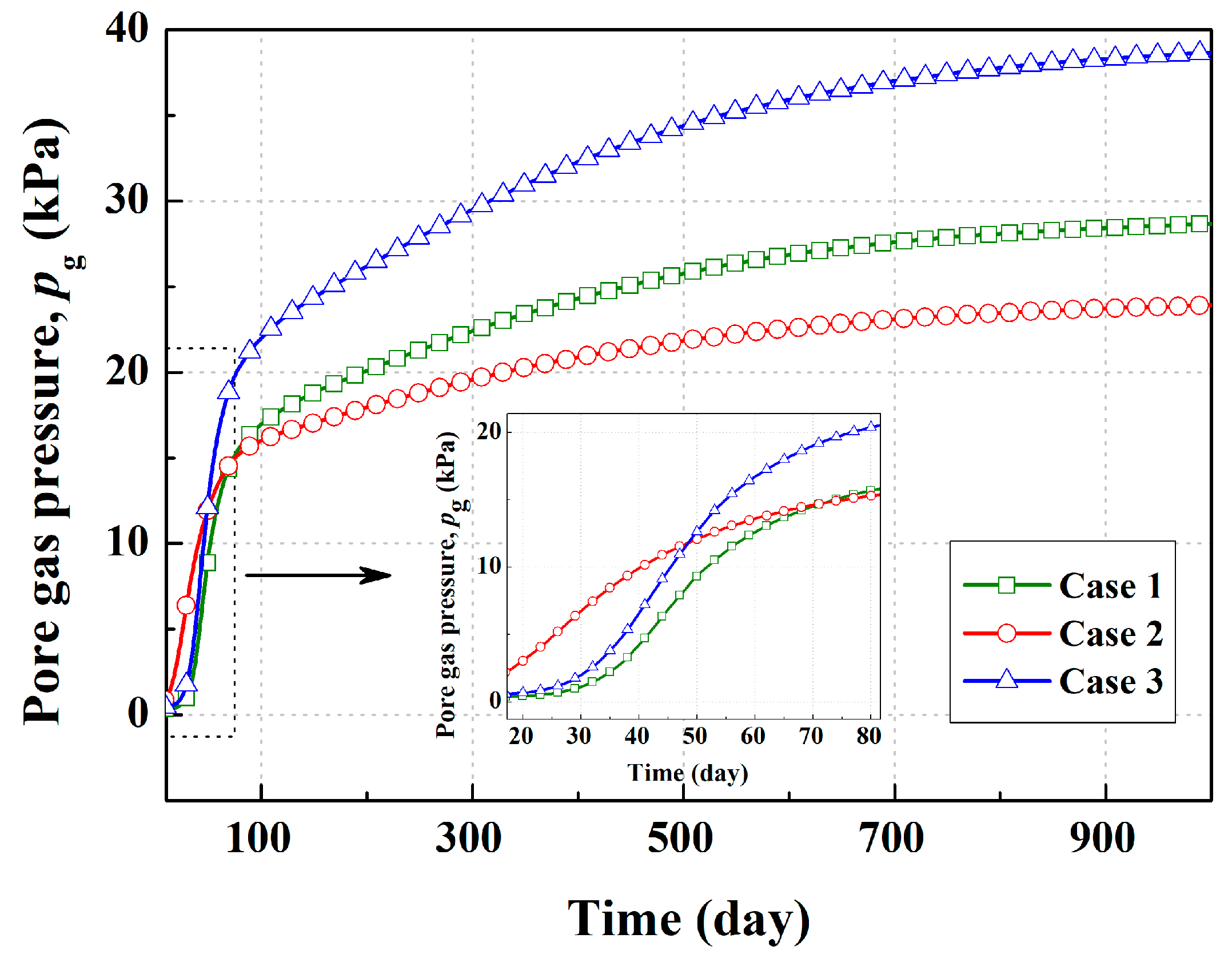
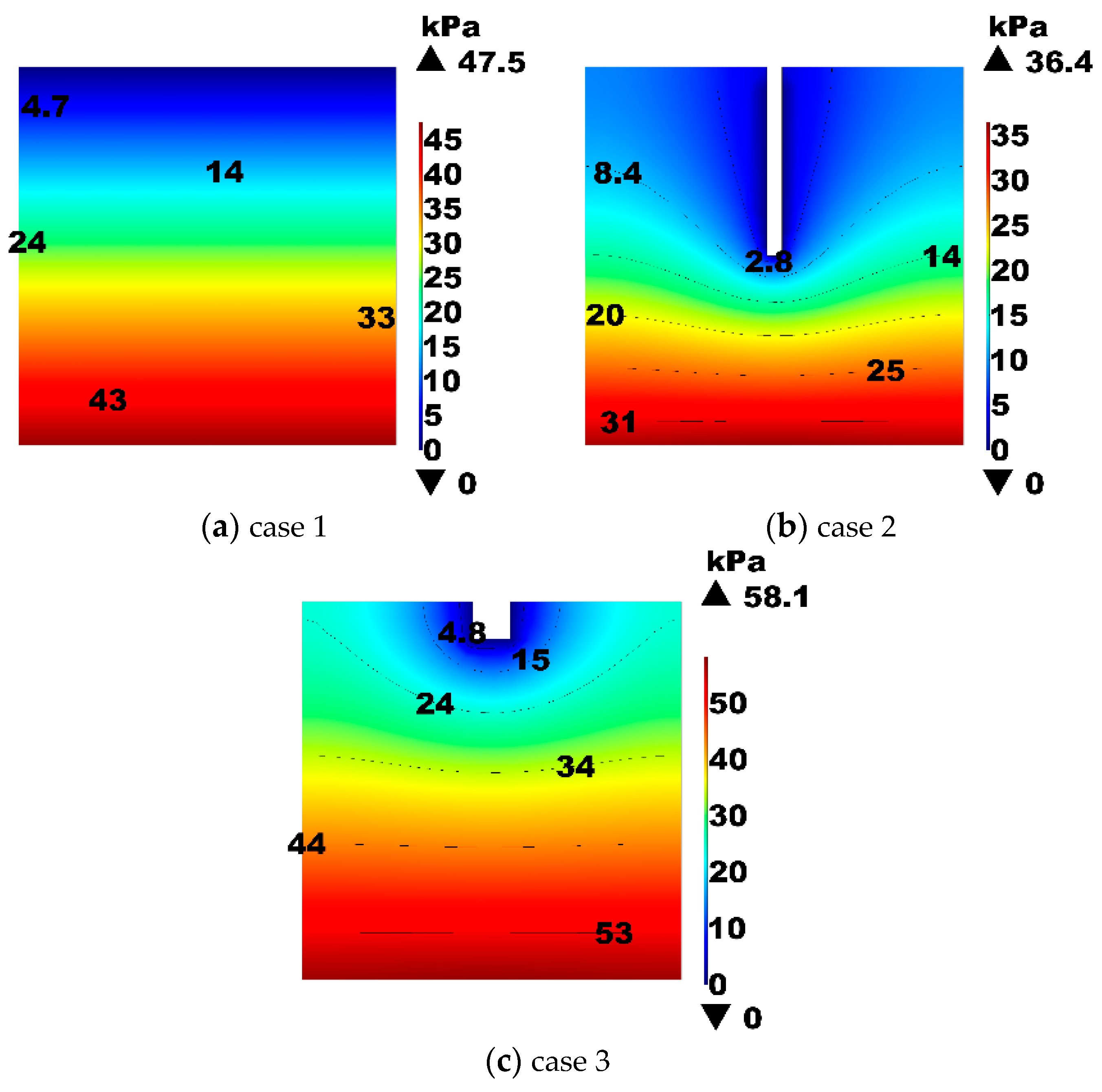
3.3. Landfill Gas Generation
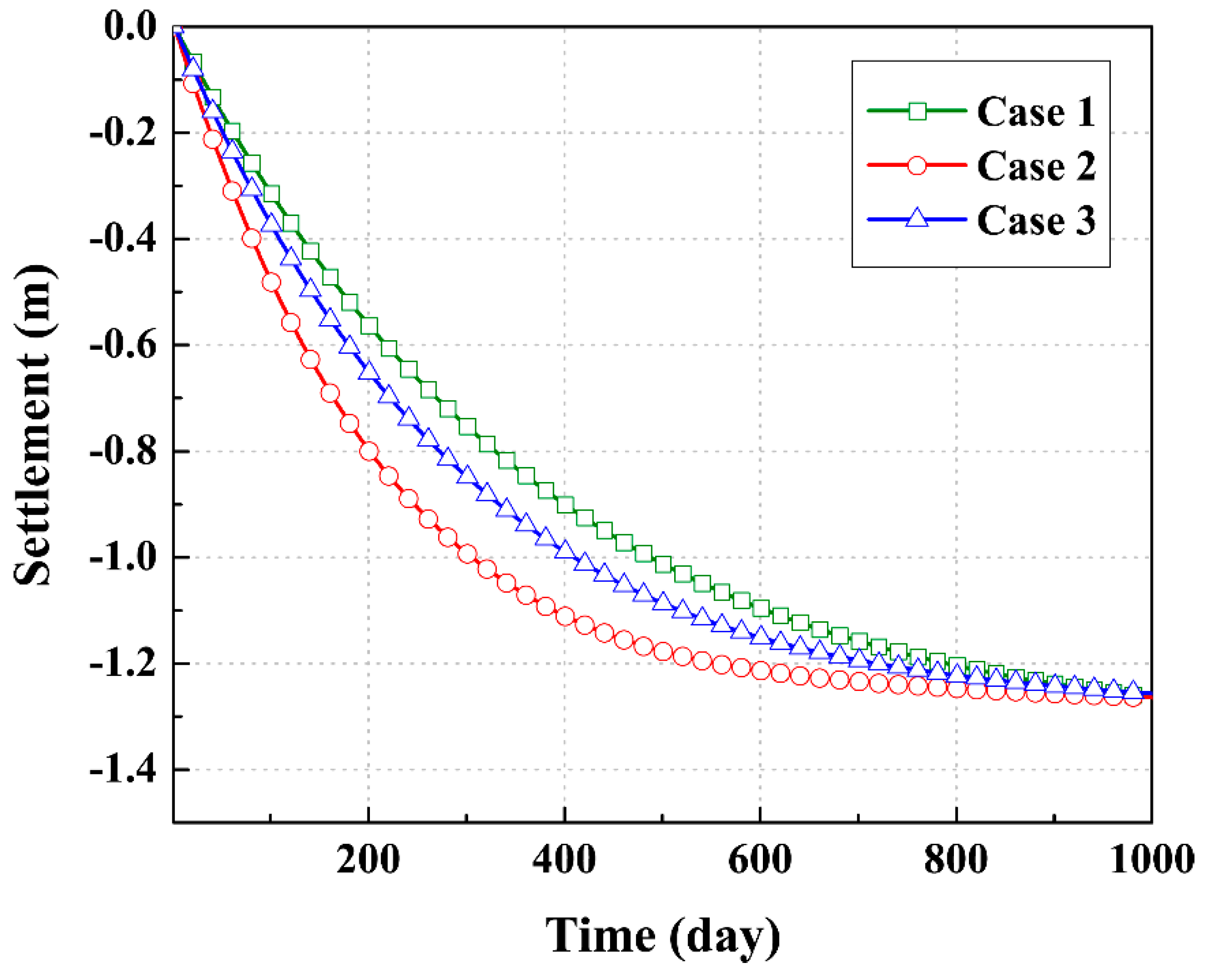
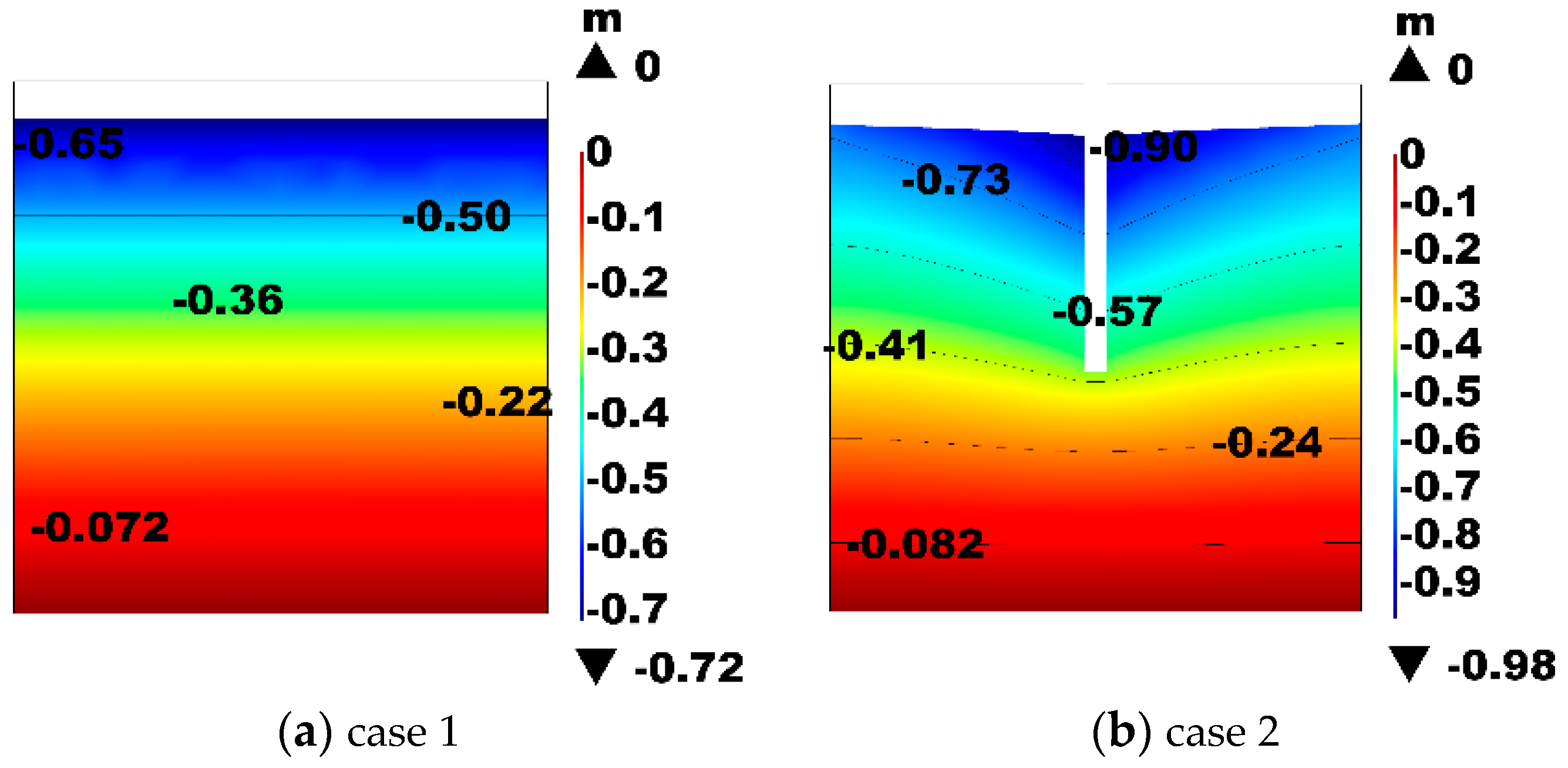
3.4. Settlement of Landfill Cells
4. Conclusions
- (1)
- The coupled model proposed in this study can well consider the hydraulic behaviors of LR in a BL by considering the fast hydrolysis of kitchen waste and leachate generation due to intraparticle water release at the early stage of the stabilization process. This model enables the investigation of the distribution of leachate and gas in a landfill, providing useful information for the design of the LR system in bioreactor landfills.
- (2)
- Recirculation of leachate has significant effects on accelerating the decomposition of MSW with high kitchen waste content, which can also remove VFA in leachate, promote landfill gas generation, and increase the early settlement in landfills. However, leachate recirculation may lead to a significant increase in pore gas pressure and obvious differential settlement in landfills. Active air extraction and reinforcement of landfill infrastructures are recommended to avoid the adverse effects of LR.
- (3)
- When the daily amount of leachate injection is certain, the vertical well can mitigate the rapid accumulation of pore gas pressure in the landfill during the stable period of landfill gas generation but has the fastest settlement rate, compared to the surface spraying and horizontal trench. The closer MSW is to the LR system, the more obvious the effect will be of the leachate injection.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Laner, D.; Crest, M.; Scharff, H.; Morris, J.W.; Barlaz, M.A. A review of approaches for the long–term management of municipal solid waste landfills. Waste Manag. 2012, 32, 498–512. [Google Scholar] [CrossRef]
- Rich, C.; Gronow, J.; Voulvoulis, N. The potential for aeration of MSW landfills to accelerate completion. Waste Manag. 2008, 28, 1039–1048. [Google Scholar] [CrossRef]
- Zhan, L.T.; Xu, H.; Chen, Y.M. Biochemical, hydrological and mechanical behaviors of high food waste content MSW landfill, preliminary findings from a large–scale experiment. Waste Manag. 2017, 63, 27–40. [Google Scholar] [CrossRef]
- Hussain, E.; Al–Ameen, J. Effect of Leachate Recirculation on Biological Stability of Municipal Solid Waste Under Simi–Arid Conditions. Al–Qadisiyah J. Eng. Sci. 2019, 12, 79–83. [Google Scholar] [CrossRef] [Green Version]
- Ritter, W.F. The History and Challenges of Wastewater Reuse in Delaware and Maryland. In Proceedings of the World Environmental and Water Resources Congress 2020: Water Resources Planning and Management and Irrigation and Drainage, Reston, VA, USA, 17–21 May 2020; pp. 109–120. [Google Scholar]
- Cui, C.Y.; Meng, K.; Xu, C.S. Analytical solution for longitudinal vibration of a floating pile in saturated porous media based on a fictitious saturated soil pile model. Comput. Geotech. 2021, 131, 103942. [Google Scholar] [CrossRef]
- Bilgili, M.S.; Demir, A.; Özkaya, B. Influence of leachate recirculation on aerobic and anaerobic decomposition of solid wastes. J. Hazard. Mater. 2007, 143, 177–183. [Google Scholar] [CrossRef] [PubMed]
- Sohoo, I.; Ritzkowski, M.; Kuchta, K. Influence of moisture content and leachate recirculation on oxygen consumption and waste stabilization in post aeration phase of landfill operation. Sci. Total Environ. 2021, 773, 145584. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Sun, X.; Zhao, Y. Comparison of semi–aerobic and anaerobic degradation of refuse with recirculation after leachate treatment by aged refuse bioreactor. Waste Manag. 2011, 31, 1202–1209. [Google Scholar] [CrossRef]
- White, J.K.; Beaven, R.P.; Powrie, W. Leachate recirculation in a landfill, Some insights obtained from the development of a simple 1–D model. Waste Manag. 2011, 31, 1210–1221. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Kim, S.; Baek, S. Acceleration of aged–landfill stabilization by combining partial nitrification and leachate recirculation, A field–scale study. J. Hazard. Mater. 2015, 285, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Barlaz, M.A.; Ham, R.K.; Schaefer, D.M. Microbial, chemical and methane production characteristics of anaerobically decomposed refuse with and without leachate recycling. Waste Manag. Res. 1992, 10, 257–267. [Google Scholar] [CrossRef]
- Chan, G.Y.S.; Chu, L.M.; Wong, M.H. Effects of leachate recirculation on biogas production from landfill co–disposal of municipal solid waste, sewage sludge and marine sediment. Environ. Pollut. 2002, 118, 393–399. [Google Scholar] [CrossRef]
- Mehta, R.; Barlaz, M.A.; Yazdani, R. Refuse decomposition in the presence and absence of leachate recirculation. J. Environ. Eng. 2002, 128, 228–236. [Google Scholar] [CrossRef]
- Demir, A.; Bilgili, M.S.; Ozkaya, B. Effect of leachate recirculation on refuse decomposition rates at landfill site, a case study. Int. J. Environ. Pollut. 2004, 21, 175–187. [Google Scholar] [CrossRef]
- Meng, K.; Cui, C.Y.; Liang, Z.M. A new approach for longitudinal vibration of a large-diameter floating pipe pile in vis-co-elastic soil considering the three-dimensional wave effects. Comput. Geotech. 2020, 128, 103840. [Google Scholar] [CrossRef]
- Chen, G.; Sun, Y.; Xu, Z. Assessment of Shallow Groundwater Contamination Resulting from a Municipal Solid Waste Landfill—A Case Study in Lianyungang, China. Water 2019, 11, 2496. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.; Liu, D.; Chen, W. Impact of landfill density on transport and hydraulic characteristics of recirculated leachate. Environ. Technol. 2019, 40, 2310–2316. [Google Scholar] [CrossRef] [PubMed]
- Top, S.; Akkaya, G.K.; Demir, A. Investigation of Leachate Characteristics in Field–Scale Landfill Test Cells. Int. J. Environ. Res. 2019, 13, 829–842. [Google Scholar] [CrossRef]
- Feng, S.J.; Cao, B.Y.; Xie, H.J. Modeling of leachate recirculation using spraying–vertical well systems in bioreactor landfills. Int. J. Geomech. 2017, 17, 04017012. [Google Scholar] [CrossRef]
- Townsend, T.G.; Wise, W.R.; Jain, P. One–dimensional gas flow model for horizontal gas collection systems at municipal solid waste landfills. J. Environ. Eng. 2005, 131, 1716–1723. [Google Scholar] [CrossRef]
- Meng, K.; Cui, C.Y.; Li, H.J. An Ontology Framework for Pile Integrity Evaluation Based on Analytical Methodology. IEEE Access 2020, 99, 72158–72168. [Google Scholar] [CrossRef]
- Fabbricino, M. Evaluating operational vacuum for landfill biogas extraction. Waste Manag. 2007, 27, 1393–1399. [Google Scholar] [CrossRef] [PubMed]
- Ritter, W.F.; Chitikela, S.R. The Mississippi River Basin Phosphorus Problem: Past History and Future Challenges to Solve It. In Proceedings of the World Environmental and Water Resources Congress 2019: Watershed Management, Irrigation and Drainage, and Water Resources Planning and Management, Reston, VA, USA, 19–23 May 2019; pp. 361–373. [Google Scholar]
- Khire, M.V.; Mukherjee, M. Leachate injection using vertical wells in bioreactor landfills. Waste Manag. 2007, 27, 1233–1247. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.; Townsend, T.G.; Tolaymat, T.M. Steady–state design of vertical wells for liquids addition at bioreactor landfills. Waste Manag. 2010, 30, 2022–2029. [Google Scholar] [CrossRef]
- Reddy, K.R.; Kumar, G.; Giri, R.K. Influence of dynamic coupled hydro–bio–mechanical processes on response of municipal solid waste and liner system in bioreactor landfills. Waste Manag. 2017, 63, 143–160. [Google Scholar] [CrossRef]
- Feng, S.J.; Lu, S.F.; Chen, H.X. Three–dimensional modelling of coupled leachate and gas flow in bioreactor landfills. Comput. Geotech. 2017, 84, 138–151. [Google Scholar] [CrossRef]
- White, J.; Robinson, J.; Ren, Q. Modelling the biochemical degradation of solid waste in landfills. Waste Manag. 2004, 24, 227–240. [Google Scholar] [CrossRef] [PubMed]
- De Cortázar, A.L.G.; Lantarón, J.H.; Fernández, O.M.; Monzón, I.T.; Lamia, M.F. Modelling for environmental assessment of municipal solid waste landfills (Part II: Biodegradation). Waste Manag. Res. 2002, 20, 514–528. [Google Scholar] [CrossRef] [PubMed]
- Wdowczyk, A.; Szymańska-Pulikowska, A. Differences in the Composition of Leachate from Active and Non-Operational Municipal Waste Landfills in Poland. Water 2020, 12, 3129. [Google Scholar] [CrossRef]
- Dho, N.Y.; Koo, J.K.; Lee, S.R. Prediction of leachate level in Kimpo metropolitan landfill site by total water balance. Environ. Monit. Assess. 2002, 73, 207–219. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.J.; Chen, Z.W.; Chen, H.X. Slope stability of landfills considering leachate recirculation using vertical wells. Eng. Geol. 2018, 241, 76–85. [Google Scholar] [CrossRef]
- Merry, S.M.; Kavazanjian, J.E.; Fritz, W.U. Reconnaissance of the July 10, 2000, Payatas landfill failure. J. Perform. Constr. Facil. 2005, 19, 100–107. [Google Scholar] [CrossRef]
- Ritter, W.F. Progress on the Chesapeake Bay TMDL and Challenges in Meeting the 2025 Pollution-Reduction Loads. In Proceedings of the World Environmental and Water Resources Congress 2019: Watershed Management, Irrigation and Drainage, and Water Resources Planning and Management, Reston, VA, USA, 19–23 May 2019; pp. 63–70. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Li, Z.; Xu, H. Coupled Analysis of Leachate Recirculation and Heat Transfer for a Landfill with Buried Waste Tyres. Open Civ. Eng. J. 2018, 12, 290–300. [Google Scholar] [CrossRef]
- Barlaz, M.A. Forest products decomposition in municipal solid waste landfills. Waste Manag. 2006, 26, 321–333. [Google Scholar] [CrossRef]
- McDougall, J. A hydro–bio–mechanical model for settlement and other behaviour in landfilled waste. Comput. Geotech. 2007, 34, 229–246. [Google Scholar] [CrossRef]
- Chen, Y.M. A fundamental theory of environmental geotechnics and its application. Chin. J. Geotech. Eng. 2014, 36, 1–46. [Google Scholar]
- Liu, H.; Luo, X.; Jiang, X. The Evaluation System of the Sustainable Development of Municipal Solid Waste Landfills and Its Application. Sustainability 2021, 13, 1150. [Google Scholar] [CrossRef]
- Vavilin, V.A.; Rytov, S.V.; Lokshina, L.Y.; Pavlostathis, S.G.; Barlaz, M.A. Distributed model of solid waste anaerobic digestion: Effects of leachate recirculation and pH adjustment. Biotechnol. Bioeng. 2003, 81, 66–73. [Google Scholar] [CrossRef]
- Xu, H.; Wang, J.; Zhan, L. Characterization of compression behaviors of high food waste content (HFWC) MSW and no food waste content (NFWC) MSW in China. Waste Manag. 2020, 103, 305–313. [Google Scholar] [CrossRef]
- Chen, Y.; Ke, H.; Fredlund, D.G. Secondary compression of municipal solid wastes and a compression model for predicting settlement of municipal solid waste landfills. J. Geotech. Geoenvironmental. Eng. 2010, 136, 706–717. [Google Scholar] [CrossRef]
- He, P.J.; Qu, X.; Shao, L.M. Leachate pretreatment for enhancing organic matter conversion in landfill bioreactor. J. Hazard. Mater. 2007, 142, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Meima, J.A.; Naranjo, N.M.; Haarstrick, A. Sensitivity analysis and literature review of parameters controlling local biodegradation processes in municipal solid waste landfills. Waste Manag. 2008, 28, 904–918. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.M.; Guo, R.Y.; Li, Y.C. A degradation model for high kitchen waste content municipal solid waste. Waste Manag. 2016, 58, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.B.; Zhan, L.T.; Chen, Y.M. Intrinsic and relative permeabilities of shredded municipal solid wastes from the Qizishan landfill. Can. Geotech. J. 2014, 51, 1243–1252. [Google Scholar] [CrossRef]
- Li, Y.C.; Liu, H.L.; Cleall, P.J. Influences of operational practices on municipal solid waste landfill storage capacity. Waste Manag. Res. 2013, 31, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Bian, X.C.; Xu, W.J.; Chen, Y.M. Storage Capacity and Slope Stability Analysis of Municipal Solid Waste Landfills. J. Perform. Constr. Facil. 2018, 32, 04018036. [Google Scholar] [CrossRef]
- Liu, J.L.; Ke, H.; Zhan, L.T.; Chen, Y.M. Simulation tests of biodegradation and compression of municipal solid waste. In Proceedings of the International Symposium on Geoenvironmental Engineering, Hangzhou, China, 8–10 September 2009; pp. 521–524. [Google Scholar]
- Chen, Y.M.; Xu, W.J.; Ling, D.S. A degradation–consolidation model for the stabilization behavior of landfilled municipal solid waste. Comput. Geotech. 2020, 118, 103341. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Z.; Guo, Q.; Wang, H.; Zhou, Y.; Ng, W.J. Pilot-scale landfill with leachate recirculation for enhanced stabilization. Biochem. Eng. J. 2016, 105, 437–445. [Google Scholar] [CrossRef]
- Xu, Q.; Tian, Y.; Wang, S.; Ko, J.H. A comparative study of leachate quality and biogas generation in simulated anaerobic and hybrid bioreactors. Waste Manag. 2015, 41, 94–100. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Values | Reference |
|---|---|---|
| mc (dry basis, wt/wt, %) | 21.4 | Chen et al. [40]; He et al. [45] |
| ml (dry basis, wt/wt, %) | 13.9 | |
| λiw (g/m3/d) | 60 | |
| b (g/m3/d) | 250 (kitchen waste), 100 (other) | Meima et al. [46]; Chen et al. [47] |
| kh (m3/g) | 0.1 | |
| a | 2.8 | |
| kmax (d–1) | 0.1 | |
| km (m3/g) | 0.06 | Meima et al. [46]; Chen et al. [47] |
| kd (d−1) | 0.01 | |
| ks (g/m3) | 4 | |
| Y | 0.08 | |
| ki (m2) | 6 × 10−12 | Feng et al. [28]; Xu et al. [48] |
| μ (kg/m/s) | 1 × 10−3 (μw), 1.4 × 10−5 (μg) | |
| α | 0.88 | |
| m | 1.6 | |
| Ss | 0.95 | |
| Sr | 0.2 | |
| Dl,c1 (m2/s) | 1.19 × 10−9 | |
| Dl,c2 (m2/s) | 1 × 10−9 | |
| n0 | 0.75 | Li et al. [49] |
| CC’ | 0.205 | Gao et al. [50] |
| CC∞’ | 0.074 | |
| sb∞ | 0.23 | Chen et al. [44] |
| βs (d−1) | 0.2 | |
| σ0 (kPa) | 13 | |
| ρd (kN/m3) | 34 | Liu et al. [51] |
| cm1 | 1.3 | - |
| cm2 | 2.1 | |
| Nm | 1.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Liu, H.; Jiang, X.; Lv, H.; Cui, C.; Huyan, Z. Numerical Model of Leachate Recirculation in Bioreactor Landfills with High Kitchen Waste Content. Water 2021, 13, 1750. https://doi.org/10.3390/w13131750
Zhang P, Liu H, Jiang X, Lv H, Cui C, Huyan Z. Numerical Model of Leachate Recirculation in Bioreactor Landfills with High Kitchen Waste Content. Water. 2021; 13(13):1750. https://doi.org/10.3390/w13131750
Chicago/Turabian StyleZhang, Peng, Hailong Liu, Xingyao Jiang, Hao Lv, Chunyi Cui, and Zhen Huyan. 2021. "Numerical Model of Leachate Recirculation in Bioreactor Landfills with High Kitchen Waste Content" Water 13, no. 13: 1750. https://doi.org/10.3390/w13131750
APA StyleZhang, P., Liu, H., Jiang, X., Lv, H., Cui, C., & Huyan, Z. (2021). Numerical Model of Leachate Recirculation in Bioreactor Landfills with High Kitchen Waste Content. Water, 13(13), 1750. https://doi.org/10.3390/w13131750








