Hydraulic Jump: A Brief History and Research Challenges
Abstract
:1. Introduction
2. State of the Art
2.1. Experimental Studies on the Internal Flow in Hydraulic Jumps
2.2. Experimental Studies on the Turbulent Features of Hydraulic Jumps
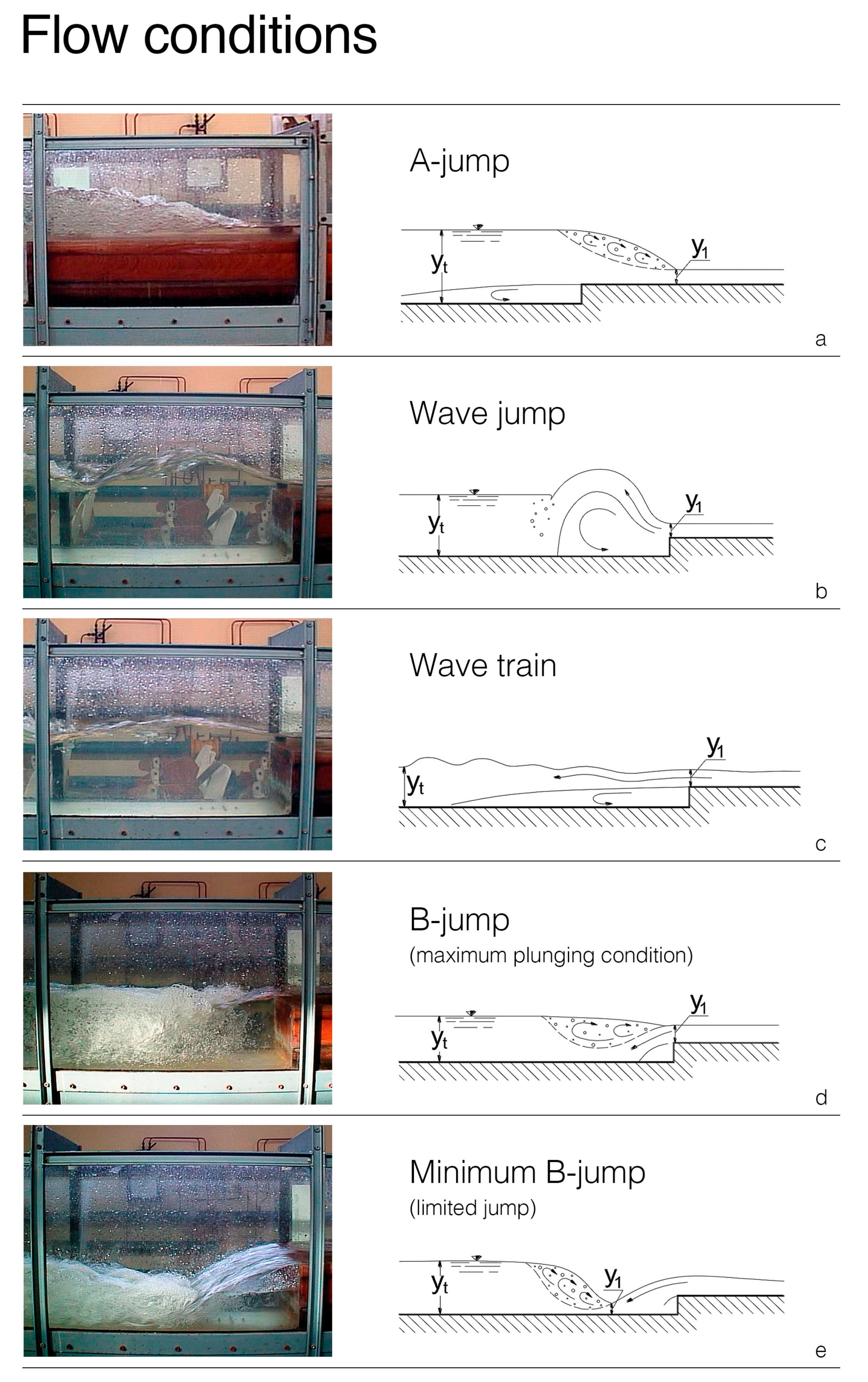
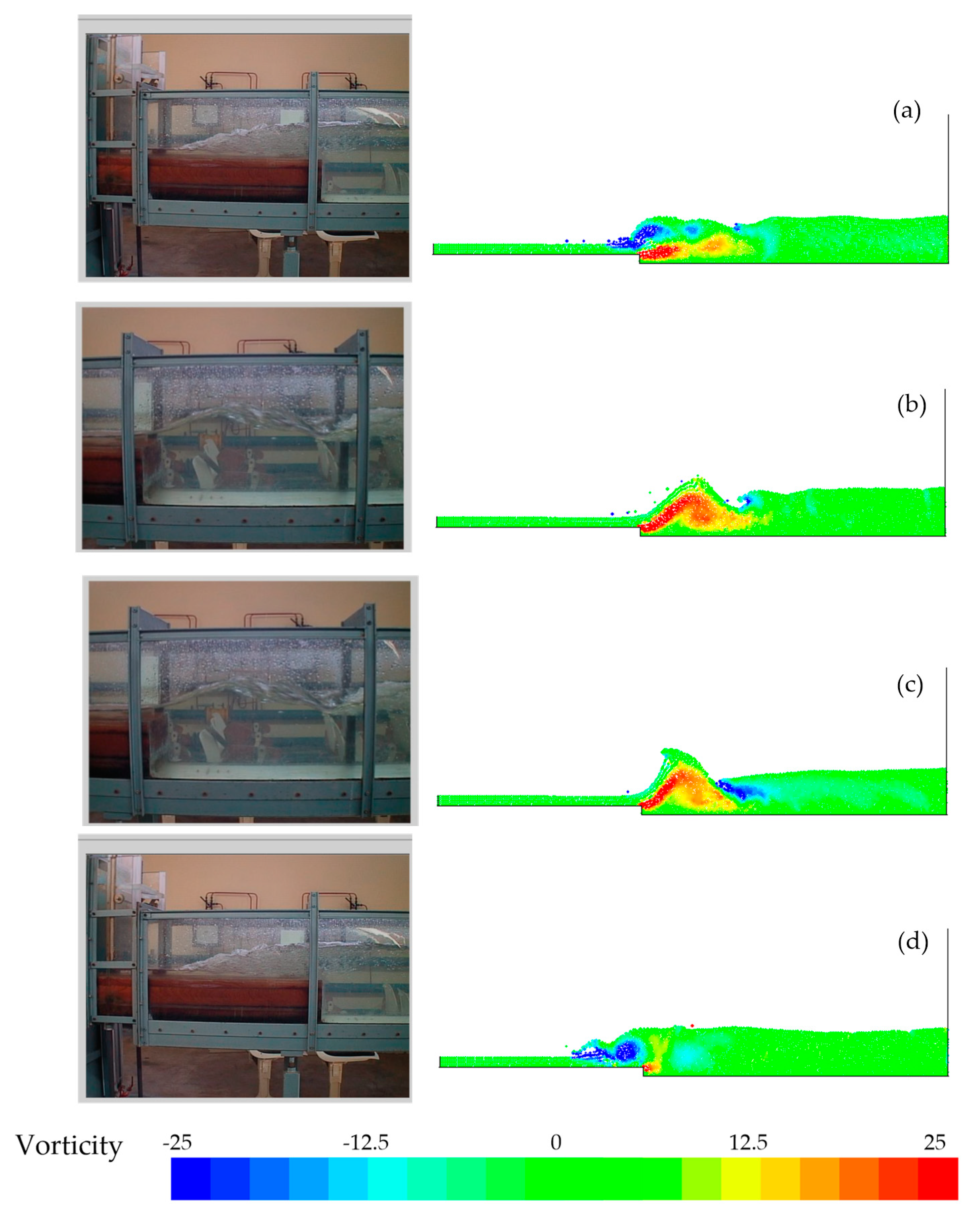
2.3. Experimental Studies on Oscillating Phenomena of Hydraulic Jumps
- oscillations of hydraulic jump types do not depend on whether the bottom is made of erodible or non-erodible material;
- a suitable time scale may be defined both for oscillations of the jump types and for fluctuations of the jump toes with a flat and outlined bottom;
- analysis of the oscillating phenomena indicates a correlation among the surface profile elevations, velocity components and pressure fluctuations;
- analysis of the oscillating phenomena indicates change configurations of the surface profile of a hydraulic jump, as a function of the air concentration present in the roller.
3. Research Challenges
3.1. Numerical Methods with an Eulerian Approach
3.2. Numerical Methods with a Lagrangian Approach
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bidone, G. Expériences sur la propagation des remous. In Memorie Della Reale Accademia delle Scienze di Torino; Natural History Museum Library: London, UK, 1820; Volume 30, pp. 195–292. [Google Scholar]
- Guglielmini, D. Della Natura de’ Fiumi; Nuova Edizione con le Annotazioni di Eustachio Manfredi: Bologna, Italy, 1739. [Google Scholar]
- Bélanger, J.B. Essai sur la Solution Numérique de Quelques Problèmes Relatifs au Mouvement Permanent des Eaux Courantes (‘Essay on the Numerical Solution of Some Problems relative to Steady Flow of Water’); Carilian-Goeury: Paris, France, 1828. [Google Scholar]
- Leutheusser, H.J.; Alemu, S. Flow separation under hydraulic jump. J. Hydraul. Res. 1978, 17, 193–206. [Google Scholar] [CrossRef]
- Harleman, D.R.F. Discussion of “Turbulence characteristics of the hydraulic jump” by Rouse, H., Siao, T. T., & Nagaratnam, S. Trans. ASCE 1959, 124, 959–962. [Google Scholar]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; United States Department of the Interior: Washington, DC, USA, 1958. [Google Scholar]
- Rajaratnam, N. The Hydraulic Jump as a Wall Jet. J. Hydraul. Div. 1965, 91, 107–132. [Google Scholar] [CrossRef]
- Leutheusser, H.J.; Kartha, V.C. Effects of inflow conditions on hydraulic jump. J. Hydraul. Div. 1972, 98, 1367–1385. [Google Scholar] [CrossRef]
- Hager, W.H.; Bretz, N.V. Hydraulic jumps at positive and negative steps. J. Hydraul. Res. 1986, 24, 237–252. [Google Scholar] [CrossRef]
- Hager, W.H.; Bremen, R. Classical hydraulic jump: Sequent depths. J. Hydraul. Res. 1989, 27, 565–585. [Google Scholar] [CrossRef]
- Hager, W.H. History of the Hydraulic Jump, United States; Bureau of Reclamation, U.S. Department of the Interior, Bureau of Reclamation, Engineering and Research Center: Washington, DC, USA, 1990.
- Wu, S.; Rajaratnam, N. Free jumps, submerged jumps and wall jets. J. Hydraul. Res. 1995, 33, 197–212. [Google Scholar] [CrossRef]
- Carollo, F.G.; Ferro, V.; Pampalone, V. New solution of classical hydraulic jump. J. Hydraul. Eng. 2009, 135, 527–531. [Google Scholar] [CrossRef]
- Vischer, D.L.; Hager, W.H. Dam Hydraulics; John Wiley Sons: Chichester, UK, 1998. [Google Scholar]
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Water Science and Technology Library; Springer Science & Business Media: Dordrecht, The Netherlands, 1992; Volume 8, ISBN 978-90-481-4106-7. [Google Scholar]
- Riegel, R.M.; Beebe, J.C. The Hydraulic Jump as a Means of Dissipating Energy; Technical Reports Part III; Miami Conservancy District: Dayton, OH, USA, 1917; pp. 60–111. [Google Scholar]
- Rehbock, T. Die Bekämpfung der Sohlen-Auskolkung bei Wehren durch Zahnschwellen. Schweiz. Bauzt. 1926, 87, 27–31. [Google Scholar]
- Safranez, K. Wechselsprung und die Energievernichtung des Wassers. Bauingenieur 1927, 8, 898–905. (In German) [Google Scholar]
- Bakhmeteff, B.A. Hydraulics of Open Channels, 1st ed.; McGraw-Hill: New York, NY, USA, 1932. [Google Scholar]
- Rouse, H. On the Use of Dimensionless Numbers. Civil Eng. 1934, 4, 563–568. [Google Scholar]
- Bakhmeteff, B.A.; Matzke, A.E. The hydraulic jump in terms of dynamic similarity. ASCE Trans. 1936, 101, 630–680. [Google Scholar]
- Rouse, H.; Siao, T.T.; Nagaratnam, S. Turbulence characteristics of the hydraulic jump. J. Hydraul. Div. 1958, 84, 1–30. [Google Scholar]
- McCorquodale, J.A.; Khalifa, A. Internal flow in hydraulic jumps. J. Hydraul. Eng. 1983, 109, 684–701. [Google Scholar] [CrossRef]
- Ehrenberger, I. Wasserbewegung in Steilen Rinnen (Susstennen). mit Besonderer Berucksichtigung der Selbstbeliiftung. Z. Osterr. Ing. Archit. 1926. No. 15/16 and 17/18 (In German) [Google Scholar]
- Resch, F.J.; Leutheusser, H.J. Le ressaut hydraulique: Measure de turbulence dans la region diphasique. (The hydraulic jump: Turbulence measurements in the two-phase flow region). J. Houille Blanche 1972, 4, 279–293. (In French) [Google Scholar] [CrossRef] [Green Version]
- Resch, F.J.; Leutheusser, H.J.; Alemu, S. Bubbly two-phase flow in the hydraulic jump. J. Hydraul. Div. 1974, 84, 137–149. [Google Scholar] [CrossRef]
- Roshko, A. Structure of turbulent shear flows: A new look. AIAA J. 1976, 14, 1349–1357. [Google Scholar] [CrossRef] [Green Version]
- Babb, A.F.; Aus, H.C. Measurements of Air in Flowing Water. J. Hydraul. Div. 1981, 107, 1615–1630. [Google Scholar] [CrossRef]
- Hoyt, J.W.; Sellin, R.H.J. Hydraulic jump as “mixing layer”. J. Hydraul. Eng. 1989, 115, 1607–1613. [Google Scholar] [CrossRef]
- Chanson, H.; Qiao, G.L. Air Bubble Entrainment and Gas Transfer at Hydraulic Jumps; Research Report No. CE149; Department of Civil Engineering, University of Queensland: Brisbane, QLD, Australia, 1994; p. 68. [Google Scholar]
- Chanson, H. Air Bubble Entrainment in Free-Surface Turbulent Flows; Experimental Investigations. Report CH46/95; Department of Civil Engineering, University of Queensland: Brisbane, QLD, Australia, 1995; p. 368. [Google Scholar]
- Chanson, H. Air entrainment in two-dimensional turbulent shear ows with partially developed in fow conditions. Int. J. Multiph. Flow 1995, 21, 1107–1121. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H.; Brattberg, T. Experimental study of the air–water shear flow in a hydraulic jump. Int. J. Multiph. Flow 2000, 26, 583–607. [Google Scholar] [CrossRef] [Green Version]
- Mossa, M.; Tolve, U. Flow visualization in bubbly two-phase hydraulic jump. J. Fluids Eng. 1998, 120, 160–165. [Google Scholar] [CrossRef]
- Gualtieri, C.; Chanson, H. Experimental Analysis of Froude Number Effect on Air Entrainment in the Hydraulic Jump. Environ. Fluid Mech. 2007, 7, 217–238. [Google Scholar] [CrossRef] [Green Version]
- Gualtieri, C.; Chanson, H. Effect of Froude number on bubble clustering in a hydraulic jump. J. Hydraul. Res. 2010, 48, 504–508. [Google Scholar] [CrossRef] [Green Version]
- Gualtieri, C.; Chanson, H. Interparticle arrival time analysis of bubble distributions in a dropshaft and hydraulic jump. J. Hydraul. Res. 2013, 51, 253–264. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H. Hydraulic Jumps: Turbulence and Air Bubble Entrainment. J. Houille Blanche 2011, 3, 5–16. [Google Scholar] [CrossRef] [Green Version]
- Kucukali, S.; Chanson, H. Turbulence Measurements in Hydraulic Jumps with Partially-Developed Inflow Conditions. Exp. Therm. Fluid Sci. 2008, 33, 41–53. [Google Scholar] [CrossRef] [Green Version]
- Murzyn, F.; Chanson, H. Experimental Investigation of Bubbly Flow and Turbulence in Hydraulic Jumps. Environ. Fluid Mech. 2009, 9, 143159. [Google Scholar] [CrossRef]
- Chachereau, Y.; Chanson, H. Bubbly flow measurements in hydraulic jumps with small inflow Froude numbers. Int. J. Multiph. Flow 2011, 37, 555–564. [Google Scholar] [CrossRef] [Green Version]
- Wang, H. Turbulence and Air Entrainment in Hydraulic Jumps. Ph.D. Thesis, School of Civil Engineering, The University of Queensland, Brisbane, QLD, Australia, 2014. [Google Scholar] [CrossRef] [Green Version]
- Felder, S.; Chanson, H. Turbulence, Dynamic Similarity and Scale Effects in High-Velocity Free-Surface Flows above a Stepped Chute. Exp. Fluids 2009, 47, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Rajaratnam, N.; Steffler, P.M.; Smy, P.R. Structure of flow in hydraulic jumps. J. Hydraul. Res. 1991, 29, 207–218. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Transition from supercritical to subcritical flow at an abrupt drop. J. Hydraul. Res. 1991, 29, 309–328. [Google Scholar] [CrossRef]
- Habib, E.; Mossa, M.; Petrillo, A. Scour downstream of hydraulic jump. In Proceedings of the Modeling, Testing & Monitoring for Hydro Powerplants Conference, Budapest, Hungary, 11–13 July 1994; pp. 591–602. [Google Scholar]
- Abdel Ghafar, A.; Mossa, M.; Petrillo, A. Scour from flow downstream of a sluice gate after a horizontal apron. In Proceedings of the 6th International Symposium on River Sedimentation, New Delhi, India, 7–11 November 1995; pp. 1069–1088. [Google Scholar]
- Chanson, H.; Toombes, L. Supercritical flow at an abrupt drop: Flow patterns and aeration. Can. J. Civil Eng. 1998, 25, 956–966. [Google Scholar] [CrossRef]
- Mossa, M. On the oscillating characteristics of hydraulic jumps. J. Hydraul. Res. 1999, 37, 541–558. [Google Scholar] [CrossRef]
- Mossa, M.; Petrillo, A.; Chanson, H. Tailwater Level Effects on Flow Conditions at an Abrupt Drop. J. Hydraul. Res. 2003, 41, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Mok, K.M.; Mossa, M. Discussion on: Relation of surface roller eddy formation and surface fluctuation in hydraulic jumps. J. Hydraul. Res. 2004, 42, 207–212. [Google Scholar] [CrossRef]
- Mossa, M.; Petrillo, A.; Chanson, H.; Yausda, Y.; Takahashi, M.; Ohtsu, I. Discussion on Tailwater level effects on flow conditions at an abrupt drop. J. Hydraul. Res. 2005, 43, 217–224. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Chanson, H. Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 2015, 141, 04015010. [Google Scholar] [CrossRef] [Green Version]
- Chachereau, Y.; Chanson, H. Free-surface fluctuations and turbulence in hydraulic jumps. Exp. Therm. Fluid Sci. 2011, 35, 896–909. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Wang, H.; Chanson, H. Turbulence and aeration in hydraulic jumps: Free-surface fluctuation and integral turbulent scale measurements. Environ. Fluid Mech. 2013, 13, 189–204. [Google Scholar] [CrossRef]
- Valero, D.; Viti, N.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water 2018, 11, 36. [Google Scholar] [CrossRef] [Green Version]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2019, 11, 28. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Steffler, P.M.; Rajaratnam, N. A numerical study of submerged hydraulic jumps. J. Hydraul. Res. 1991, 29, 293–308. [Google Scholar] [CrossRef]
- Chippada, S.; Ramaswamy, B.; Wheeler, M.F. Numerical simulation of hydraulic jump. Int. J. Numer. Methods Eng. 1994, 37, 1381–1397. [Google Scholar] [CrossRef]
- Qingchao, L.; Drewes, U. Turbulence characteristics in free and forced hydraulic jumps. J. Hydraul. Res. 1994, 32, 877–898. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, Y. Numerical simulation of hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2005, 10, 52–57. [Google Scholar]
- Souders, D.T.; Hirt, C.W. Modeling entrainment of air at turbulent free surfaces. In Proceedings of the World Water and Environmental Resources Congress 2004, Salt Lake City, UT, USA, 27 June–1 July 2004. [Google Scholar]
- Gonzlez, A.E.; Bombardelli, F.A. Two-phase-flow theoretical and numerical models for hydraulic jumps, including air entrainment. In Proceedings of the XXXI IAHR Congress 2005, Seoul, Korea, 11–16 September 2005. [Google Scholar]
- Ma, J.; Oberai, A.A.; Lahey, R.T., Jr.; Drew, D.A. Modeling air entrainment and transport in a hydraulic jump using two-fluid RANS and DES turbulence models. Heat Mass Transf. 2011, 47, 911–919. [Google Scholar] [CrossRef]
- Witt, A.; Gulliver, J.; Shen, L. Simulating air entrainment and vortex dynamics in a hydraulic jump. Int. J. Multiph. Flow 2015, 72, 165–180. [Google Scholar] [CrossRef] [Green Version]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- Wei, W.; Hong, Y.; Liu, Y. Numerical Simulation on Hydraulic Characteristics of Free Hydraulic Jump on Corrugated Beds of Stilling Basin. J. Syst. Simul. 2017, 29, 918–925. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to nonspherical stars. Monthly Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L. A numerical approach to the testing of fusion process. Astronom. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M. Multi-phase simulation of infected respiratory cloud transmission in air. AIP Adv. 2021, 11. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Darlymple, R.A.; Crespo, A.J.C. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- De Padova, D.; Meftah, M.B.; De Serio, F.; Mossa, M.; Sibilla, S. Characteristics of breaking vorticity in spilling and plunging waves. Environ. Fluid Mech. 2020, 20, 233–260. [Google Scholar] [CrossRef]
- López, D.; Marivela, R.; Garrote, L. Smoothed particle hydrodynamics model applied to hydraulic structures: A hydraulic jump test case. J. Hydraul. Res. 2010, 48, 142–158. [Google Scholar] [CrossRef]
- Federico, I.; Marrone, S.; Colagrossi, A.; Aristodemo, F.; Antuono, M. Simulating 2D open channel flows through an SPH model. Eur. J. Mech. B/Fluids 2012, 34, 35–46. [Google Scholar] [CrossRef]
- Jonsson, P.; Andreasson, P.; Gunnar, J.; Hellström, I.; Jonsén, P.; Staffan Lundström, T. Smoothed Particle Hydrodynamic simulation of hydraulic jump using periodic open boundaries. Appl. Math. Model. 2016, 40, 8391–8405. [Google Scholar] [CrossRef]
- Chern, M.J.; Syamsuri, S. Effect of corrugated bed on hydraulic jump characteristic using SPH method. J. Hydraul. Eng. 2012, 139, 221–232. [Google Scholar] [CrossRef]
- Gu, S.; Bo, F.; Luo, M.; Kazemi, E.; Zhang, Y.; Wei, J. SPH Simulation of Hydraulic Jump on Corrugated Riverbeds. Appl. Sci. 2019, 9, 436. [Google Scholar] [CrossRef] [Green Version]
- De Padova, D.; Mossa, M.; Sibilla, S.; Torti, E. 3D SPH modeling of hydraulic jump in a very large channel. J. Hydraul. Res. 2010, 51, 158–173. [Google Scholar] [CrossRef]
- Chanson, H.; Montes, J.S. Characteristics of undular hydraulic jump: Experimental apparatus and flow patterns. J. Hydraul. Eng. 1995, 121, 129–144. [Google Scholar] [CrossRef] [Green Version]
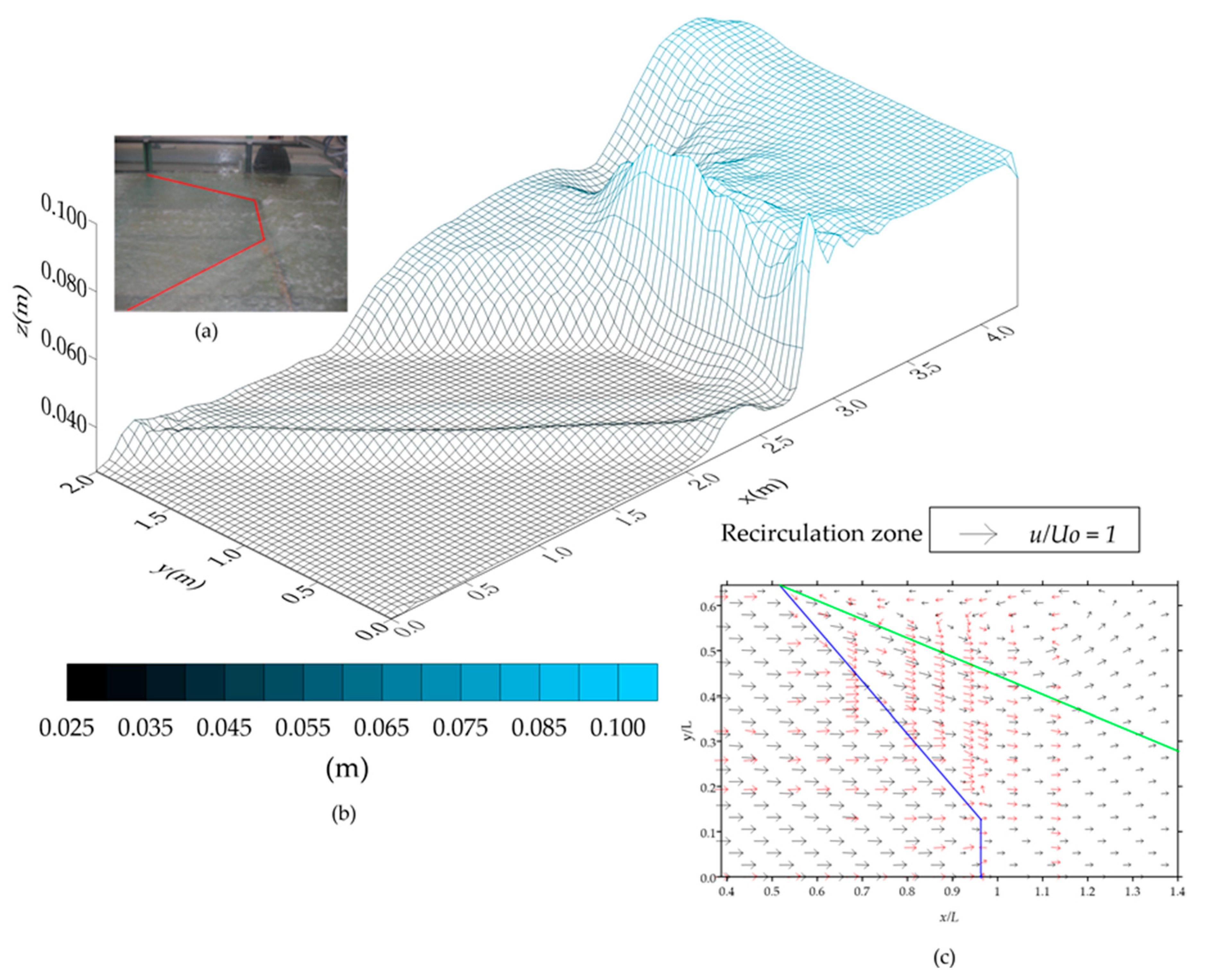
- Meftah, M.B.; De Serio, F.; Mossa, M.; Pollio, A. Analysis of the velocity field in a large rectangular channel with lateral shockwave. Environ. Fluid Mech. 2007, 7, 519–536. [Google Scholar] [CrossRef]
- Meftah, M.B.; De Serio, F.; Mossa, M.; Pollio, A. Experimental study of recirculating flows generated by lateral shock waves in very large channels. Environ. Fluid Mech. 2008, 8, 215–238. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M.; Pollio, A. Considerations on shock wave/boundary layer interaction in undular hydraulic jumps in horizontal channels with a very high aspect ratio. Eur. J. Mech. B Fluids 2010, 29, 415–429. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH modelling of hydraulic jump oscillations at an abrupt drop. Water 2017, 9, 790. [Google Scholar] [CrossRef] [Green Version]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH numerical investigation of the characteristics of an oscillating hydraulic jump at an abrupt drop. J. Hydrodyn. 2018, 30, 106–113. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Padova, D.; Mossa, M. Hydraulic Jump: A Brief History and Research Challenges. Water 2021, 13, 1733. https://doi.org/10.3390/w13131733
De Padova D, Mossa M. Hydraulic Jump: A Brief History and Research Challenges. Water. 2021; 13(13):1733. https://doi.org/10.3390/w13131733
Chicago/Turabian StyleDe Padova, Diana, and Michele Mossa. 2021. "Hydraulic Jump: A Brief History and Research Challenges" Water 13, no. 13: 1733. https://doi.org/10.3390/w13131733
APA StyleDe Padova, D., & Mossa, M. (2021). Hydraulic Jump: A Brief History and Research Challenges. Water, 13(13), 1733. https://doi.org/10.3390/w13131733






