Hydrodynamic Performance and Design Evolution of Wedge-Shaped Blocks for Dam Protection against Overtopping
Abstract
1. Introduction and Background
2. Materials and Methods
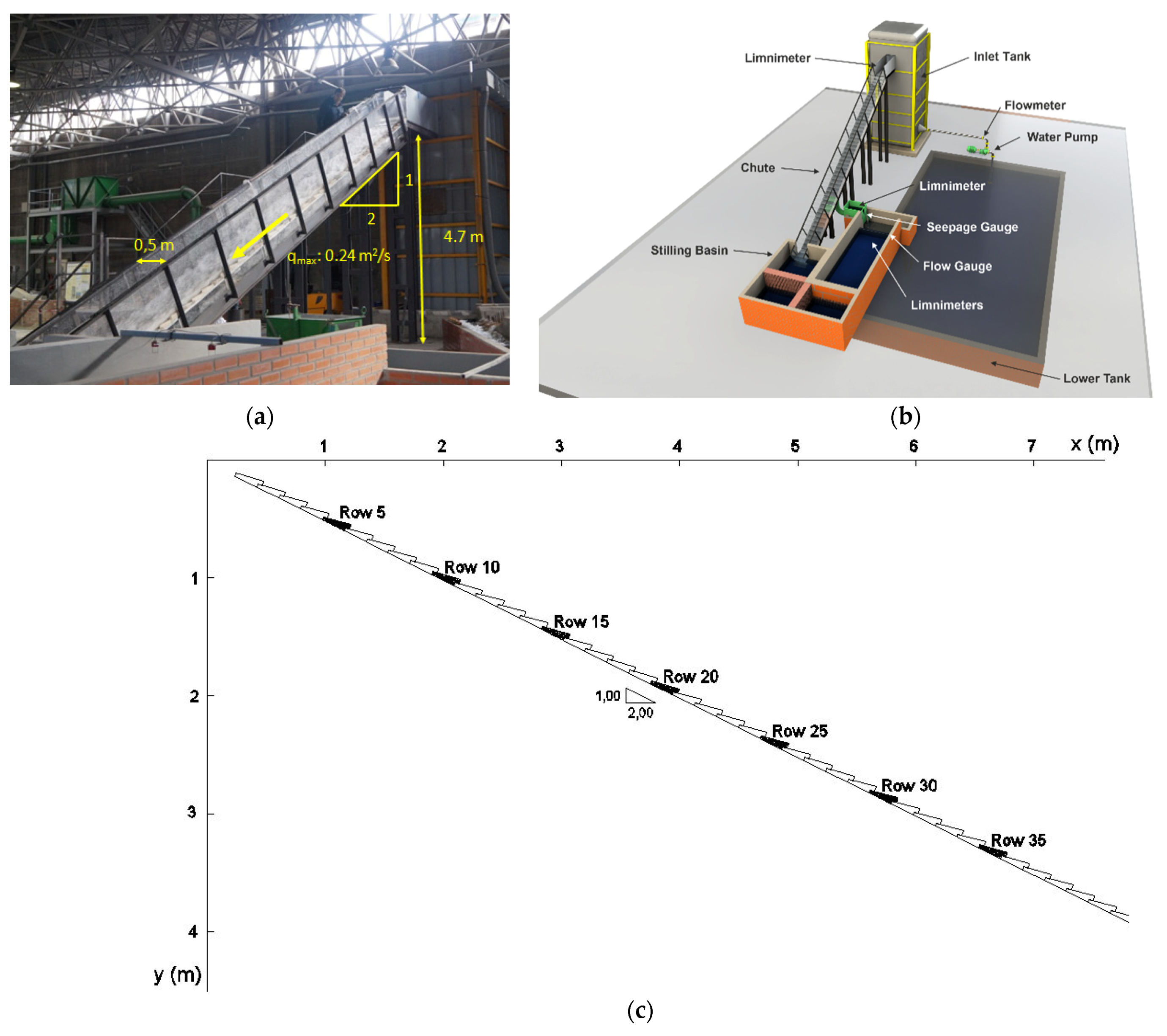
2.1. Experimental Facility
- Measuring devices for water levels and discharge of skimming and seepage flows:
- Electromagnetic flowmeter to measure the pumped flow rate.
- Triangular thin-plate weir to measure the flow that leaks through the open joints between adjacent blocks and seeps through the granular layer.
- Electromagnetic limnimeters (4) for measuring the water level at the following points: the inlet tank, the upstream end of the chute, the abovementioned triangular thin-plate weir and the rectangular thin-plate weir at the end of the stilling basin.
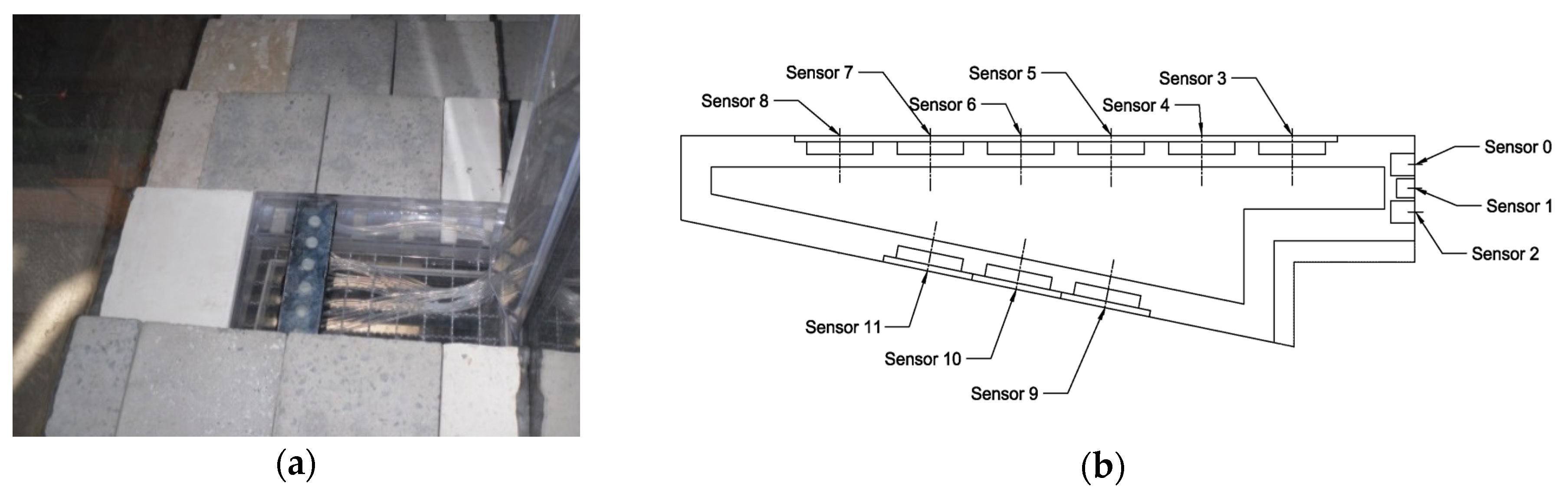
- Pressure measurement system to register the water pressures at several points on the block tread, base and the riser step of the WSBs [27], formed by:
- A set of 12 Messtech submersible XA-700 pressure transducers connected to measuring tubes installed on one of the measuring blocks.
- A pressure gauge (Scanivalve DSA3207 Corp. model) with 12 sockets measuring tubes installed on a second measuring block.
2.2. Flow Test Characterization
2.2.1. Flow Regimes
2.2.2. Inception Point
2.2.3. Uniform Flow Area
2.3. Testing Program
3. Results and Discussion
3.1. Hydrodynamic Pressures
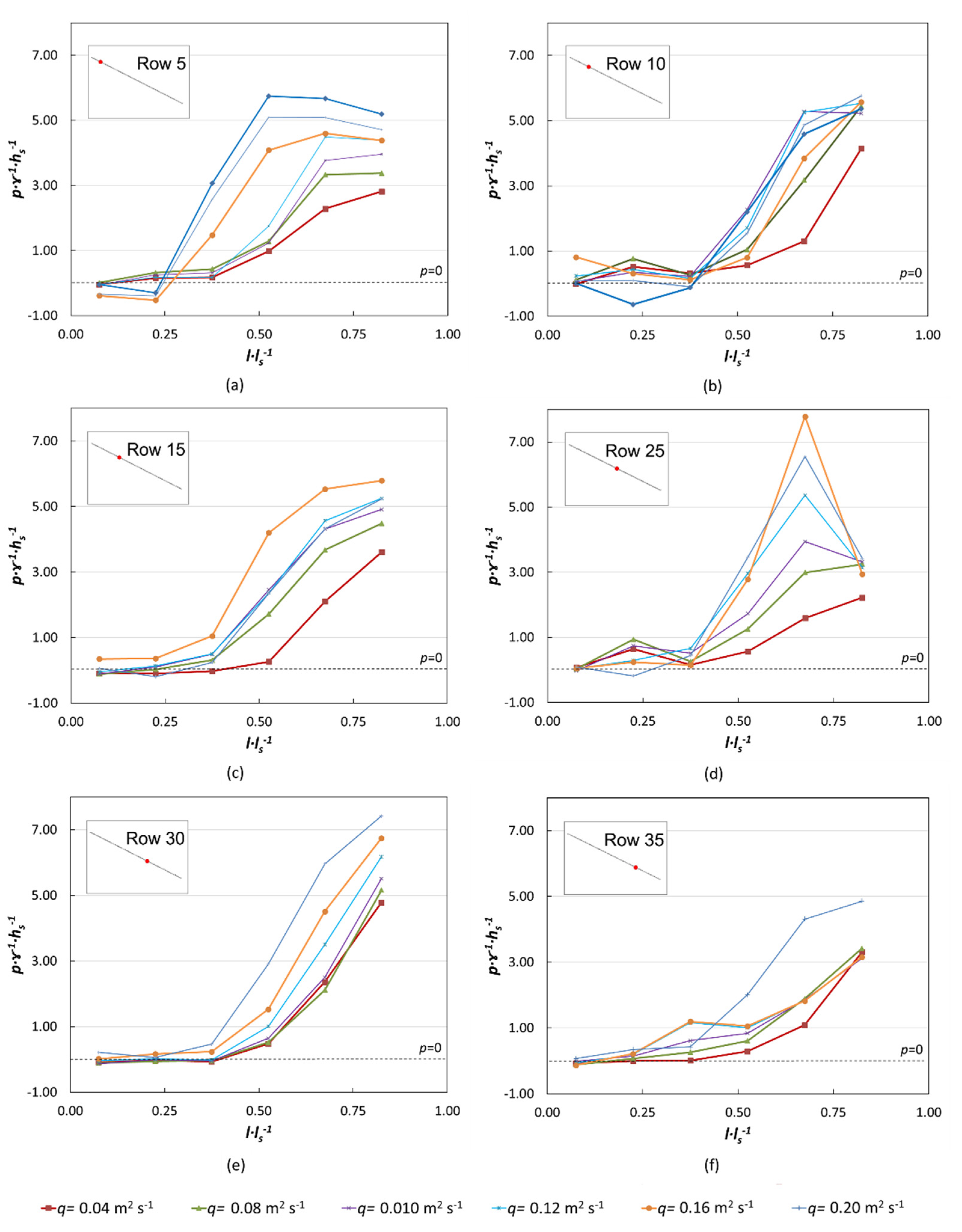
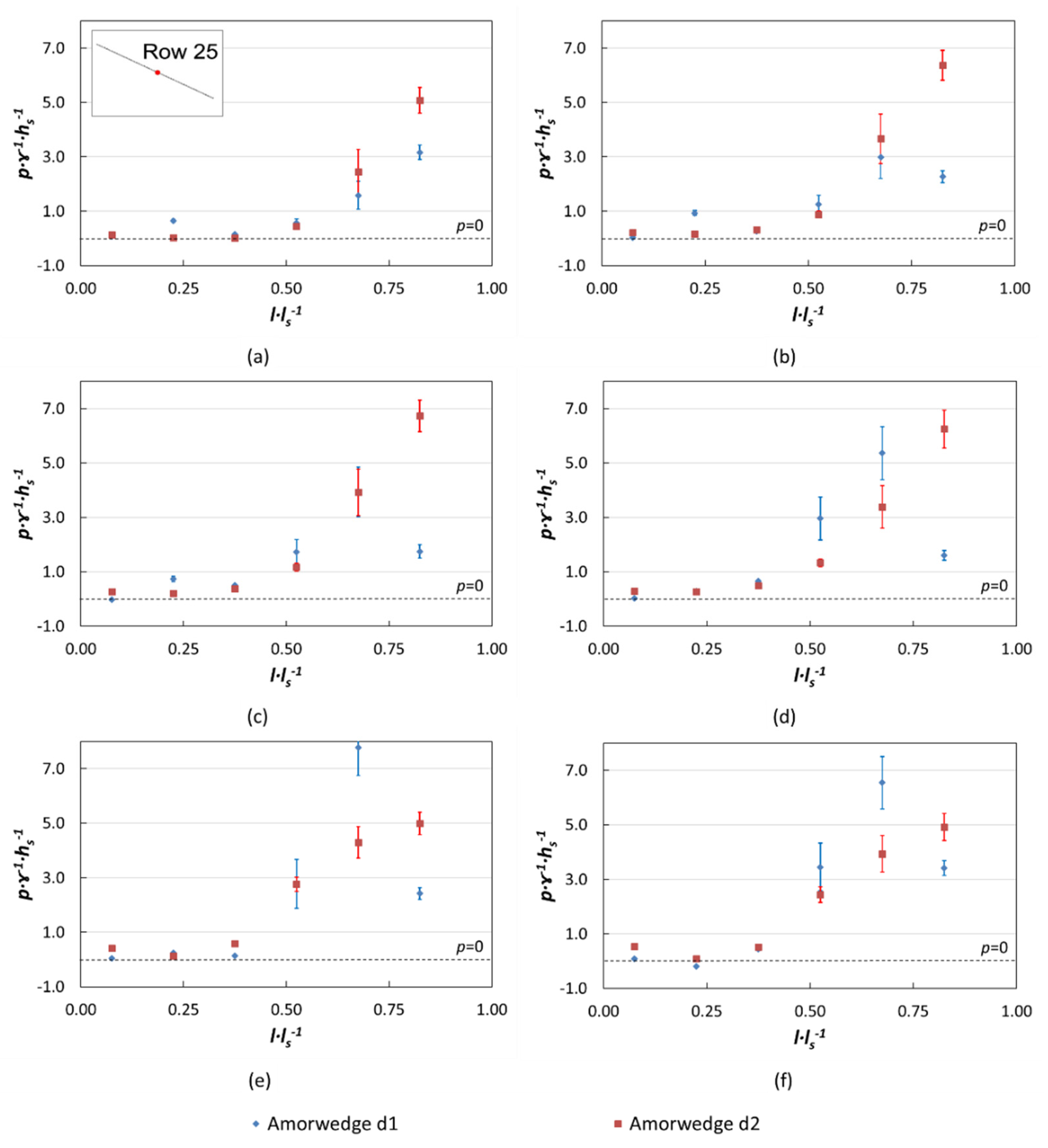
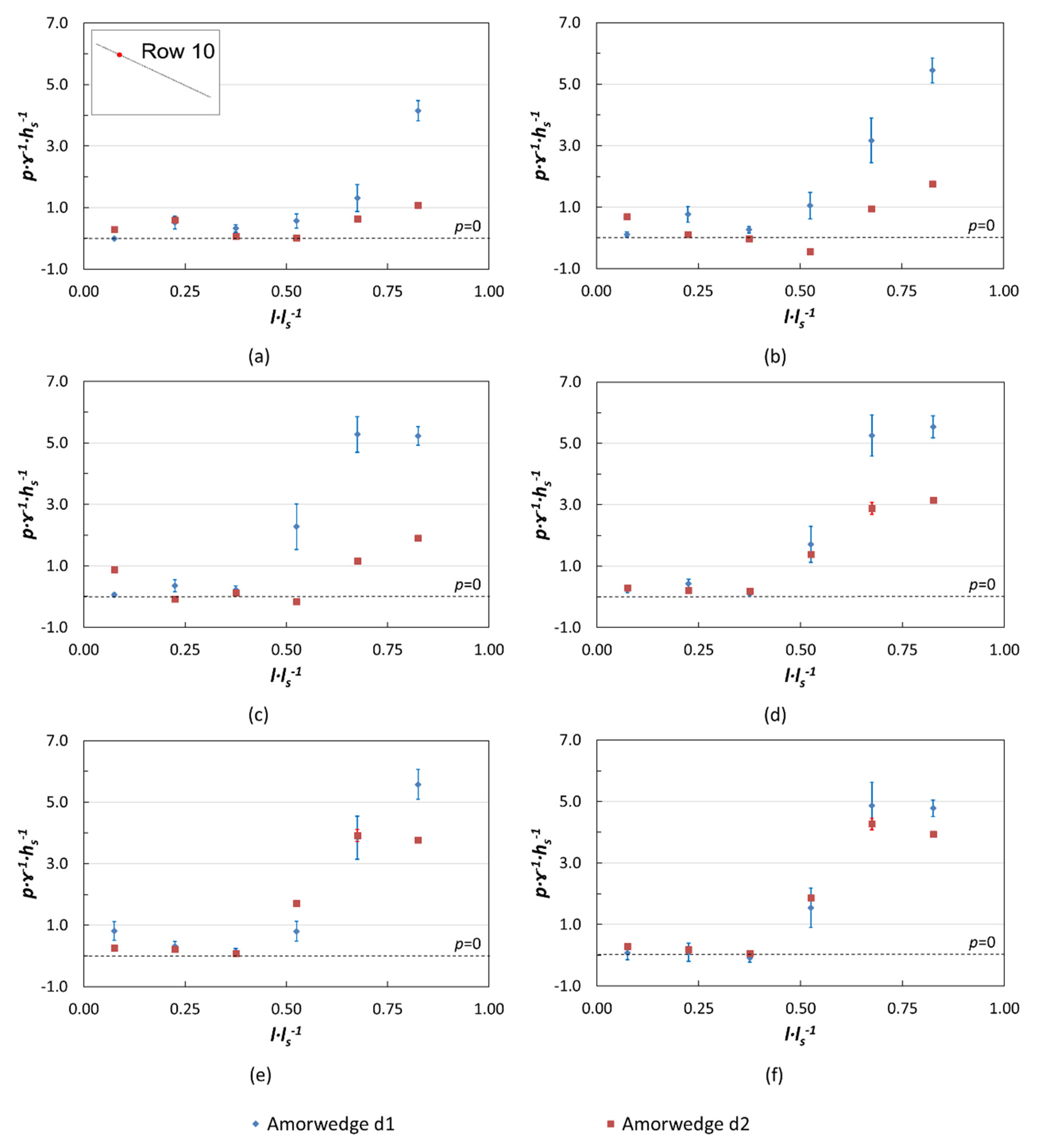
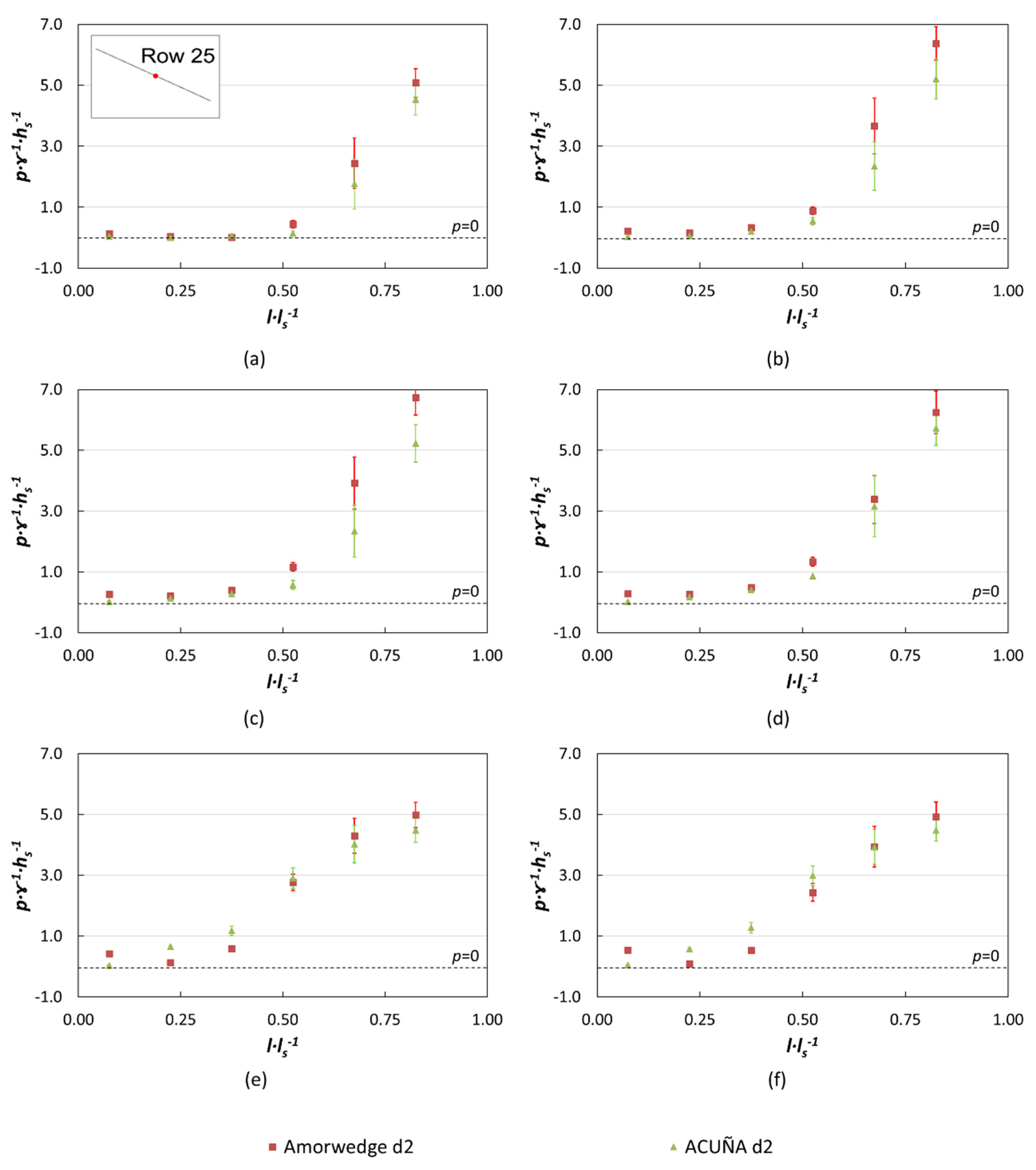
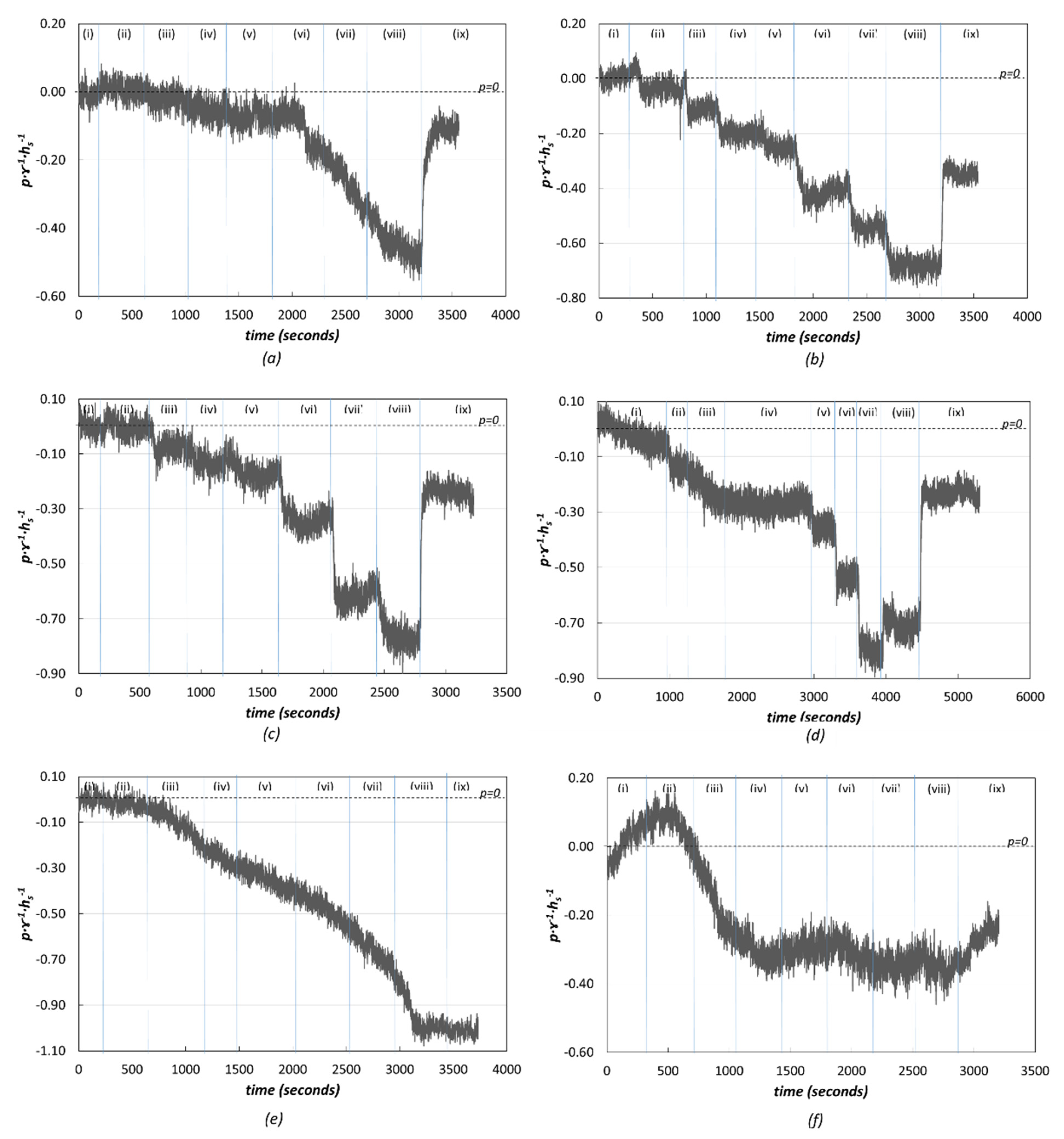
3.1.1. Pressures on the Block Tread
Armorwedge™ Block (w1) Tests with Free Draining Conditions (d1)
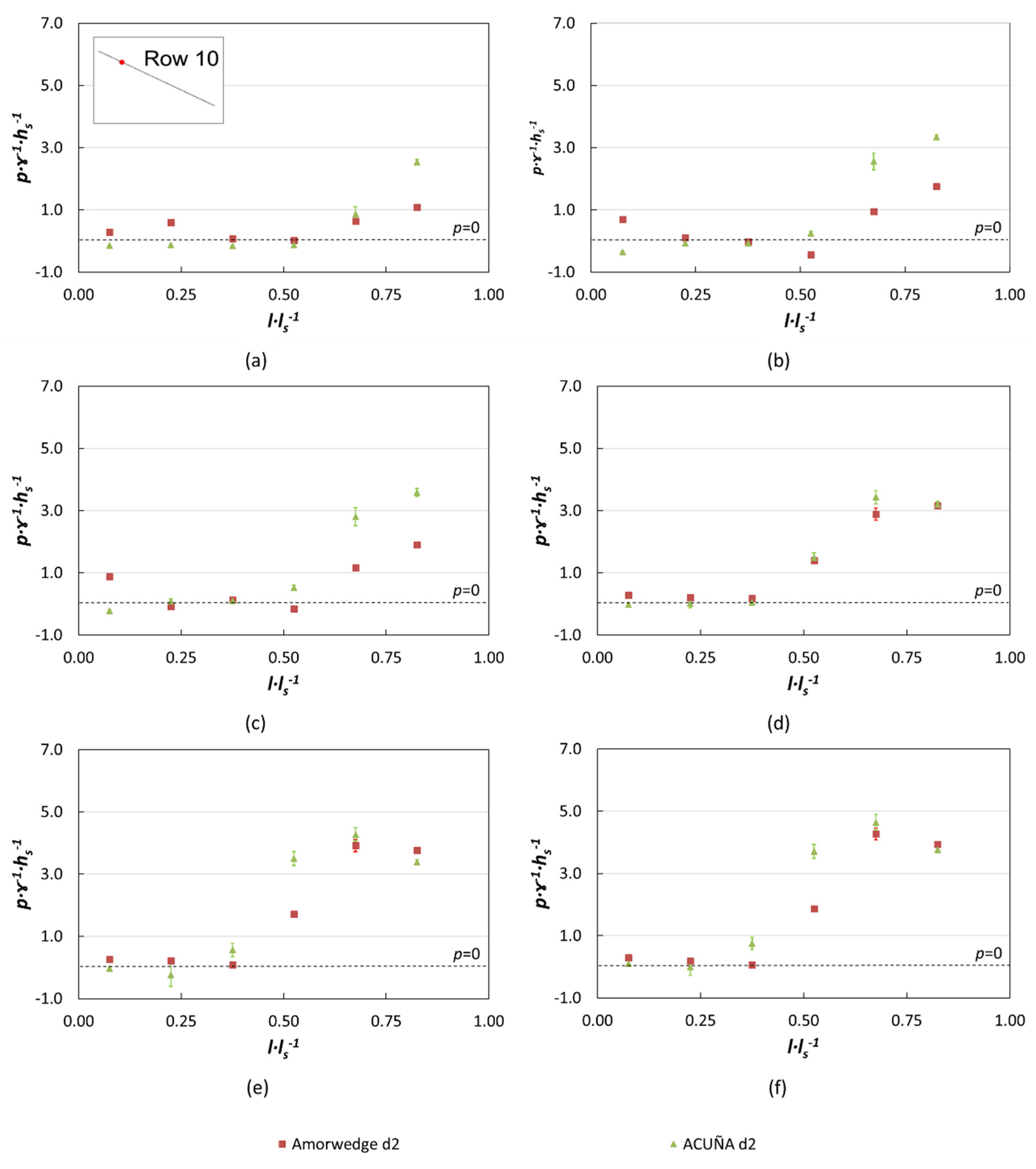
Effect of Drainage Layer (d2) on ArmorwedgeTM Block (w1)
Comparison of the ArmorwedgeTM (w1) and ACUÑA (w2) Blocks
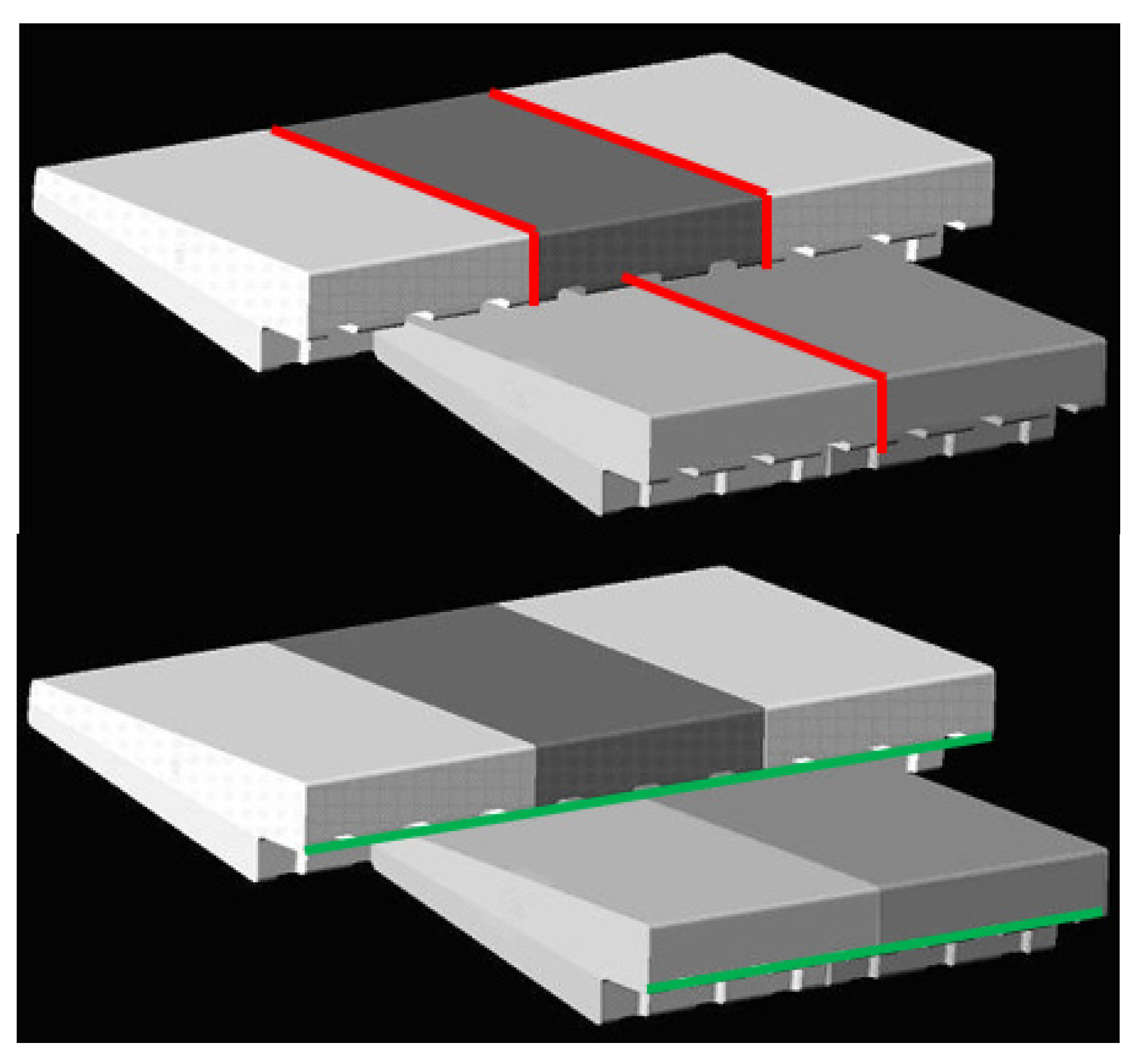
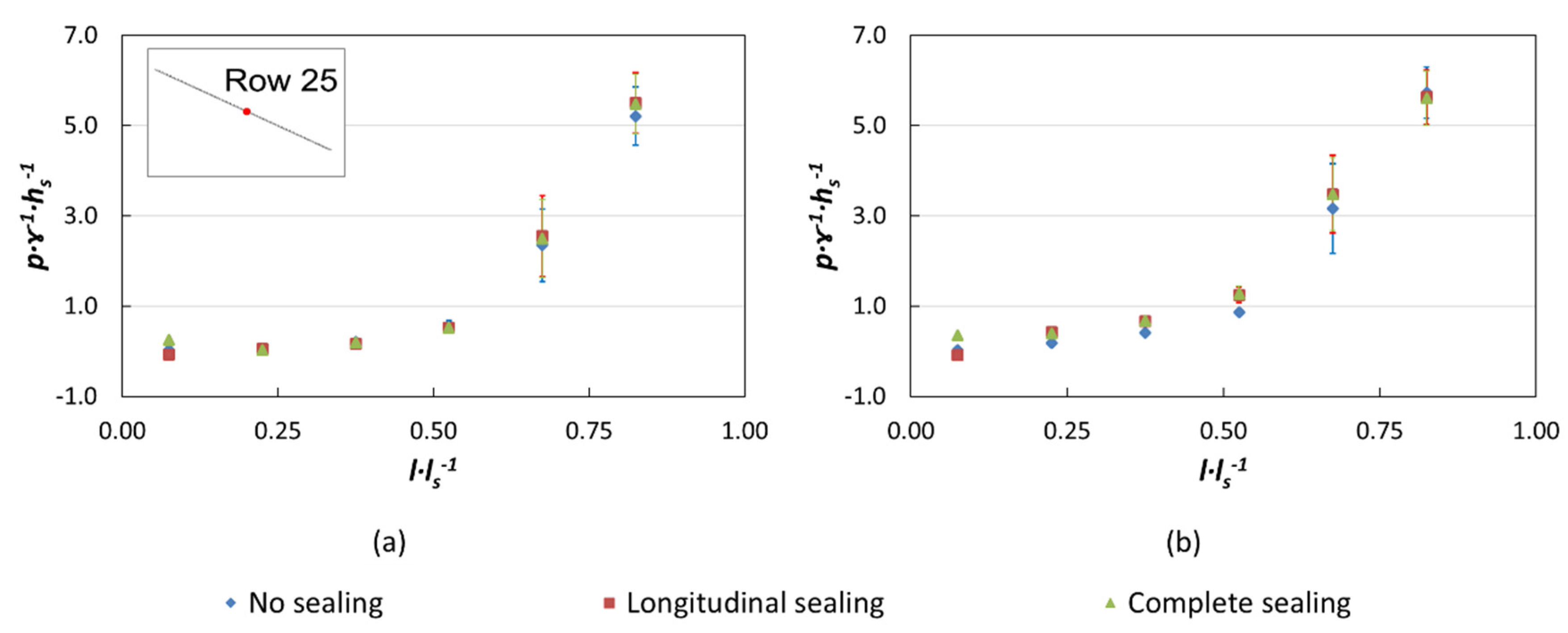
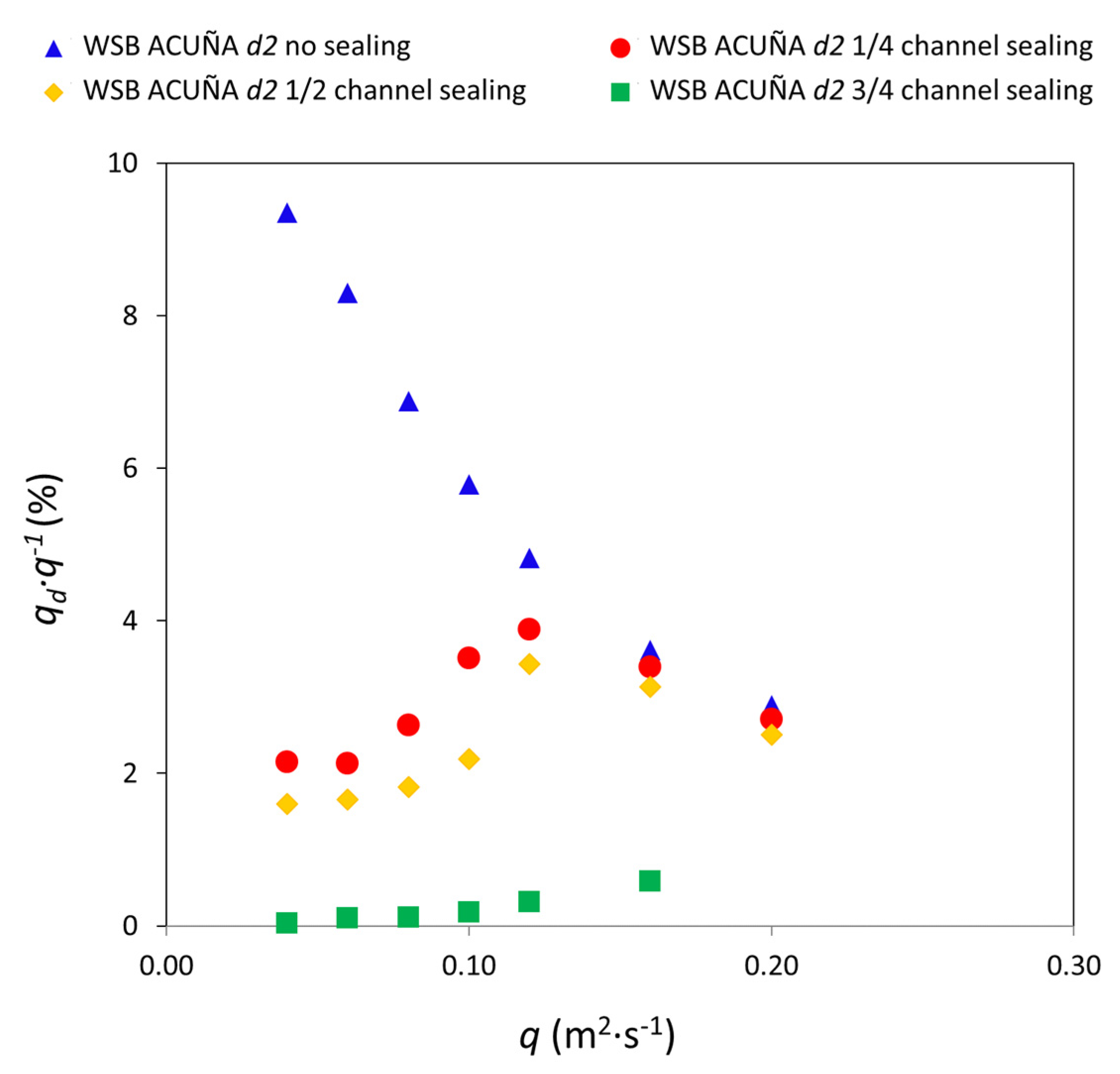
Effect of Sealing Joints between Blocks
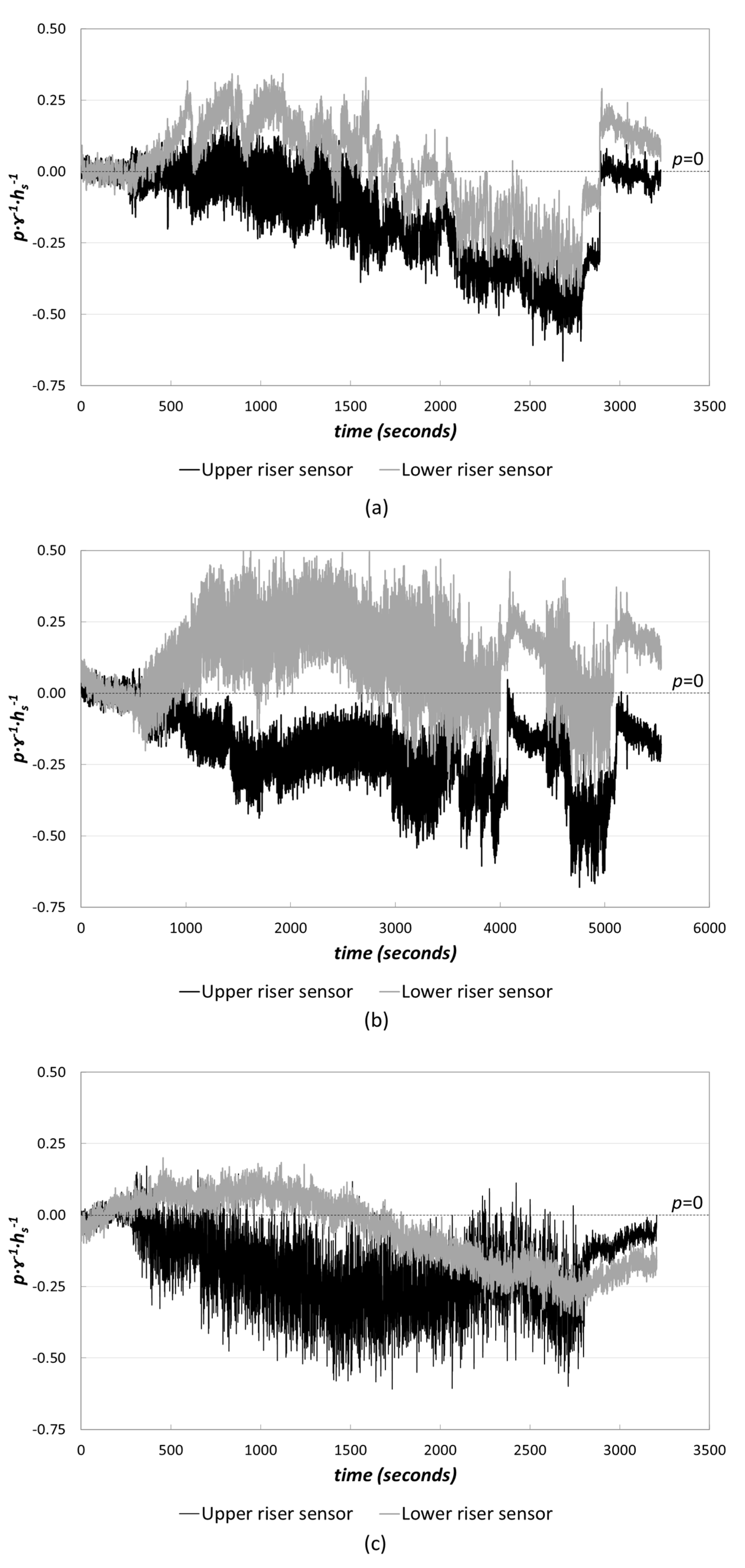
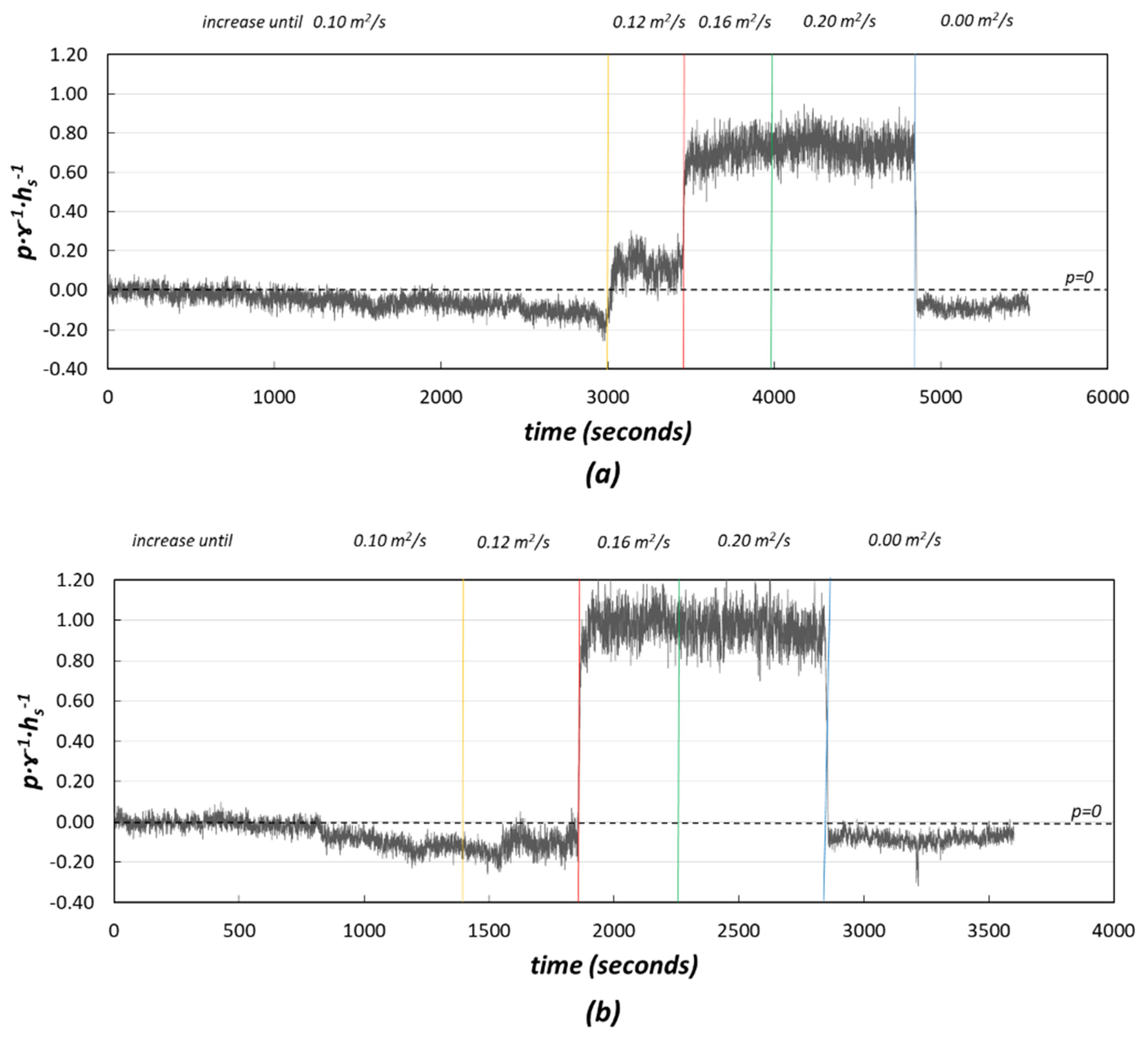
3.1.2. Pressures on the Block Riser
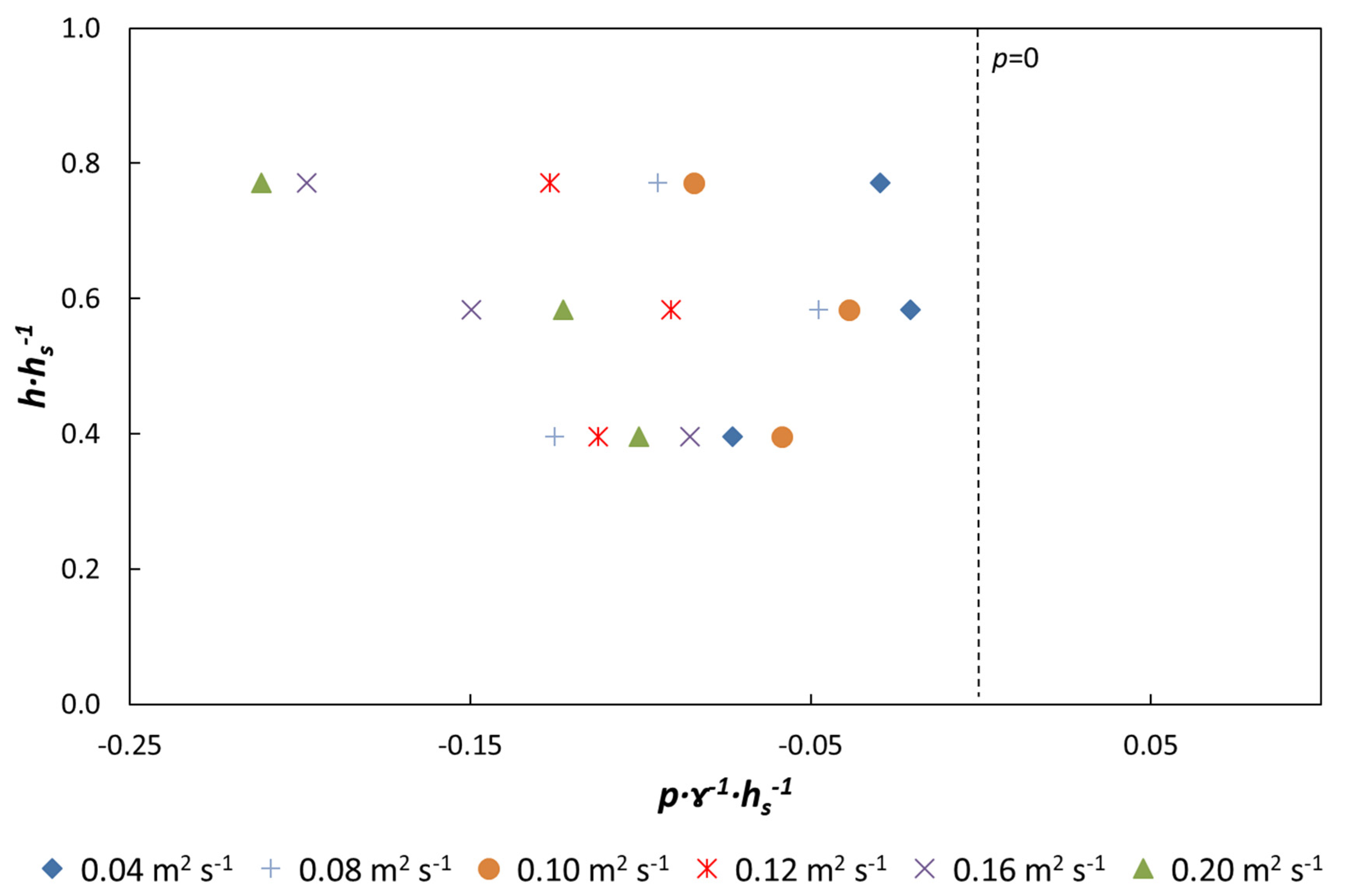
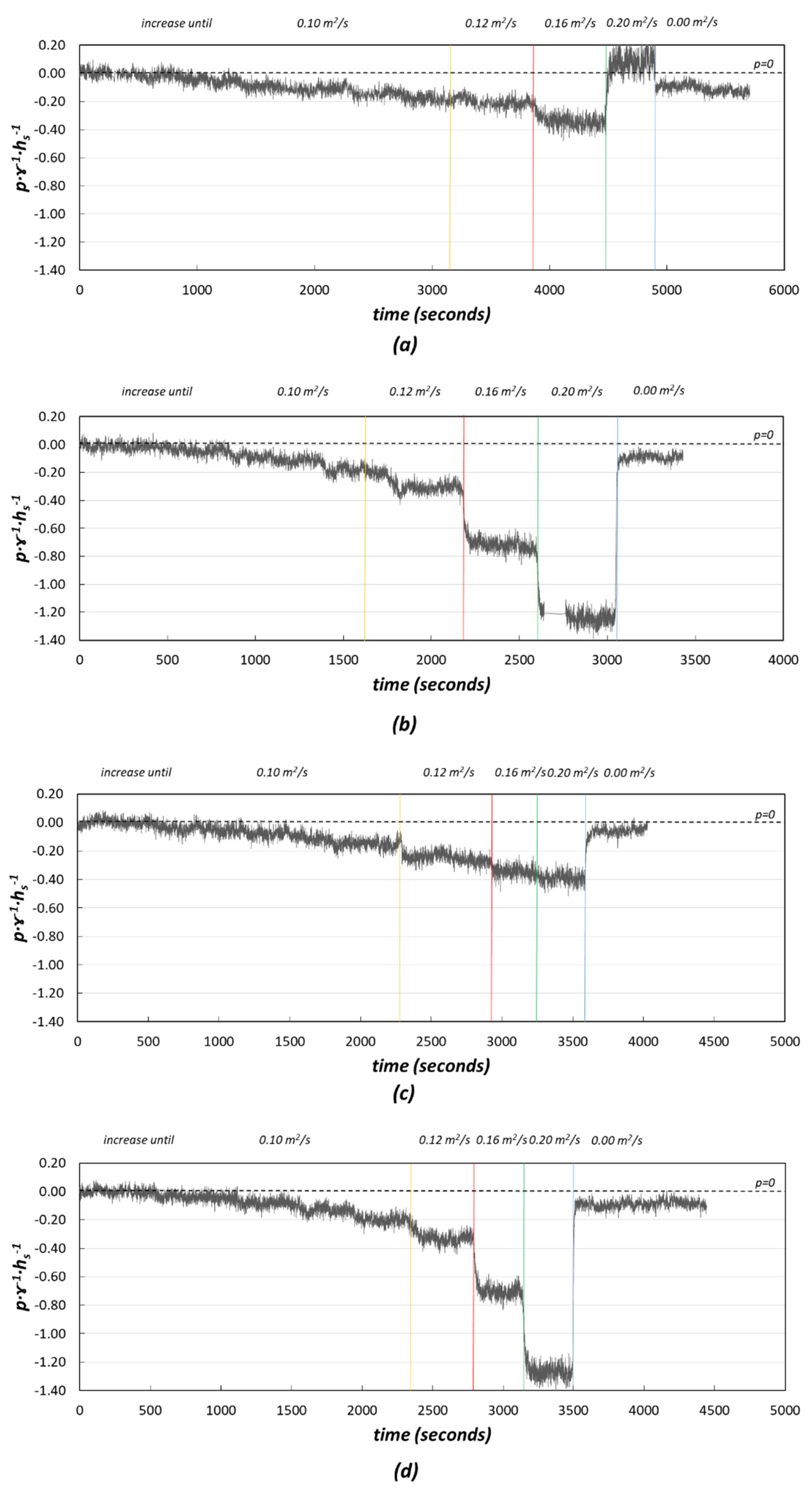
3.1.3. Pressures on the Base of the Block
ArmorwedgeTM Block (w1) Tests in Free Draining Scenario (d1)
Comparison of the ArmorwedgeTM (w1) and ACUÑA (w2) Blocks
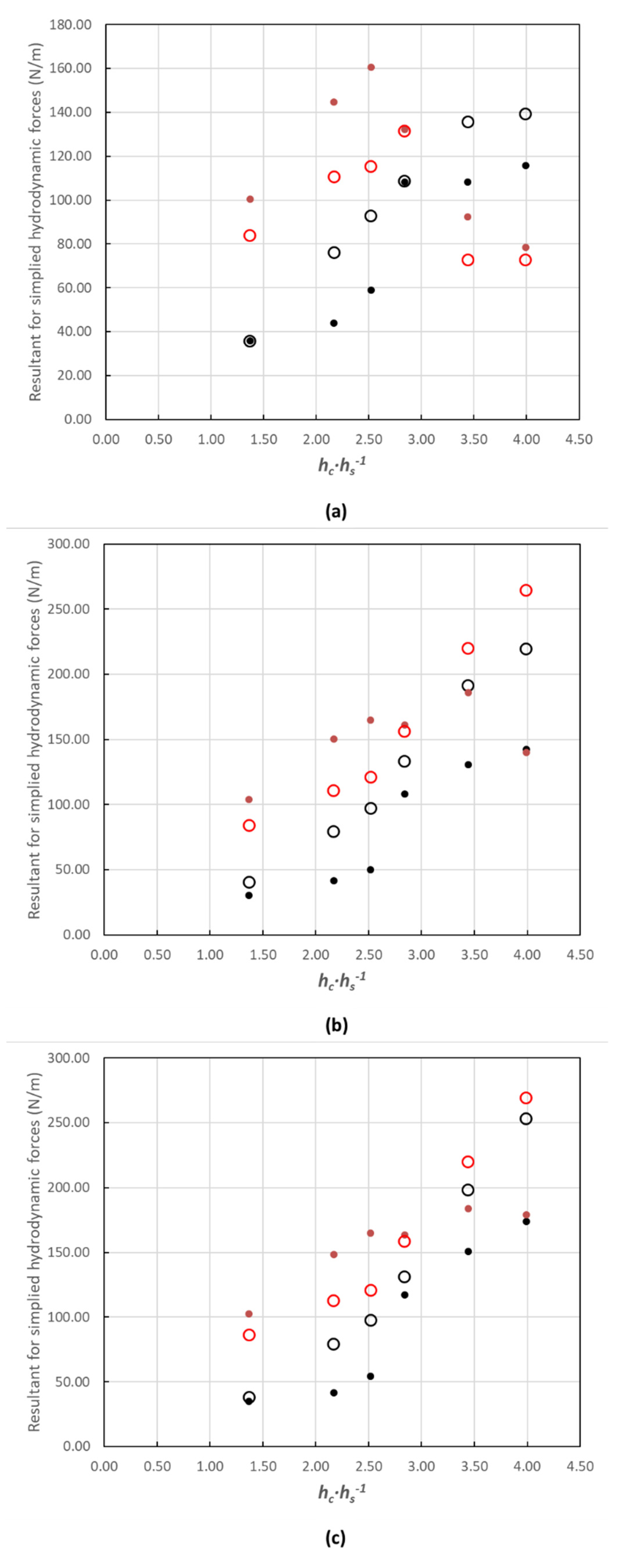
3.2. Hydrodynamic Forces on the WSBs
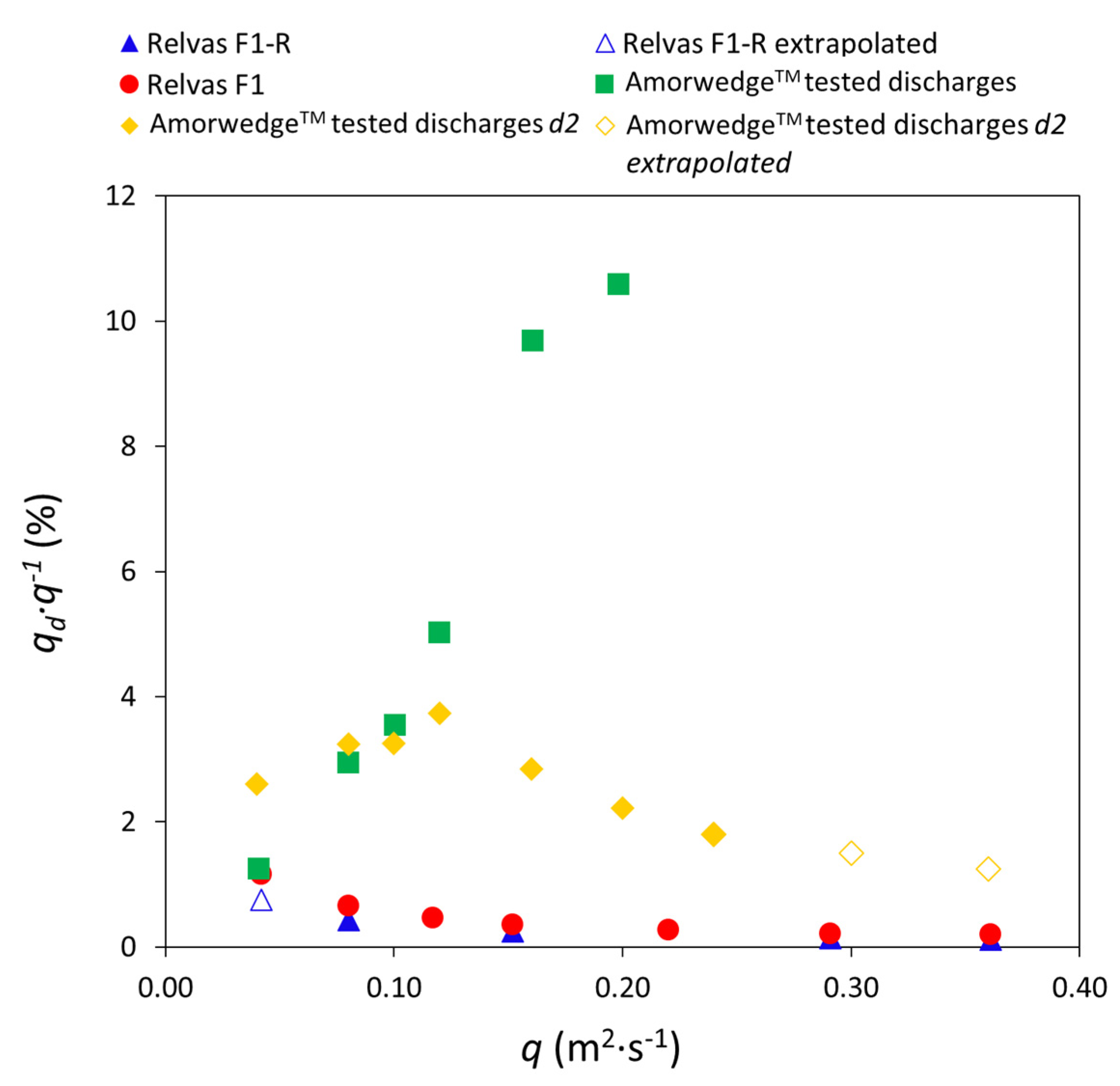
3.3. Drainage Flow
3.4. Effect of the Joints among WSBs on the Drainage Flow
4. Conclusions
- Hydrodynamic pressures on the blocks tread were similar for the ArmorwedgeTM and ACUÑA blocks, although a slightly higher pressure was observed on the ACUÑA block for the highest discharge flows in the lower part of the chute. Although a limited effect, this is favorable for the stability of the block.
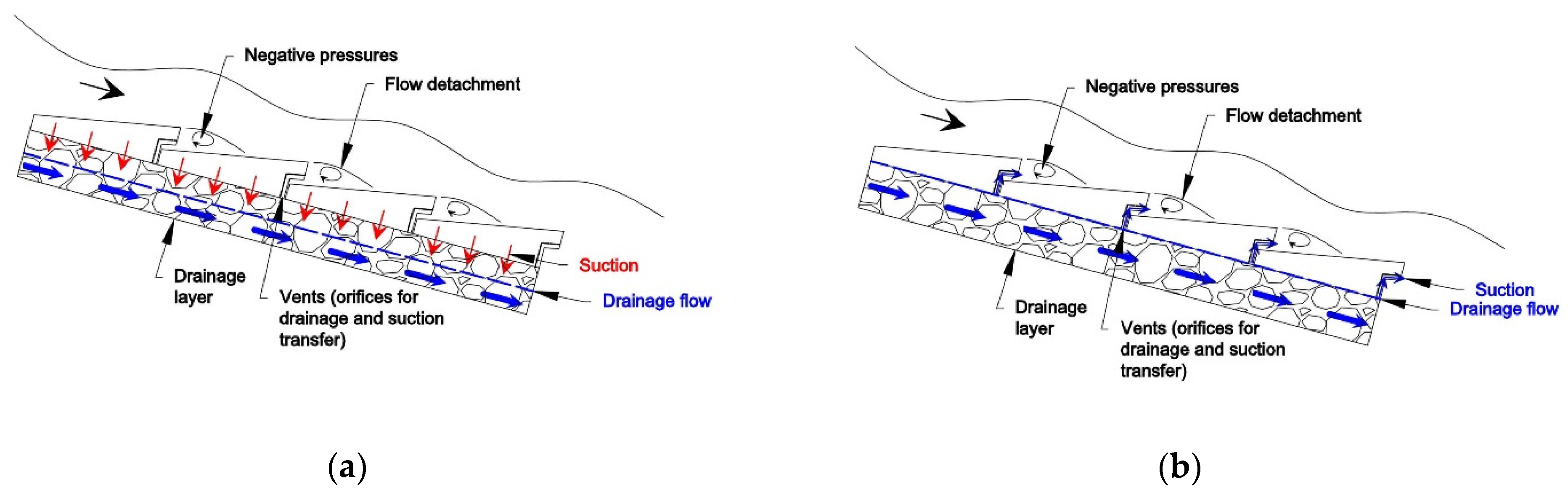
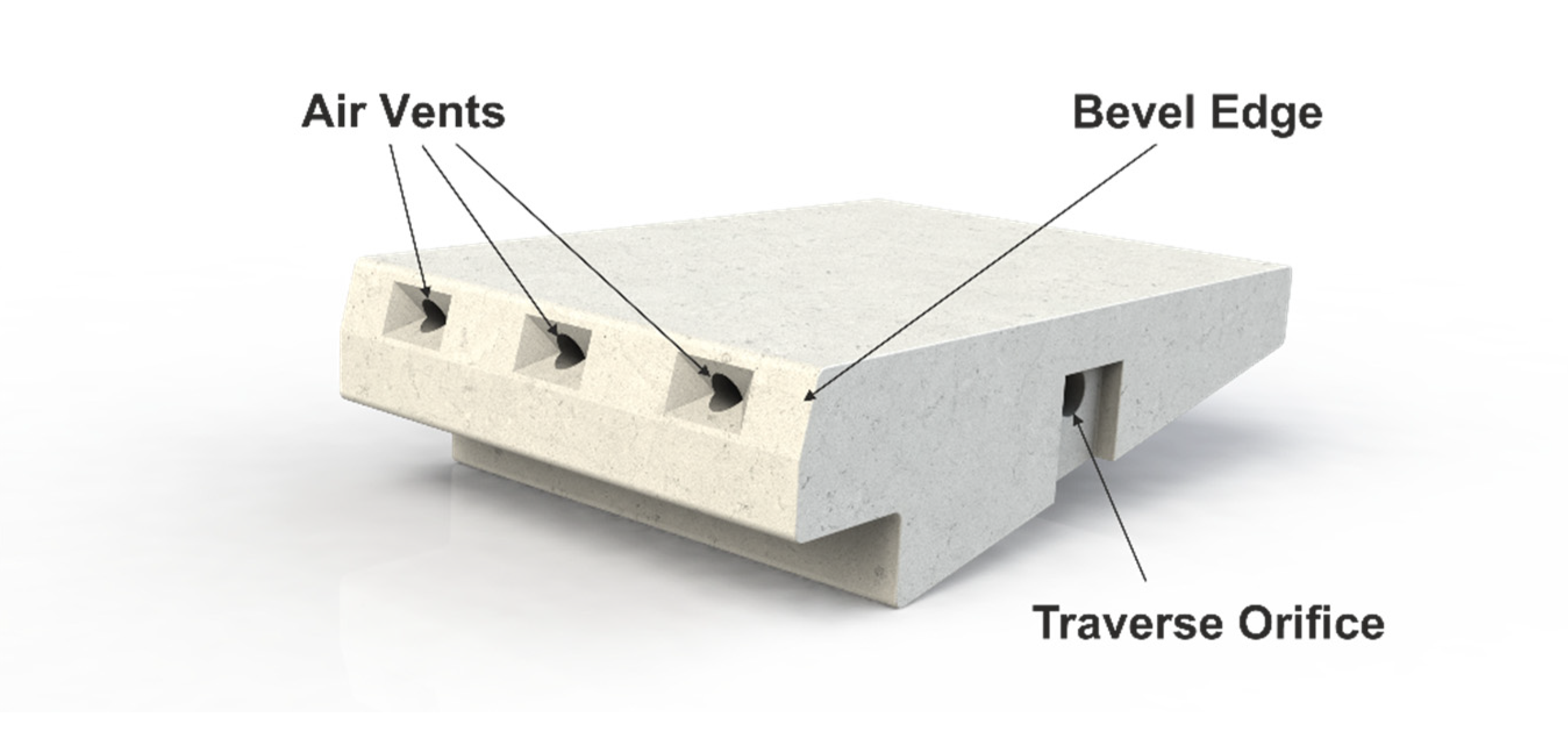
- Pressure records in the riser of the ACUÑA block were negative or close to zero, with the greatest suction located in the upper third of the riser. This fact was also previously observed by numerical modeling and led to the new WSB design, ACUÑA, with air vents in the upper part of the riser.
- Negative suction pressures were registered at the base of the two types of blocks when the drainage layer was not saturated. This is favorable for the stability of the block. The suction at the base was higher when the longitudinal joints between blocks were sealed. The effect of sealing just the upper part of the chute was remarkable. The leakage towards the drainage layer was significantly reduced, delaying or avoiding its saturation and, hence, the uplift force.
- The drainage flow rate increased significantly with the inlet discharge flow when the drainage layer was not saturated; however, it (expressed as a fraction of the inlet flow) decreased with inlet flow if the drainage layer was saturated.
- It should be noted that in some cases, positive pressures, although low, were detected in the lower part of the riser. In these cases, the air vents presumably allowed the water to enter the drainage layer if air vents were located at the base of the riser, as was the case for the ArmorwedgeTM block.
- In the upper part of the channel, the hydrodynamic stabilizing force increased systematically with the discharge flow. The ACUÑA block was more stable than the ArmorwedgeTM block for all the tested cases. In the lower part of the channel, the stabilizing force was reduced with the discharge flow due to the saturation of the drainage layer and uplift pressures appearing at the base of the block. In this situation, the ArmorwedgeTM block was more stable than the ACUÑA block.
- When the joints between blocks were sealed, and the drainage layer was unsaturated, the stabilizing forces increased with the discharge flow, and the ACUÑA block was more stable than the ArmorwedgeTM block for all cases with the skimming flow regime.
- In both WSBs, the longitudinal joints between blocks were the source of the highest percentage of the total leakage flow. In addition, these leaks came mostly from the upper area of the flume.
- Although joint sealing is not a usual practice, it is advisable to consider the benefits and implement a cost-effective way for sealing the joints in new WSB dam protection against overtopping or spillways, especially in the upper sections.
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cu | uniformity coefficient |
| d1 | free drainage condition |
| d2 | the granular layer drainage condition |
| D10 | size of which 10% of the particles, in weight, are finer (m) |
| D50 | size of which 50% of the particles, in weight, are finer (m) |
| F* | roughness Froude number |
| hc | critical depth |
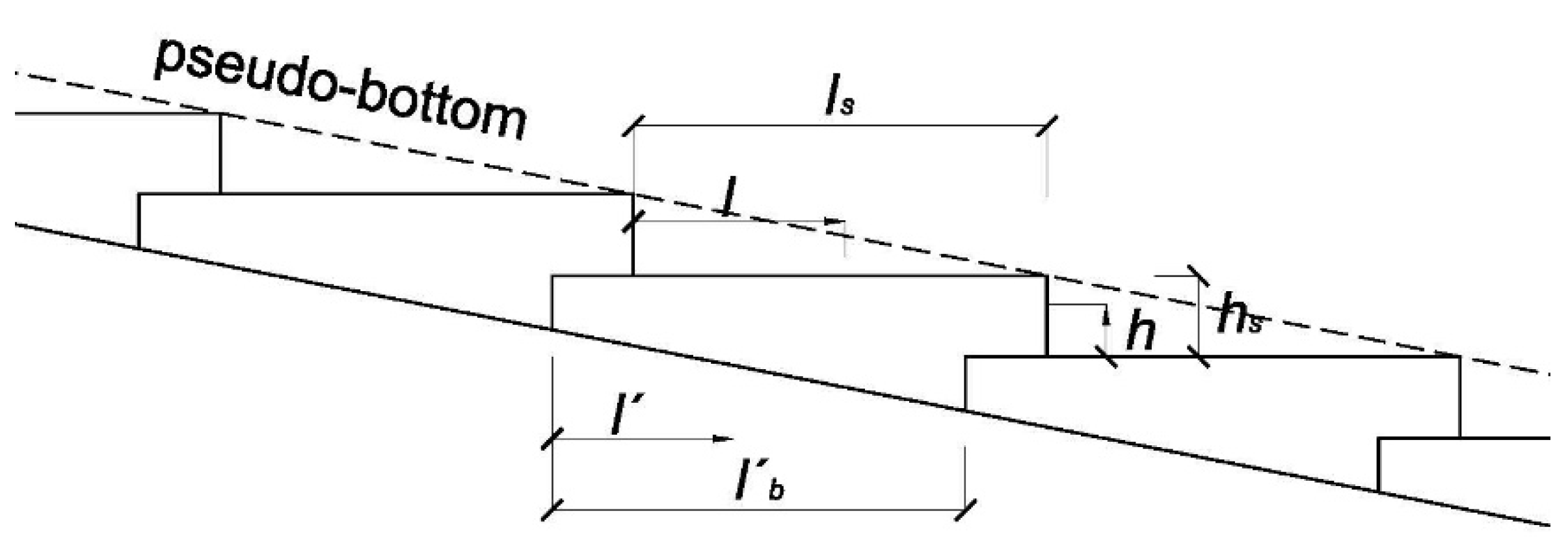
| hs | height of the block riser |
| Li | longitudinal distance between the critical depth position on the crest of the dam and the horizontal face where the inception point is located |
| Lu | longitudinal position from the dam or flume crest of the beginning of the quasi-uniform region |
| l | the partially exposed length of the top surface of the block |
| ls | the total exposed length of the top surface of the block |
| L′ | partial length of the base of the block |
| L′b | the total length of the base of the block |
| p | average hydrodynamic pressure |
| q | flow-rate inlet in the chute |
| qd | drainage flow-rate |
| w1 | ArmorwedgeTM block |
| w2 | ACUÑA block |
| x | coordinate horizontal to the crest of the dam |
| y | coordinate perpendicular to the crest of the dam |
| γ | water volumic weight |
| θ | the angle of the slope of the chute |
References
- FEMA. Technical Manual: Overtopping Protection for Dams; U.S. Department of Homeland Security: Washington, DC, USA, 2014.
- Grinchuk, A.S.; Pravdivets, Y.P.; Shekhtman, N.V. Test of earth slope revetments permitting flow of water at large specific discharges. Hydrotech. Constr. 1977, 11, 22–26. [Google Scholar] [CrossRef]
- Hewlett, H.; Baker, R.; May, R.; Pravdivets, Y.P. Design of Stepped-Block Spillways; Construction Industry Research and Information Association: London, UK, 1997. [Google Scholar]
- Pravdivets, Y.P.; Slissky, S.M. Passing floodwaters over embankment dams. Int. Water Power Dam Constr. 1981, 33, 30–32. [Google Scholar]
- Baker, R.; Gardiner, K. Construction and performance of a wedge block spillway at Brushes Clough reservoir. In Proceedings of the 8th Conference of the British Dam Society on Reservoir Safety and the Environment, Exeter, UK, 14–17 September 1994; pp. 214–223. [Google Scholar]
- Baker, R.; Pravdivets, Y.; Hewlett, H. Design considerations for the use of wedge-shaped precast concrete blocks for dam spillways. Proc. Inst. Civ. Eng. Water Marit. Eng. 1994, 106, 317–323. [Google Scholar] [CrossRef]
- Baker, R.; Gardiner, K.D. Building blocks. Int. Water Power Dam Constr. 1995, 47, 2. [Google Scholar]
- Bramley, M.; May, R.; Baker, R. Performance of Wedge-Shaped Blocks in High Velocity Flow—CIRIA Research Project 407 Stage 1 Report; CIRIA: London, UK, 1989; 163p. [Google Scholar]
- Bramley, M.; May, R.; Baker, R. Performance of Wedge-Shaped Blocks in High Velocity Flow—CIRIA Research Project 407 Stage 2 Laboratory Study; CIRIA: London, UK, 1991; 112p. [Google Scholar]
- Cloppper, P.E. Hydraulic Stability of Articulated Concrete Block Revetment Systems during Overtopping Flow; Federal Highway Administration: McLean, VA, USA, 1989.
- Slovensky, G.G., Jr. Near-Prototype Testing of Wedge-Block Overtopping Protection. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 1993. [Google Scholar]
- Gaston, M.L. Air Entrainment and Energy Dissipation on a Stepped Block Spillway. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 1995. [Google Scholar]
- Frizell, K.H. Protecting embankment dams with concrete stepped overlays. Hydro Rev. 1997, 16, 36–45. [Google Scholar]
- Frizell, K.H. ArmorwedgeTM Analysis Report: Block Size Scaling and Bedding Information, 2007; (Confidencial).
- Thornton, C.I.; Robeson, M.D.; Varyu, D.R. ArmorwedgeTM Data Report 2006 Testing for Armortec Erosion Control Solutions; Unpublished manuscript (Confidential).
- Relvas, A.T.; Pinheiro, A.N. Closure of “Inception Point and Air Concentration in Flows on Stepped Chutes Lined with Wedge-Shaped Concrete Blocks”. J. Hydraul. Eng. 2010, 136, 86–88. [Google Scholar] [CrossRef]
- Relvas, A.T. Descarregadores de Cheias de Blocos de Betão Prefabricados em Forma de Cunha sobre Barragens de Aterro. Ph.D. Thesis, Instituto Superior Técnico, Universidade Tecnica de Lisboa, Lisbon, Portugal, 2008. (In Portuguese). [Google Scholar]
- Relvas, A.T.; Pinheiro, A.N. Inception Point and Air Concentration in Flows on Stepped Chutes Lined with Wedge-Shaped Concrete Blocks. J. Hydraul. Eng. 2008, 134, 1042–1051. [Google Scholar] [CrossRef]
- Relvas, A.T.; Pinheiro, A.N. Stepped chutes lined with wedge-shaped concrete blocks: Hydrodynamic pressures on blocks and stability analysis. Can. J. Civ. Eng. 2011, 38, 338–349. [Google Scholar] [CrossRef]
- Relvas, A.T.; Pinheiro, A.N. Velocity Distribution and Energy Dissipation along Stepped Chutes Lined with Wedge-Shaped Concrete Blocks. J. Hydraul. Eng. 2011, 137, 423–431. [Google Scholar] [CrossRef]
- Morán, R. Wedge-shaped Blocks: A Historical Review. In Proceedings of the 2nd International Seminar on Dam Protections against Overtopping Protections 2016, Colorado State University (CSU), Fort Collins, CO, USA, 7–9 September 2016; Available online: https://mountainscholar.org/handle/10217/179790 (accessed on 16 February 2017).
- Morán, R.; Toledo, M.A. Design and construction of the Barriga dam spillway through an improved wedge-shaped block technology. Can. J. Civ. Eng. 2014, 41, 924–927. [Google Scholar] [CrossRef]
- Pether, R.; Marsh, P.; Cartwright, P. An innovative new spillway for bruton flood storage reservoir. Dams Reserv. 2009, 19, 67–72. [Google Scholar] [CrossRef]
- Booth, N. Technical visit: Grane Valley reservoir spillway improvements. Dams Reserv. 2012, 22, 113–115. [Google Scholar] [CrossRef]
- Thomson, D. United Efforts at Grane Valley Reservoir. Water Power and Dams Construction. 2014. Available online: http://www.waterpowermagazine.com/features/featureunited-efforts-at-grane-valley-reservoir-4273851/ (accessed on 26 May 2014).
- Morton, D.; Binnie, M.; Christopher; Crowson, D.; Herrington, J.; Marsh, P.; Seaton, M. Norton Fitzwarren Flood Alleviation Dam. Available online: http://www.hyderconsulting.com/insights/Documents/ (accessed on 6 April 2016).
- Caballero, F.J.; Toledo, M.A.; San Mauro, J.; Salazar, F. Physical and numerical modeling for understanding the hydraulic behavior of wedge-shaped-blocks (WSB) spillways. In Dam Protections against Overtopping and Accidental Leakage; CRC Press: Boca Raton, FL, USA, 2015; pp. 193–206. ISBN 978-1-138-02808-1. [Google Scholar]
- Caballero, F.J.; San Mauro, J.; Toledo, M.A.; Moran, R.; Salazar, F. Advances in the understanding of the hydraulic behavior of wedge-shape block spillways. In Proceedings of the 2nd International Seminar on Dam Protections against Overtopping, Protections 2016, Colorado State University (CSU), Fort Collins, CO, USA, 7–9 September 2016; Available online: https://mountainscholar.org/handle/10217/179781 (accessed on 16 February 2017).
- San Mauro, J.; Larese, A.; Salazar, F.; Irazábal, J.; Morán, R.; Toledo, M.Á. Hydraulic and stability analysis of the supporting layer of wedge-shaped blocks. In Proceedings of the 2nd International Seminar on Dam Protections against Overtopping and Accidental Leakage, Protections 2016, Colorado State University (CSU), Fort Collins, CO, USA, 7–9 September 2016; Available online: https://mountainscholar.org/handle/10217/179782 (accessed on 16 February 2017).
- Caballero, F.J.; San Mauro, J.; Toledo, M.A.; Morán, R.; Salazar, F.; Moreno, E. A new evolution on the wedge-shaped block for overtopping protection of embankment dams. In Proceedings of the 3nd International Seminar on Dam Protections against Overtopping, Protections 2018, Grange-over-Sands, UK, 6–8 June 2018; Available online: http://eprints.hrwallingford.co.uk/1519/ (accessed on 2 April 2020).
- Mauro, J.S.; Toledo, M.; Salazar, F.; Caballero, F.F.J. A methodology for the design of dam spillways with wedge shaped blocks based on numerical modeling. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2019, 35. Available online: https://www.scipedia.com/public/San_Mauro_et_al_2018a (accessed on 8 February 2019). [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Gabriel-Martín, I.; Sordo-Ward, Á.; Garrote, L. Influence of initial reservoir level on the allocation of seasonal maximum conservation levels/Influencia del nivel inicial en la definición de resguardos estacionales en presas. Ing. Agua 2018, 22, 225–238. Available online: https://polipapers.upv.es/index.php/ia/article/view/9526 (accessed on 8 February 2019). (In Spanish). [CrossRef]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; Granados, I. Hydrological Risk Analysis of Dams: The Influence of Initial Reservoir Level Conditions. Water 2019, 11, 461. [Google Scholar] [CrossRef]
- Garijo, C.; Mediero, L.; Garrote, L. Usefulness of AEMET generated climate projections for climate change impact studies on floods at national-scale (Spain)/Utilidad de las proyecciones climáticas generadas por AEMET para estudios de impacto del cambio climático sobre avenidas a escala nacional. Ing. Agua 2018, 22, 153–166. Available online: https://polipapers.upv.es/index.php/IA/article/view/9312 (accessed on 8 February 2019). (In Spanish) [CrossRef]
- Garijo, C.; Mediero, L. Assessment of Changes in Annual Maximum Precipitations in the Iberian Peninsula under Climate Change. Water 2019, 11, 2375. [Google Scholar] [CrossRef]
- Quintero, F.; Mantilla, R.; Anderson, C.; Claman, D.; Krajewski, W. Assessment of Changes in Flood Frequency Due to the Effects of Climate Change: Implications for Engineering Design. Hydrology 2018, 5, 19. [Google Scholar] [CrossRef]
- Soriano, E.; Mediero, L.; Garijo, C. Quantification of Expected Changes in Peak Flow Quantiles in Climate Change by Combining Continuous Hydrological Modelling with the Modified Curve Number Method. Water Resour. Manag. 2020, 34, 4381–4397. [Google Scholar] [CrossRef]
- Chamani, M.R.; Rajaratnam, N. Onset of skimming flow on stepped spillways. J. Hydraul. Eng. 1999, 125, 969–971. [Google Scholar] [CrossRef]
- André, S. High Velocity Aerated Flow on Stepped Chutes with Macro-Roughness Elements. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland, 2004. [Google Scholar]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Chanson, H. State of the art of the hydraulic design of stepped chute spillways. Int. J. Hydropower Dams 1994, 1, 33–42. [Google Scholar]
- Matos, J. Emulsionamento de Ar e Dissipação de Energia do Escoamento em Descarregadores em Degraus. Ph.D. Thesis, Technical University of Lisbon, Lisbon, Portugal, 1999. [Google Scholar]
- Yasuda, Y.; Ohtsu, I. Flow resistance of skimming flow in stepped channels. In Proceedings of the 28th IAHR Congress, Graz, Austria, 22–27 August 1999; Volume B14. [Google Scholar]
- Mateos, I.; Elviro, G. Initiation of aeration in stepped spillways. In Proceedings of the 27th IAHR Congress, Theme D, ASCE, San Francisco, CA, USA, 10–15 August 1997; pp. 589–594. [Google Scholar]
- Chanson, H. Hydraulic design of stepped spillways and downstream energy dissipators. Dam Eng. 2001, 11, 205–242. [Google Scholar]
- Boes, R.; Minor, H.E. Guidelines for the Hydraulic Design of Stepped Spillways. In Proceedings of the International Workshop on Hydraulics of Stepped Spillways, Zurich, Switzerland, 22–24 March 2000; Minor, H.-E., Hager, W., Eds.; Balkema: Boca Raton, FL, USA, 2000; pp. 163–170. [Google Scholar]
- Christodoulou, G. Design of stepped spillways for optimal energy dissipation. Int. J. Hydropower Dams 1999, 5, 90–93. [Google Scholar]
- Frizell, K.H.; Smith, D.H.; Ruff, J.F. Stepped overlays proven for use in protecting overtopped embankment dams. In Proceedings of the ASDSO Annual Conference on Dam Safety, Boston, MA, USA, 9–13 September 1994; pp. 11–14. [Google Scholar]

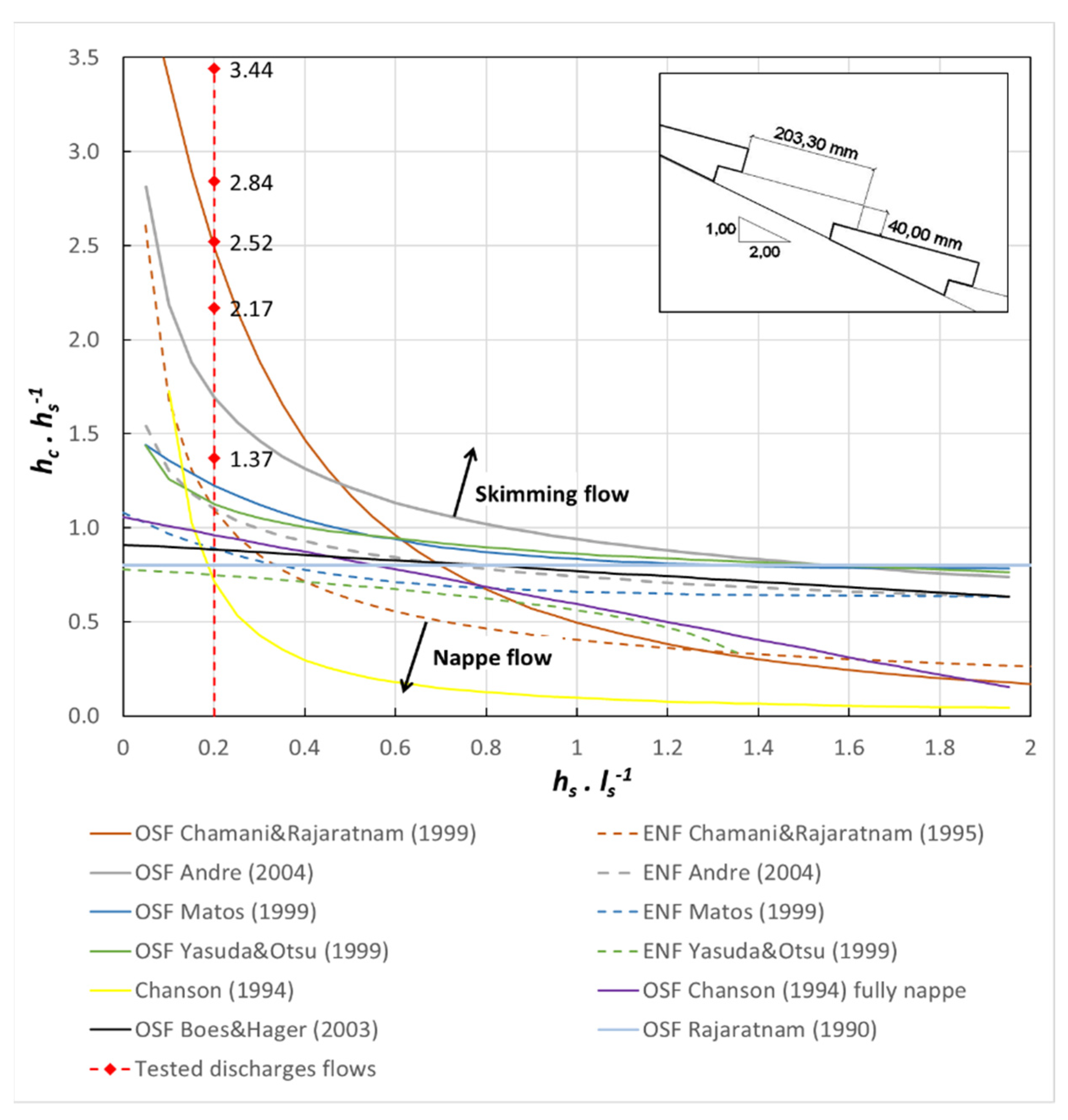
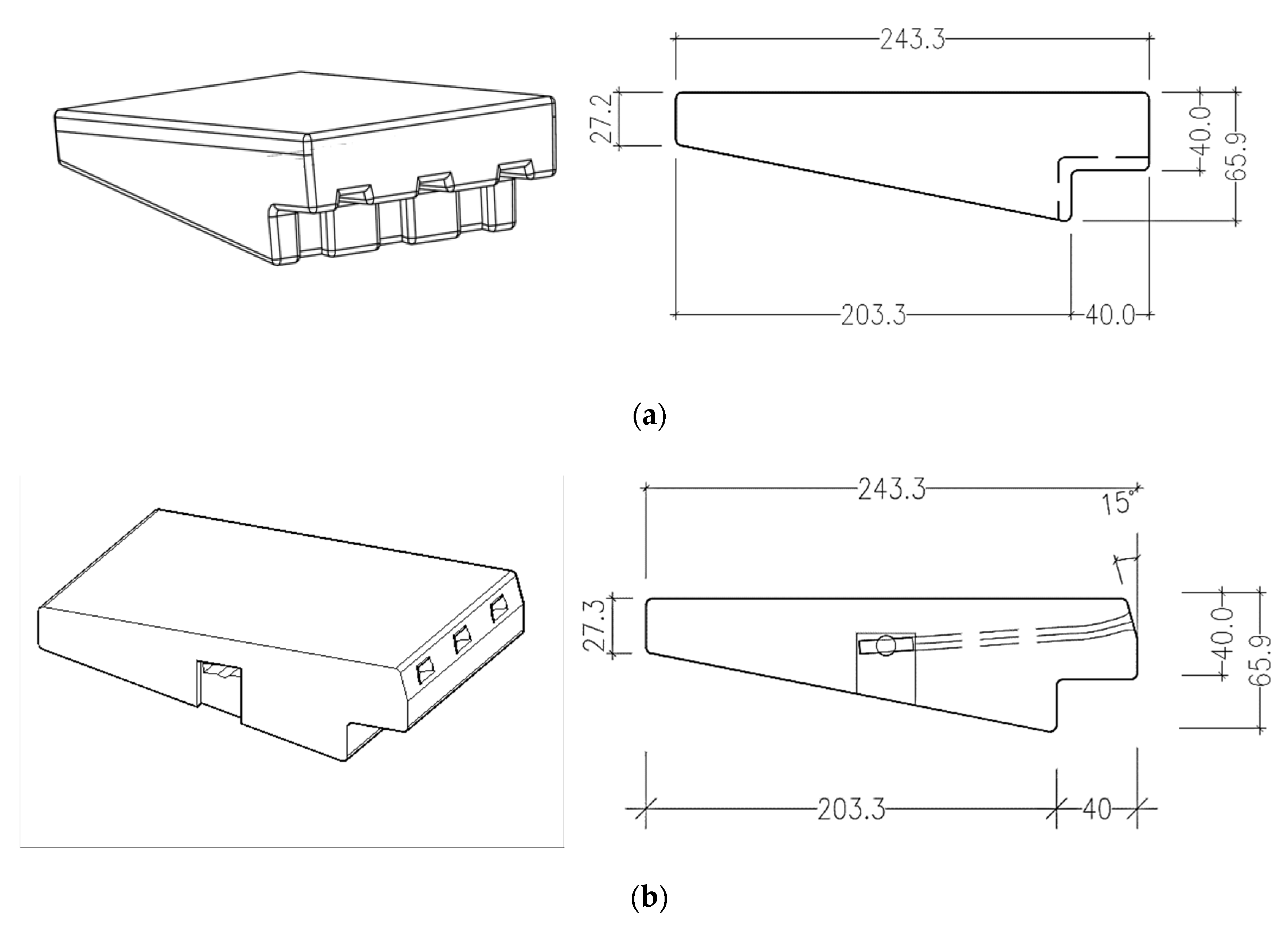


| h′ (hc hs−1) | 4.51 | 3.99 | 3.44 | 2.84 | 2.52 | 2.17 | 1.37 |
| q (m2 s−1) | 0.24 | 0.20 | 0.16 | 0.12 | 0.10 | 0.08 | 0.04 |
| Flow Rate q (m2 s−1) | H′ (hc hs−1) | Row Number | Distance of the Inception Point Li | |||
|---|---|---|---|---|---|---|
| Observed | Observed Interval | Relvas [18] | Chanson [43] | Matos [44] | ||
| 0.04 | 1.37 | 3 | 673–880 | 779 | 684 | 617 |
| 0.08 | 2.17 | 4–5 | 1035–1293 | 1283 | 1121 | 1035 |
| 0.10 | 2.52 | 5–6 | 1190–1500 | 1507 | 1314 | 1223 |
| 0.12 | 2.84 | 6 | 1293–1500 | 1718 | 1496 | 1401 |
| 0.16 | 3.44 | 6–7 | 1293–1707 | 2114 | 1837 | 1737 |
| 0.20 | 3.99 | 7–8 | 1500–1914 | 2482 | 2154 | 2053 |
| 0.24 | 4.51 | 9–10 | 1914–2328 | 2831 | 2453 | 2352 |
| Flow Rate q (m2 s−1) | h′ (hc hs−1) | Uniform Flow Depth Location (m) | |||||
|---|---|---|---|---|---|---|---|
| CIRIA Guide Hewlett et al. [3] | Boes and Minor [48] | Relvas [18] | |||||
| Distance (m) | Row | Distance (m) | Row | Distance (m) | Row | ||
| 0.04 | 1.37 | 1.09 | 5 | 1.83 | 8 | 1.56 | 7 |
| 0.08 | 2.17 | 1.73 | 8 | 2.91 | 13 | 2.57 | 12 |
| 0.10 | 2.52 | 2.01 | 9 | 3.38 | 16 | 3.01 | 14 |
| 0.12 | 2.84 | 2.27 | 10 | 3.81 | 18 | 3.44 | 16 |
| 0.16 | 3.44 | 2.75 | 13 | 4.62 | 22 | 4.23 | 20 |
| 0.20 | 3.99 | 3.20 | 15 | 5.36 | 25 | 4.96 | 23 |
| 0.24 | 4.51 | 3.61 | 17 | 6.05 | 28 | 5.66 | 27 |
| WSB | Drainage Conditions | q (m2 s−1) | Measured Variables | Joints and Air Vents Conditions | Number of Tests Performed |
|---|---|---|---|---|---|
| w1 | d1 | 0.04–0.24 | P on rows 5 and 25/L | Without sealing | 3 |
| P on rows 10 and 30/L | Without sealing | 2 | |||
| P on rows 15 and 35/L | Without sealing | 2 | |||
| P on rows 15 and 43/L | Without sealing | 1 | |||
| L | Without sealing | 1 | |||
| L | LJ sealing | 1 | |||
| L | LJ and TJ sealing | 1 | |||
| w2 | d1 | 0.04–0.24 | L | Without sealing | 1 |
| LJ sealing | 1 | ||||
| LJ and TJ sealing | 1 | ||||
| d2 | 0.04–0.20 | P on rows 10 and 25/L | Without sealing | 2 | |
| LJ sealing | 2 | ||||
| LJ and TJ sealing | 2 | ||||
| w1 | d2 | 0.04–0.20 | P on rows 10 and 25/L | Without sealing | 1 |
| LJ sealing | 1 | ||||
| LJ and TJ sealing | 1 | ||||
| w2 | d2 | 0.04–0.20 | L | Without sealing | 1 |
| LJ and TJ sealing of rows 1 to 8. | 1 | ||||
| LJ/TJ/AV sealing of rows 1 to 8. | 1 | ||||
| LJ and TJ sealing of rows 1 to 16. | 1 | ||||
| LJ/TJ/AV sealing of rows 1 to 16. | 1 | ||||
| LJ and TJ sealing of rows 1 to 24. | 1 | ||||
| LJ/TJ/AV sealing of rows 1 to 24. | 1 | ||||
| LJ and TJ sealing of rows 1 to 32. | 1 | ||||
| LJ/TJ/AV sealing of rows 1 to 32. | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caballero, F.J.; Toledo, M.Á.; Moran, R.; San Mauro, J. Hydrodynamic Performance and Design Evolution of Wedge-Shaped Blocks for Dam Protection against Overtopping. Water 2021, 13, 1665. https://doi.org/10.3390/w13121665
Caballero FJ, Toledo MÁ, Moran R, San Mauro J. Hydrodynamic Performance and Design Evolution of Wedge-Shaped Blocks for Dam Protection against Overtopping. Water. 2021; 13(12):1665. https://doi.org/10.3390/w13121665
Chicago/Turabian StyleCaballero, Francisco Javier, Miguel Ángel Toledo, Rafael Moran, and Javier San Mauro. 2021. "Hydrodynamic Performance and Design Evolution of Wedge-Shaped Blocks for Dam Protection against Overtopping" Water 13, no. 12: 1665. https://doi.org/10.3390/w13121665
APA StyleCaballero, F. J., Toledo, M. Á., Moran, R., & San Mauro, J. (2021). Hydrodynamic Performance and Design Evolution of Wedge-Shaped Blocks for Dam Protection against Overtopping. Water, 13(12), 1665. https://doi.org/10.3390/w13121665









