Abstract
Spillways with Highly Converging Chutes (HCCs) are a non-conventional alternative that can be applied to achieve a higher outflow capacity when the weir length exceeds the width of the valley at the toe of gravity or arch dams. This kind of spillway has been used in the past, but no general studies have yet been published. This article summarizes experimental research work aiming to increase the knowledge of the effect of some design parameters of HCCs on the energy dissipation in the stilling basin at the toe of the dam. As a comparison reference, we use the Type I stilling basins, widely known by the technical dam engineering community. The obtained results show that spillways with HCCs are a promising alternative to traditional designs, combining the ability to increase the weir length with a high capacity to dissipate energy through the impingement effect of the frontal and the side jets inside the stilling basin.
Keywords:
spillway; dam; stilling basin; bucket; chute; flood; weir; safety; protection; dam protection 1. Introduction
Increasing flooding due to climate change along with more restrictive modern criteria for dam safety have necessitated comprehensive reviews of the design of the spillways of existing dams. Thus, recent research [1,2,3,4,5,6,7,8] has been conducted to deepen our knowledge of methods for increasing the discharge capacity of spillways. In addition, new technical guidelines for dam protection against overtopping [9,10,11] have been published to ensure dam safety during extreme floods, when the spillway is not able to pass the outlet discharge and the dam crest is overtopped.
The use of highly convergent chutes (HCCs) can be a cost-effective alternative to increase the length of the spillway weir (i.e., increase the spillway capacity) in concrete dams. This type of spillway is characterized by a concrete chute downstream that changes the direction of the inlet flow and leads it to a central area of the river valley (Figure 1a). Thus, the wall of this chute is highly convergent (Figure 1b) in comparison with the usual design criteria for the maximum convergence of the sidewalls of spillway chutes [12].
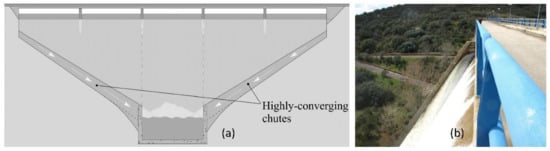
Figure 1.
(a) Scheme of the HCCs of a gravity dam from downstream [13]. (b) View of one of the HCCs of Torre de Abraham Dam (Spain) in operation (courtesy of José R. González).
HCCs have been successfully adopted in several cases such as the Hammam Grouz Dam (Algeria); Vatnsfell (Iceland); Asari, Atagi, Chubetsu, Haidsuka, Kodama, Fukutomi, Fukashiro, Nunome, Ishigoya, Masudagawa, Onbe, Oonagami, Origawa, Sasakura, Shikogawa, Shinmiyagawa, Tomada, and Yasutomi Dams (Japan); Pagade Dam (Portugal); and Baíña, Doña Ana, Rambla del Moro, Torre de Abraham, Vilasouto, and Zapardiel Dams (Spain) [13,14]. There is also a case of HCCs being used to protect the downstream toe of the dam against potential scour caused by overtopping flow (Tygart Dam, USA) [15]. A similar design of converging walls was applied to prevent scour at the abutment groin areas for the overtopping protection of embankment dams formed by lifts of roller-compacted concrete (Spring Creek Dam, USA) [5,11,16,17,18].
Even though HCCs have been successfully applied, design criteria and knowledge are lacking on the performance of the energy dissipation in comparison with other alternatives such as stilling basins or flip buckets. Thus, in most cases, the experience of the engineer, with the support of either physical or numerical modeling (or both), has been the only resource used to construct a suitable design. This context motivated the beginning of a new research effort, aimed to determine the effect of HCCs in the energy dissipation of the Type I stilling basin, as originally defined by the Bureau of Reclamation (BOR) [19]. This article summarizes part of our experimental research.
2. Aim and Scope
As mentioned above, the general aim of this study was to conduct experimental research on the energy dissipation of HCCs in Type I stilling basins to enable cost-effective design when adapting the stilling basins of existing dams to the operation of new flow inlets from newly added HCCs for purposes such as [13]:
- Increasing the spillway capacity.
- Protecting the downstream toe of the dam abutments against potential scour caused by overtopping.
- Enhancing the reservoir storage by increasing the full supply level, preserving the existing freeboards and the former capacity of the spillway.
In addition, the findings of the study are helpful for designing HCCs in new dam projects, where the length of the spillway weir may exceed the width of the floodplain of the river downstream, and the preferred option for the energy dissipation is a stilling basin.
The Type I basin mainly achieves energy dissipation through the formation of a hydraulic jump inside it when the inlet discharge (hereinafter referred to as frontal discharge) from the chute enters the basin following its longitudinal direction [19,20,21,22]. However, when side jets from HCCs impinge the flow from the frontal discharge, their collision causes a highly turbulent and complex pattern of flow within the basin [23]. This fact leads to a new energy dissipation process that differs drastically from the one provoked by a hydraulic jump.
Our secondary goals were:
- To establish objective criteria for the suitable hydraulic conditions of the flow downstream from the stilling basin to enable the appropriate restitution of the flow to the riverbed according to widely accepted technical guidelines.
- To perform a conceptual study of the effect of key HCCs design parameters on the energy dissipation at the stilling basin.
- To assess the design adaptation needs of existing stilling basins depending on the increase in the outlet discharge.
- To obtain experimental data to calibrate and validate numerical models for future research.
3. Methodology
This research was based on a set of tests performed at the hydraulic laboratory of the engineering college of Caminos, Canales y Puertos of the Universidad Politécnica de Madrid (Spain). The methodology of the research is summarized below through a brief description of the experimental facility and the procedures followed during the tests.
3.1. Experimental Facility
The experimental facility was used to simulate a typical gravity dam profile where different configurations of the spillway could be set. The physical model was obtained from previous studies on this topic [13], and was specifically adapted for the current investigation. The facility had the following features:
- Maximum length of the weir (Ww): 5 m
- Height of the weir over the bottom of the stilling basin (Hw): 1.5 m
- Vertical upstream slope of the cross-section of the gravity dam
- Downstream slope of the cross-section of the gravity dam: 0.8 H:V
- Width of the stilling basin (Wb): 1 m
- Maximum length of the stilling basin (Lb): 3.7 m
- Maximum height of the sidewalls of the stilling basin (Hb): 0.5 m
The model was set up to allow changing the length of the weir by adding (or removing) 0.5 m-wide steel plates (up to a maximum of 4 plates on each side of the central meter), which could be fixed to the upstream face of the dam body by screws (Figure 2). Thus, the weir length could be set to 1 m (as shown in Figure 2) for the case of frontal discharge only; and 2, 3, 4, to a maximum of 5 m for the tests where side jets (Qs) and frontal (Qf) discharges were combined. In every test, the symmetry of the inlet flow at the stilling basin remained unchanged. Two vertical steel plates (inlet plates in Figure 2), transversely placed to the longitudinal axis of the gravity dam, were placed on both sides of the upstream area of the weir to maintain appropriate inlet conditions over the weir, i.e., to ensure an orthogonal direction of the inlet flow with respect to the longitudinal axis of the weir in all tests.
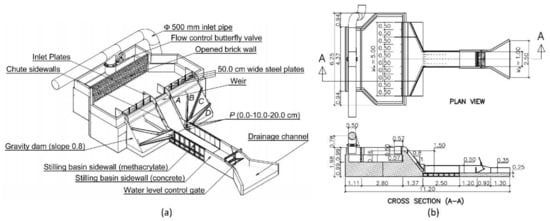
Figure 2.
Experimental facility: (a) 3D scheme with the main parts and the setup configurations A, B, C and D, and (b) plan view and longitudinal cross-section.
In the case of the inlet with only frontal discharge (i.e., 1 m long weir), the steel sidewalls of the chute were vertical; this configuration was termed A. In addition, three couples of steel HCCs (configurations B, C, and D) were formed to be able to change the direction of the side jets (Figure 2). The direction was defined by the angle of the bottom of the HCCs (α) with respect to the horizontal plane, projected in the front view vertical plane, as shown in Figure 3. These angles were 47° for configuration B, 28° for C, and 10° for D.
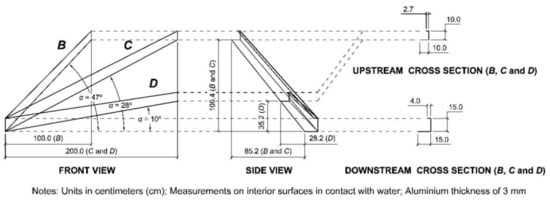
Figure 3.
Drawings of the converging chutes for setup configurations B, C, and D.
For each HCCs configuration, the chutes were attached to the downstream slope of the gravity dam by steel supports. As mentioned above, the bottom of the HCCs had a constant slope with the horizontal plane. The width of the bottom of the HCCs changed linearly from 10 cm in the upstream cross-section to 15 cm at the downstream end, which was located next to the sidewall of the stilling basin. The sidewall of the converging chute was vertical, 10 cm high in the upstream cross-section and 15 cm at the downstream end (Figure 3). In every cross-section, the top of the vertical sidewall was closed by a 5 cm wide deflector, parallel to the bottom of the converging chute, to both prevent spilling and allow the water to flip, forming a rolling wave as shown in Figure 1b. In addition, the height of the step from the bottom of the basin to the bottom of the downstream section of the HCCs (P) could be modified during the tests.
The stilling basin was formed by a 3.7 m-long, 1 m-wide rectangular channel located at the toe of the dam in front of the central meter of the weir. The bottom of the channel had a horizontal slope. From upstream to downstream, the first 2.5 m of the channel was composed of transparent methacrylate that was reinforced externally with steel frames. The bottom of this part of the channel had 49 threaded holes used to install dynamic pressure devices underneath. Likewise, the last 1.2 m of the channel was formed by a brick wall covered by cement mortar. A gate for the control of the downstream water elevation was installed at the end of this area. Downstream of the stilling basin, the outlet flow dropped into the returning channel of the laboratory, which sent the outlet flow back to the main tank of the laboratory. A calibrated thin-plate weir was installed inside the returning channel to measure the discharge during the tests.
The required discharge in each test was achieved using a variable-speed pump drive, which was automatically controlled by the flowmeter installed at the inlet pipe. The maximum available discharge of the pumping system was 0.25 m3 s−1.
3.2. Instrumentation
The experimental facility was equipped with the following items:
- An electromagnetic flowmeter installed at the inlet pipe of the facility. The measured discharge was used as the variable controlling the inlet flow provided by the pumping system.
- An ultrasonic limnimeter for measuring the water level at the inlet tank, placed upstream of the gravity dam.
- A total of 21 dynamic pressure gauges located at the bottom of the stilling basin (Figure 4). The measurements analyzed in this study were those obtained from the 11 sensors located along the longitudinal axis of the basin.
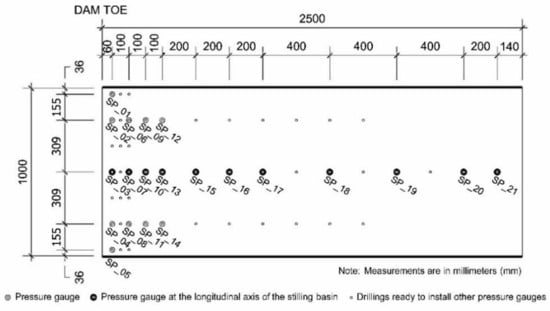 Figure 4. Plan view of the location of the dynamic pressure devices at the bottom of the stilling basin. The flow traveled from left to right, being the left border of the dam toe.
Figure 4. Plan view of the location of the dynamic pressure devices at the bottom of the stilling basin. The flow traveled from left to right, being the left border of the dam toe. - A set of three limnimeters attached to a movable carriage located at the stilling basin, 3.2 m downstream of the dam toe.
- An electronic limnimeter located upstream of the rectangular thin-plate weir at the returning channel, downstream of the model. This sensor provided an indirect measurement of the testing discharge through the calibrated rating curve of the weir.
- Photo and video cameras. The images showed the elapsed time of each test provided by the large chronometer located next to the right sidewall of the experimental facility.
- A self-programmed data acquisition system to gather real-time measurements of the devices. The system included acquisition cards controlled by a laptop computer.
3.3. Research Approach
The research work was divided into three phases. The first phase included the general approach, the selection of the parameters of the study, and the definition of the scope. After this phase, we concluded that it was necessary to establish a comparison framework to objectively evaluate the energy dissipation criteria. This work was conducted in phase two. Finally, the core of the experimental research on the performance of stilling basins with HCCs was performed in phase three. This work is briefly described below.
3.3.1. Phase 1: Scope and Selection of Parameters
The parameters Hb, Hw, Lb, and Wb; the geometry of the HCCs corresponding to each configuration (B, C, and D); and the geometry of the gravity dam, including the shape of the weir, remained unchanged in every test. The size of the experimental facility limited the maximum suitable discharge to 0.15 m3 s−1. The parameters that were modified during the tests were P, the ratio (KQ) between the discharge from the side jets (Qs) and the total discharge (Q), and the value of the angle of the bottom of the HCCs with respect the horizontal plane (α). The reference case for the comparison of each test was the one corresponding to frontal discharge only (i.e., Qf = Q), with energy dissipation achieved by a classical hydraulic jump.
3.3.2. Phase 2: Determination of the Acceptance Criteria for the Energy Dissipation
The index selected to establish the flow condition at the exit of the stilling basin was the coefficient of variation (CV) of the dynamic pressure measured at the pressure gauges located along the longitudinal axis of the stilling basin. The objective of this selection was to characterize the degree of turbulence at the end of the basin. For this purpose, we decided to use CV because it could be obtained from the measurements of the dynamic pressure (p). To apply a criterion based on the CV index, we needed to determine the reference values of the index according to widely accepted technical guidelines. As such, a set of tests with only frontal discharge (i.e., without discharge from side jets) was performed at the experimental facility. The tailwater elevation downstream of the stilling basin was imposed by the control gate for different discharges between 0.010 and 0.150 m3 s−1 until a stable hydraulic jump was generated with its upstream end located at the toe of the dam. The water depth downstream the jump was termed df2. Applying the hydraulic jump equation [24] between the inlet (subscript 1) and outlet (subscript 2) sections of the hydraulic jump, the water depth of the flow entering the hydraulic jump (df1) could be calculated as follows (Equation (1)):
where Ff2 is the Froude number of the flow downstream of the hydraulic jump, which can be obtained through:
The average velocity (Vf2) corresponding to the inlet cross-section of the basin is related to the discharge (Q) according to Equation (3):
As the value of df2 and Q were known through the measurements for the tests (Wb is constant and equal to 1 m), Vf2 was obtained using Equation (3). Then, substituting Vf2 in Equation (2), Ff2 was calculated (Equation (2)). Finally, df1 and Vf1 were determined applying Equations (1) and (3), respectively (changing subindex 2 for 1 in Equation (3)).
The process described above was aimed at indirectly determining the inlet conditions (i.e., df1 and Vf1). This was considered necessary due to the low and fluctuating values of df1 that were reached during the tests. This finding prevented the accurate measurement of the values of df1, so we used the more reliable measurements of the water depth registered downstream of the hydraulic jump.
Once the values of df1, Vf1, and Ff1 were known, the length of the basin with only frontal discharge (Lf) was obtained following the recommendations of BOR [19] according to Figure 5.
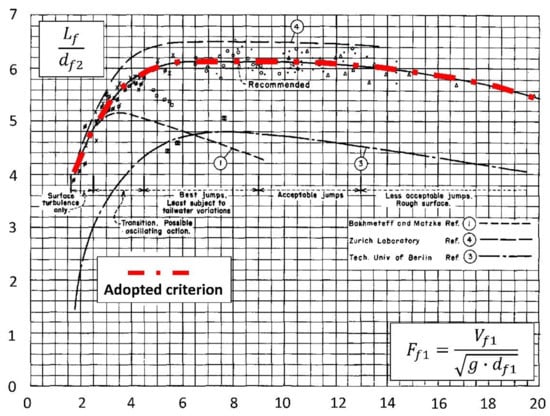
Figure 5.
Length of the Type I basin recommended by the BOR (Adapted from Ref. [19]).
Then, after the hydraulic jump was developed and stable, in steady-state conditions, dynamic pressures (p) were registered at the pressure gauges located along the longitudinal axis of the stilling basin over 20 s. Thus, it was possible to obtain the CV (Equation (4)) of each of the series of records corresponding to each device.
where σp is the standard deviation of the pressure values, and is the mean of the pressure values.
A linear interpolation between two consecutive CV values in adjacent devices was used to calculate the CV corresponding to the length of the stilling basin recommended by the BOR (CVf). This CVf was adopted as the reference index for each tested discharge (Q, coincident with Qf in phase 2). Next, the sets of pairs (Q, Lf) and (Q, CVf) could be obtained and applied as an acceptance criterion of the energy dissipation of the basins with inlet flows from HCCs. In this phase, the maximum discharge was limited by the length of the jump. Thus, for discharges above 0.147 m3 s−1, this length was so high that the jump was out of the area of the basin equipped with pressure sensors and it was not possible to obtain the CVf. The total of 49 tests were conducted in phase 2.
3.3.3. Phase 3: Core of the Experimental Research
Once the acceptance criteria were determined in phase 2, the test program was set up according to the scope of the research determined in phase 1. A total of 649 tests were performed in phase 3, as summarized in Table 1.

Table 1.
Number of tests performed in phase 3.
Tests were performed for the following target discharges (QT): 0.010, 0.025, 0.050, 0.100, and 0.150 m3 s−1. The target discharge was defined as the flowrate that was required by the pumping system for the inlet discharge at the facility. However, the variability in the discharge values registered by the flowmeter necessitated a more reliable measurement of the flow discharge (Q). The values of QT and Q were similar for each test.
Thus, the series of QT values indicated above were applied for every geometrical configuration (i.e., at every couple of values of α and KQ) when possible. In some cases, for the highest value of QT (0.150 m3 s−1), the maximum sidewall height was not high enough to obtain the needed water depth to produce a suitable dissipation of energy. Conversely, the tests with a lower value of QT (0.010 m3 s−1) were considered useless after the review of the registered pressure data. Therefore, the tests corresponding to this target discharge were not considered in the discussion.
It was also necessary to adopt criteria to establish the tailwater depth (d*) in each test. The variability in Q prevented setting up preset tailwater depths for all tests. Thus, the lowest water depth in each test was determined through our direct observations when the water flow upstream the control gate was considered as subcritical. When possible, three higher water depths were applied in each test for a total of 4. The objective was to test higher tailwater levels to achieve suitable energy dissipation with partially or totally submerged conditions within the basin. Then, after a certain tailwater depth was fixed for each test, the dynamic pressure was registered in the pressure gauges over 20 s. Finally, during data post-processing, the required length of the basin (L*) for each d* was determined by linearly interpolating the CVf (corresponding to the acceptance criteria for each Q) between the CV registered in the consecutive pressure gauges located along the longitudinal axis of the basin (i.e., gauges SP_03, SP_07, SP_10, SP_13, SP_15, SP_16, SP_17, SP_18, SP_19, and SP_20). An example of this is shown in Figure 6.
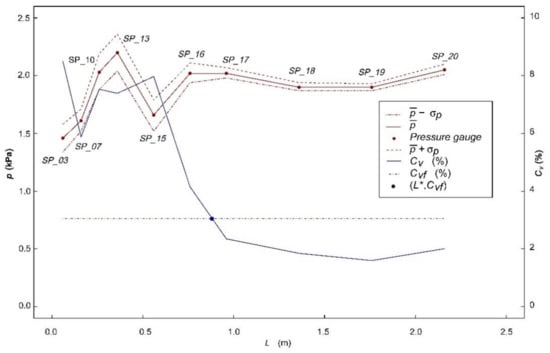
Figure 6.
Example of the determination of the required length of the HCCs basin (L*) in phase 3 tests. The figure shows the results obtained from the measurements of the dynamic pressure gauges located in the longitudinal axis of the basin: mean dynamic pressure (), standard deviation (σp), and coefficient of variation (CV).
Thus, a relevant result for each test was a pair of values (d*, L*), which met the acceptance criteria determined in phase 2, that is, the pair of values needed to dissipate the energy of the same discharge (Q) in similar conditions (i.e., the same coefficient of variation of dynamic pressures along the axis of the basin) as in Type I stilling basins. In this way, we compared the pairs (d*, L*) and (df2, Lf) to evaluate the required size depending on the inlet conditions.
4. Results and Discussion
This section is divided into three parts: (1) a discussion of the results obtained in phase 2, including the determination of the acceptance criteria for the dissipation of energy; (2) the influence of each of the parameters considered in the operation of the stilling basin with an inlet from HCCs (i.e., P, α, and KQ) are discussed; and (3) general conclusions about the flow pattern observed during the tests are provided.
4.1. Energy Dissipation Criteria
As shown in the example in Figure 6, the CV decreases with increasing distance from the dam toe. As expected, also increases with L given that the water depth is higher when subcritical flow conditions are achieved. The CV value that strictly fulfills the acceptance criteria for each particular discharge (Q) can be obtained through a linear interpolation between the immediately higher and lower values of CVf in Figure 6 as the intersection between the horizontal line (CVf) and the CV corresponding to each test.
A summary of the results of the tests conducted in phase 2 is presented in Figure 7.
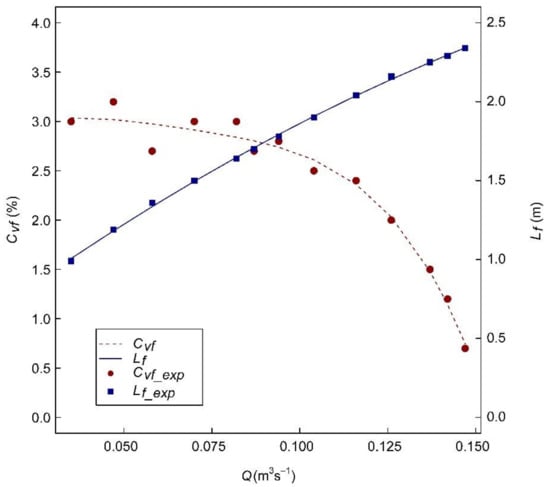
Figure 7.
Evolution of the CVf and Lf for different discharges tested in phase 2.
The evolution of CVf with Q (coincident with Qf in this phase) shows that the interval of the registered values ranges between 0.5% and 3.0%. This evolution shows a gradual decrease as Q increases in the range of flow rates used in the tests. The CVf values were not reliable for Q below 0.034 m3 s−1. As described in Section 3.3, for discharges above 0.147 m3 s−1, the length of the hydraulic jump exceeded the area of the basin where dynamic pressures could be registered. Therefore, the CVf values that could be experimentally obtained ranged from 0.034 and 0.147 m3 s−1. Within this interval, the CVf could be fitted to a fourth-grade polynomic expression (Equation (5)) with a coefficient of determination of 0.96.
For discharges below 0.034 m3 s−1, the CVf considered for the acceptance criteria was constant, with a value of 3.05% (i.e., the minimum available discharge in this phase). As the maximum discharge used in phase 3 was 0.162 m3 s−1, which is close to 0.147 m3 s−1, a constant CVf value of 0.5 % was adopted for discharges higher than 0.147 m3 s−1. The criteria to assess the energy dissipation can be modified depending on the conditions (such as geological or environmental conditions, the potential scour, or others) of the downstream riverbed. However, as indicated in the methodology, in this case, the intention was to establish a consistent approach with the widely accepted criteria for Type I basins.
The results of the length of the hydraulic jump with frontal discharge (Lf) for different discharges are shown in Figure 7. The results were adjusted to a simple linear regression (Equation (6)):
Th results displayed in Figure 8 are the combinations of L* and d* of every test performed in this study. Thus, every symbol represents one of the tests performed in phases 2 and 3. The red dots are the combinations of L* and d* that fulfilled the energy dissipation criteria obtained in phase 2.
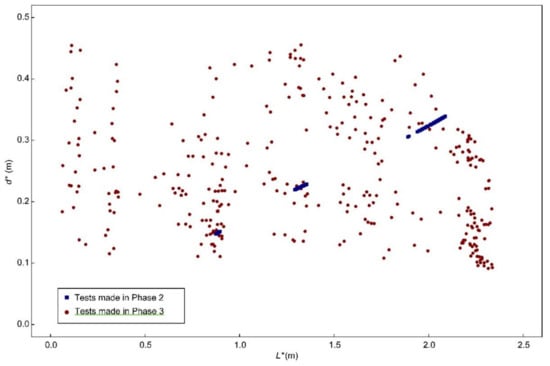
Figure 8.
Combinations of d* (m) and L* (m) of the phase 2 tests conducted to formulate the energy dissipation criteria with only frontal flow, and the phase 3 tests that fulfilled such criteria with side jet flow.
4.2. Influence of the Parameters on the Performance of the Stilling Basin
The discussion begins with the analysis of the parameter P, as we observed signs that this parameter may be the easiest to interpret among those considered in the research. After the effect of P is discussed, parameters α and KQ are jointly analyzed, specifically for the cases where P was more effective in terms of energy dissipation.
4.2.1. Analysis of the Height of the Bottom of the HCCs over the Bottom of the Basin (P)
The results in Table 2 show the percentage of tests that fulfilled the following conditions: d* < df2 (termed as condition I), L* < Lf, (condition II), and both I and II, for different values of P and QT. The latter condition (i.e., I and II) represents the percentage of cases where the size of the basin needed to dissipate the energy with side inlets from HCCs is smaller than the size with only frontal flow (i.e., with a dissipation achieved by a hydraulic jump). For this analysis, the freeboard needed for the sidewall height was neglected, so that the comparison focused only on the water depth and the length of the basin (note that the width of the basin was constant for every test) required to fulfill the acceptance criteria for the dissipation of energy.

Table 2.
Number of tests that met the energy dissipation criteria for different basin dimension conditions for different values of P.
Table 3 presents the values of the rates between the mean value of df2 with respect to the mean value of d* (), and the mean value of Lf with respect the mean value of L* ().

Table 3.
Values of the rates between the mean value of df2 with respect to the mean value of d* (), and the mean value of Lf with respect the mean value of L* () for every value of P.
The results presented in Table 2 show that the frequency of fulfillment of conditions I and II (and both simultaneously) increased when P was lower. This finding was evident for the representative target discharges (i.e., 0.025, 0.050, and 0.100 m3 s−1) among the tests conducted. Thus, for representative values of QT, and when P equals zero, 56.8% to 70% of the tests complied with d* < df2. Likewise, 75% to 100% of the tests complied with L* < Lf, and 39.4% to 47.8% fulfilled both conditions. Therefore, if P is zero, i.e., if the bottom of the HCCs enters the basin at the same elevation of the sill of the basin, it is more likely that a smaller basin would be required. In other words, HCCs can be used to increase the capacity of existing spillways without any change in the original basin, especially when P is zero. In most of the tests performed with P equaling 0.20 m, both d* and L* were higher than when P was zero. This finding led to infer that the higher the depth of entry to the basin, the greater the dissipation of energy. This was observed especially when the basin operated in submergence conditions (i.e., when the tailwater level was high enough that the side jets impinged into the water mass).
Table 3 provides results that are useful for quantifying the changes in mean values of d* and L* in comparison with df2 and Lf, respectively. In the table, values higher than one indicate that the tailwater depths and lengths of the basin (when HCCs are in operation) are lower than those corresponding to a classical hydraulic jump with only frontal flow for the same QT. Focusing on representative target discharges (i.e., 0.025, 0.050, and 0.100 m3 s−1), and considering the rate, the ranges of values are 0.93 to 1.09 for P = 0 m, 0.96 to 1.08 for P = 0.1 m, and 0.90 to 0.94 for P = 0.2 m. The rate has a wider range of variation: 1.30 to 1.54 for P = 0 m, 0.64 to 1.24 for P = 0.1 m, and 0.58 to 1.18 for P = 0.2 m. Thus, the results presented in Table 3 indicate that the differences between the height of the basin (i.e., d* and df2) for HCCs or hydraulic jump are not significant. Conversely, the effect of the operation of HCCs can achieve reductions of up to 54% of the required length of the basin, which can be meaningful from an economical point of view in actual cases. However, in some of the tests with P values of 0.10 or 0.20 m, reductions in d* and L* were also achieved; so, in some cases, it may be possible to design HCCs with inlets raised from the bottom of the basin that provide good performance.
4.2.2. Influence of the Angle between the Bottom of the HCCs with Respect to the Horizontal Plane (α) and the Discharge Rate of the Side Jets (KQ)
As discussed in Section 4.2.1, the length of the basin (L*) was proven to be the parameter with the most potential for optimization. Therefore, the discussion firstly focuses on the response of L* to the tested values of α and KQ. As shown in Figure 9, which depicts results of the tests for a P of zero, most of the highest reductions in L* occurred for the lowest value of α (i.e., 10°). Such reductions are especially relevant for higher values of KQ (i.e., 0.75 and 0.80). The possible reason for this result may be the higher energy dissipation achieved by the impingement of the side jets. Thus, the lowest value of α (10°) more directly impinges the side jets, which produces a quasi-frontal impact. In addition, the higher the values of KQ, the higher the proportion of the discharge involved in the impact dissipation of the side jets in relation to the frontal discharge. Therefore, the results show that the combination of both effects has significative consequences for the reduction in L*.
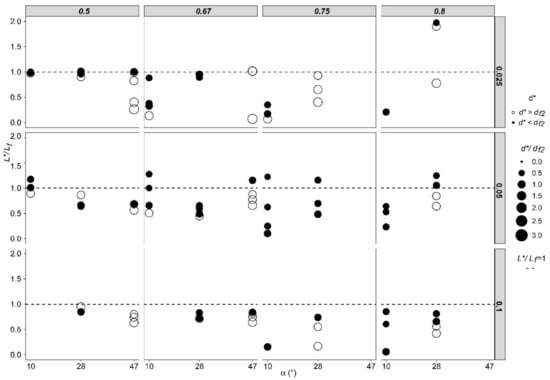
Figure 9.
The L*/Lf (−) rate with respect to α (°) for tests with a P of zero. The figure is organized in a matrix layout, with vertical columns representing KQ (−) and horizontal rows QT (m3 s−1). Filled circle represent cases where d* < df2; empty circles represent d* > df2. The size of every circle represents the d*/df2 (−) rate.
Next, we discuss the effect of d*. As shown in Figure 10, the angle α does not seem to have a critical effect on the required tailwater elevation. Thus, the values of d* are not far from the value of the conjugated water elevation (df2), with a usual range of variation in d*/df2 between 0.50 to 1.50. In general, with some exceptions (see QT 0.025 m3 s−1 and KQ 0.8), the higher the α, the higher the d*. However, this tendency is not evident, as noted in the following cases: QT 0.1 m3 s−1 and KQ 0.67, QT 0.1 m3 s−1 and KQ 0.75, and QT 0.05 m3 s−1 and KQ 0.5. However, no conclusive conclusions could be drawn about the effect of KQ on the value of d*.
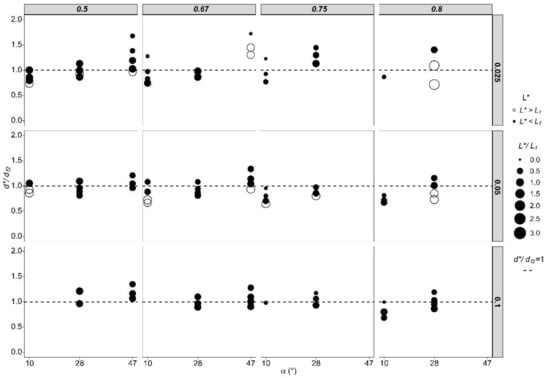
Figure 10.
d*/df2 (−) with respect to α (°) for tests when P is zero. The figure is organized in a matrix layout, with vertical columns representing KQ (−) and horizontal rows representing QT (m3 s−1). Filled circles represent cases where L* < Lf; empty circles represent L* > Lf. The size of every circle represents L*/Lf (−).
Another remarkable conclusion from both Figure 9 and Figure 10 is that in every test, there was always a pair of values of d* and L* that was less than the corresponding df2 and Lf, values (every filled circle below the dotted line in each figure). That is, it is highly probable that a smaller basin size can be found that can dissipate the energy. In other words, it may be possible to adapt an existing stilling basin to dissipate the energy of a larger outflow discharge without varying the size of the basin. This conclusion can be useful in cases where an increase in the capacity of the spillway is needed in gravity (or arch-gravity) dams with a stilling basin as the energy dissipator.
4.3. Effect of Submergence on Flow Distribution
The flow pattern originating in the area where the front and side jets meet causes three-dimensional and highly turbulent functioning. Thus, the hydraulic behavior and the energy dissipation pattern are essentially different than those that occur in a hydraulic jump. As shown in Figure 11a1,a2 and Video S1, where low tailwater was used to meet the required dissipation criteria, the impingement of the jets causes a rise in the water level at the toe of the dam, approximately coinciding with the longitudinal axis of the basin. Such concentration of the flow at the center of the basin generates lateral flow toward the sidewalls that spreads downstream (Figure 11a1).

Figure 11.
Pictures showing the hydraulic conditions in a stilling basin with low ((a1,a2), views from downstream and left side, respectively) and high submergence ((b1,b2), same positions as a1 and a2, respectively) due to different tailwater elevations in the test with QT = 0.050 m3 s−1, α = 28° (configuration B), P = 0, and KQ = 0.80.
Conversely, as illustrated in Figure 11b1,b2 and Video S2, when the energy dissipation is achieved with higher tailwater elevations (i.e., higher submergence condition), the propagation of shockwaves is reduced, and the downstream flow distributes uniformly along the width of the basin. The effect of submergence described above for this test setup was observed in most of the cases. Therefore, we concluded that operation of the basin in higher submergence conditions can effectively achieve more uniform distribution of the flow downstream the basin.
In addition to the effect of submergence, there are other aspects that can be analyzed for a particular case through numerical modeling with specific software (CALA) developed during the research project [2,3,25]. This software was calibrated and validated by the experimental results presented in this paper, which may help the technical community apply the findings of this paper to real-sized cases.
5. Conclusions
The experimental research summarized in this article showed that the use of HCCs spillways with symmetric side jet inlets can effectively dissipate the flow energy in the stilling basins of gravity dams, with a likely reduction in the size of the corresponding Type I basin. This is particularly interesting for cases where the outflow capacity of an existing spillway needs to be increased and the stilling basin has already been built. It can also be applied in cases where it is intended to protect the downstream toe of the dam against erosion due to overtopping.
The methodology included a comprehensive study of the coefficient of variation of the dynamic pressures at the outlet area of Type I basins with a hydraulic jump dissipation pattern. In this study, we obtained an objective dissipation criterion to be met by the tests performed with side jet inlets from HCCs.
In general, the test setup with the inlet of the HCCs at the bottom of the basin (i.e., when P was 0) resulted in the minimum sizes of the HCCs basins, with average reductions in the length of the basin (L*) from 23% to 35% in comparison with Type I basin. The results of the required tailwater depths (d*) are closer to those needed by Type I basins (average reductions up to 8%, and average increases up to 7%). In any case, there were tests in which reductions in both L* and d* were achieved from the corresponding values (Lf and df2) of the Type I basins for a given flow discharge.
Among the tests with the inlet of the HCCs at the bottom of the basin, greater size reductions were achieved when the direction of the impingement of the symmetrical side jets was more frontal (α = 10°) and most of the water flow in comparison with the frontal flow was from the HCCs side jets (KQ was 0.8).
Finally, the observations of the flow pattern in the HCC basins showed that operation in submergence conditions usually caused a more uniform distribution of the flow along the whole width of the basin. Conversely, lower tailwater elevations led to the formation of shockwaves along the basin and flow concentrations in some areas of its cross-section.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/w13101343/s1. Video S1: VideoFig11a, Video S2: VideoFig11b.
Author Contributions
Conceptualization, M.Á.T. and R.M.; methodology, J.P.; formal analysis, R.M.; investigation, J.P.; data curation, R.P.; writing—original draft preparation, R.M.; writing—review and editing, M.Á.T.; visualization, R.P.; supervision, M.Á.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministerio de Ciencia e Innovación of Spain within the CALA research project (grant number RTC-2016-4581-5).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
MDPI Research Data Policies.
Acknowledgments
The authors would like to acknowledge collaboration with the Red de Aulas CIMNE. The authors would also like to acknowledge Javier Caballero, Ricardo Monteiro-Alves, Víctor Flórez, Begoña Labalde, Jaime García, Javier San Mauro, Fernando Salazar, and Eugenio Oñate for supporting this research.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| CV | coefficient of variation of the water pressure, expressed in percentage. |
| CVf | coefficient of variation of the pressure downstream the BOR’s Type I stilling basin, expressed in percentage. |
| df1 | water depth of the flow entering the jump in BOR’s Type I basin. |
| df2 | water depth downstream of the BOR’s Type I basin. |
| d* | water depth downstream of the basin after energy dissipation with side jets discharge. |
| Ff1 | Froude number at the entrance of the hydraulic jump. |
| Ff2 | Froude number downstream the hydraulic jump. |
| Hb | maximum height of the sidewalls of the stilling basin, equals to 0.5 m. |
| Hw | height of the weir over the bottom of the stilling basin, equals to 1.5 m. |
| KQ | discharge rate of the side jets (i.e., Qs/Q). |
| L | horizontal distance from the toe of the dam along the longitudinal axis of the basin. |
| Lb | maximum length of the stilling basin of the experimental facility: 3.7 m. |
| Lf | length of the basin recommended by the BOR criteria for Type I basins. |
| L* | length of the basin required to a suitable energy dissipation with side jets discharge. |
| p | pressure. |
| mean of the pressure values. | |
| P | height of the step from the bottom of the basin to the bottom of the downstream section of the HCCs. |
| Q | total discharge. |
| Qf | frontal discharge. |
| Qs | side discharge from the HCCs inlet. |
| QT | target discharge. |
| Vf1 | velocity of the flow entering the jump in BOR’s Type I basin. |
| Vf2 | velocity of the flow downstream of the BOR’s Type I basin. |
| Wb | width of the stilling basin, equals 1 m. |
| Ww | maximum length of the weir, equals 5 m. |
| α | angle of the bottom of the HCCs with respect the horizontal plane, projected in the front view vertical plane. |
| σp | standard deviation of the pressure values. |
References
- San Mauro, J.; Morera, L.; Salazar, F.; Rossi, R.; Toledo, M.; Morán, R.; Martínez, B.; Caballero, F.; Oñate, E. Modelación Física Y Numérica De Aliviaderos Con Cajeros Altamente Convergentes. In Proceedings of the III Jornadas De Ingeniería Del Agua, Valencia, Spain, 23–24 October 2013. [Google Scholar]
- Larese, A.; Salazar, F.; San Mauro, J.; Oñate, E.; Toledo, M.; Morán, R. Advanced Computational Methods for Dam Protections Against Overtopping. In Proceedings of the Protections 2018 (3rd International Conference on Protection against Overtopping), Grange-over-Sands, UK, 6–8 June 2018. [Google Scholar]
- Mauro, S.; Salazar, F. Mejora De La Seguridad Hidrológica E Incremento De La Capacidad De Embalse De Presas De Fábrica Mediante Aliviaderos Con Cajeros Altamente Convergentes. 2019. Available online: https://www.scipedia.com/public/Peraita_et_al_2019a (accessed on 1 October 2020).
- Lempérière, F.; Vigny, J.; Deroo, L. New Methods and Criteria for Designing Spillways could Reduce Risks and Costs Significantly; Hydropower & Dams: Wallington, UK, 2012; pp. 120–128. [Google Scholar]
- Hunt, S.L. Design of Converging Stepped Spillways. Ph.D. Thesis, Colorado State Univeristy, Fort Collins, CO, USA, 2008. [Google Scholar]
- Hunt, S.L.; Kadavy, K.C.; Abt, S.R.; Temple, D.M. Impact of Converging Chute Walls for Roller Compacted Concrete Stepped Spillways. J. Hydraul. Eng. 2008, 134, 1000–1003. [Google Scholar] [CrossRef]
- Schleiss, A. From Labyrinth to Piano Key Weirs—A Historical Review. In Proceedings of the Labyrinth and Piano Key Weirs; Apple Academic Press: Palm Bay, FL, USA, 2011; pp. 3–15. [Google Scholar]
- Macián-Pérez, J.F.; Vallés-Morán, F.J.; Sánchez-Gómez, S.; De-Rossi-Estrada, M.; García-Bartual, R. Experimental Characterization of the Hydraulic Jump Profile and Velocity Distribution in a Stilling Basin Physical Model. Water 2020, 12, 1758. [Google Scholar] [CrossRef]
- NVE. Guidelines for Embankment Dams. Guideline 4/2012. Norwegian Water Resources and Energy Directorate. 2012. Available online: https://www.nve.no/damsikkerhet-og-kraftforsyningsberedskap/damsikkerhet/regelverk/veileder-for-fyllingsdammer/ (accessed on 1 October 2020).
- Portland Cement Association. Design Manual for RCC Spillways and Overtopping Protection, 1st ed.; Portland Cement Association: Skokie, IL, USA, 2002; p. 100. [Google Scholar]
- FEMA. Technical Manual: Overtopping Protection for Dams; U.S. Department of Homeland Security: Washington, DC, USA, 2014.
- United States Bureau of Reclamation. Design of Small Dams; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987.
- Morera, L.; San Mauro, J.; Salazar, F.; Toledo, M.Á. Highly-Converging Chutes as an Overtopping Protection for Concrete Dams: Physical and Numerical Modelling; Taylor & Francis Group: London, UK, 2015. [Google Scholar]
- Yang, J. Investigations at Vatnsfell. Int. Water Power Dam. Constr. 2007, 59, 9. [Google Scholar]
- Zaitsoff, M. Overtopping modifications to Tygart Dam. In Proceedings of the National Dam Safety Technical Seminar: Overtopping Protection for Dams, Portland, OR, USA, 13–15 May 2003; pp. 20–21. [Google Scholar]
- Talbot, J.; Robinson, K.; Kadavy, K. Hydraulic Model Study of a Roller Compacted Concrete Stepped Spillway with Converging Chute Walls. In Proceedings of the Association of State Dam Safety Officials Annual Conference, Pittsburg, PA, USA, 7–10 September 1997. [Google Scholar]
- Hunt, S.L.; Temple, D.M.; Abt, S.R.; Kadavy, K.C.; Hanson, G. Converging Stepped Spillways: Simplified Momentum Analysis Approach. J. Hydraul. Eng. 2012, 138, 796–802. [Google Scholar] [CrossRef]
- Hunt, S.L.; Kadavy, K.C.; Abt, S.R.; Temple, D.M. Impact of Converging Chute Walls for RCC Stepped Spillways. Impacts Glob. Clim. Chang. 2005, 1–12. [Google Scholar] [CrossRef]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1978.
- Barjastehmaleki, S. Spillway Stilling Basins and Plunge Pools Lining Design. Ph.D. Thesis, University of Trieste, Trieste, Italy, 2016. [Google Scholar]
- Babaali, H.; Shamsai, A.; Vosoughifar, H. Computational Modeling of the Hydraulic Jump in the Stilling Basin with Convergence Walls using CFD Codes. Arab. J. Sci. Eng. 2015, 40, 381–395. [Google Scholar] [CrossRef]
- Vischer, D.; Hager, W. Energy Dissipators. Oceanogr. Lit. Rev. 1996, 1, 87. [Google Scholar]
- Martín-Vide, J. The Design of Converging Overfall Spillways. Int. J. Hydropower Dams 1995, 2, 87. [Google Scholar]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- San Mauro, J.; Salazar, F.; Morán, R.; Peraita, J.; Toledo, M.Á.; Conde, M.J.; Flórez, V.; Labalde, B.; Alcalde, F. Aliviaderos Con Cajeros Altamente Convergentes. ¿Posible Solución Para La Presa De Oroville? In Proceedings of the V Jornadas de Ingeniería del Agua, A Coruña, Spain, 24–26 October 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).