The Use of a Uniform Technique for Harmonization and Generalization in Assessing the Flood Discharge Frequencies of Long Return Period Floods in the Danube River Basin
Abstract
:1. Introduction
- -
- Maximum annual discharges must be independent and stochastic;
- -
- Processes influencing the runoff process are stationary with respect to time (homogeneity of the series);
- -
- Statistical characteristics of the measured data series (series of maximum annual discharge) represent the past, presence, and future.
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Log-Pearson III Probability Distribution
2.2.2. Conditions of Qmax Series
2.2.3. Parameter Estimation: Simple Case
2.2.4. Historical Floods
2.2.5. Skew Coefficients in Log-Pearson III Distribution—Regionalization
3. Results
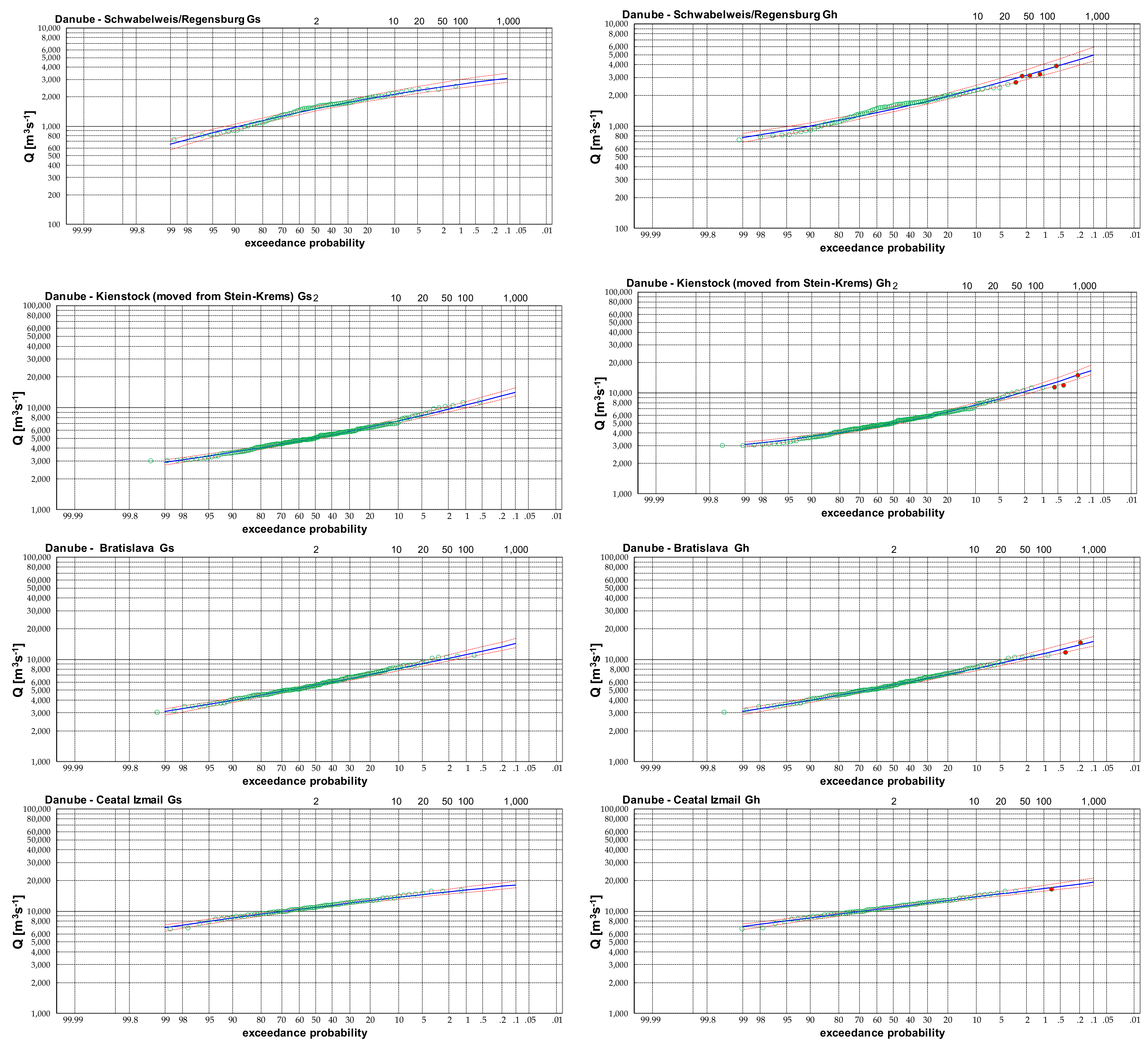
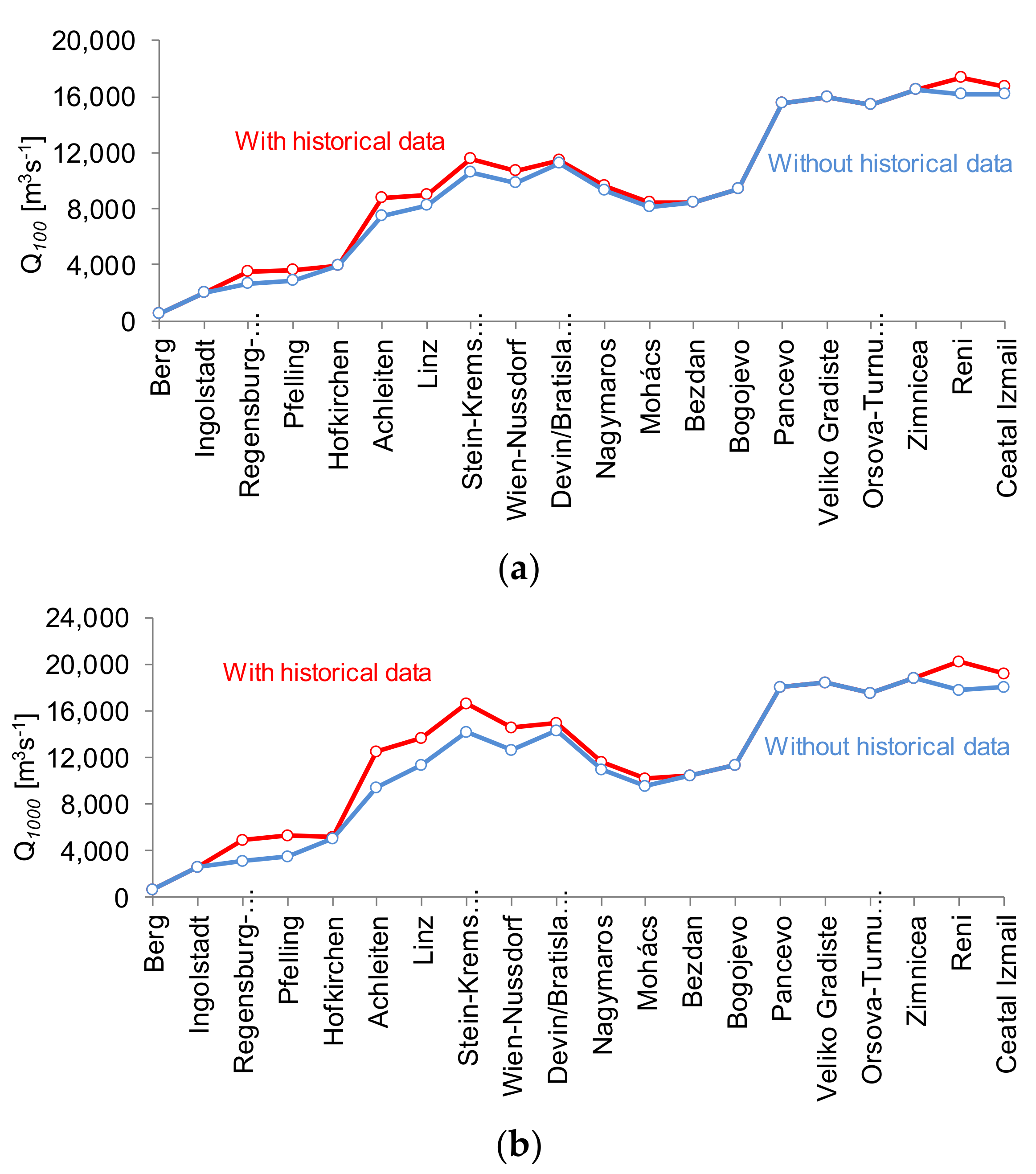
3.1. Estimation of the T-Year Design Discharges along the Danube River
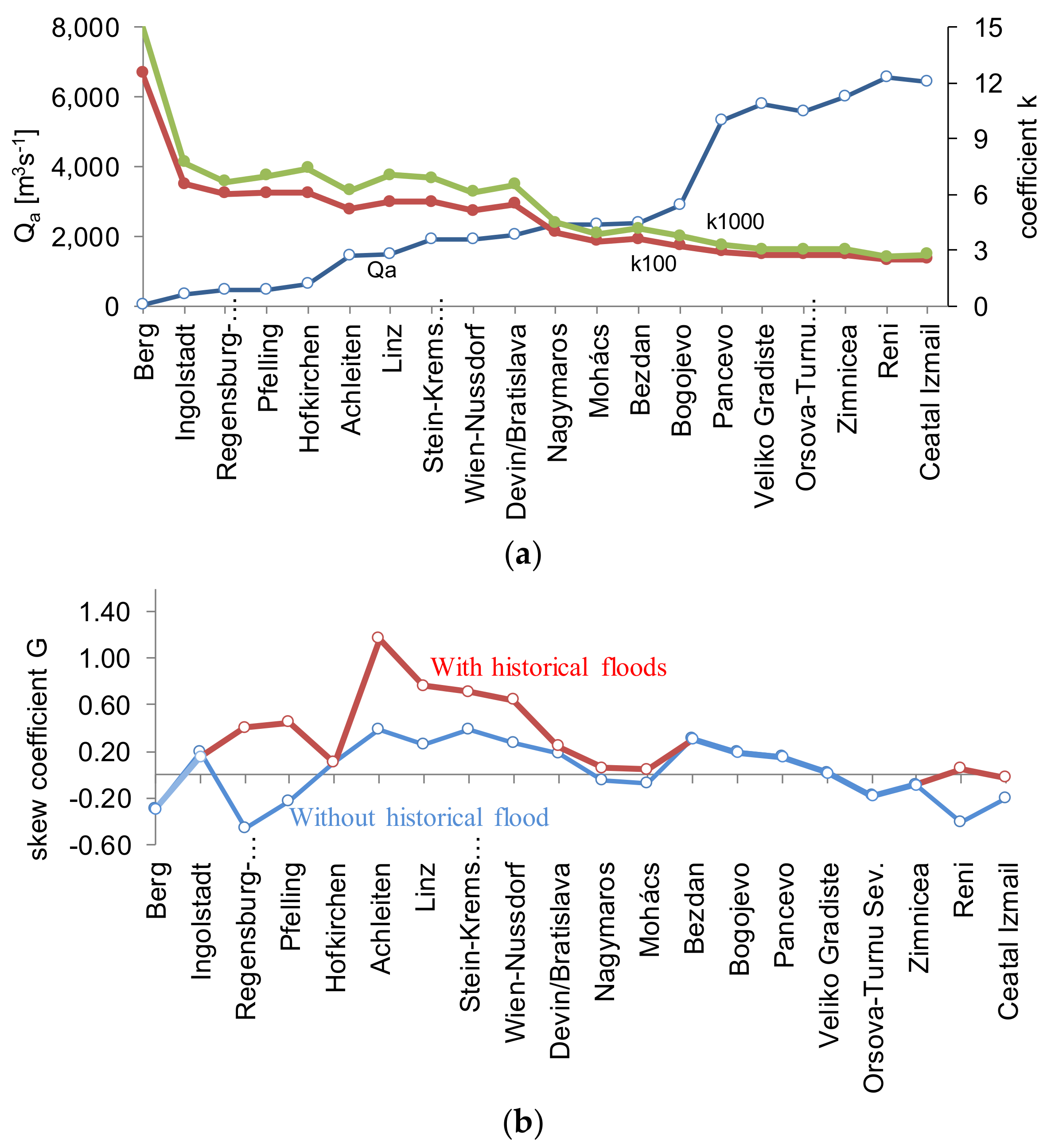
3.2. Regionalization of the Skew Coefficients of the LPIII Probability Curves for the Danube River
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernández, L.; Scherer, M.; Emil, J. Gumbel’s last course on the “Statistical theory of extreme values”: A conversation with Tuncel, M. Yegulalp. Extremes 2018, 21, 97–113. [Google Scholar] [CrossRef] [Green Version]
- Gumbel, E.J. Statistical Theory of Extreme Values and Some Practical Applications; Applied Mathematics Series; US Government Printing Office: Washington, DC, USA, 1954; 60p.
- Kresser, W. The Flooding of the Danube; Springer Verlag: Vienna, Austria, 1957; 95p. (In German) [Google Scholar]
- Merz, R.; Blöschl, G. Flood frequency hydrology: 1. Temporal, spatial, and causal expansion of information. Water Resour. Res. 2008, 44, 08432. [Google Scholar] [CrossRef] [Green Version]
- Merz, R.; Blöschl, G. Flood frequency hydrology: 2. Combining data evidence. Water Resour. Res. 2008, 44, 08433. [Google Scholar] [CrossRef]
- Elleder, L. Reconstruction of the 1784 flood hydrograph for the Vltava River in Prague, Czech Republic. Glob. Planet. Chang. 2010, 70, 117–124. [Google Scholar] [CrossRef]
- Elleder, L.; Herget, J.; Roggenkamp, T.; Niesen, A. Historic floods in the city of Prague—A reconstruction of peak discharges for 1481–1825 based on documentary sources. Hydrol. Res. 2012, 44, 202–214. [Google Scholar] [CrossRef]
- Kjeldsen, T.; Macdonald, N.; Lang, M.; Mediero, L.; Albuquerque, T.; Bogdanowicz, E.; Brázdil, R.; Castellarin, A.; David, V.; Fleig, A.; et al. Documentary evidence of past floods in Europe and their utility in flood frequency estimation. J. Hydrol. 2014, 517, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Strupczewski, W.G.; Kochanek, K.; Bogdanowicz, E. Historical floods in flood frequency analysis: Is this game worth the candle? J. Hydrol. 2017, 554, 800–816. [Google Scholar] [CrossRef]
- Wetter, O. The potential of historical hydrology in Switzerland. Hydrol. Earth Syst. Sci. 2017, 21, 5781–5803. [Google Scholar] [CrossRef] [Green Version]
- Brázdil, R.; Kundzewicz, Z.W.; Benito, G. Historical hydrology for studying flood risk in Europe. Hydrol. Sci. J. 2006, 51, 739–764. [Google Scholar] [CrossRef]
- Pekárová, P.; Miklánek, P.; Melo, M.; Halmová, D.; Pekár, J.; Bačová Mitková, V. Flood Marks along the Danube River between Passau and Bratislava; Veda: Bratislava, Slovakia, 2014; 102p, ISBN 978-80-224-1408-1. [Google Scholar]
- Szolgay, J.; Kohnová, S.; Hlavčová. Uncertainties in determining the design flood. Environment 2003, 37, 194–199. (In Slovak) [Google Scholar]
- Rogger, M.; Kohl, B.; Pirkl, H.; Viglione, A.; Komma, J.; Kirnbauer, R.; Merz, R.; Blöschl, G. Runoff models and flood frequency statistics for design flood estimation in Austria—Do they tell a consistent story? J. Hydrol. 2012, 456–457, 30–43. [Google Scholar] [CrossRef]
- Coxon, G.; Freer, J.; Westerberg, I.K.; Wagener, T.; Woods, R.; Smith, P.J. A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations. Water Resour. Res. 2015, 51, 5531–5546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lam, D.; Thompson, C.; Croke, J.; Sharma, A.; Macklin, M.; Thompson, C. Reducing uncertainty with flood frequency analysis: The contribution of paleoflood and historical flood information. Water Resour. Res. 2017, 53, 2312–2327. [Google Scholar] [CrossRef] [Green Version]
- Šraj, M.; Viglione, A.; Parajka, J.; Blöschl, G. The influence of non-stationarity in extreme hydrological events on flood frequency estimation. J. Hydrol. Hydromech. 2016, 64, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Leščešen, I.; Dolinaj, D. Regional Flood Frequency Analysis of the Pannonian Basin. Water 2019, 11, 193. [Google Scholar] [CrossRef] [Green Version]
- Stănescu, V.A. Regional Analysis of the Annual Peak Discharges in the Danube Catchment. Follow-Up Volume No.VII to the Danube Monograph; Regional Cooperation of the Danube Countries: Bucharest, Romania, 2004; 64p. [Google Scholar]
- Cunnane, C. Statistical distributions for flood frequency analysis. In Operational Hydrology Report (WMO); WMO: Geneva, Switzerland, 1989. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; U.S. Geological Survey: Reston, VA, USA, 2002; Volume 323. [Google Scholar]
- Flynn, K.M.; Kirby, W.H.; Hummel, P.R. User’s Manual for Program PeakFQ Annual Flood-Frequency AnalysisUsing Bulletin 17B Guidelines; Chapter B4; U.S. Geological Survey: Reston, VA, USA, 2006; p. 42. [Google Scholar]
- Khosravi, G.; Majidi, A.; Nohegar, A. Determination of suitable probability distribution for annual mean and peak discharges estimation (Case study: Minab river-Barantin gauge, Iran). Int. J. Probab. Stat. 2012, 1, 160–163. [Google Scholar] [CrossRef] [Green Version]
- Langat, P.K.; Kumar, L.; Koech, R. Identification of the Most Suitable Probability Distribution Models for Maximum, Minimum, and Mean Streamflow. Water 2019, 11, 734. [Google Scholar] [CrossRef] [Green Version]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological statistics. Hydrol. Sci. J. 2005, 50, 381–404. [Google Scholar]
- Bobée, B. The Log Pearson type 3 distribution and its application in hydrology. Water Resour. Res. 1975, 11, 681–689. [Google Scholar] [CrossRef]
- Pilon, P.J.; Adamowski, K. Asymptotic variance of flood quantile in log Pearson Type III distribution with historical information. J. Hydrol. 1993, 143, 481–503. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. The Log-Pearson type III distribution and its application in flood frequency analysis. I: Distribution characteristics. J. Hydrol. Eng. 2007, 12, 482–491. [Google Scholar]
- Pawar, U.; Hire, P. Flood Frequency Analysis of the Mahi Basin by Using Log Pearson Type III Probability Distribution. Hydrospatial Anal. 2018, 2, 102–112. [Google Scholar] [CrossRef]
- Phien, H.N.; Ajirajah, T.J. Applications of the log Pearson type-3 distribution in hydrology. J. Hydrol. 1984, 73, 359–372. [Google Scholar] [CrossRef]
- Cohn, T.A.; Stedinger, J.R. Use of historical information in a maximum-likelihood framework. J. Hydrol. 1987, 96, 215–223. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency analysis of extreme events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 18. [Google Scholar]
- Griffis, V.W.; Stedinger, J.R. The Log-Pearson type III distribution and its application in flood frequency analysis. II: Parameter Estimation Methods. J. Hydrol. Eng. 2007, 12, 492–500. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. Log-Pearson type 3 distribution and its application in flood frequency analysis, III—sample skew and weighted skew estimators. J. Hydrol. Eng. 2009, 14, 121–130. [Google Scholar] [CrossRef]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models. Water Resources Research Report; Department of Civil and Environmental Engineering, The University of Western Ontario: London, ON, Canada, 2011; pp. 1–54. [Google Scholar]
- Horváthová, B. Povodeň to nie je len veľká voda (Flood Is Not Only High Water); Veda: Bratislava, Slovakia, 2003; 224p. (In Slovak) [Google Scholar]
- Kiss, A.; Laszlovszky, J. 14th–16th-century Danube floods and long-term water level changes in archaeological and sedimentary evidence in the western and central Carpathian Basin: An overview with documentary comparison. J. Env. Geogr. 2013, 6, 1–11. [Google Scholar]
- Melo, M.; Pekárová, P.; Dujsiková, C.; Melová, K. Povodeň na Dunaji v roku 1895 časť I: V historických dokumentoch. (The flood on the Danube in 1895 part I: In historical documents). Acta Hydrol. Slovaca 2012, 13, 271–279. (In Slovak) [Google Scholar]
- Melo, M.; Pekárová, P.; Miklánek, P.; Melová, K.; Dujsíková, C. Use of historical sources in a study of the 1895 floods on the Danube River and its tributaries. Geogr. Pannonica 2014, 18, 108–116. [Google Scholar]
- Mikhailov, V.N.; Morozov, V.N.; Cheroy, N.I.; Mikhailova, M.V.; Zavyalova, E.F. Extreme flood on Danube River in 2006. Russ. Meteorol. Hydrol. 2008, 1, 80–89. [Google Scholar]
- Pekárová, P.; Halmová, D.; Bačová Mitková, V.; Miklánek, P.; Pekár, J.; Škoda, P. Historic flood marks and flood frequency analysis of the Danube River at Bratislava, Slovakia. J. Hydrol. Hydromech. 2013, 61, 326–333. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Nester, T.; Komma, J.; Parajka, J.; Perdigão, R.A.P. The June 2013 flood in the Upper Danube basin, and comparisons with the 2002, 1954 and 1899 floods. Hydrol. Earth Syst. Sci. 2013, 17, 9533–9573. [Google Scholar] [CrossRef] [Green Version]
- Cheng, K.S.; Chiang, J.L.; Hsu, C.W. Simulation of probability distributions commonly used in hydrological frequency analysis. Hydrol. Process 2007, 21, 51–60. [Google Scholar] [CrossRef]
- IACWD. Guidelines for Determining Flood Flow Frequency, Bulletin 17-B; Technical Report; Interagency Committee on Water Data, Hydrology Subcommittee: Reston, VA, USA, 1982; 194p. [Google Scholar]
- Stedinger, J.R.; Griffis, V.W. Flood Frequency Analysis in the United States: Time to Update. J. Hydrol. Eng. 2008, 13, 199–204. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, R.M. Probability plotting position formulas for flood records with historical information. J. Hydrol. 1987, 96, 185–199. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Stedinger, J.R. Plotting position for historical floods and their precision. WRR 1987, 23, 715–727. [Google Scholar]
- Hammett, K.M.; DelCharco, M.J. Estimating the Magnitude and Frequency of Floods for Streams in West-Central Florida; U.S. Geological Survey Scientific Investigations Report 2005-5080; U.S. Geological Survey: Reston, VA, USA, 2001; 15p, plus apps. [Google Scholar]
- England, J.F., Jr.; Cohn, T.A.; Faber, B.A.; Stedinger, J.R.; Thomas, W.O., Jr.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R., Jr. Guidelines for Determining Flood Flow Frequency—Bulletin 17C; Techniques and Methods: Book 4, Chapter B5; U.S. Geological Survey: Reston, VA, USA, 2018; 148p. [Google Scholar] [CrossRef] [Green Version]
- McCuen, R.H.; Smith, E. Origin of floods skew. J. Hydrol. Eng. 2008, 13. [Google Scholar] [CrossRef]
- Bondar, C.; Panin, N. The Danube Delta Hydrologic Database and Modelling. GeoEcoMarina 2001, 5, 5–53. [Google Scholar]
- Bačová Mitková, V.; Pekárová, P.; Miklánek, P.; Pekár, J. Hydrological simulation of flood transformations in the upper Danube River: Case study of large flood events. J. Hydrol. Hydromech. 2016, 64, 337–348. [Google Scholar] [CrossRef] [Green Version]
- Stănescu, V.A.; Ungureanu, V.; Domokos, M. Regionalization of the Danube catchment for the estimation of the distribution functions of annual peak discharges. J. Hydrol. Hydromech. 2001, 49, 407–427. [Google Scholar]
- Engeland, K.; Wilson, D.; Borsányi, P.; Roald, L.; Holmqvist, E. Use of historical data in flood frequency analysis: A case study for four catchments in Norway. Hydrol. Res. 2018, 49, 466–486. [Google Scholar] [CrossRef]
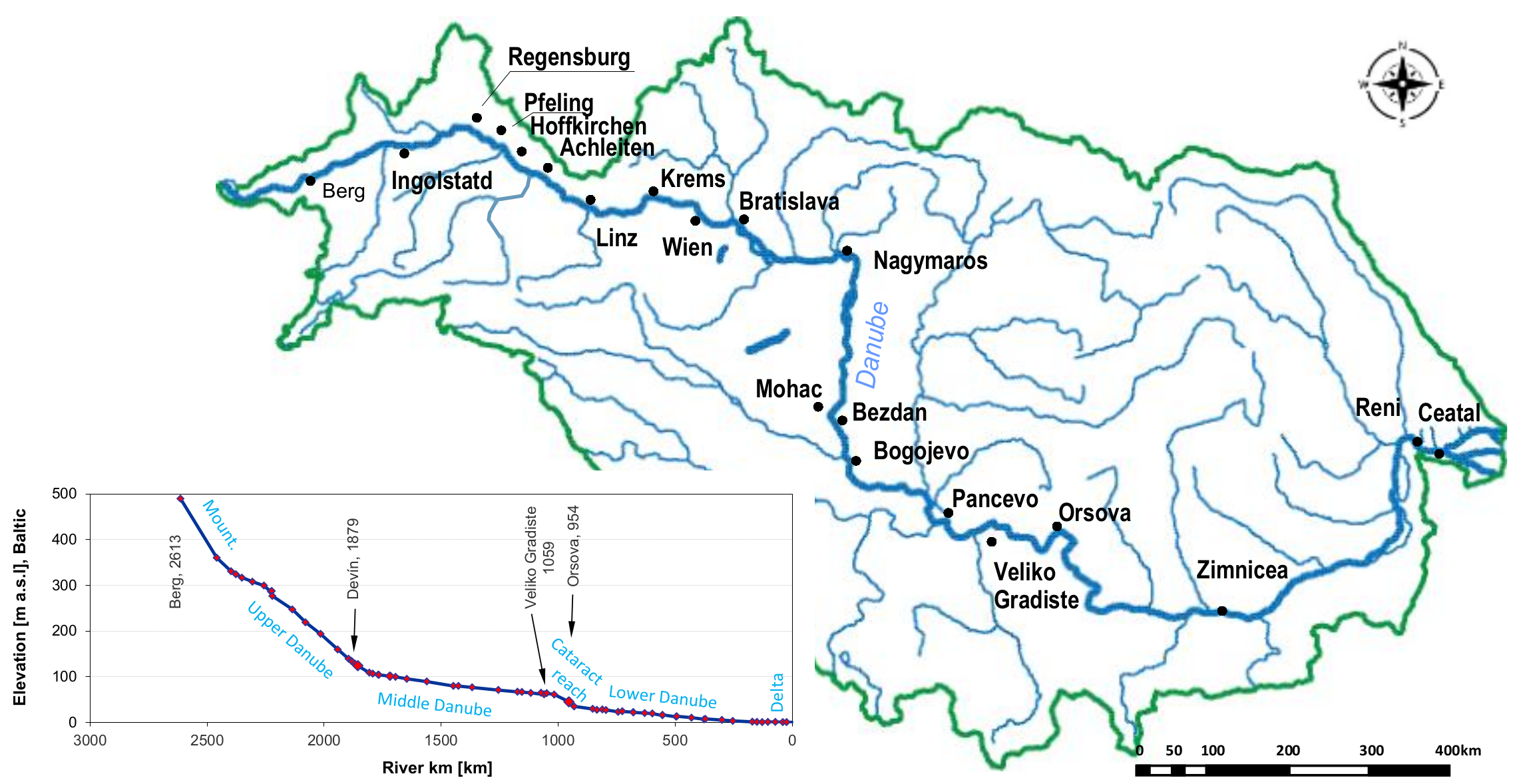
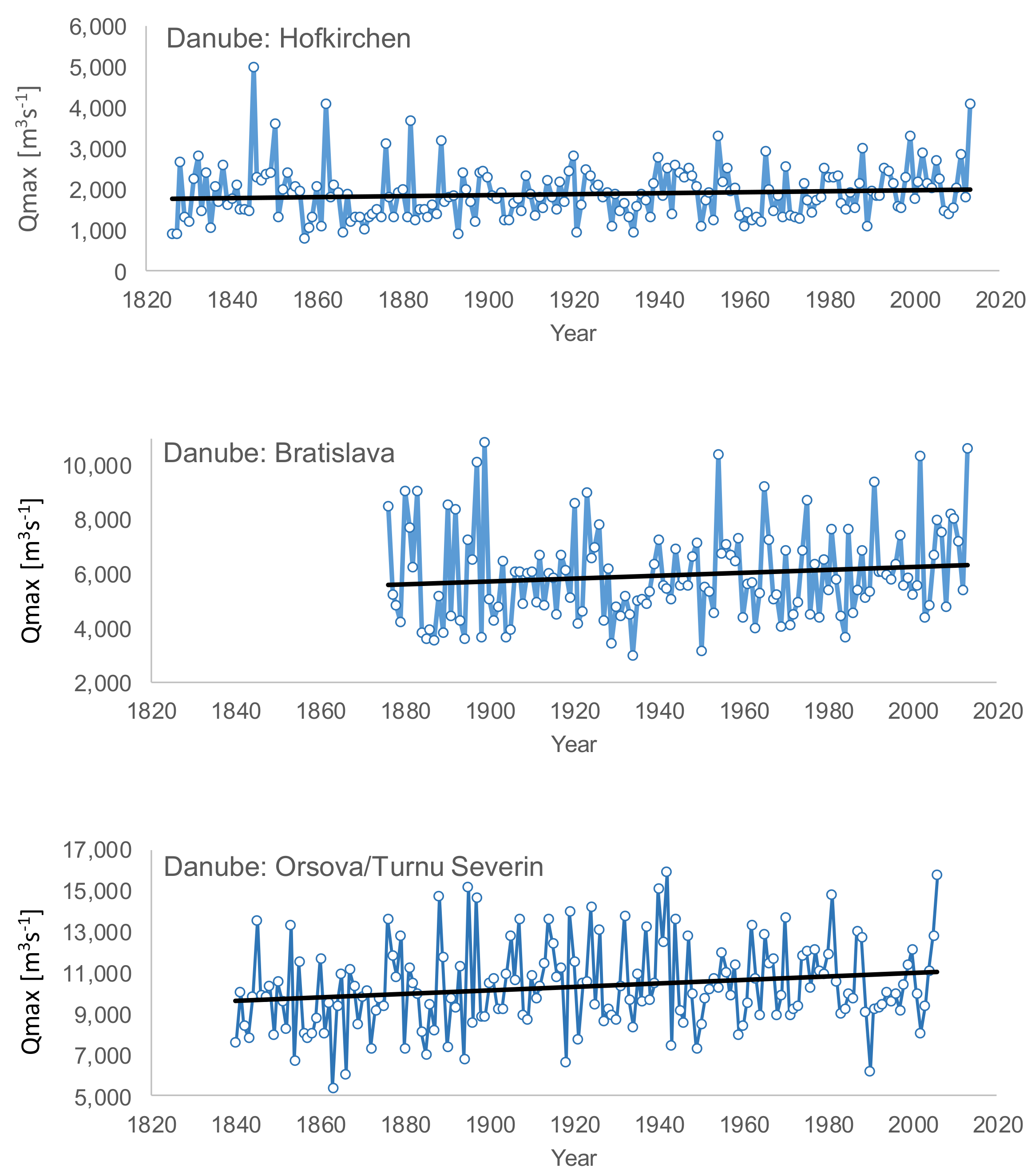
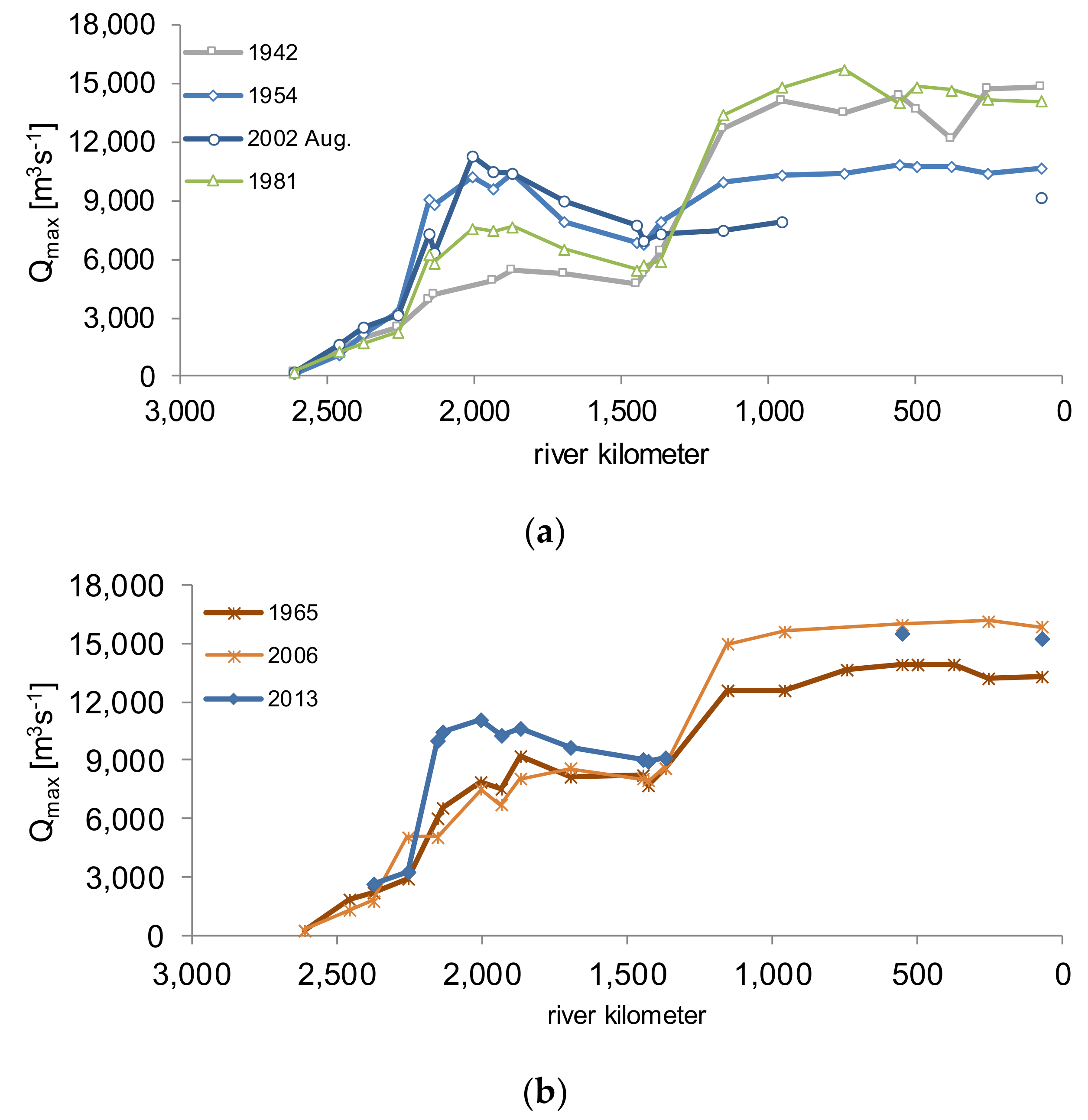

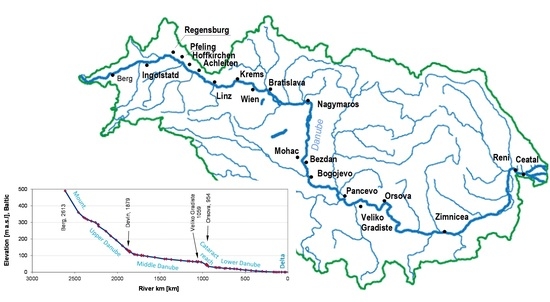
| Gauge | River km | Period | Country | Area [km2] | LAT | LONG | Elevation [m a.s.l] | Qamax [m3s−1] |
|---|---|---|---|---|---|---|---|---|
| Berg | 2613 | 1930–2007 | GE | 4047 | 48.27 | 9.73 | 489.48 | 204 |
| Ingolstadt | 2458.3 | 1940–2007 | GE | 20,001 | 48.75 | 11.42 | 359.97 | 1110 |
| Regensburg-Schwabelweis | 2376.1 | 1924–2007 | GE | 35,399 | 49.02 | 12.14 | 324.06 | 1532 |
| Pfelling | 2300 | 1926–2007 | GE | 37,757 | 48.88 | 12.75 | 307.73 | 1516 |
| Hofkirchen | 2256.9 | 1826–2013 | GE | 47,496 | 48.68 | 13.12 | 299.17 | 1896 |
| Achleiten | 2150 | 1901–2007 | GE | 76,653 | 48.58 | 13.5 | 287.27 | 4146 |
| Linz | 2135.2 | 1821–2013 | AT | 79,490 | 48.31 | 14.3 | 247.06 | 3670 |
| Stein-Krems (Kienstock) | 2002.7 | 1828–2006 | AT | 96,045 | 48.38 | 15.46 | 193.32 | 5372 |
| Wien-Nussdorf | 1934.1 | 1828–2006 | AT | 101,731 | 48.25 | 16.3 | 157 | 5301 |
| Devin/Bratislava | 1868.8 | 1876–2013 | SK | 131,338 | 48.14 | 17.1 | 132.86 | 5884 |
| Nagymaros | 1694.6 | 1893–2007 | HU | 183,534 | 47.78 | 18.95 | 99.37 | 5598 |
| Mohács | 1446.8 | 1930–2007 | HU | 209,064 | 46 | 18.67 | 79.19 | 5063 |
| Bezdan | 1425.5 | 1940–2006 | SR | 210,250 | 45.85 | 18.87 | 79.29 | 4974 |
| Bogojevo | 1367.4 | 1940–2006 | SR | 251,593 | 45.53 | 19.08 | 76.11 | 5675 |
| Pancevo | 1153.3 | 1940–2006 | SR | 525,009 | 44.87 | 20.46 | 65.98 | 10,147 |
| Veliko Gradiste | 1060 | 1931–2007 | SR | 570,375 | 44.8 | 21.4 | 60.83 | 10,529 |
| Orsova-Turnu Severin | 955 | 1840–2006 | RO | 576,232 | 44.7 | 22.42 | 44.76 | 10,295 |
| Zimnicea | 554 | 1931–2010 | RO | 658,400 | 43.63 | 25.36 | 16.06 | 11,087 |
| Reni | 132 | 1921–2010 | UKR | 805,700 | 45.45 | 28.27 | 4 | 11,217 |
| Ceatal Izmail | 72 | 1931–2010 | RO | 807,000 | 45.22 | 28.73 | 0.2 | 11,173 |
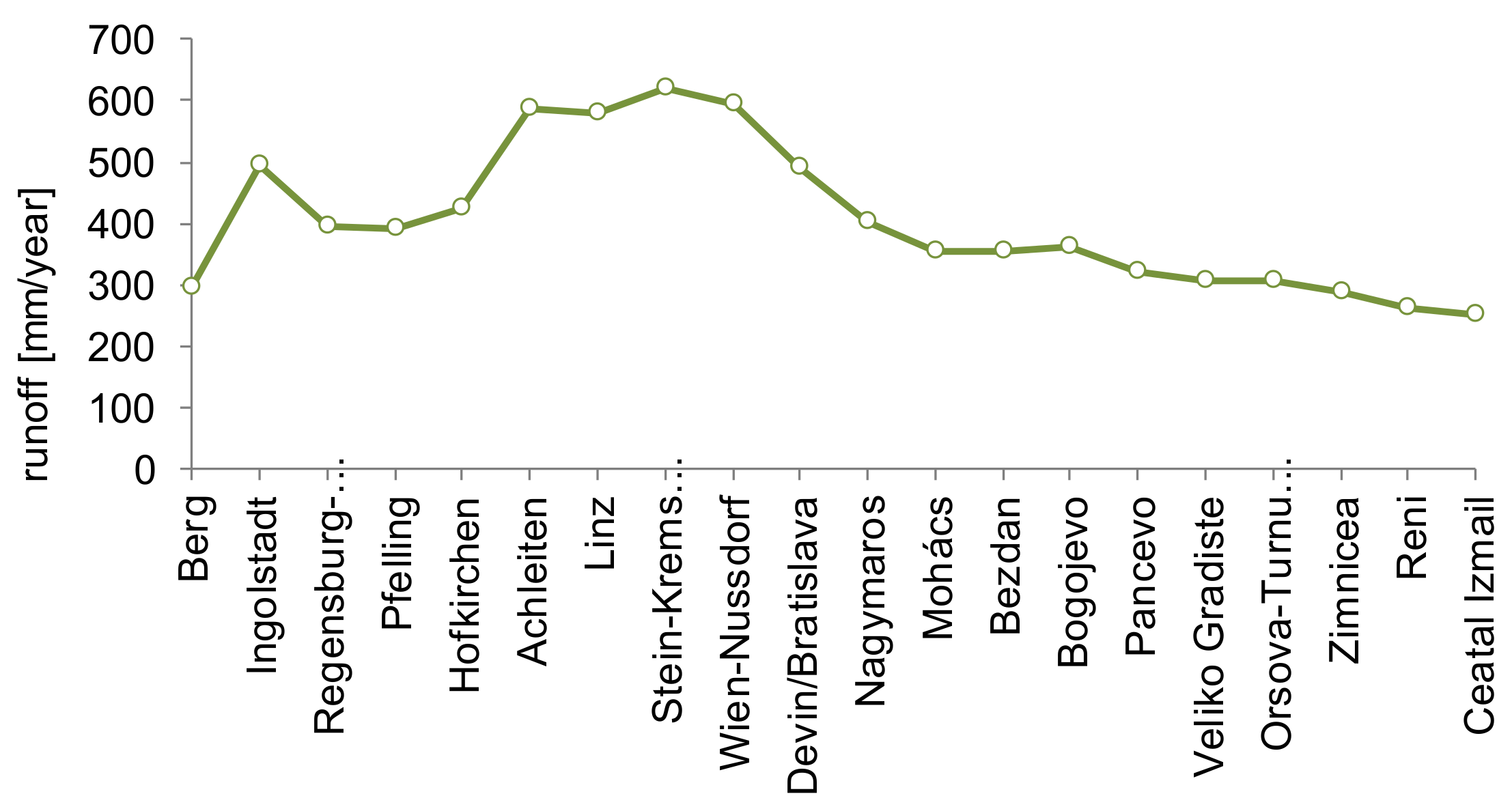
| Without Estimated Historical Maxima | R [mm] | Gs | 10 [Year] | 50 [Year] | 100 [Year] | 200 [Year] | 500 [Year] | 1000 [Year] |
|---|---|---|---|---|---|---|---|---|
| Berg | 296 | −0.30 | 324 | 432 | 476 | 518 | 573 | 613 |
| Ingolstadt | 494 | 0.15 | 1514 | 1891 | 2050 | 2209 | 2421 | 2583 |
| Regensburg-Schwabelweis | 396 | −0.46 | 2125 | 2530 | 2675 | 2809 | 2969 | 3081 |
| Pfelling | 392 | −0.23 | 2144 | 2649 | 2846 | 3034 | 3273 | 3447 |
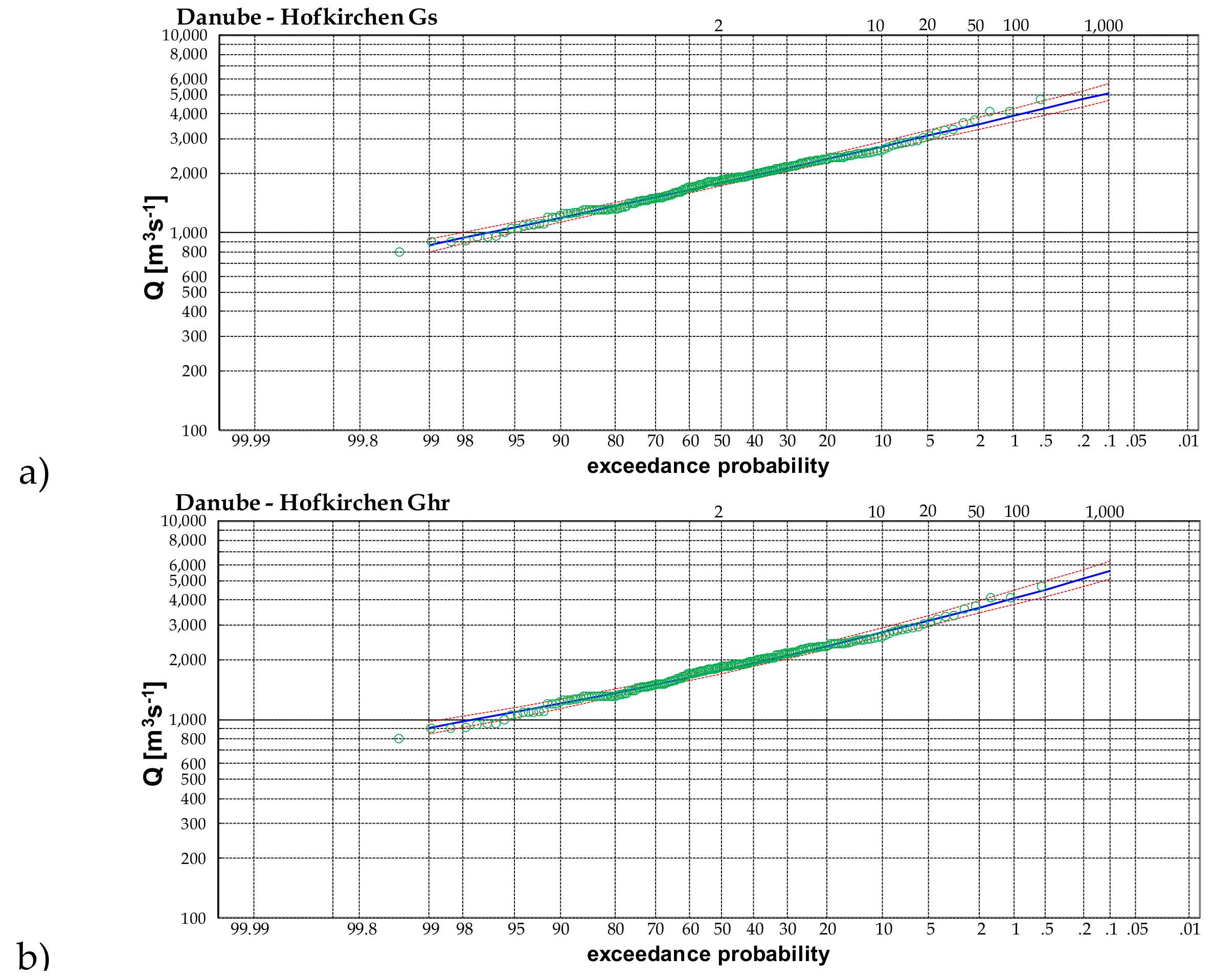
| Hofkirchen | 425 | 0.09 | 2356 | 3547 | 3897 | 4250 | 4724 | 5091 |
| Achleiten | 587 | 0.39 | 5486 | 6835 | 7422 | 8020 | 8835 | 9473 |
| Linz | 581 | 0.26 | 4641 | 7352 | 8205 | 9092 | 10,323 | 11,304 |
| Stein-Krems (Kienstock) | 621 | 0.39 | 7397 | 9605 | 10,592 | 11,613 | 13,028 | 14,154 |
| Wien-Nussdorf | 596 | 0.27 | 7187 | 9046 | 9847 | 10,658 | 11,756 | 12,610 |
| Devin/Bratislava | 492 | 0.18 | 8116 | 10,273 | 11,192 | 12,119 | 13,365 | 14,328 |
| Nagymaros | 401 | −0.05 | 7325 | 8712 | 9257 | 9783 | 10,457 | 10,955 |
| Mohács | 355 | −0.08 | 6548 | 7708 | 8157 | 8589 | 9138 | 9541 |
| Bezdan | 354 | 0.30 | 6452 | 7847 | 8437 | 9029 | 9823 | 10,435 |
| Bogojevo | 363 | 0.19 | 7334 | 8810 | 9418 | 10,020 | 10,815 | 11,418 |
| Pancevo | 320 | 0.15 | 12,611 | 14,661 | 15,483 | 16,285 | 17,326 | 18,105 |
| Veliko Gradiste | 307 | 0.02 | 13,128 | 15,167 | 15,962 | 16,728 | 17,708 | 18,430 |
| Orsova-Turnu Severin | 307 | −0.19 | 12,901 | 14,754 | 15,445 | 16,094 | 16,901 | 17,481 |
| Zimnicea | 288 | −0.09 | 13,776 | 15,769 | 16,528 | 17,248 | 18,155 | 18,815 |
| Reni | 262 | −0.40 | 13,918 | 15,596 | 16,183 | 16,715 | 17,352 | 17,793 |
| Ceatal Izmail | 251 | −0.21 | 13,677 | 15,492 | 16,161 | 16,785 | 17,557 | 18,108 |
| With Estimated Historical Maxima | Gh | 10 [Year] | 50 [Year] | 100 [Year] | 200 [Year] | 500 [Year] | 1000 [Year] | Year of Historical Max. |
|---|---|---|---|---|---|---|---|---|
| Regensburg-Schwabelweis | 0.40 | 2306 | 3140 | 3525 | 3931 | 4505 | 4970 | 1845, 1850, 1862, 1882, 2013 |
| Pfelling | 0.45 | 2320 | 3224 | 3651 | 4105 | 4756 | 5290 | 1845, 1862, 1850, 1882, 2013 |
| Achleiten | 1.17 | 5778 | 7754 | 8710 | 9743 | 11,244 | 12,495 | 1862, 1899, 2013 |
| Linz | 0.76 | 4621 | 7880 | 9027 | 10,276 | 12,104 | 13,639 | 1501 |
| Stein-Krems (Kienstock) | 0.71 | 7545 | 10,255 | 11,554 | 12,952 | 14,974 | 16,650 | 1501, 1787, 2013 |
| Wien-Nussdorf | 0.64 | 7328 | 9620 | 10,678 | 11,792 | 13,366 | 14,642 | 1501, 1787, 2013 |
| Devin/Bratislava | 0.24 | 8194 | 10,485 | 11,477 | 12,487 | 13,860 | 14,931 | 1501, 1787 |
| Nagymaros | 0.06 | 7421 | 8955 | 9574 | 10,182 | 10,975 | 11,570 | 2013 |
| Mohács | 0.04 | 6658 | 7966 | 8491 | 9004 | 9669 | 10,167 | 2013 |
| Reni | 0.05 | 14,156 | 16,485 | 17,403 | 18,291 | 19,434 | 20,281 | 1897 |
| Ceatal Izmail | −0.03 | 13,816 | 15,905 | 16,712 | 17,484 | 18,466 | 19,186 | 1876 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bačová Mitková, V.; Pekárová, P.; Halmová, D.; Miklánek, P. The Use of a Uniform Technique for Harmonization and Generalization in Assessing the Flood Discharge Frequencies of Long Return Period Floods in the Danube River Basin. Water 2021, 13, 1337. https://doi.org/10.3390/w13101337
Bačová Mitková V, Pekárová P, Halmová D, Miklánek P. The Use of a Uniform Technique for Harmonization and Generalization in Assessing the Flood Discharge Frequencies of Long Return Period Floods in the Danube River Basin. Water. 2021; 13(10):1337. https://doi.org/10.3390/w13101337
Chicago/Turabian StyleBačová Mitková, Veronika, Pavla Pekárová, Dana Halmová, and Pavol Miklánek. 2021. "The Use of a Uniform Technique for Harmonization and Generalization in Assessing the Flood Discharge Frequencies of Long Return Period Floods in the Danube River Basin" Water 13, no. 10: 1337. https://doi.org/10.3390/w13101337