Rainwater Harvesting Techniques to Face Water Scarcity in African Drylands: Hydrological Efficiency Assessment
Abstract
1. Introduction
2. Geographical and Climatological Context
3. Materials and Methods
3.1. The Numerical Model
- The potential evapotranspiration equation is based on a single climatic data widely available, the temperature:where is the air temperature in °C, is the percentage of total daytime hours in which the evapotranspiration occurs (approximately 12 h) out of total daytime hours of the year (365 × 12 h), and is a parameter for calibration.
- The is adjusted for a specific crop using a crop coefficient , resulting in:where represents the crop evapotranspiration under standard conditions and is the crop coefficient that accounts for the evapotranspiration capability during each growth stage of an individual crop . Values of are listed in the FAO Irrigation and drainage paper 56 [51].
- When the soil becomes dry, a limited amount of water is available for plant root extraction. If the depletion of the soil water storage overcomes a threshold, the crop is said to be water stressed and its crop transpiration capability is reduced by a water stress coefficient
- The water stress coefficient [0,1] can be determined by the equationwhere and are the water content at wilting point and field capacity, respectively, and is the soil water depletion fraction, which is characteristic for each crop and represents the fraction of the total available water that the plant can uptake without suffering stress.
3.2. Model Set-Up
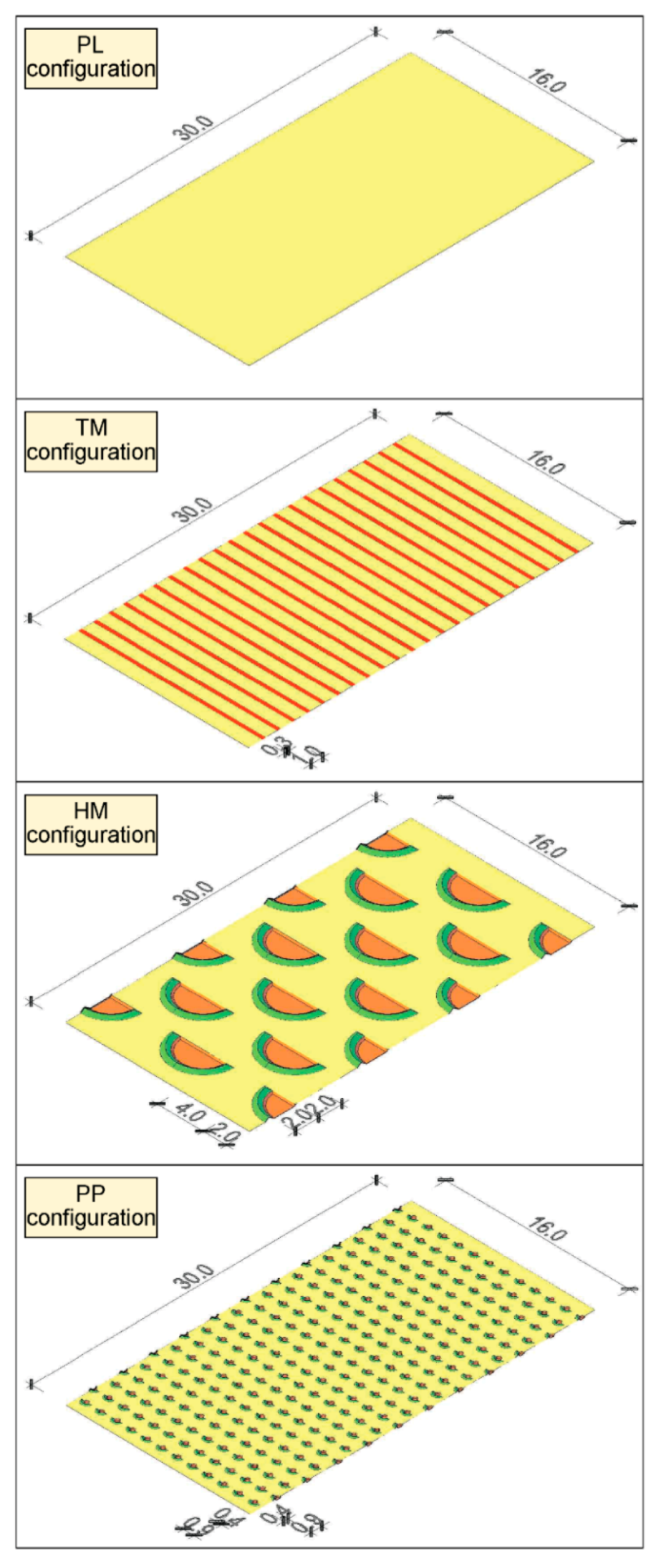
3.2.1. Geometry
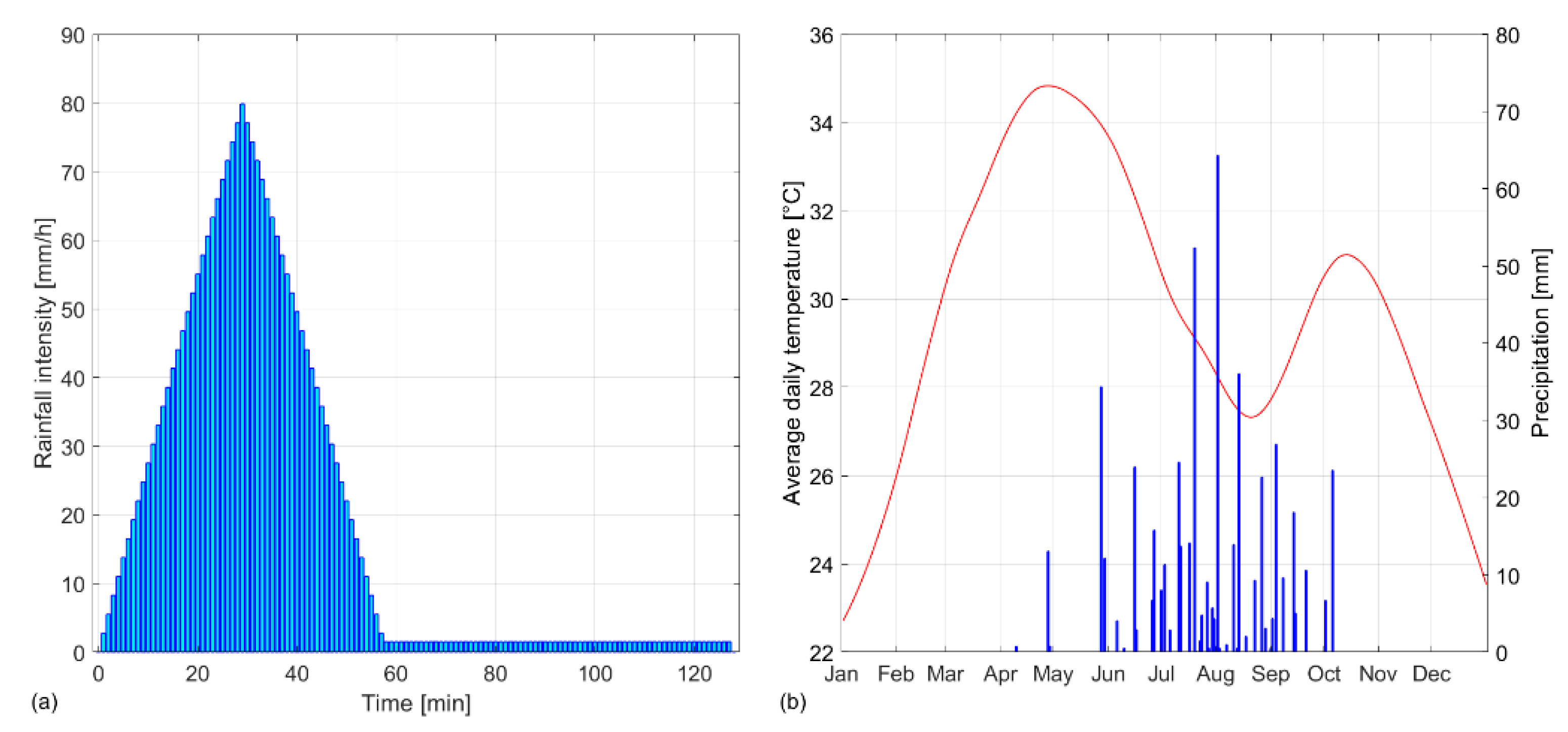
3.2.2. Meteorological Data
3.2.3. Input Parameters
- -
- the previous six parameters, corresponding to the simulation closest to the mean model behavior, and the four soil parameters (Table 3);
- -
- the phenological parameters for each analyzed crop (Table 4). During the growing period, the evapotranspiration potential of the given crop will vary accordingly to the development of its height and leafage. The growing season can be divided into four different growth stages labeled as follows: (initial), (development), (mid-season), (late-season). To each stage is associated a distinct value of crop coefficient .
3.3. Evaluation of the Hydrological Efficiency
- -
- outflow reduction: calculated as the reduction on the cumulated volume of water that flows out of the domain with and without the implementation of RHWT ( and , respectively)
- -
- infiltration increase: calculated as the increase on the cumulated volume of water infiltrated in the subsurface with and without the implementation of RHWT ( and , respectively)
- -
- stress mitigation: calculated as the increase on soil moisture needed to reach the availability threshold with and without the implementation of RHWT ( and , respectively)
4. Results
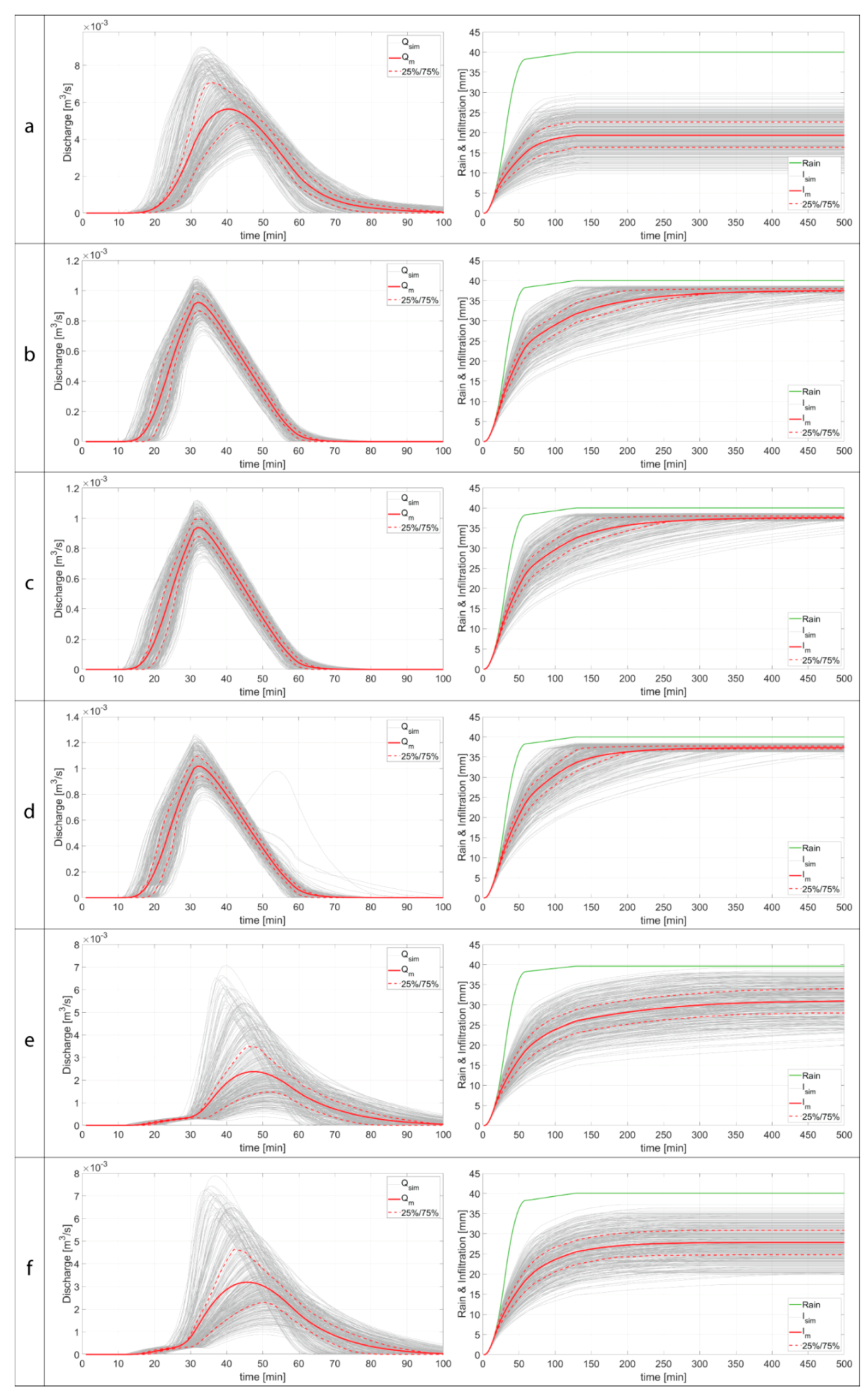
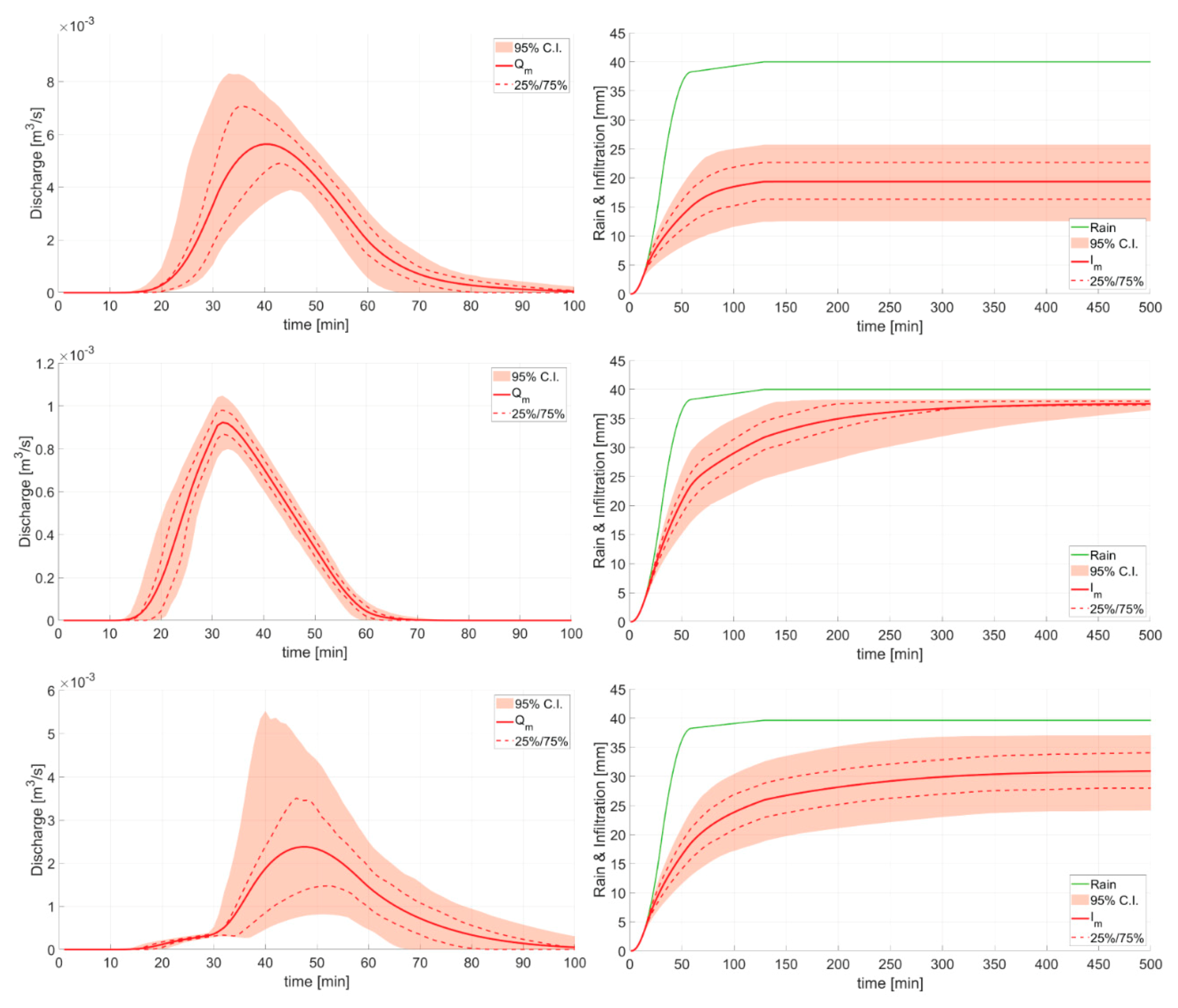
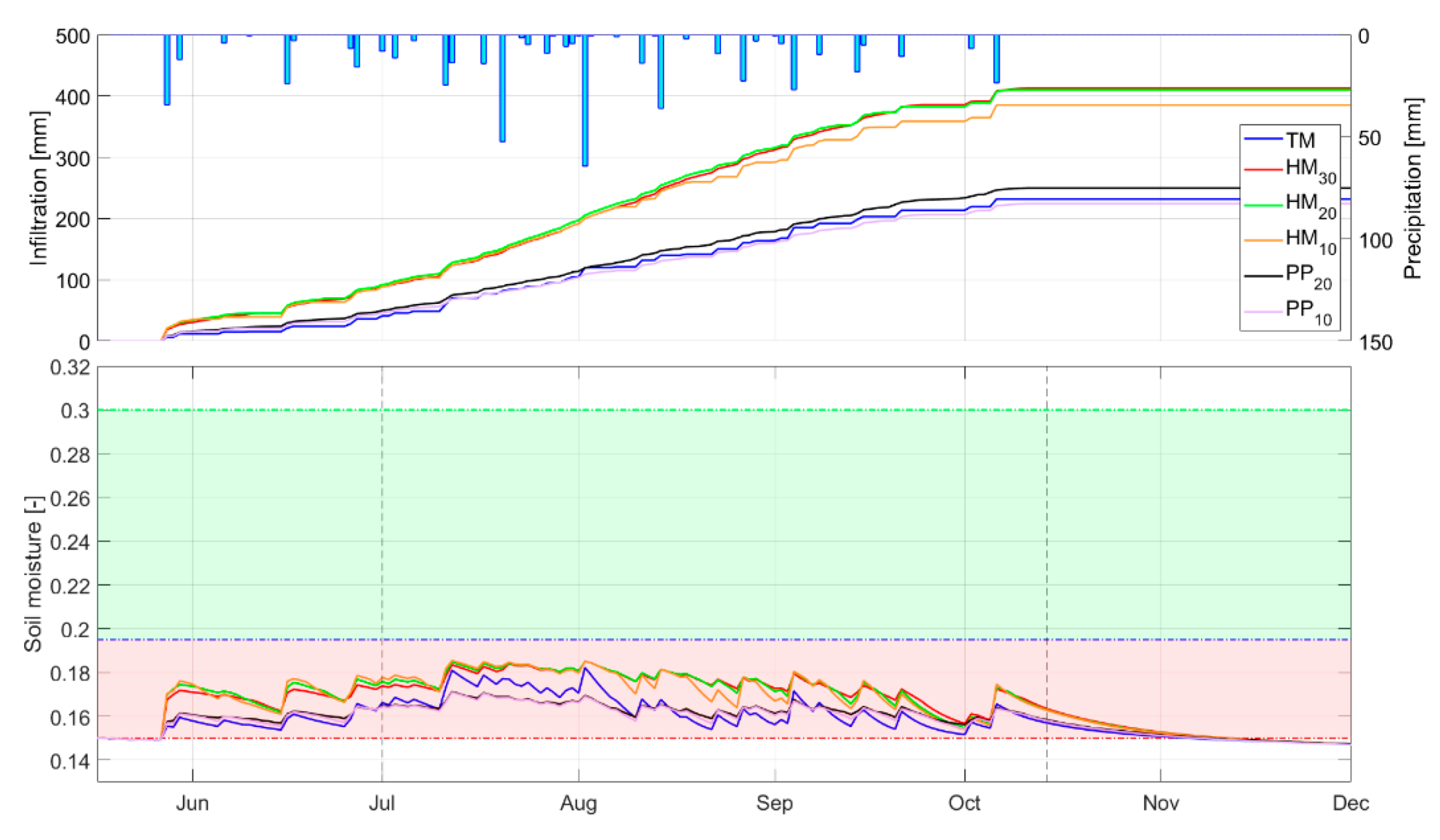
4.1. Hydrological Behaviour
4.2. Hydrological Efficiency Assessment
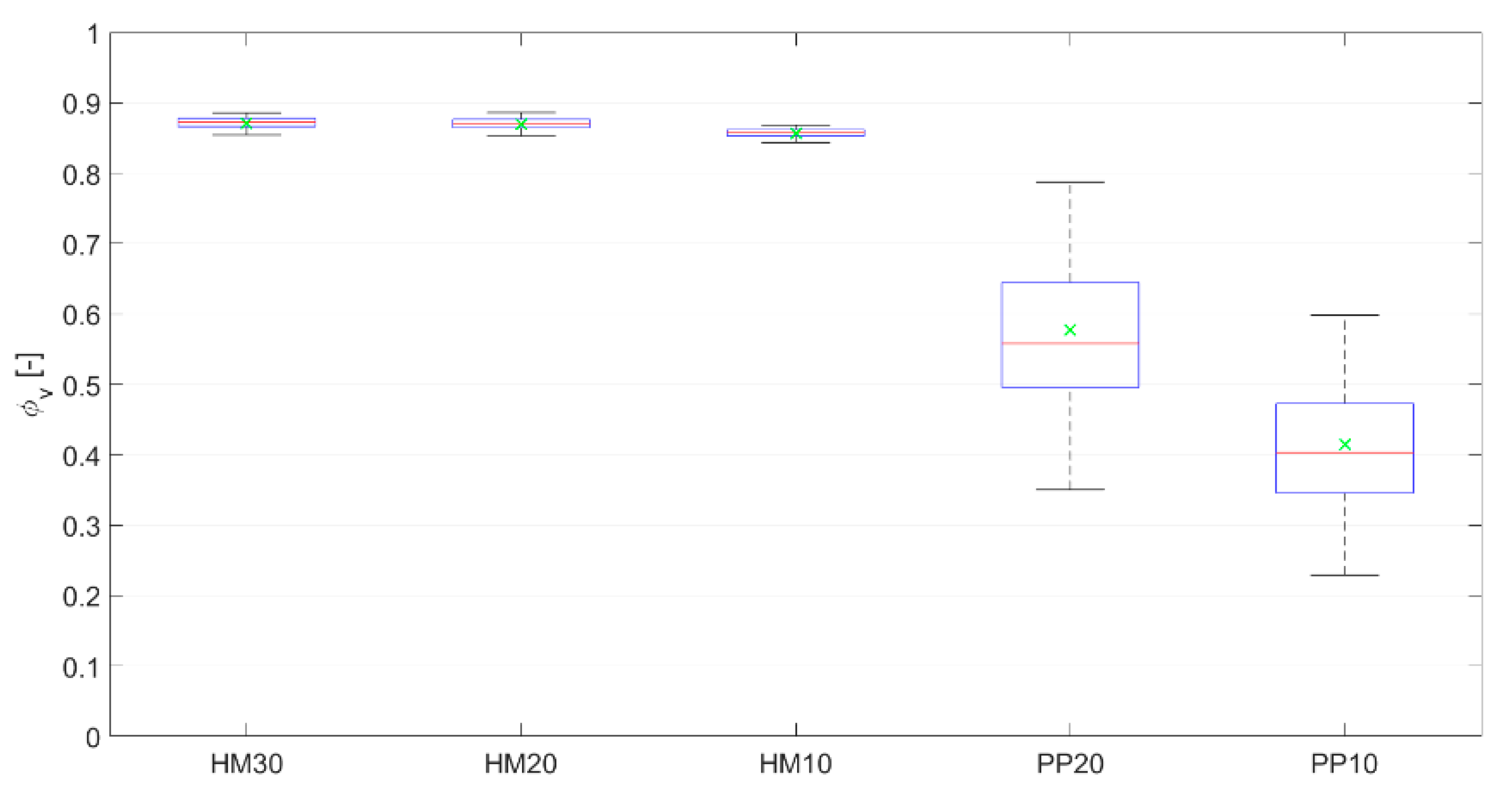
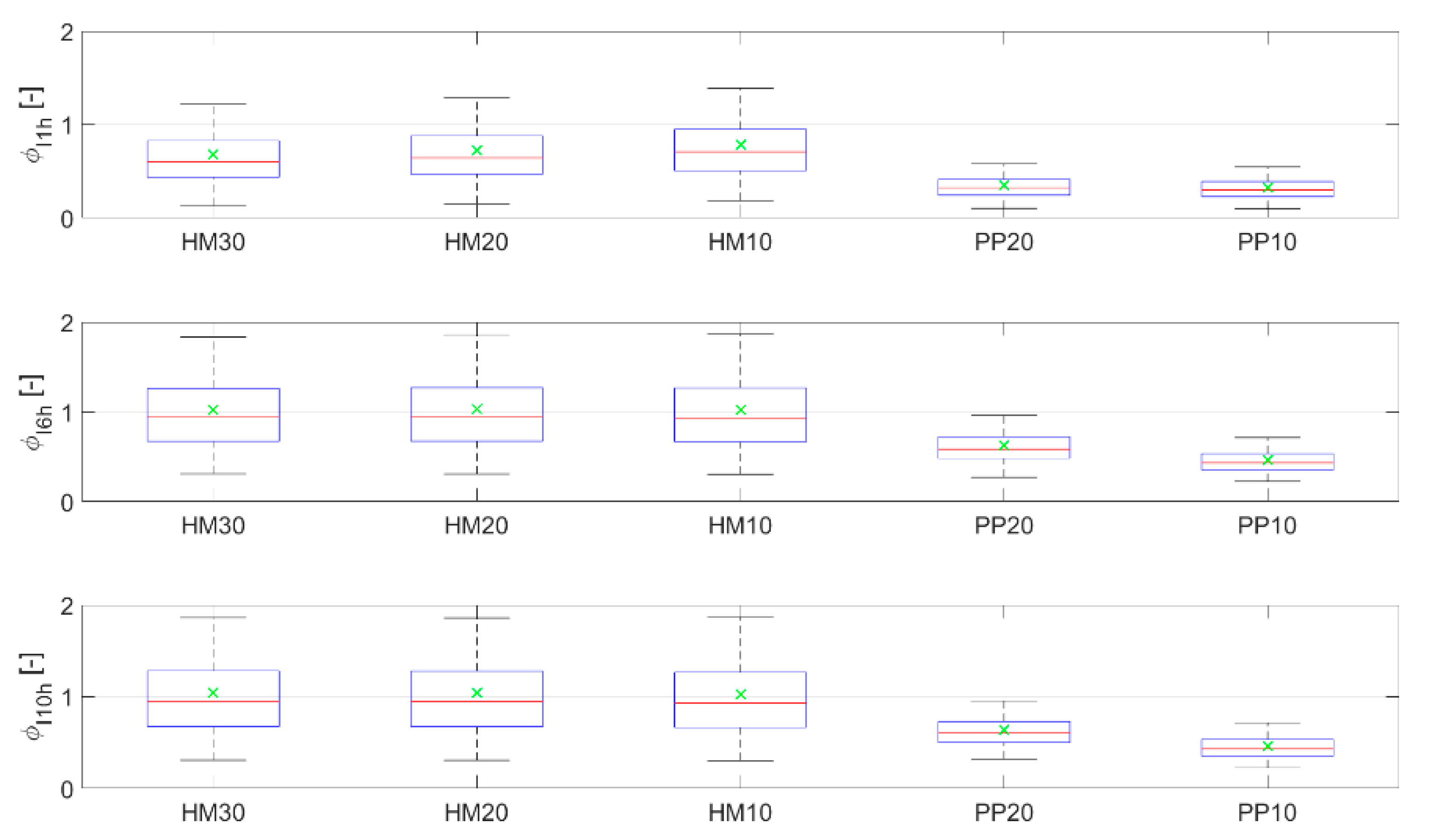
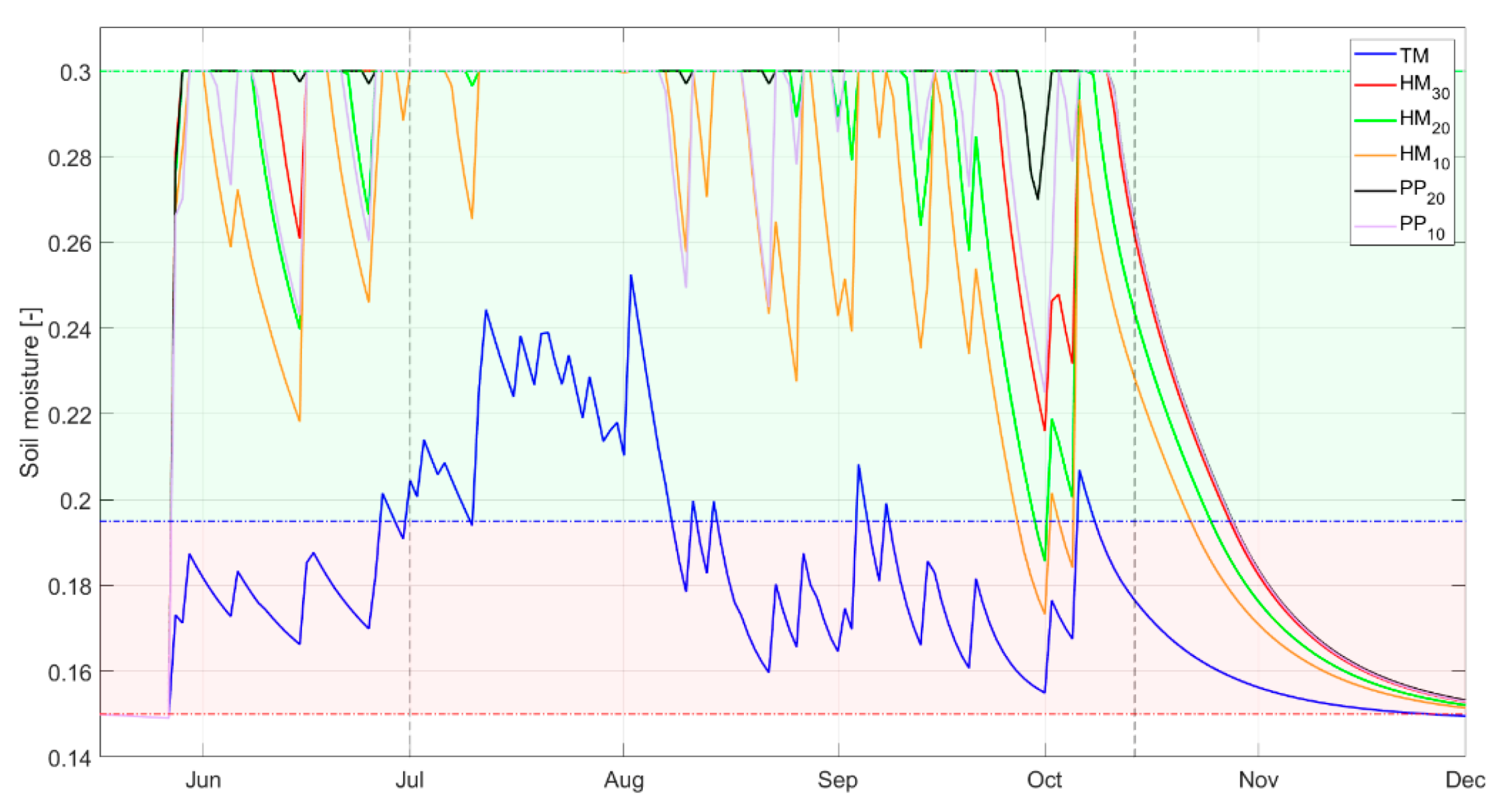
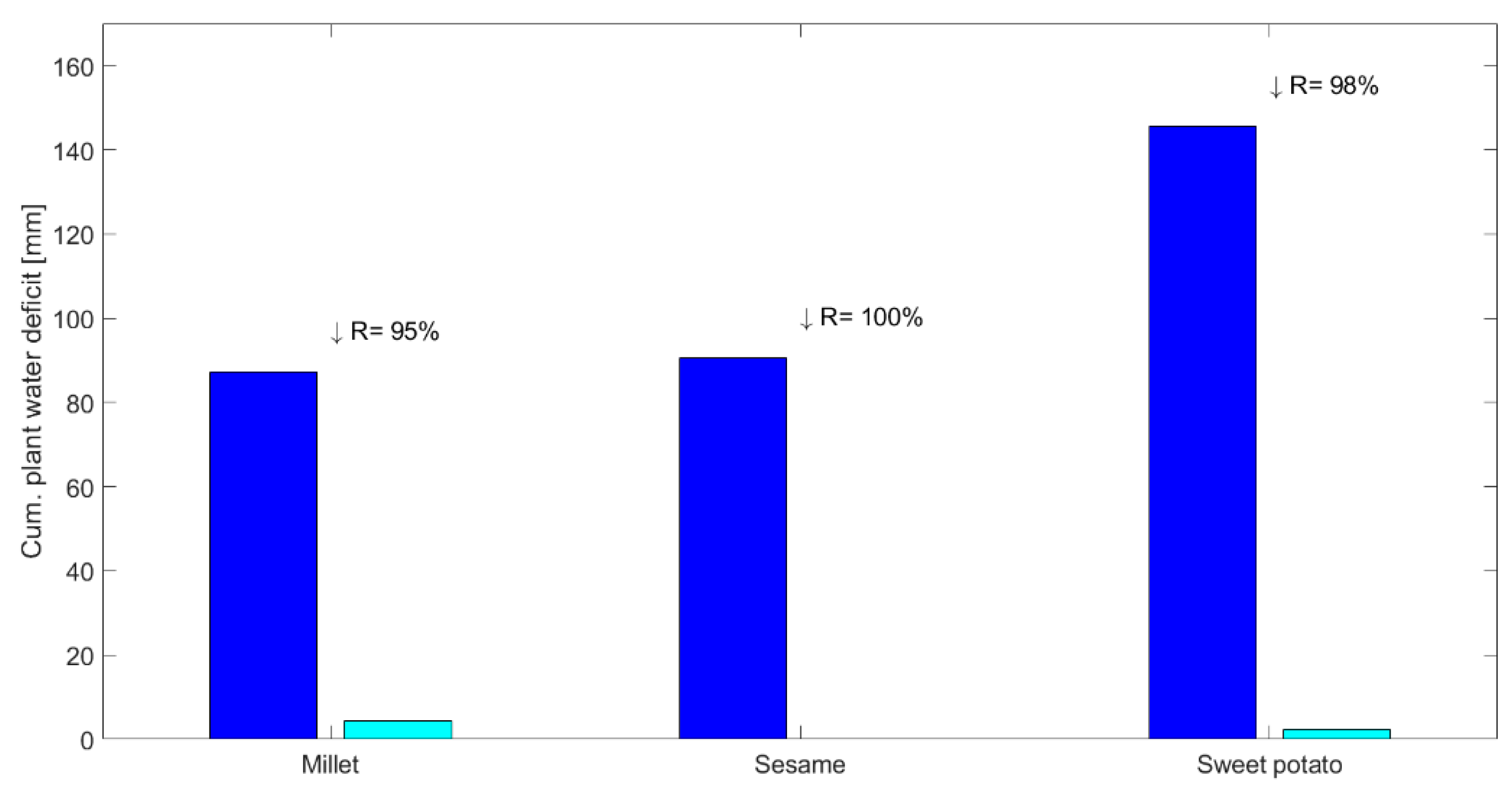
4.3. Water Stress Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Searchinger, T.; Hanson, C.; Waite, R.; Lipinski, B. Achieving Replacement Level Fertility. 2013. Available online: https://www.wri.org/publication/achieving-replacement-level-fertility (accessed on 13 May 2020).
- Potts, M.; Henderson, C.; Campbell, M. The Sahel: A Malthusian Challenge? Environ. Resour. Econ. 2013, 55, 501–512. [Google Scholar] [CrossRef]
- Winterbottom, R.; Reij, C.; Garrity, D.; Glover, J.; Hellums, D.; Mcgahuey, M.; Scherr, S. Improving Land and Water Management. 2013. Available online: https://www.climatelearningplatform.org/sites/default/files/resources/improving_land_and_water_management_0.pdf (accessed on 13 May 2020).
- Breman, H.; Groot, J.J.R.; van Keulen, H. Resource limitations in Sahelian agriculture. Glob. Environ. Chang. 2001, 11, 59–68. [Google Scholar] [CrossRef]
- National Centers for Environmental Information. Available online: https://www.ncdc.noaa.gov/cag/global/time-series/africa/land/1/7/1910-2019?trend=true&trend_base=10&firsttrendyear=1880&lasttrendyear=2019 (accessed on 14 February 2020).
- Taylor, C.M.; Belušić, D.; Guichard, F.; Parker, D.J.; Vischel, T.; Bock, O.; Harris, P.P.; Janicot, S.; Klein, C.; Panthou, G. Frequency of extreme Sahelian storms tripled since 1982 in satellite observations. Nature 2017, 544, 475–478. [Google Scholar] [CrossRef]
- Balme, M.; Vischel, T.; Lebel, T.; Peugeot, C.; Galle, S. Assessing the water balance in the Sahel: Impact of small scale rainfall variability on runoff. J. Hydrol. 2006, 331, 336–348. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Andersson, J.C.M.; Müller, E.N.; Hattermann, F.F. Climate or land use? - Attribution of changes in river flooding in the Sahel zone. Water 2015, 7, 2796–2820. [Google Scholar] [CrossRef]
- Amogu, O.; Esteves, M.; Vandervaere, J.-P.; Malam Abdou, M.; Panthou, G.; Rajot, J.-L.; Souley Yéro, K.; Boubkraoui, S.; Lapetite, J.-M.; Dessay, N.; et al. Runoff evolution due to land-use change in a small Sahelian catchment. Hydrol. Sci. J. 2015, 60, 78–95. [Google Scholar] [CrossRef]
- Tamagnone, P.; Massazza, G.; Pezzoli, A.; Rosso, M. Hydrology of the Sirba River: Updating and Analysis of Discharge Time Series. Water 2019, 11, 156. [Google Scholar] [CrossRef]
- Bigi, V.; Pezzoli, A.; Rosso, M. Past and Future Precipitation Trend Analysis for the City of Niamey (Niger): An Overview. Climate 2018, 6, 73. [Google Scholar] [CrossRef]
- Seidou, O. Climate Change May Result in More Water Availability in Parts of the African Sahel. In Innovations and Interdisciplinary Solutions for Underserved Areas, Proceedings of Second International Conference, InterSol 2018, Kigali, Rwanda, March 24–25; Springer: Berlin, Germany, 2018; ISBN 978-3-319-98877-1. [Google Scholar]
- Tabor, J.A. Improving crop yields in the Sahel by means of water-harvesting. J. Arid Environ. 1995, 30, 83–106. [Google Scholar] [CrossRef]
- Malley, Z.J.U.; Kayombo, B.; Willcocks, T.J.; Mtakwa, P.W. Ngoro: An indigenous, sustainable and profitable soil, water and nutrient conservation system in Tanzania for sloping land. Soil Tillage Res. 2004, 77, 47–58. [Google Scholar] [CrossRef]
- Assefa, S.; Biazin, B.; Muluneh, A.; Yimer, F.; Haileslassie, A. Rainwater harvesting for supplemental irrigation of onions in the southern dry lands of Ethiopia. Agric. Water Manag. 2016, 178, 325–334. [Google Scholar] [CrossRef]
- Walker, S.; Tsubo, M.; Hensley, M. Quantifying risk for water harvesting under semi-arid conditions. Agric. Water Manag. 2005, 76, 94–107. [Google Scholar] [CrossRef]
- Zougmoré, R.; Zida, Z.; Kambou, N.F. Role of nutrient amendments in the success of half-moon soil and water conservation practice in semiarid Burkina Faso. Soil Tillage Res. 2003, 71, 143–149. [Google Scholar] [CrossRef]
- Hensley, M.; Bennie, A.; Van Rensburg, L.; Botha, J. Review of ‘plant available water’ aspects of water use efficiency under irrigated and dryland conditions. Water SA 2011, 37, 771–780. [Google Scholar] [CrossRef]
- Zakari, S.; Ouédraogo, M.; Abasse, T.; Zougmoré, R. Farmer’s Prioritization and Adoption of Climate-Smart Agriculture (CSA) Technologies and Practices. J. Agric. Environ. Sci. 2019, 8, 176–185. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Climate-Smart Agriculture Sourcebook; Food and Agriculture Organization of the United Nations: Rome, Italy, 2014; ISBN 978-92-5-107720-7. [Google Scholar]
- Al-Seekh, S.H.; Mohammad, A.G. The Effect of Water Harvesting Techniques on Runoff, Sedimentation, and Soil Properties. Environ. Manag. 2009, 44, 37–45. [Google Scholar] [CrossRef]
- Rockström, J.; Karlberg, L.; Wani, S.P.; Barron, J.; Hatibu, N.; Oweis, T.; Bruggeman, A.; Farahani, J.; Qiang, Z. Managing water in rainfed agriculture—The need for a paradigm shift. Agric. Water Manag. 2010, 97, 543–550. [Google Scholar] [CrossRef]
- Zouré, C.; Queloz, P.; Koïta, M.; Niang, D.; Fowé, T.; Yonaba, R.; Consuegra, D.; Yacouba, H.; Karambiri, H. Modelling the water balance on farming practices at plot scale: Case study of Tougou watershed in Northern Burkina Faso. Catena 2019, 173, 59–70. [Google Scholar] [CrossRef]
- Reij, C.; Tappan, G.; Smale, M. Agroenvironmental Transformation in the Sahel: Another Kind of “Green Revolution”. Int. Food Policy Res. Inst. 2009, 914, 52. [Google Scholar]
- Mounirou, L.A.; Zouré, C.O.; Yonaba, R.; Paturel, J.-E.; Mahé, G.; Niang, D.; Yacouba, H.; Karambiri, H. Multi-scale analysis of runoff from a statistical perspective in a small Sahelian catchment under semi-arid climate. Arab. J. Geosci. 2020, 13, 154. [Google Scholar] [CrossRef]
- Mounirou, L.A.; Yacouba, H.; Karambiri, H.; Paturel, J.-E.; Mahé, G. Measuring runoff by plots at different scales: Understanding and analysing the sources of variation. Comptes Rendus Geosci. 2012, 344, 441–448. [Google Scholar] [CrossRef]
- Defersha, M.B.; Melesse, A.M. Field-scale investigation of the effect of land use on sediment yield and runoff using runoff plot data and models in the Mara River basin, Kenya. CATENA 2012, 89, 54–64. [Google Scholar] [CrossRef]
- Vaezi, A.R. Modeling Runoff from Semi-Arid Agricultural Lands in Northwest Iran. Pedosphere 2014, 24, 595–604. [Google Scholar] [CrossRef]
- Hernández-Bernal, N. Water Harvesting as a Tool to Allow Environmental Recovery in a Semi-Arid Region in Brazil. Available online: https://search.informit.com.au/documentSummary;dn=889490390692042;res=IELENG (accessed on 14 February 2020).
- Welderufael, W.A.; Le Roux, P.A.L.; Hensley, M. Quantifying rainfall–runoff relationships on the Dera Calcic Fluvic Regosol ecotope in Ethiopia. Agric. Water Manag. 2008, 95, 1223–1232. [Google Scholar] [CrossRef]
- Verbist, K.; Cornelis, W.M.; Gabriels, D.; Alaerts, K.; Soto, G. Using an inverse modelling approach to evaluate the water retention in a simple water harvesting technique. Hydrol. Earth Syst. Sci. 2009, 13, 1979–1992. [Google Scholar] [CrossRef]
- Tamagnone, P.; Comino, E.; Rosso, M. Rainwater harvesting techniques as an adaptation strategy for flood mitigation. J. Hydrol. 2020, 586, 124880. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métod. Numér. Para Cálculo Diseño En Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Xu, H.; Wu, M. A First Estimation of County-Based Green Water Availability and Its Implications for Agriculture and Bioenergy Production in the United States. Water 2018, 10, 148. [Google Scholar] [CrossRef]
- Schyns, J.F.; Hoekstra, A.Y.; Booij, M.J.; Hogeboom, R.J.; Mekonnen, M.M. Limits to the world’s green water resources for food, feed, fiber, timber, and bioenergy. Proc. Natl. Acad. Sci. USA 2019, 116, 4893–4898. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian standardized rainfall index revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- HarvestChoice Long-Term Annual Rainfall (mm, 1960–2014). Available online: https://harvestchoice.org/data/pre_mean (accessed on 4 December 2019).
- Dame, M.C.W.; University of Notre Dame. Country Index // Notre Dame Global Adaptation Initiative // University of Notre Dame. Available online: https://gain.nd.edu/our-work/country-index/ (accessed on 2 July 2020).
- Todzo, S.; Bichet, A.; Diedhiou, A. Intensification of the hydrological cycle expected in West Africa over the 21st century. Earth Syst. Dyn. 2020, 11, 319–328. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel: Recent trends of extreme rainfall in the west african sahel. Int. J. Climatol. 2014, 34, 3998–4006. [Google Scholar] [CrossRef]
- Kandji, S.T.; Verchot, L.; Mackensen, J. Climate Change and Variability in the Sahel Region: Impacts and Adaptation Strategies in the Agricultural Sector. 2006. Available online: http://www.worldagroforestry.org/publication/climate-change-and-variability-sahel-region-impacts-and-adaptation-strategies (accessed on 14 May 2020).
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Cea, L.; Legout, C.; Darboux, F.; Esteves, M.; Nord, G. Experimental validation of a 2D overland flow model using high resolution water depth and velocity data. J. Hydrol. 2014, 513, 142–153. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications: The shallow water equations for overland flow applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef]
- Cea, L.; Legout, C.; Grangeon, T.; Nord, G. Impact of model simplifications on soil erosion predictions: Application of the GLUE methodology to a distributed event-based model at the hillslope scale: Impact of model simplifications on soil erosion predictions. Hydrol. Process. 2016, 30, 1096–1113. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Effect of rainfall uncertainty on the performance of physically based rainfall–runoff models. Hydrol. Process. 2019, 33, 160–173. [Google Scholar] [CrossRef]
- Cea, L.; Fraga, I.; Puertas, J.; Álvarez, M.; Bermúdez, M.; Coquerez, S.; Salsón, S.; Pettazzi, A. Influencia de la densidad espacial de estaciones pluviométricas y de la disponibilidad de datos radar en los hidrogramas de tormenta calculados con un modelo hidrológico distribuido: Aplicación a una cuenca de 24 Km2 en el Noroeste de España. In Proceedings of the IV Jornadas de Ingeniería del Agua, JIA2015, Córdoba, Spain, 21–22 October 2015; p. 10. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill series in water resources and environmental engineering; McGraw-Hill: New York, NY, USA, 1988; ISBN 978-0-07-010810-3. [Google Scholar]
- Famiglietti, J.S.; Wood, E.F. Multiscale modeling of spatially variable water and energy balance processes. Water Resour. Res. 1994, 30, 3061–3078. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; Food and Agriculture Organization: Rome, Italy, 1977; Volume 24. [Google Scholar]
- Allan, R.; Pereira, L.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Mekdaschi Studer, R.; Liniger, H. Water Harvesting: Guidelines to Good Practice; Centre for Development and Environment (CDE): Bern, Switzerland, 2013; ISBN 978-3-905835-35-9. [Google Scholar]
- WOCAT. Available online: https://qcat.wocat.net/en/wocat/ (accessed on 27 February 2019).
- Mathon, V.; Laurent, H.; Lebel, T. Mesoscale Convective System Rainfall in the Sahel. J. Appl. Meteorol. 2002, 41, 1081–1092. [Google Scholar] [CrossRef]
- Galle, S.; Grippa, M.; Peugeot, C.; Moussa, I.B.; Cappelaere, B.; Demarty, J.; Mougin, E.; Panthou, G.; Adjomayi, P.; Agbossou, E.K.; et al. AMMA-CATCH, a Critical Zone Observatory in West Africa Monitoring a Region in Transition. Vadose Zone J. 2018, 17, 180062. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Peugeot, C.; Cappelaere, B.; Vieux, B.E.; Séguis, L.; Maia, A. Hydrologic process simulation of a semiarid, endoreic catchment in Sahelian West Niger. 1. Model-aided data analysis and screening. J. Hydrol. 2003, 279, 224–243. [Google Scholar] [CrossRef]
- Delestre, O.; Esteves, M. Rainfall Overland flow Simulations and Real Events in Niger. 2010. Available online: https://hal.archives-ouvertes.fr/hal-00521133/ (accessed on 4 February 2020).
- Van de Giesen, N.; Stomph, T.J.; de Ridder, N. Surface runoff scale effects in West African watersheds: Modeling and management options. Agric. Water Manag. 2005, 72, 109–130. [Google Scholar] [CrossRef]
- Abdou, M.M.; Vandervaere, J.-P.; Descroix, L.; Bouzou, I.; Maiga, O.F.; Abdou, S.; Seyni, B.B.; Daouda, L.O. Évolution de la Conductivité Hydraulique d’un sol Sableux Cultivé du Niger. Available online: https://hal.ird.fr/ird-02153170/document (accessed on 26 November 2019).
- Valentin, C. Surface crusts of semi-arid sandy soils: Types, functions and management. In Proceedings of the Management of Tropical Sandy Soils for Sustainable Agriculture, Khon Kaen, Thailand, 27 November–2 December 2005; p. 12, ISBN 978-974-7946-96-3. [Google Scholar]
- Brocca, L.; Melone, F.; Moramarco, T. Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 2011, 25, 2801–2813. [Google Scholar] [CrossRef]
- Komariah, S.M. The development of water harvesting research for agriculture. Rev. Agric. Sci. 2013, 1, 31–42. [Google Scholar] [CrossRef]
- Barry, B.; Olaleye, A.O.; Zougmoré, R.; Fatondji, D. Rainwater Harvesting Technologies in the Sahelian Zone of West Africa and the Potential for Outscaling; (Working Paper 126); International Water Management Institute: Colombo, Sri Lanka, 2008; p. 40. ISBN 978-92-9090-684-1. [Google Scholar]
- Li, C.; Hoffland, E.; Kuyper, T.W.; Yu, Y.; Zhang, C.; Li, H.; Zhang, F.; van der Werf, W. Syndromes of production in intercropping impact yield gains. Nat. Plants 2020, 6, 653–660. [Google Scholar] [CrossRef]
- Roose, E.; Kabore, V.; Guenat, C. Zai Practice: A West African Traditional Rehabilitation System for Semiarid Degraded Lands, a Case Study in Burkina Faso. Arid Soil Res. Rehabil. 1999, 13, 343–355. [Google Scholar] [CrossRef]

| Configurations | Excavation Depth (cm) | Identification Code |
|---|---|---|
| Plain | 0 | PL |
| Traditional sowing method | 0 | TM |
| Half-moon | 10 | HM10 |
| 20 | HM20 | |
| 30 | HM30 | |
| Planting pits | 10 | PP10 |
| 20 | PP20 |
| Parameter | Sampling Range | Unit | Source | |
|---|---|---|---|---|
| Manning coefficient () | [0.02–0.7] | s/m1/3 | [59,60,61] | |
| Suction () | [110–290] | mm | [48] | |
| Total porosity () | [0.33–0.48] | - | [26,48] | |
| Initial saturation () | [0.07–0.1] | - | [62] | |
| Hydraulic conductivity | () | [0.5–3] crusted 1 | mm/h | [48,59,60,62,63] |
| () | [10–40] tilled 1 | |||
| Parameter | Values | Unit | |
|---|---|---|---|
| Manning coefficient () | 0.34 | s/m1/3 | |
| Suction () | 122.16 | mm | |
| Total porosity () | 0.3 | - | |
| Initial saturation () | 0.5 | - | |
| Hydraulic conductivity | () | 0.89 | mm/h |
| () | 18.11 | ||
| () | 0.5 | ||
| Pore size distribution index | 0.5 | - | |
| Field capacity | 0.25 | - | |
| Wilting point | 0.15 | - | |
| Type | Crop | Depletion Factor (-) | Crop Coefficient (days) | Lengths of Growth Stages (days) | Growing Season | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | Length (Days) | Period | ||||||
| Cereals | Millet | 0.55 | 0.3 | 1 | 0.3 | 15 | 25 | 40 | 25 | 105 | Jul–Oct |
| Oil seed | Sesame | 0.6 | 0.35 | 1.1 | 0.25 | 20 | 30 | 40 | 20 | 110 | Jun–Sep |
| Root crop | Sweet potato | 0.65 | 0.5 | 1.15 | 0.65 | 15 | 30 | 50 | 30 | 125 | Jun–Oct |
| PL | HM30 | HM20 | HM10 | PP20 | PP10 | ||
|---|---|---|---|---|---|---|---|
| Manning coefficient () | −0.34 | −0.13 | −0.09 | −0.30 | −0.41 | −0.45 | |
| Suction () | −0.32 | −0.33 | −0.33 | −0.33 | −0.37 | −0.37 | |
| Total porosity () | −0.20 | −0.21 | −0.21 | −0.20 | −0.20 | −0.20 | |
| Initial saturation () | 0.01 | −0.02 | −0.02 | 0.02 | 0.02 | 0.02 | |
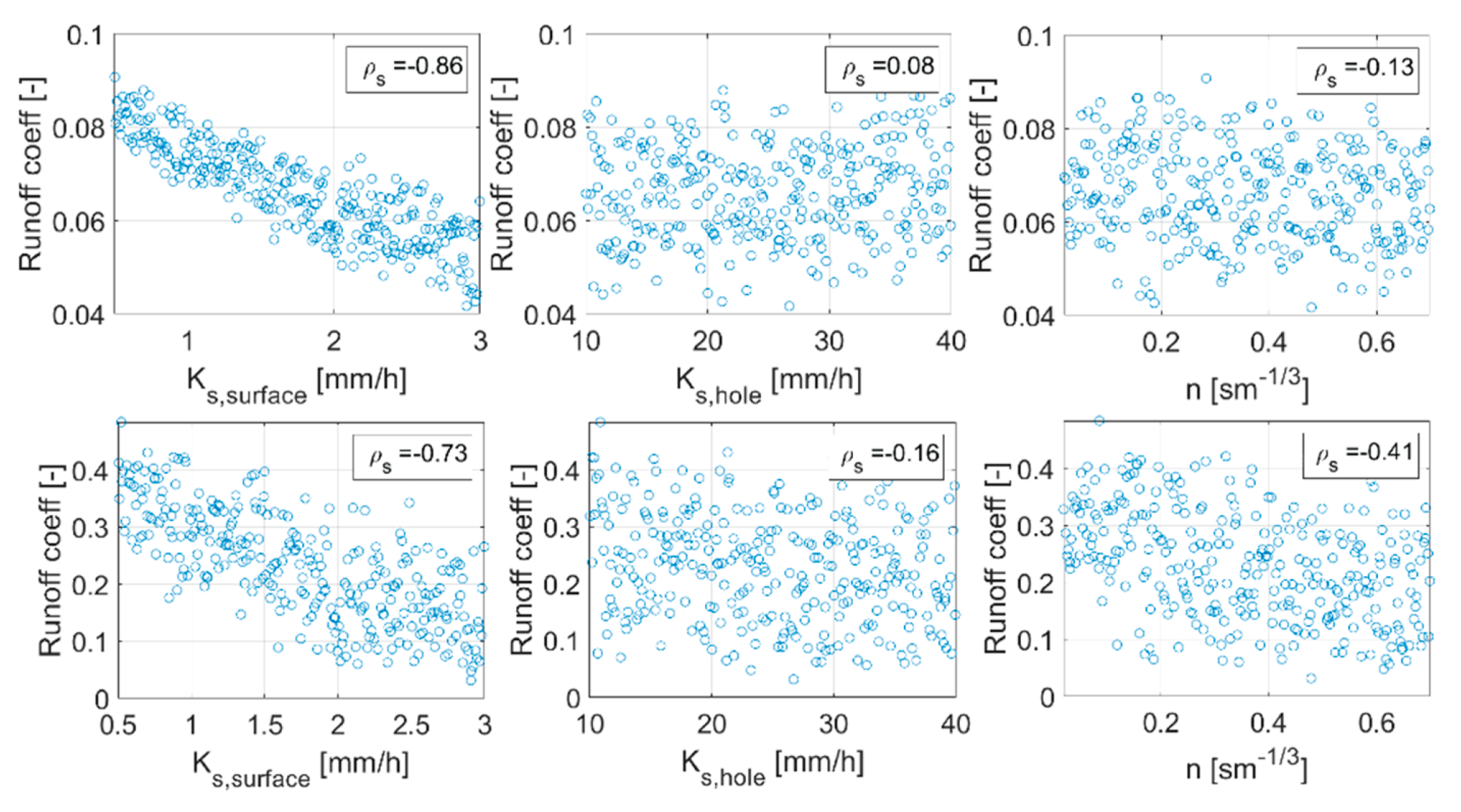
| Hydraulic conductivity | () | −0.82 | −0.86 | −0.86 | −0.83 | −0.73 | −0.71 |
| () | - | 0.08 | 0.09 | 0.07 | −0.16 | −0.15 | |
| RWHT | |
|---|---|
| HM30 | 23.02 |
| HM20 | 22.92 |
| HM10 | 20.72 |
| PP20 | 3.75 |
| PP10 | 2.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamagnone, P.; Cea, L.; Comino, E.; Rosso, M. Rainwater Harvesting Techniques to Face Water Scarcity in African Drylands: Hydrological Efficiency Assessment. Water 2020, 12, 2646. https://doi.org/10.3390/w12092646
Tamagnone P, Cea L, Comino E, Rosso M. Rainwater Harvesting Techniques to Face Water Scarcity in African Drylands: Hydrological Efficiency Assessment. Water. 2020; 12(9):2646. https://doi.org/10.3390/w12092646
Chicago/Turabian StyleTamagnone, Paolo, Luis Cea, Elena Comino, and Maurizio Rosso. 2020. "Rainwater Harvesting Techniques to Face Water Scarcity in African Drylands: Hydrological Efficiency Assessment" Water 12, no. 9: 2646. https://doi.org/10.3390/w12092646
APA StyleTamagnone, P., Cea, L., Comino, E., & Rosso, M. (2020). Rainwater Harvesting Techniques to Face Water Scarcity in African Drylands: Hydrological Efficiency Assessment. Water, 12(9), 2646. https://doi.org/10.3390/w12092646







