Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydraulic Models
2.1.1. Iber
2.1.2. SWMM 5.1
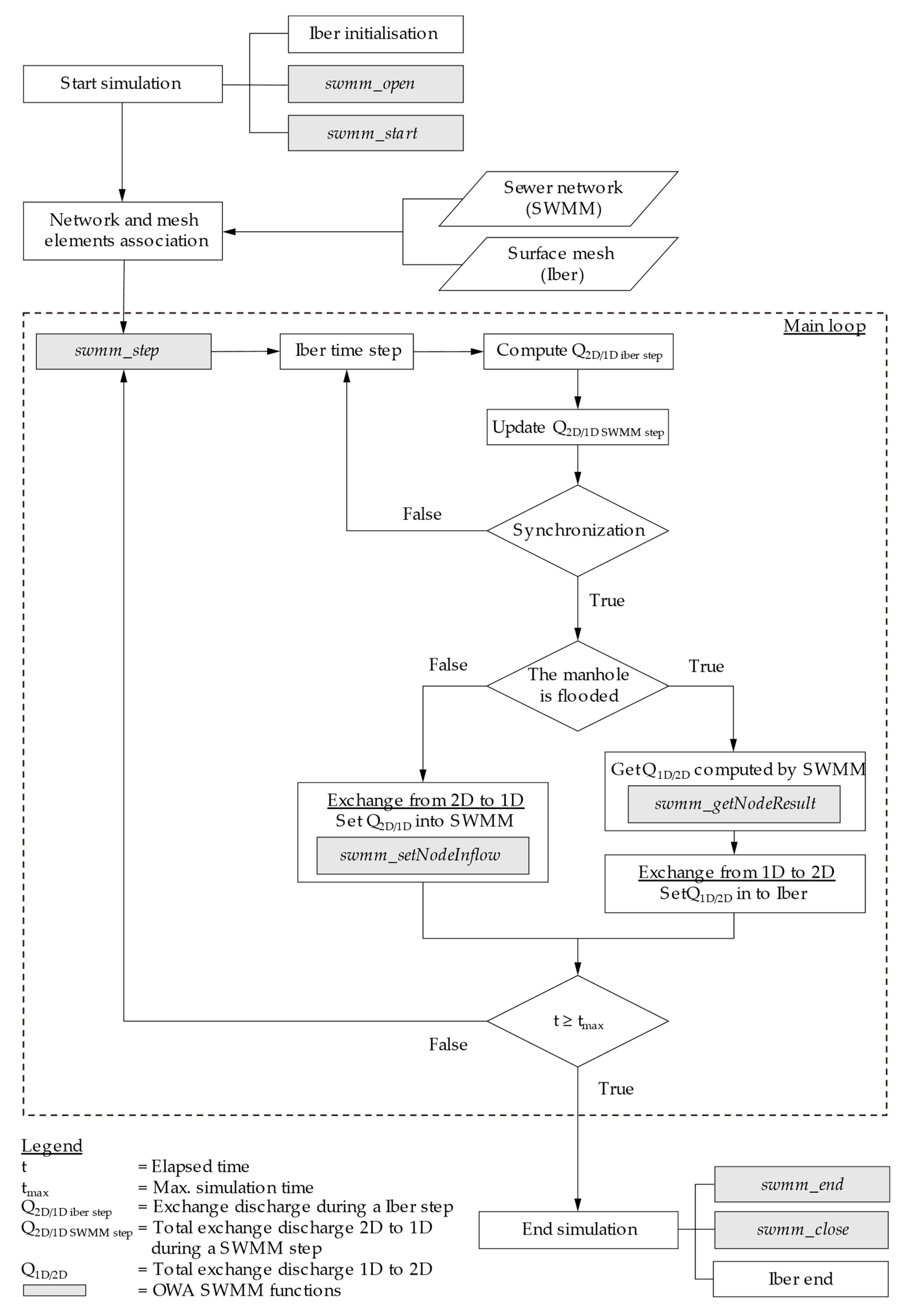
2.2. Linking Methodology
3. Case Studies and Results
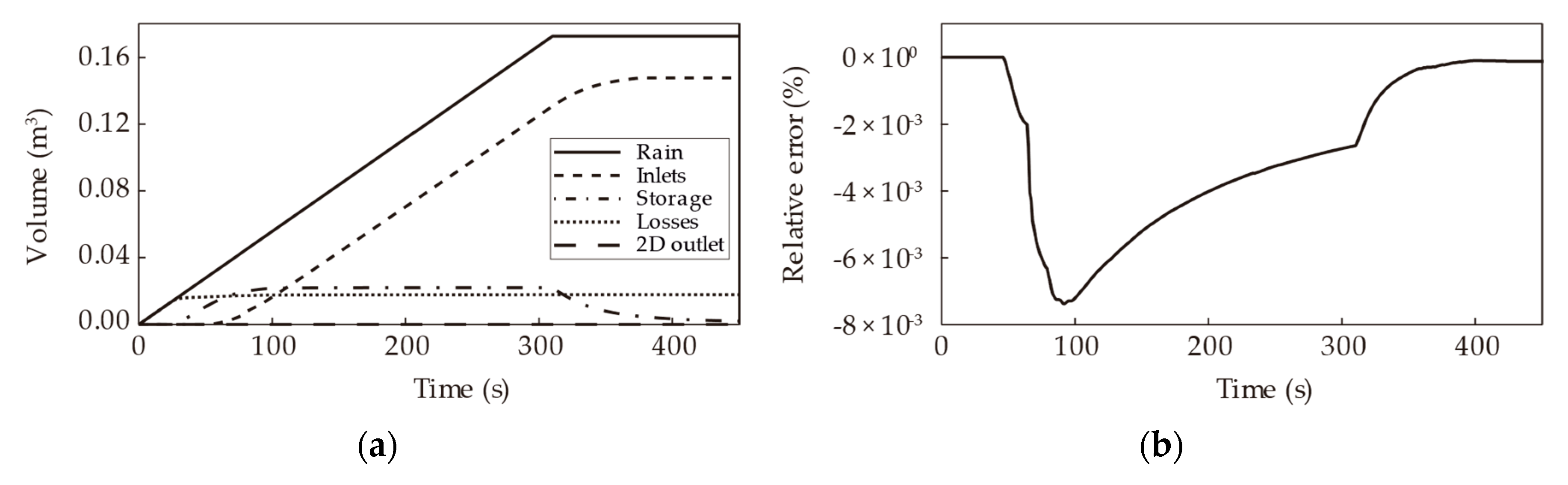
3.1. Simplified Urban Street
3.1.1. Case Study Description
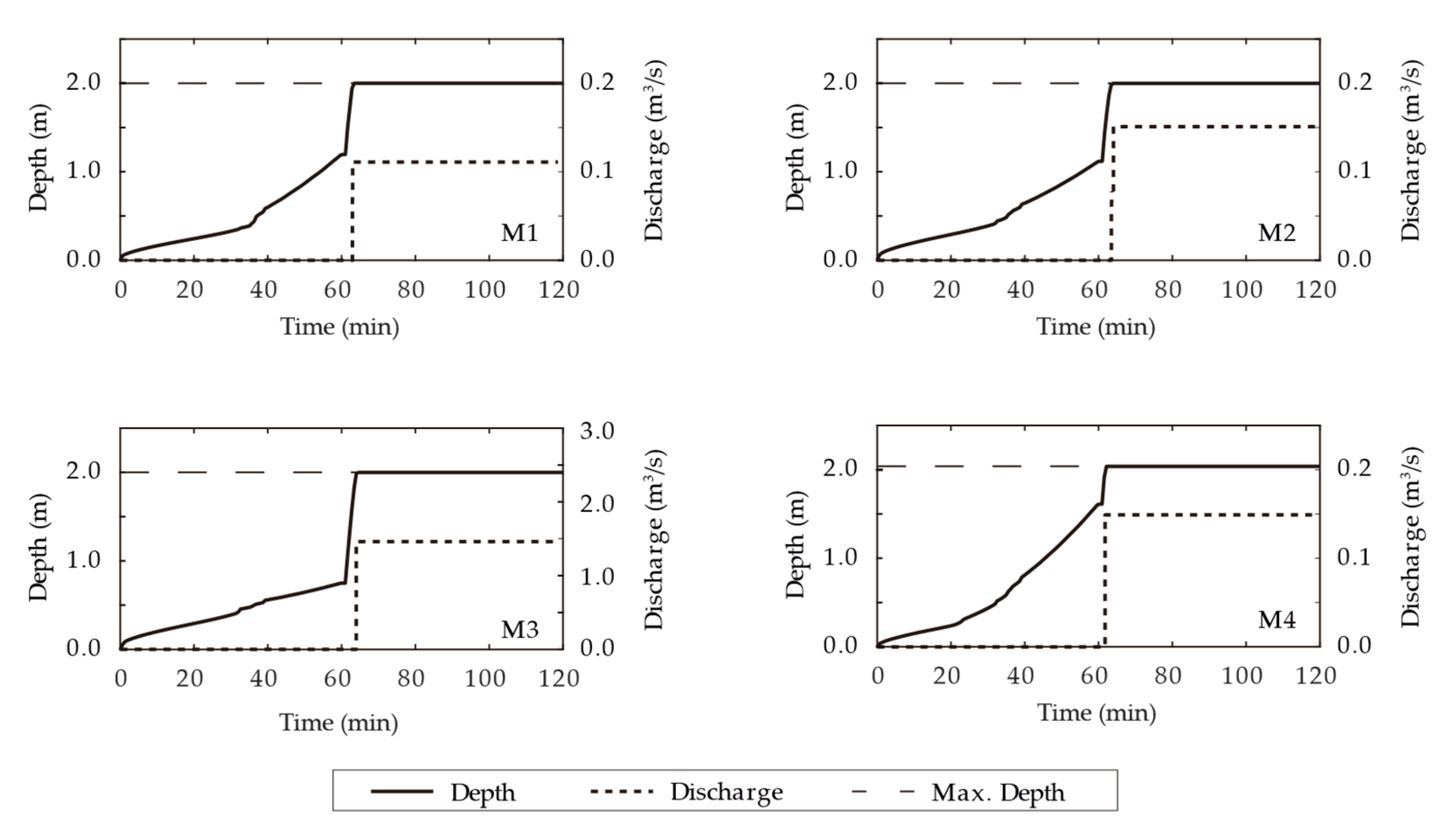
3.1.2. Results
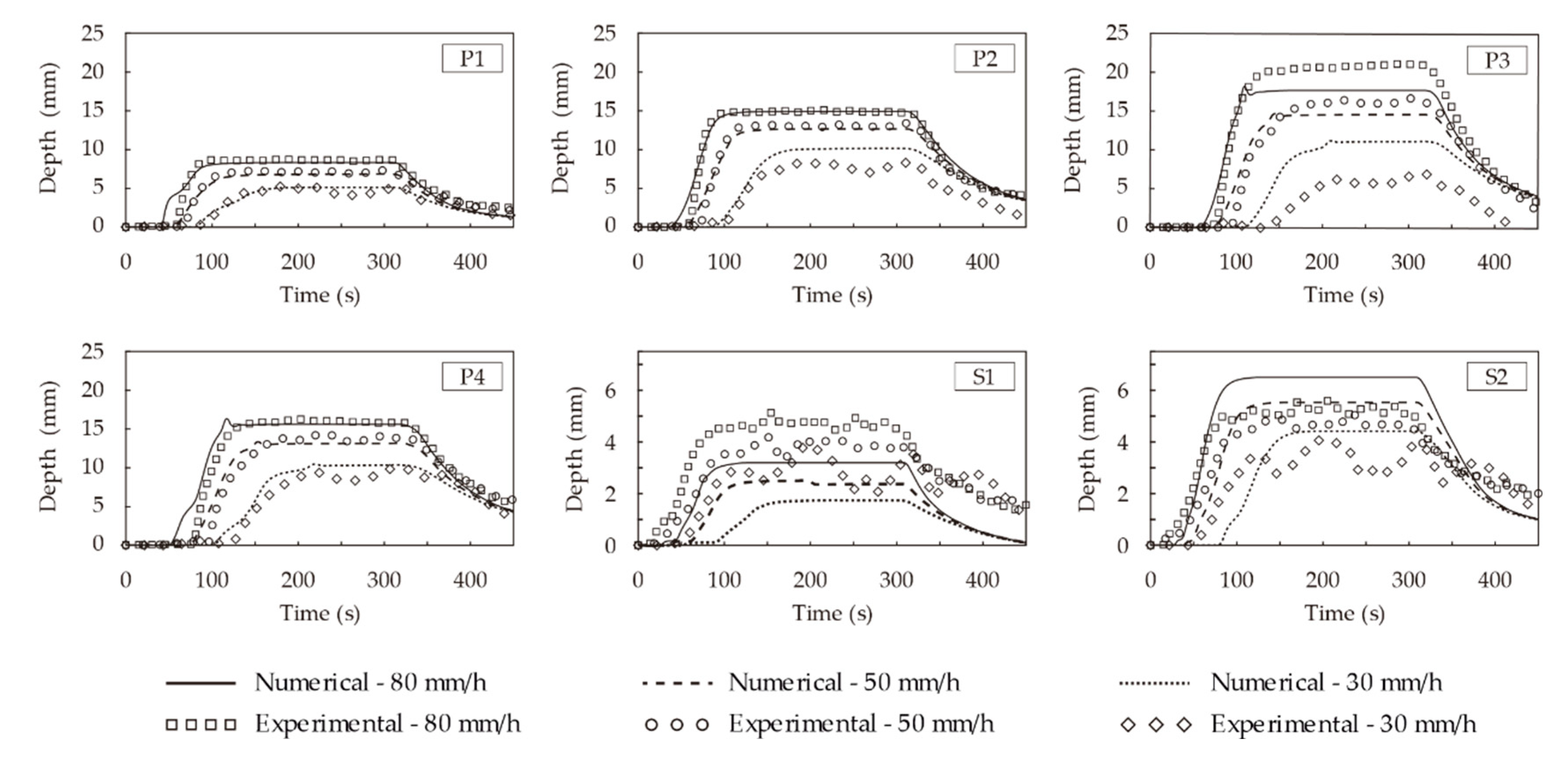
3.2. Full-Scale Urban Drainage Physical Model
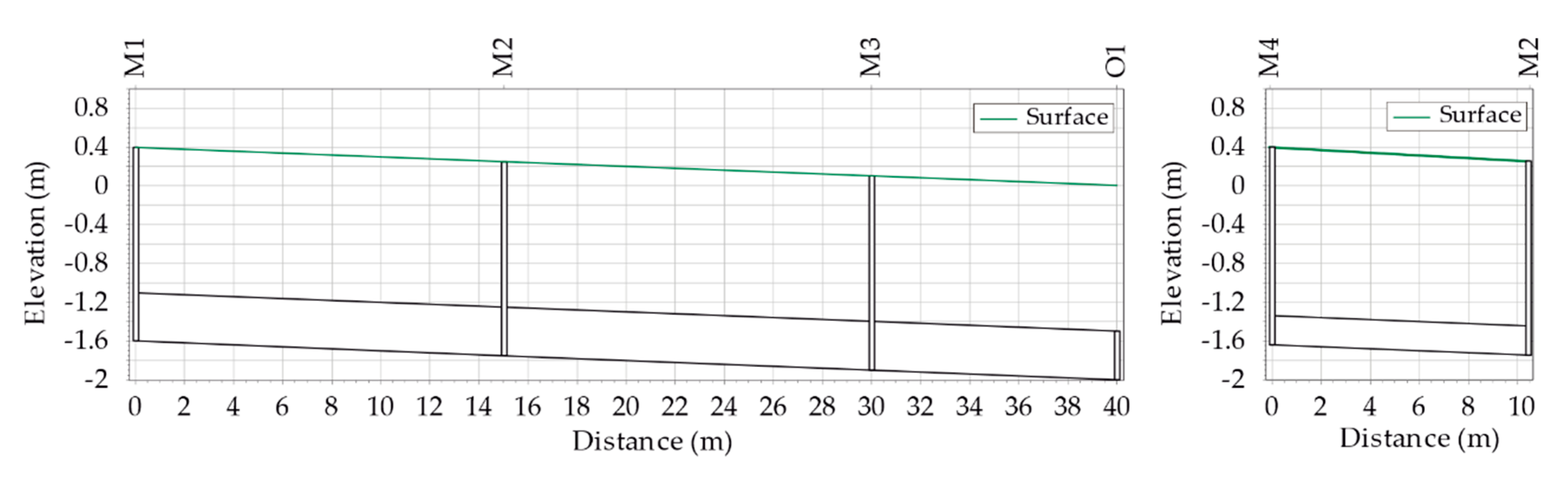
3.2.1. Case Study Description
3.2.2. Results
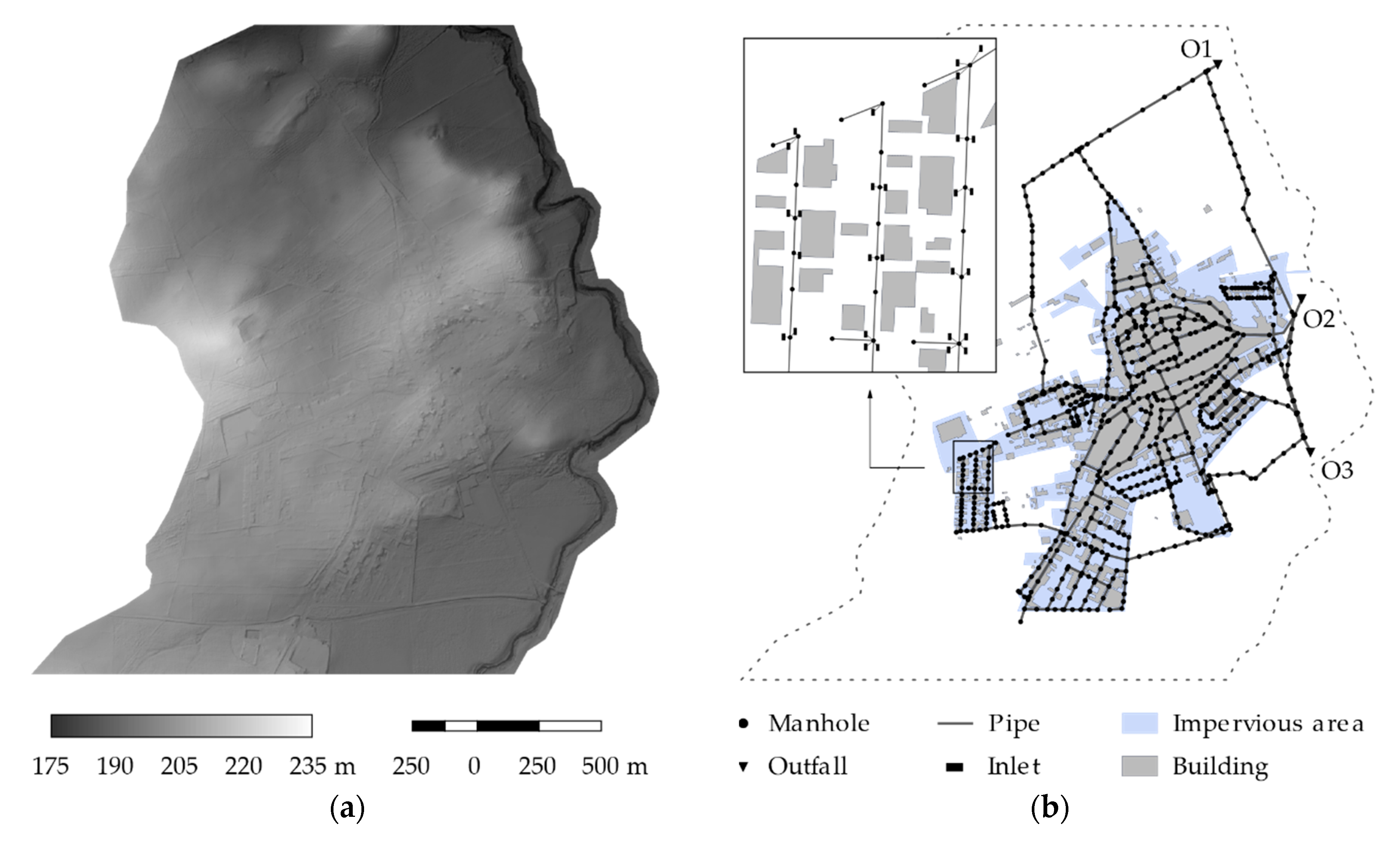
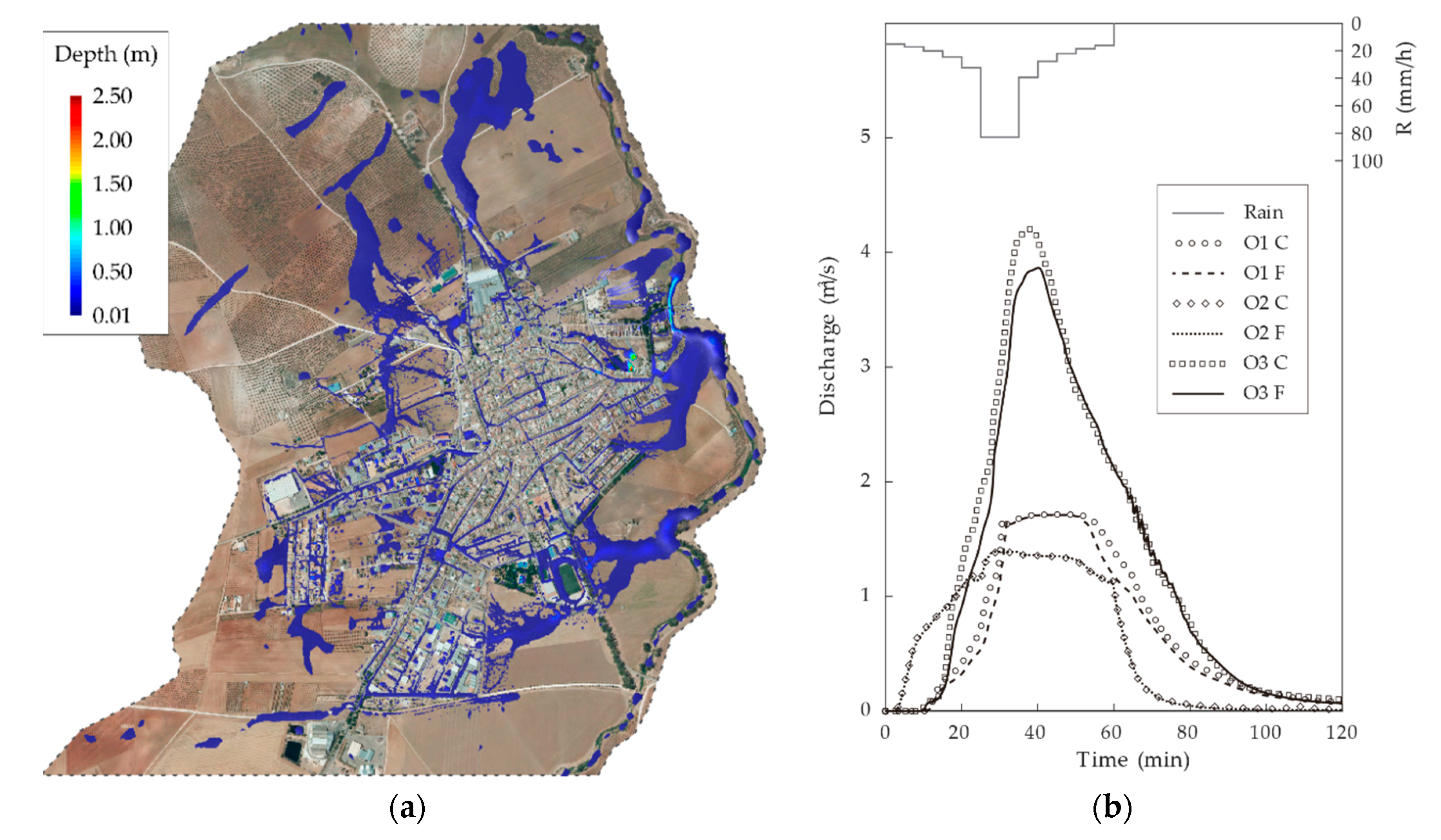
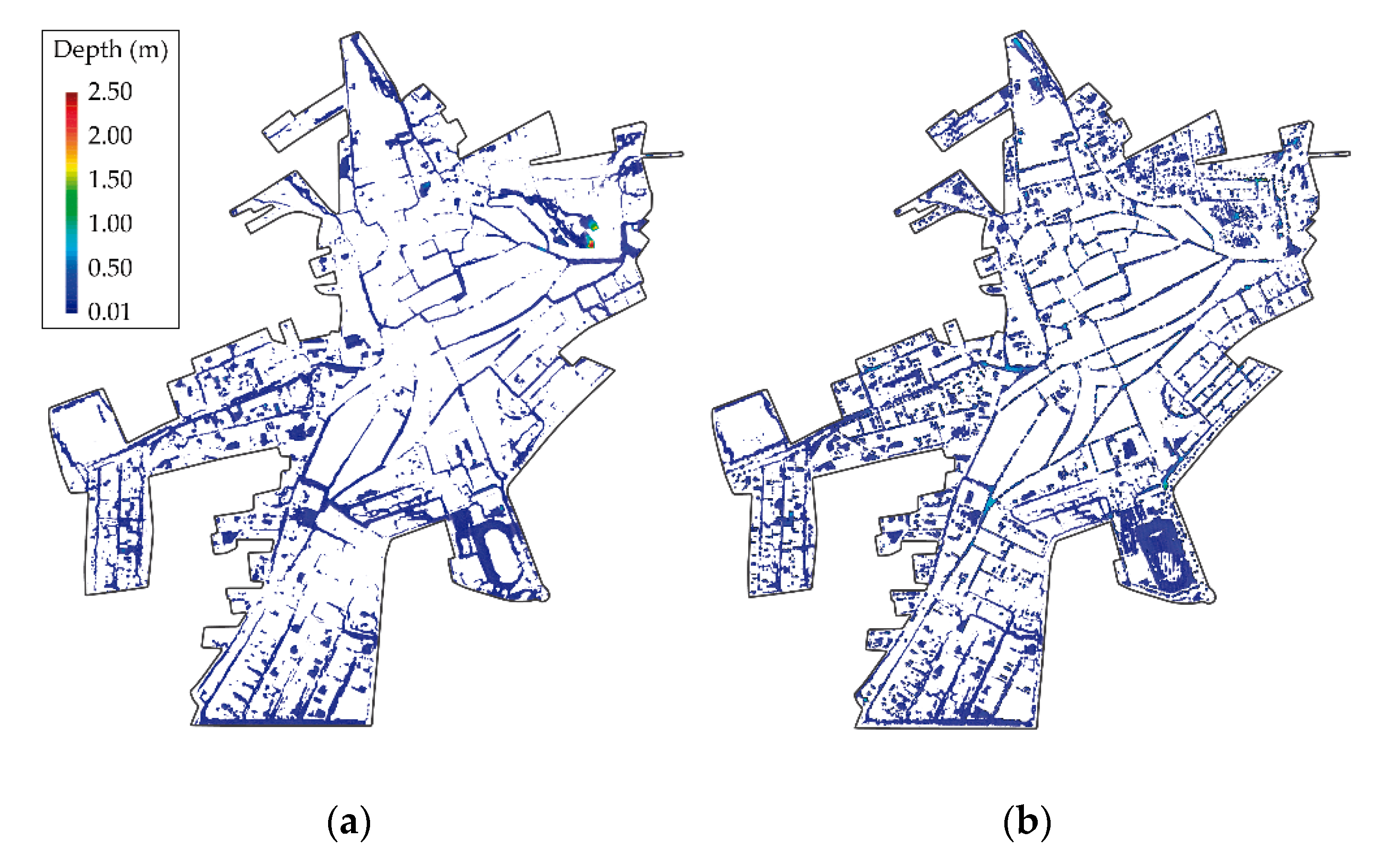
3.3. Real Urban Settlement
3.3.1. Case Study Description
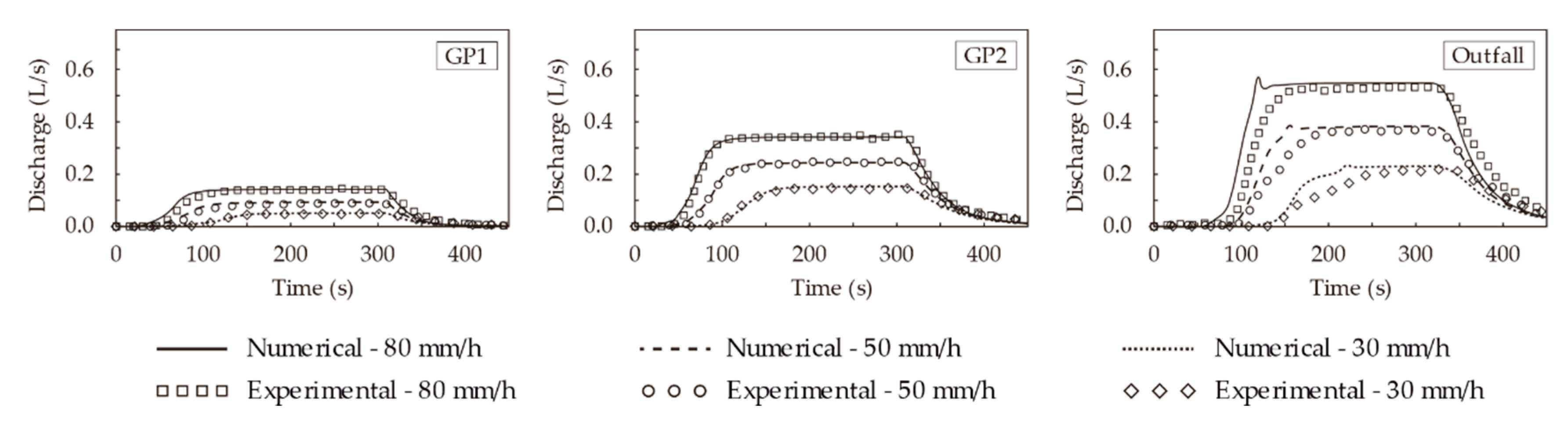
3.3.2. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cea, L.; Garrido, M.; Puertas, J.; Jácome, A.; Del Río, H.; Suárez, J. Overland flow computations in urban and industrial catchments from direct precipitation data using a two-dimensional shallow water model. Water Sci. Technol. 2010, 62, 1998–2008. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J.; Suarez, J.; Jimenez, V.; Jacome, A. Global sensitivity and GLUE-Based uncertainty analysis of a 2D-1D dual urban drainage model. J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- Chen, A.S.; Leandro, J.; Djordjević, S. Modelling sewer discharge via displacement of manhole covers during flood events using 1D/2D SIPSON/P-DWave dual drainage simulations. Urban Water J. 2016, 13, 830–840. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Chen, A.S.; Djordjević, S. A comparison of three dual drainage models: Shallow water vs local inertial vs diffusive wave. J. Hydroinform. 2017, 19, 331–348. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, Č. An approach to simulation of dual drainage. Water Sci. Technol. 1999, 39, 95–103. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Djordjevi, S.; Savi, D.A. Comparison of 1D/1D and 1D/2D coupled (Sewer/Surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Fraga Cadórniga, I. Desarrollo de un modelo dual 1D/2D para el cálculo del drenaje urbano: Modelo numérico y validación experimental. Ph.D. Thesis, Universidade da Coruña, A Coruña, Spain, 2015. [Google Scholar]
- Aragón-Hernández, J.L. Modelación numérica integrada de los procesos hidráulicos en el drenaje urbano. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. [Google Scholar]
- Leandro, J.; Martins, R. A methodology for linking 2D overland flow models with the sewer network model SWMM 5.1 based on dynamic link libraries. Water Sci. Technol. 2016, 73, 3017–3026. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Validation of a 1D-2D dual drainage model under unsteady part-full and surcharged sewer conditions. Urban Water J. 2017, 14, 74–84. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1.; EPA/600/R-14/413b; National Risk Management Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2015; p. 352.
- Hsu, M.H.; Chen, S.H.; Chang, T.J. Dynamic inundation simulation of storm water interaction between sewer system and overland flows. J. Chin. Inst. Eng. Trans. Chin. Inst. Eng. Ser. A Chung Kuo K. Ch’eng Hsuch K’an 2002, 25, 171–177. [Google Scholar] [CrossRef]
- Pathirana, A.; Tsegaye, S.; Gersonius, B.; Vairavamoorthy, K. A simple 2-D inundation model for incorporating flood damage in urban drainage planning. Hydrol. Earth Syst. Sci. 2011, 15, 2747–2761. [Google Scholar] [CrossRef]
- Jahanbazi, M.; Egger, U. Application and comparison of two different dual drainage models to assess urban flooding. Urban Water J. 2014, 11, 584–595. [Google Scholar] [CrossRef]
- Kim, S.E.; Lee, S.; Kim, D.; Song, C.G. Stormwater inundation analysis in small and medium cities for the climate change using EPA-SWMM and HDM-2D. J. Coast. Res. 2018, 85, 991–995. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. Influence of sewer network models on urban flood damage assessment based on coupled 1D/2D models. J. Flood Risk Manag. 2018, 11, S717–S728. [Google Scholar] [CrossRef]
- Adeogun, A.G.; Pathirana, A.; Daramola, M.O. Others 1D-2D hydrodynamic model coupling for inundation analysis of sewer overflow. JEAS J. Eng. Appl. Sci. 2012, 7, 356–362. [Google Scholar] [CrossRef]
- Delelegn, S.W.; Pathirana, A.; Gersonius, B.; Adeogun, A.G.; Vairavamoorthy, K. Multi-objective optimisation of cost-benefit of urban flood management using a 1D2D coupled model. Water Sci. Technol. 2011, 63, 1053–1059. [Google Scholar] [CrossRef] [PubMed]
- Seyoum, S.D.; Vojinovic, Z.; Price, R.K.; Weesakul, S. Coupled 1D and noninertia 2D flood inundation model for simulation of urban flooding. J. Hydraul. Eng. 2012, 138, 23–34. [Google Scholar] [CrossRef]
- Phillips, B.C.; Yu, S.; Thompson, G.R.; Silva, N. De 1D and 2D Modelling of Urban Drainage Systems using XP-SWMM and TUFLOW. In Proceedings of the 10th International Conference on Urban Drainage, Copenhagen, Denmark, 21–26 August 2005. [Google Scholar]
- Bisht, D.S.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE URBAN: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- SWMM5 Modeling with PCSWMM. Available online: https://www.pcswmm.com/ (accessed on 6 September 2020).
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Metod. Numer. Calc. Disen. Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- SWMM-Docs: Open Water Analytics Stormwater Management Model. Available online: http://wateranalytics.org/Stormwater-Management-Model/index.html (accessed on 17 July 2020).
- Bladé Castellet, E.; Cea, L.; Corestein, G. Numerical modelling of river inundations. Ing. Agua 2014, 18, 68. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A simple and efficient unstructured finite volume scheme for solving the shallow water equations in overland flow applications. J. Am. Water Resour. Assoc. 2015, 5, 2. [Google Scholar] [CrossRef]
- García-Feal, O.; González-Cao, J.; Gómez-Gesteira, M.; Cea, L.; Domínguez, J.M.; Formella, A. An accelerated tool for flood modelling based on Iber. Water 2018, 10, 1459. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Effect of rainfall uncertainty on the performance of physically based rainfall–runoff models. Hydrol. Process. 2019, 33, 160–173. [Google Scholar] [CrossRef]
- Cea, L.; Legout, C.; Darboux, F.; Esteves, M.; Nord, G. Experimental validation of a 2D overland flow model using high resolution water depth and velocity data. J. Hydrol. 2014, 513, 142–153. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model Reference Manual Volume II—Hydraulics; U.S. Environmental Protection Agency: Washington, DC, USA, 2017.
- Chen, A.S.; Djordjević, S.; Leandro, J.; Savić, D.A. The urban inundation model with bidirectional flow interaction between 2D overland surface and 1D sewer networks. Novatech 2007 2007, 465–472. [Google Scholar]
- Lopes, P.; Leandro, J.; Carvalho, R.F.; Páscoa, P.; Martins, R. Numerical and experimental investigation of a gully under surcharge conditions. Urban Water J. 2015, 12, 468–476. [Google Scholar] [CrossRef]
- Gómez, M.; Russo, B. Methodology to estimate hydraulic efficiency of drain inlets. Proc. Inst. Civ. Eng. Water Manag. 2011, 164, 81–90. [Google Scholar] [CrossRef]
- Flood risk management. Engineering. University of Exeter. Available online: https://emps.exeter.ac.uk/engineering/research/cws/research/flood-risk/rapids.html (accessed on 30 July 2020).
- Naves, J. Wash-off and Sediment Transport Experiments in a Full-Scale Urban Drainage Physical Model. Ph.D. Thesis, Universidade da Coruña, A Coruña, Spain, 2019. [Google Scholar]
- Naves, J.; Anta, J.; Puertas, J.; Regueiro-Picallo, M.; Suárez, J. Using a 2D shallow water model to assess Large-Scale Particle Image Velocimetry (LSPIV) and Structure from Motion (SfM) techniques in a street-scale urban drainage physical model. J. Hydrol. 2019, 575, 54–65. [Google Scholar] [CrossRef]
- Naves, J.; Anta, J.; Suárez, J.; Puertas, J. Hydraulic, wash-off and sediment transport experiments in a full-scale urban drainage physical model. Sci. Data 2020, 7, 1–13. [Google Scholar] [CrossRef]
- Naves, J.; Anta, J.; Suárez, J.; Puertas, J. Washtreet—Hydraulic, wash-off and sediment transport experimental data obtained in an urban drainage physical model. Sci. Data 2019. [Google Scholar] [CrossRef]
- Cea, L.; Legout, C.; Grangeon, T.; Nord, G. Impact of model simplifications on soil erosion predictions: Application of the GLUE methodology to a distributed event-based model at the hillslope scale. Hydrol. Process. 2016, 30, 1096–1113. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Experimental study of the water depth and rainfall intensity effects on the bed roughness coefficient used in distributed urban drainage models. J. Hydrol. 2013, 505, 266–275. [Google Scholar] [CrossRef]
- Jaafar, H.H.; Ahmad, F.A.; Beyrouthy, N. El GCN250, new global gridded curve numbers for hydrologic modeling and design. Sci. Data 2019, 1–9. [Google Scholar] [CrossRef]
- Leutnant, D.; Döring, A.; Uhl, M. Swmmr—An R package to interface SWMM. Urban Water J. 2019, 16, 68–76. [Google Scholar] [CrossRef]
- Arias, J.S. Máximas Lluvias Diarias en España Peninsular; Seria Monográfica del Ministerio de Fomento: Madrid, Spain, 1999; p. 55. [Google Scholar]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. https://doi.org/10.3390/w12092647
Sañudo E, Cea L, Puertas J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water. 2020; 12(9):2647. https://doi.org/10.3390/w12092647
Chicago/Turabian StyleSañudo, Esteban, Luis Cea, and Jerónimo Puertas. 2020. "Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM" Water 12, no. 9: 2647. https://doi.org/10.3390/w12092647
APA StyleSañudo, E., Cea, L., & Puertas, J. (2020). Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water, 12(9), 2647. https://doi.org/10.3390/w12092647





