Next Article in Journal
Estimation of Water Quality Parameters with High-Frequency Sensors Data in a Large and Deep Reservoir
Next Article in Special Issue
Modified Hiltner Dew Balance to Re-Estimate Dewfall Accumulation as a Reliable Water Source in the Negev Desert
Previous Article in Journal
Dynamic Evaluation of Sustainable Water Resource Systems in Metropolitan Areas: A Case Study of the Beijing Megacity
Previous Article in Special Issue
Baseline Groundwater Quality before Shale Gas Development in Xishui, Southwest China: Analyses of Hydrochemistry and Multiple Environmental Isotopes (2H, 18O, 13C, 87Sr/86Sr, 11B, and Noble Gas Isotopes)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 12
Issue 9
10.3390/w12092630
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Where Does the Chilean Aconcagua River Come from? Use of Natural Tracers for Water Genesis Characterization in Glacial and Periglacial Environments

by
Sebastián Andrés Crespo
1,*,
Céline Lavergne
2,3,
Francisco Fernandoy
4,
Ariel A. Muñoz
1,
Leandro Cara
5 and
Simón Olfos-Vargas
1
1
Instituto de Geografía, Facultad de Ciencias del Mar y Geografía, Pontificia Universidad Católica de Valparaíso, Valparaíso 2362807, Chile
2
Laboratory of Aquatic Environmental Research, Centro de Estudios Avanzados, Universidad de Playa Ancha, Viña del Mar 2581782, Chile
3
HUB Ambiental UPLA, Universidad de Playa Ancha, Valparaíso 234000, Chile
4
Laboratorio de Análisis Isotópico (LAI), Facultad de Ingeniería, Universidad Andrés Bello, Viña del Mar 2531015, Chile
5
Instituto Argentino de Nivología, Glaciología y Ciencias Ambientales (IANIGLA-CONICET), Mendoza 5500, Argentina
*
Author to whom correspondence should be addressed.
Water 2020, 12(9), 2630; https://doi.org/10.3390/w12092630
Submission received: 1 August 2020 / Revised: 4 September 2020 / Accepted: 12 September 2020 / Published: 21 September 2020
(This article belongs to the Special Issue Application of Isotopic Data to Water Resource Management)
Browse Figures
Versions Notes

Abstract

:
The Aconcagua river basin (Chile, 32 °S) has suffered the effects of the megadrought over the last decade. The severe snowfall deficiency drastically modified the water supply to the catchment headwaters. Despite the recognized snowmelt contribution to the basin, an unknown streamflow buffering effect is produced by glacial, periglacial and groundwater inputs, especially in dry periods. Hence, each type of water source was characterized and quantified for each season, through the combination of stable isotope and ionic analyses as natural water tracers. The δ18O and electric conductivity were identified as the key parameters for the differentiation of each water source. The use of these parameters in the stable isotope mixing “simmr” model revealed that snowmelt input accounted 52% in spring and only 22–36% during the rest of the year in the headwaters. While glacial supply contributed up to 34%, both groundwater and periglacial exhibited a remarkable contribution around 20% with some seasonal variations. Downstream, glacial contribution averaged 15–20%, groundwater seasonally increased up to 46%, and periglacial input was surprisingly high (i.e., 14–21%). The different water sources contribution quantification over time for the Aconcagua River reported in this work provides key information for water security in this territory.

1. Introduction

Chile is among the most vulnerable countries to climate change [1]. Changing climatic conditions have already been observed in Central Chile, with significant increases in mean temperature and decreases in mean precipitation [2,3,4,5]. The propagation of this meteorological drought through the water cycle has resulted in severe decreases in streamflow (and thus water availability) over Central Chile since 2010 and has been called the “Megadrought” [6]. This extraordinary event occurred in the hottest decade of the last 100 years and would seem to have no analogy in the last millennium, according to precipitation and streamflow reconstructions in the area [6,7]. Long-term climate projections also do not present an encouraging picture for this region of the Andes, as they indicate a warming trend and a greater recurrence of droughts in the coming decades [8,9,10].
The Valparaíso region (Central Chile), the second most populated region of Chile [11], exhibits the largest amount of over-allocated aquifers in the country (n = 28) and presents an unbalanced relationship between water supply (40.7 m3 s−1) and water demand (55.5 m3 s−1). This annual deficit is projected to reach 37.6 m3 s−1 in 2026 [12], and the Aconcagua river basin could experience water scarcity in 34% of years moving forward if agricultural water demand remains constant, and future discharge is similar to historical [13], concerning a present and future territorial development limitation. As the main river in this region, the Aconcagua river (Figure 1) with 33.1 m3 s−1 of annual flow [14] supplies the second most productive valley of the country [15] and provides freshwater for more than 1 million inhabitants considering the water intake for the Valparaíso metropolitan area supply [11]. The main hydrological system water recharge [16] has a clearly nivo-glacial origin, but it is strongly influenced by high interannual variability of Andean winter snowfall, ranging from 5% to 250% of the annual historical average [17,18]. Even when the main water source corresponds to snowmelt (i.e., in normal to abundant snow load years), this interannual variability rises the necessity to analyze different water source contribution in addition to snow (e.g., groundwater, glacial and periglacial) that provide basal flow in dry periods.
The socio-economic development and subsistence of the region is strongly linked to the meltwater from the Andes, which also includes the buffering effect of glaciers in dry periods [19,20]. However, this information has not been estimated in this basin yet for other water sources than snowmelt. In its 7340 km2 [16], the basin contains 717 ice bodies covering 136 km2, which are distributed over the 869 km2 of the uppermost catchment area and play a vital role as buffers against droughts in dry years [21]. As was proposed by Peña and Nazarala [22] for the whole Central Andes, this cryoforms contribute to approximately 67% of the total summer flow. The glacial melt streamflow buffer effect limits the drought, so droughts in the Central Andes do not reach more critical situations [19,20]. However, as a result of reduced rainfall and increased temperatures at high elevations, a widespread retreat of glaciers has been reported in the region [19,23,24,25,26]. In the Aconcagua River Basin, a glacial area reduction of 30 km2 was observed along the period 1955–2003, with small glaciers being proportionally the most affected [27]. Predictions have shown that the Juncal Norte glacier could lose up to 70% of its area by the end of the 21st century [28]. It is estimated that these processes of negative variations in fronts and areas experienced in glaciers of the central Andes are largely due to the elevation of the 0 °C isotherm in the region [4].
The study of water stable isotopes constitutes a baseline for determining the origin of plant and animal tissues that incorporate this water in a constitutive form, (i.e., when the tissue is formed). This information was also spatially displayed through a set of isoscapes and electric conductivity maps, which serve as a baseline for the spatial characterization of water sources and water delivery opportunities by each water source. Using this information, it will be possible to determine the origin of tissues such as feathers, hairs or seeds, becoming possible to infer dietary habits and migratory patterns, with high applicability for social, geographic, ecological and forensic studies [29,30,31].
Differences in glacio-genesis features and melting conditions provide distinct air and sediment contact times of each water source and thus different chemical characteristics in terms of ionic and stable isotope water composition [20,32]. This specific chemical composition could allow the identification of every water source and the quantification of their input contribution for each season. The electric conductivity and 18O composition were successfully used in the Bhagirathi River (Himalayas) to trace water from ice, snow and rainwater [33]. In the Garonne Valley (France), Lambs et al. also identified runoff water from high altitudes using stable oxygen isotope and electric conductivity [34]. Pu et al., using only 18O composition from different water sources in the Baishui River catchment (China), built a hydrograph separation between rain and melt water contributions to the river, without distinction between snow, groundwater and ice melting contributions [35]. In the Mendoza River basin (Central Andes, Argentina), Crespo et al., found clear differences in ionic and stable isotope chemistry between the main mountain ranges of the catchment basin related to different precipitation systems (Pacific and Atlantic moisture) and geological settings [32]. In another study in the same catchment basin, Crespo et al. [20] showed that glacial input accounted for 50%, periglacial 15%, groundwater 18% and snowmelt 17% of the total contribution [20]. In that study, Crespo et al. [20] highlighted that more than 83% of water input originates from “not-snow” water source in dry periods in the Mendoza River basin and pointed out the importance of quantifying the water source contribution from a large diversity of sources.
As was mentioned, the Andean region between 29 °S and 35 °S experienced the most extreme and prolonged drought in the instrumental record [36]. Deciphering the water source contribution is crucial to generate strategies promoting the adaptation actions for water security under the climate change projections for Central Chile, where the Aconcagua basin is located. This study used new methodology combination to identify the contribution of different water sources in a dry water cycle to the Aconcagua River and estimated their contribution throughout the different seasons of the year. These issues are relevant to have precise information on the spatiotemporal contribution of water inputs in order to achieve a long-term harmonious development strategy.

2. Materials and Methods

2.1. Sampling and Chemical Analysis

A total of 103 water samples were taken in this study. In eight sites were obtained the river samples (n = 48) over six seasonal sampling periods (summer, autumn, winter and spring 2018 and summer and autumn 2019). During these sampling campaigns, 18 samples of the different water sources representing the glacial and periglacial environment, groundwater and snow catchments were sampled (Table 1).
In addition, precipitation samples were collected with rain collectors (n = 4), located at Valparaíso (0 m a.s.l.) and at Parque Andino Juncal (2479 m a.s.l.). The collectors were PVC pipes (2.5 cm in diameter, 1 m long) with a funnel at the top to improve uptake. They were filled with a light mineral oil layer inside to prevent evaporation. Moreover, snow samples (n = 14) from 1563 to 2906 m a.s.l. were taken immediately after storm events, removing the superficial 10 cm. Finally, stagnant water samples (n = 12) were taken from Laguna del Inca, Del Nacimiento Wetland and a wetland near the Juncal Norte Glacier (Figure 1).
For isotopic analysis, water samples were collected in 50 mL tubes (Falcon, Corning, NY, USA), immediately filtered and sealed with thermoplastic cohesive (PARAFILM, Neenah, WI, USA) to prevent evaporation. Isotopic analysis was performed at the Laboratorio de Análisis Isotópico at the Andres Bello University, Viña del Mar (Chile) by a “Los Gatos Research” OA-ICOS, with analytical uncertainty for δ18O and δ2H less than 0.1 ‰ and 0.8 ‰, respectively. The standardization was based on the Vienna Standard Mean Ocean Water (VSMOW) scale.
For ionic analysis, the samples were collected in clean 1L plastic bottles and frozen at −20 °C until analysis. In these samples, electrical conductivity and the following ions were analyzed: sulfate (SO42−), nitrate (NO3−), phosphate (PO43−), chloride (Cl−), fluoride (F−), aluminum (Al), bromide (Br), calcium (Ca), magnesium (Mg), sodium (Na), potassium (P), iron (Fe), barium (Br), manganese (Mn), silicium (Si) and strontium (Sr). The analyses were carried out at the Alfred Wegener Institute (AWI) (Potsdam, Germany). Anion determinations were performed by ion chromatography (Thermo-scientific ICS2100). The detection limits were: 0.02, 0.135, 0.089, 0.004, 0.133 and 0.014 for F−, Cl−, SO42−, Br−, NO3− and PO43−, respectively. An ICP-OES (inductively coupled plasma—optical emission spectrometry) was used to determine the cation composition: Mg, K, Na, Fe, Al, Ba, Sr, Si and P. The detection limit was 1 ppm.

2.2. Statistical Analysis

All statistical analyses were performed with R software version 3.5.1 [37] in R Studio environment Version 1.0.153. The raw dataset of ionic elements and isotopic composition was first cleaned by removing the samples not used in the GLMM model. Aluminum, bromide and phosphate were not detected in the remaining samples and were removed. Moreover, iron and manganese were only detected in one sample and were not considered for the current analysis. Hence, the working dataset was composed of 11 ionic and 3 isotopic variables. Pearson correlations were used in order to identify significant relationships between chemical components (corrplot function, “corrplot” package [38]).
Three principal component analysis were performed (dudi.pca function, “ade4” package [39]) with only ionic components, only isotopic data or both ionic components and isotopic data, respectively. The use of the procruste comparison tests allowed to confirm that the interpretation of both chemical and isotopic PCA was similar (p < 0.01, protest function, “vegan” package [40]). Hence, the final PCA combined both chemical components and the isotopic data.
Generalized linear and non-linear mixed-effects models (GLMM, “nlme” package) were used to determine the water source differences significance [41]. It was done with the two variables most correlated with the two main axes of variation in the PCA (see “Section 3”). The variables “season” and “water source” (i.e., glacial and periglacial environments, groundwater and snow) were considered as fixed factors. In this analysis, the linear models were adjusted considering different intercepts (each water source in each season of the year), in relation to which the rest of the values or categories of variables were compared. The “sampling sites” were considered as random factors to avoid pseudo-replications due to repeated measurements at the same site over time [42,43].
To quantify the contribution from the different water sources, data from electric conductivity and δ18O were used in a Bayesian model where each value was combined with 100,000 pseudo replicates. The stable isotope mixing model (“simmr” package) performs the analysis of the contribution of the different water sources (snow, rock glacier, glacier and groundwater) and requires the use of two tracers (in this case: electric conductivity and δ18O) [44]. This model is based on Gaussian parsimony and expressed the contributions in average values for the different water sources with credibility intervals (95%), which means that the reported effect has 95% probability of falling within this range [20]. The water sources selected were the more representative of the possible water inputs to the main rivers in the Cordillera Principal. Because observation boreholes are missing from the mountain areas in the Aconcagua river basin, the groundwater samples were taken from perennial springs and agricultural boreholes. While these boreholes were situated downstream the analyzed area, they are suitable as a source of water as they are recharged from the Principal Cordillera through a high density of connected fractured aquifers [45,46].

2.3. Isoscape and Electric Conductivity Maps

QGIS software version 3.10.0 was used to produce the electric conductivity maps and isoscapes [47]. The basin delimitation was carried out using Hydrologic modelling, Spatial Analysis Raster, GRASS version 7.6. The shapefiles of the basins were organized for each season of the year. The products are at a scale of 1:130,000, projected to UTM zone 19 S and with reference system SIRGAS WGS 84. The secondary shapefiles were obtained from Infraestructura de Datos Geoespaciales Chile [21].

2.4. Snow Covered Area Analysis

In order to identify the snow contribution, a satellite Snow Covered Area (SCA) product was used. The SCA was obtained from the transformation of the Fractional Snow Cover (FSC), provided by MODIS Terra & Aqua products v6 (MOD10A1, MYD10A1), to a binary product through a threshold of presence/absence of snow. The FSC is calculated from the normalized snow index (NDSI), which is the most widely used index for the determination of snow by optical sensors [48,49]. The threshold applied for NDSI transformation to SCA was 0.4. It was globally used by the SCA MODIS Terra & Aqua products v5, and deprecated in version 6 [50]. The main problem for the snow detection through optical sensors is the presence of clouds. In this work, an algorithm developed by Cara et al. was used [51]. It performs a combination of SCA products, obtaining a daily layer without loss information due to clouds. Afterwards, SCA depletion curves were made for the period 1 July 2017 to 30 June 2019 using 1460 images.

3. Results

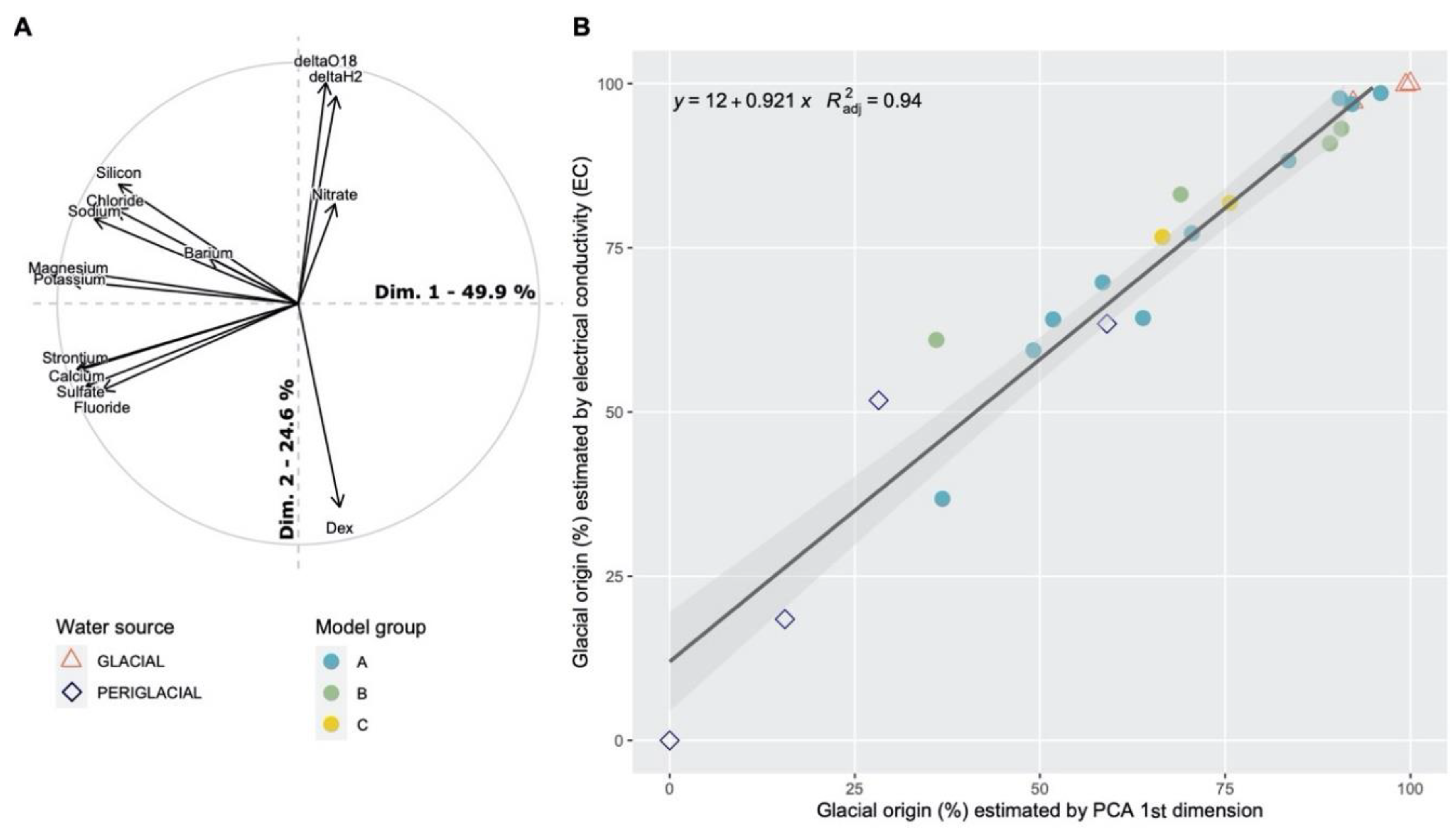
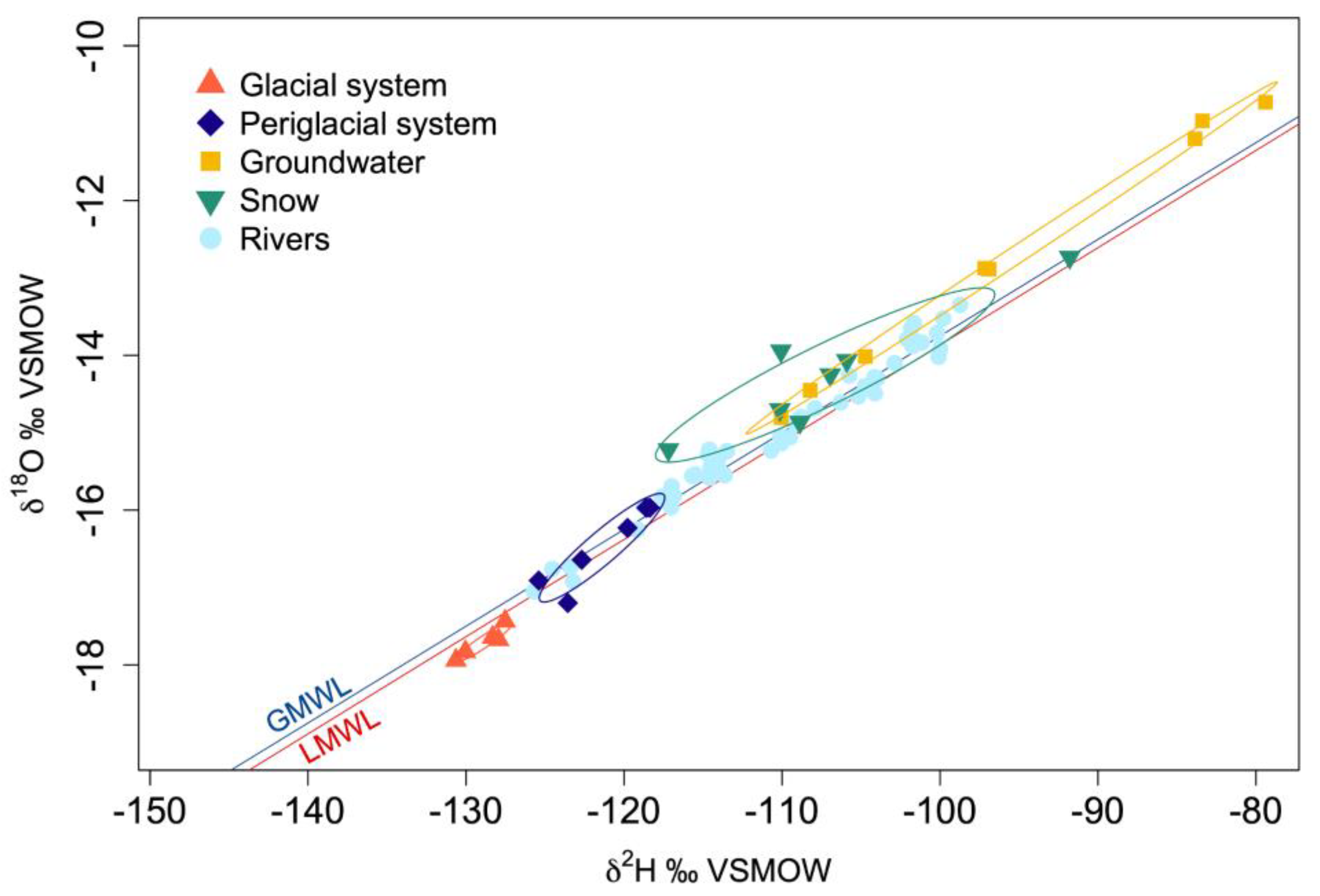
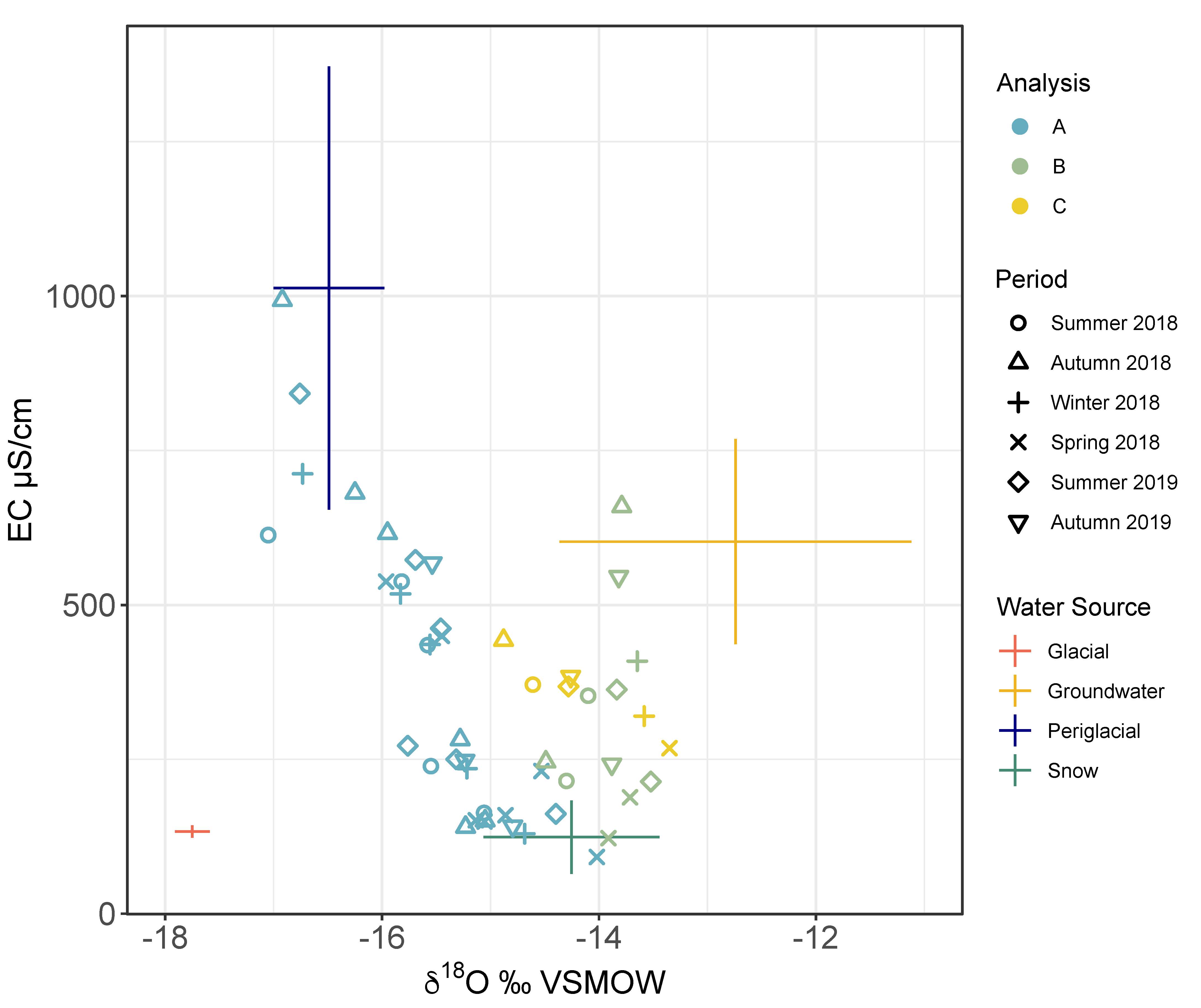
3.1. Source Differentiation Using Natural Tracers

Ionic and stable isotope composition act as chemical, natural tracers for the differentiation of water sources [20,32,52]. During the study period, a low winter precipitation and earlier snow melting allowed us to define more precisely the stable isotope composition from different water sources. A principal component analysis (PCA) was performed based on the ionic composition (11 chemical components and electrical conductivity) and isotopic data. The two first dimensions represented 76.04% of the total variation of the dataset, with 52.93% of the total variation depicted in the first dimension mainly characterized by the electrical conductivity (12.07% of relative contribution on the first dimension). The most influential variable on the second dimension was δ18O with 23.92% of relative contribution on the second dimension (Figure 2).
To go further, we computed a similar PCA without the electrical conductivity (Figure 2A); the first-dimension coordinates were extracted, and the relation between these principal coordinates and the electrical conductivity was plotted (Figure 2B). This correlation allowed to well discriminate glacial and periglacial sources with glacial samples exhibiting lower nutrient concentrations and lower conductivity. Hence, these issues confirmed that electrical conductivity is a satisfactory indicator to discriminate between glacial and periglacial origin. As it is also easy to measure in situ, it provides a good glacial/periglacial origin marker useful directly in the field.
As highlighted by the PCA results, the electrical conductivity and δ18O were the most important variables allowing to discriminate the water sources and were thus included in generalized linear mixed effects models to predict the origin of the water in the whole set of samples including samples without chemical data. Then, these two variables were independently tested for their capacity to discriminate between water sources. By considering the whole set of data with also groundwater samples, the δ18O allowed to make the distinction between the water discharged by the glacial system from groundwater and snow catchments (p < 0.001) but not significantly from the periglacial system (Table 1; Akaike weight = 1, R2 = 0.89) as also can be observed in Figure 3. The second model based on the electric conductivity confirmed the PCA findings and showed that this variable is suitable to significantly make the difference between glacial, groundwater and periglacial water sources (p < 0.001) but not from snow catchment (Table 2; Akaike weight = 1, R2 = 0.88).

3.2. Quantification of Glacier, Snow and Groundwater Contribution to the Upper Aconcagua River Basin

Based on the results of the PCA, the variables that mostly explained the two dimensions (water isotopic composition (δ18O) and electric conductivity (EC)) were used in a stable isotope mixing model within a Bayesian framework (“simmr”) (Table 3 and Figure 4). Four water sources contributing to the upper Aconcagua river basin were assumed (i.e., glacial, periglacial, groundwater and snow).
We quantified the contribution from different water sources throughout seasons. To validate the different water sources contribution, we compared the results of three analyses comprising the upper catchment area (869 km2), which holds more than 90% of the glaciers of the whole Aconcagua river basin [21]. In a first analysis we considered all the rivers draining to the Juncal River in point A (Figure 1) as repetitions: Ojos de Agua, Juncalillo and Juncal rivers (analysis A, mean catchment altitude: 3583 m a.s.l., Table 4). In the second analysis (B), we considered the resulting water sources contribution from Blanco and Peñón rivers, both located downstream from A, at the same longitude and with similar mean catchment elevation (3445 m a.s.l.). Analysis C (3417 m a.s.l.) referred to the water sources contributions to the Juncal River before the joining with Blanco River (Point C in Figure 1). The proportions given by the different analysis were compared, to contrast and validate the results (Table 4).

3.2.1. Snow System

Characterizing snow chemical composition is complicated because what precipitates as snow will not directly drain into rivers as rain does. The snowpack accumulates and stands most of the winter until spring arrives and starts to melt. From the melting point, the snow drains along the catchment and will get enriched with sediments.
To correctly characterize the snow melt water chemistry, samples were taken from seasonal active streams from spring that are fed exclusively from snow catchments melting. Here, all the snow melt of the catchment is mixed and loaded with sediments as normally occurs, producing a representative water mix, concerning ion enrichment, to be incorporated in the “simmr” model that can be compared directly to the other water sources analyzed in this work.
A stable isotope local meteoric water line at 33 °S was established using winter precipitation samples. The resulting equation is δ2H = 7.9874 × δ18O + 10.892 (R2 = 0.9974), which falls close to the LMWL developed at the same latitude and reported by Taucare et al.: δ2H = 8.076 × δ18O + 11.42 (R2 = 0.97) (Figure 3 and Figure S1) [45]. Snow catchments samples fall over the LMWL (Figure S1), which indicates that the water is not largely affected by evaporation during run-off. Thus, this represents an opportunity to confirm the representativeness of surface water samples originating from solid precipitation as snow melt tracers in mountain regions, and therefore better suited than punctual precipitation events, since the snow melt will integrate water from different altitudes and residence time (with the representative ionic enrichment) that will finally contributes to rivers and surface waters from the region.
The maximum snow input was during the spring season, with 49% mean water contribution (Table 4 and Figure 5). The snow contribution in rivers draining to the highest area (analysis A) was 52% in spring, 44% for analysis B and 51% for analysis C. The minimum snow contribution was detected in autumn 2018, averaging 27%. In that season, analysis A presented 22% of snowmelt contribution and 29% for B and C. By autumn 2019, the snow contribution rises to 34% on average, due to an early light snowfall, which melted quickly, being detected in this analysis. Therefore, in autumn 2019, an increase in snowmelt contribution was observed in all the “simmr” analysis with 36%, 30% and 35% for A, B and C, respectively.

3.2.2. Glacial Environment

Glacier melt contributions were maximum in summer (2018: 25; 2019: 22%) and autumn (2018: 22; 2019: 20%). The glacial contribution was fairly stable throughout the year for the area represented by analysis A but not for B and C. While in A the glacial contribution was close to 30% (i.e., 21% in spring and 34% in summer), in the area represented by the analysis B, the proportion remains stable (close to 20%) throughout the year only falling sharply in winter to 13%. In C, the proportion of glaciers was also quite regular, around 17% and falling in both winter and spring to 12% and 10%, respectively (Table 4).
The minimum glacial contribution was observed in spring, where snowmelt preceded glacial ice melt and mostly dominated the runoff. In spring, an average glacial contribution of 18% was observed for all analysis. For A and B analysis, the spring glacial contribution was 21 and 22%, respectively. Downstream, analysis C showed a drop in glacial contribution to 10%.

3.2.3. Periglacial Environment

The periglacial environment was represented in this study by sub-basins mostly covered with rock glaciers, the principal geomorphological expression of this environment. The water contribution of this source was very stable along the studied period. It represented a mean contribution around 17%, except in autumn and spring. Because the snowmelt contribution was dominant in spring, lower periglacial contribution was retrieved falling to 11%, 12% and 8% for A, B and C, respectively. The analysis also coincided in the periglacial peak water contribution in autumn 2018 (i.e., 25%). This could be due to a thermal inertia resulting in higher temperature in deeper soil layers at this time of the year compared to surface temperatures [55]. That internal temperature would generate the water contribution continuity by melting of the active layer of these periglacial cryoforms, increasing their relative contribution in a period with almost no precipitations. The proportion of this contribution in autumn 2018 was 30%, 20% and 21% for A, B and C, respectively. In 2019, this contribution declined due to the increase in the snow input from an early light snowfall and fast melting, representing only 19% for A analysis results, 18% for B and 14% for C.

3.2.4. Groundwater

Groundwater contribution was variable along the seasons for the different Aconcagua river studied areas, but as it occurred with glacial and periglacial environments water inputs, it presented its minimum contribution in spring (23%). In this season, the lowest contribution was recorded in analysis A (16%), followed by B (22%) and up to 32% for C. The maximum groundwater contribution was observed in winter, averaging 34%. This contribution varied as follows: 21% in analysis A, downstream in B represented 46% and 37% in C, and appeared relevant to maintain basal flows in dry years.
The co-isotope line of groundwaters sampled along this work shows a slight deviation from the 33 °S LMWL as defined by Taucare et al. and also from the co-isotope line defined for snow and rain samples in this work (Figure S2) [45]. The groundwater line (slope 7.17) reflects limited evaporation, assuming that the 33 °S LMWL (slope 8.07) is representative of precipitation for this region. The slight lower slope shows that the evaporation of recharge water before infiltration is short. If the time of exposition were longer, then a much stronger effect on the co-isotope line could be expected, as the water remains exposed to the atmosphere for a longer time period. Taucare et al. report a much higher degree of evaporation of spring and groundwater in their study (slope 3.54) [45]. The intercept of the evaporation line of groundwater and the 33 °S LMWL occurs at δ18O = −17.6‰, which is a more depleted value than the value informed by Taucare et al. [45] (δ18O = −12.6‰). Using the same altitude-isotope gradient (−0.3‰ 100 m−1) from Taucare et al., we can infer that the recharge zone of groundwater for the present study occurs much higher in the mountain at around 3700 m a.s.l. [45]. Therefore, there is a strong evidence for the groundwater being recharged on the Cordillera Principal, as previously pointed out.

3.2.5. Stagnant Waters

To identify the water source origin of stagnant water from the upper catchments, an additional “simmr” model for the Inca Lagoon, Del Nacimiento wetland and a wetland located in the proglacial part of the Juncal Norte glacier was performed (Table 5). Even when they were sampled at different seasons, the electric conductivity and the isotopic composition presented low variation (i.e., average of 2.6% of variation) along the sampling period (Table S1).
The result of the analysis for the Inca Lagoon showed a dominant snow contribution (76%), followed by a glacial environment contribution (14%), which coincides with the small glaciers identified in the sub-basin draining to the lagoon and the predominant snow contribution in this ski area. In contrast, Del Nacimiento wetland showed a dominant glacial water source input (46%), followed by periglacial water input (30%) and only a smaller snow contribution (12%). This result is coherent with the location of this wetland, located at around 3 kms from the proglacial area of the Juncal Norte glacier and periglacial geoforms observed in the area. Additionally, a small wetland located close to the Juncal Norte glacier (0.3 km) was sampled, on the bottom of a snowy mountain slope. The results were coherent with field observations, showing 45% of glacial input and 35% of snow input.

4. Discussion

The aim of this work was to understand and estimate the water contribution from glacial, periglacial, precipitation and groundwater sources to the headwaters forming the Aconcagua river. The 2018–2019 water cycle (Figure S3) was framed into a dry period called “Megadrought” since 2010 in Central Chile [36]. This decadal drought ranges precipitation deficits between 25% and 45% and the Aconcagua’s river reference station for snow accumulation “Portillo” (2880 m a.s.l.) showed −71% of snow water equivalent, its worst record in more than 50 years [6,56]. As a result, in 2019, the Aconcagua river streamflow was −84% lower of mean annual streamflow (compared with the historical average 1981–2010) [56]. In view of that extreme situation, the president of the Republic of Chile signed a decree of water scarcity for the entire Aconcagua river basin [57].

4.1. Water Source Discrimination and Quantification

Although the Aconcagua river is defined as mostly formed by snow and rain contributions, in its upper part, where the bulk of the snowpack is accumulated (analysis A), the river was fed mostly by other water sources (except in spring) for the dry analyzed period. Between 66% and 73% of the streamflows were supplied by glacial, periglacial and groundwater inputs in all the seasons out of the spring, when declines to 51% (Table S2), due to the dominance of snowmelt water input. The average contribution of the different water sources shows that the main water input throughout the analyzed period was snow (35%), followed by groundwater (28%), glacial contribution (21%) and periglacial contribution (17%) (Table S3). However, in the river headwaters represented by analysis A, a greater proportional contribution from glaciers was observed throughout the year. Thus, although snow continues to be the main water input source (31%), it was followed by the glacial (28%), then by the periglacial (22%) and finally by groundwater with 19% (Table S3). Downstream (analysis C), snow continues to be dominant (38%), with an increasing groundwater input (33%), and 15% and 13% water contributions from glacial and periglacial systems, respectively. The tributaries of analysis B are represented by snowmelt (35%), followed by groundwater (31%), glacial (20%) and periglacial (15%) water input.
When comparing the results of the present work with the previous of Rodriguez et al. carried out in the Juncal River basin along the dry water cycle 2011–2012 there are some relevant similarities but also differences [58]. Based on geographical source analysis, they identify and quantify three different sources of flow in the basin, namely, South, West and East, instead of different water sources differentiation. They conclude that most of the Juncal river catchment can be attributed to the Southern basin region, strongly related to glacier presence and low ion concentrations, and supplying 53% of the average water contribution in summer (26 November 2011, to 31 March 2012). At the east side of the Andes, in the Mendoza river basin, an analysis carried out by Crespo et al., reported a similar 52.75% of glacial environment water contribution for the melting season (November 2013 to March 2014) [20]. In the present work, for a more extensive area comprising the Juncal, Juncalillo and Ojos de Agua rivers, in a time period strictly representative of summer instead of spring and summer as in Rodriguez et al.’s work, the glacial contribution was 34% in 2018 and 29% in 2019 (Table 4). In the named “West basin region”, associated with quick-flowing snowmelt, Rodriguez et al. [58] report 20% average water contribution. In the present work this proportion was 25% in average, with 24% and 26% for 2018 and 2019, respectively, while Crespo et al. [20] presented 17.25% for the Mendoza River. The “East basin region”, related to high ion concentrations proper to high rock-water interaction and a depleted isotopic signal proper of high-elevation accumulation zones, showed 27% average water contribution in the 2011–2012 summer period analyzed by Rodriguez et al. [58]. This proportion was similar to the summed up 30.25% water input contribution from rock glaciers and groundwater reported in Crespo et al. [20], with 16.25% and 14%, respectively. The 2018 and 2019 averaged summer periglacial contribution in this work was 23.5%, while the groundwater was 20%, resulting in a summed-up contribution of 43.5% for both water sources (Analysis A, Table 4).
As was explained in Section 3.2.4, there is strong evidence of the groundwater being recharged on the Cordillera Principal [45,46]. Besides the winter base flow role of groundwater, representing 28% of the global average contribution along the whole year for all the analysis (Table S3), the catchment and aquifer recharge areas of the basin protection should be carefully reconsidered, since it could be diffusely contaminated. Even when the mentioned studies are not comparable because of the different study areas and analyzed periods, they were conducted in the same geological province (Cordillera Principal) and in dry water cycles framed by the megadrought [6]. The rivers are formed in the lower hypsometric part of the basin, where some free and confined aquifers will intercept them, becoming a constant water input along seasons and constituting the river basal flow to which the other sources, variable in time, are added by superficial draining. This can be seen in the largest winter contribution of groundwater (34%) in Table 4.
Finally, concerning water source contribution quantification in water bodies, we identify and quantify the water source contribution to stagnant waters as the Inca lagoon and two wetlands. This probes (1) the utility of the used methodology for discerning water origin in the catchment and (2) the necessity of an holistic protection concept of the water cycle in the headwaters area of the Aconcagua River basin.

4.2. Geochemical Water Information to be Used in Climate Change Adaptation and Territorial Resilience Planning

The understanding of the seasonal changes in the water contribution from different sources in the Aconcagua basin has evidenced the crucial role of the glaciers in providing water in dry periods. In addition to the streamflow buffer effect provided by glacial, periglacial and groundwater sources shown in this work, these water systems play also a crucial role as water reservoirs for the future. As reported by Segovia Rocha and Videla [59], the cryoforms water equivalent in the Valparaíso region represents 2.9 km3, equivalent to more than 30 times the water maximum storage of The Peñuelas lake (0.095 km3), which is the major water reservoir of the region [59,60]. Concerning the rise in temperature observed in the last five decades in the Aconcagua river Basin (1.2 °C) and the expected addition of another 1–3 °C by 2081–2100, a negative tendency of rainfall is expected for central Chile over the same time period, most likely related to a combination of oceanic conditions and anthropogenic forcing, accelerating snowmelt timing, evapotranspiration increase and glacier shrinkage [6,13,26]. The central Andean glaciers at 33 °S presented a 46% shrinkage since 1956, and this deglacierization will continue [26]. All of these processes would have major implications for agricultural, hydroelectricity and domestic water supply [13]. Despite the glacial and periglacial environments relevance functions as aquifer recharge, water supply in dry years and strategic reserves of high quality fresh water, there are no legal provisions for the protection of glacial bodies until the present day in Chile. This situation highlights the urgent necessity to generate a specific glacial and periglacial environment protection law [26].
In addition, considering that the streamflows will have an earlier peak of spring and will increase the proportional contribution from summer glacial melt, this information could be used to optimize the water distribution and storage during the melting season, when is more needed in the region [13]. The information provided in this work could also be used in the current discussion of the Climate Change Law in the Chilean parliament and climate change adaptation and water security policies. The importance of glacial and periglacial environments contribution to streamflows and aquifer recharge is highlighted when comparing with the northern Petorca river basin, without glaciers. Today the Petorca river basin is considered an icon of the water crisis in Chile, where the riverbed is currently dry, and water conflicts arise in these hidro-social territories [7].
The seasonal characterization of different basin areas through natural tracers, spatially displayed through a set of isoscapes and electric conductivity maps (Figures S4 and S5), can also constitute a baseline for determining the origin of plant and animal tissues that incorporate this water in a constitutive form, i.e., when the tissue is formed. Using this information could be possible to determine the origins of tissues such as feathers, hairs or seeds, becoming possible to infer dietary habits and migratory patterns, with high applicability for social, geographic, ecological and forensic studies [29,30,31].

5. Conclusions

By the use of creative combination of chemical tracers and flow measurements, the current work presents the first understanding study estimating the water contribution from glacial, periglacial, snow and groundwater sources to the Chilean Aconcagua river basin catchment over a year.
Although in normal to abundant snow load years the head catchment is dominated by snowmelt water contribution, in dry hydrological cycles, the streamflow becomes largely dominated by other water sources. Likewise, this analysis was strongly affected by seasonality, when the different water sources played their leading role in a different way for each area of the upper basin analyzed. The total analysis average water input from sources different than snow ranged seasonally from 66% to 73%, dropping to 51% in spring when the snowmelt became a dominant input. The upper catchment (analysis A) glacial supply stood out (24–34%), being lower only in spring (21%). The summer glacial inputs were 34% and 29% for 2018 and 2019, respectively. As expected, the snow contribution became clearly dominant in spring (52%), while for the rest of the year remained between 22% and 36%. Groundwater contribution also remained stable throughout the seasons (19–21%), decreasing only in spring to 16%. The 19–24% periglacial water contribution was remarkable, reaching a maximum in autumn (30%) and a minimum in spring (11%) (Table 4).
Downstream, as observed in analysis B and C, glacial contributions dropped and other water sources become more relevant. The difference in contributions between analyses B and C is very small for all the water sources in all the seasons, since they offer almost the same proportions (Table 4). A striking exception to this rule is the higher proportion of the spring groundwater input and winter snowmelt in C. Also noteworthy were the high contributions of groundwater which, except in spring, were between 25% and 46% in B and between 30% and 37% in C. Likewise surprising is the high periglacial contribution in summer and autumn, with contributions between 15% and 20% in B and between 14% and 21% in C, respectively.
Finally, we were able to identify and separate the different water sources contributing to the Aconcagua river and quantify them for the first time, highlighting the contribution relevance of water sources different than snow in arid hydrological cycles, such as the analyzed in this study. This work provides key information for developing adaptation strategies for the territory for both, current and future water management.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4441/12/9/2630/s1.

Author Contributions

Conceptualization, S.A.C.; methodology, S.A.C., C.L. and F.F.; field campaigns, S.A.C., C.L. and S.O.-V.; validation, S.A.C., C.L., F.F. and A.A.M.; statistical analysis, S.C. and C.L.; investigation, S.A.C., C.L., F.F. and L.C.; resources, S.A.C. and A.A.M.; data curation, S.A.C., C.L., F.F. and S.O.-V.; writing—original draft preparation, S.A.C.; writing—review and editing, S.A.C., C.L., F.F. and A.A.M.; Mapping and spatial analysis, S.A.C., L.C. and S.O.-V.; supervision, S.A.C.; project administration, S.A.C.; funding acquisition, S.A.C., A.A.M., C.L. and F.F. All authors have read and agreed to the published version of the manuscript.

Funding

The research work was supported by ANID FONDECYT Postdoctoral project No. 3180682, led by S.A.C. specifically. Authors S.A.C. and A.A.M. thanks to project ANID FONDAP No.1511009. C. Lavergne was funded by ANID FONDECYT Postdoctoral project No.3180374. A. Muñoz was supported by ANID FONDECYT No.1201714. The authors also acknowledge the Research Nucleus in Nature Based Solutions of the Pontifical Catholic University of Valparaíso (PUCV) 39.431/2020.

Acknowledgments

To Isabella Aguilera, Karin Klock, Ivonne Quintanilla, Luis Muñoz Gaete, Isadora Schneider, Ezequiel Toum and Julio Segura for lab support. To Catherine Kenrick, Tomas Dinges, Juli Vidal and Anibal from the “Parque Andino Juncal” for access permission and fieldwork support. To Ana María Córdova, David Poblete, Marcelo Madariaga, Lucas Dominguez, Lisbet Cartacho, Christian Bringas, Valeria Atucha, Guillermo Fuentes, Montserrat Ternicien and Isadora Schneider for fieldwork support. We appreciate the collaboration of APRs Las Coimas and La Troya, and Rodrigo Ahumada and Agrícola Uniagri for facilitating our field works. Finally, we would like to especially acknowledge Paul Overduin from the Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research (AWI) and to Laboratorio de Análisis Isotópicos (Andres Bello University), for their analytical support and data validation.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Contribución Nacional Tentativa De Chile (Indc) Para El Acuerdo Climático París; 2015. Available online: https://mma.gob.cl/wp-content/uploads/2015/09/INDC_1609c1.pdf (accessed on 15 September 2020).
  2. Boisier, J.P.; Aceituno, P. Changes in surface and upper-air temperature along the arid coast of Northern Chile. In Proceedings of the 8 ICSHMO, Foz de Iguaçu, Brazil, 24–28 April 2006. [Google Scholar]
  3. Falvey, M.; Garreaud, R.D. Regional cooling in a warming world: Recent temperature trends in the southeast Pacific and along the west coast of subtropical South America (1979–2006). J. Geophys. Res. Atmos. 2009, 114, 1–16. [Google Scholar] [CrossRef]
  4. Carrasco, J.F.; Osorio, R.; Casassa, G. Secular trend of the equilibrium-line altitude on the western side of the southern Andes, derived from radiosonde and surface observations. J. Glaciol. 2008, 54, 538–550. [Google Scholar] [CrossRef] [Green Version]
  5. Boisier, J.P.; Rondanelli, R.; Garreaud, R.D.; Muñoz, F. Anthropogenic and natural contributions to the Southeast Pacific precipitation decline and recent megadrought in central Chile. Geophys. Res. Lett. 2016, 43, 413–421. [Google Scholar] [CrossRef] [Green Version]
  6. Garreaud, R.D.; Boisier, J.P.; Rondanelli, R.; Montecinos, A.; Sepúlveda, H.H.; Veloso-Aguila, D. The Central Chile Mega Drought (2010–2018): A climate dynamics perspective. Int. J. Climatol. 2020, 40, 421–439. [Google Scholar] [CrossRef]
  7. Muñoz, A.A.; Klock-Barría, K.; Alvarez-Garreton, C.; Aguilera-Betti, I.; González-Reyes, Á.; Lastra, J.A.; Chávez, R.O.; Barría, P.; Christie, D.; Rojas-Badilla, M.; et al. Water crisis in Petorca Basin, Chile: The combined effects of a mega-drought and water management. Water 2020, 12, 648. [Google Scholar] [CrossRef] [Green Version]
  8. Bradley, R.S.; Keimig, F.T.; Diaz, H.F. Projected temperature changes along the American cordillera and the planned GCOS network. Geophys. Res. Lett. 2004, 31, 2–5. [Google Scholar] [CrossRef] [Green Version]
  9. Stocker, T.; Intergovernmental Panel on Climate Change, Working Group I. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; ISBN 9781107661820. [Google Scholar]
  10. CR2 Report to the Nation. The 2010–2015 Mega-Drought: A Lesson for the Future. Inf. Nación 2015. Available online: www.cr2.cl/megasequia (accessed on 15 September 2020).
  11. Nacional Estadísticas, I. De Síntesis De Resultados Censo 2017; Instituto Nacional de Estadísticas (INE): Santiago, Chile, 2018; Available online: https://www.censo2017.cl/descargas/home/sintesis-de-resultados-censo2017.pdf (accessed on 15 September 2020).
  12. Política Nacional para los Recursos Hídricos 2015; Grafnika Impresores: Santiago, Chile, 2015. Available online: https://www.interior.gob.cl/media/2015/04/recursos_hidricos.pdf (accessed on 15 September 2020).
  13. Webb, M.J.; Winter, J.M.; Spera, S.A.; Chipman, J.W.; Osterberg, E.C. Water, agriculture, and climate dynamics in central Chile’s Aconcagua River Basin. Phys. Geogr. 2020, 1–21. [Google Scholar] [CrossRef]
  14. DGA. Información Hídrica de las Cuencas Priorizadas, Fichas Temáticas, Cuenca Aconcagua; Dirección General de Aguas: Santiago, Chile, 2015; Available online: https://www.mop.cl/Prensa/Documents/08_Rio_Aconcagua.pdf (accessed on 15 September 2020).
  15. Janke, J.R.; Ng, S.; Bellisario, A. An inventory and estimate of water stored in firn fields, glaciers, debris-covered glaciers, and rock glaciers in the Aconcagua River Basin, Chile. Geomorphology 2017, 296, 142–152. [Google Scholar] [CrossRef]
  16. DGA. Cuenca del Aconcagua: Diagnostico y Clasificacion de los Cursos y Cuerpos de Agua Segun Objetivos de Calidad; Dirección General de Aguas: Santiago, Chile, 2004; Available online: https://web.archive.org/web/20150924102033/http://www.sinia.cl/1292/articles-31018_Bueno.pdf (accessed on 15 September 2020).
  17. Compagnucci, R.H.; Vargas, W.M. Inter-annual variability of the Cuyo rivers’ streamflow in the Argentinean Andean mountains and ENSO events. Int. J. Climatol. 1998, 18, 1593–1609. [Google Scholar] [CrossRef]
  18. Masiokas, M.H.; Villalba, R.; Luckman, B.H.; Le Quesne, C.; Aravena, J.C. Snowpack variations in the central Andes of Argentina and Chile, 1951–2005: Large-scale atmospheric influences and implications for water resources in the region. J. Clim. 2006, 19, 6334–6352. [Google Scholar] [CrossRef]
  19. Leiva, J.C. Recent fluctuations of the Argentinian glaciers. Glob. Planet. Change 1999, 22, 169–177. [Google Scholar] [CrossRef]
  20. Crespo, S.; Fernandoy, F.; Cara, L.; Klarian, S.; Lavergne, C. First snow, glacier and groundwater contribution quantification in the Upper Mendoza River basin using 2H and 18O. Isotopes Environ. Health Stud. 2020. [Google Scholar] [CrossRef] [PubMed]
  21. Glaciares. 2015. Available online: http://www.ide.cl/index.php/medio-ambiente/item/1665-glaciares-2015 (accessed on 31 July 2020).
  22. Snowmelt-Runoff Simulation Model of a Central Chile Andean basin with Relevant Orographic Effects—Resultados de su Búsqueda—Bases de Datos Bibliográficos Pascal y Francis. Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=8327953 (accessed on 28 July 2020).
  23. Rivera, A.; Acuna, C.; Casassa, G.; Bown, F. Use of remotely sensed and field data to estimate the contribution of Chilean glaciers to eustatic sea-level rise. Ann. Glaciol. 2002, 34, 367–372. [Google Scholar] [CrossRef] [Green Version]
  24. Dussaillant, I.; Berthier, E.; Brun, F.; Masiokas, M.; Hugonnet, R.; Favier, V.; Rabatel, A.; Pitte, P.; Ruiz, L. Two decades of glacier mass loss along the Andes. Nat. Geosci. 2019, 12, 802–808. [Google Scholar] [CrossRef]
  25. Masiokas, M.H.; Rivera, A.; Espizua, L.E.; Villalba, R.; Delgado, S.; Aravena, J.C. Glacier fluctuations in extratropical South America during the past 1000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 242–268. [Google Scholar] [CrossRef]
  26. Ruiz Pereira, S.F.; Veettil, B.K. Glacier decline in the Central Andes (33 °S): Context and magnitude from satellite and historical data. J. South Am. Earth Sci. 2019, 94, 102249. [Google Scholar] [CrossRef]
  27. Bown, F.; Rivera, A.; Acuña, C. Recent glacier variations at the Aconcagua basin, central Chilean Andes. Ann. Glaciol. 2008, 48, 43–48. [Google Scholar] [CrossRef] [Green Version]
  28. Ragettli, S.; Immerzeel, W.W.; Pellicciotti, F. Contrasting climate change impact on river flows from high-altitude catchments in the Himalayan and Andes Mountains. Proc. Natl. Acad. Sci. USA 2016, 113, 9222–9227. [Google Scholar] [CrossRef] [Green Version]
  29. Terzer, S.; Wassenaar, L.I.; Araguás-Araguás, L.J.; Aggarwal, P.K. Global isoscapes for δ 18 O and δ 2 H in precipitation: Improved prediction using regionalized climatic regression models. Hydrol. Earth Syst. Sci 2013, 17, 1–16. [Google Scholar] [CrossRef]
  30. Ehleringer, J.R.; Chesson, L.A.; Valenzuela, L.O.; Tipple, B.J.; Martinelli, L.A. Stable isotopes trace the truth: From adulterated foods to crime scenes. Elements 2015, 11, 259–264. [Google Scholar] [CrossRef]
  31. Lachniet, M.S.; Lawson, D.E.; Stephen, H.; Sloat, A.R.; Patterson, W.P. Isoscapes of δ 18 O and δ 2 H reveal climatic forcings on Alaska and Yukon precipitation. Water Resour. Res. 2016, 52, 6575–6586. [Google Scholar] [CrossRef] [Green Version]
  32. Crespo, S.; Aranibar, J.; Gomez, L.; Schwikowski, M.; Bruetsch, S.; Cara, L.; Villalba, R. Ionic and stable isotope chemistry as indicators of water sources to the Upper Mendoza River basin, Central Andes of Argentina. Hydrol. Sci. J. 2017, 62, 588–605. [Google Scholar] [CrossRef] [Green Version]
  33. Lambs, L. Correlation of conductivity and stable isotope 18O for the assessment of water origin in river system. Chem. Geol. 2000, 164, 161–170. [Google Scholar] [CrossRef] [Green Version]
  34. Lambs, L.; Loubiat, M.; Richardson, W. The use of stable isotope to evaluate water mixing and water use by flood plain trees along the Garonne valley. Isotopes Environ. Health Stud. 2003, 39, 301–310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Pu, T.; He, Y.; Zhu, G.; Zhang, N.; Du, J.; Wang, C. Characteristics of water stable isotopes and hydrograph separation in Baishui catchment during the wet season in Mt.Yulong region, south western China. Hydrol. Process. 2013, 27, 3641–3648. [Google Scholar] [CrossRef]
  36. Garreaud, R.D.; Alvarez-Garreton, C.; Barichivich, J.; Pablo Boisier, J.; Christie, D.; Galleguillos, M.; LeQuesne, C.; McPhee, J.; Zambrano-Bigiarini, M. The 2010-2015 megadrought in central Chile: Impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef] [Green Version]
  37. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
  38. Friendly, M. Corrgrams: Exploratory displays for correlatigon matrices. Am. Stat. 2002, 56, 316–324. [Google Scholar] [CrossRef]
  39. Dray, S.; Dufour, A.-B. The ade4 package: Implementing the duality diagram for ecologists. J. Stat. Softw. 2007, 22, 1–20. [Google Scholar] [CrossRef] [Green Version]
  40. Oksanen, J.; Blanchet, F.G.; Kindt, R.; Legendre, P.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; Steven, M.H.H.; Wagner, H. Vegan: Community Ecology Package; R Package Version 2.0-7: Vienna, Austria, 2013. [Google Scholar]
  41. Pinheiro, J. Nlme: Linear and Nonlinear Mixed-Effects Models, R Package Version 3.1-103; 2013, Volume 3, p. 111. Available online: http://cran.r-project.org/web/packages/nlme/index.html (accessed on 15 September 2020).
  42. Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
  43. Crawley, M.J. The R Book; John Wiley & Sons, Ltd.: Chichester, UK, 2007; ISBN 9780470515075. [Google Scholar]
  44. Parnell, A.; Inger, R. Stable Isotope Mixing Models in R with Simmr. Available online: https://cran.r-project.org/web/packages/simmr/vignettes/simmr.html (accessed on 16 September 2020).
  45. Taucare, M.; Daniele, L.; Viguier, B.; Vallejos, A.; Arancibia, G. Groundwater resources and recharge processes in the Western Andean Front of Central Chile. Sci. Total Environ. 2020, 722. [Google Scholar] [CrossRef]
  46. Taucare, M.; Viguier, B.; Daniele, L.; Heuser, G.; Arancibia, G.; Leonardi, V. Connectivity of fractures and groundwater flows analyses into the Western Andean Front by means of a topological approach (Aconcagua Basin, Central Chile). Hydrogeol. J. 2020. [Google Scholar] [CrossRef]
  47. QGIS Development Team 2020. Open Source Geospatial Foundation. 2020. Available online: http://qgis.osgeo.org (accessed on 15 September 2020).
  48. Hall, D.K.; Riggs, G.A. Normalized-difference snow index (Ndsi). Encycl. Earth Sci. Ser. 2011, 779–780. [Google Scholar] [CrossRef] [Green Version]
  49. Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
  50. Riggs, G.A.; Hall, D.K.; Salomonson, V.V. MODIS Sea Ice Products User Guide to Collection 5; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2006; Volume 49. Available online: https://modis-snow-ice.gsfc.nasa.gov/uploads/siug_c5.pdf (accessed on 15 September 2020).
  51. Cara, L.; Masiokas, M.; Viale, M.; Villalba, R. Análisis De La Cobertura Nival De La Cuenca Superior Del Río Mendoza a Partir De Imágenes Modis. Meteorológica 2016, 41, 21–36. [Google Scholar]
  52. Ohlanders, N.; Rodriguez, M.; McPhee, J. Stable water isotope variation in a Central Andean watershed dominated by glacier and snowmelt. Hydrol. Earth Syst. Sci. 2013, 17, 1035–1050. [Google Scholar] [CrossRef] [Green Version]
  53. Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
  54. DGA MOP—Chile. Available online: https://snia.mop.gob.cl/BNAConsultas/reportes (accessed on 9 December 2019).
  55. Trombotto, D.; Ahumada, A. Los Fenomenos Periglaciales. Identificación, Determinación y Aplicación; Fondo. Miguel Lillo.; Opera Lilloana: Tucumán, Argentina, 2005; ISBN 950-668-010-8. [Google Scholar]
  56. Dirección general de aguas, Ministerio de Obras Públicas. Boletin no498, Información Pluviométrica, Fluviométrica, Estado de Embalses y Aguas Subterráneas. 2019. Available online: https://dga.mop.gob.cl/productosyservicios/informacionhidrologica/Informacin%20Mensual/Boletin_10_Octubre_2019.pdf (accessed on 15 September 2020).
  57. Ministerio del Interior y Seguridad Pública. CVE 1616675—Diario Oficial de la República de Chile; Ministerio del Interior y Seguridad Pública: Santiago de Chile, Chile, 2019; Available online: https://www.diariooficial.interior.gob.cl/publicaciones/2019/07/10/42400/01/1616675.pdf (accessed on 15 September 2020).
  58. Rodriguez, M.; Ohlanders, N.; Pellicciotti, F.; Williams, M.; McPhee, J. Estimating runoff from a glaciarized catchment using natural tracers in the semi-arid Andes cordillera. Hydrol. Process. 2016, 30, 3609–3626. [Google Scholar] [CrossRef]
  59. Rocha, A.S.; Giering, Y.V. Caracterización glaciológica de Chile Glaciological characterization of Chile. 2017, 24, 3–24. [Google Scholar]
  60. DGA 2020. Región de Valparaiso—Gobierno de Chile. Available online: http://pronostico.dga.cl/detalle5Region.html#embalse (accessed on 2 September 2020).
Water 12 02630 g001 550
Figure 1. Study area digital elevation model, sampling sites and ice bodies. A, B and C refer to the sub-basins outlet location considered in the “simmr” model analysis.
Figure 1. Study area digital elevation model, sampling sites and ice bodies. A, B and C refer to the sub-basins outlet location considered in the “simmr” model analysis.
Water 12 02630 g001
Water 12 02630 g002 550
Figure 2. Principal component analysis (PCA) based on both ionic (nitrate, chloride, sodium, silicon, barium, potassium, magnesium, fluoride, calcium, strontium, sulfate) and isotopic (deltaO18: δ18O, deltaH2: δ2H, Dex: deuterium excess) data. (A) Correlation circle positioning the variables studied. The correlation of the electrical conductivity values and the coordinates of the first dimension of the PCA (B) highlighted that electrical conductivity is suitable for glacial/periglacial origin discrimination.
Figure 2. Principal component analysis (PCA) based on both ionic (nitrate, chloride, sodium, silicon, barium, potassium, magnesium, fluoride, calcium, strontium, sulfate) and isotopic (deltaO18: δ18O, deltaH2: δ2H, Dex: deuterium excess) data. (A) Correlation circle positioning the variables studied. The correlation of the electrical conductivity values and the coordinates of the first dimension of the PCA (B) highlighted that electrical conductivity is suitable for glacial/periglacial origin discrimination.
Water 12 02630 g002
Water 12 02630 g003 550
Figure 3. Stable isotope (δ18O and δ2H) scatter plot of rivers and water sources. The blue line represents the Global Meteoric Water Line (GMWL) according to Craig’s equation [53]. The red line represents the Local Meteoric Water Line (LMWL), was constructed with our data at 33 °S and follows the equation: δ2H = 7.9874 × δ18O + 10.892 (R2 = 0.9974), close to the LMWL at 33 °S reported by Taucare et al.: δ2H = 8.076 × δ18O + 11.42 (R2 = 0.97) [45].
Figure 3. Stable isotope (δ18O and δ2H) scatter plot of rivers and water sources. The blue line represents the Global Meteoric Water Line (GMWL) according to Craig’s equation [53]. The red line represents the Local Meteoric Water Line (LMWL), was constructed with our data at 33 °S and follows the equation: δ2H = 7.9874 × δ18O + 10.892 (R2 = 0.9974), close to the LMWL at 33 °S reported by Taucare et al.: δ2H = 8.076 × δ18O + 11.42 (R2 = 0.97) [45].
Water 12 02630 g003
Water 12 02630 g004 550
Figure 4. “Simmr” isospace plot of different water sources contributing to the upper Aconcagua River basin. The different water source references (i.e., glacial, periglacial, groundwater and snow) and samples used for each model analysis (A, B and C) were plotted in color. Shapes were used to represent the six sampling periods and water source references. The sources are identified by the colors (i.e., glacial in red up-oriented, groundwater in orange, periglacial in night blue and snow in dark green). Vertical and horizontal bars represented the standard deviation of the water sources.
Figure 4. “Simmr” isospace plot of different water sources contributing to the upper Aconcagua River basin. The different water source references (i.e., glacial, periglacial, groundwater and snow) and samples used for each model analysis (A, B and C) were plotted in color. Shapes were used to represent the six sampling periods and water source references. The sources are identified by the colors (i.e., glacial in red up-oriented, groundwater in orange, periglacial in night blue and snow in dark green). Vertical and horizontal bars represented the standard deviation of the water sources.
Water 12 02630 g004
Water 12 02630 g005 550
Figure 5. Percentage of the total snow covered area for each sub-basin composing the Aconcagua River catchment area along the analyzed period (2017–2019). The SWE refers to the snow water equivalent in mm, at Portillo station, and Aconcagua at Blanco River refers to the streamflow of the Aconcagua river after the join of the Juncal and Blanco rivers. Both, SWE and streamflow, were measured by Dirección General de Aguas de Chile [54].
Figure 5. Percentage of the total snow covered area for each sub-basin composing the Aconcagua River catchment area along the analyzed period (2017–2019). The SWE refers to the snow water equivalent in mm, at Portillo station, and Aconcagua at Blanco River refers to the streamflow of the Aconcagua river after the join of the Juncal and Blanco rivers. Both, SWE and streamflow, were measured by Dirección General de Aguas de Chile [54].
Water 12 02630 g005
Table
Table 1. Mean, standard deviation (SD) and confidence interval δ18O composition for water sources in comparison with the Glacial system. Akaike weight w = 1; R2 = 0.89.
Table 1. Mean, standard deviation (SD) and confidence interval δ18O composition for water sources in comparison with the Glacial system. Akaike weight w = 1; R2 = 0.89.
VariableMean [δ18O‰]SDCI (2.5–97.5%)p-Value
Glacial−17.700.74−19.16 & −16.24
Periglacial1.211.17−1.08 & 3.510.301
Groundwater4.710.912.92 & 6.50<0.001
Snow catchment3.440.891.70 & 5.19<0.001
Table
Table 2. Mean, standard deviation (SD) and confidence interval (CI) for electric conductivity of different water sources in comparison with the glacial system. Akaike weight w = 1; R2 = 0.88.
Table 2. Mean, standard deviation (SD) and confidence interval (CI) for electric conductivity of different water sources in comparison with the glacial system. Akaike weight w = 1; R2 = 0.88.
VariableMean [µS cm−1]SDCI (2.5–97.5%)p-Value
Glacial134.3106.8−75.10 & 343.75
Periglacial878.8164.9555.72 & 1201.97<0.001
Groundwater496.1131.8237.82 & 754.33<0.001
Snow catchment−10.4129.3−263.90 & 243.150.936
Table
Table 3. Stable isotopes and electric conductivity mean and standard deviation values for the different water sources analyzed.
Table 3. Stable isotopes and electric conductivity mean and standard deviation values for the different water sources analyzed.
Water Sourceδ18O ‰SDδ2H ‰SDδ d‰SDEC µS cm−1SDnMean Altitude/Depth
Glacial−17.700.19−128.891.3712.740.541331154173
Periglacial−16.490.51−121.402.9010.501.79101335963712
Snow catchment−14.250.81−107.277.736.763.031245973328
Groundwater−13.031.52−97.7610.886.471.355841707857/−93
Note: For glacial environment were considered as representative the samples obtained in summer. For periglacial water sources were considered the samples obtained in summer and autumn. Snow catchment samples were obtained during the seasonal snow melt, in spring, when the pure snow fed streams were active. The mean altitude was calculated as an average of the basins analyzed with QGIS and are expressed in meters above sea level [47]. For boreholes, depth was expressed in meters.
Table
Table 4. Proportional contribution of each water source to the headwaters of the Aconcagua River basin according to different “simmr” analysis.
Table 4. Proportional contribution of each water source to the headwaters of the Aconcagua River basin according to different “simmr” analysis.
Water Source/SeasonASD AB 19-49SD BC 51SD CAnalysis AverageAnalysis SD Dif.
Summer 2018 A−CB−CA−B
Glacial0.340.140.210.170.180.110.250.140.170.040.13
Periglacial0.230.120.140.110.160.090.170.110.070.03−0.03
Snow0.240.140.400.220.370.180.330.18−0.13−0.040.06
Groundwater0.190.110.250.170.300.150.250.14−0.11−0.040.00
Autumn 2018
Glacial0.300.140.190.140.190.110.220.130.110.000.11
Periglacial0.300.160.200.150.210.110.240.140.090.000.10
Snow0.220.130.290.190.290.160.270.16−0.070.00−0.07
Groundwater0.190.100.320.190.320.160.280.15−0.130.00−0.13
Winter 2018
Glacial0.300.130.130.090.120.080.180.100.180.010.17
Periglacial0.230.130.120.070.090.060.150.090.140.020.11
Snow0.260.150.290.170.420.200.330.18−0.16−0.13−0.03
Groundwater0.210.120.460.160.370.170.340.15−0.160.09−0.25
Spring 2018
Glacial0.210.100.220.200.100.070.180.120.110.12−0.01
Periglacial0.110.070.120.110.080.050.100.080.040.05−0.01
Snow0.520.170.440.260.510.220.490.220.01−0.070.08
Groundwater0.160.110.220.180.320.190.230.16−0.16−0.10−0.06
Summer 2019
Glacial0.290.130.220.180.160.100.220.140.130.070.07
Periglacial0.240.130.150.110.140.080.170.110.100.010.10
Snow0.260.150.370.220.370.180.330.18−0.11−0.01−0.11
Groundwater0.210.120.260.180.330.160.270.15−0.12−0.07−0.05
Autumn 2019
Glacial0.240.130.190.150.160.100.200.130.080.040.05
Periglacial0.190.130.180.130.140.080.170.110.050.040.01
Snow0.360.180.300.200.350.180.340.190.00−0.050.05
Groundwater0.210.130.330.200.350.160.300.16−0.14−0.03−0.11
Note: A: refers to the “simmr”analysis of the rivers from the upper headwater of the basin considered as replicates (mean elevation 3583 m a.s.l.); B: considers Peñon and Blanco rivers (3445 m a.s.l. average altitude); C: analysis of the Juncal River before joining the Blanco River (mean area altitude: 3417 m a.s.l.)
Table
Table 5. Proportional contribution of each water source to the stagnant waters of the head catchments at the Aconcagua River basin according to “simmr” analysis.
Table 5. Proportional contribution of each water source to the stagnant waters of the head catchments at the Aconcagua River basin according to “simmr” analysis.
SiteGlacialSDPeriglacialSDSnowSDGroundwaterSD
Inca lagoon0.140.100.030.020.760.110.060.04
Del Nacimiento wetland0.460.160.300.130.120.090.120.11
Juncal Norte wetland0.450.140.080.070.350.150.120.07

Share and Cite

MDPI and ACS Style

Crespo, S.A.; Lavergne, C.; Fernandoy, F.; Muñoz, A.A.; Cara, L.; Olfos-Vargas, S. Where Does the Chilean Aconcagua River Come from? Use of Natural Tracers for Water Genesis Characterization in Glacial and Periglacial Environments. Water 2020, 12, 2630. https://doi.org/10.3390/w12092630

AMA Style

Crespo SA, Lavergne C, Fernandoy F, Muñoz AA, Cara L, Olfos-Vargas S. Where Does the Chilean Aconcagua River Come from? Use of Natural Tracers for Water Genesis Characterization in Glacial and Periglacial Environments. Water. 2020; 12(9):2630. https://doi.org/10.3390/w12092630

Chicago/Turabian Style

Crespo, Sebastián Andrés, Céline Lavergne, Francisco Fernandoy, Ariel A. Muñoz, Leandro Cara, and Simón Olfos-Vargas. 2020. "Where Does the Chilean Aconcagua River Come from? Use of Natural Tracers for Water Genesis Characterization in Glacial and Periglacial Environments" Water 12, no. 9: 2630. https://doi.org/10.3390/w12092630

APA Style

Crespo, S. A., Lavergne, C., Fernandoy, F., Muñoz, A. A., Cara, L., & Olfos-Vargas, S. (2020). Where Does the Chilean Aconcagua River Come from? Use of Natural Tracers for Water Genesis Characterization in Glacial and Periglacial Environments. Water, 12(9), 2630. https://doi.org/10.3390/w12092630

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop