A Simple Time-Varying Sensitivity Analysis (TVSA) for Assessment of Temporal Variability of Hydrological Processes
Abstract
1. Introduction
2. TVSA Function Description
2.1. Code Description
2.2. Objective Functions
2.2.1. Nash–Sutcliffe Efficiency (NSE)
2.2.2. Root Mean Square Error (RMSE)
2.2.3. Nash–Sutcliffe Efficiency Calculated on Inverse Streamflows (NSEiQ)
2.2.4. Kling–Gupta Efficiency (KGE)
2.3. Convergence Analysis
3. Application Example
3.1. Study Area and Data
3.2. Description of the Model
3.3. TVSA Implementation
4. Results and Discussion
4.1. Computational Cost
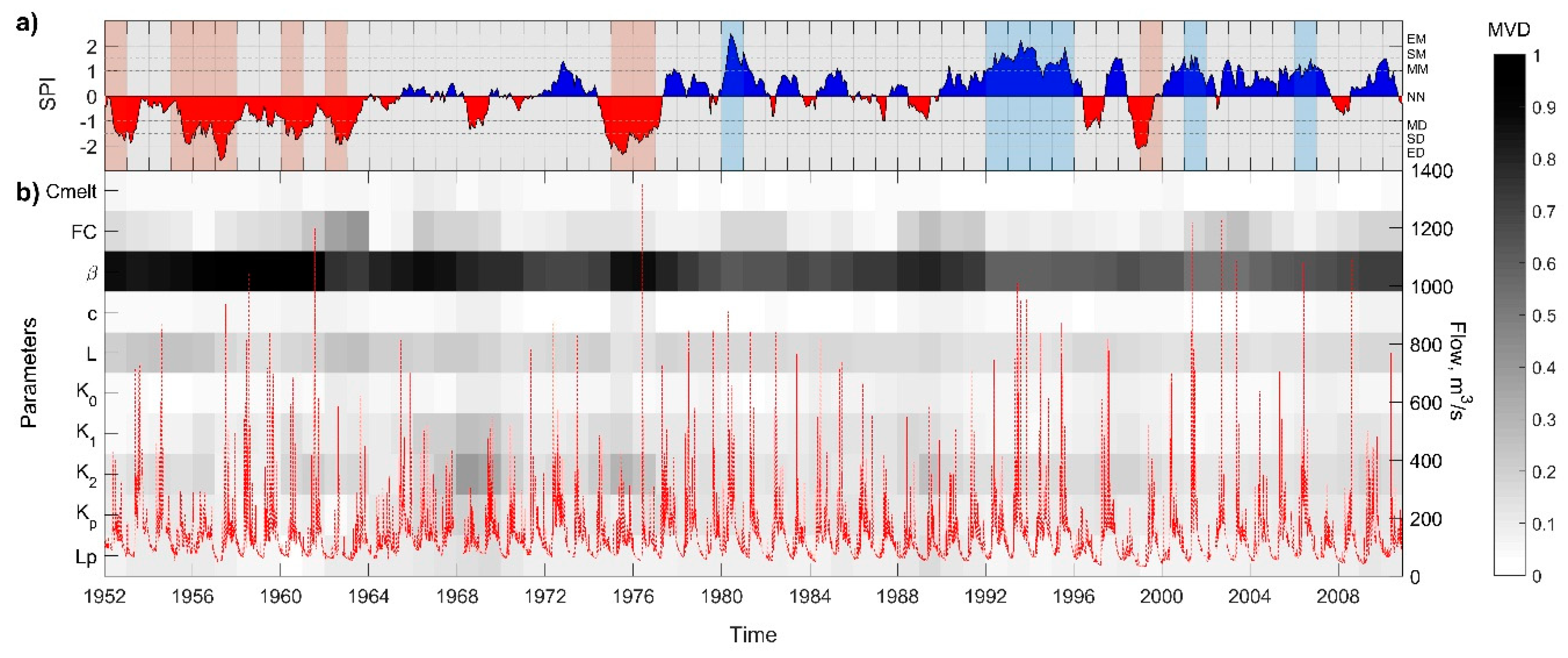
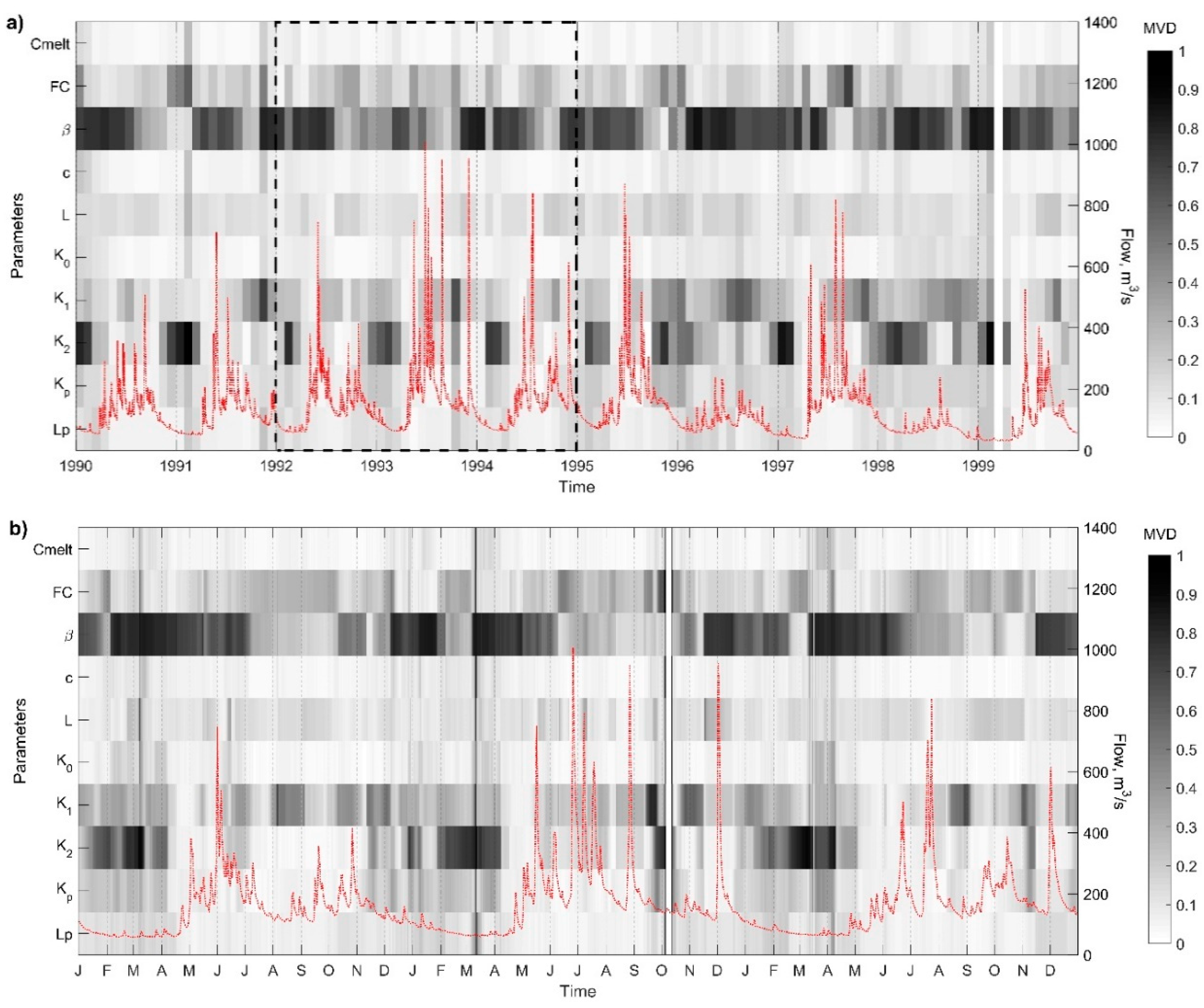
4.2. Temporal Variability of Hydrological Processes
4.3. Size of the Window of Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Pianosi, F.; Sarrazin, F.; Wagener, T. A Matlab toolbox for Global Sensitivity Analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Devak, M.; Dhanya, C.T. Sensitivity analysis of hydrological models: Review and way forward. J. Water Clim. Chang. 2017, 8, 557–575. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis; Wiley: Chichester, UK, 2008. [Google Scholar]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A.; Cariboni, J. From screening to quantitative sensitivity analysis. A unified approach. Comput. Phys. Commun. 2011, 182, 978–988. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 2. Application. Water Resour. Res. 2016, 52, 440–455. [Google Scholar] [CrossRef]
- Razavi, S.; Gupta, H.V. A new framework for comprehensive, robust, and efficient global sensitivity analysis: 1. Theory. Water Resour. Res. 2016, 52, 423–439. [Google Scholar] [CrossRef]
- Khorashadi Zadeh, F.; Nossent, J.; Sarrazin, F.; Pianosi, F.; van Griensven, A.; Wagener, T.; Bauwens, W. Comparison of variance-based and moment-independent global sensitivity analysis approaches by application to the SWAT model. Environ. Model. Softw. 2017, 91, 210–222. [Google Scholar] [CrossRef]
- Cukier, R.I.; Fortuin, C.M.; Shuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in peel inlet-II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Sobol, M.I. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based oncumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Razavi, S.; Sheikholeslami, R.; Gupta, H.V.; Haghnegahdar, A. VARS-TOOL: A toolbox for comprehensive, efficient, and robust sensitivity and uncertainty analysis. Environ. Model. Softw. 2019, 112, 95–107. [Google Scholar] [CrossRef]
- Wagener, T.; McIntyre, N.; Lees, M.J.; Wheater, H.S.; Gupta, H.V. Towards reduced uncertainty in conceptual rainfall-runoff modelling: Dynamic identifiability analysis. Hydrol. Process. 2003, 17, 455–476. [Google Scholar] [CrossRef]
- Guse, B.; Pfannerstill, M.; Strauch, M.; Reusser, D.E.; Lüdtke, S.; Volk, M.; Gupta, H.; Fohrer, N. On characterizing the temporal dominance patterns of model parameters and processes. Hydrol. Process. 2016, 30, 2255–2270. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. Understanding the time-varying importance of different uncertainty sources in hydrological modelling using global sensitivity analysis. Hydrol. Process. 2016, 30, 3991–4003. [Google Scholar] [CrossRef]
- Ghasemizade, M.; Baroni, G.; Abbaspour, K.; Schirmer, M. Combined analysis of time-varying sensitivity and identifiability indices to diagnose the response of a complex environmental model. Environ. Model. Softw. 2017, 88, 22–34. [Google Scholar] [CrossRef]
- Zhao, Y.; Nan, Z.; Yu, W.; Zhang, L. Calibrating a hydrological model by stratifying frozen ground types and seasons in a cold alpine basin. Water 2019, 11, 985. [Google Scholar] [CrossRef]
- Wagener, T.; Kollat, J. Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox. Environ. Model. Softw. 2007, 22, 1021–1033. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. From maps to movies: High-resolution time-varying sensitivity analysis for spatially distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 5109–5125. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. Technical note: Method of Morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 2893–2903. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Wagener, T. Time-varying sensitivity analysis clarifies the effects of watershed model formulation on model behavior. Water Resour. Res. 2013, 49, 1400–1414. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Habib, E. Application of a Conceptual Hydrologic Model in Teaching Hydrologic Processes. Int. J. Eng. Educ. 2010, 26, 963–973. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Medina, Y.; Muñoz, E. Analysis of the Relative Importance of Model Parameters in Watersheds with Different Hydrological Regimes. Water 2020, 12, 2376. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Wagener, T.; van Werkhoven, K.; Reed, P.; Tang, Y. Multiobjective sensitivity analysis to understand the information content in streamflow observations for distributed watershed modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Demissie, M. Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT ISWS CR 2004-08; Illinois State Water Survey: Champaign, IL, USA, 2004; Available online: http://hdl.handle.net/2142/94220 (accessed on 20 July 2019).
- Le Moine, N. Le Bassin Versant de Surface vu par le Souterrain: Une Voie D’amélioration des Performances et du Réalisme des Modèles Pluie-Débit? Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2008. [Google Scholar]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; McMillan, H.; Gupta, H. Use of an entropy-based metric in multiobjective calibration to improve model performance. Water Resour. Res. 2014, 50, 8066–8083. [Google Scholar] [CrossRef]
- Patil, S.D.; Stieglitz, M. Comparing spatial and temporal transferability of hydrological model parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model—Its Structure and Applications; SMHI RH No. 4; SMHI: Norrköping, Sweden, 1992. [Google Scholar]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Seibert, J. Multi-criteria calibration of a conceptual runoff model using a genetic algorithm. Hydrol. Earth Syst. Sci. 2000, 4, 215–224. [Google Scholar] [CrossRef]
- Muñoz, E.; Rivera, D.; Vergara, F.; Tume, P.; Arumí, J.L. Identifiability analysis: Towards constrained equifinality and reduced uncertainty in a conceptual model. Hydrol. Sci. J. 2014, 59, 1690–1703. [Google Scholar] [CrossRef]
- Kollat, J.B.; Reed, P.M.; Wagener, T. When are multiobjective calibration trade-offs in hydrologic models meaningful? Water Resour. Res. 2012, 48, W3520. [Google Scholar] [CrossRef]
- Medina, Y.; Muñoz, E. Estimation of Annual Maximum and Minimum Flow Trends in a Data-Scarce Basin. Case Study of the Allipén River Watershed, Chile. Water 2020, 12, 162. [Google Scholar] [CrossRef]
- Seibert, J.; Vis, M.J.P. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef]
- World Meteorological Organization. Standardized Precipitation Index User Guide. Available online: https://public.wmo.int/en/resources/library/standardized-precipitation-index-user-guide (accessed on 24 June 2020).
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Zelelew, M.B.; Alfredsen, K. Sensitivity-guided evaluation of the HBV hydrological model parameterization. J. Hydroinform. 2013, 15, 967–990. [Google Scholar] [CrossRef]
- Massmann, C.; Wagener, T.; Holzmann, H. A new approach to visualizing time-varying sensitivity indices for environmental model diagnostics across evaluation time-scales. Environ. Model. Softw. 2014, 51, 190–194. [Google Scholar] [CrossRef]


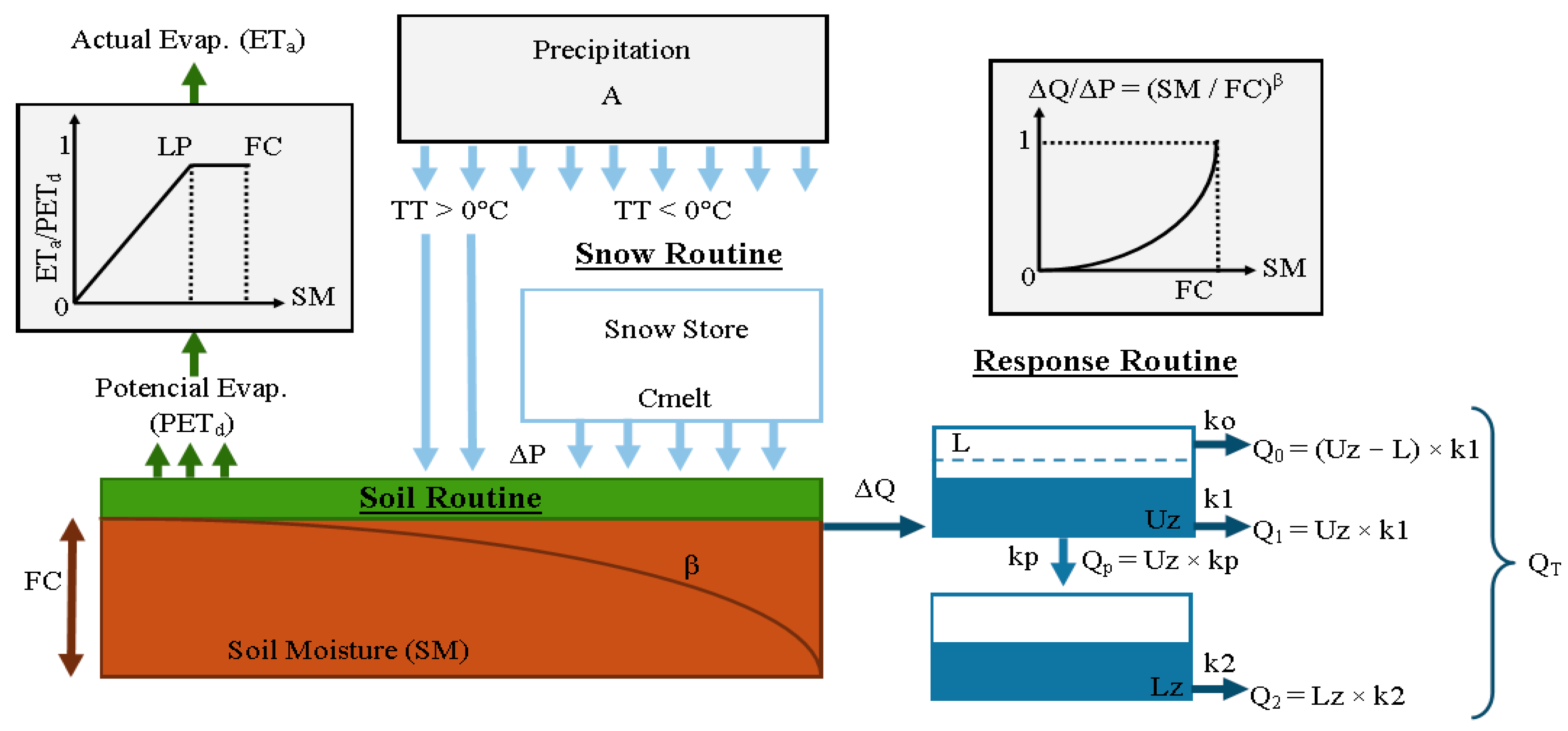

| Parameter | Description | Range |
|---|---|---|
| Mass balance | ||
| A | Precipitation modification parameter | 0.8–2.5 |
| Snow Module | ||
| TT (°C) | Threshold temperature that indicates the initiation of snowmelt (normally, 0 °C) | 0 |
| Cmelt | Fraction of snow that melts above the threshold temperature (TT) from the beginning of snowmelt. | 0.5–7 |
| Moisture module | ||
| FC (mm) | Field capacity (storage in the soil layer) | 0–2000 |
| Empirical coefficient that represents the soil moisture variation in the area | 0–7 | |
| LP | Fraction of field capacity to calculate the permanent wilting point (PWP = LP × FC) | 0.3–1 |
| C () | Correction factor for potential evapotranspiration | 0.01–0.3 |
| Response module | ||
| L (mm) | Threshold for quick runoff response | 0–100 |
| () | Quick response coefficient (upper reservoir) | 0.3–0.6 |
| () | Slow response coefficient (upper reservoir) | 0.1–0.2 |
| () | Lower reservoir response coefficient | 0.01–0.1 |
| () | Maximum flow coefficient for percolation | 0.01–0.1 |
| SPI Values | Category |
|---|---|
| 2 and above | Extremely wet (EM) |
| 1.5 to 1.99 | Severely wet (SM) |
| 1.0 to 1.49 | Moderately wet (MM) |
| −0.99 to 0.99 | Normal or near normal (NN) |
| −1.0 to −1.49 | Moderate drought (MD) |
| −1.5 to −1.99 | Severe drought (SD) |
| −2 and below | Extreme drought (ED) |
| Method | Evaluations to Reach Convergence | Time of Model Evaluation (s) | Time for SI Calculation and Objective Functions (s) | Memory (%) |
|---|---|---|---|---|
| RSA | 10,000 | 122 | 5.55 | 75 |
| PAWN | 19,000 | 231 | 7.36 | 98 |
| Morris | >22,000 * | 246 | – | Out of memory |
| Sobol (TE) | >22,000 * | 246 | – | Out of memory |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, Y.; Muñoz, E. A Simple Time-Varying Sensitivity Analysis (TVSA) for Assessment of Temporal Variability of Hydrological Processes. Water 2020, 12, 2463. https://doi.org/10.3390/w12092463
Medina Y, Muñoz E. A Simple Time-Varying Sensitivity Analysis (TVSA) for Assessment of Temporal Variability of Hydrological Processes. Water. 2020; 12(9):2463. https://doi.org/10.3390/w12092463
Chicago/Turabian StyleMedina, Yelena, and Enrique Muñoz. 2020. "A Simple Time-Varying Sensitivity Analysis (TVSA) for Assessment of Temporal Variability of Hydrological Processes" Water 12, no. 9: 2463. https://doi.org/10.3390/w12092463
APA StyleMedina, Y., & Muñoz, E. (2020). A Simple Time-Varying Sensitivity Analysis (TVSA) for Assessment of Temporal Variability of Hydrological Processes. Water, 12(9), 2463. https://doi.org/10.3390/w12092463




