Simulation of a Hydrostatic Pressure Machine with Caffa3d Solver: Numerical Model Characterization and Evaluation
Abstract
1. Introduction
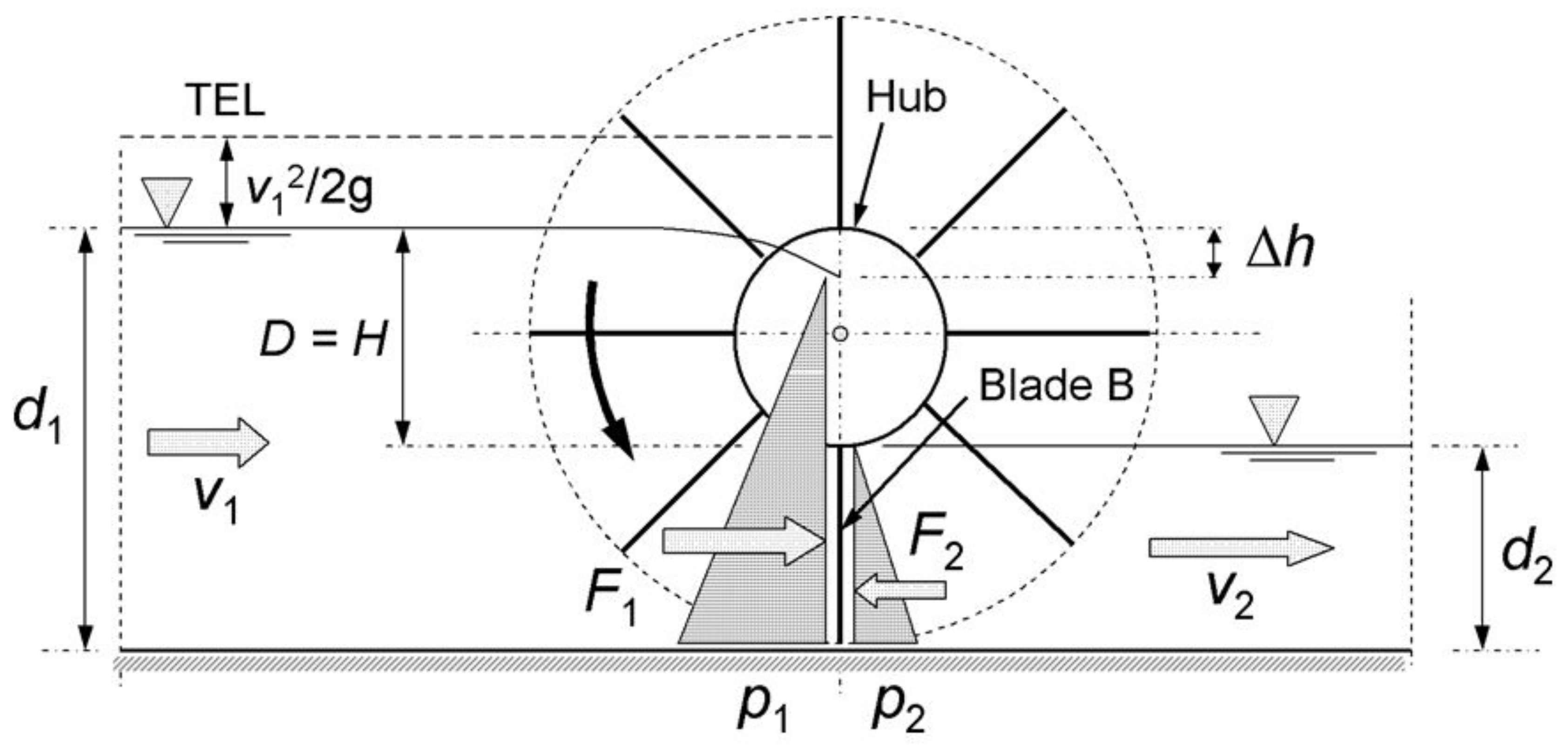
2. Materials and Methods
2.1. Rotation of the Wheel
2.2. Free Surface Flow
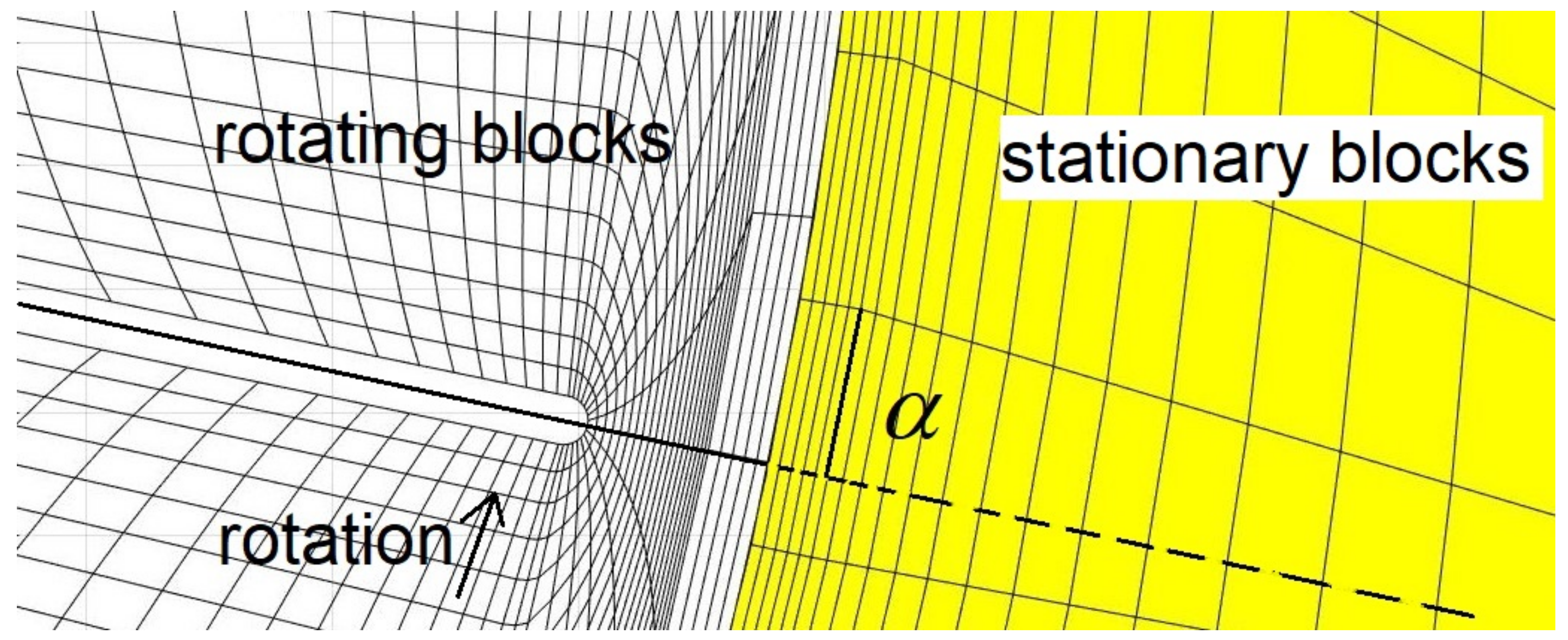
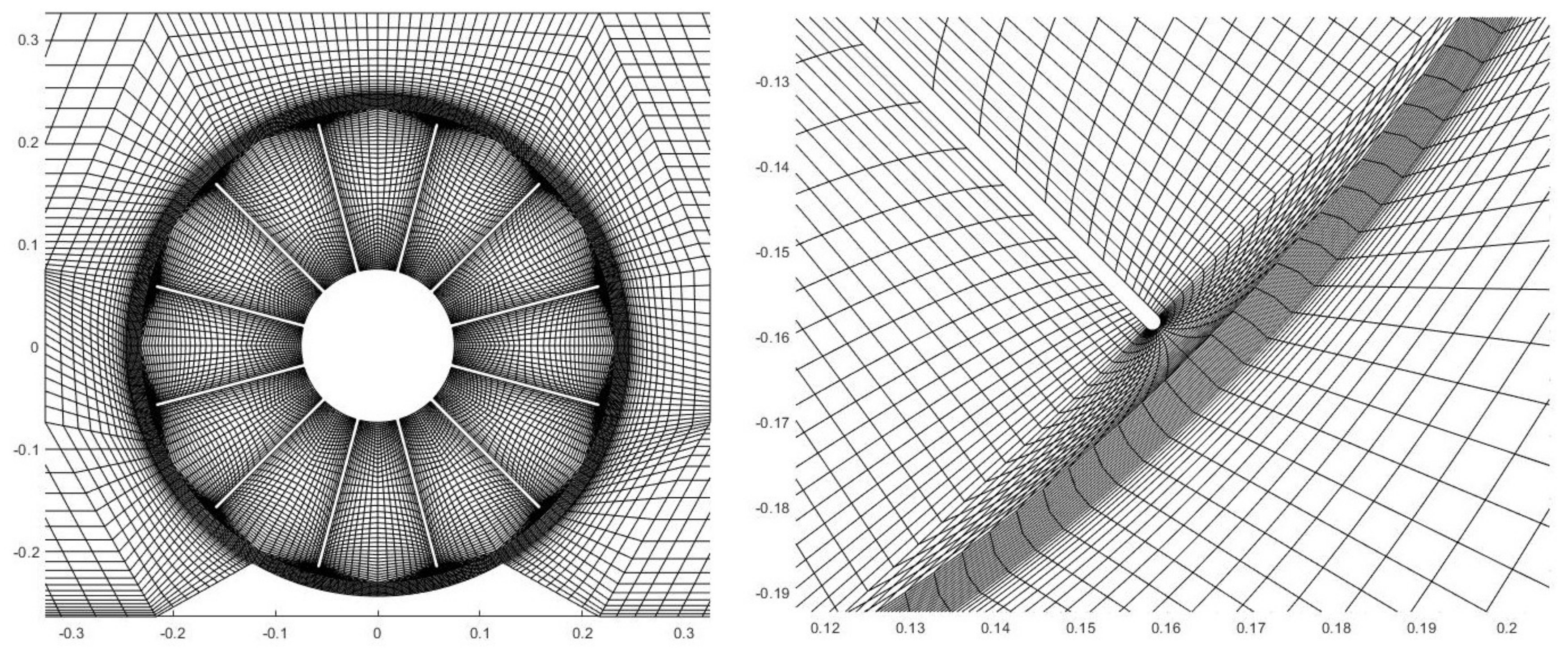
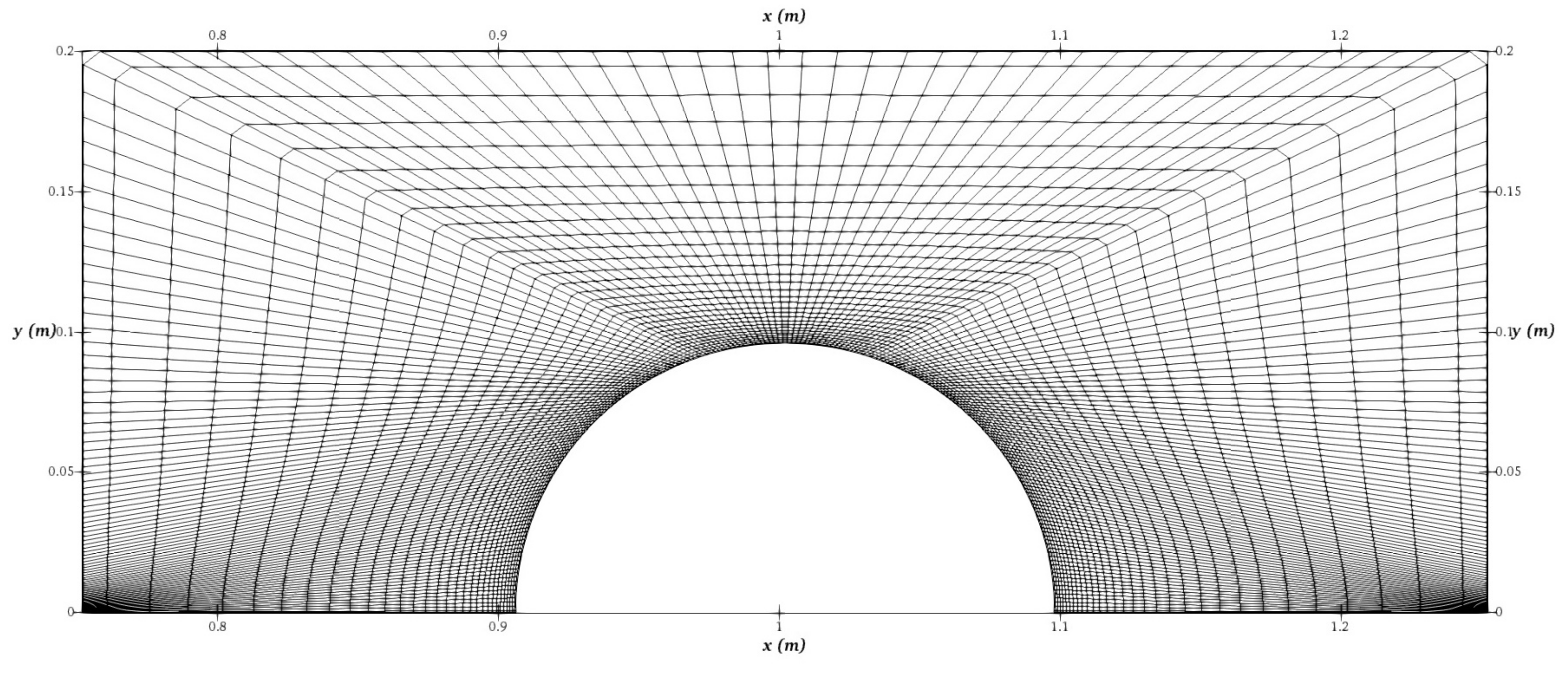
2.3. Model Geometry and Meshing
2.4. Boundary Conditions
2.5. Other Configuration Parameters
2.6. Power Calculation
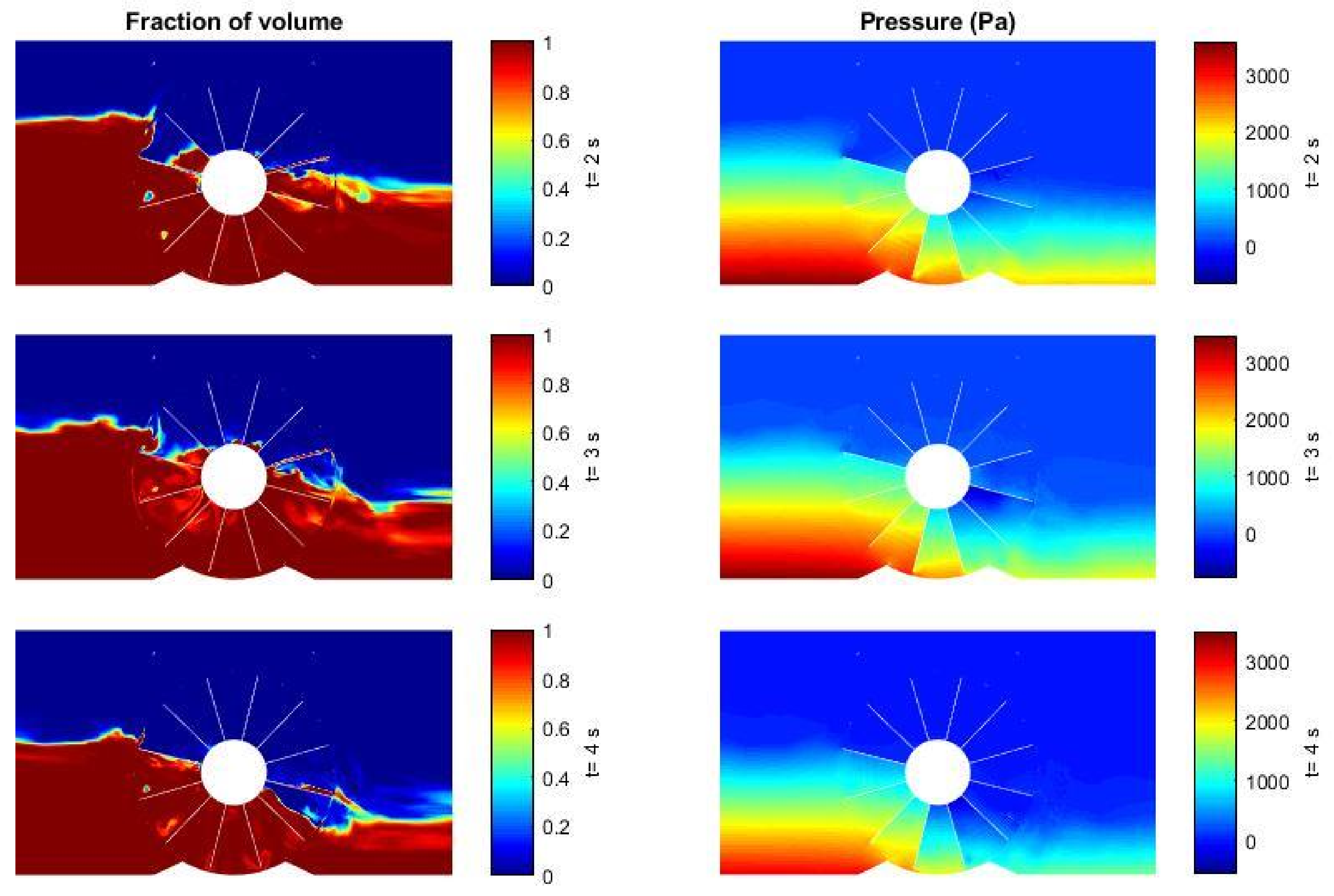
3. Results and Discussion
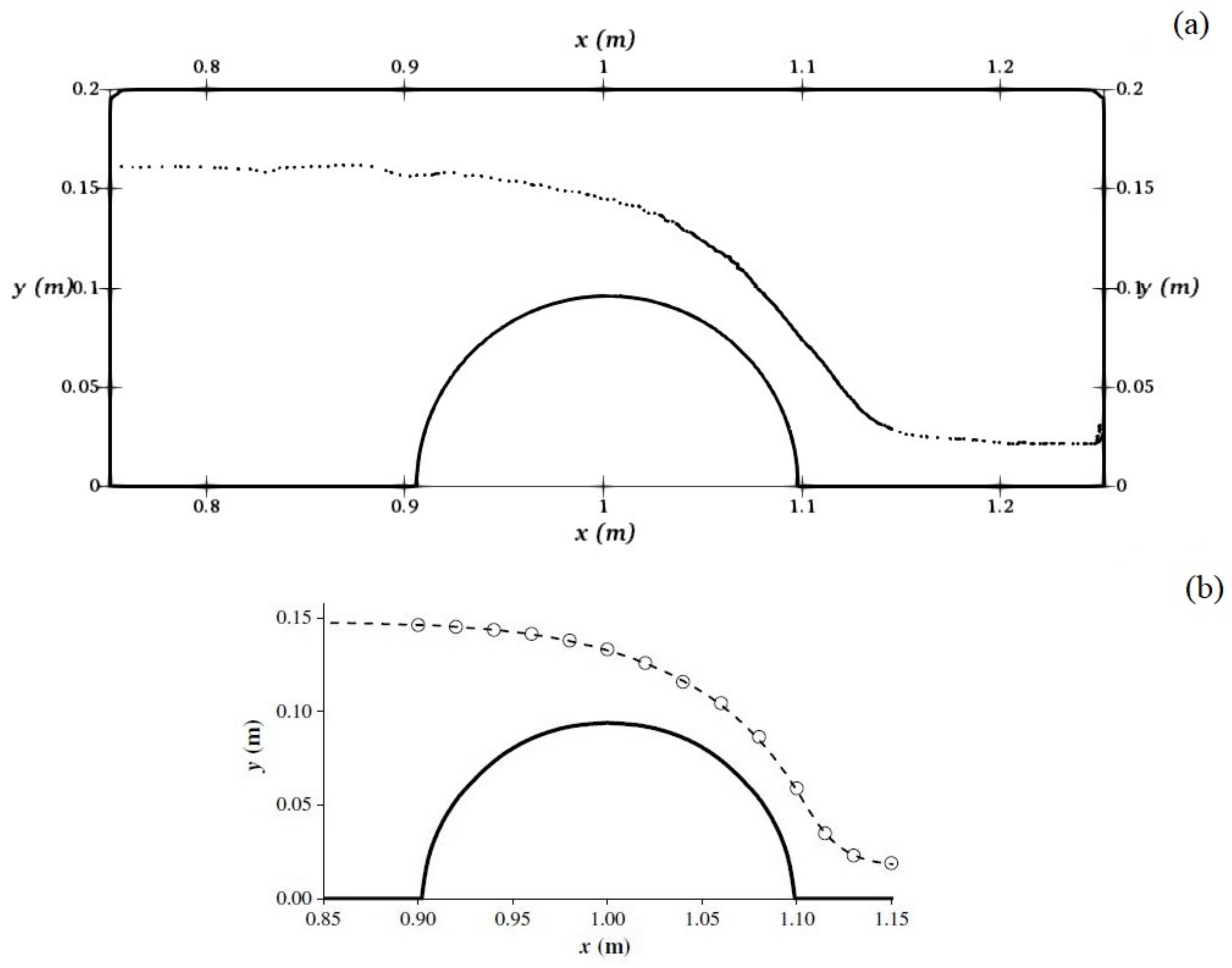
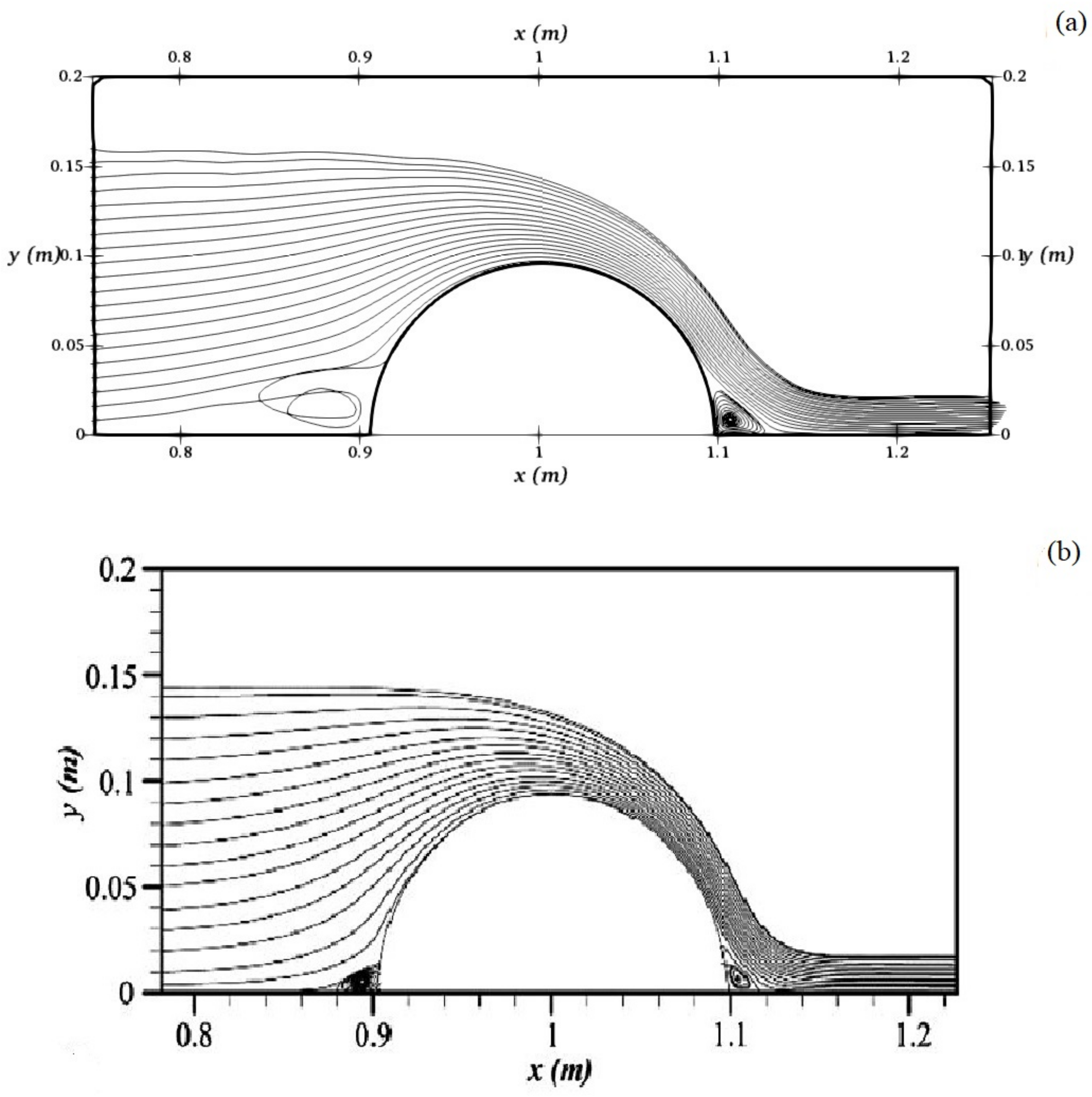
3.1. VOF Assessment
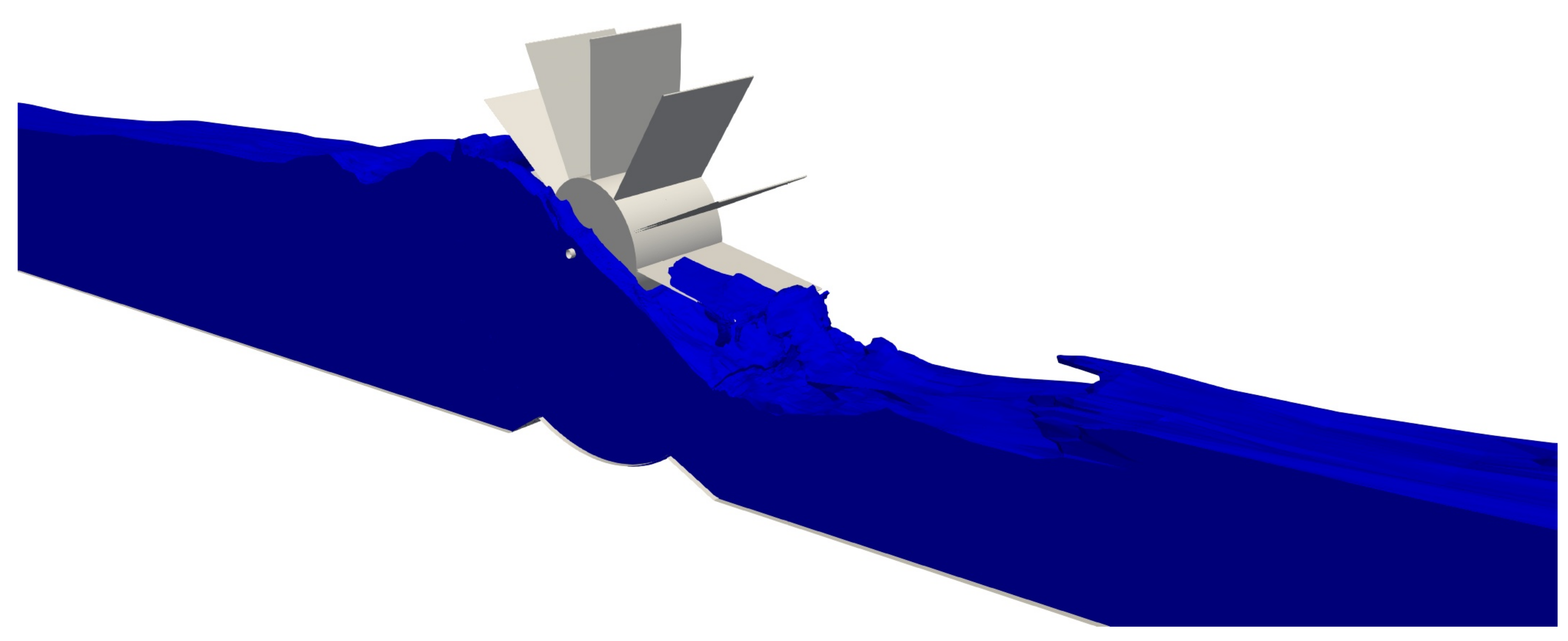
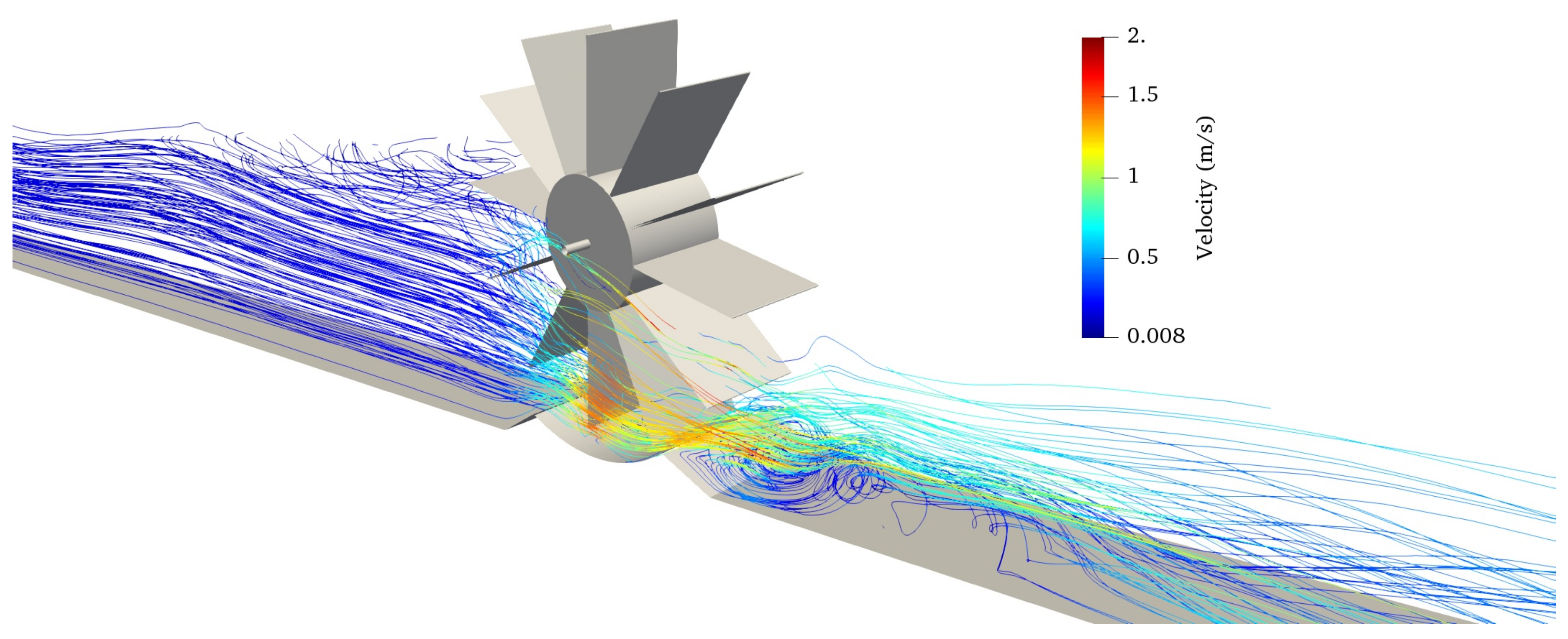
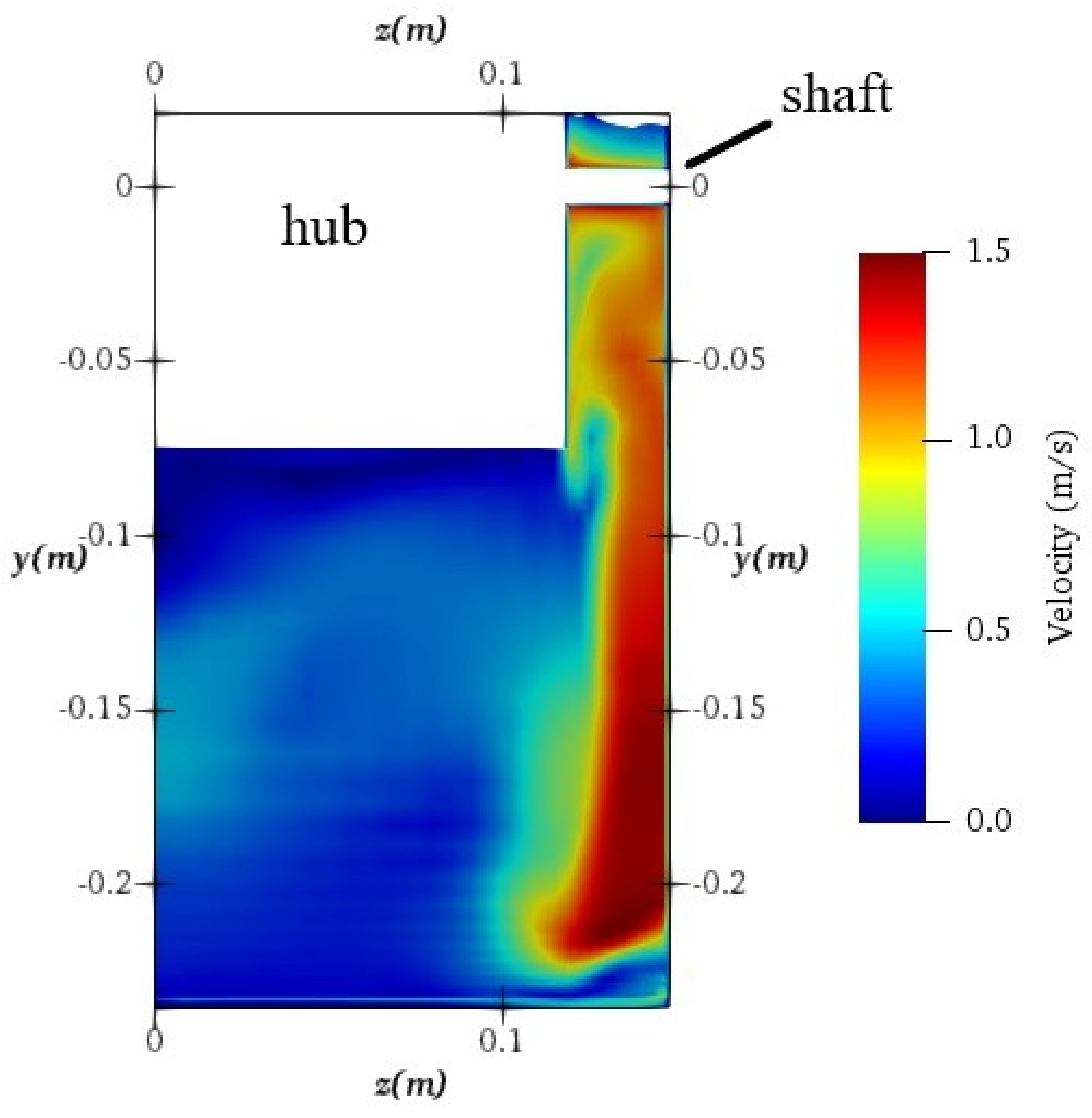
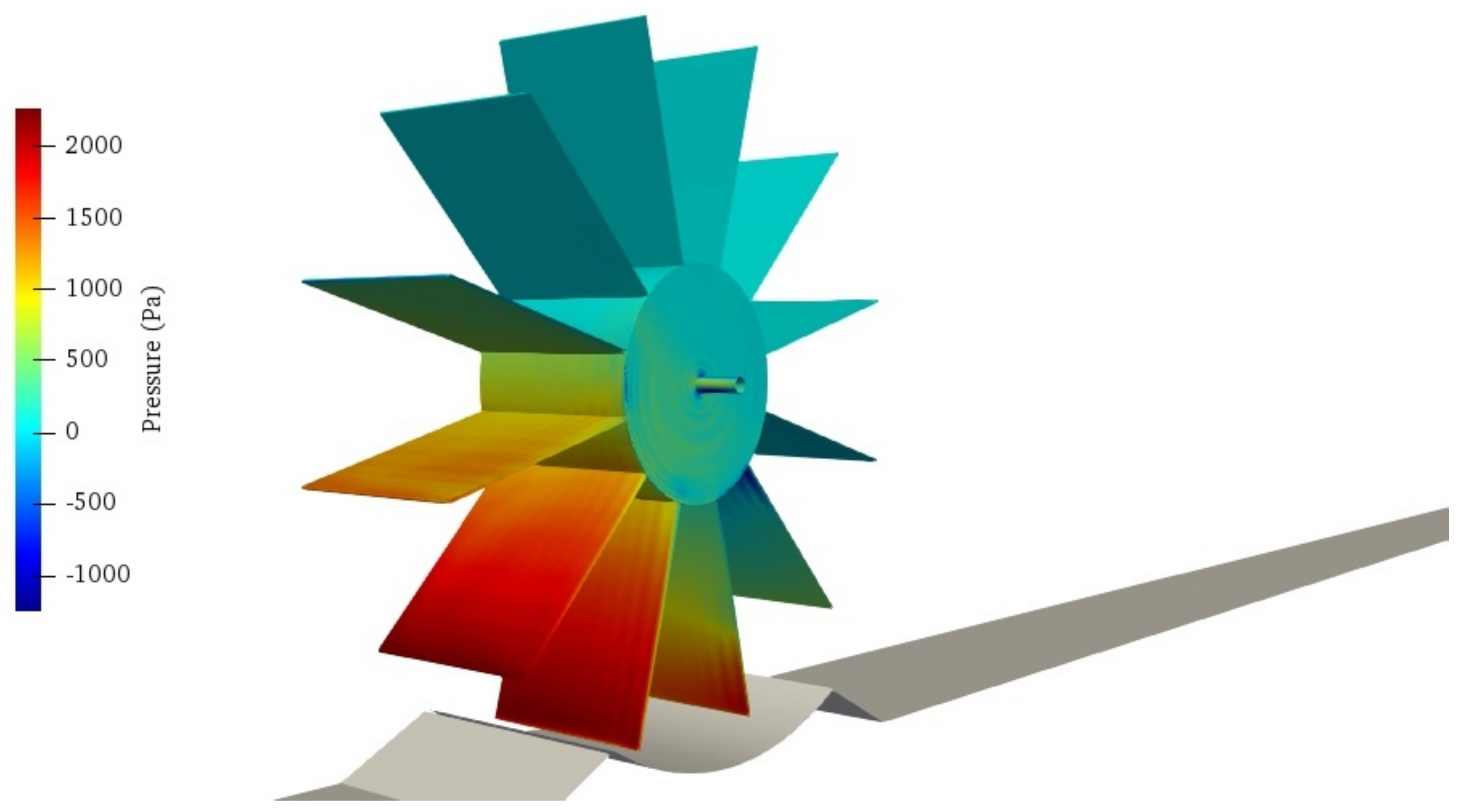
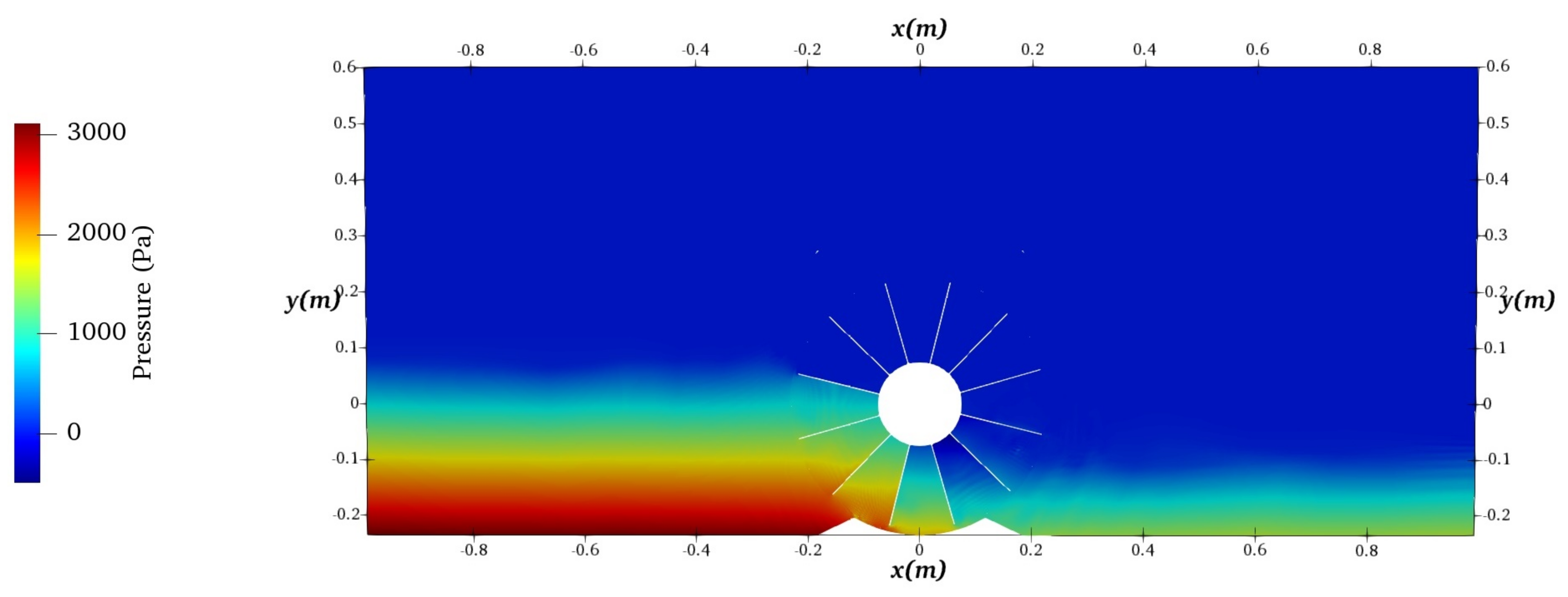
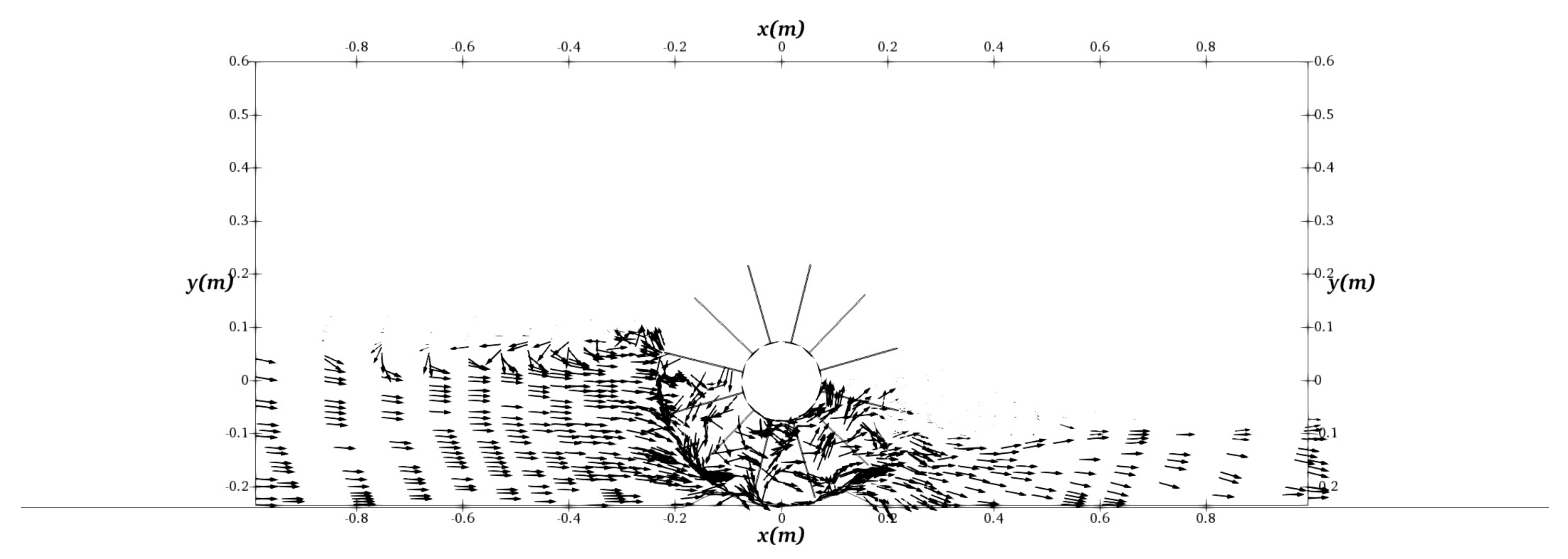
3.2. Simulation of a HPM
4. Conclusions
- to add the vertical wall normal to the flow at the section of the rotation axis, in order to reduce the gap between the wheel and the lateral walls, while maintaining the channel wider than the wheel, in order to enable the filling and emptying process;
- to perform a mesh independence analysis while maintaining low values of ;
- to assess other turbulence techniques and associated models (particularly the model for RANS already implemented in the solver);
- to incorporate the continuous calculation (at each time step) of torque and shaft power into the solver.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paish, O. Small hydro power: technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Elbatran, A.H.; Yaakob, O.B.; Ahmed, Y.M.; Shabara, H.M. Operation, performance and economic analysis of low head micro-hydropower turbines for rural and remote areas: A review. Renew. Sustain. Energy Rev. 2015, 43, 40–50. [Google Scholar] [CrossRef]
- Sari, M.A.; Badruzzaman, M.; Cherchi, C.; Swindle, M.; Ajami, N.; Jacangelo, J.G. Recent innovations and trends in in-conduit hydropower technologies and their applications in water distribution systems. J. Environ. Manag. 2018, 228, 416–428. [Google Scholar] [CrossRef] [PubMed]
- Samora, I.; Hasmatuchi, V.; Münch-Alligné, C.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Experimental characterization of a five blade tubular propeller turbine for pipe installation. Renew. Energy 2016, 95, 356–366. [Google Scholar] [CrossRef]
- Vagnoni, E.; Andolfatto, L.; Richard, S.; Münch-Alligné, C.; Avellan, F. Hydraulic performance evaluation of a micro-turbine with counter rotating runners by experimental investigation and numerical simulation. Renew. Energy 2018, 126, 943–953. [Google Scholar] [CrossRef]
- Senior, J.; Wiemann, P.; Müller, G. The Rotary Hydraulic Pressure Machine for Very Low HEAD Hydropower Sites. Available online: http://www.hylow.eu/knowledge/all-download-documents/ (accessed on 7 August 2020).
- Viollet, P.-L. From the water wheel to turbines and hydroelectricity. Technological evolution and revolutions. Comptes Rendus MéCanique 2017, 345, 570–580. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Performance characteristics, power losses and mechanical power estimation for a brestshot water wheel. Energy 2015, 87, 315–325. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Optimization of breastshot water wheels performance using different inflow configurations. Renew. Energy 2016, 97, 243–251. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Gravity water wheels as a micro hydropower energy source: A review based on historic data, design methods, efficiencies and modern optimizations. Renew. Sustain. Energy Rev. 2018, 97, 414–427. [Google Scholar] [CrossRef]
- Cleynen, O.; Kerikous, E.; Hoerner, S.; Thévenin, D. Characterization of the performance of a free-stream water wheel using computational fluid dynamics. Energy 2018, 165, 1392–1400. [Google Scholar] [CrossRef]
- Zhao, M.; Zheng, Y.; Yang, C.; Zhang, Y.; Tang, Q. Performance Investigation of the Immersed Depth Effects on a Water Wheel Using Experimental and Numerical Analyses. Water 2020, 12, 982. [Google Scholar] [CrossRef]
- Senior, J.; Saenger, N.; Müller, G. New hydropower converters for very low head differences. J. Hydraul. Res. 2010, 48, 703–714. [Google Scholar] [CrossRef]
- Linton, N.P. Trials and Development of a Hydrostatic Pressure Wheel. Ph.D. Thesis, Faculty of Engineering and The Environment, University of Southampton, Southampton, UK, 2013. [Google Scholar]
- Narrain, A.G. Low Head Hydropower for Local Energy Solutions. Ph.D. Thesis, Delft University of Technology and UNESCO-IHE Institute for Water Education, Delft, The Netherlands, 2017. [Google Scholar]
- Licari, M.; Benoit, M.; Anselmet, F.; Kocher, V.; Clément, S.; le Faucheux, P. Study of low-head hydrostatic pressure water wheels for harnessing hydropower on small streams. In Proceedings of the 24 Congrès Français de Mécanique, Brest, France, 26–30 August 2019. [Google Scholar]
- Paudel, S.; Linton, N.; Zanke, U.; Saenger, N. Experimental investigation on the effect on channel width on flexible rubber blade water wheel performance. Renew. Energy 2013, 52, 1–7. [Google Scholar] [CrossRef]
- Butera, I.; Fontan, S.; Poggi, D.; Quaranta, E.; Revelli, R. Experimental Analysis of Effect of channel Geometry and Water Levels on Rotary Hydrostatic Pressure Machine. J. Hydraul. Eng. 2020, 146, 04019071. [Google Scholar] [CrossRef]
- Schneider, S.; Müller, G.; Saenger, N. HYLOW Project Report: Converter Technology Development—HPM and HPC; Internal Task Report 2.3; Not published.
- Usera, G.; Vernet, A.; Ferré, A. A parallel block-structured finite volume method for flows in complex geometry with sliding interfaces. Flow Turbul. Combust 2008, 81, 471–495. [Google Scholar] [CrossRef]
- Ferziger, J.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Usera, G.; Mendina, M. CFD Challenge: Solutions using open source flow solver caffa3d. In MBRi with immersed boundary condition. In Proceedings of the ASME 2012 Summer Bioengineering Conference, Farjardo, Puerto Rico, 20–23 June 2012. [Google Scholar]
- Berg, P.; Roloff, C.; Beuing, O.; Voss, S.; Sugiyama, S.-I.; Aristokleous, N.; Anayiotos, A.S.; Ashton, N.; Revell, A.; Bressloff, N.W.; et al. The Computational Fluid Dynamics Rupture Challenge 2013-Phase II: Variability of Hemodynamics Simulations in Two Intracranial Aneurysms. J. Biomech. Eng. 2015, 137, 121008. [Google Scholar]
- Mühle, F.; Schottler, J.; Bartl, J.; Futrzynski, R.; Evans, S.; Bernini, L.; Schito, P.; Draper, M.; Guggeri, A.; Kleusberg, E.; et al. Blind test comparison on the wake behind a yawed wind turbine. Wind. Energy Sci. 2018, 3, 883–903. [Google Scholar] [CrossRef]
- Mendina, M.; Draper, M.; Kelm-Soares, A.P.; Narancio, G.; Usera, G. A general purpose parallel block structured open source incompressible flow solver. Clust. Comput. 2014, 17, 231–241. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Ketabdari, M.J. Chapter 15:Free Surface Flow Simulation Using VOF Method. In Numerical Simulation—From Brain Imaging to Turbuloent Flows; Lopez-Ruiz, R., Ed.; IntechOpen: London, UK, 2016. [Google Scholar]
- Ubbink, O.; Issa, R.I. A method for computing sharp fluid interfaces on arbitrary meshes. J. Comput. Phys. 1999, 153, 26–50. [Google Scholar] [CrossRef]
- Hogg, P.W.; Gu, X.J.; Emerson, D.R. An implicit algorithm for capturing sharp fluid interfaces in the volume of fluid advection method. In Proceedings of the European Conference on Computational Fluid Dynamics, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Vachaparambil, K.J.; Einarsud, K.E. Comparison of surface tension models for the Volume of Fluid method. J. Eng. Math. 1988, 22, 3–13. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Akoz, M.S.; Gumus, V.; Kirkgoz, M.S. Numerical Simulation of Flow over a Semicylinder Weir. J. Irrig. Drain. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Forbes, L.K. Critical free-surface flow over a semi-circular obstruction. J. Eng. Math. 1988, 22, 3–13. [Google Scholar] [CrossRef]
- Abadie, T.; Aubin, J.; Legendre, D. On the combined effects of surface tension force calculation and interface advection on spurious currents within Volume of Fluid and Level Set frameworks. J. Comput. Phys. 2015, 297, 611–636. [Google Scholar] [CrossRef]
- Jamet, D.; Torres, D.; Brackbill, J.U. On the theory and computation of surface tension: the elimination of parasitic currents through energy conservation in the second-gradient method. J. Comput. Phys. 2002, 182, 262–276. [Google Scholar] [CrossRef]
- Harvie, D.J.E.; Davidson, M.R.; Rudman, M. An analysis of parasitic current generation in Volume of Fluid simulations. Appl. Math. Model. 2006, 30, 1056–1066. [Google Scholar] [CrossRef]
- Pan, Z.; Weibel, J.A.; Garimella, S.V. Spurious Current Suppression in VOF-CSF Simulation of Slug Flow through Small Channels. Processes 2019, 7, 542. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pienika, R.; Usera, G.; Ramos, H.M. Simulation of a Hydrostatic Pressure Machine with Caffa3d Solver: Numerical Model Characterization and Evaluation. Water 2020, 12, 2419. https://doi.org/10.3390/w12092419
Pienika R, Usera G, Ramos HM. Simulation of a Hydrostatic Pressure Machine with Caffa3d Solver: Numerical Model Characterization and Evaluation. Water. 2020; 12(9):2419. https://doi.org/10.3390/w12092419
Chicago/Turabian StylePienika, Rodolfo, Gabriel Usera, and Helena M. Ramos. 2020. "Simulation of a Hydrostatic Pressure Machine with Caffa3d Solver: Numerical Model Characterization and Evaluation" Water 12, no. 9: 2419. https://doi.org/10.3390/w12092419
APA StylePienika, R., Usera, G., & Ramos, H. M. (2020). Simulation of a Hydrostatic Pressure Machine with Caffa3d Solver: Numerical Model Characterization and Evaluation. Water, 12(9), 2419. https://doi.org/10.3390/w12092419





