Application of the Segregation Potential Model to Freezing Soil in a Closed System
Abstract
1. Introduction
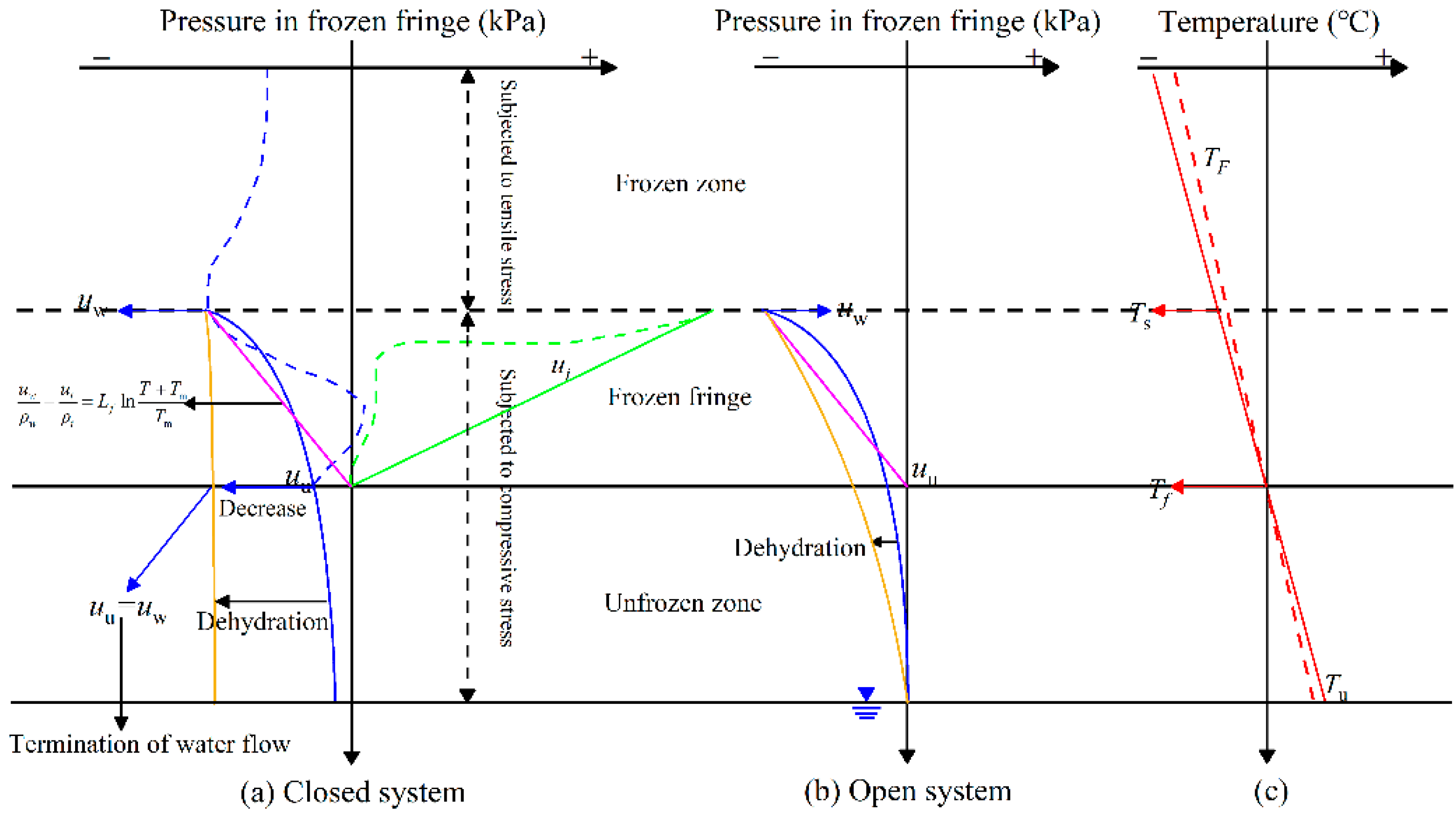
2. The Segregation Potential
3. Frost Heaving Test
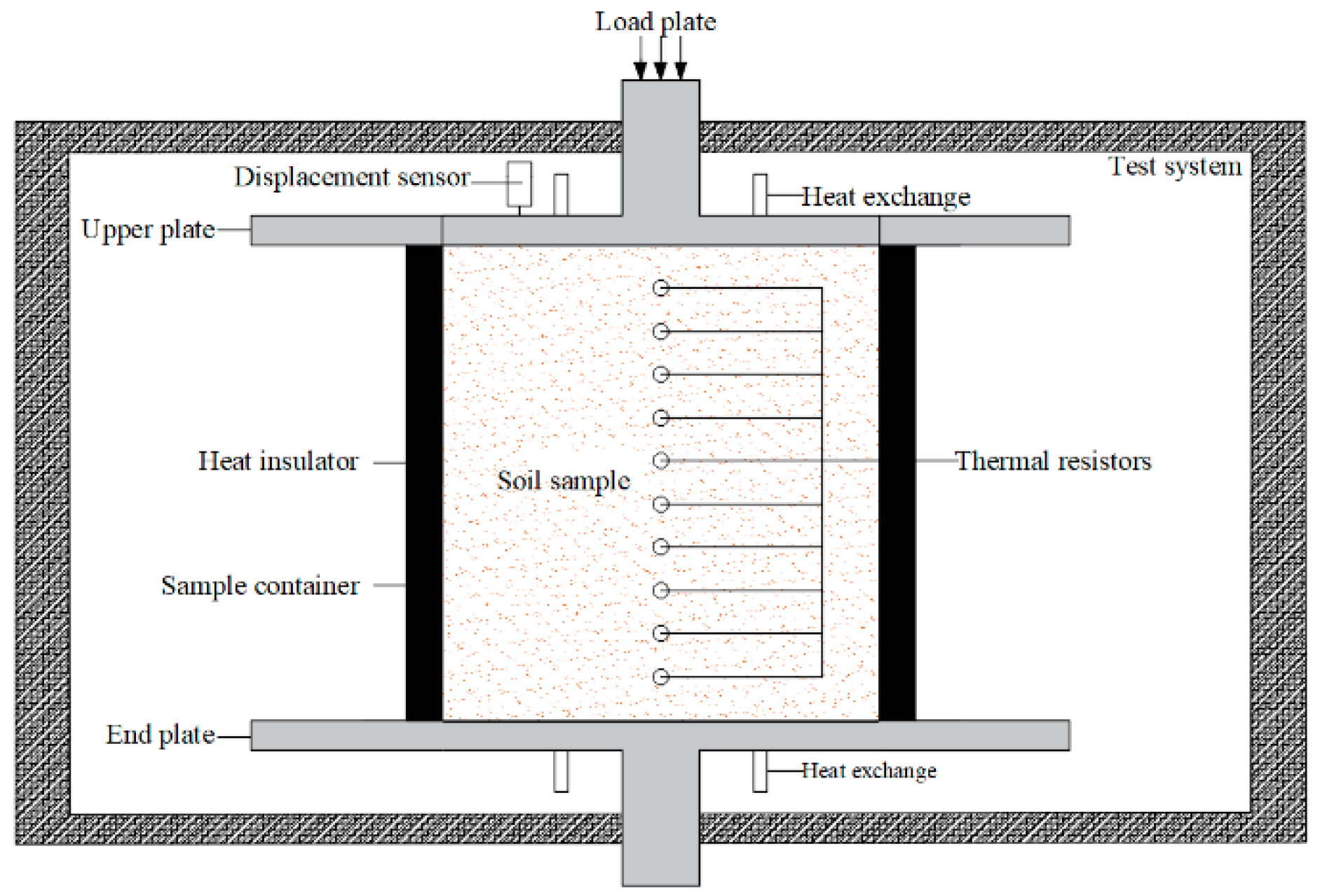
3.1. Material and Method
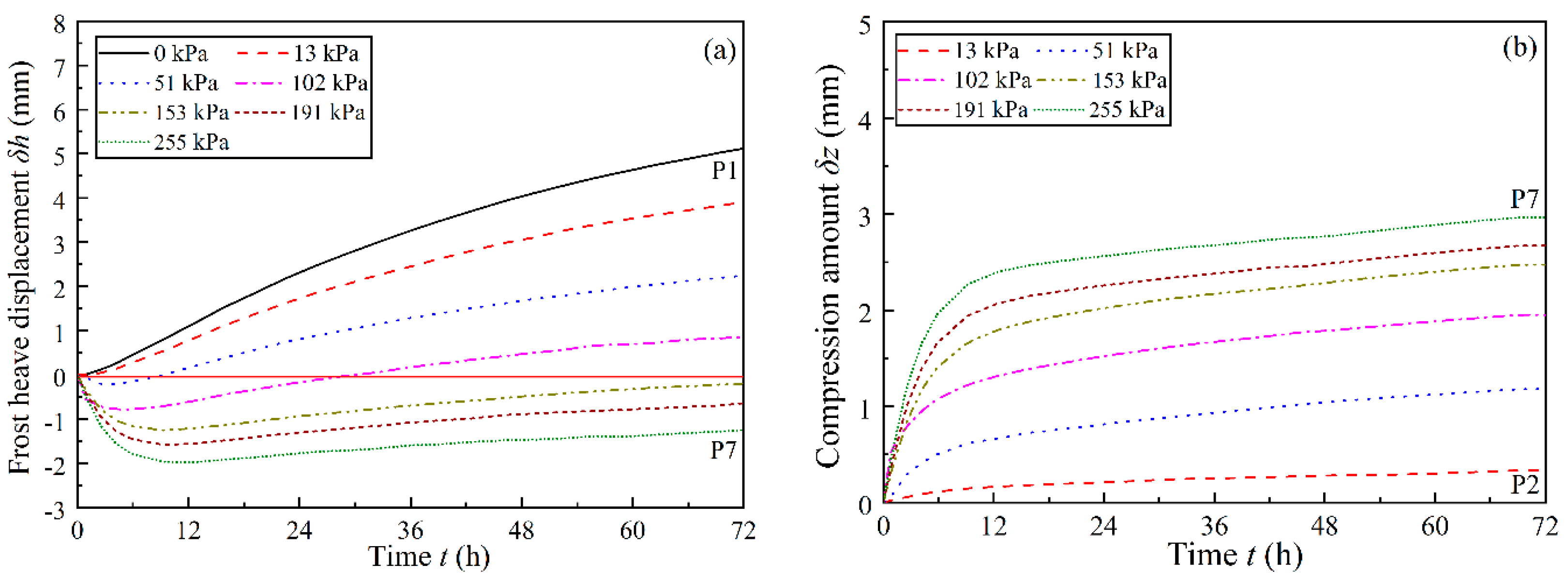
3.2. Test Results
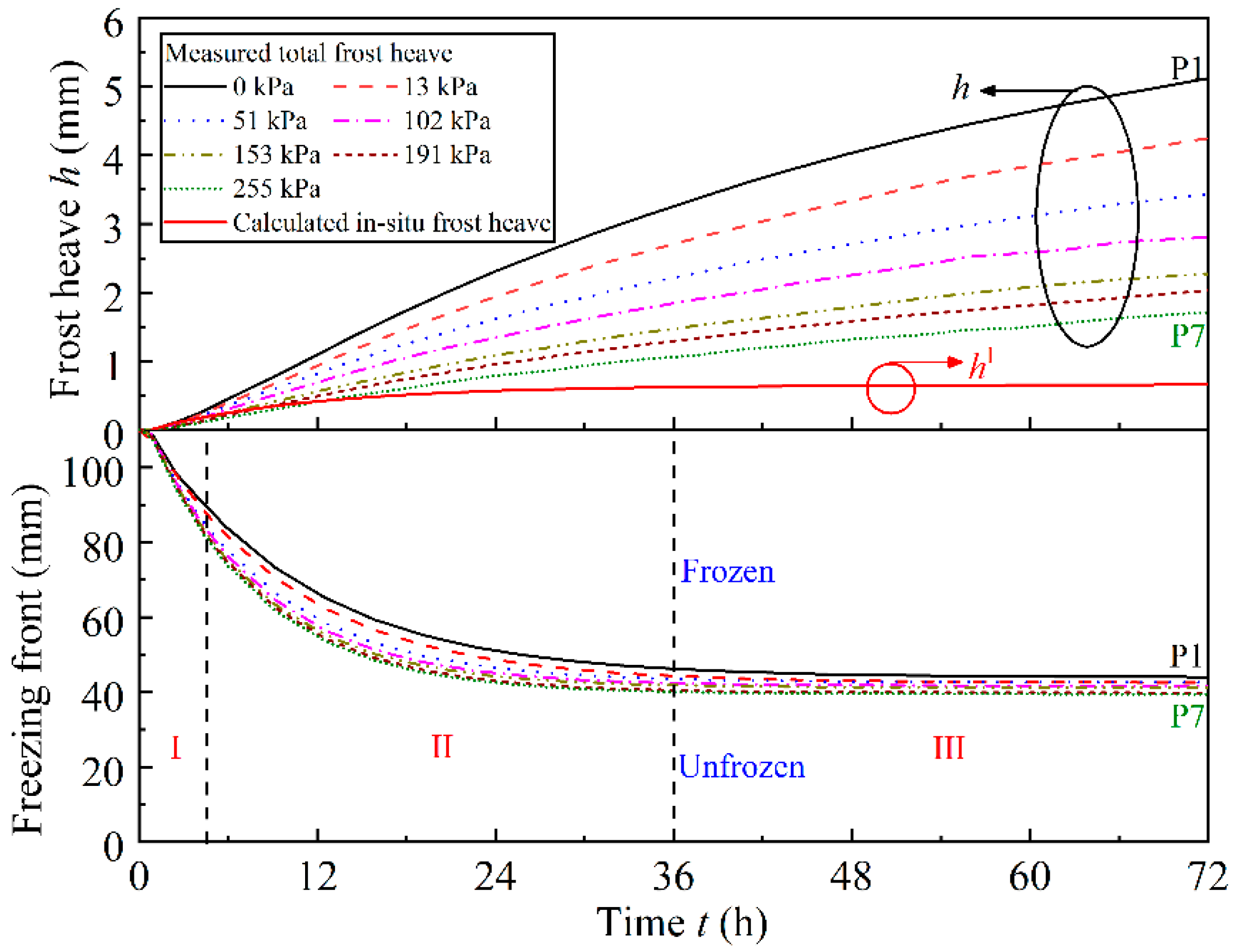
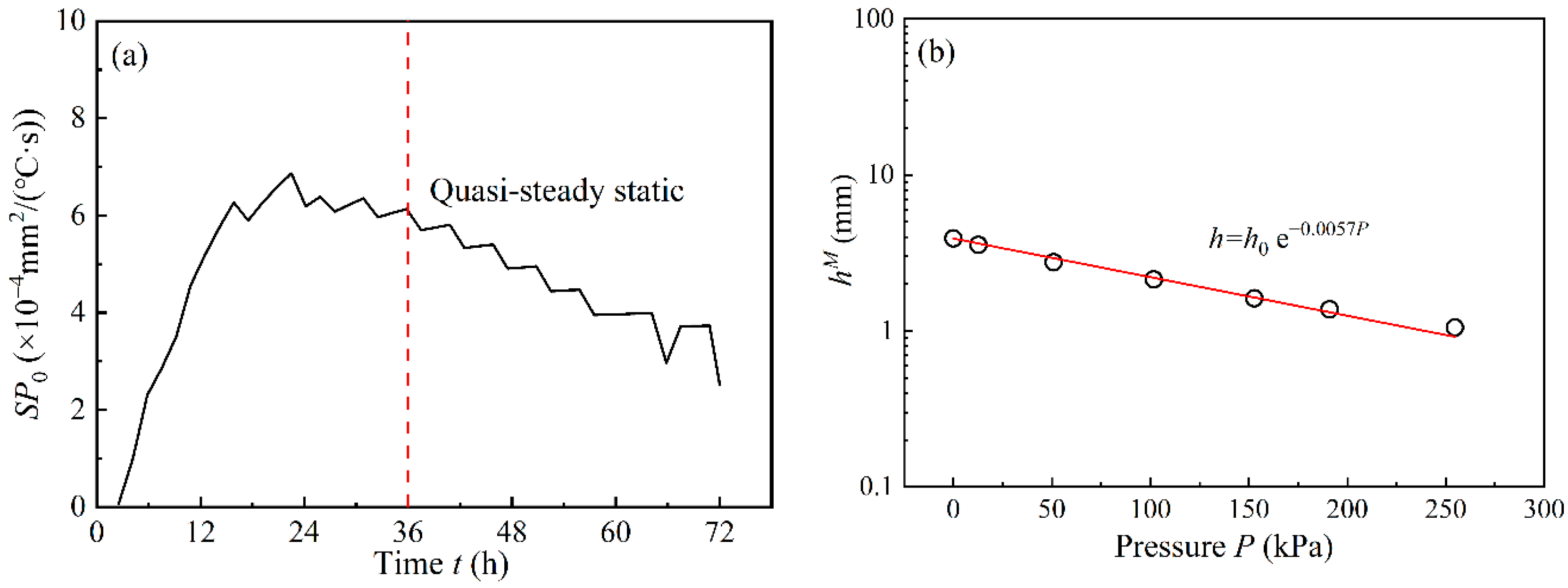
3.3. Calculation of Segregation Potential from the Frost Heaving Test
4. Determination of the Segregation Potential from Numerical Simulation Results
4.1. Simulation Method
4.1.1. Assumption
- (1)
- Darcy’s law is applicable for water migration during the soil freezing processes.
- (2)
- The soil in the study is isotropic and elastic.
4.1.2. Equilibrium Equations
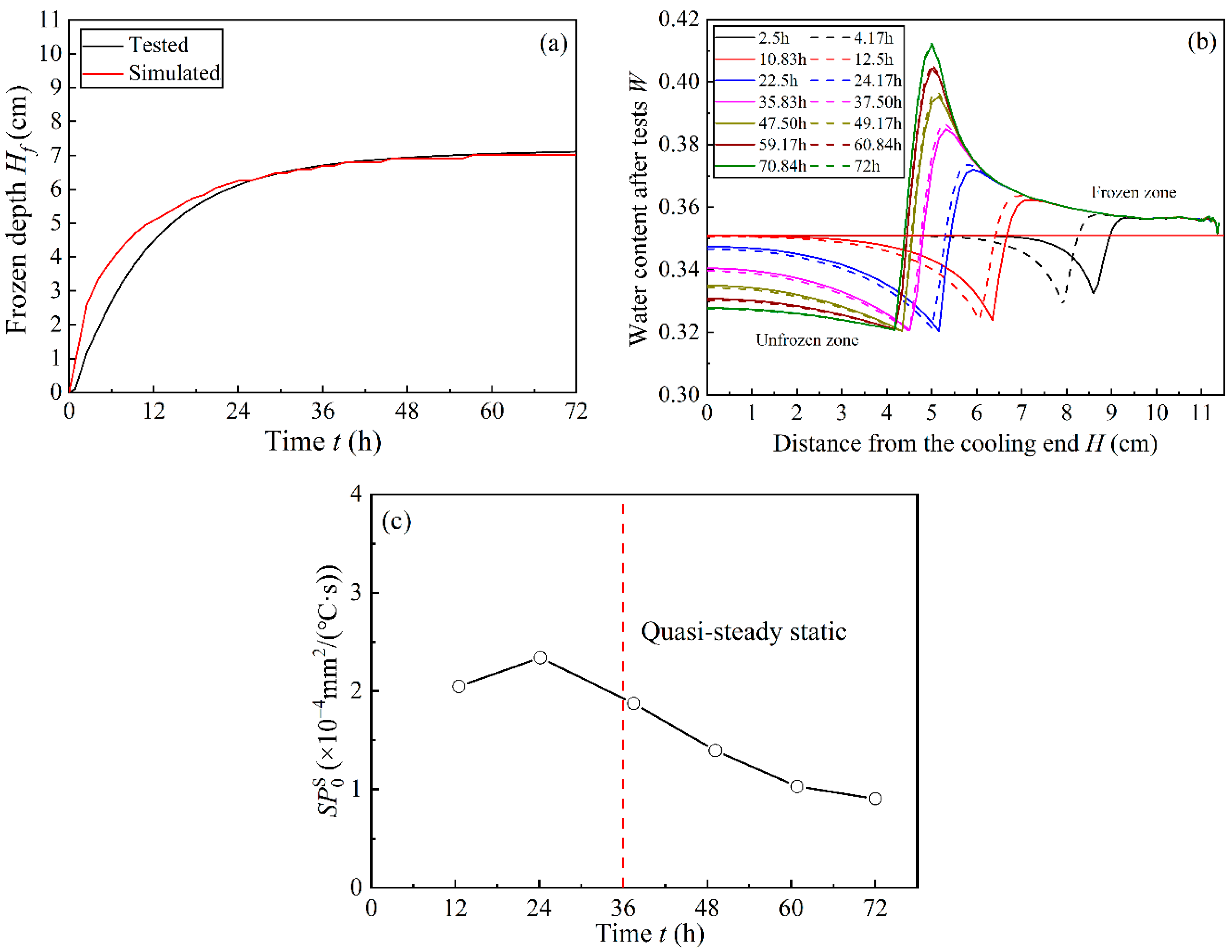
4.2. Simulation Results
5. Approach to Applying the Segregation Potential Model in Closed Systems
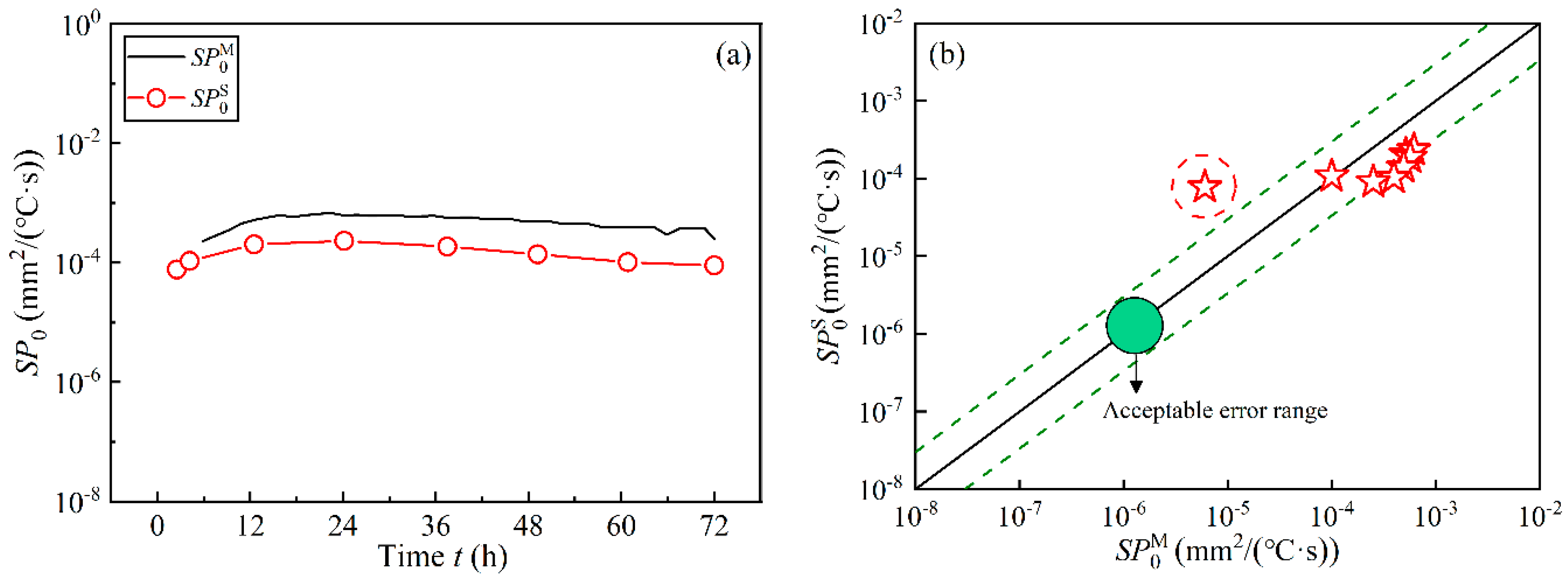
5.1. Comparison of the and
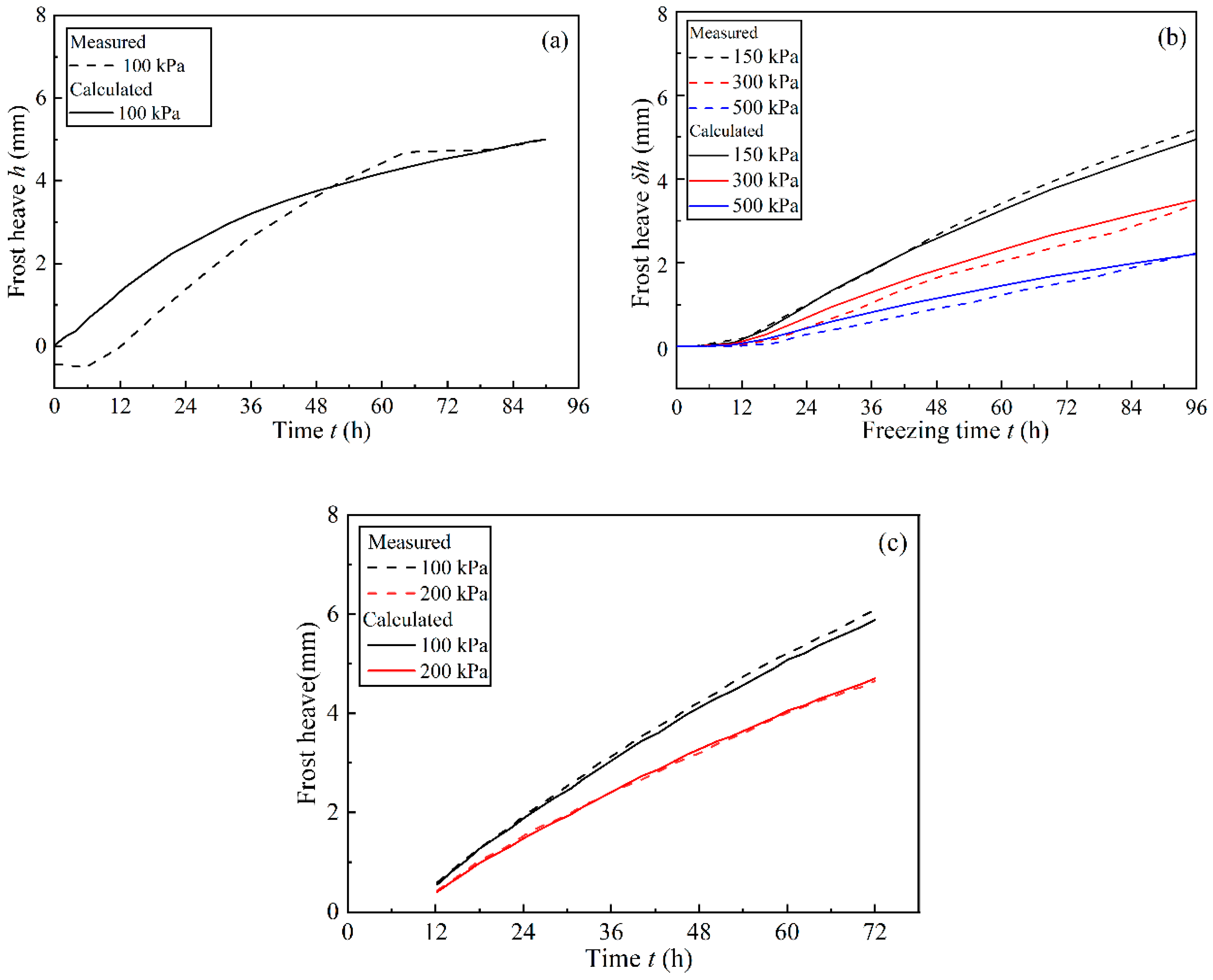
5.2. Applying the Segregation Potential Model in a Closed System
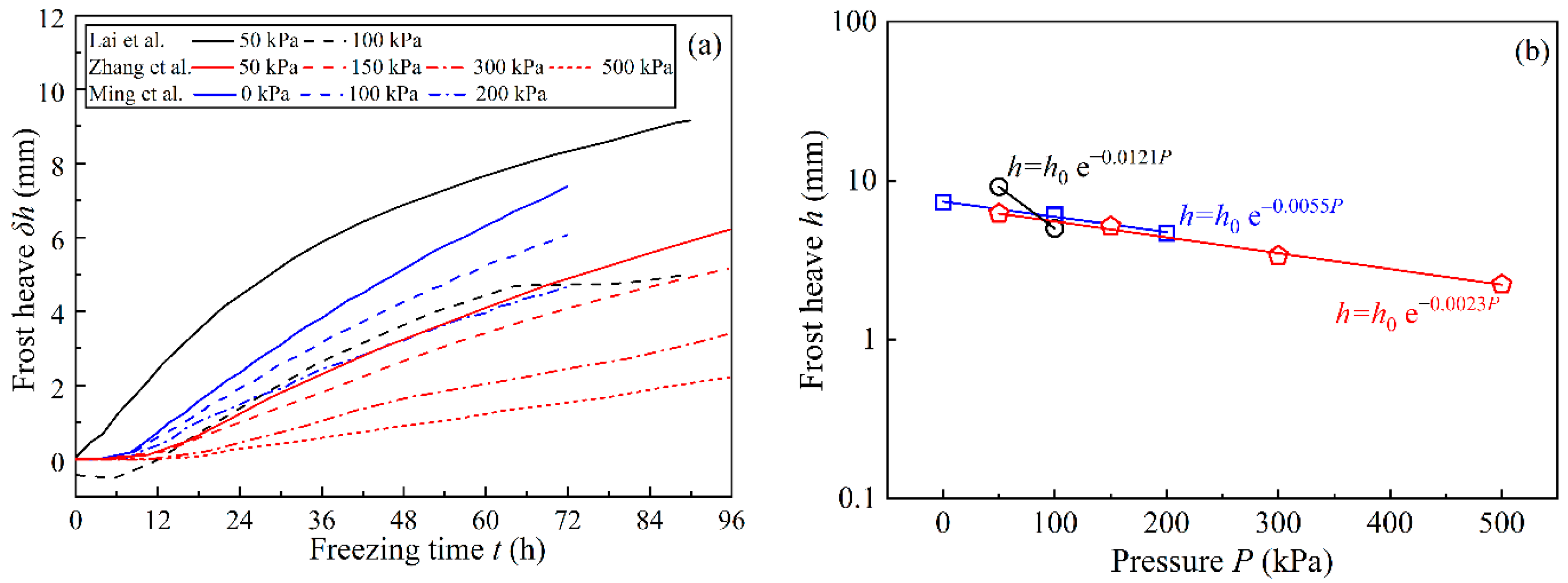
5.3. Further Validation of the Model in a Closed System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kraatz, S.; Jacobs, J.M.; Miller, H.J. Spatial and temporal freeze-thaw variations in Alaskan roads. Cold Reg. Sci. Technol. 2019, 157, 149–162. [Google Scholar] [CrossRef]
- Wu, X.Y.; Niu, F.J.; Lin, Z.J.; Luo, J.; Zheng, H.; Shao, Z.J. Delamination frost heave in embankment of high speed railway in high altitude and seasonal frozen region. Cold Reg. Sci. Technol. 2018, 153, 25–32. [Google Scholar] [CrossRef]
- Wang, Y.P.; Jin, H.J.; Li, G.Y. Investigation of the freeze-thaw states of foundation soils in permafrost areas along the China–Russia Crude Oil Pipeline (CRCOP) route using ground-penetrating radar (GPR). Cold Reg. Sci. Technol. 2016, 126, 10–21. [Google Scholar] [CrossRef]
- Yang, Z.H.; Dutta, U.; Xiong, F.; Biswas, N.; Benz, H. Seasonal frost effects on the dynamic behavior of a twenty-story office building. Cold Reg. Sci. Technol. 2008, 51, 76–84. [Google Scholar] [CrossRef]
- Qin, Z.P.; Lai, Y.M.; Tian, Y.; Yu, F. Frost-heaving mechanical model for concrete face slabs of earthen dams in cold regions. Cold Reg. Sci. Technol. 2019, 161, 91–98. [Google Scholar] [CrossRef]
- Miller, R.D. Lens initiation in secondary heaving. In Proceedings of the International Symposium on Frost Action in Soils, Luleå, Sweden, 16–18 February 1977. [Google Scholar]
- O’Neill, K.; Miller, R.D. Exploration of a rigid ice model of frost heave. Water Resour. Res. 1985, 21, 281–296. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Zhu, M. Frost heave modelling using porosity rate function. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 703–722. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.Y. A model for predicting the hydraulic conductivity of warm saturated frozen soil. Build. Sci. 2020, 179, 106939. [Google Scholar] [CrossRef]
- Edlefsen, N.E.; Anderson, A.B.C. Thermodynamics of soil moisture. Hilgardia 1943, 12, 117–123. [Google Scholar] [CrossRef]
- Miyata, Y.; Akagawa, S. An experimental study of dynamic solid-liquid phase equilibrium in a poroius medium. JSME Int. J. Ser. B 1998, 41, 590–600. [Google Scholar] [CrossRef]
- Bronfenbrener, L.; Bronfenbrener, R. Modeling frost heave in freezing soils. Cold Reg. Sci. Technol. 2010, 61, 43–64. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Li, D.Q. Numerical analysis of coupled water, heat and stress in saturated freezing soil. Cold Reg. Sci. Technol. 2012, 72, 43–49. [Google Scholar] [CrossRef]
- Lai, Y.M.; Pei, W.S.; Zhang, M.Y.; Zhou, J.Z. Study on theory model of hydro-thermal-mechanical interaction process in saturated freezing silty soil. Int. J. Heat Mass Transf. 2014, 78, 805–819. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. The segregation potential of a freezing soil. Can. Geotech. J. 1981, 18, 482–491. [Google Scholar] [CrossRef]
- Nixon, J.F. Field frost heave predictions using the segregation potential concept. Can. Geotech. J. 1982, 19, 526–529. [Google Scholar] [CrossRef]
- Ma, W.; Zhang, L.; Yang, C. Discussion of the applicability of the generalized Clausius–Clapeyron equation and the frozen fringe process. Earth Sci. Rev. 2015, 142, 47–59. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. A mechanistic theory of ice lens formation in fine-grained soils. Can. Geotech. J. 1980, 17, 473–486. [Google Scholar] [CrossRef]
- Konrad, J.M.; Morgenstern, N.R. Frost heave prediction of chilled pipelines buried in unfrozen soils. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1984, 21, 100–115. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Wei, C.F.; Lai, Y.M.; Wei, H.Z.; Tian, H.H. Application of the generalized clapeyron equation to freezing point depression and unfrozen water content. Water Resour. Res. 2018, 54, 9412–9431. [Google Scholar] [CrossRef]
- Campbell, G.S. Soil Physics with Basic: Transport Models for Soil-Plant Systems; Elsevier: Amsterdam, The Netherlands, 1985; Volume 14. [Google Scholar]
- Xu, X.Z.; Wang, J.C.; Zhang, L.X. Frozen Soil Physics Science; Science Press: Beijing, China, 2010. [Google Scholar]
- Sheng, D.C.; Zhang, S.; Yu, Z.W.; Zhang, J.S. Assessing frost susceptibility of soils using PCHeave. Cold Reg. Sci. Technol. 2013, 95, 27–38. [Google Scholar] [CrossRef]
- Ji, Y.K.; Zhou, G.Q.; Zhao, X.D.; Wang, J.Z.; Wang, T.; Lai, Z.J.; Mo, P.Q. On the frost heaving-induced pressure response and its dropping power-law behaviors of freezing soils under various restraints. Cold Reg. Sci. Technol. 2017, 142, 25–33. [Google Scholar] [CrossRef]
- Harlan, R.L. Analysis of coupled heat-fluid transport in partially. Water Resour. Res. 1973, 9, 1314–1323. [Google Scholar] [CrossRef]
- Taylor, G.S.; Luthin, J.N. A model for coupled heat and moisture transfer during soil freezing. Can. Geotech. J. 1978, 15, 548–555. [Google Scholar] [CrossRef]
- Ming, F.; Chen, L.; Li, D.Q.; Wei, X.B. Estimation of hydraulic conductivity of saturated frozen soil from the soil freezing characteristic curve. Sci. Total Environ. 2020, 698, 134132. [Google Scholar] [CrossRef]
- Lebeau, M.; Konrad, J.M. A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, M.Y.; Lu, J.G.; Pei, W.S.; Yan, Z.R. Effect of hydro-thermal behavior on the frost heave of a saturated silty clay under different applied pressures. Appl. Therm. Eng. 2017, 117, 462–467. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, Y.; Li, D.Q. Experimental and theoretical investigations into the formation of ice lenses in deformable porous media. Geosci. J. 2016, 20, 667–679. [Google Scholar] [CrossRef]



| Sand (%) | Silt (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 110 | 100 | 0.351 | 0.228 | 0.351 | 1.43 | −0.18 | 89.8 | 9.92 | 0.28 |
| Test Number | External Pressure | Controlled Temperature (°C) | |
|---|---|---|---|
| Cool End | Warm End | ||
| P1-P7 | 0, 13, 51,102, 153, 191, 255 (kPa) | −2 | 1 |
| P1-P7 | 0, 13, 51,102, 153, 191, 255 (kPa) | 20 | |
| (kPa) | RMSE | Average |
|---|---|---|
| 13 | 0.26 | 0.13 |
| 51 | 0.19 | |
| 102 | 0.02 | |
| 153 | 0.04 | |
| 191 | 0.11 | |
| 255 | 0.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Sheng, Y.; Huang, L.; Huang, X.; He, B. Application of the Segregation Potential Model to Freezing Soil in a Closed System. Water 2020, 12, 2418. https://doi.org/10.3390/w12092418
Zhang X, Sheng Y, Huang L, Huang X, He B. Application of the Segregation Potential Model to Freezing Soil in a Closed System. Water. 2020; 12(9):2418. https://doi.org/10.3390/w12092418
Chicago/Turabian StyleZhang, Xiyan, Yu Sheng, Long Huang, Xubin Huang, and Binbin He. 2020. "Application of the Segregation Potential Model to Freezing Soil in a Closed System" Water 12, no. 9: 2418. https://doi.org/10.3390/w12092418
APA StyleZhang, X., Sheng, Y., Huang, L., Huang, X., & He, B. (2020). Application of the Segregation Potential Model to Freezing Soil in a Closed System. Water, 12(9), 2418. https://doi.org/10.3390/w12092418





