Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study
Abstract
1. Introduction
- To improve the quality of the data and to choose the best model input scenario by applying data pre-processing techniques.
- To select the optimum values of ANN hyperparameters by using the Backtracking Search Algorithm and Artificial Neural Network (BSA-ANN) technique. Moreover, to evaluate how BSA-ANN performs in comparison with a CSA-ANN algorithm.
- To assess the performance of the novel methodology to predict medium-term municipal water demand in relation to some lags time of observed water consumption.
- To reduce the uncertainty for decision makers by using a novel and refined model, which involves data pre-processing methods (to improve the quality of data and select the model input), and employing a more sophisticated approach for model prediction (using combined techniques to enhance the accuracy of results, and the stand-alone ANN to confirm the results of the hybrid model).
2. Study Area and Data Collection
3. Methodology
3.1. Data Pre-processing
3.2. Artificial Neural Network (ANN)
3.3. Backtracking Search Algorithm (BSA)
3.4. Evaluation Model
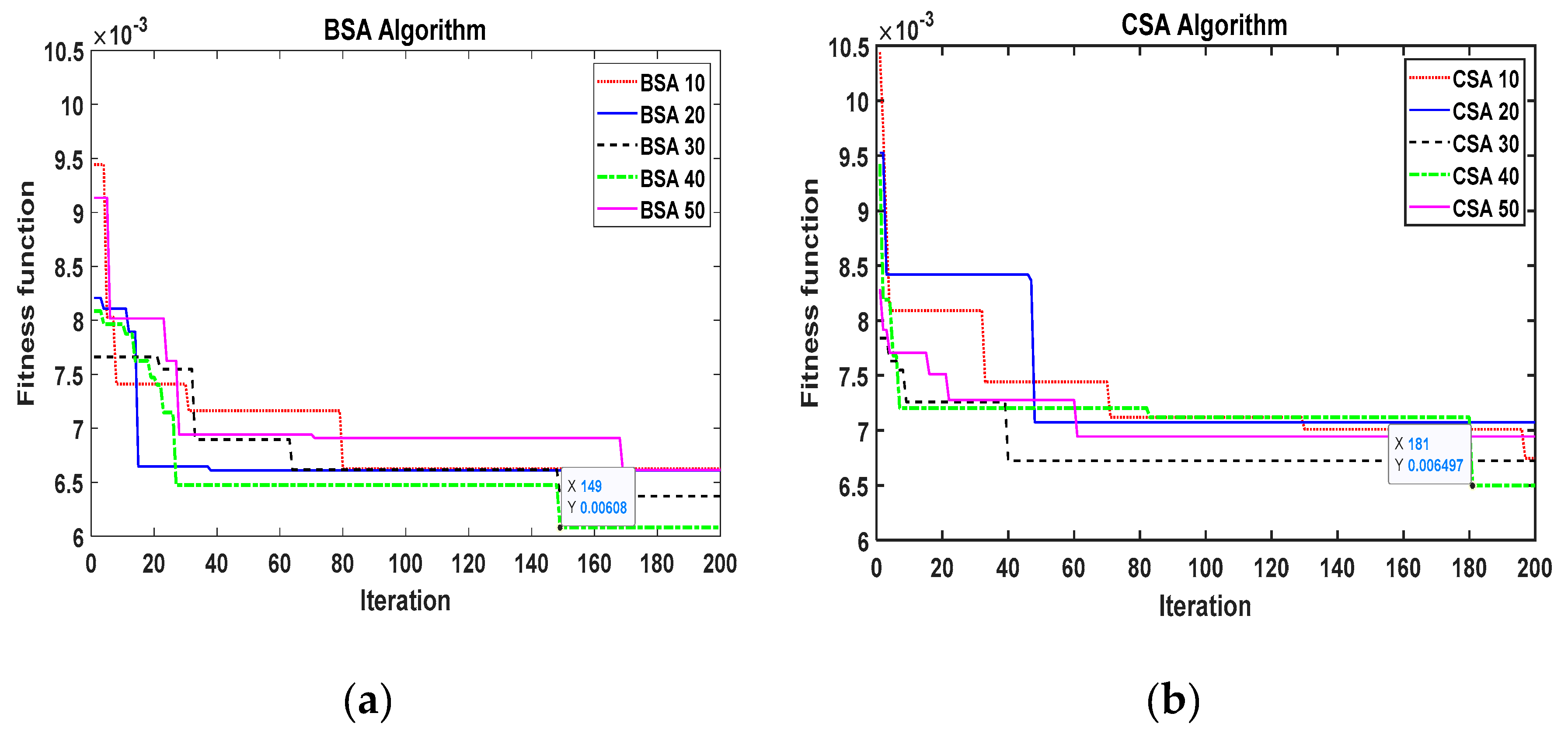
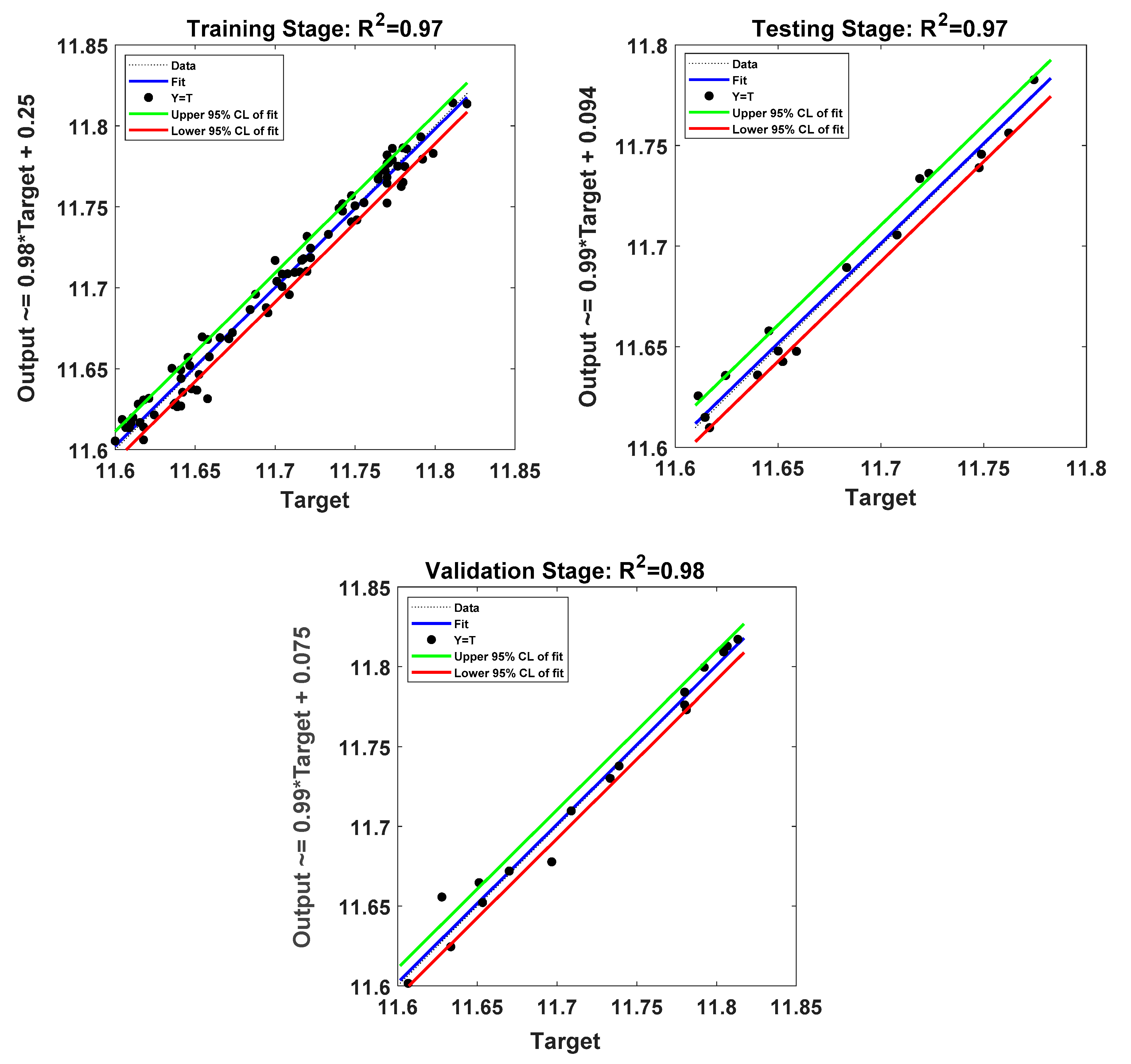
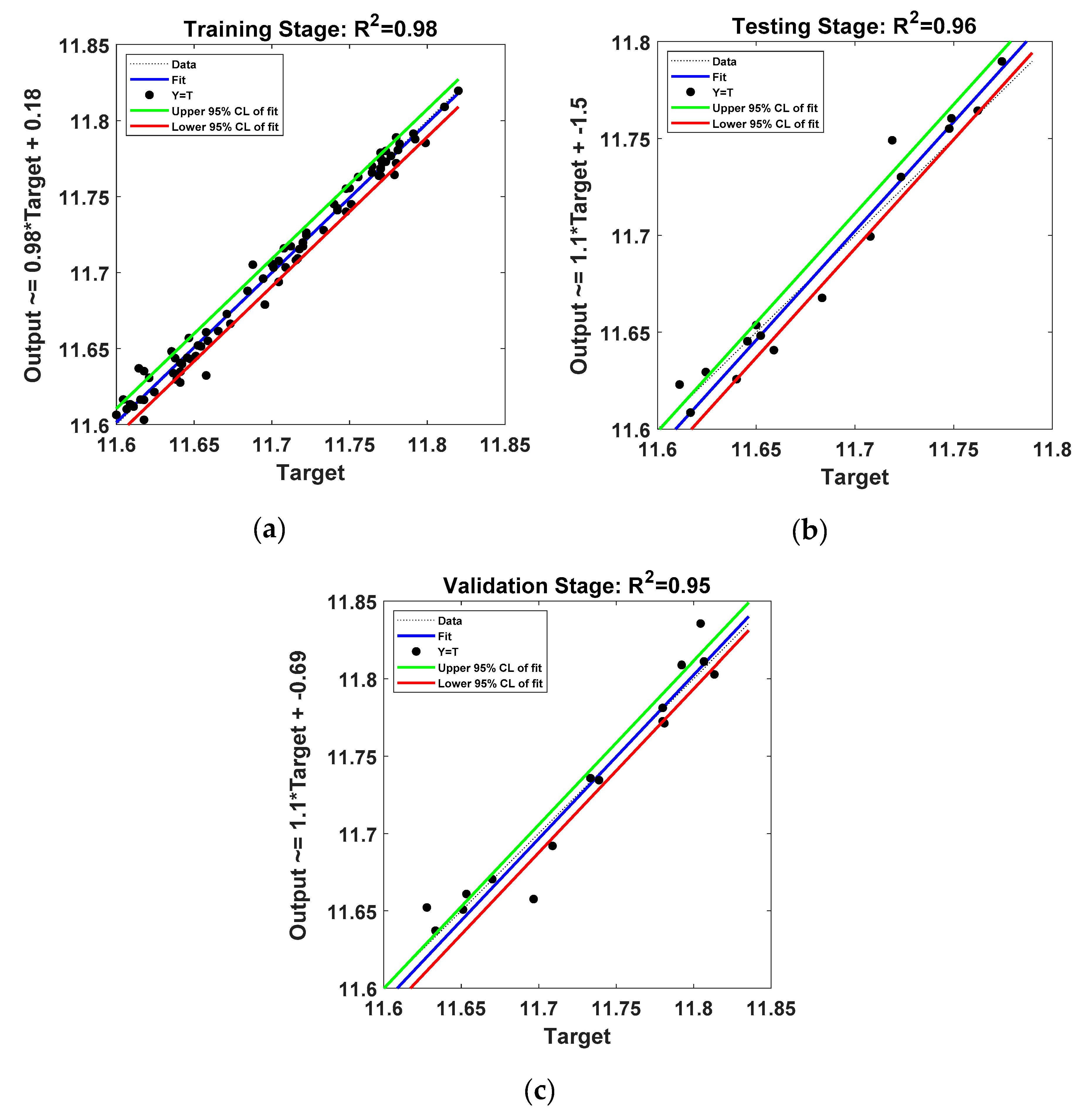
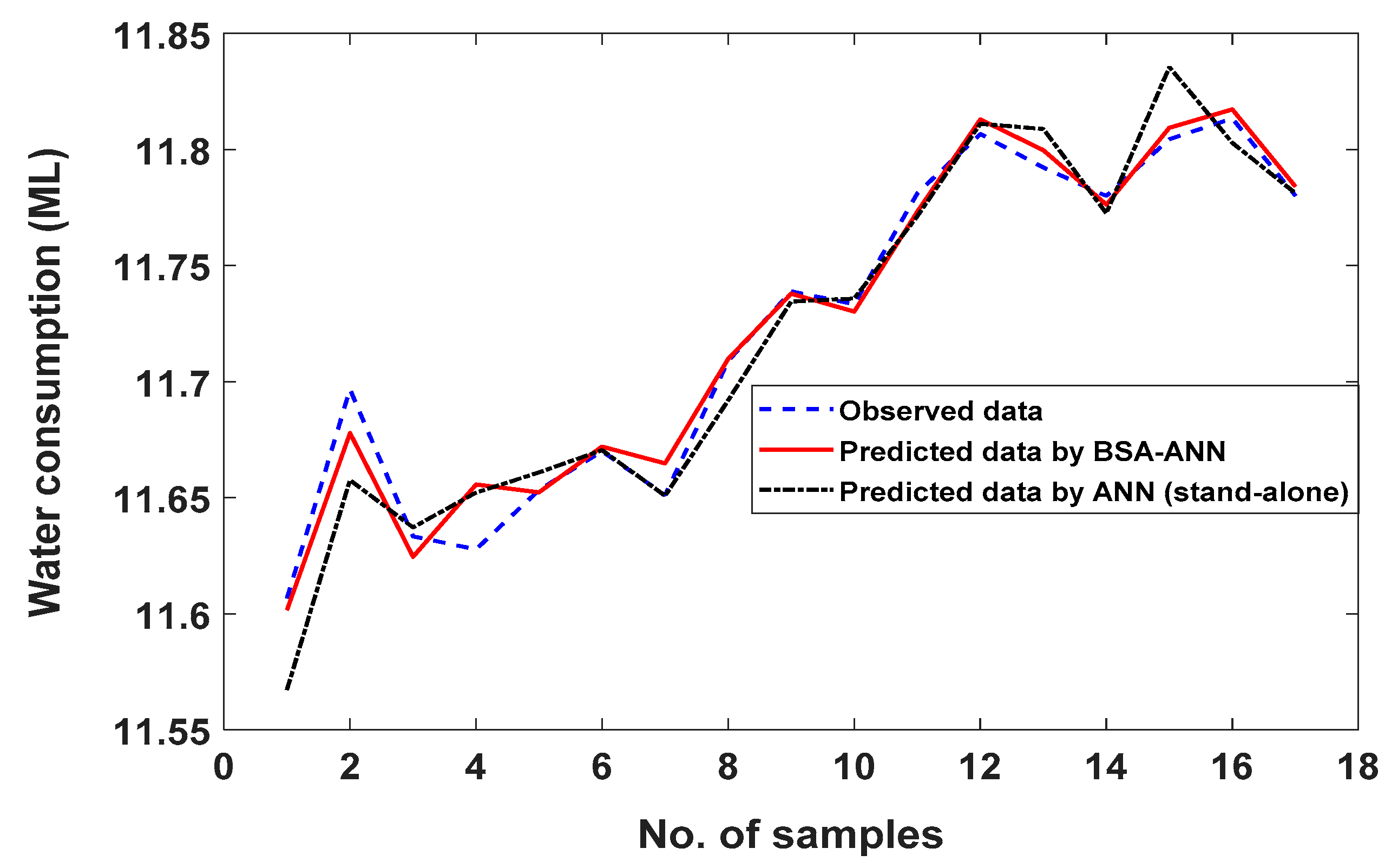
4. Results and Discussion
4.1. Development Model Input
4.2. Application Hybrid Heuristic Algorithms-ANN Techniques
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farhan, S.L.; Abdelmonem, M.G.; Nasar, Z.A. The Urban Transformation of Traditional City Centres: Holy Karbala as a Case Study. Int. J. Arch. Res. ArchNet IJAR 2018, 12, 53–67. [Google Scholar] [CrossRef]
- Ebrahim Banihabib, M.; Mousavi-Mirkalaei, P. Extended linear and non-linear auto-regressive models for forecasting the urban water consumption of a fast-growing city in an arid region. Sustain. Cities Soc. 2019, 48. [Google Scholar] [CrossRef]
- Farhan, S.L.; Hashim, I.A.J.; Naji, A.A. The Sustainable House: Comparative Analysis of Houses in Al Kut Neighborhoods-Iraq. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 1031–1036. [Google Scholar]
- Farhan, S.L.; Jasim, I.A.; Al-Mamoori, S.K. The Transformation of The City of Najaf, Iraq: Analysis, Reality and Future Prospects. J. Urban Regen. Renew. 2019, 13, 1–12. [Google Scholar]
- Zubaidi, S.L.; Kot, P.; Hashim, K.; Alkhaddar, R.; Abdellatif, M.; Muhsin, Y.R. Using LARS–WG model for prediction of temperature in Columbia City, USA. IOP Conf. Ser. Mater. Sci. Eng. 2019, 584, 1–9. [Google Scholar] [CrossRef]
- Osman, Y.Z.; Abdellatif, M.; Al-Ansari, N.; Knutsson, S.; Jawad, S. Climate Change and Future Precipitation in An Arid Environment of The Middle East: Case Study of Iraq. J. Environ. Hydrol. 2017, 25, 1–18. [Google Scholar]
- Zubaidi, S.L.; Al-Bugharbee, H.; Muhsen, Y.R.; Hashim, K.; Alkhaddar, R.M.; Hmeesh, W.H. The Prediction of Municipal Water Demand in Iraq: A Case Study of Baghdad Governorate. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 274–277. [Google Scholar]
- Hashim, K.S.; Al-Saati, N.H.; Alquzweeni, S.S.; Zubaidi, S.L.; Kot, P.; Kraidi, L.; Hussein, A.H.; Alkhaddar, R.; Shaw, A.; Alwash, R. Decolourization of Dye Solutions by Electrocoagulation: An Investigation of The Effect of Operational Parameters. IOP Conf. Ser. Mater. Sci. Eng. 2019, 584, 1–8. [Google Scholar] [CrossRef]
- Hashim, K.S.; Hussein, A.H.; Zubaidi, S.L.; Kot, P.; Kraidi, L.; Alkhaddar, R.; Shaw, A.; Alwash, R. Effect of Initial Ph Value on The Removal of Reactive Black Dye from Water by Electrocoagulation (EC) Method. J. Phys. Conf. Ser. 2019, 1294, 1–6. [Google Scholar] [CrossRef]
- Ashoori, N.; Dzombak, D.A.; Small, M.J. Identifying water price and population criteria for meeting future urban water demand targets. J. Hydrol. 2017, 555, 547–556. [Google Scholar] [CrossRef]
- Toth, E.; Bragalli, C.; Neri, M. Assessing the significance of tourism and climate on residential water demand: Panel-data analysis and non-linear modelling of monthly water consumptions. Environ. Model. Softw. 2018, 103, 52–61. [Google Scholar] [CrossRef]
- Hashim, K.S.; Kot, P.; Zubaidi, S.L.; Alwash, R.; Al Khaddar, R.; Shaw, A.; Al-Jumeily, D.; Aljefery, M.H. Energy Efficient Electrocoagulation Using Baffle-Plates Electrodes for Efficient Escherichia Coli Removal from Wastewater. J. Water Process. Eng. 2020, 33, 1–7. [Google Scholar] [CrossRef]
- Msiza, I.S.; Nelwamondo, F.V.; Marwala, T. Water demand forecasting using multi-layer perceptron and radial basis functions. In Proceedings of the International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007. [Google Scholar]
- Kusangaya, S.; Warburton Toucher, M.L.; van Garderen, E.A. Evaluation of uncertainty in capturing the spatial variability and magnitudes of extreme hydrological events for the uMngeni catchment, South Africa. J. Hydrol. 2018, 557, 931–946. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.H.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Ghalehkhondabi, I.; Ardjmand, E.; Young, W.A., 2nd; Weckman, G.R. Water demand forecasting: Review of soft computing methods. Environ. Monit. Assess. 2017, 189, 313. [Google Scholar] [CrossRef]
- de Souza Groppo, G.; Costa, M.A.; Libânio, M. Predicting water demand: A review of the methods employed and future possibilities. Water Supply 2019. [Google Scholar] [CrossRef]
- Gato, S.; Jayasuriya, N.; Roberts, P. Forecasting residential water demand: Case study. J. Water Resour. Plan. Manag. 2007, 133, 309–319. [Google Scholar] [CrossRef]
- Gato, S.; Jayasuriya, N.; Roberts, P. Temperature and rainfall thresholds for base use urban water demand modelling. J. Hydrol. 2007, 337, 364–376. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel approach for predicting monthly water demand by combining singular spectrum analysis with neural networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- Boyd, G.; Na, D.; Li, Z.; Snowling, S.; Zhang, Q.; Zhou, P. Influent Forecasting for Wastewater Treatment Plants in North America. Sustainability 2019, 11, 1764. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Z.; Snowling, S.; Siam, A.; El-Dakhakhni, W. Predictive models for wastewater flow forecasting based on time series analysis and artificial neural network. Water Sci. Technol. 2019, 80, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Seo, Y.; Kwon, S.; Choi, Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology 2018, 5, 54. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene Expression Programming Coupled with Unsupervised Learning: A Two-Stage Learning Process in Multi-Scale, Short-Term Water Demand Forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef]
- Polomˇcic´, D.; Gligoric´, Z.; Bajic´, D.; Cvijovic´, C.E. A Hybrid Model for Forecasting Groundwater Levels Based on Fuzzy C-Mean Clustering and Singular Spectrum Analysis. Water 2017, 9, 541. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, W.; Zhou, P. Performance of statistical and machine learning ensembles for daily temperature downscaling. Theor. Appl. Clim. 2020, 140, 571–588. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Comparison of different heuristic and decomposition techniques for river stage modeling. Environ. Monit. Assess. 2018, 190, 392. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Hameed, M.; Sharqi, S.S.; Yaseen, Z.M.; Afan, H.A.; Hussain, A.; Elshafie, A. Application of artificial intelligence (AI) techniques in water quality index prediction: A case study in tropical region, Malaysia. Neural Comput. Appl. 2016, 28, 893–905. [Google Scholar] [CrossRef]
- Bayatvarkeshi, M.; Mohammadi, K.; Kisi, O.; Fasihi, R. A new wavelet conjunction approach for estimation of relative humidity: Wavelet principal component analysis combined with ANN. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Mouatadid, S.; Adamowski, J. Using extreme learning machines for short-term urban water demand forecasting. Urban Water J. 2016, 14, 630–638. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-Term Water Demand Forecast Based on Deep Learning Method. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M.; Ali, J.A. Accurate wireless sensor localization technique based on hybrid pso-ann algorithm for indoor and outdoor track cycling. IEEE Sens. J. 2016, 16, 529–541. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M. A Wireless Sensor Network with Soft Computing Localization Techniques for Track Cycling Applications. Sensors 2016, 16, 1043. [Google Scholar] [CrossRef] [PubMed]
- Zubaidi, S.L.; Ortega-Martorell, S.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Gharghan, S.K.; Ahmed, M.S.; Hashim, K. A Method for Predicting Long-Term Municipal Water Demands Under Climate Change. Water Resour. Manag. 2020, 34, 1265–1279. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Nigussie, T.A. Monthly water demand prediction using wavelet transform, first-order differencing and linear detrending techniques based on multilayer perceptron models. Urban Water J. 2018, 15, 177–181. [Google Scholar] [CrossRef]
- Pacchin, E.; Gagliardi, F.; Alvisi, S.; Franchini, M. A Comparison of Short-Term Water Demand Forecasting Models. Water Resour. Manag. 2019, 33, 1481–1497. [Google Scholar] [CrossRef]
- Rasifaghihi, N.; Li, S.S.; Haghighat, F. Forecast of urban water consumption under the impact of climate change. Sustain. Cities Soc. 2020, 52. [Google Scholar] [CrossRef]
- Eggimann, S.; Mutzner, L.; Wani, O.; Schneider, M.Y.; Spuhler, D.; Moy de Vitry, M.; Beutler, P.; Maurer, M. The Potential of Knowing More: A Review of Data-Driven Urban Water Management. Environ. Sci. Technol. 2017, 51, 2538–2553. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lu, W. Monthly Rainfall Forecasting Using Echo State Networks Coupled with Data Preprocessing Methods. Water Resour. Manag. 2017, 32, 659–674. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Shi, X.; Hong, Y. Wavelet-Nonlinear Cointegration Prediction of Irrigation Water in the Irrigation District. Water Resour. Manag. 2019, 33, 2941–2954. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Ali, J.A. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Díaz, P.; Pérez-Cisneros, M.; Cuevas, E.; Avalos, O.; Gálvez, J.; Hinojosa, S.; Zaldivar, D. An Improved Crow Search Algorithm Applied to Energy Problems. Energies 2018, 11, 571. [Google Scholar] [CrossRef]
- Abou El Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Shalaby, A.S. Application of the Crow Search Algorithm for Economic Environmental Dispatch. In Proceedings of the Nineteenth International Middle East Power Systems Conference (MEPCON), Menoufia University, Nasr City, Egypt, 19–21 December 2017; pp. 78–83. [Google Scholar]
- Abdelaziz, A.Y.; Fathy, A. A novel approach based on crow search algorithm for optimal selection of conductor size in radial distribution networks. Eng. Sci. Technol. Int. J. 2017, 20, 391–402. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Al-Bugharbee, H.; Ortega-Martorell, S.; Gharghan, S.K.; Olier, I.; Hashim, K.S.; Al-Bdairi, N.S.S.; Kot, P. A Novel Methodology for Prediction Urban Water Demand by Wavelet Denoising and Adaptive Neuro Fuzzy Inference System Approach. Water 2020, 12, 1628. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Zhou, P.; Li, Z.; Snowling, S.; Baetz, B.W.; Na, D.; Boyd, G. A random forest model for inflow prediction at wastewater treatment plants. Stoch. Environ. Res. Risk Assess. 2019, 33, 1781–1792. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid Hydrological Data-Driven Approach for Daily Streamflow Forecasting. J. Hydrol. Eng. 2020, 25. [Google Scholar] [CrossRef]
- Gedefaw, M.; Hao, W.; Denghua, Y.; Girma, A.; Khamis, M.I. Variable selection methods for water demand forecasting in Ethiopia: Case study Gondar town. Cogent Environ. Sci. 2018, 4. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, J.; Leng, G.; Yang, Y.; Gao, Q.; Fan, Y.; Luo, J. The Potential Utility of Satellite Soil Moisture Retrievals for Detecting Irrigation Patterns in China. Water 2018, 10, 1505. [Google Scholar] [CrossRef]
- Kim, K.; Joo, H.; Han, D.; Kim, S.; Lee, T.; Kim, H.S. On Complex Network Construction of Rain Gauge Stations Considering Nonlinearity of Observed Daily Rainfall Data. Water 2019, 11, 1578. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A Probabilistic Short-Term Water Demand Forecasting Model Based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Pacchin, E.; Alvisi, S.; Franchini, M. A Short-Term Water Demand Forecasting Model Using a Moving Window on Previously Observed Data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- Bata, M.T.H.; Carriveau, R.; Ting, D.S.K. Short-Term Water Demand Forecasting Using Nonlinear Autoregressive Artificial Neural Networks. J. Water Resour. Plan. Manag. 2020, 146. [Google Scholar] [CrossRef]
- RW. Rand Water’s Integrated Annual Report; RW: Johannesburg, South Africa, 2013; p. 236. [Google Scholar]
- Muringathuparambil, R.J.; Musango, J.K.; Brent, A.C.; Currie, P. Developing building typologies to examine energy efficiency in representative low cost buildings in Cape Town townships. Sustain. Cities Soc. 2017, 33, 1–17. [Google Scholar] [CrossRef]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Pearson Education, Inc.: London, UK, 2013. [Google Scholar]
- Al-Bugharbee, H.; Trendafilova, I. A Fault Diagnosis Methodology for Rolling Element Bearings Based on Advanced Signal Pretreatment And Autoregressive Modelling. J. Sound Vib. 2016, 369, 246–265. [Google Scholar] [CrossRef]
- Hassani, H.; Webster, A.; Silva, E.S.; Heravi, S. Forecasting U.S. Tourist arrivals using optimal Singular Spectrum Analysis. Tour. Manag. 2015, 46, 322–335. [Google Scholar] [CrossRef]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Khan, M.A.R.; Poskitt, D.S. Forecasting stochastic processes using singular spectrum analysis: Aspects of the theory and application. Int. J. Forecast. 2017, 33, 199–213. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Kot, P.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H. Short-Term Water Demand Prediction in Residential Complexes: Case Study in Columbia City, USA. In Proceedings of the 2018 11th International Conference on Developments in eSystems Engineering (DeSE), Cambridge, UK, 2–5 September 2018; pp. 31–35. [Google Scholar]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef]
- Nguyen-ky, T.; Mushtaq, S.; Loch, A.; Reardon-Smith, K.; An-Vo, D.-A.; Ngo-Cong, D.; Tran-Cong, T. Predicting water allocation trade prices using a hybrid Artificial Neural Network-Bayesian modelling approach. J. Hydrol. 2018, 567, 781–791. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Yonaba, H.; Anctil, F.; Fortin, V. Comparing Sigmoid Transfer Functions for Neural Network Multistep Ahead Streamflow Forecasting. J. Hydrol. Eng. 2010, 15, 275–283. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E.; Gunen, M.A.; Atasever, U.H. Weighted differential evolution algorithm for numerical function optimization: A comparative study with cuckoo search, artificial bee colony, adaptive differential evolution, and backtracking search optimization algorithms. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Z.; Sun, Y.; Su, Q.; Xia, X. A novel modified BSA inspired by species evolution rule and simulated annealing principle for constrained engineering optimization problems. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Stergiou, N. Nonlinear Analysis for Human Movement Variability; CRC Press: Cleveland, OH, USA, 2016. [Google Scholar]
- Aldrich, C.; Auret, L. Unsupervised Process Monitoring and Fault Diagnosis with Machine Learning Methods; Springer: Berlin, Germany, 2013. [Google Scholar]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
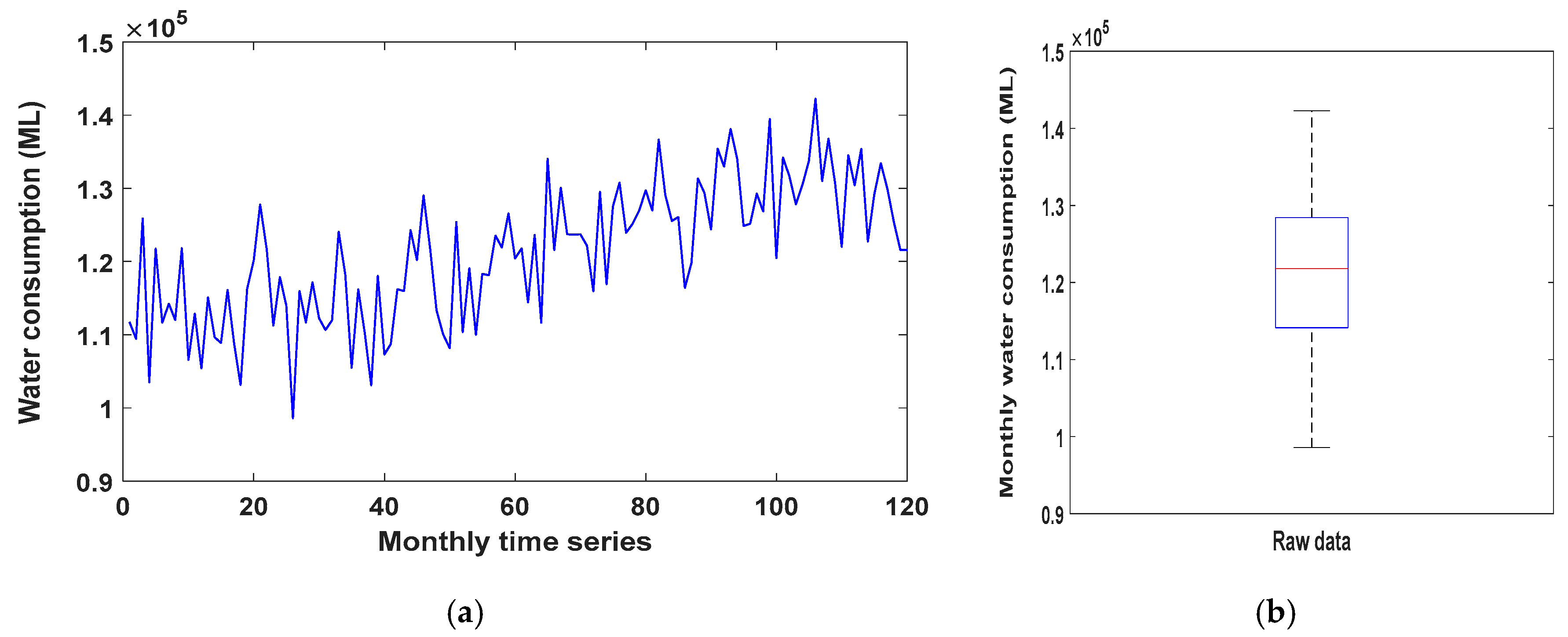
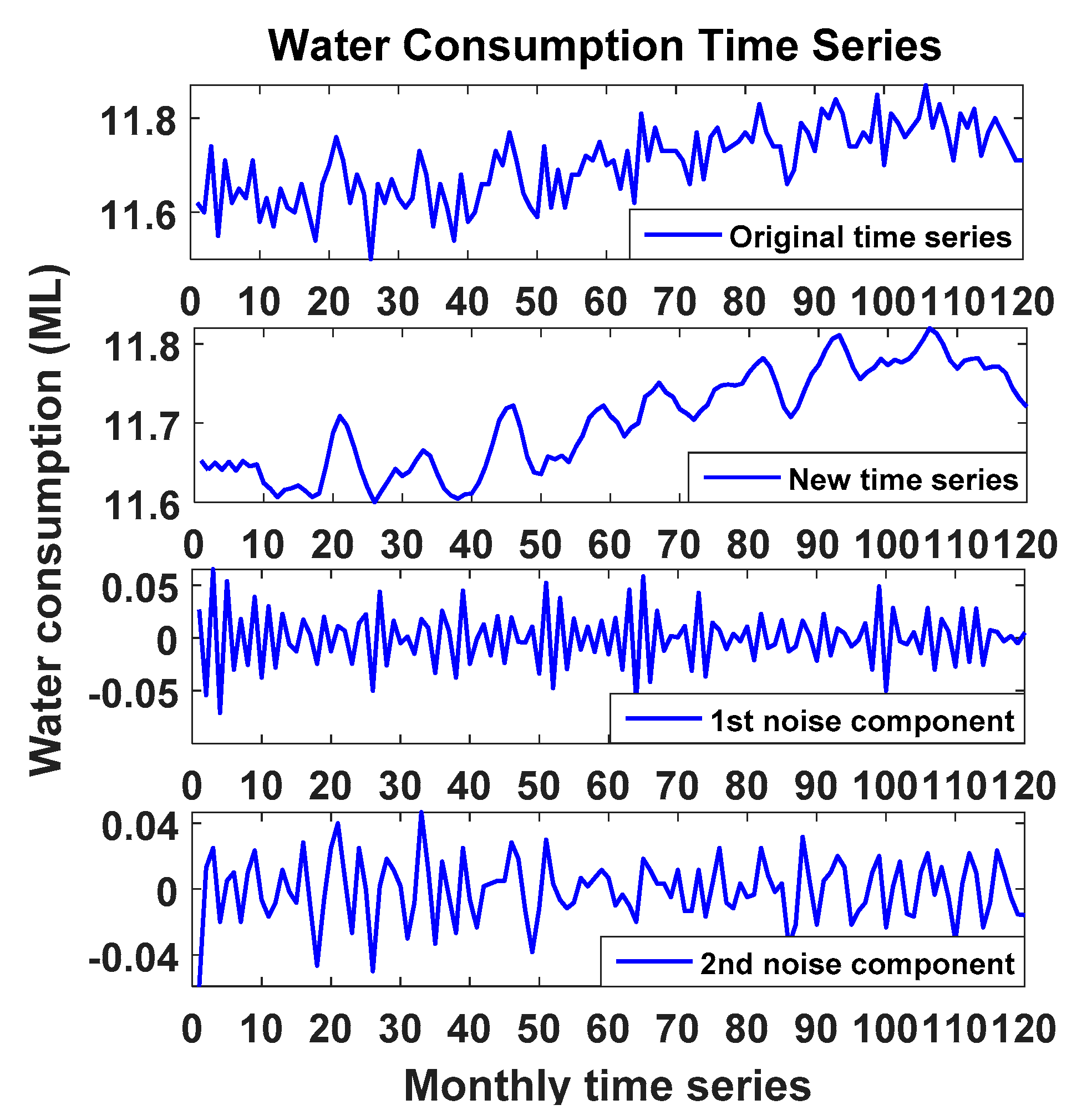
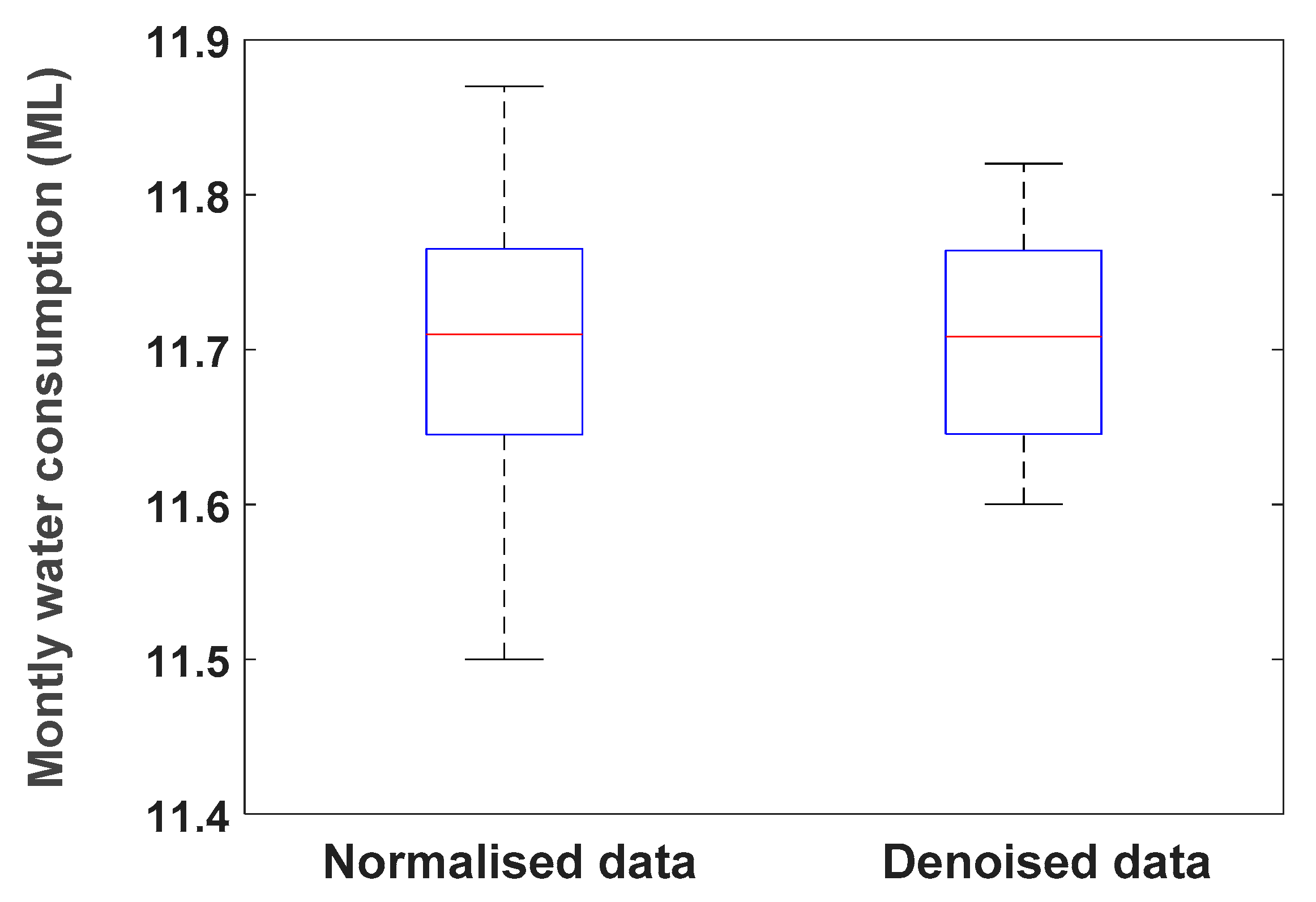
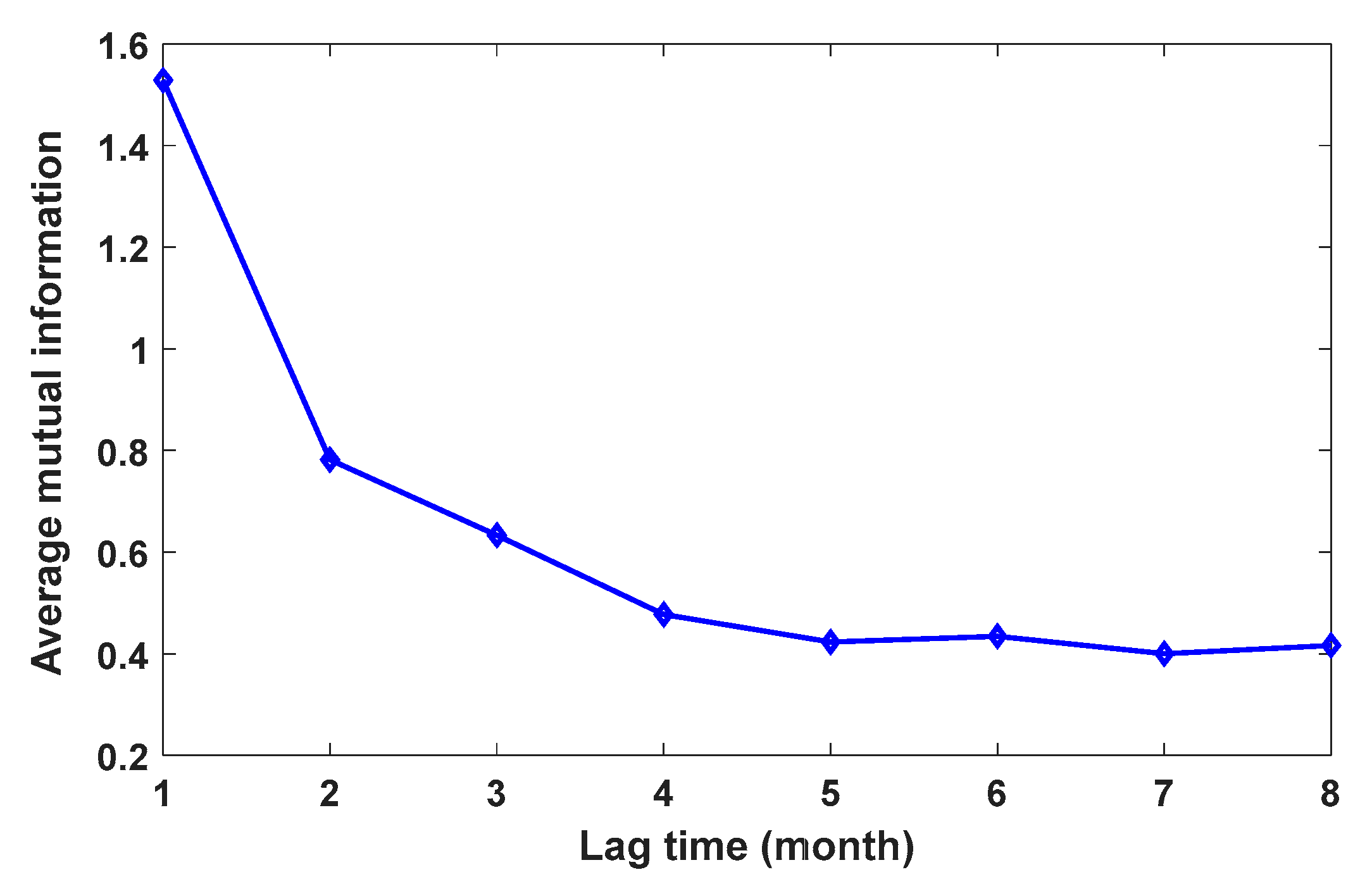
| Parameter | Type |
|---|---|
| Number of inputs | Estimated by Mutual Information (MI) technique |
| Number of outputs | Our target, which is water demand |
| Number of hidden layers | Two hidden layers |
| Number of neurons in hidden layer N1 | Estimated by metaheuristic algorithm |
| Number of neurons in hidden layer N2 | Estimated by metaheuristic algorithm |
| Learning rate coefficient | Estimated by metaheuristic algorithm |
| Learning algorithm | Levenberg-Marquardt (LM) |
| Activation function in hidden layer N1 | Tansigmoidal activation function |
| Activation function in hidden layer N2 | Linear activation function |
| Number of epochs | 1000 iterations |
| Water Consumption (ML) | Cmax | Cmin | Cmean | CStd | T |
|---|---|---|---|---|---|
| Training set | 11.81 | 11.60 | 11.70 | 0.062 | 82 |
| Testing set | 11.82 | 11.61 | 11.71 | 0.070 | 17 |
| Validation set | 11.79 | 11.61 | 11.72 | 0.057 | 17 |
| Model | Data Stage | RMSE | MAE | MARE | CE |
|---|---|---|---|---|---|
| BSA-ANN | Training | 0.0091 | 0.0075 | 0.00064 | 0.999 |
| Testing | 0.0090 | 0.0079 | 0.00044 | 0.972 | |
| Validation | 0.0099 | 0.0071 | 0.00040 | 0.979 | |
| ANN (stand-alone) | Training | 0.0078 | 0.0058 | 0.00049 | 1.0 |
| Testing | 0.0138 | 0.0112 | 0.00063 | 0.935 | |
| Validation | 0.0181 | 0.0129 | 0.00072 | 0.931 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zubaidi, S.L.; Ortega-Martorell, S.; Al-Bugharbee, H.; Olier, I.; Hashim, K.S.; Gharghan, S.K.; Kot, P.; Al-Khaddar, R. Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water 2020, 12, 1885. https://doi.org/10.3390/w12071885
Zubaidi SL, Ortega-Martorell S, Al-Bugharbee H, Olier I, Hashim KS, Gharghan SK, Kot P, Al-Khaddar R. Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water. 2020; 12(7):1885. https://doi.org/10.3390/w12071885
Chicago/Turabian StyleZubaidi, Salah L., Sandra Ortega-Martorell, Hussein Al-Bugharbee, Ivan Olier, Khalid S. Hashim, Sadik Kamel Gharghan, Patryk Kot, and Rafid Al-Khaddar. 2020. "Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study" Water 12, no. 7: 1885. https://doi.org/10.3390/w12071885
APA StyleZubaidi, S. L., Ortega-Martorell, S., Al-Bugharbee, H., Olier, I., Hashim, K. S., Gharghan, S. K., Kot, P., & Al-Khaddar, R. (2020). Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water, 12(7), 1885. https://doi.org/10.3390/w12071885










