Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Measurements
2.1.2. Series of Annual Maximum Precipitation
2.2. Methods for Design Value Estimation
2.2.1. Method of Reduced Variate
2.2.2. Testing New Methods
Modified Maximum Likelihood Estimation
Bayesian Approach
2.3. Analysis
Goodness-of-Fit Test Scores
3. Results
3.1. Comparison of Methods
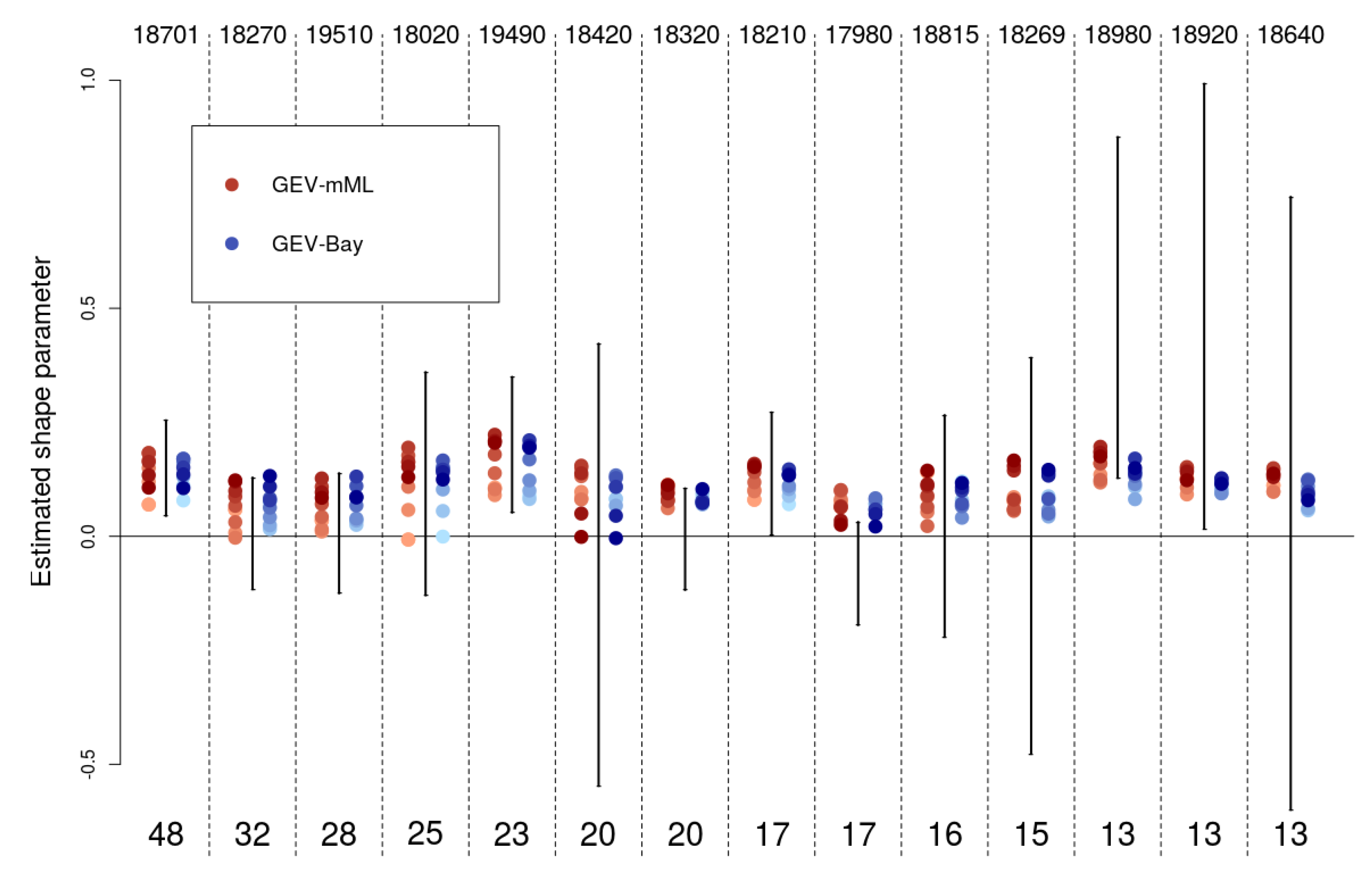
3.2. The Shape Parameter
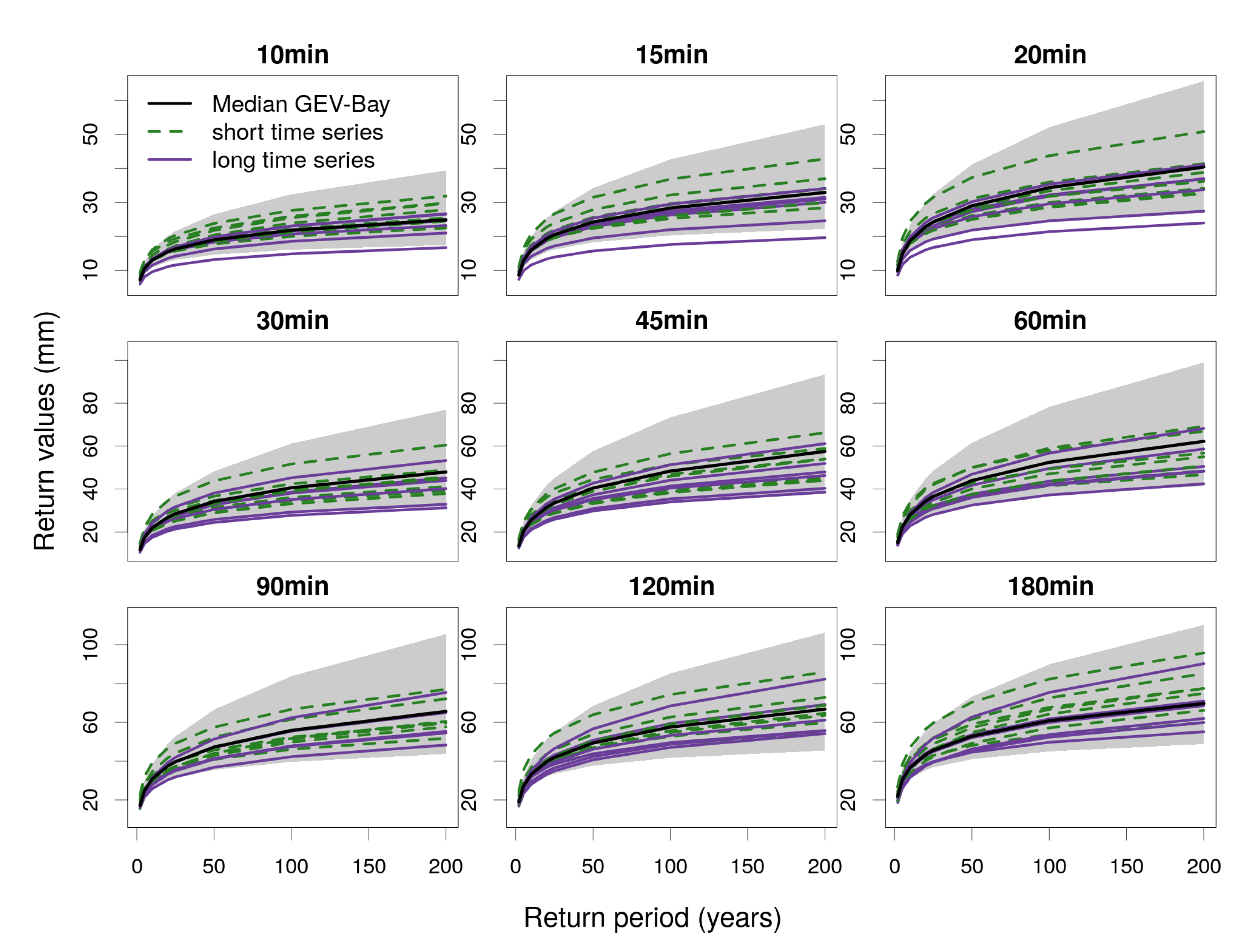
3.3. Assessment of Uncertainty
4. Discussion
5. Conclusions
6. Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sorteberg, A.; Lawrence, D.; Dyrrdal, A.V.; Mayer, S.; Engeland, K. Climatic Changes in short-duration Extreme Precipitation and Rapid Onset Flooding—Implications for Design Values; Technical Report 1; Norwegian Centre for Climate Services: Oslo, Norway, 2018. [Google Scholar]
- Hodges, K.I.; Lee, R.W.; Bengtsson, L. A comparison of extratropical cyclones in recent reanalyses ERA-Interim, NASA MERRA, NCEP CFSR, and JRA-25. J. Clim. 2011, 24, 4888–4906. [Google Scholar] [CrossRef]
- Azad, R.; Sorteberg, A. Extreme daily precipitation in coastal western Norway and the link to atmospheric rivers. J. Geophys. Res. Atmos. 2017, 122, 2080–2095. [Google Scholar] [CrossRef]
- Dyrrdal, A.V.; Lenkoski, A.; Thorarinsdottir, T.L.; Stordal, F. Bayesian hierarchical modeling of extreme hourly precipitation in Norway. Environmetrics 2015, 26, 89–106. [Google Scholar] [CrossRef]
- Dyrrdal, A.V.; Skaugen, T.; Stordal, F.; Førland, E.J. Estimating extreme areal precipitation in Norway from a gridded dataset. Hydrol. Sci. J. 2016, 61, 483–494. [Google Scholar] [CrossRef]
- Frauenfelder, R.; Solheim, A.; Isaksen, K.; Romstad, B.; Dyrrdal, A.V.; Ekseth, K.H.; Harbitz, A.; Harbitz, C.B.; Haugen, J.E.; Hygen, O.; et al. Impacts of extreme weather events on transport infrastructure in Norway. Nat. Hazards Earth Syst. Sci. Discuss. 2017, 1–24. [Google Scholar] [CrossRef]
- Handmer, J.; Honda, Y.; Kundzewicz, Z.W.; Arnell, N.; Benito, G.; Hatfield, J.; Mohamed, I.F.; Peduzzi, P.; Wu, S.; Sherstyukov, B.; et al. Changes in impacts of climate extremes: Human systems and ecosystems. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation. A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change (IPCC); Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; pp. 231–290. [Google Scholar]
- NOU. Overvann i byer og tettsteder—Som problem og ressurs. In English: Stormwater In Cities and Towns—As A Problem and Resource; Technical Report 16; Official Norwegian Reports; Norwegian Government Security and Service Organisation: Oslo, Norway, 2015. [Google Scholar]
- Li, H.; Gao, H.; Zhou, Y.; Xu, C.Y.; Ortega M., R.Z.; Sælthun, N.R. Usage of SIMWE model to model urban overland flood: A case study in Oslo. Hydrol. Res. 2020, 51, 366–380. [Google Scholar] [CrossRef]
- Bernard, M.M. Formulas for rainfall intensities of long duration. Trans. Am. Soc. Civ. Eng. 1932, 96, 592–606. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Hosking, J.R.; Wallis, J.R. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Olsson, J.; Södling, J.; Berg, P.; Wern, L.; Eronn, A. Short-duration rainfall extremes in Sweden: A regional analysis. Hydrol. Res. 2019, 50, 945–960. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L.; Willems, P. Regional frequency analysis of extreme rainfall in Belgium based on radar estimates. Hydrol. Earth Syst. Sci. 2017, 21, 5385. [Google Scholar] [CrossRef]
- Fukutome, S.; Schindler, A.C.A. Meteoswiss Extreme Value Analyses: User Manual and Documentation, 3rd ed.; Technical Report 255; Meteo Swiss: Zurich, Switzerland, 2018; p. 80. [Google Scholar]
- Huard, D.; Mailhot, A.; Duchesne, S. Bayesian estimation of intensity–duration–frequency curves and of the return period associated to a given rainfall event. Stoch. Environ. Res. Risk Assess. 2010, 24, 337–347. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation/Statistiques de valeurs extrêmes et estimation de précipitations extrêmes: I. Recherche théorique. Hydrol. Sci. J. 2004, 49, 590. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: II. Empirical investigation of long rainfall records/Statistiques de valeurs extrêmes et estimation de précipitations extrêmes: II. Recherche empirique sur de longues séries de précipitations. Hydrol. Sci. J. 2004, 49, 610. [Google Scholar] [CrossRef]
- Ragulina, G.; Reitan, T. Generalized extreme value shape parameter and its nature for extreme precipitation using long time series and the Bayesian approach. Hydrol. Sci. J. 2017, 62, 863–879. [Google Scholar] [CrossRef]
- Gumbel, E.; Lieblein, J. Statistical Theory of Extreme Values and Some Practical Applications: A Series of Lectures; U.S. Government Printing Office: Washington, DC, USA, 1954; Volume 33, p. 51.
- Gumbel, E.J. Statistics of Extremes; Dover Publications: New York, NY, USA, 2004; Unabridged Republication of the Edition Published by Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Němec, J. Engineering Hydrology; McGraw-Hill Publishing Company Limited: London, UK, 1972. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Book Company: Singapore, 1988. [Google Scholar]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity–duration–frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- Fusek, M.; Hellebrand, R.; Michálek, J. Modelling precipitation extremes in the Czech Republic: Update of intensity-duration-frequency curves. Est. J. Earth Sci. 2016, 65, 234–247. [Google Scholar] [CrossRef]
- Prescott, P.; Walden, A. Maximum likelihood estimation of the parameters of the generalized extreme-value distribution. Biometrika 1980, 67, 723–724. [Google Scholar] [CrossRef]
- Van de Vyver, H. Bayesian estimation of rainfall intensity–duration–frequency relationships. J. Hydrol. 2015, 529, 1451–1463. [Google Scholar] [CrossRef]
- Coles, S.; Pericchi, L.R.; Sisson, S. A fully probabilistic approach to extreme rainfall modeling. J. Hydrol. 2003, 273, 35–50. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics, JR Statist. J. R. Stat. Society. Ser. B (Methodol.) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kyselỳ, J. A cautionary note on the use of nonparametric bootstrap for estimating uncertainties in extreme-value models. J. Appl. Meteorol. Climatol. 2008, 47, 3236–3251. [Google Scholar] [CrossRef]
- Holešovskỳ, J.; Fusek, M.; Blachut, V.; Michálek, J. Comparison of precipitation extremes estimation using parametric and nonparametric methods. Hydrol. Sci. J. 2016, 61, 2376–2386. [Google Scholar] [CrossRef][Green Version]
- Bayes, T. LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S. Philos. Trans. Royal Soc. Lond. 1763, 53, 370–418. [Google Scholar]
- Richey, M. The Evolution of Markov Chain Monte Carlo Methods. Am. Math. Mon. 2010, 117, 383–413. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Frei, C.; Fukutome, S. gevXgpd: Extreme Value Analysis, R package version 1.4.2; GitHub: Zurich, Switzerland, 2014. [Google Scholar]
- Gilleland, E.; Katz, R.W. extRemes 2.0: An Extreme Value Analysis Package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef]
- Luceño, A. Fitting the generalized Pareto distribution to data using maximum goodness-of-fit estimators. Comput. Stat. Data Anal. 2006, 51, 904–917. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov–Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Laio, F. Cramer–von Mises and Anderson-Darling goodness of fit tests for extreme value distributions with unknown parameters. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Berkhof, J.; Van Mechelen, I.; Hoijtink, H. Posterior predictive checks: Principles and discussion. Comput. Stat. 2000, 15, 337–354. [Google Scholar] [CrossRef]
- Van de Schoot, R.; Kaplan, D.; Denissen, J.; Asendorpf, J.B.; Neyer, F.J.; Van Aken, M.A. A gentle introduction to Bayesian analysis: Applications to developmental research. Child Dev. 2014, 85, 842–860. [Google Scholar] [CrossRef]
- Reich, B.J.; Shaby, B.A. A hierarchical max-stable spatial model for extreme precipitation. Ann. Appl. Stat. 2012, 6, 1430. [Google Scholar] [CrossRef]
- Doorn, N.; Hansson, S.O. Should probabilistic design replace safety factors? Philos. Technol. 2011, 24, 151–168. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Brath, A.; Montanari, A. Reliability of different depth-duration-frequency equations for estimating short-duration design storms. Water Resour. Res. 2006, 42, 151–168. [Google Scholar] [CrossRef]
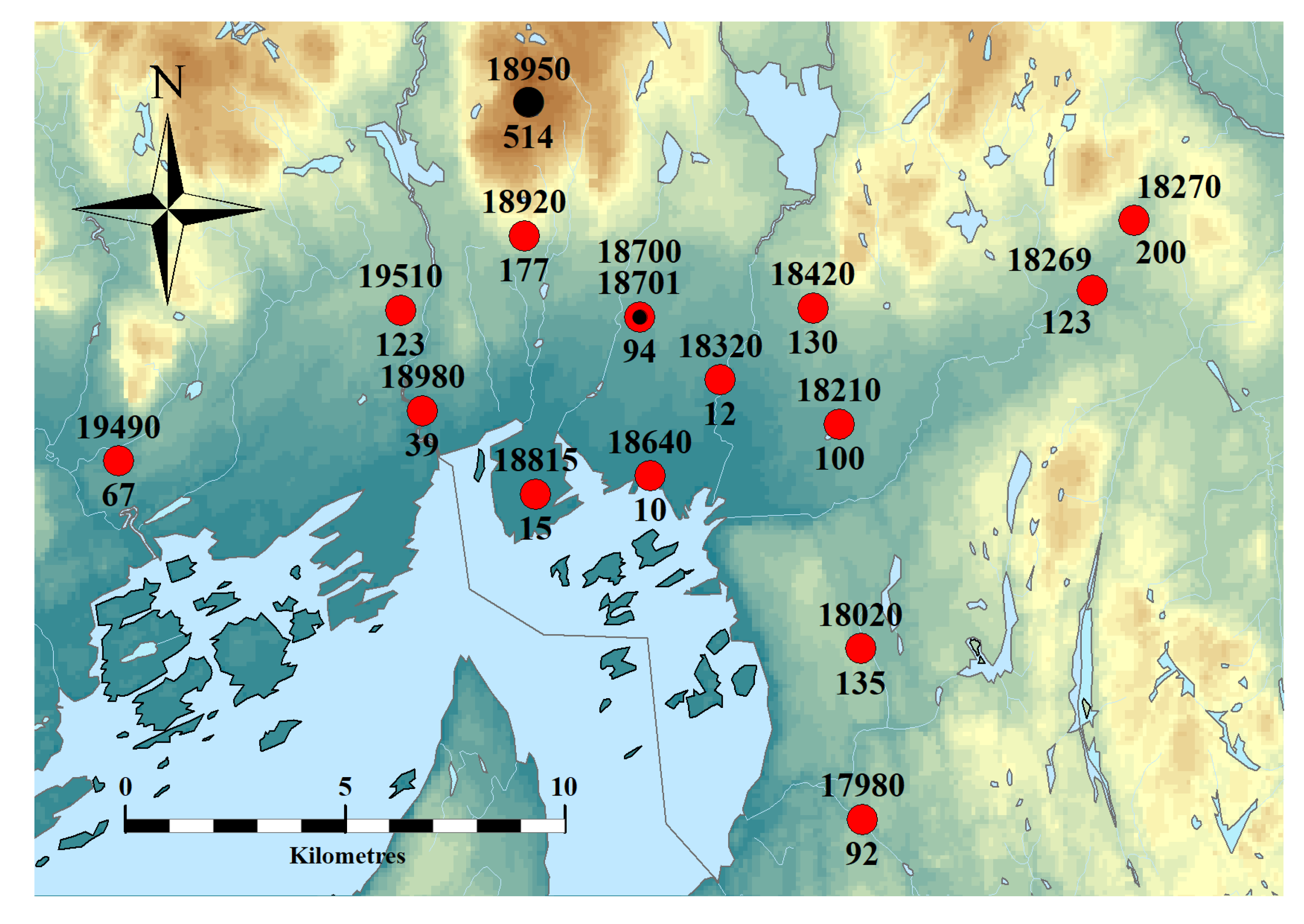

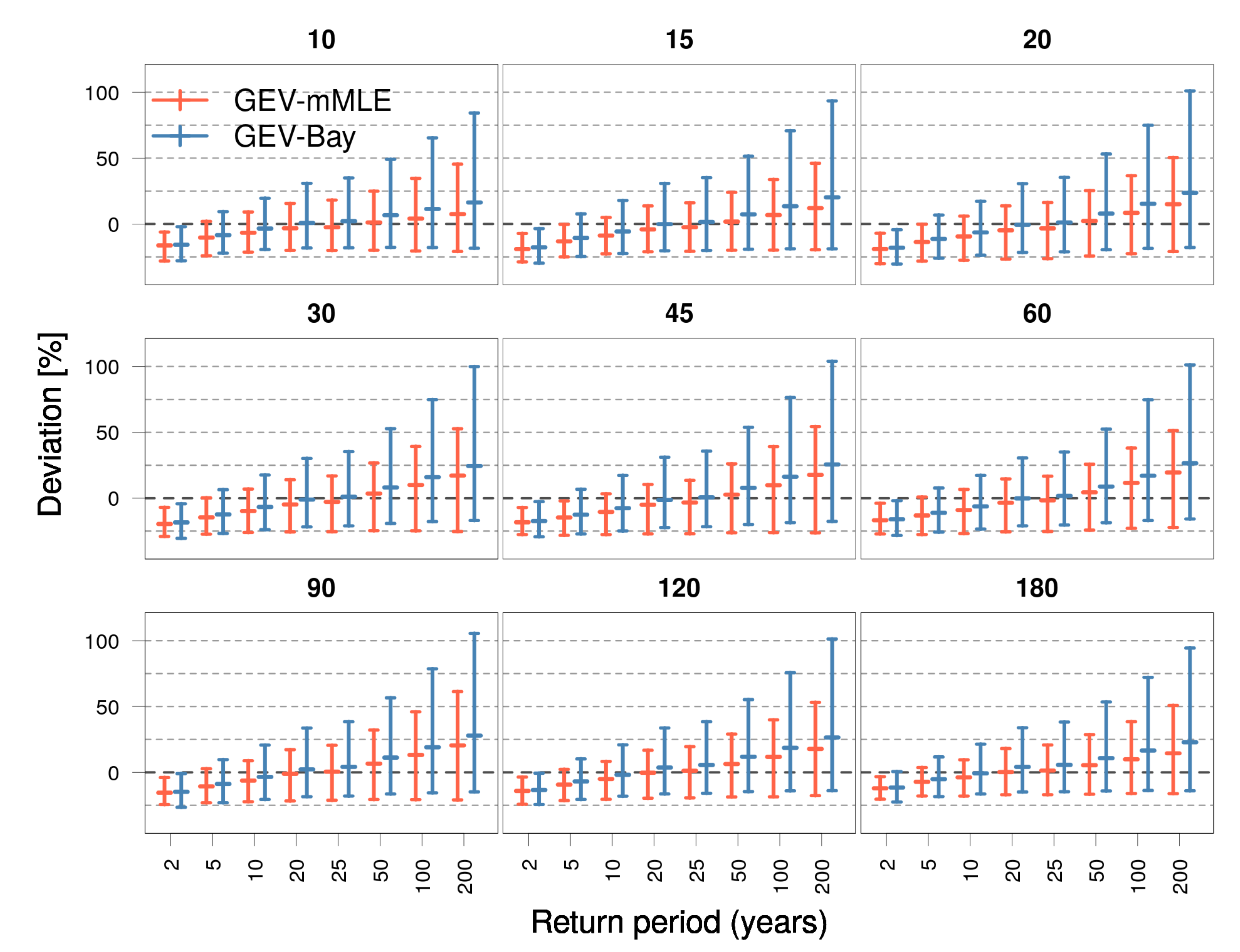
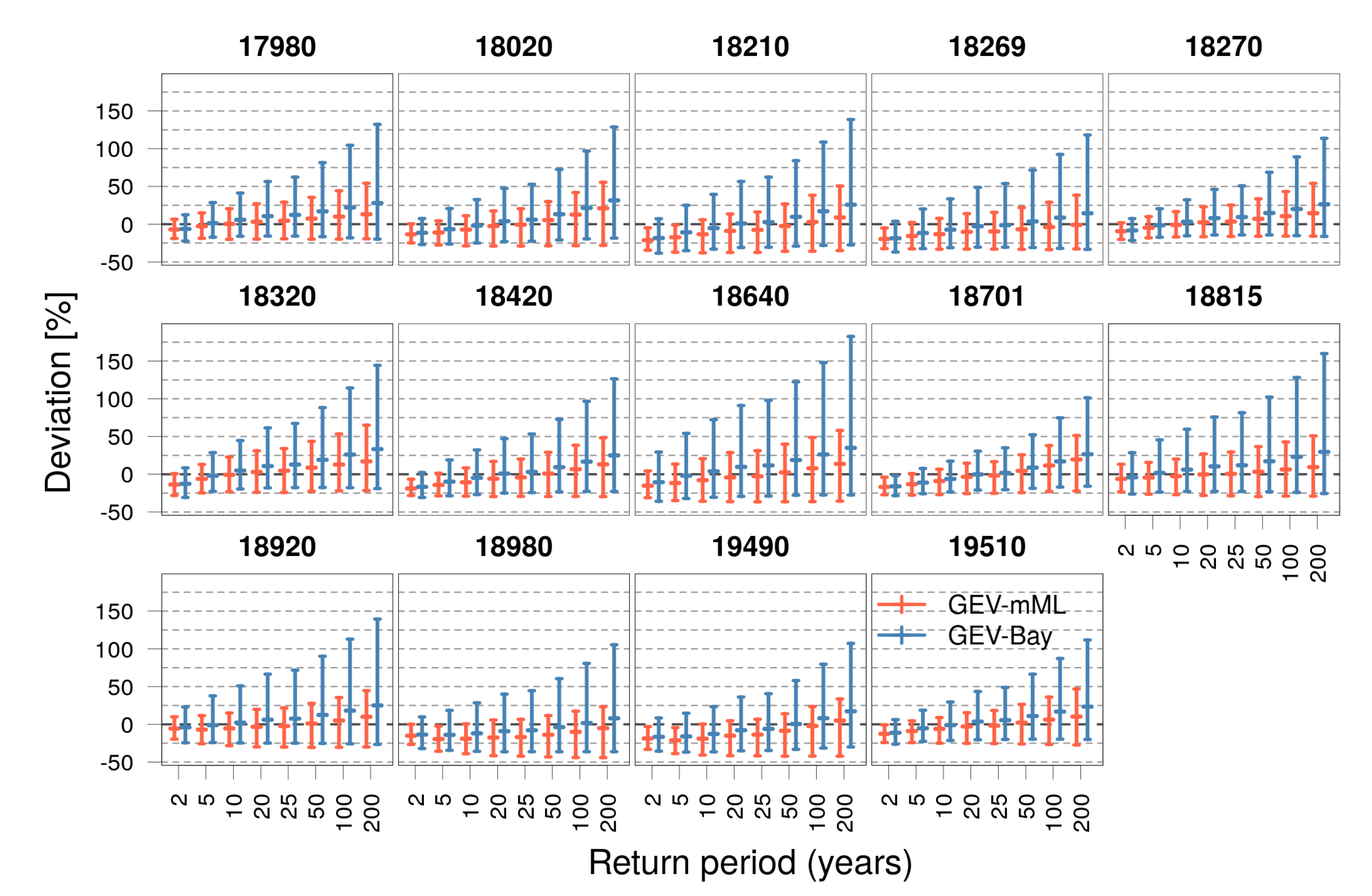
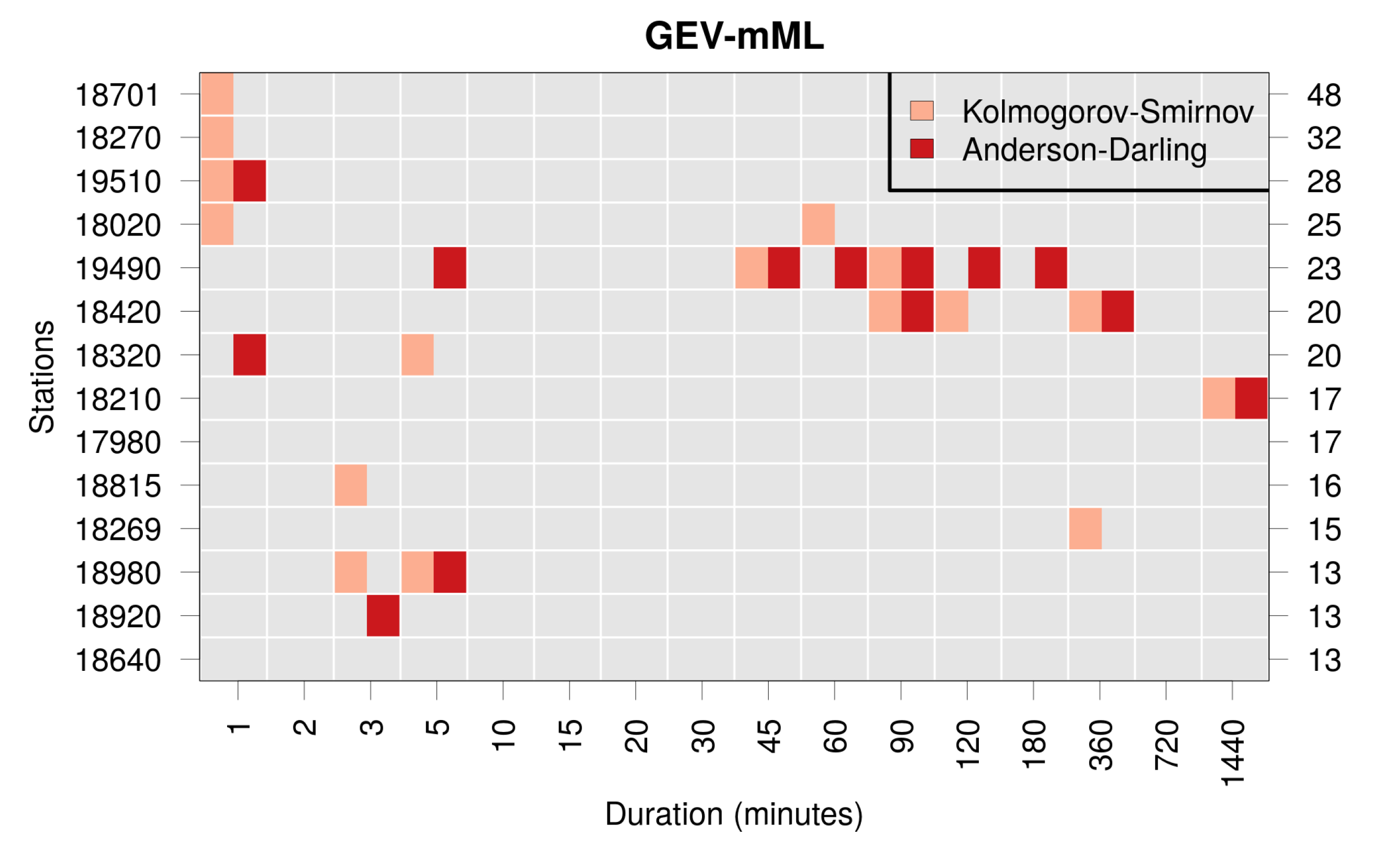

| ID | Station Name | Operational Period | Number of Seasons | ||
|---|---|---|---|---|---|
| From | To | N-Highest | AM | ||
| 17980 | Oslo-Ljabruveien | 1 January 2000 | - | 20 | 17 |
| 18020 | Oslo-Lambertseter | 15 May 1985 | - | 35 | 25 |
| 18210 | Oslo-Hovin | 15 January 1999 | - | 20 | 17 |
| 18269 | Oslo-Haugenstua | 1 January 2000 | - | 16 | 15 |
| 18270 | Oslo-Vestli | 18 April 1974 | - | 37 | 32 |
| 18320 | Oslo-Hausmannsgate | 21 June 1984 | 4 November 2013 | 29 | 20 |
| 18420 | Oslo-Disen | 2 June 1998 | - | 21 | 20 |
| 18640 | Oslo-Vestre Vika | 22 May 1974 | 3 October 1998 | 15 | 13 |
| 18701 | Oslo-Blindern plu | 16 April 1968 | - | 52 | 48 |
| 18815 | Oslo-Bygdøy | 1 January 2000 | - | 18 | 16 |
| 18920 | Oslo-Besserud | 29 September 1998 | - | 17 | 13 |
| 18980 | Oslo-Lilleaker | 1 January 2000 | - | 14 | 13 |
| 19490 | Gjettum | 1 July 1970 | - | 34 | 23 |
| 19510 | Øvrevoll | 19 May 1967 | - | 38 | 28 |
| Test Score | Computational Form |
|---|---|
| Kolmogorov–Smirnov statistic | |
| Right-tail Anderson–Darling statistic |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lutz, J.; Grinde, L.; Dyrrdal, A.V. Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty. Water 2020, 12, 1735. https://doi.org/10.3390/w12061735
Lutz J, Grinde L, Dyrrdal AV. Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty. Water. 2020; 12(6):1735. https://doi.org/10.3390/w12061735
Chicago/Turabian StyleLutz, Julia, Lars Grinde, and Anita Verpe Dyrrdal. 2020. "Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty" Water 12, no. 6: 1735. https://doi.org/10.3390/w12061735
APA StyleLutz, J., Grinde, L., & Dyrrdal, A. V. (2020). Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty. Water, 12(6), 1735. https://doi.org/10.3390/w12061735





