Flood Risk Evaluation in Ungauged Coastal Areas: The Case Study of Ippocampo (Southern Italy)
Abstract
:1. Introduction
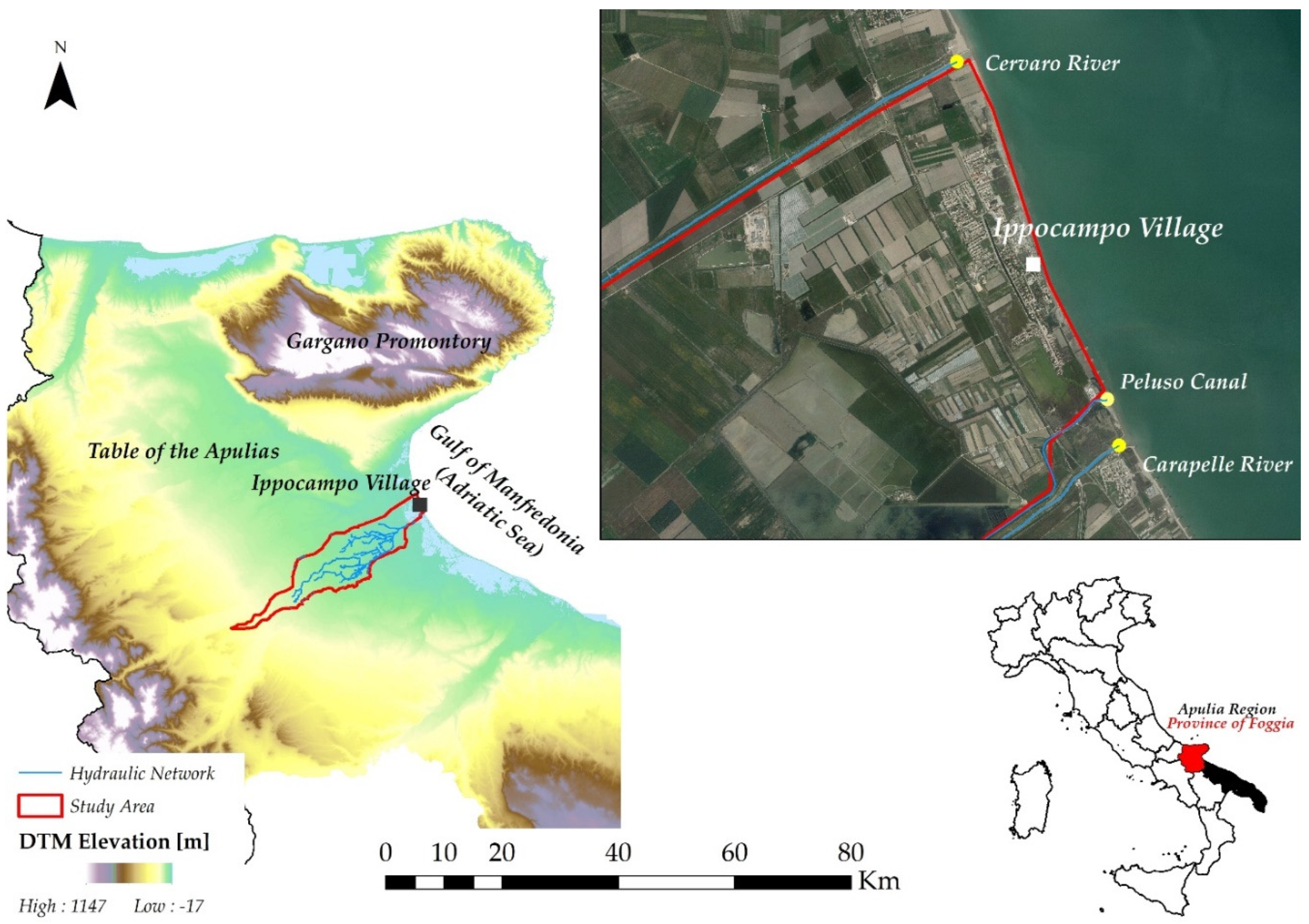
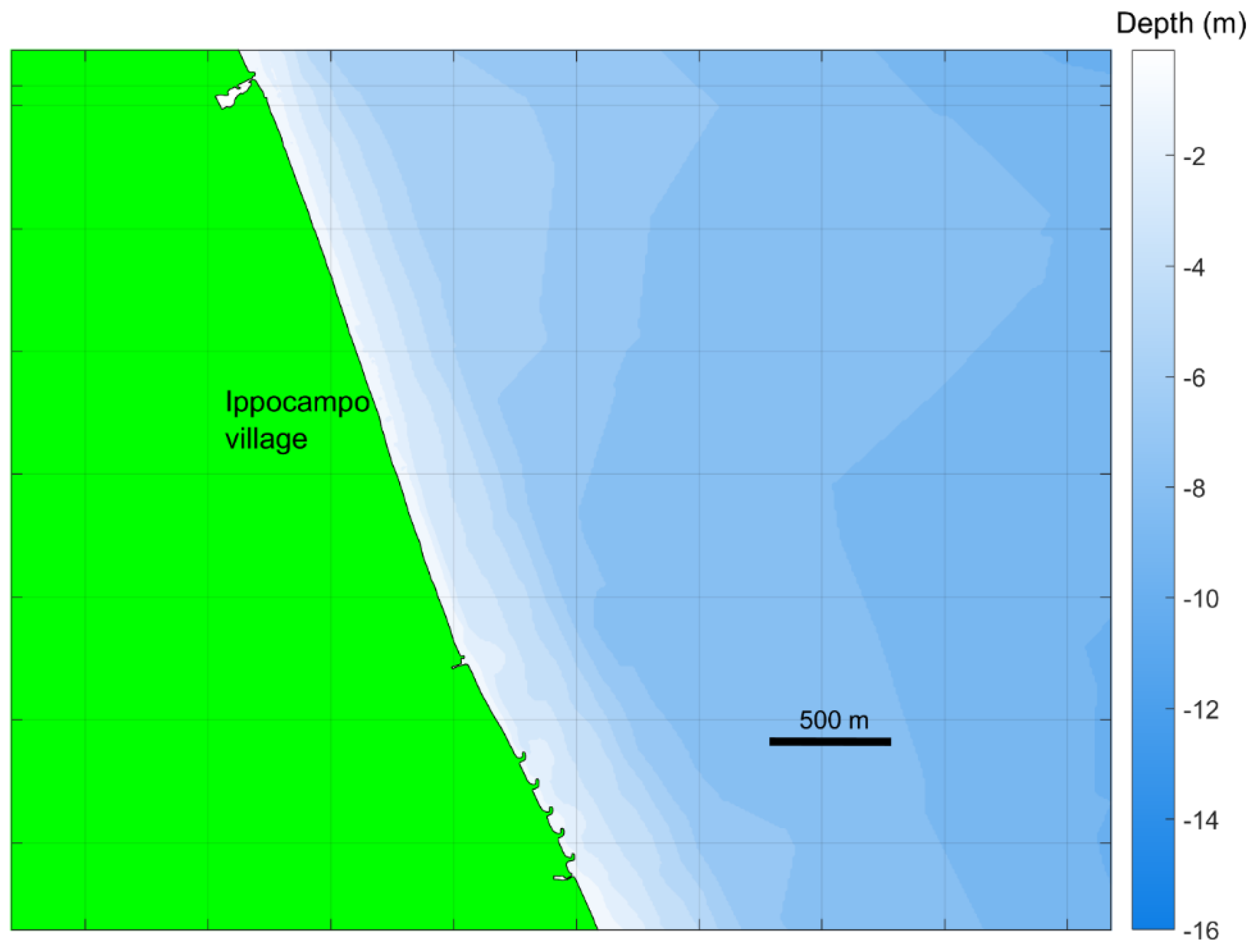
2. The Study Area
3. Materials and Methods
3.1. Numerical Model Description
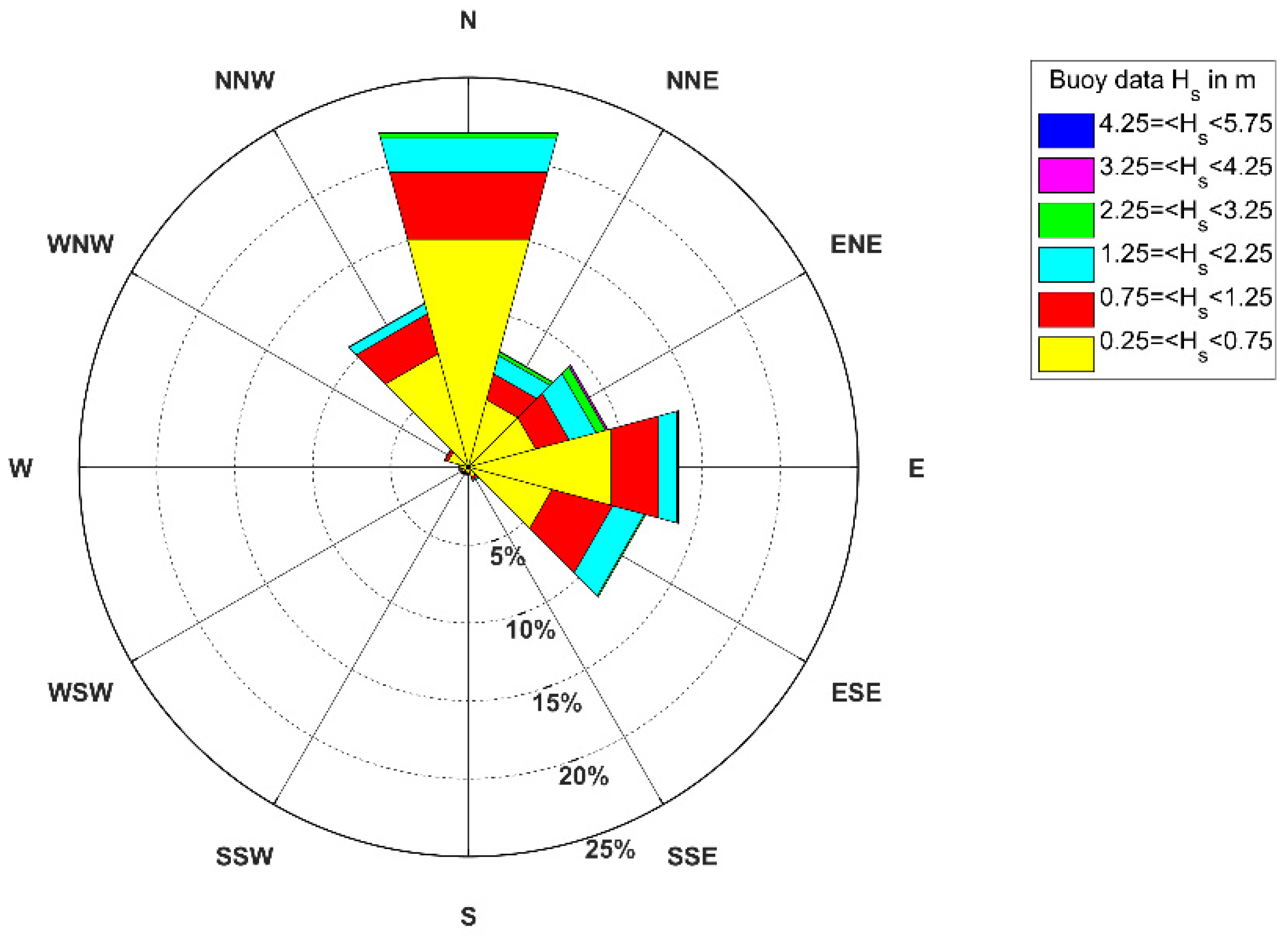
3.2. Rough Data Collection
3.3. Hydrologic Modeling
3.4. Coastal Modeling
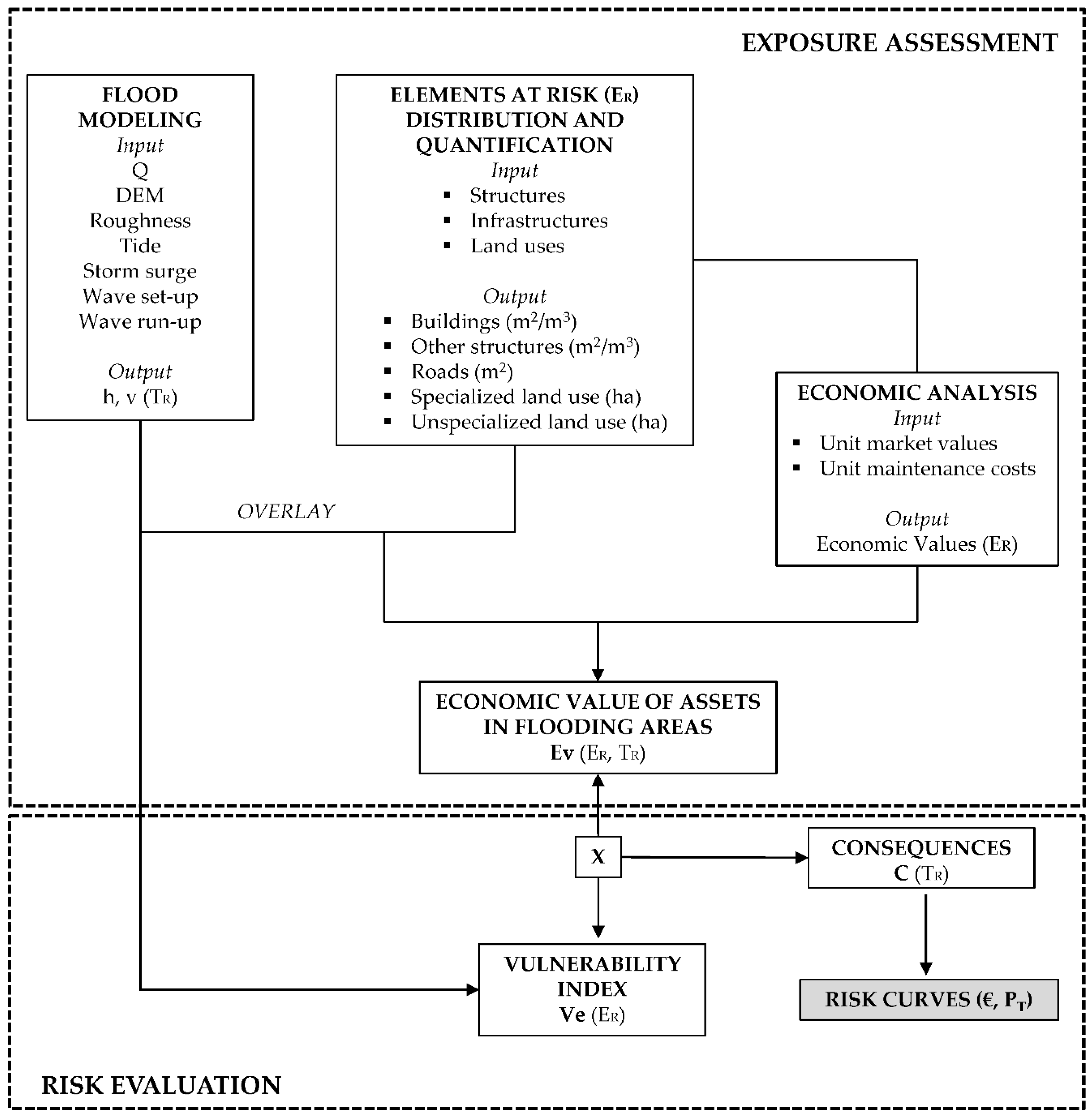
3.5. Risk Assessment
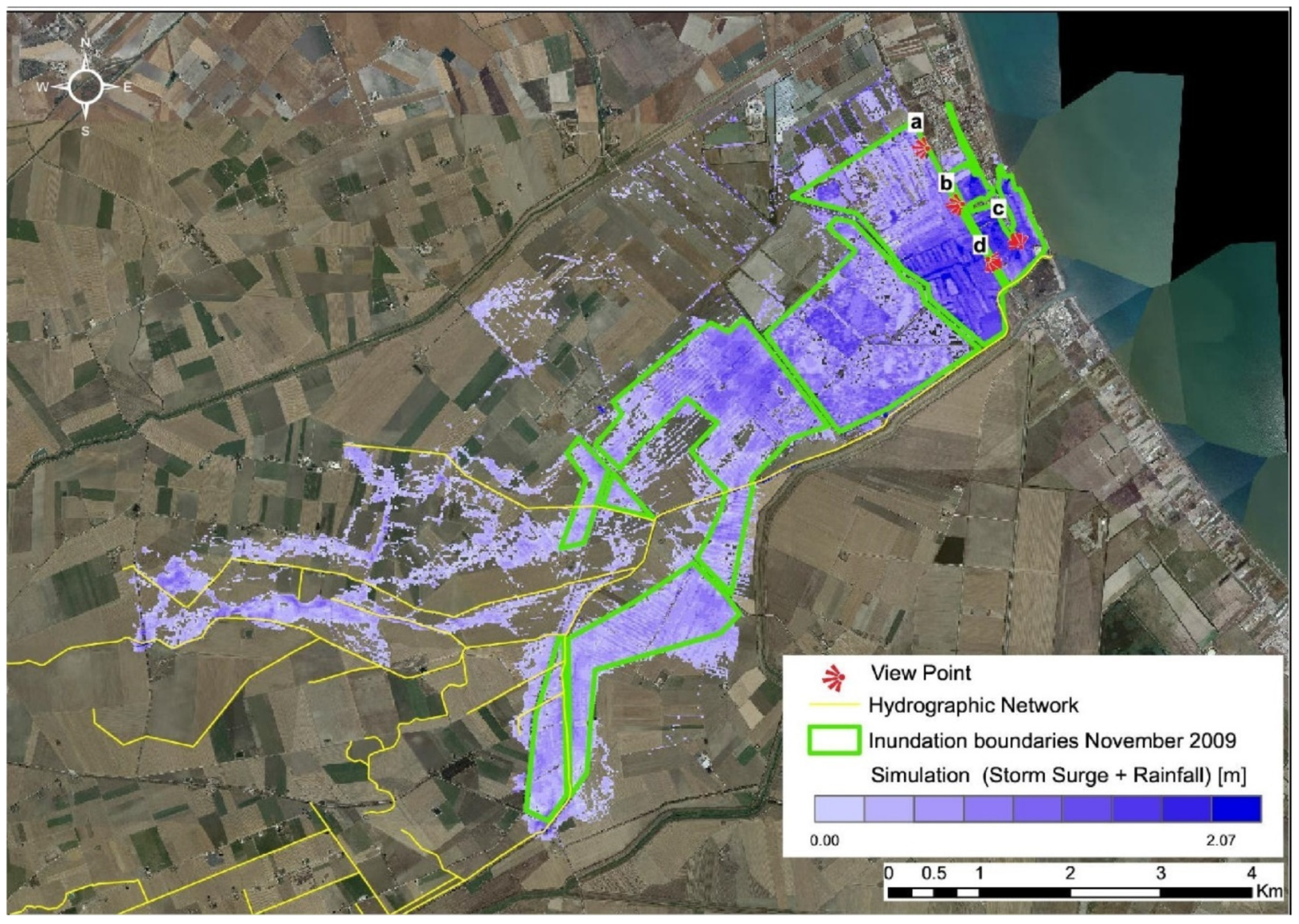
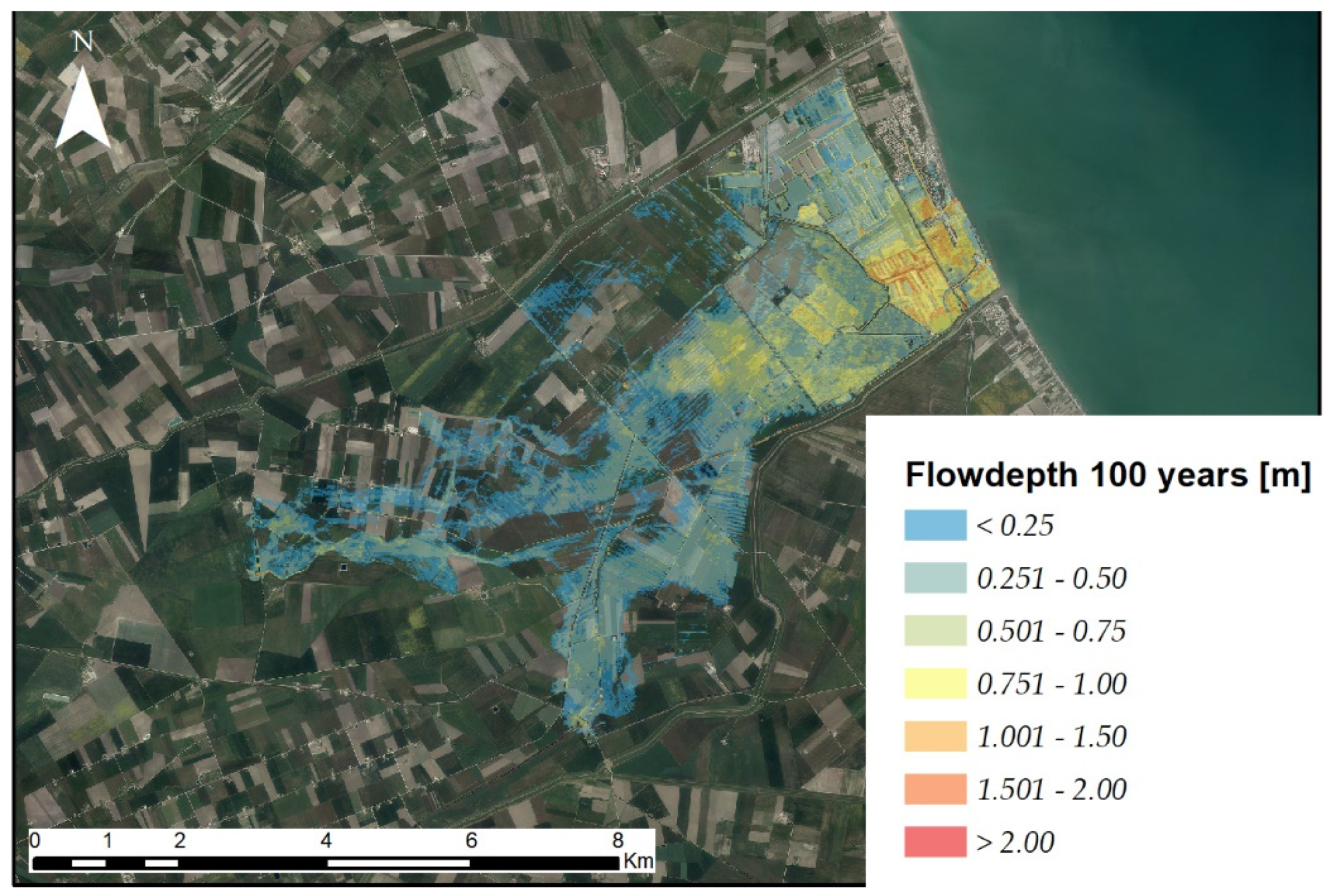
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Recanatesi, F.; Petroselli, A.; Ripa, M.N.; Leone, A. Assessment of stormwater runoff management practices and BMPs under soil sealing: A study case in a peri-urban watershed of the metropolitan area of Rome (Italy). J. Environ. Manag. 2017, 201, 6–18. [Google Scholar] [CrossRef]
- Apollonio, C.; Balacco, G.; Novelli, A.; Tarantino, E.; Piccinni, A.F. Land Use Change Impact on Flooding Areas: The Case Study of Cervaro Basin (Italy). Sustainability 2016, 8, 996. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Ardoin-Bardin, S.; Bonell, M.; Dorninger, M.; Goodrich, D.; Gutknecht, D.; Matamoros, D.; Merz, B.; Shand, P.; Szolgay, J. At what scales do climate variability and land cover change impact on flooding and low flows? Hydrol. Process. 2007, 21, 1241–1247. [Google Scholar] [CrossRef]
- Novelli, A.; Tarantino, E.; Caradonna, G.; Apollonio, C.; Balacco, G.; Piccinni, F. Improving the ANN Classification Accuracy of Landsat Data Through Spectral Indices and Linear Transformations (PCA and TCT) Aimed at LU/LC Monitoring of a River Basin. In Proceedings of the 16th International Conference on Computational Science and Its Applications, Beijing, China, 4–7 July 2016. [Google Scholar]
- Nardi, F.; Vivoni, E.R.; Grimaldi, S. Investigating a floodplain scaling relation using a hydrogeomorphic delineation method. Water Resour. Res. 2006, 42, W09409. [Google Scholar] [CrossRef]
- Hill, A.R. Stream chemistry and riparian zones. In Streams and Ground Waters; Jones, J., Mulholland, P., Eds.; Elsevier: New York, NY, USA, 1999; pp. 83–110. [Google Scholar]
- Katsuyama, M.; Ohte, N.; Kabeya, N. Effects of bedrock permeability on hillslope and riparian groundwater dynamics in a weathered granite catchment. Water Resour. Res. 2005, 41, W01010. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Entekhabi, D.; Bras, R.L.; Ivanov, V.Y.; Van Horne, M.P.; Grassotti, C.; Hoffman, R.N. Extending the Predictability of Hydrometeorological Flood Events Using Radar Rainfall Nowcasting. J. Hydrometeorol. 2006, 7, 660–677. [Google Scholar] [CrossRef]
- Townsend, P.A. Relationships between vegetation patterns and hydroperiod on the Roanoke River floodplain, North Carolina. Plant Ecol. 2001, 156, 43–58. [Google Scholar] [CrossRef]
- Jung, M.; Burt, T.P.; Bates, P.D. Toward a conceptual model of floodplain water table response. Water Resour. Res. 2004, 40, W12409. [Google Scholar] [CrossRef]
- Williams, W.A.; Jensen, M.E.; Winne, J.C.; Redmond, R.L. An automated technique for delineating and characterizing valley-bottom settings. Environ. Monit. 2000, 64, 105–114. [Google Scholar] [CrossRef]
- Petroselli, A.; Grimaldi, S. Design hydrograph estimation in small and fully ungauged basins: A preliminary assessment of EBA4SUB framework. J. Flood Risk Manag. 2018, 11, S197–S210. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A. Do we still need the Rational Formula? An alternative empirical procedure for peak discharge estimation in small and ungauged basins. Hydrol. Sci. J. 2015, 60, 67–77. [Google Scholar] [CrossRef]
- Młyński, D.; Petroselli, A.; Walega, A. Flood frequency analysis by an event-based rainfall-runoff model in selected catchments of southern Poland. Soil Water Res. 2018, 13, 170–176. [Google Scholar]
- Neumann, B.; Vafeidis, A.T.; Zimmermann, J.; Nicholls, R.J. Future Coastal Population Growth and Exposure to Sea-Level Rise and Coastal Flooding—A Global Assessment. PLoS ONE 2015, 10, e0118571. [Google Scholar] [CrossRef] [PubMed]
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative Analysis of Coastal Flooding Vulnerability and Hazard Assessment at National Scale. J. Mar. Sci. Eng. 2017, 5, 51. [Google Scholar] [CrossRef] [Green Version]
- Bruno, M.F.; Molfetta, M.G.; Pratola, L.; Mossa, M.; Nutricato, R.; Morea, A.; Nitti, D.O.; Chiaradia, M.T. A Combined Approach of Field Data and Earth Observation for Coastal Risk Assessment. Sensors 2019, 19, 1399. [Google Scholar] [CrossRef] [Green Version]
- Archetti, R.; Damiani, L.; Bianchini, A.; Romagnoli, C.; Abbiati, M.; Addona, F.; Airoldi, L.; Cantelli, L.; Gaeta, M.G.; Molfetta, M.G.; et al. Innovative strategies, monitoring and analysis of the coastal erosion risk: The STIMARE project. In Proceedings of the 29th International Ocean and Polar Engineering Conference, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Bates, P.D.; Dawson, R.J.; Hall, J.W.; Horritt, M.S.; Nicholls, R.J.; Wicks, J.; Hassan, M.A. Simplified two-dimensional numerical modelling of coastal flooding and example applications. Coast. Eng. 2005, 52, 793–810. [Google Scholar] [CrossRef]
- Postacchini, M.; Lalli, F.; Memmola, F.; Bruschi, A.; Bellafiore, D.; Lisi, I.; Zitti, G.; Brocchini, M. A model chain approach for coastal inundation: Application to the bay of Alghero. Estuar. Coast. Shelf Sci. 2019, 219, 56–70. [Google Scholar] [CrossRef]
- Krestenitis, Y.N.; Androulidakis, Y.S.; Kontos, Y.N.; Georgakopoulos, G. Coastal inundation in the north-eastern mediterranean coastal zone due to storm surge events. J. Coast. Conserv 2011, 15, 353–368. [Google Scholar] [CrossRef]
- Martinelli, L.; Zanuttigh, B.; Corbau, B. Assessment of coastal flooding hazard along the Emilia Romagna littoral. Coast. Eng. 2010, 57, 1042–1058. [Google Scholar] [CrossRef]
- Perini, L.; Calabrese, L.; Salerno, G.; Ciavola, P.; Armaroli, C. Evaluation of coastal vulnerability to flooding: Comparison of two different methodologies adopted by the Emilia-Romagna region (Italy). Nat. Hazards Earth Syst. Sci. 2016, 16, 18. [Google Scholar] [CrossRef] [Green Version]
- Teng, J.; Jakeman, A.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Tang, H.S.; Steven, I.; Chien, J.; Temimi, M.; Blain, C.A.; Ke, Q.; Kraatz, S. Vulnerability of population and transportation infrastructure at the east bank of Delaware Bay due to coastal flooding in sea-level rise conditions. Nat. Hazards 2013, 69, 141–163. [Google Scholar] [CrossRef]
- Joyce, J.; Chang, N.B.; Harji, R.; Ruppert, T.; Singhofen, P. Cascade impact of hurricane movement, storm tidal surge, sea level rise and precipitation variability on flood assessment in a coastal urban watershed. Clim. Dyn. 2018, 51, 383–409. [Google Scholar] [CrossRef]
- Ray, T.; Stepinski, E.; Sebastian, A.; Bedient, P.B. Dynamic Modeling of Storm Surge and Inland Flooding in a Texas Coastal Floodplain. J. Hydraul. Eng. 2011, 137, 1103–1110. [Google Scholar] [CrossRef]
- Torres, J.M.; Bass, B.; Irza, N.; Fang, Z.; Proft, J.; Dawson, C.; Kiani, M.; Bedient, P. Characterizing the hydraulic interactions of hurricane storm surge and rainfall–runoff for the Houston–Galveston region. Coast. Eng. 2015, 106, 7–19. [Google Scholar] [CrossRef] [Green Version]
- Ulbrich, U.; Lionello, P.; Belusic, D.; Jacobeit, J.; Knippertz, P.; Kuglitsch, F.G.; Leckebusch, G.C.; Luterbacher, J.; Maugeri, M.; Maheras, P.; et al. iClimate of the Mediterranean: Synoptic patterns, temperature, precipitation, winds and their extremes. In Climate of the Mediterranean Region—From the Past to the Future; Elsevier: Sydney, NSW, Australia, 2012; pp. 301–346. [Google Scholar]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.-P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate change and interconnected risks to sustainable development in the Mediterranean. Nat. Clim. Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef] [Green Version]
- Pasquali, D.; Bruno, M.; Celli, D.; Damiani, L.; Di Risio, M. A simplified hindcast method for the estimation of extreme storm surge events in semi-enclosed basins. Appl. Ocean Res. 2019, 85, 45–52. [Google Scholar] [CrossRef]
- Penning-Rowsell, E.C. The Benefits of Flood and Coastal Risk Management: A Handbook of Assessment Techniques 2010; Flood Hazard Research Centre: London, UK, 2010. [Google Scholar]
- De Moel, H.; Jongman, B.; Kreibich, H.; Merz, B.; Penning-Rowsell, E.; Ward, P.J. Flood risk assessments at different spatial scales. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 865–890. [Google Scholar] [CrossRef] [Green Version]
- Lamb, R.; Keef, C.; Tawn, J.A.; Laeger, S.; Meadowcroft, I.; Surendran, S.; Dunning, P.; Batstone, C. A new method to assess the risk of local and widespread flooding on rivers and coasts. J. Flood Risk Manag. 2010, 3, 323–336. [Google Scholar] [CrossRef]
- Autorità di Bacino Distrettuale dell’Appennino Meridionale Sede Puglia(ex Autorità di Bacino della Puglia), Piano Stralcio di Assetto Idrogeologico (PAI). Available online: http://www.adb.puglia.it (accessed on 11 March 2020).
- O’Brien, J.S. Modeling tsunami waves and ocean storm surges with FLO-2D. In Proceedings of the American Water Resources Association, 2005 Summer Specialty Conference, Institutions for SIMOP, Honolulu, HI, USA, 27–29 June 2005. [Google Scholar]
- Pezzoli, A.; Cartacho, D.L.; Arasaki, E.; Alfredini, P.; Sakai, R.O. Extreme events assessment methodology coupling rainfall and tidal levels in the coastal flood plain of the São Paulo North Coast (Brazil) for engineering projects purposes. J. Clim. Weather Forecast. 2013, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Pellicani, R.; Van Westen, C.J.; Spilotro, G. Assessing landslide exposure in areas with limited landslide information. Landslides 2014, 11, 463–480. [Google Scholar] [CrossRef]
- Pellicani, R.; Parisi, A.; Iemmolo, G.; Apollonio, C. Economic Risk Evaluation in Urban Flooding and Instability-Prone Areas: The Case Study of San Giovanni Rotondo (Southern Italy). Geosciences 2018, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Barbano, A.; Braca, G.; Bussettini, M.; Dessì, B.; Inghilesi, R.; Lastoria, B.; Monacelli, G.; Morucci, S.; Piva, F.; Sinapi, L.; et al. Proposta Metodologica per L’aggiornamento delle Mappe di Pericolosità e di Rischio—Attuazione della Direttiva 2007/60/CE Relativa alla Valutazione e alla Gestione dei Rischi da Alluvioni (Decreto Legislativo n.49/2010); ISPRA: Rome, Italy, 2012. Available online: http://www.isprambiente.gov.it/files/pubblicazioni/manuali-lineeguida/MLG_82_2012.pdf (accessed on 11 March 2020).
- Huizinga, J.; de Moel, H.; Szewczyk, W. Global Flood Depth-Damage Functions—Methodology and the Database with Guidelines; Joint Research Centre, Publications Office of the European Union: Luxembourg, 2017. [Google Scholar] [CrossRef]
- Sezione di Protezione Civile—Regione Puglia, Annali Idrologici. Available online: http://www.protezionecivile.puglia.it (accessed on 11 March 2020).
- Council Directive 92/43/EEC of the Council of The European Communities of 21 May 1992 on the Conservation of Natural Habitats and of Wild Fauna and Flora. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:31992L0043 (accessed on 11 March 2020).
- Damiani, L.; Petrillo, A.; Ranieri, G. The Erosion along the Apulian Coast Near the Ofanto River. In Coastal Engineering V; WIT Press: Southampton, UK, 2003; Volume 70, pp. 407–418. [Google Scholar]
- FLO-2D Inc. FLO-2D Users Manual; FLO-2D Inc.: Nutrioso, AR, USA, 2001. [Google Scholar]
- Autorità di Bacino Distrettuale dell’Appennino Meridionale Sede Puglia(ex Autorità di Bacino della Puglia)—Sistema Informativo Meteo Oceanografico delle coste Pugliesi (SIMOP). Available online: http://93.51.158.171/web/simop/home (accessed on 17 March 2020).
- Damiani, L.; Bruno, M.F.; Molfetta, M.G.; Nobile, B. Coastal zone monitoring in apulia region: First analysis on meteomarine climate. In Proceedings of the 5th International Symposium on Environmental Hydraulics (ISEH 2007), Tempe, AZ, USA, 4–7 December 2007. [Google Scholar]
- NDBC. NDBC Technical Document 09-02, Handbook of Automated Data Quality Control Checks and Procedures; NDBC: Hancock County, MS, USA, 2009.
- Bruno, M.F.; Molfetta, M.G.; Petrillo, A.F. The influence of interannual variability of mean sea level in the Adriatic Sea on extreme values. J. Coast. Res. 2014, 70, 241–246. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains USGS Survey Water Supply Paper 2339; USGS: Denver, CO, USA, 1989; pp. 1–38. [CrossRef] [Green Version]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Book Company: New York, NY, USA, 1959; p. 113. [Google Scholar]
- Copertino, V.A.; Fiorentino, M. Valutazione Delle Piene in Puglia; Tipolitografia La Modernissima: Lamezia Terme, Italy, 1994. [Google Scholar]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-Component Extreme Value Distribution for Flood Frequency Analysis. Water Resour. Res. 1984, 20, 847–856. [Google Scholar] [CrossRef]
- Fiorentino, V.; Gabriele, S.; Rossi, F.; Versace, P. Hierarchical approach for regional flood frequency analysis. In Regional Flood Frequency Analysis; Singh, V.P., Ed.; D. Reidel: Norwell, MA, USA, 1987; pp. 35–49. [Google Scholar]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Penta, A. Distribuzione di probabilità del massimo annuale dell’altezza di pioggia giornaliera su un bacino. In Proceedings of the Atti XIV Convegno di Idraulica e Costruzioni Idrauliche, Napoli, Italy, 10–12 October 1974. [Google Scholar]
- U.S. Department of Agriculture. Urban Hydrology for Small Watersheds. Technical Release 55 (TR-55), 2nd ed.; Natural Resources Conservation Service, Conservation Engineering Division: Washington, DC, USA, 1986.
- Zhang, W.Y. Application of NRCS-CN method for estimation of watershed runoff and disaster risk. Geomat. Nat. Hazards Risk 2019, 10, 2220–2238. [Google Scholar] [CrossRef] [Green Version]
- Satheeshkumar, S.; Venkateswaran, S.; Kannan, R. Rainfall–runoff estimation using SCS–CN and GIS approach in the Pappiredipatti watershed of the Vaniyar sub basin, South India. Model. Earth Syst. Environ. 2017, 3, 24. [Google Scholar] [CrossRef]
- Mockus, V. Letter from Victor Mockus to Orrin Ferris; U.S. Department of Agriculture Soil Conservation Service: Lanham, MD, USA, 1964.
- Fiorentino, M. La valutazione dei volumi di piena nelle reti di drenaggio urbano. Idrotecnica 1985, 3, 141–152. [Google Scholar]
- Bacchi, B.; Franchini, M.; Galeati, G.; Ranzi, R. Parametrizzazione e regionalizzazione della curva di riduzione dei massimi annuali delle portate medie su assegnata durata. In Proceedings of the Atti del XXVII Convegno di Idraulica e Costruzioni Idrauliche, Potenza, Italy, 16–19 September 2000; Volume 2, pp. 129–136. [Google Scholar]
- Fiorentino, M.; Margiotta, M.R. La valutazione dei volumi di piena e il calcolo semplificato dell’effetto di laminazione di grandi invasi. In Tecniche per la Difesa Dall’Inquinamento; G.Frega, Editoriale BIOS: Cosenza, Italy, 1997; pp. 203–222. [Google Scholar]
- Doodson, A.T. The analysis of tidal observations for 29 days. Int. Hydrogr. Rev. 1954, 31, 63–71. [Google Scholar]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- De Girolamo, P.; Contini, P. Impatto morfologico di opere a mare: Casi di studio. In Proceedings of the Atti VIII Convegno AIOM, Lerici, Italy, 28–29 May 1998. [Google Scholar]
- U.S. Army Engineer Waterways Experiment Station; U.S. Government Printing Office. Shore Protection Manual, 4th ed.; U.S. Army Engineer Waterways Experiment Station, U.S. Government Printing Office: Washington, DC, USA, 1984; Volume 2.
- Franco, L.; Piscopia, R.; Corsini, S.; Inghilesi, R. L’Atlante Delle Onde nei Mari Italiani Italian Wave Atlas, Full Final Report; APAT-University of Roma Tre, AIPCN Italian Section and Italia Navigando: Roma, Italy, 2004. [Google Scholar]
- Goda, Y. Statistical Variability of Sea State Parameters as a Function of Wave Spectrum. Coast. Eng. Jpn. 1988, 31, 39–52. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef] [Green Version]
- Ris, R.C.; Holthuijsen, L.H.; Booij, N. A third-generation wave model for coastal regions: 2. Verification. J. Geophys. Res. 1999, 104, 7667–7681. [Google Scholar] [CrossRef]
- Hunt, J.N. On the damping of gravity waves propagated over a permeable surface. J. Geophys. Res. 1959, 64, 437–442. [Google Scholar] [CrossRef]
- Komar, P.D. Beach Processes and Sedimentation; Simon & Schuster: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Nielsen, P.; Hanslow, D.J. Wave Runup Distributions on Natural Beaches. J. Coast. Res. 1991, 7, 1139–1152. [Google Scholar]
- Massel, S.R.; Pelinovsky, E.N. Run-Up of Dispersive and Breaking Waves on Beaches. Oceanologia 2001, 43, 61–97. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- McCall, R.T.; van Thiel de Vries, J.S.M.; Plant, N.G.; van Dongeren, A.R.; Roelvink, J.A.; Thompson, D.M.; Reniers, A.J. Two-dimensional time dependent hurricane overwash and erosion modeling at Santa Rosa Island. Coast. Eng. 2010, 57, 668–683. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Glade, T. Vulnerability assessment in landslide risk analysis. Die Erde 2003, 134, 121–138. [Google Scholar]
- The Mekong River Commission Secretariat. Best Practise Guidelines for Flood Risk Assessment; The Mekong River Commission Secretariat: Vientiane, Laos, 2009. [Google Scholar]
- Lee, E.M.; Jones, D.K.C. Landslide Risk Assessment, 2nd ed.; ICE Publishing: London, UK, 2014; pp. 497–509. [Google Scholar]
- SIT Puglia, Cartografia Tematica. Available online: http://www.sit.puglia.it/portal/portale_cartografie_tecniche_tematiche/home (accessed on 11 March 2020).
- Klerk, W.J.; Winsemius, H.C.; van Verseveld, W.J.; Bakker, A.M.R.; Diermanse, F.L.M. The co-incidence of storm surges and extreme discharges within the rhine–meuse delta. Environ. Res. Lett. 2015, 10, 035005. [Google Scholar] [CrossRef] [Green Version]
- Bevacqua, E.; Maraun, D.; Hobæk Haff, I.; Widmann, M.; Vrac, M. Multivariate statistical modelling of compound events via pair-copula constructions: Analysis of floods in Ravenna (Italy). Hydrol. Earth Syst. Sci. 2017, 21, 2701–2723. [Google Scholar] [CrossRef] [Green Version]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Autorità di Bacino del Fiume Tevere, Piano Stralcio di Assetto Idrogeologico (PAI). Available online: http://www.abtevere.it (accessed on 11 March 2020).


| Sub-Catchment | CN(III) | Q Peak (m3/s) | |||
|---|---|---|---|---|---|
| TR = 1 year | TR = 30 years | TR = 50 years | TR = 100 years | ||
| TRIBUTARY 1 | 87 | 11.08 | 29.64 | 34.75 | 41.70 |
| TRIBUTARY 2 | 86 | 1.05 | 13.26 | 15.48 | 18.56 |
| TRIBUTARY 3 | 88 | 0.83 | 9.39 | 10.92 | 13.04 |
| CHANNEL 1 | 88 | 0.59 | 7.51 | 8.76 | 10.51 |
| CHANNEL 2 | 90 | 0.53 | 4.66 | 5.36 | 6.33 |
| CHANNEL 3 | 90 | 0.66 | 5.33 | 6.12 | 7.19 |
| CHANNEL 4 UPSTREAM | 90 | 1.02 | 12.19 | 14.20 | 16.99 |
| CHANNEL 4 DOWNSTREAM | 87 | 0.32 | 2.97 | 3.43 | 4.06 |
| PELUSO 1 | 89 | 20.70 | 55.35 | 64.90 | 77.87 |
| PELUSO 2 | 92 | 0.13 | 1.24 | 1.43 | 1.69 |
| PELUSO 3 | 92 | 0.09 | 0.95 | 1.11 | 1.32 |
| PELUSO 4 | 89 | 0.02 | 0.29 | 0.33 | 0.40 |
| Sea Level | TR = 1 year | TR = 30 years | TR = 50 years | TR = 100 years |
|---|---|---|---|---|
| Hm0 (m) | 3.4 | 5.63 | 6.03 | 6.04 |
| R2% (m) | 0.68 | 1.12 | 1.20 | 1.27 |
| Tidal residual (m) | 0.28 | 0.36 | 0.38 | 0.4 |
| Astronomical tide (m) | 0.2 | 0.2 | 0.2 | 0.2 |
| Total sea level (m) | 1.16 | 1.68 | 1.78 | 1.87 |
| Categories of Elements at Risk | Vulnerability (Ve) | ||
|---|---|---|---|
| h (m); v (m/s) | |||
| Buildings | Ve(h) = 0.5∙h | ||
| Other structures | 0.5∙h | if v < 2 | |
| Ve(h,v) = | |||
| 0.35∙h∙(1 + 0.25∙v) | if v ≥ 2 | ||
| Specialized land use | Ve(h,v) = | h | if v < 0.25 |
| h∙(1 + v) | if v ≥ 0.25 | ||
| Unspecialized land use | Ve(h,v) = | 0.25∙h | if v < 0.25 |
| 0.25∙h∙(1 + v) | if v ≥ 0.25 | ||
| Infrastructures | Ve(h)—Damage function from [40,41] | ||
| Elements at Risk | TR | Exceedance Probability | Amount (sqm) | Economic Value | Consequences | Total Economic Losses |
|---|---|---|---|---|---|---|
| Buildings | 1 | 1 | 163 | €891,831 | €163,634 | |
| Other structures | 1 | 1 | 365 | €35,470 | €4661 | |
| Road | 1 | 1 | 36,762 | €1,028,209 | €207,380 | |
| Specialized land use | 1 | 1 | 1903 | €4563 | €1783 | |
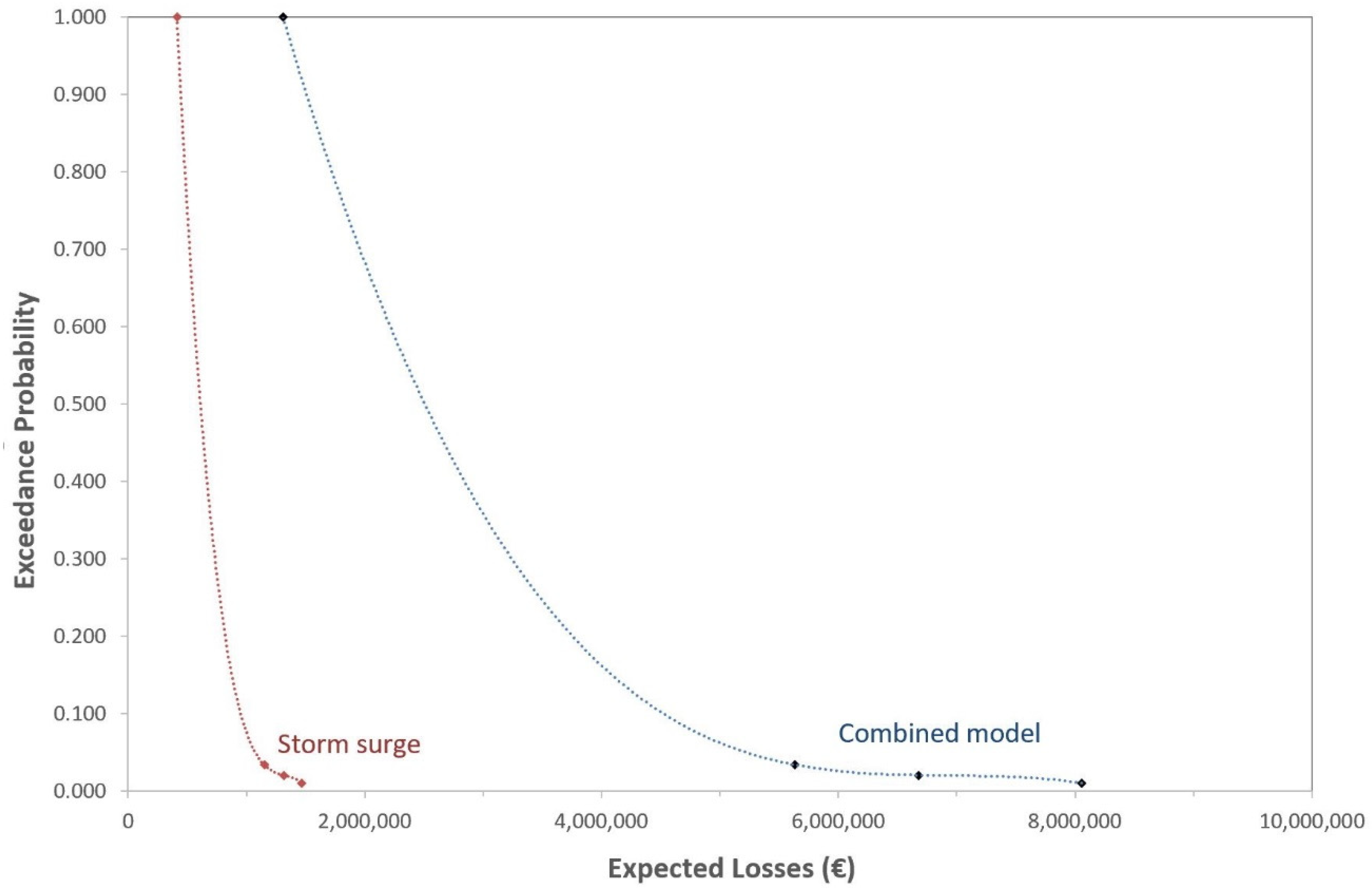
| Unspecialized land use | 1 | 1 | 585,449 | €315,691 | €34,665 | €412,123 |
| Buildings | 30 | 0.033 | 1864 | €3,432,475 | €633,715 | |
| Other structures | 30 | 0.033 | 632 | €61,271 | €13,060 | |
| Road | 30 | 0.033 | 57,393 | €1,604,410 | €414,963 | |
| Specialized land use | 30 | 0.033 | 1903 | €4563 | €4080 | |
| Unspecialized land use | 30 | 0.033 | 728,335 | €421,024 | €84,052 | €1,149,870 |
| Buildings | 50 | 0.02 | 2234 | €4,379,509 | €774,118 | |
| Other structures | 50 | 0.02 | 632 | €61,271 | €13,640 | |
| Road | 50 | 0.02 | 59,299 | €1,657,620 | €435,358 | |
| Specialized land use | 50 | 0.02 | 1925 | €4616 | €4212 | |
| Unspecialized land use | 50 | 0.02 | 739,636 | €427,151 | €88,295 | €1,315,623 |
| Buildings | 100 | 0.01 | 2407 | €4,721,521 | €880,093 | |
| Other structures | 100 | 0.01 | 632 | €61,271 | €14,794 | |
| Road | 100 | 0.01 | 64,811 | €1,811,336 | €474,252 | |
| Specialized land use | 100 | 0.01 | 1,925.01 | €4616 | €4319 | |
| Unspecialized land use | 100 | 0.01 | 759,036 | €441,781 | €96,043 | €1,469,500 |
| Elements at Risk | TR | Exceedance Probability | Amount (sqm) | Economic Value | Consequences | Total Economic Losses |
|---|---|---|---|---|---|---|
| Buildings | 1 | 1 | 917 | €1,777,765 | €271,608 | |
| Other structures | 1 | 1 | 365 | €31,210 | €3689 | |
| Road | 1 | 1 | 98,534 | €2,703,967 | €517,629 | |
| Specialized land use | 1 | 1 | 56,000 | €127,087 | €49,089 | |
| Unspecialized land use | 1 | 1 | 4,050,000 | €6,241,545 | €466,578 | €1,308,593 |
| Buildings | 30 | 0.033 | 5967 | €10,291,706 | €1,867,053 | |
| Other structures | 30 | 0.033 | 633 | €61,568 | €13,090 | |
| Road | 30 | 0.033 | 270,945 | €7,408,776 | €1,592,121 | |
| Specialized land use | 30 | 0.033 | 316,000 | €559,501 | €251,005 | |
| Unspecialized land use | 30 | 0.033 | 12,780,000 | €21,062,380 | €1,912,155 | €5,635,423 |
| Buildings | 50 | 0.02 | 7030 | €11,999,597 | €2,233,376 | |
| Other structures | 50 | 0.02 | 633 | €61,568 | €13,759 | |
| Road | 50 | 0.02 | 302,982 | €8,278,693 | €1,817,806 | |
| Specialized land use | 50 | 0.02 | 400,000 | €683,770 | €319,958 | |
| Unspecialized land use | 50 | 0.02 | 14,440,000 | €23,938,683 | €2,291,826 | €6,676,725 |
| Buildings | 100 | 0.01 | 7931 | €13,425,906 | €2,678,795 | |
| Other structures | 100 | 0.01 | 633 | €61,568 | €14,847 | |
| Road | 100 | 0.01 | 350,619 | €9,558,971 | €2,125,702 | |
| Specialized land use | 100 | 0.01 | 524,000 | €861,115 | €412,420 | |
| Unspecialized land use | 100 | 0.01 | 16,680,000 | €27,819,598 | €2,826,192 | €8,057,956 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apollonio, C.; Bruno, M.F.; Iemmolo, G.; Molfetta, M.G.; Pellicani, R. Flood Risk Evaluation in Ungauged Coastal Areas: The Case Study of Ippocampo (Southern Italy). Water 2020, 12, 1466. https://doi.org/10.3390/w12051466
Apollonio C, Bruno MF, Iemmolo G, Molfetta MG, Pellicani R. Flood Risk Evaluation in Ungauged Coastal Areas: The Case Study of Ippocampo (Southern Italy). Water. 2020; 12(5):1466. https://doi.org/10.3390/w12051466
Chicago/Turabian StyleApollonio, Ciro, Maria Francesca Bruno, Gabriele Iemmolo, Matteo Gianluca Molfetta, and Roberta Pellicani. 2020. "Flood Risk Evaluation in Ungauged Coastal Areas: The Case Study of Ippocampo (Southern Italy)" Water 12, no. 5: 1466. https://doi.org/10.3390/w12051466





