The Effect of Habitat Structure Boulder Spacing on Near-Bed Shear Stress and Turbulent Events in a Gravel Bed Channel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Data Filtering
2.3. Calculation of Bed Shear Stress
2.4. Quadrant Analysis
- Quadrant 1: outward interactions ()
- Quadrant 2: ejection events ()
- Quadrant 3: inward interactions ()
- Quadrant 4: sweep events ().
3. Results and Discussion
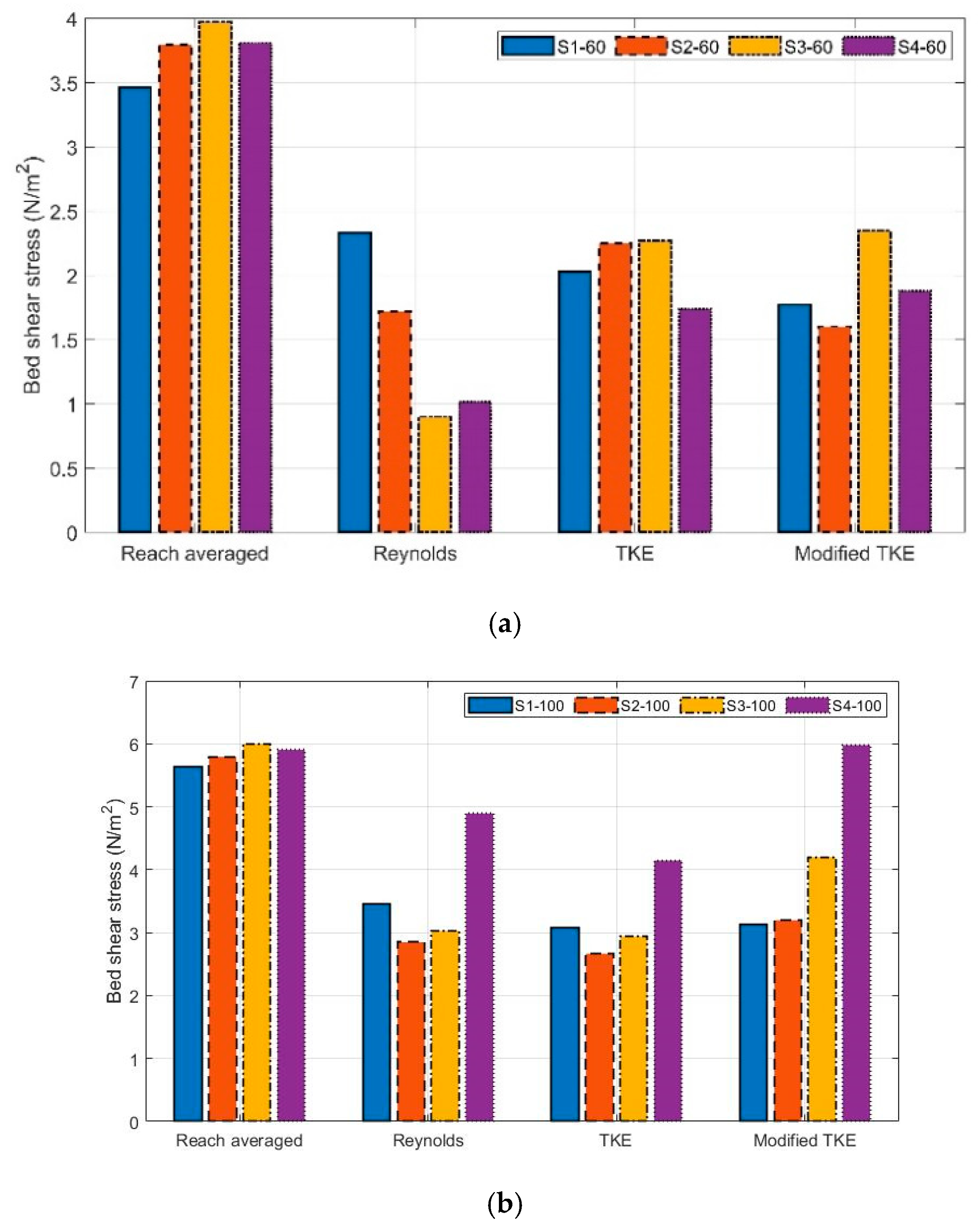
3.1. Near-Bed Shear Stress
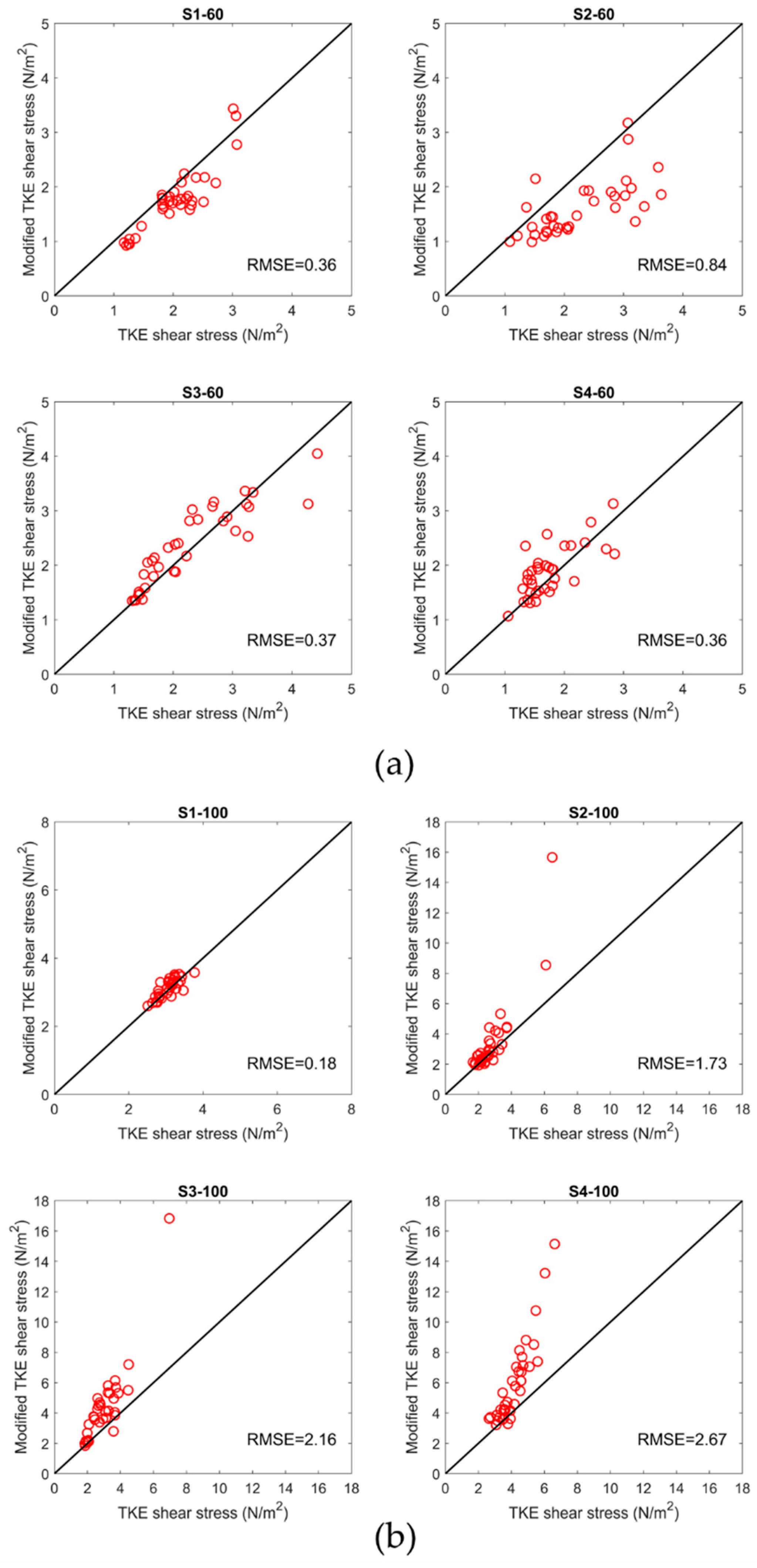
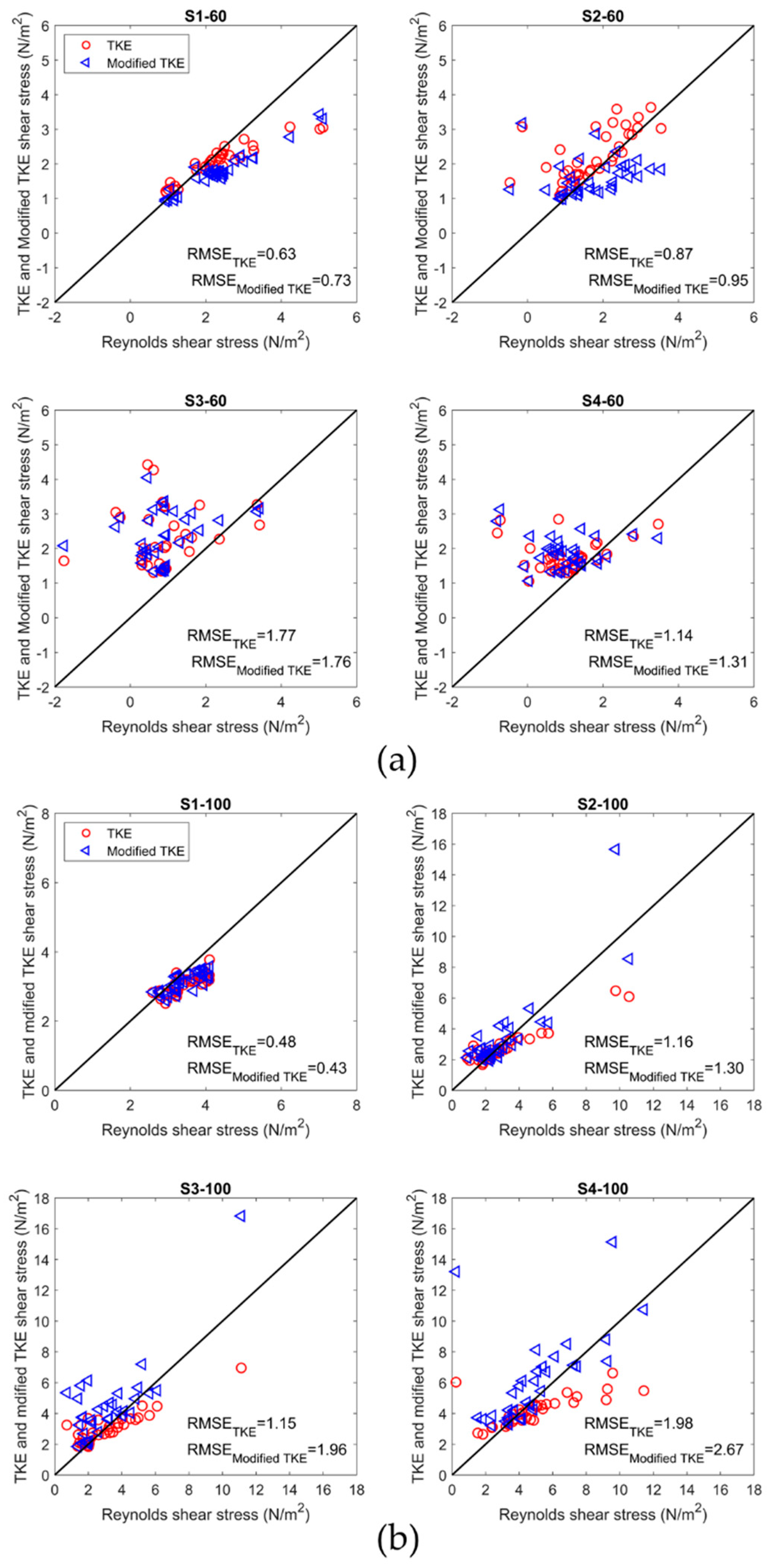
3.2. Relative Performance of the Reynolds, TKE, and Modified TKE Methods
3.3. Spatial Distribution of Near-Bed Shear Stress
3.4. Near-Bed Turbulent Events
4. Conclusions
- For all scenarios, the reach-averaged method led to a significantly higher reach-averaged bed shear stress. For the unsubmerged condition, the Reynolds method resulted in a significantly lower near-bed shear stress between the point-methods, while, at submerged condition, all the point-methods showed very similar results.
- At unsubmerged condition, the effect of the boulder spacing on the variation of near-bed shear stress estimated from the Reynolds method was different from the TKE and modified TKE methods, while, at submerged condition, all of the point-methods showed a similar trend.
- At submerged condition, the densest boulder spacing led to the highest near-bed shear stress for all point-methods. However, for the unsubmerged condition, maximum near-bed shear stress varied for different methods and boulder spacing.
- At unsubmerged condition, the TKE and modified TKE methods can be used interchangeably for estimation of the near-bed shear stress in the presence of boulders; however, applying appropriate and coefficients is required to obtain more reliable results. For a comprehensive comparison of the Reynolds method with two other point-methods, more measurements are necessary, especially at unsubmerged condition.
- At unsubmerged condition, denser boulder spacing led to a more uniform contribution of turbulent events to the Reynolds shear stress. At submerged condition, decreased ejection events downstream of boulders in the large and medium boulder spacing may reduce the sediment entrainment and suspension.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, M.P.; O’donoghue, T.; Alsina, J.M.; Baldock, T.E. Direct bed shear stress measurements in bore-driven swash. Coast. Eng. 2009, 56, 853–867. [Google Scholar] [CrossRef] [Green Version]
- Howe, D.; Blenkinsopp, C.E.; Turner, I.L.; Baldock, T.E.; Puleo, J.A. Direct measurements of bed shear stress under swash flows on steep laboratory slopes at medium to prototype scales. J. Mar. Sci. Eng. 2019, 7, 358. [Google Scholar] [CrossRef] [Green Version]
- Mirfenderesk, H.; Young, I.R. Direct measurements of the bottom friction factor beneath surface gravity waves. Appl. Ocean Res. 2003, 25, 269–287. [Google Scholar] [CrossRef]
- Park, J.H.; Do Kim, Y.; Park, Y.S.; Jo, J.A.; Kang, K. Direct measurement of bottom shear stress under high-velocity flow conditions. Flow Meas. Instrum. 2016, 50, 121–127. [Google Scholar] [CrossRef]
- Park, J.H.; Do Kim, Y.; Park, Y.S.; Jung, D.G. Direct measurement of bed shear stress using adjustable shear plate over a wide range of Froude numbers. Flow Meas. Instrum. 2019, 65, 122–127. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows, IAHR; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Babaeyan-Koopaei, K.; Ervine, D.A.; Carling, P.A.; Cao, Z. Velocity and turbulence measurements for two overbank flow events in River Severn. J. Hydraul. Eng. 2002, 128, 891–900. [Google Scholar] [CrossRef]
- Wilcock, P.R. Estimating local bed shear stress from velocity observations. Water Resour. Res. 1996, 32, 3361–3366. [Google Scholar] [CrossRef]
- Williams, J.J. Drag and sediment dispersion over sand waves. Estuar. Coast. Shelf Sci. 1995, 41, 659–687. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D.; McEwan, I.; Griffiths, G. Spatially averaged open-channel flow over rough bed. J. Hydraul. Eng. 2001, 127, 123–133. [Google Scholar] [CrossRef]
- Kim, S.-C.; Friedrichs, C.T.; Maa, J.-Y.; Wright, L.D. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Comparing different methods of bed shear stress estimates in simple and complex flow fields. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2004, 29, 1403–1415. [Google Scholar] [CrossRef]
- Lichtneger, P.; Sindelar, C.; Schobesberger, J.; Hauer, C.; Habersack, H. Experimental investigation on local shear stress and turbulence intensities over a rough non-uniform bed with and without sediment using 2D particle image velocimetry. Int. J. Sediment Res. 2020, 35, 193–202. [Google Scholar] [CrossRef]
- Kostaschuk, R.; Villard, P.; Best, J. Measuring velocity and shear stress over dunes with acoustic Doppler profiler. J. Hydraul. Eng. 2004, 130, 932–936. [Google Scholar] [CrossRef]
- Sime, L.C.; Ferguson, R.I.; Church, M. Estimating shear stress from moving boat acoustic Doppler velocity measurements in a large gravel bed river. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Federal Interagency Stream Restoration Working Group (15 US Federal Agencies). Stream Corridor Restoration: Principles, Processes, and Practices; GPO Item No. 0120-A; FISRWG: Washington, DC, USA, 1998. [Google Scholar]
- Kang, S.; Hill, C.; Sotiropoulos, F. On the turbulent flow structure around an instream structure with realistic geometry. Water Resour. Res. 2016, 52, 7869–7891. [Google Scholar] [CrossRef]
- Marttila, H.; Turunen, J.; Aroviita, J.; Tammela, S.; Luhta, P.-L.; Muotka, T.; Kløve, B. Restoration increases transient storages in boreal headwater streams. River Res. Appl. 2018, 34, 1278–1285. [Google Scholar] [CrossRef]
- Henry, C.P.; Amoros, C.; Roset, N. Restoration ecology of riverine wetlands: A 5-year post-operation survey on the Rhone River, France. Ecol. Eng. 2002, 18, 543–554. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhu, D.Z.; Rajaratnam, N. Mean flow characteristics in a rock-ramp-type fish pass. J. Hydraul. Eng. 2014, 140, 156–168. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhu, D.Z.; Rajaratnam, N. Turbulence characteristics in a rock-ramp-type fish pass. J. Hydraul. Eng. 2015, 141, 04014075. [Google Scholar] [CrossRef]
- Baki, A.B.M.; Zhang, W.; Zhu, D.Z.; Rajaratnam, N. Flow structures in the vicinity of a submerged boulder within a boulder array. J. Hydraul. Eng. 2016, 143, 04016104. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Tsakiris, A.G. Boulder effects on turbulence and bedload transport. In Gravel-Bed Rivers; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2017; pp. 33–72. [Google Scholar]
- Tsakiris, A.G.; Papanicolaou, A.N.T.; Hajimirzaie, S.M.; Buchholz, J.H.J. Influence of collective boulder array on the surrounding time-averaged and turbulent flow fields. J. Mt. Sci. 2014, 11, 1420–1428. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Dermisis, D.C.; Elhakeem, M. Investigating the role of clasts on the movement of sand in gravel bed rivers. J. Hydraul. Eng. 2011, 137, 871–883. [Google Scholar] [CrossRef]
- Hardy, R.J.; Best, J.L.; Lane, S.N.; Carbonneau, P.E. Coherent flow structures in a depth-limited flow over a gravel surface: The role of near-bed turbulence and influence of Reynolds number. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Van Rijn, L.C. Critical movement of large rocks in currents and waves. Int. J. Sediment Res. 2019, 34, 387–398. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Kramer, C.M.; Tsakiris, A.G.; Stoesser, T.; Bomminayuni, S.; Chen, Z. Effects of a fully submerged boulder within a boulder array on the mean and turbulent flow fields: Implications to bedload transport. Acta Geophys. 2012, 60, 1502–1546. [Google Scholar] [CrossRef]
- Yager, E.M.; Kirchner, J.W.; Dietrich, W.E. Calculating bed load transport in steep boulder bed channels. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Shamloo, H.; Rajaratnam, N.; Katopodis, C. Hydraulics of simple habitat structures. J. Hydraul. Res. 2001, 39, 351–366. [Google Scholar] [CrossRef]
- Dey, S.; Sarkar, S.; Bose, S.K.; Tait, S.; Castro-Orgaz, O. Wall-wake flows downstream of a sphere placed on a plane rough wall. J. Hydraul. Eng. 2011, 137, 1173–1189. [Google Scholar] [CrossRef]
- Monsalve, A.; Yager, E.M. Bed surface adjustments to spatially variable flow in low relative submergence regimes. Water Resour. Res. 2017, 53, 9350–9367. [Google Scholar] [CrossRef]
- Ghilardi, T.; Schleiss, A. Influence of immobile boulders on bedload transport in a steep flume. In Proceedings of the 34th IAHR World Congress, Brisbane, Australia, 26 June–1 July 2011; pp. 3473–3480. [Google Scholar]
- Ghilardi, T.; Schleiss, A. Steep flume experiments with large immobile boulders and wide grain size distribution as encountered in alpine torrents. In Proceedings of the International conference on fluvial Hydraulics, San José, Costa Rica, 5–7 September 2012; Taylor & Francis Group, CRC Press: London, UK, 2012; pp. 407–414. [Google Scholar]
- Papanicolaou, A.N.; Tsakiris, A.G.; Wyssmann, M.A.; Kramer, C.M. Boulder Array Effects on Bedload Pulses and Depositional Patches. J. Geophys. Res. Earth Surf. 2018, 123, 2925–2953. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Diplas, P.; Dancey, C.L.; Balakrishnan, M. Surface Roughness Effects in Near-Bed Turbulence: Implications to Sediment Entrainment. J. Eng. Mech. 2001, 127, 211–218. [Google Scholar] [CrossRef]
- Shih, W.; Diplas, P.; Celik, A.O.; Dancey, C. Accounting for the role of turbulent flow on particle dislodgement via a coupled quadrant analysis of velocity and pressure sequences. Adv. Water Resour. 2017, 101, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.W.; Liu, Y.; Stoesser, T. Influence of Boulder Concentration on Turbulence and Sediment Transport in Open-Channel Flow Over Submerged Boulders. J. Geophys. Res. Earth Surf. 2017, 122, 2392–2410. [Google Scholar] [CrossRef]
- Tang, C.; Li, Y.; Acharya, K.; Du, W.; Gao, X.; Luo, L.; Yu, Z. Impact of intermittent turbulent bursts on sediment resuspension and internal nutrient release in Lake Taihu, China. Environ. Sci. Pollut. Res. 2019, 26, 16519–16528. [Google Scholar] [CrossRef] [PubMed]
- Salim, S.; Pattiaratchi, C.; Tinoco, R.; Coco, G.; Hetzel, Y.; Wijeratne, S.; Jayaratne, R. The influence of turbulent bursting on sediment resuspension under fluvial unidirectional currents. Earth Surf. Dyn. 2016, 5, 399–415. [Google Scholar] [CrossRef] [Green Version]
- Mohajeri, S.H.; Righetti, M.; Wharton, G.; Romano, G.P. On the structure of turbulent gravel bed flow: Implications for sediment transport. Adv. Water Resour. 2016, 92, 90–104. [Google Scholar] [CrossRef]
- Lacey, R.J.; Rennie, C.D. Laboratory investigation of turbulent flow structure around a bed-mounted cube at multiple flow stages. J. Hydraul. Eng. 2012, 138, 71–84. [Google Scholar] [CrossRef]
- Bretón, F.; Baki, A.B.M.; Link, O.; Zhu, D.Z.; Rajaratnam, N. Flow in nature-like fishway and its relation to fish behaviour. Can. J. Civ. Eng. 2013, 40, 567–573. [Google Scholar] [CrossRef]
- Polatel, C. Large-Scale Roughness Effect on Free-Surface and Bulk Flow Characteristics in Open-Channel Flows. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2006. [Google Scholar]
- Tan, L.; Curran, J.C. Comparison of Turbulent Flows over Clusters of Varying Density. J. Hydraul. Eng. 2012, 138, 1031–1044. [Google Scholar] [CrossRef]
- Paphitis, D. Sediment movement under unidirectional flows: An assessment of empirical threshold curves. Coast. Eng. 2001, 43, 227–245. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-channel Flow Measurements with a Laser Doppler Anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Dombroski, D.E.; Crimaldi, J.P. The accuracy of acoustic Doppler velocimetry measurements in turbulent boundary layer flows over a smooth bed. Limnol. Oceanogr. Methods 2007, 5, 23–33. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Cea, L.; Puertas, J.; Pena, L. Velocity measurements on highly turbulent free surface flow using ADV. Exp. Fluids 2007, 42, 333–348. [Google Scholar] [CrossRef]
- Wahl, T.L. Analyzing ADV data using WinADV. In Proceedings of the Joint Conference on Water Resources Engineering and Water Resources Planning and Managmenet, Minneapolis, MI, USA, 30 July-2 August 2000. [Google Scholar]
- Strom, K.B.; Papanicolaou, A.N. ADV measurements around a cluster microform in a shallow mountain stream. J. Hydraul. Eng. 2007, 133, 1379–1389. [Google Scholar] [CrossRef]
- Martin, V.; Fisher, T.S.R.; Millar, R.G.; Quick, M.C. ADV data analysis for turbulent flows: Low correlation problem. In Proceedings of the Hydraulic Measurements and Experimental Methods 2002, Estes Park, CO, USA, 28 July–1 August 2002; pp. 1–10. [Google Scholar]
- Nikora, V.I.; Goring, D.G. ADV measurements of turbulence: Can we improve their interpretation? J. Hydraul. Eng. 1998, 124, 630–634. [Google Scholar] [CrossRef]
- Lacey, R.W.J.; Roy, A.G. Fine-scale characterization of the turbulent shear layer of an instream pebble cluster. J. Hydraul. Eng. 2008, 134, 925–936. [Google Scholar] [CrossRef]
- Buffin-Bélanger, T.; Roy, A.G. Effects of a pebble cluster on the turbulent structure of a depth-limited flow in a gravel-bed river. Geomorphology 1998, 25, 249–267. [Google Scholar] [CrossRef]
- Curran, J.C.; Tan, L. The effect of cluster morphology on the turbulent flows over an armored gravel bed surface. J. Hydro-Environ. Res. 2014, 8, 129–142. [Google Scholar] [CrossRef]
- Liu, D.; Liu, X.; Fu, X.; Wang, G. Quantification of the bed load effects on turbulent open-channel flows: Les-Dem Simulation of Sediment in Turbulent Flow. J. Geophys. Res. Earth Surf. 2016, 121, 767–789. [Google Scholar] [CrossRef]
- Guan, D.; Agarwal, P.; Chiew, Y.-M. Quadrant Analysis of Turbulence in a Rectangular Cavity with Large Aspect Ratios. J. Hydraul. Eng. 2018, 144, 04018035. [Google Scholar] [CrossRef]
- Sadeque, M.A.; Rajaratnam, N.; Loewen, M.R. Flow around Cylinders in Open Channels. J. Eng. Mech. 2008, 134, 60–71. [Google Scholar] [CrossRef]
- Hajimirzaie, S.M.; Tsakiris, A.G.; Buchholz, J.H.J.; Papanicolaou, A.N. Flow characteristics around a wall-mounted spherical obstacle in a thin boundary layer. Exp. Fluids 2014, 55, 1762. [Google Scholar] [CrossRef]
- Zexing, X.; Chenling, Z.; Qiang, Y.; Xiekang, W.; Xufeng, Y. Hydrodynamics and bed morphological characteristics around a boulder in a gravel stream. Water Supply 2020, 20, 395–407. [Google Scholar] [CrossRef]
- Morris, H.M. Flow in rough conduits. Trans. ASME 1955, 120, 373–398. [Google Scholar]
- Nakagawa, H.; Nezu, I. Prediction of the contributions to the Reynolds stress from bursting events in open-channel flows. J. Fluid Mech. 1977, 80, 99–128. [Google Scholar] [CrossRef]

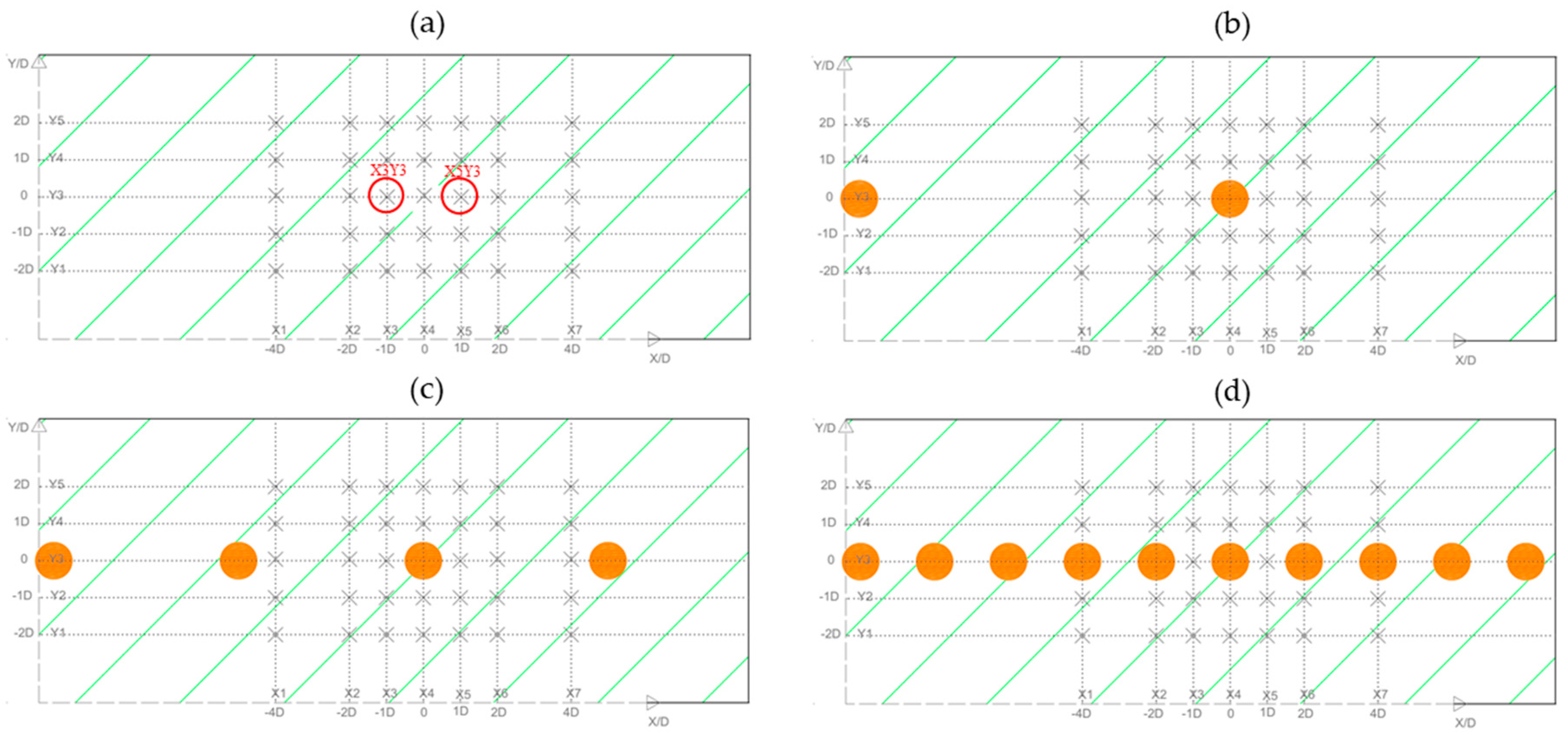
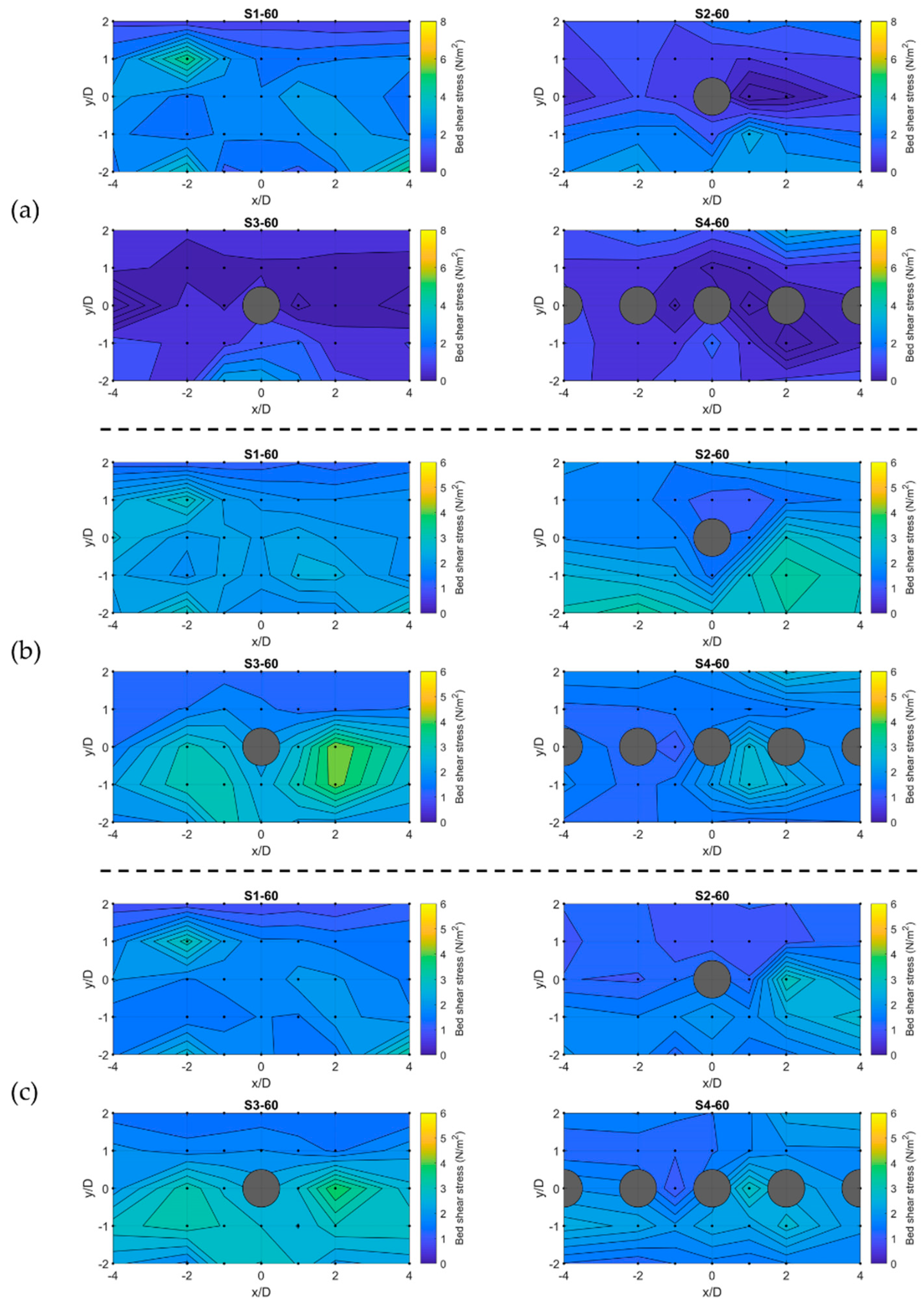
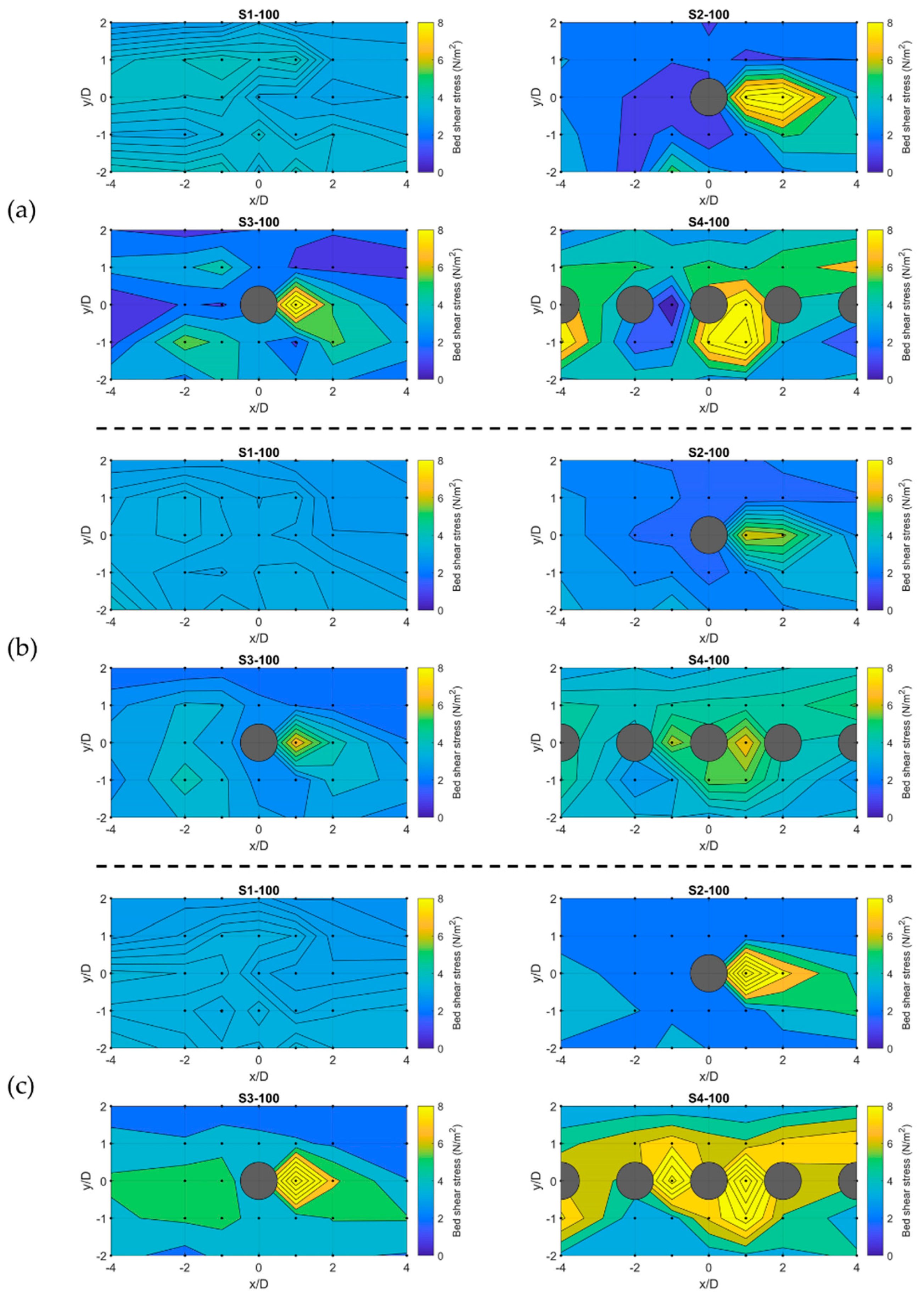
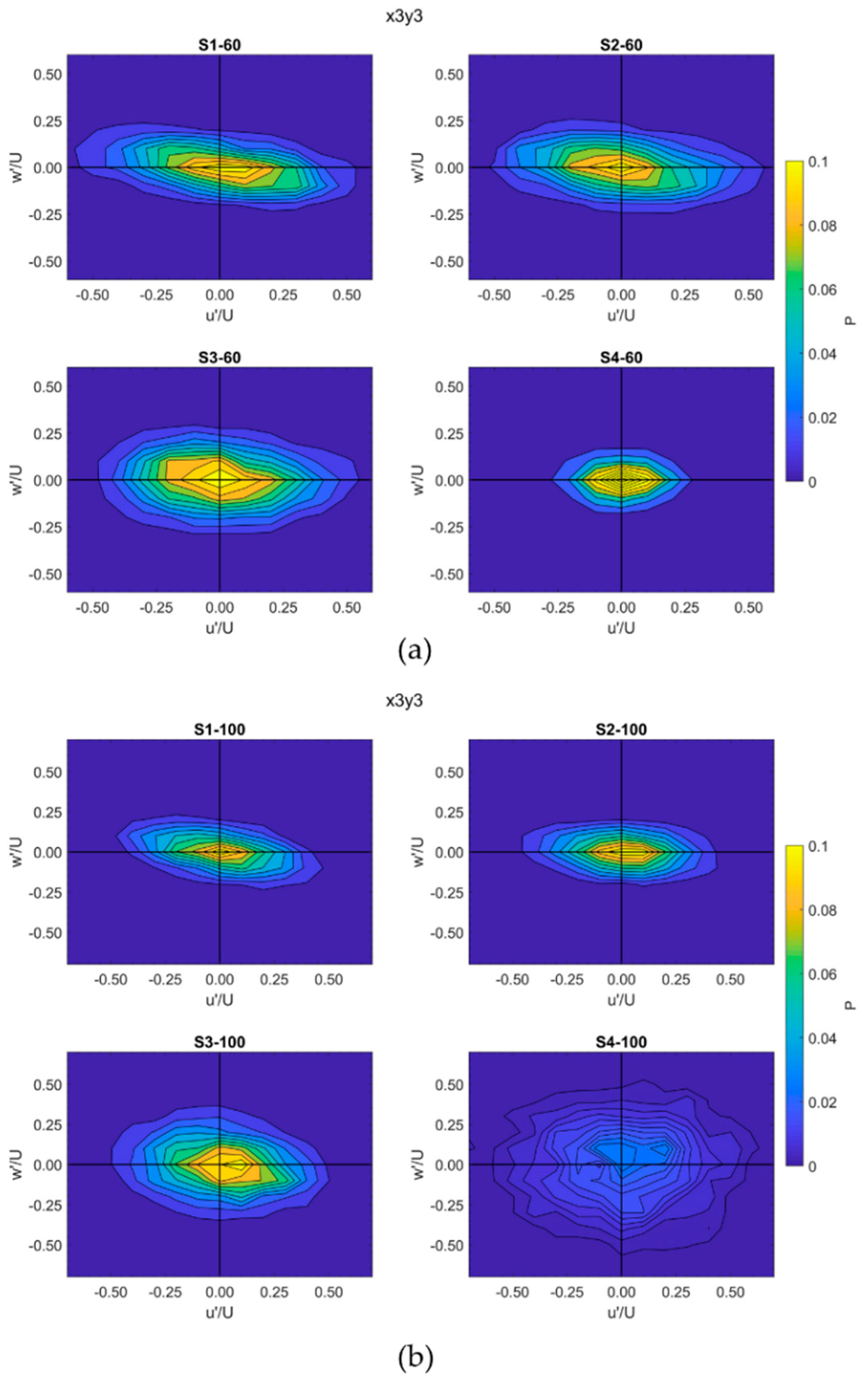

| Scenario | Flow Rate (L/s) | Boulder Spacing | Reach-Averaged Flow Depth (m) | Submergence Ratio |
|---|---|---|---|---|
| S1-60 | 60 | Infinity | 0.082 | - |
| S2-60 | 10D | 0.092 | 0.73 | |
| S3-60 | 5D | 0.098 | 0.78 | |
| S4-60 | 2D | 0.093 | 0.74 | |
| S1-100 | 100 | Infinity | 0.151 | - |
| S2-100 | 10D | 0.157 | 1.25 | |
| S3-100 | 5D | 0.165 | 1.32 | |
| S4-100 | 2D | 0.161 | 1.29 |
| Parameter | P | |||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | Outward | Ejection | Inward | Sweep | Outward | Ejection | Inward | Sweep |
| S1-60 | −0.05 | 0.55 | −0.04 | 0.41 | 0.03 | 0.36 | 0.03 | 0.27 |
| S2-60 | −0.29 | 0.74 | −0.26 | 0.74 | 0.12 | 0.30 | 0.10 | 0.30 |
| S3-60 | −1.50 | 2.17 | −1.50 | 1.83 | 0.21 | 0.30 | 0.21 | 0.25 |
| S4-60 | −10.10 | 12.01 | −9.77 | 8.86 | 0.25 | 0.29 | 0.24 | 0.22 |
| S1-100 | −0.07 | 0.51 | −0.06 | 0.50 | 0.04 | 0.32 | 0.04 | 0.31 |
| S2-100 | −0.74 | 1.25 | −0.64 | 1.11 | 0.18 | 0.31 | 0.16 | 0.27 |
| S3-100 | −0.51 | 1.14 | −0.58 | 0.93 | 0.14 | 0.32 | 0.16 | 0.26 |
| S4-100 | −12.17 | 12.29 | −11.62 | 12.49 | 0.25 | 0.25 | 0.24 | 0.26 |
| Parameter | P | |||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | Outward | Ejection | Inward | Sweep | Outward | Ejection | Inward | Sweep |
| S1-60 | −0.02 | 0.45 | −0.03 | 0.38 | 0.01 | 0.33 | 0.02 | 0.28 |
| S2-60 | 1.24 | −0.57 | 1.14 | −0.84 | 0.30 | 0.14 | 0.27 | 0.20 |
| S3-60 | 4.98 | −2.92 | 3.24 | −4.30 | 0.32 | 0.19 | 0.21 | 0.28 |
| S4-60 | 1.41 | −0.90 | 1.48 | −1.00 | 0.28 | 0.18 | 0.29 | 0.20 |
| S1-100 | −0.08 | 0.59 | −0.10 | 0.49 | 0.05 | 0.34 | 0.06 | 0.28 |
| S2-100 | −0.06 | 0.22 | −0.03 | 0.72 | 0.04 | 0.15 | 0.02 | 0.49 |
| S3-100 | −0.02 | 0.23 | −0.03 | 0.62 | 0.02 | 0.17 | 0.02 | 0.45 |
| S4-100 | −0.05 | 0.39 | −0.03 | 0.49 | 0.03 | 0.27 | 0.02 | 0.34 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golpira, A.; Huang, F.; Baki, A.B.M. The Effect of Habitat Structure Boulder Spacing on Near-Bed Shear Stress and Turbulent Events in a Gravel Bed Channel. Water 2020, 12, 1423. https://doi.org/10.3390/w12051423
Golpira A, Huang F, Baki ABM. The Effect of Habitat Structure Boulder Spacing on Near-Bed Shear Stress and Turbulent Events in a Gravel Bed Channel. Water. 2020; 12(5):1423. https://doi.org/10.3390/w12051423
Chicago/Turabian StyleGolpira, Amir, Fengbin Huang, and Abul B.M. Baki. 2020. "The Effect of Habitat Structure Boulder Spacing on Near-Bed Shear Stress and Turbulent Events in a Gravel Bed Channel" Water 12, no. 5: 1423. https://doi.org/10.3390/w12051423





