A GIS Approach to Analyzing the Spatial Pattern of Baseline Resilience Indicators for Community (BRIC)
Abstract
:1. Introduction
2. Materials and Methods
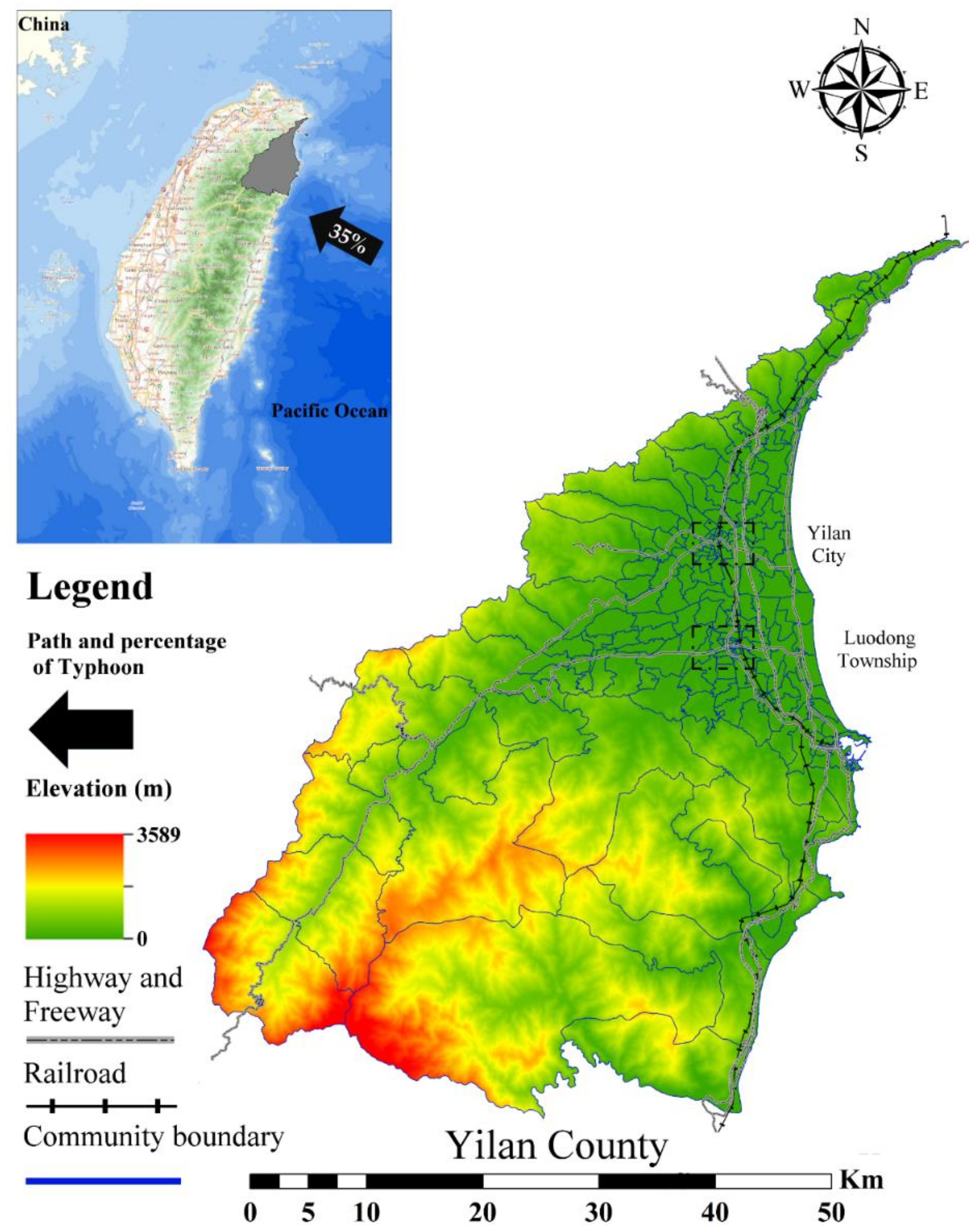
2.1. Study Site
2.2. Resilience Indicator
2.3. Spatial Pattern Analysis
2.4. Geographically Weighted Regression (GWR)
3. Results
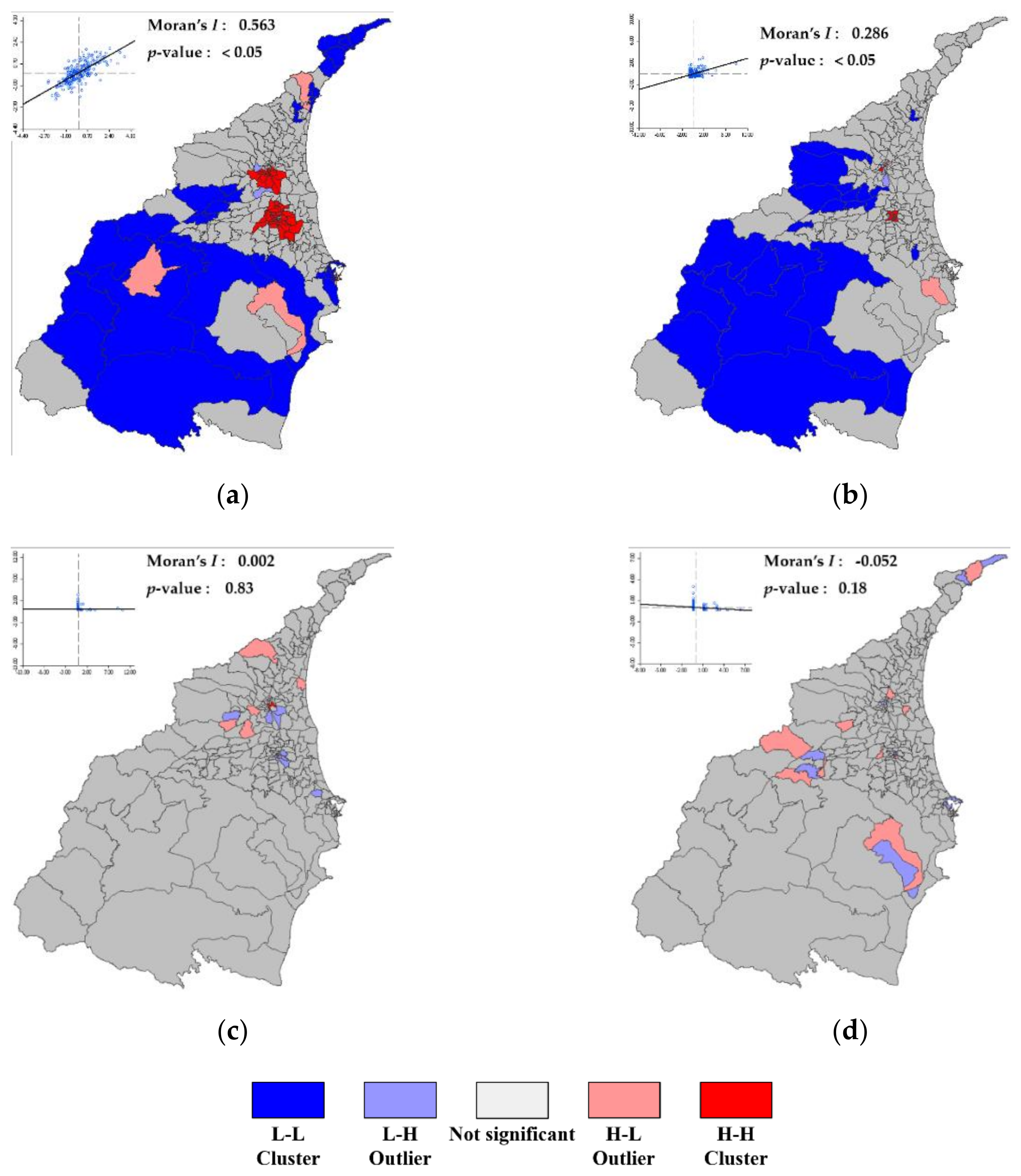
3.1. Global Spatial Autocorrelation Analysis
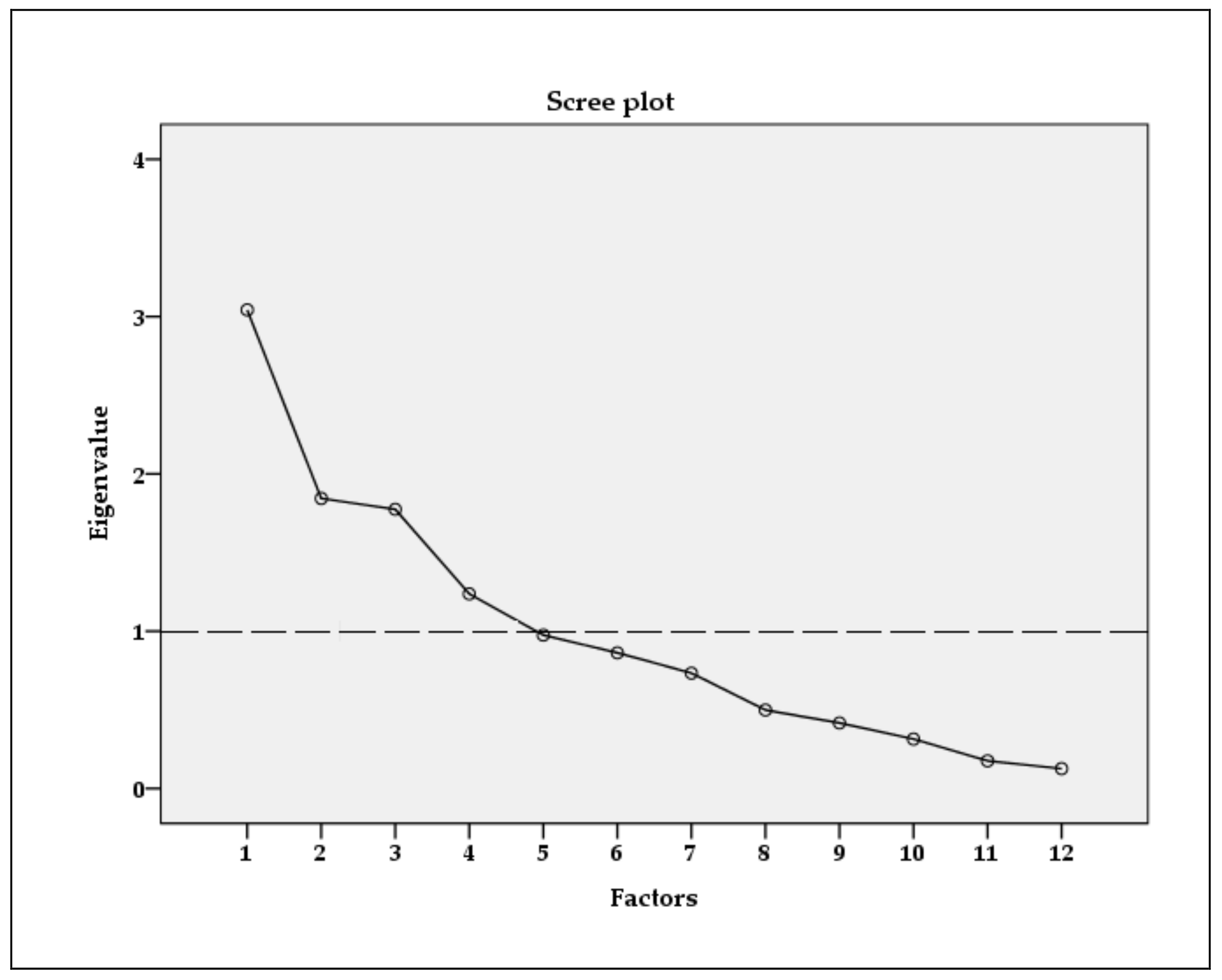
3.2. Principal Component Analysis
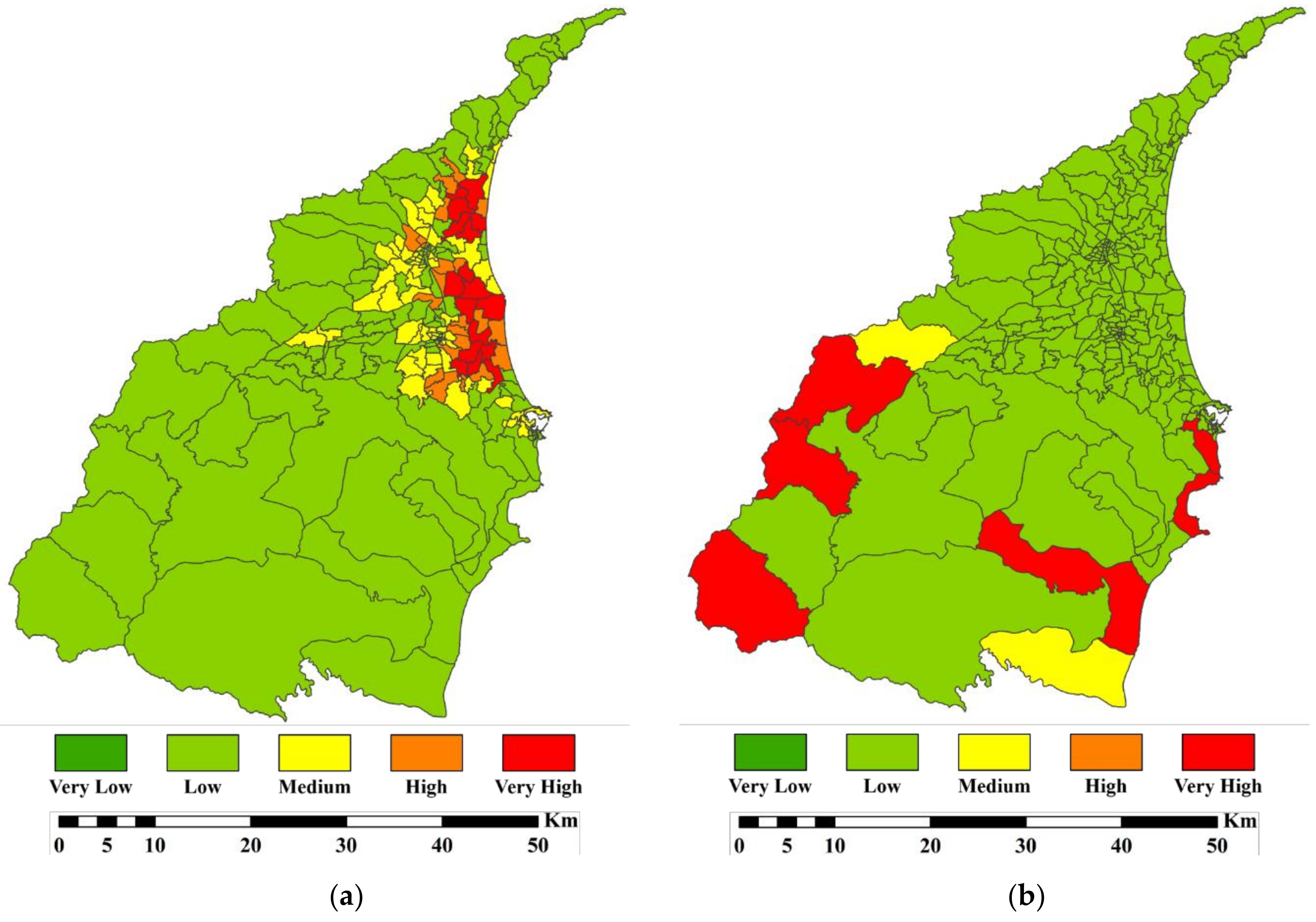
3.3. The Spatial Pattern of Components
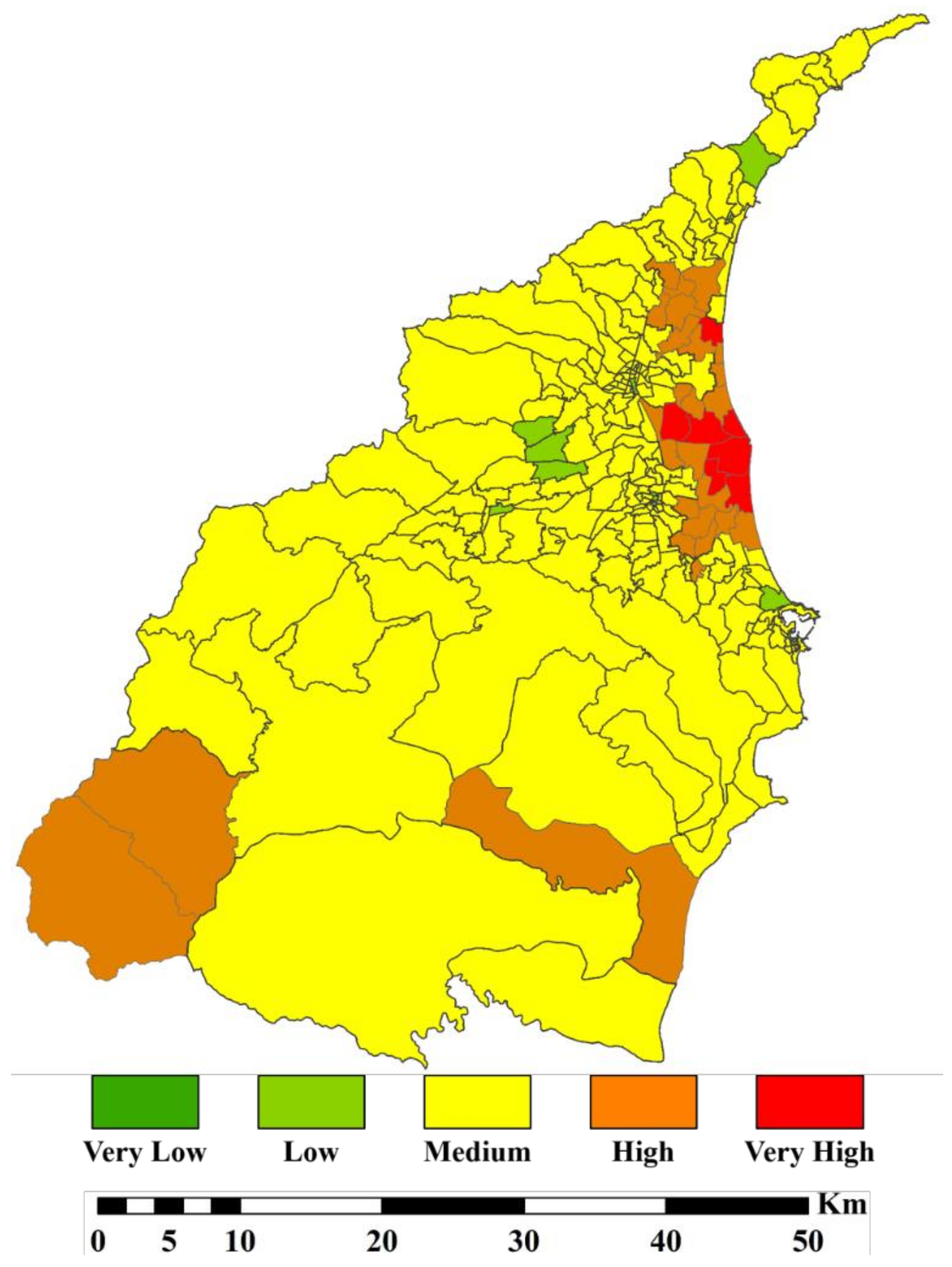
3.4. BRIC
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Doorn, N. Resilience indicators: Opportunities for including distributive justice concerns in disaster management. J. Risk Res. 2015, 20, 711–731. [Google Scholar] [CrossRef] [Green Version]
- Intergovernmental Panel on Climate Change (IPCC). “Technical Summary.” Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Eds.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Winderl, T. Disaster Resilience Measurements: Stocktaking of Ongoing Efforts in Developing System for Measuring Resilience; UNDP: New York, NY, USA, 2014; pp. 18–29. [Google Scholar]
- Manyena, B.; Machingura, F.; O’Keefe, P. Disaster Resilience Integrated Framework for Transformation (DRIFT): A new approach to theorising and operationalising resilience. World Dev. 2019, 123, 104587. [Google Scholar] [CrossRef]
- Cutter, S.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Chang. 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Klein, R.J.T.; Nicholls, R.J.; Thomalla, F. Resilience to Natural Hazards: How Useful Is this Concept? Environ. Hazards 2003, 5, 35–45. [Google Scholar] [CrossRef]
- Manyena, B. The concept of resilience revisited. Disasters 2006, 30, 434–450. [Google Scholar] [CrossRef]
- Cutter, S. The landscape of disaster resilience indicators in the USA. Nat. Hazards 2015, 80, 741–758. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Wang, J. A Way to Sustainability: Perspective of Resilience and Adaptation to Disaster. Sustainability 2016, 8, 737. [Google Scholar] [CrossRef] [Green Version]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Prior, T.; Hagmann, J. Measuring resilience: Methodological and political challenges of a trend security concept. J. Risk Res. 2013, 17, 281–298. [Google Scholar] [CrossRef]
- Adger, W.N. Social Vulnerability to Climate Change and Extremes in Coastal Vietnam. World Dev. 1999, 27, 249–269. [Google Scholar] [CrossRef]
- Adger, W.N. Social and ecological resilience: Are they related? Prog. Hum. Geogr. 2000, 24, 347–364. [Google Scholar] [CrossRef]
- Adger, W.N.; Hughes, T.P.; Folke, C.; Carpenter, S.R.; Rockström, J. Social-Ecological Resilience to Coastal Disasters. Science 2005, 309, 1036–1039. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, S.; Walker, B.; Anderies, J.M.; Abel, N. From Metaphor to Measurement: Resilience of What to What? Ecosystems 2001, 4, 765–781. [Google Scholar] [CrossRef]
- Folke, C. Resilience: The Emergence of a Perspective for Social-ecological Systems Analyses. Global Environ. Chang. 2006, 16, 253–267. [Google Scholar] [CrossRef]
- Gunderson, L. Ecological and Human Community Resilience in Response to Natural Disasters. Ecol. Soc. 2010, 15, 18–29. [Google Scholar] [CrossRef]
- Walker, B.; Holling, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, Adaptability and Transformability in Social-ecological Systems. Ecol. Soc. 2004, 9, 5–13. [Google Scholar] [CrossRef]
- Barnett, J. Adapting to Climate Change in Pacific Island Countries: The Problem of Uncertainty. World Dev. 2001, 29, 977–993. [Google Scholar] [CrossRef] [Green Version]
- Norris, L.F.; Stevens, S.P.; Pfefferbaum, B.; Wyche, K.F.; Pfefferbaum, R.L. Community Resilience as a Metaphor, Theory, Set of Capacities, and Strategy for Disaster Readiness. Am. J. Community Psychol. 2007, 41, 127–150. [Google Scholar] [CrossRef]
- Cutter, S.; Burton, C.G.; Emrich, C.T. Disaster Resilience Indicators for Benchmarking Baseline Conditions. J. Homel. Secur. Emerg. Manag. 2010, 7, 1–22. [Google Scholar] [CrossRef]
- Jordan, E.; Javernick-Will, A. Indicators of Community Recovery: Content Analysis and Delphi Approach. Nat. Hazards Rev. 2013, 14, 21–28. [Google Scholar] [CrossRef]
- Twigger-Ross, C.; Coates, T.; Deeming, H.; Orr, P.; Ramsden, M.; Stafford, J. Community Resilience Research: Final Report on Theoretical Research and Analysis of Case Studies Report to the Cabinet Office and Defence Science and Technology Laboratory; Collingwood Environmental Planning Ltd.: London, UK, 2011. [Google Scholar]
- Manyena, S.B.; O’Brien, G.; O’Keefe, P.; Rose, J. Disaster resilience: A bounce back or bounce forward ability? Local Environ. 2011, 16, 417–424. [Google Scholar]
- Wardekker, A.; De Jong, A.; Knoop, J.M.; Van Der Sluijs, J.P. Operationalising a resilience approach to adapting an urban delta to uncertain climate changes. Technol. Forecast. Soc. Chang. 2010, 77, 987–998. [Google Scholar] [CrossRef] [Green Version]
- Prashar, S.; Shaw, R.; Takeuchi, Y. Assessing the resilience of Delhi to climate-related disasters: A comprehensive approach. Nat. Hazards 2012, 64, 1609–1624. [Google Scholar] [CrossRef]
- Pfefferbaum, R.L.; Pfefferbaum, B.; Van Horn, R.L.; Klomp, R.W.; Norris, F.H.; Reissman, D.B. The Communities Advancing Resilience Toolkit (CART). J. Public Health Manag. Pr. 2013, 19, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Pfefferbaum, B.; Pfefferbaum, R.L.; Van Horn, R.L. Community resilience interventions: Participatory, assessmentbased, action-oriented processes. Am. Behav. Sci. 2015, 59, 238–253. [Google Scholar] [CrossRef]
- Cohen, O.; Leykin, D.; Lahad, M.; Goldberg, A.; Aharonson-Daniel, L. The conjoint community resiliency assessment measure as a baseline for profiling and predicting community resilience for emergencies. Technol. Forecast. Soc. Chang. 2013, 80, 1732–1741. [Google Scholar] [CrossRef]
- White, R.K.; Edwards, W.C.; Farrar, A.; Plodinec, M.J. A Practical Approach to Building Resilience in America’s Communities. Am. Behav. Sci. 2014, 59, 200–219. [Google Scholar] [CrossRef]
- Cox, R.S.; Hamlen, M. Community Disaster Resilience and the Rural Resilience Index. Am. Behav. Sci. 2014, 59, 220–237. [Google Scholar] [CrossRef]
- Wilkin, J.; Biggs, E.; Tatem, A.J. Measurement of Social Networks for Innovation within Community Disaster Resilience. Sustainability 2019, 11, 1943. [Google Scholar] [CrossRef] [Green Version]
- Cui, K.; Han, Z.; Wang, D. Resilience of an Earthquake-Stricken Rural Community in Southwest China: Correlation with Disaster Risk Reduction Efforts. Int. J. Environ. Res. Public Health 2018, 15, 407. [Google Scholar] [CrossRef] [Green Version]
- Cuthbertson, J.; Llanes, J.M.R.; Robertson, A.; Archer, F. Current and Emerging Disaster Risks Perceptions in Oceania: Key Stakeholders Recommendations for Disaster Management and Resilience Building. Int. J. Environ. Res. Public Health 2019, 16, 460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eisenman, D.; Chandra, A.; Fogleman, S.; Magana, A.; Hendricks, A.; Wells, K.; Williams, M.; Tang, J.; Plough, A. The Los Angeles County Community Disaster Resilience Project — A Community-Level, Public Health Initiative to Build Community Disaster Resilience. Int. J. Environ. Res. Public Health 2014, 11, 8475–8490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chun, H.; Chi, S.; Hwang, B.-G. A Spatial Disaster Assessment Model of Social Resilience Based on Geographically Weighted Regression. Sustainability 2017, 9, 2222. [Google Scholar] [CrossRef] [Green Version]
- Sherrieb, K.; Norris, F.H.; Galea, S. Measuring Capacities for Community Resilience. Soc. Indic. Res. 2010, 99, 227–247. [Google Scholar] [CrossRef]
- Sherrieb, K.; Louis, C.A.; Pfefferbaum, R.L.; Pfefferbaum, J.B.; Diab, E.; Norris, L.F. Assessing community resilience on the US coast using school principals as key informants. Int. J. Disaster Risk Reduct. 2012, 2, 6–15. [Google Scholar] [CrossRef]
- Peacock, W.G.; Brody, S.D.; Seitz, W.A.; Merrell, W.J.; Vedlitz, A.; Zahran, S.; Harriss, R.C.; Stickney, R. Advancing Resilience of Coastal Localities: Developing, Implementing, and Sustaining the Use of Coastal Resilience Indicators: A Final Report; Final report for NOAA CSC grant no. NA07NOS4730147; Hazard Reduction and Recovery Center: College Station/Houston, TX, USA, 2010. [Google Scholar]
- Yoon, D.K.; Kang, J.E.; Brody, S.D. A measurement of community disaster resilience in Korea. J. Environ. Plan. Manag. 2015, 59, 1–25. [Google Scholar] [CrossRef]
- Scherzer, S.; Lujala, P.; Rød, J.K. A community resilience index for Norway: An adaptation of the Baseline Resilience Indicators for Communities (BRIC). Int. J. Disaster Risk Reduct. 2019, 36, 101107. [Google Scholar] [CrossRef]
- Cutter, S.; Ash, K.; Emrich, C.T. The geographies of community disaster resilience. Glob. Environ. Chang. 2014, 29, 65–77. [Google Scholar] [CrossRef]
- Cutter, S.; Ash, K.; Emrich, C.T. Urban–Rural Differences in Disaster Resilience. Ann. Am. Assoc. Geogr. 2016, 106, 1236–1252. [Google Scholar] [CrossRef]
- Burton, C.G. A Validation of Metrics for Community Resilience to Natural Hazards and Disasters Using the Recovery from Hurricane Katrina as a Case Study. Ann. Assoc. Am. Geogr. 2014, 105, 67–86. [Google Scholar] [CrossRef]
- Pendall, R.; Foster, K.A.; Cowell, M. Resilience and regions: Building understanding of the metaphor. Camb. J. Reg. Econ. Soc. 2009, 3, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Miles, S.B.; Chang, S.E. ResilUS: A Community Based Disaster Resilience Model. Cartogr. Geogr. Inf. Sci. 2011, 38, 36–51. [Google Scholar] [CrossRef]
- Frazier, T.G.; Thompson, C.M.; Dezzani, R.J.; Butsick, D. Spatial and temporal quantification of resilience at the community scale. Appl. Geogr. 2013, 42, 95–107. [Google Scholar] [CrossRef]
- Center Weather Bureau. Typhoon Database. Available online: https://rdc28.cwb.gov.tw/TDB/ (accessed on 5 February 2020).
- Directorate-General of Budget, Accounting and Statistics. STATDB. Available online: https://statdb.dgbas.gov.tw/pxweb/Dialog/statfile9.asp (accessed on 5 February 2020).
- Singh-Peterson, L.; Salmon, P.M.; Goode, N.; Gallina, J. Translation and evaluation of the Baseline Resilience Indicators for Communities on the Sunshine Coast, Queensland Australia. Int. J. Disaster Risk Reduct. 2014, 10, 116–126. [Google Scholar] [CrossRef]
- Cai, H.; Lam, N.S.-N.; Qiang, Y.; Zou, L.; Correll, R.M.; Mihunov, V.V. A synthesis of disaster resilience measurement methods and indices. Int. J. Disaster Risk Reduct. 2018, 31, 844–855. [Google Scholar] [CrossRef]
- Mayunga, J.S. Understanding and Applying the Concept of Community Disaster Resilience: A Capital-Based Approach. In Summer Academy for Social Vulnerability and Resilience Building; JOUR: Munich, Germany, 2007. [Google Scholar]
- Aldrich, D.P. Social, not physical, infrastructure: The critical role of civil society in disaster recovery. Disasters 2012, 36, 398–419. [Google Scholar] [CrossRef] [PubMed]
- Aldrich, D.P.; Meyer, M.A. Social Capital and Community Resilience. Am. Behav. Sci. 2014, 59, 254–269. [Google Scholar] [CrossRef]
- Ross, A.D. Local Disaster Resilience: Administrative and Political Perspectives; Routledge Press: New York, NY, USA, 2014. [Google Scholar]
- Moran, P.A.P. The Interpretation of Statistical Maps. J. R. Stat. Soc. Ser. B 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 2010, 27, 93–115. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. A Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Villagra, P.; Quintana, C. Disaster Governance for Community Resilience in Coastal Towns: Chilean Case Studies. Int. J. Environ. Res. Public Health 2017, 14, 1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sen, A. Commodities and Capabilities; Oxford University Press: Cambridge, UK, 1985. [Google Scholar]
- Nussbaum, M.C. Women and Human Development; Cambridge University Press (CUP): Cambridge, UK, 2000. [Google Scholar]
- Gardoni, P.; Murphy, C. Recovery from natural and man-made disasters as capabilities restoration and enhancement. Int. J. Sustain. Dev. Plan. 2008, 3, 317–333. [Google Scholar] [CrossRef]
- Murphy, C.; Gardoni, P. The Acceptability and the Tolerability of Societal Risks: A Capabilities-based Approach. Sci. Eng. Ethics 2007, 14, 77–92. [Google Scholar] [CrossRef] [PubMed]


| Variables | Mean | SD | Moran’s I | p-Value |
|---|---|---|---|---|
| Annual Income | 273,953.751 | 220,415.705 | 0.365 | <0.05 |
| Population With a College Diploma | 613.600 | 487.833 | 0.556 | <0.05 |
| Population Between 20 to 50 Years Old | 911.540 | 588.782 | 0.277 | <0.05 |
| Presidential Election Vote Rate | 0.636 | 0.041 | 0.388 | <0.05 |
| Number of Social-Civic Groups | 0.965 | 1.258 | 0.124 | <0.05 |
| Capacity of Emergency Shelters | 167.626 | 252.061 | 0.063 | 0.10 |
| Number of Clinics | 1.231 | 2.812 | 0.407 | <0.05 |
| Number of Licensed Medical Personnel | 10.596 | 74.772 | 0.017 | 0.41 |
| Number of Hospital Beds | 11.884 | 73.422 | −0.013 | 0.81 |
| Number of Pharmacies | 0.536 | 1.106 | 0.283 | <0.05 |
| Number of Emergency Services Stations | 0.086 | 0.310 | −0.068 | 0.12 |
| Number of Ambulances | 0.124 | 0.379 | −0.018 | 0.69 |
| Neighbors | R2 | Adjusted R2 | AICc | StdResid Moran’s I | p-Value |
|---|---|---|---|---|---|
| 45 | 0.508 | 0.316 | 626.696 | 0.087 | 0.031 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, C.-H.; Liaw, S.-C. A GIS Approach to Analyzing the Spatial Pattern of Baseline Resilience Indicators for Community (BRIC). Water 2020, 12, 1401. https://doi.org/10.3390/w12051401
Sung C-H, Liaw S-C. A GIS Approach to Analyzing the Spatial Pattern of Baseline Resilience Indicators for Community (BRIC). Water. 2020; 12(5):1401. https://doi.org/10.3390/w12051401
Chicago/Turabian StyleSung, Chien-Hao, and Shyue-Cherng Liaw. 2020. "A GIS Approach to Analyzing the Spatial Pattern of Baseline Resilience Indicators for Community (BRIC)" Water 12, no. 5: 1401. https://doi.org/10.3390/w12051401
APA StyleSung, C.-H., & Liaw, S.-C. (2020). A GIS Approach to Analyzing the Spatial Pattern of Baseline Resilience Indicators for Community (BRIC). Water, 12(5), 1401. https://doi.org/10.3390/w12051401





