The Effect of Unsteady Water Discharge through Dams of Hydroelectric Power Plants on Hydrodynamic Regimes of the Upper Pools of Waterworks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Development of a Hydrodynamic Model in a Two-Dimensional Formulation
2.2. Model of Unsteady Flow in a Two-Dimensional Formulation of RiverFlow2D, Basic Equations
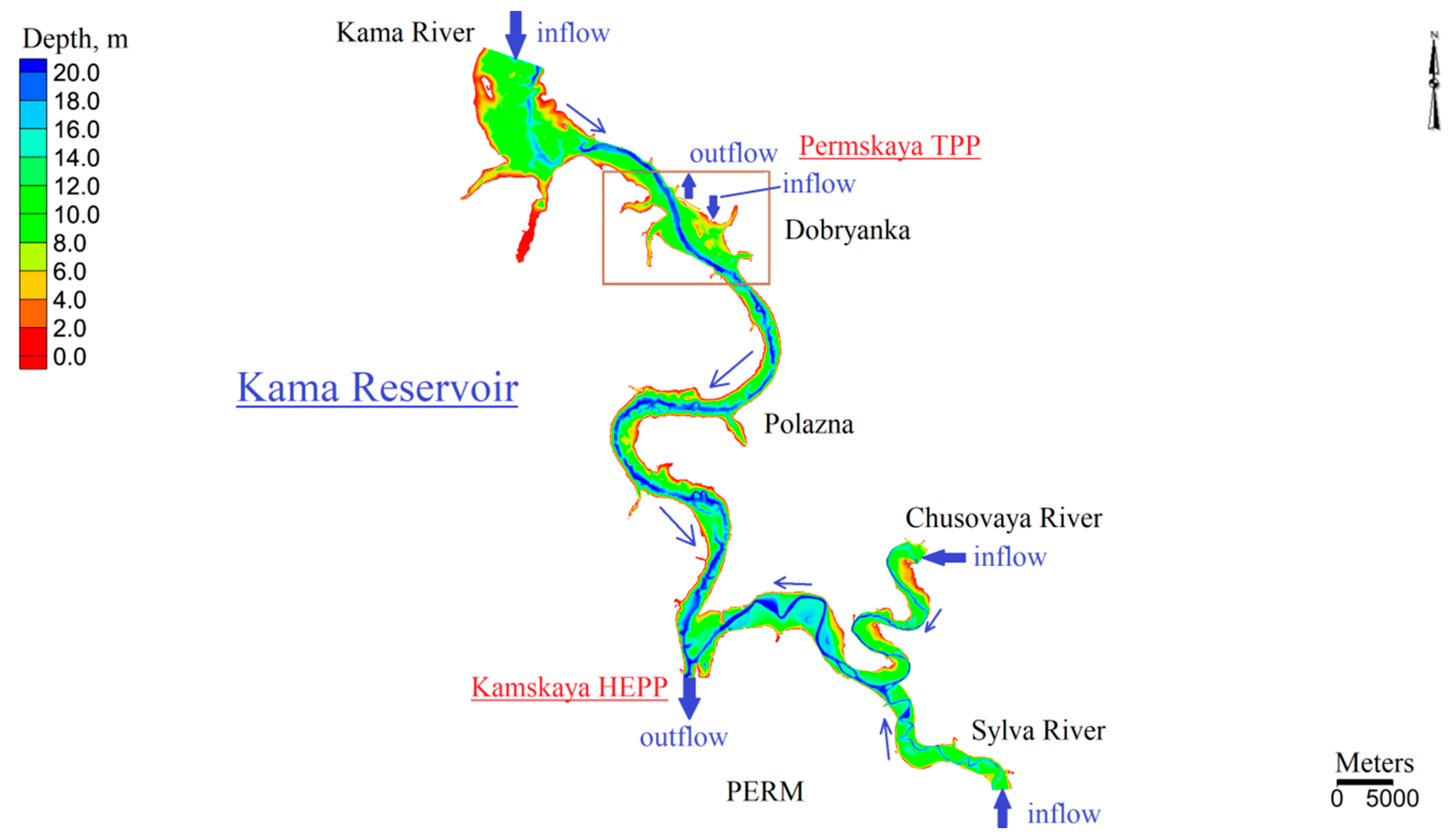
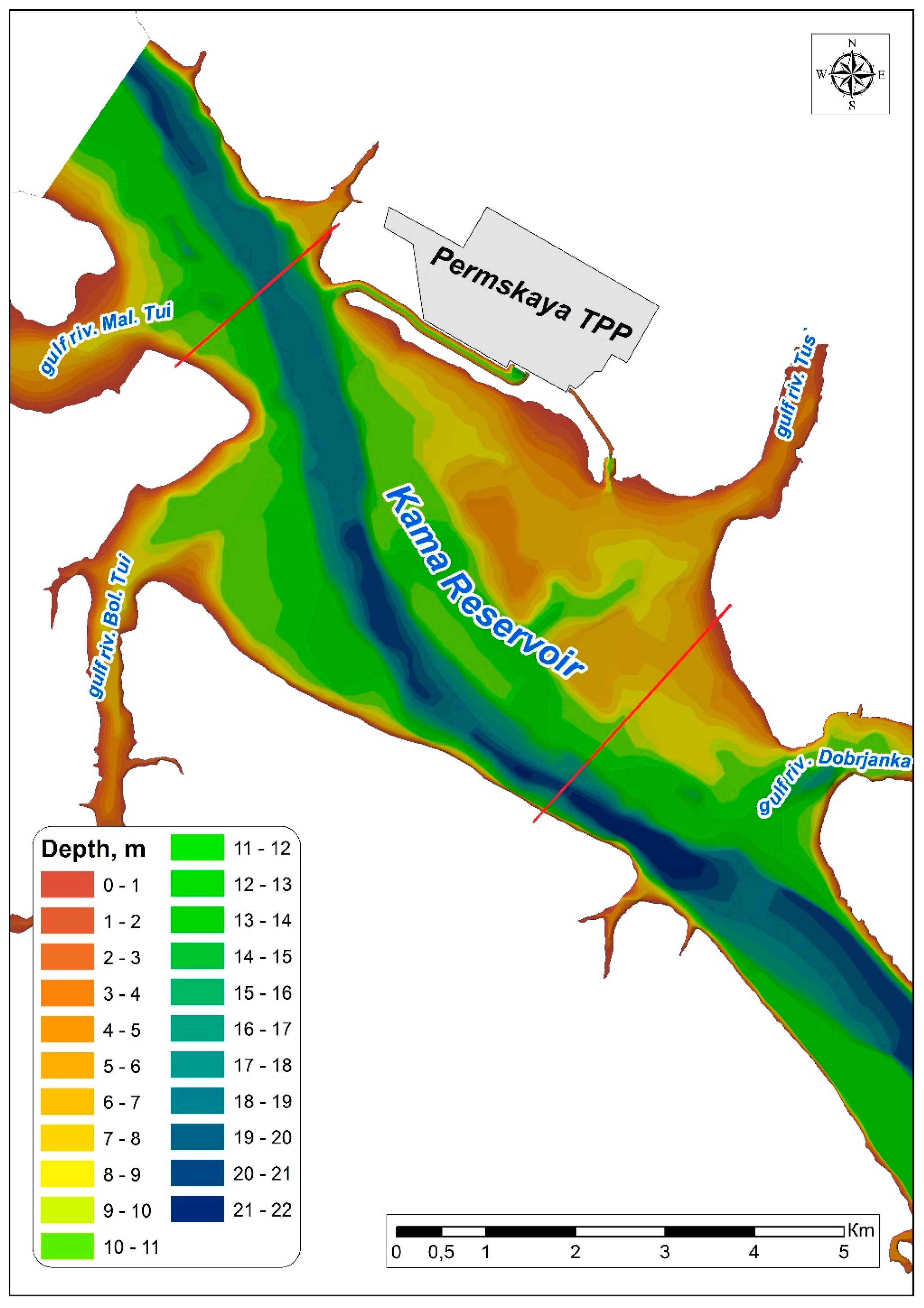
2.3. Construction of a Two-Dimensional Hydrodynamic Model of a Section of the Kama Reservoir and Initial Data Assignment
2.4. Initial Data for 2D Modeling
- -
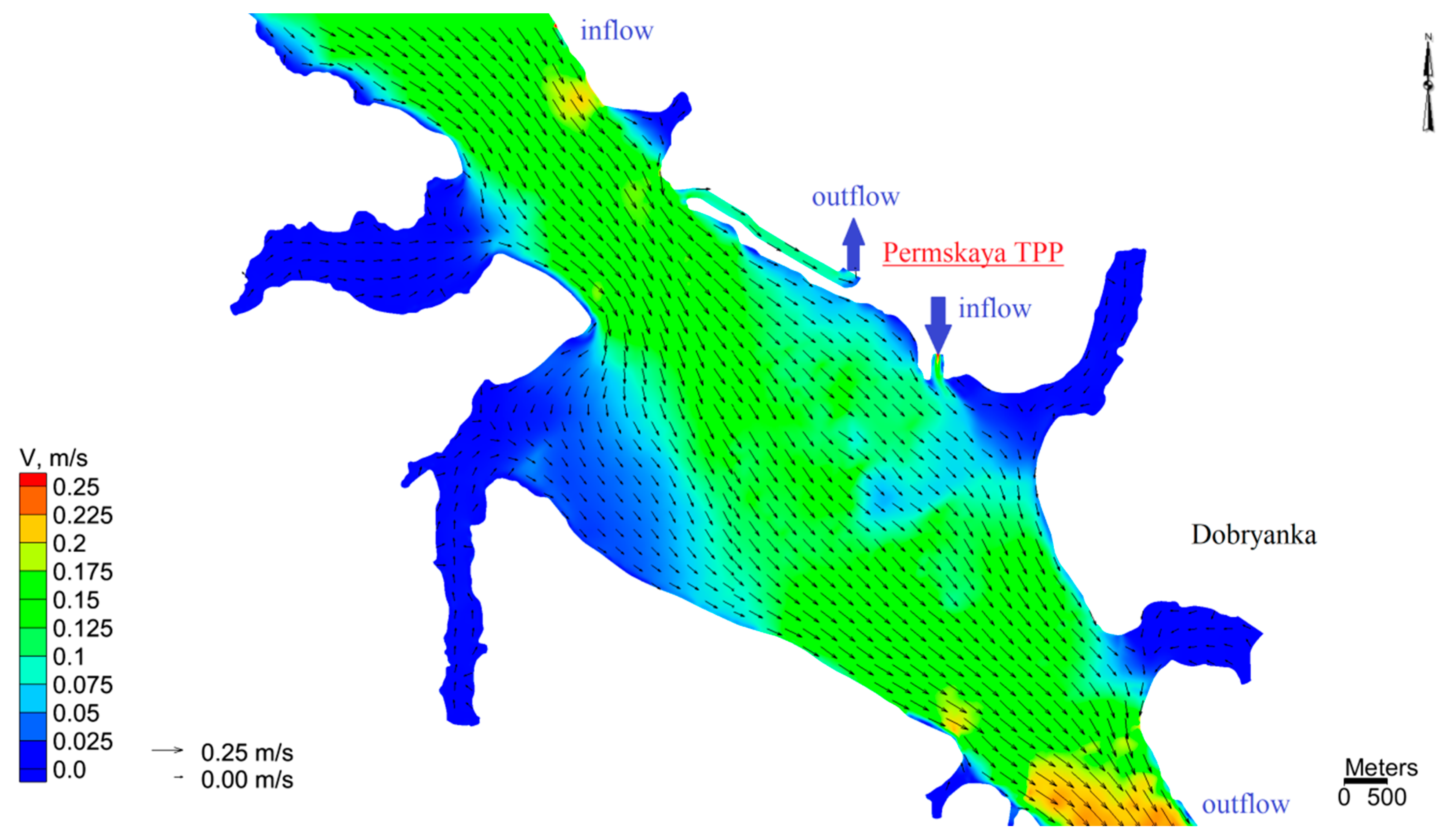
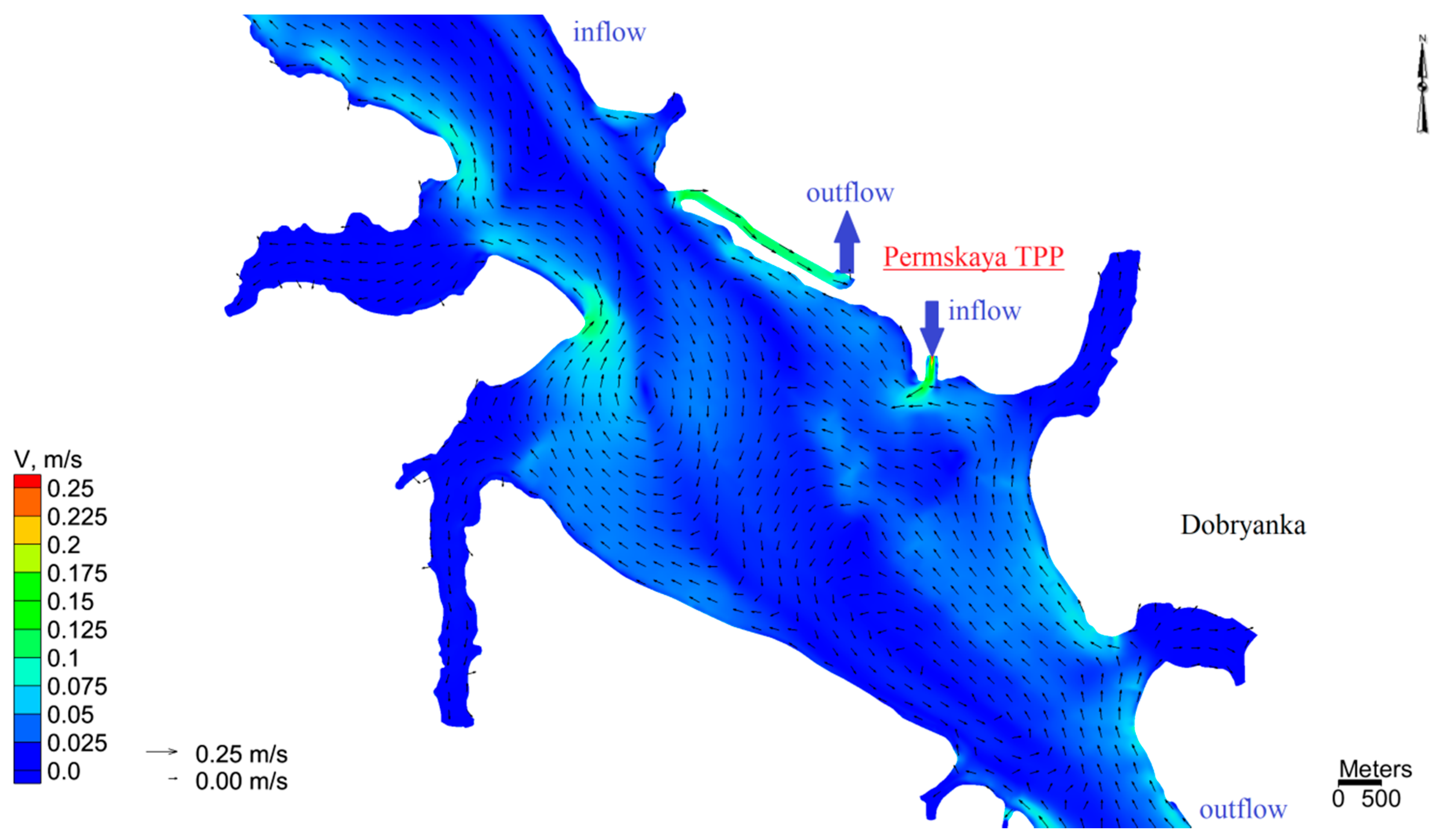
- The flow rate of water entering the Kama reservoir (Kama River—1675 m3/s, Chusovaya—226 m3/s and Sylva—159 m3/s) was considered constant at 2060 m3/s for 5 days. This is taken on the basis of the average annual summer inflow of water entering the Kama reservoir along its main tributaries, the Kama, Chusovaya and Sylva rivers;
- -
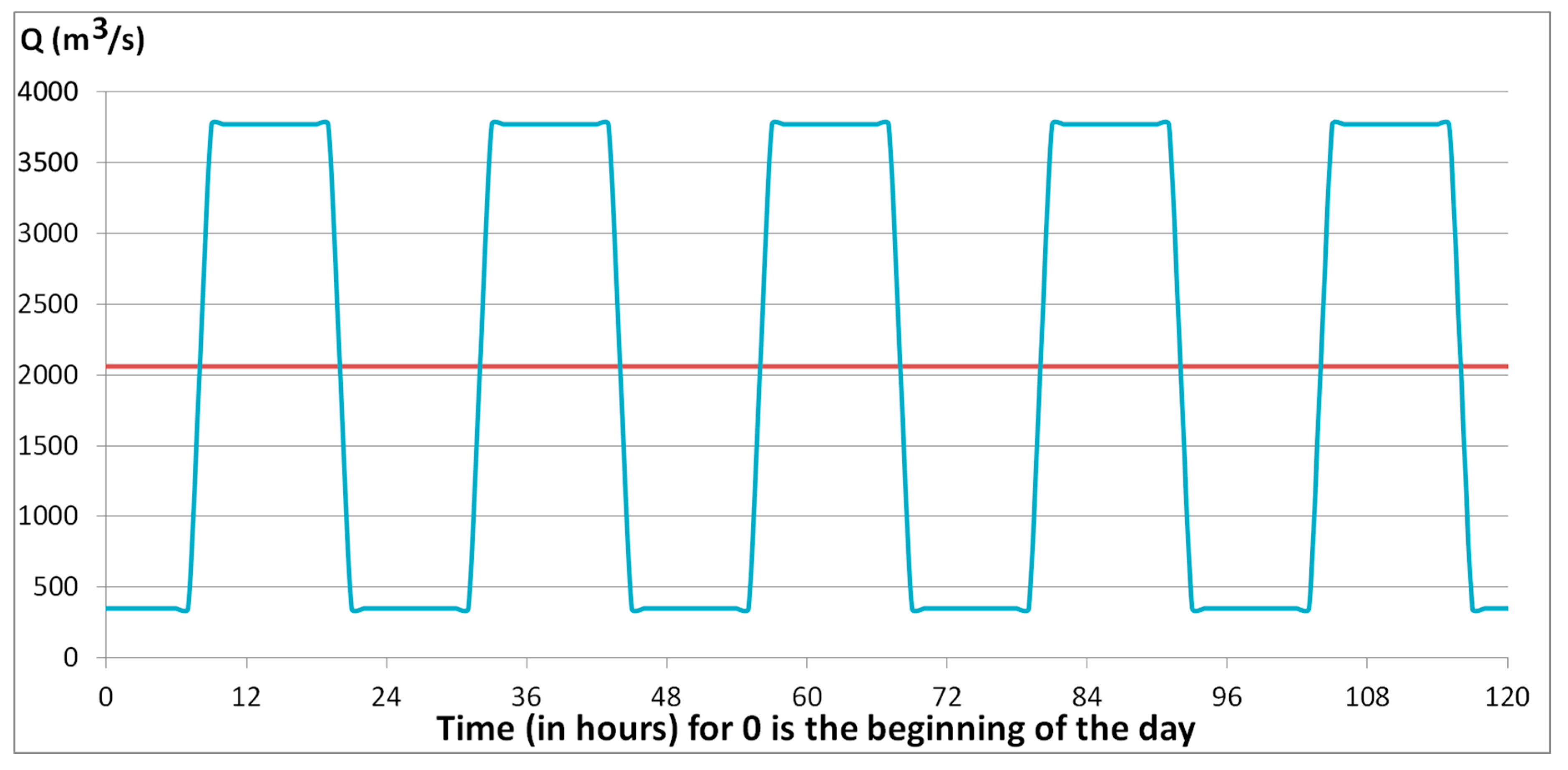
- The discharge flow rate of water at the Kamskaya HEPP (Kama river) for 5 days was varied according to the following scheme: the initial discharge flow rate of 350 m3/s for 10 h, then after 2 h the discharge flow rate rose to 3770 m3/s, then within 10 h constant flow rate of 3770 m3/s, then decrease in 2 h of discharge flow rate to 350 m3/s, then again after 10 h rise to 3770 m3/s and so on within 5 days. A two-hour drop in water discharge flow rate occurred in the time interval from 7 to 9 p.m., and a rise in water discharge flow rate occurred in the time interval from 7 to 9 a.m. These flow rates were taken from the conditions of maximum and minimum load on the Kama hydroelectric station in summer conditions. The maximum and minimum peaks were taken as constants. In real conditions, the discharge flow rate of water during the day can vary quite strongly. The schedule of water discharge flow rates by tributaries of the Kama reservoir and water discharge from the Kamskaya HEPP is shown in Figure 2, the beginning of the day (0 a.m.) is taken as “0”;
- -
- The flow rates of water intake and discharge at the Permskaya TPP (the Kama River, city of Dobryanka) were considered constant and equal to 42.5 m3/s for 5 days. This value was obtained from the average long-term data of the Permskaya TPP in the summer period with the continuous operation of two power units.
2.5. Three-Dimensional Hydrodynamical Model
2.6. Model of Unsteady Flow in a Three-Dimensional Formulation, Basic Equations
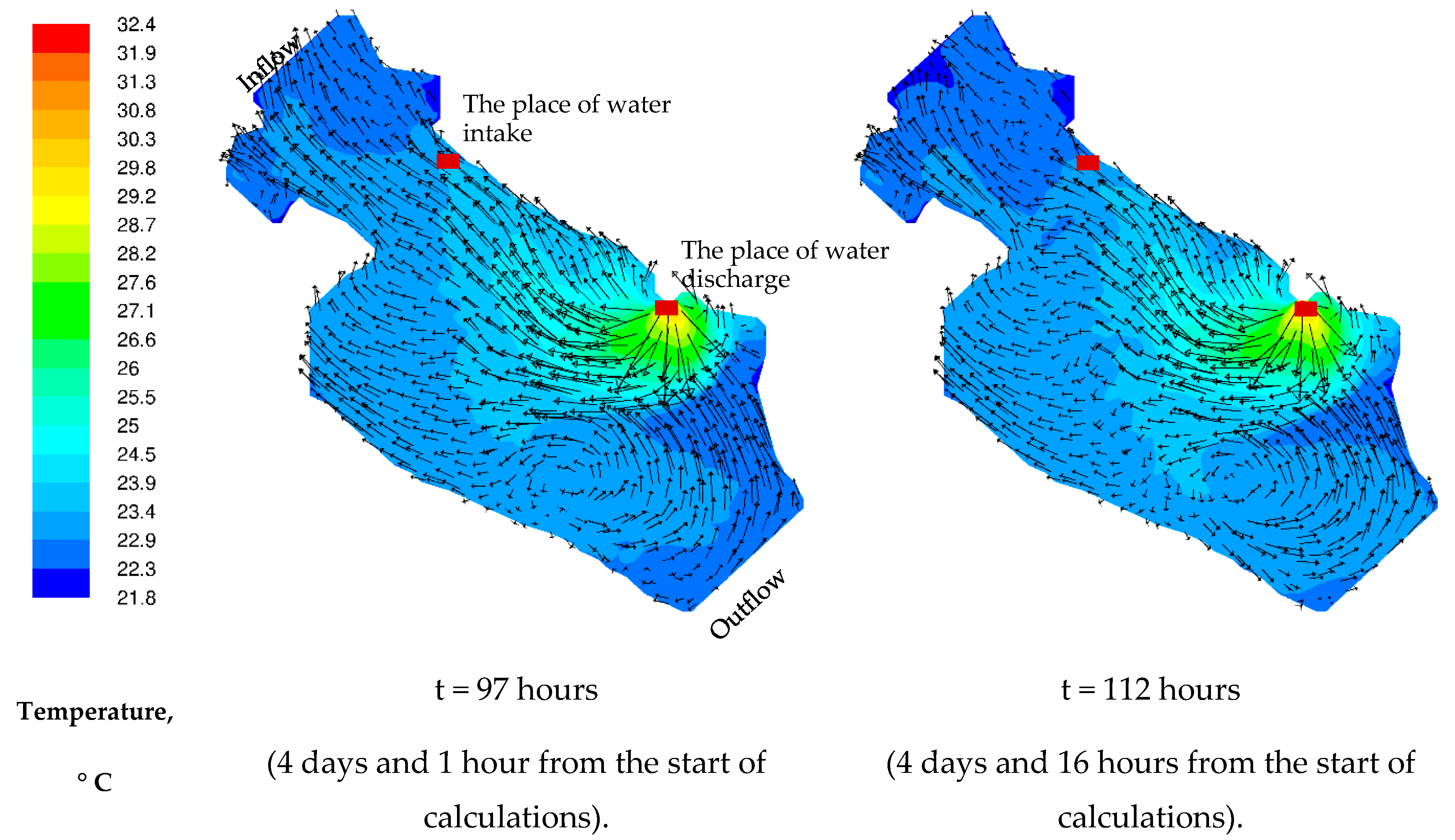
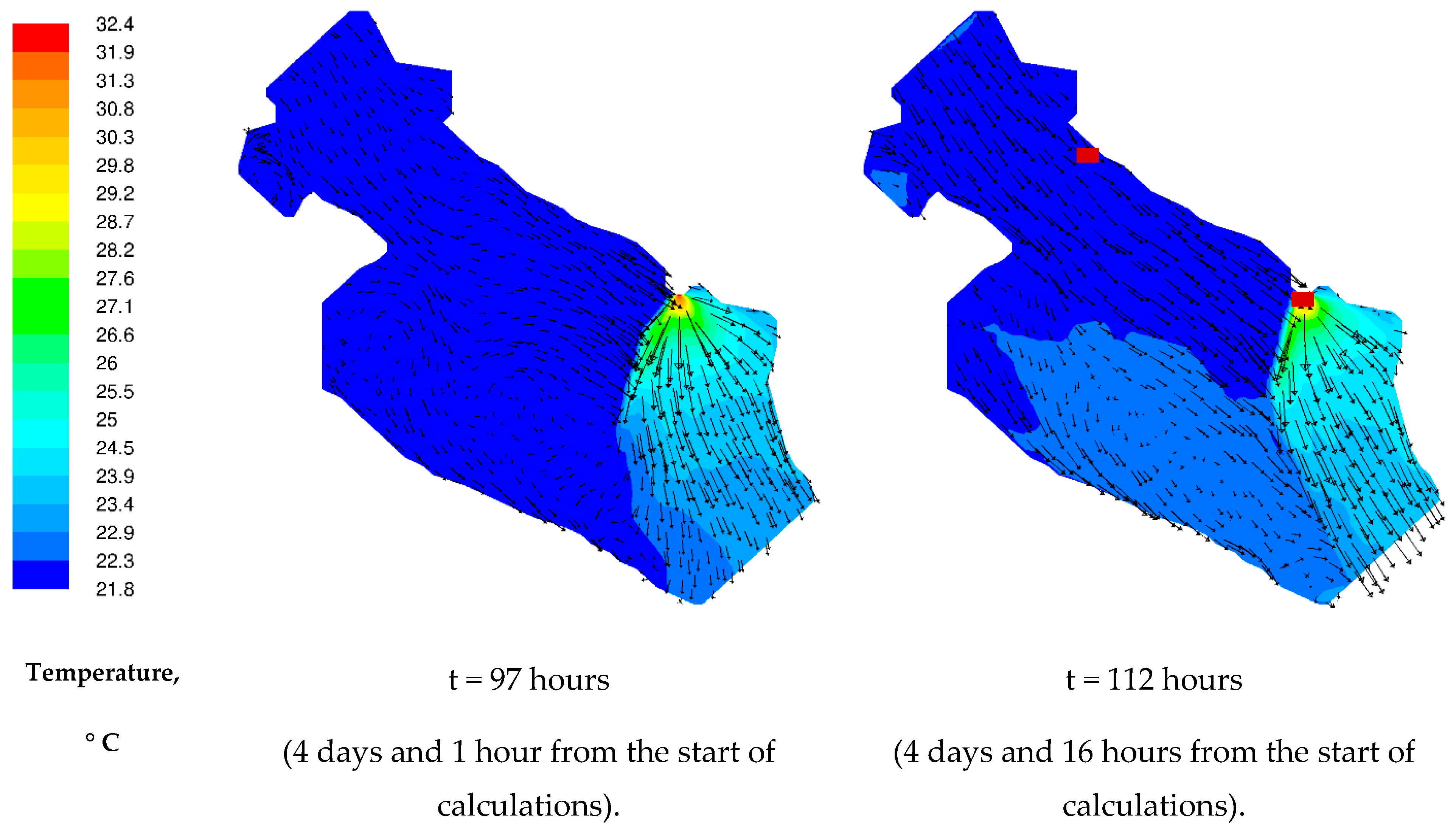
2.7. Boundary Conditions for 3D Modeling
- -
- at the bottom of the river and on its banks, the no-slip conditions and constant temperature were set ;
- -
- at the input of the computational domain, the time-variable velocity of the main flow, determined in two-dimensional modeling was set the temperature was set as equal to the background temperature of the river ;
- -
- in places of water intake and discharge, a constant water velocity and a constant temperature were set: at the inlet of the working channel and at the outlet of the working channel ;
- -
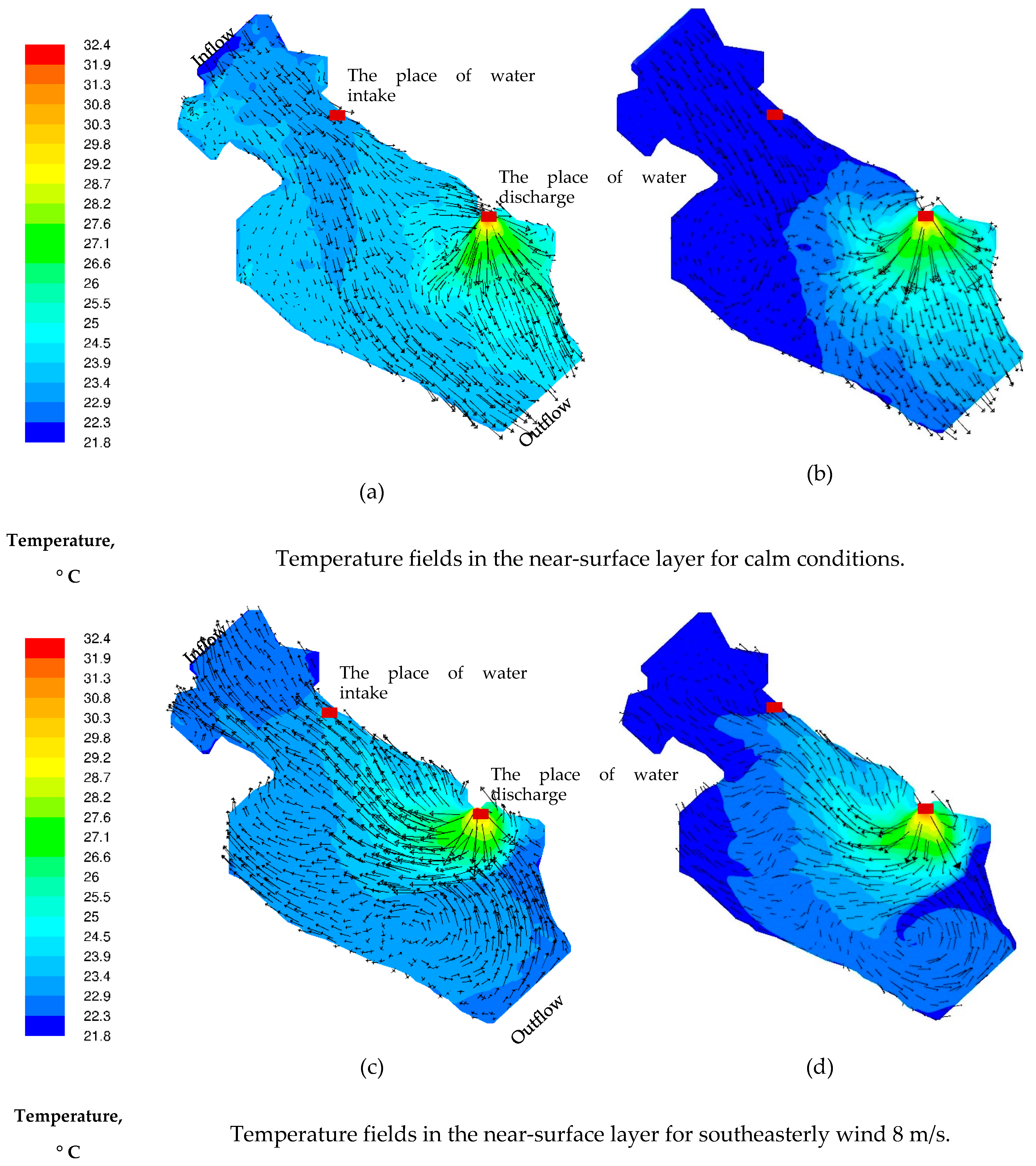
- the upper boundary of the fluid was considered free, the wind effect was taken into account—shear stresses were set in accordance with the formula presented in [32], where is the air density, is the dimensionless coefficient of wind stress and is the wind velocity at a distance of 10 m from the water surface. According to [32], for wind velocities from the range 1 m/s < < 15 m/s, the dimensionless parameter has the form . The calculations were made for wind velocity m/s, so the value was used. For the temperature on the surface of the water, a linear law of heat transfer was set; taking into account the heating of the surface from the surrounding air, the heat transfer coefficient was selected on the basis of field measurements.
2.8. Construction of a Three-Dimensional Hydrodynamic Model of a Section of the Kama Reservoir
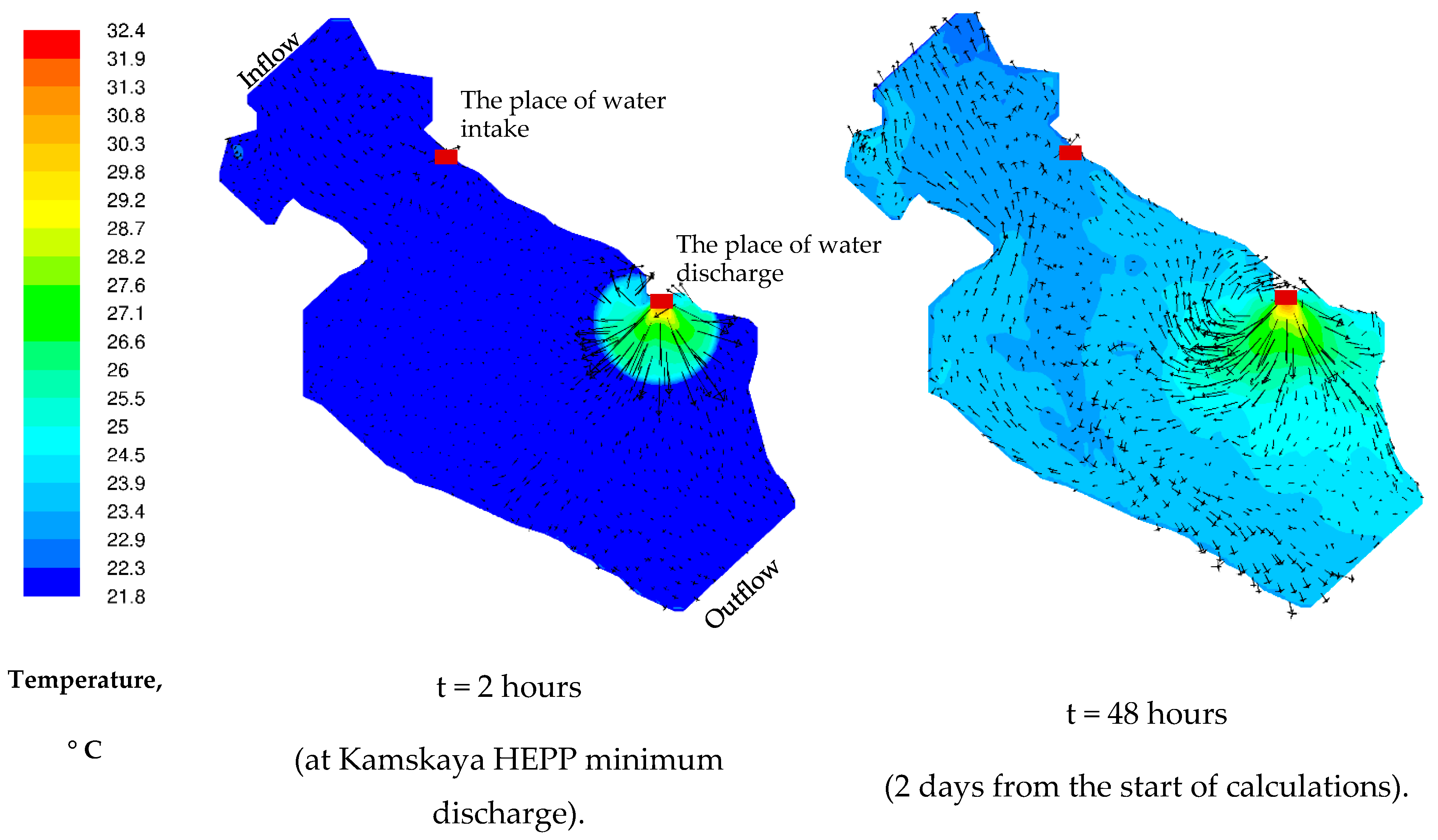
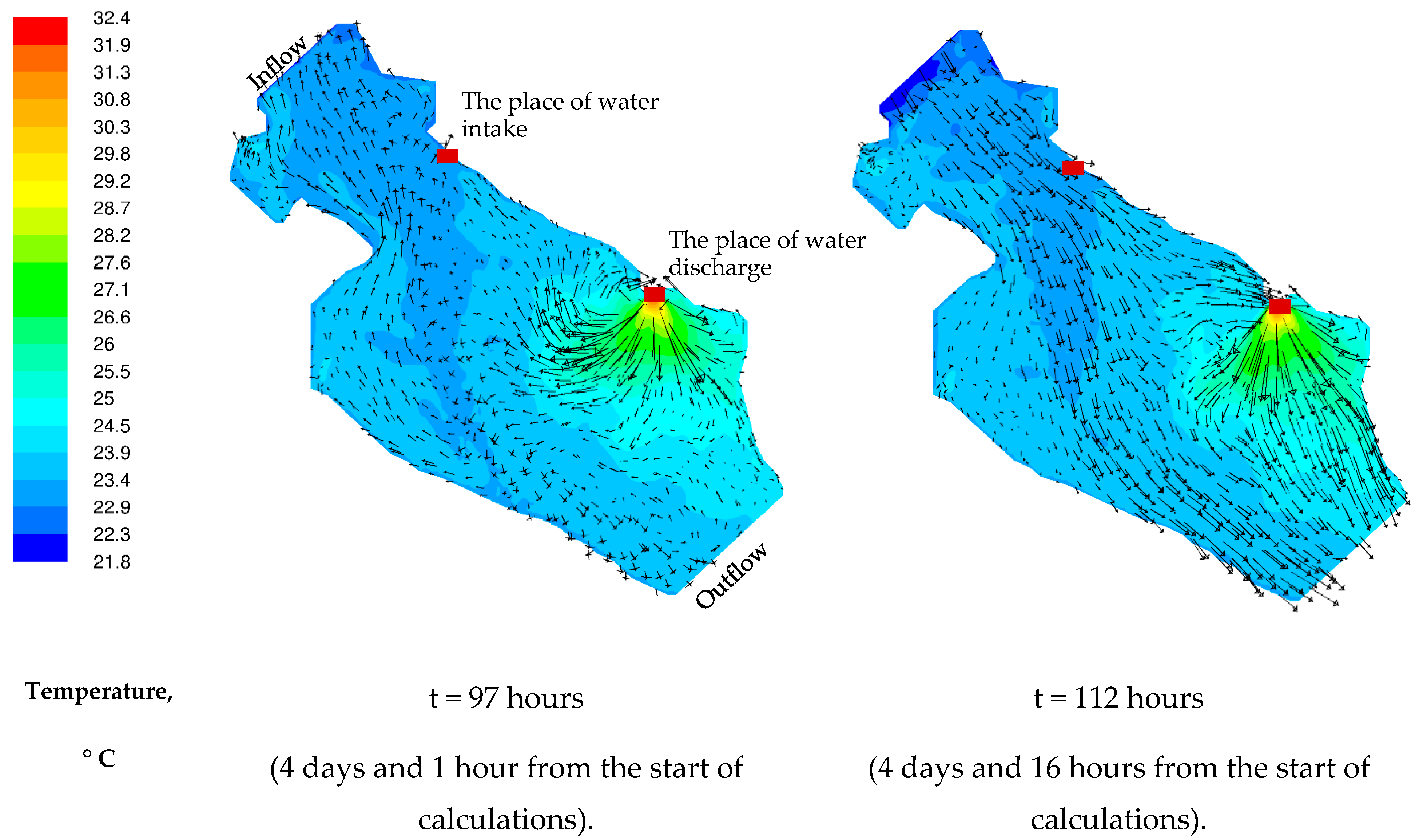
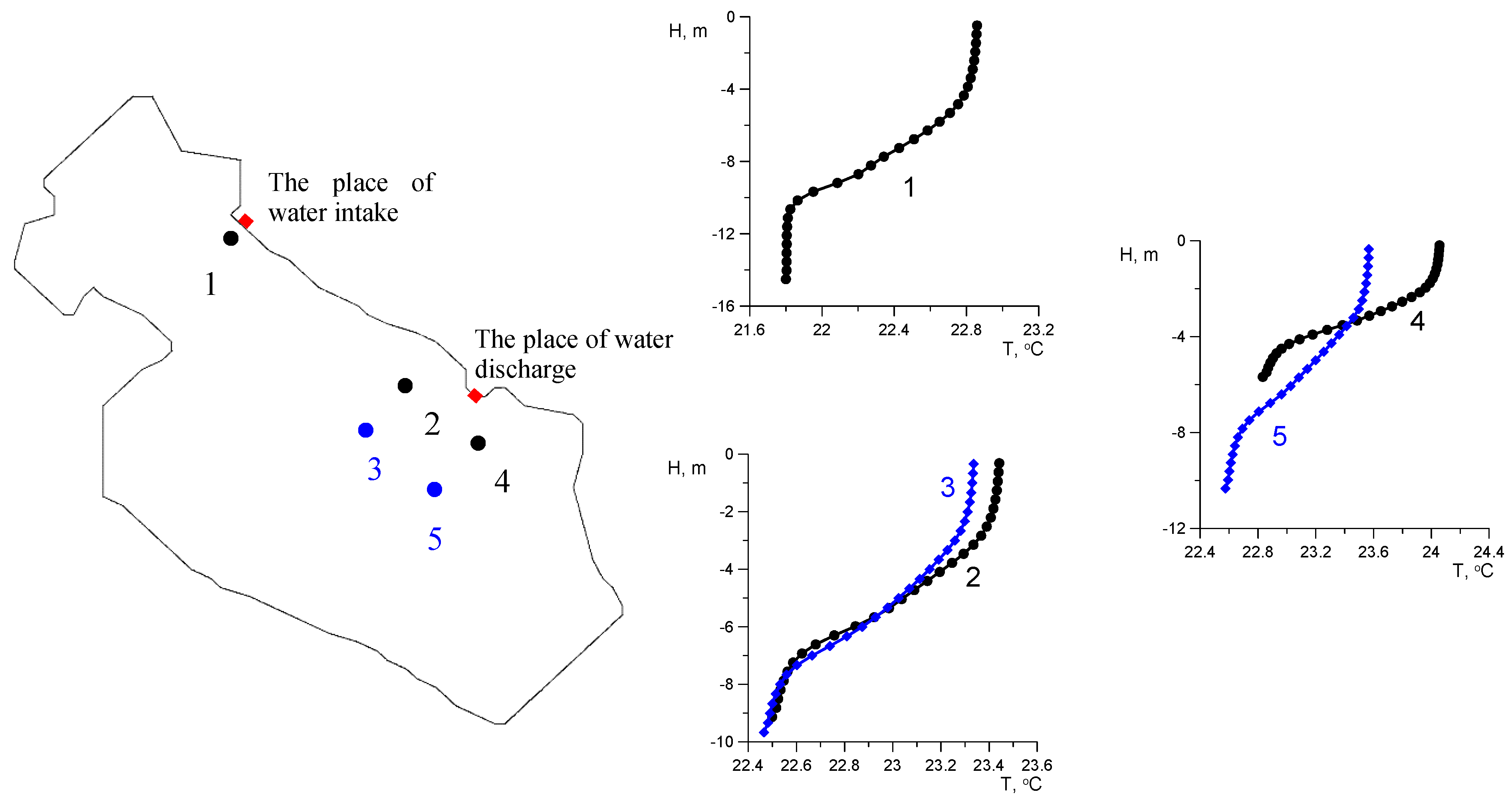
3. Results
3.1. The Results of Two-Dimensional Numerical Simulation
3.2. Results of 3D Numerical Modeling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abbaspour, A.H.J.; Moghimi, P.; Kayhan, K. Modeling of thermal pollution in coastal area and its economical and environmental assessment. Int. J. Environ. Sci. Technol. 2005, 2, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Madden, N.; Lewis, A.; Davis, M. Thermal effluent from the power sector: An analysis of once-through cooling system impacts on surface water temperature. Environ. Res. Lett. 2013, 8, 035006. [Google Scholar] [CrossRef]
- Hester, E.T.; Bauman, K.S. Stream and retention pond thermal response to heated summer runoff from urban impervious surfaces. J. Am. Water Res. Assoc. 2013, 49, 328–342. [Google Scholar] [CrossRef]
- Raptis, C.E.; Pfister, S. Global freshwater thermal emissions from steam-electric power plants with oncethrough cooling systems. Energy 2016, 97, 46–57. [Google Scholar] [CrossRef]
- Issakhov, A.; Mashenkova, A. Numerical study for the assessment of pollutant dispersion from a thermal power plant under the different temperature regimes. Int. J. Environ. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Alcamo, J.; Flörke, M.; Märker, M. Future long-term changes in global water resources driven by socio-economic and climatic changes. Hydrol. Sci. J. 2007, 52, 247–275. [Google Scholar] [CrossRef]
- Directive 2006/44/EC of the European Parliament. 2006. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=uriserv:OJ.L_.2006.264.01.0020.01.ENG (accessed on 4 May 2020).
- Van Vliet, M.T.H.; Franssen, W.H.P.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river discharge and water temperature under climate change. Glob. Environ. Chang. 2013, 23, 450–464. [Google Scholar] [CrossRef]
- Ptak, M.; Sojka, M.; Kałuża, T.; Choiński, A.; Nowak, B. Long-term water temperature trends of the Warta River in the years 1960–2009. Ecohydrol. Hydrobiol. 2019, 19, 441–451. [Google Scholar] [CrossRef]
- Webb, B.W.; Nobilis, F. Long-term changes in river temperature and the influence of climatic and hydrological factors. Hydrol. Sci. J. 2007, 52, 74–85. [Google Scholar] [CrossRef]
- Ptak, M.; Sojka, M.; Choiński, A.; Nowak, B. Effect of environmental conditions and morphometric parameters on surface water temperature in Polish lakes. Water 2018, 10, 580. [Google Scholar] [CrossRef] [Green Version]
- Ling, F.; Foody, G.M.; Du, H.; Ban, X.; Li, X.; Zhang, Y.; Du, Y. Monitoring thermal pollution in rivers downstream of dams with Landsat ETM+ thermal infrared images. Remote Sens. 2017, 9, 1175. [Google Scholar] [CrossRef] [Green Version]
- Issakhov, A. Mathematical modeling of thermal process to aquatic environment with different hydro meteorological conditions. Sci. World J. 2014, 2014, 678095. [Google Scholar] [CrossRef] [PubMed]
- Issakhov, A. Mathematical modeling of the discharged heat water effect on the aquatic environment from thermal power plant. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 229–238. [Google Scholar] [CrossRef]
- Miara, A.; Vorosmarty, C.J. A dynamic model to assess tradeoffs in power production and riverine ecosystem protection. Environ. Sci. Process. Impacts 2013, 15, 1113–1126. [Google Scholar] [CrossRef]
- Stewart, R.J.; Wollheim, W.M.; Miara, A.; Vörösmarty, C.J.; Fekete, B.; Lammers, R.B.; Rosenzweig, B. Horizontal cooling towers: Riverine ecosystem services and the fate of thermoelectric heat in the contemporary Northeast US. Environ. Res. Lett. 2013, 8, 025010. [Google Scholar] [CrossRef] [Green Version]
- Miara, A.; Cohen, S.M.; Macknick, J.; Vorosmarty, C.J.; Corsi, F.; Sun, Y.; Tidwell, V.C.; Newmark, R.; Fekete, B.M. Climate-Water Adaptation for Future US Electricity Infrastructure. Environ. Sci. Technol. 2019, 53, 14029–14040. [Google Scholar] [CrossRef]
- Issakhov, A.; Zhandaulet, Y. Numerical Study of Technogenic Thermal Pollution Zones’ Formations in the Water Environment from the Activities of the Power Plant. Environ. Model. Asess. 2020, 25, 203–218. [Google Scholar] [CrossRef]
- Durán-Colmenares, A.; Barrios-Piña, H.; Ramírez-León, H. Numerical Modeling of Water Thermal Plumes Emitted by Thermal Power Plants. Water 2016, 8, 482. [Google Scholar] [CrossRef] [Green Version]
- Hester, E.T.; Doyle, M.W. Human Impacts to River Temperature and Their Effects on Biological Processes: A Quantitative Synthesis. J. Am. Water Resour. Assoc. 2011, 47, 571–587. [Google Scholar] [CrossRef]
- Issakhov, A. Mathematical modeling of the discharged heat water effect on the aquatic environment from thermal power plant under various operational capacities. Appl. Math. Model. 2016, 40, 1082–1096. [Google Scholar] [CrossRef]
- McGuirk, J.J.; Rodi, W. A depth-averaged mathematical model for the near field of the side discharge into open-channel flow. J. Fluid Mech. 1978, 86, 761–781. [Google Scholar] [CrossRef]
- Park, S.W.; Chung, M.K. Prediction of 2-dimensional unsteady thermal discharge into a reservoir. J. Korean Soc. Mech. Eng. 1983, 7, 451–460. [Google Scholar]
- Lyubimova, T.; Lepikhin, A.; Konovalov, V.; Parshakova, Y.; Tiunov, A. Formation of the density currents in the zone of confluence of two rivers. J. Hydrol. 2014, 508, 328–342. [Google Scholar] [CrossRef]
- Lyubimova, T.; Lepikhin, A.; Parshakova, Y.; Lyakhin, Y.; Tiunov, A. The modelling of the formation of technogenic thermal pollution zones in large reservoirs. Int. J. Heat Mass Transf. 2018, 126 Pt A, 342–352. [Google Scholar] [CrossRef]
- Lyubimova, T.; Lepikhin, A.; Parshakova, Y.; Lyakhin, Y.; Tiunov, A. Application of hydrodynamic modeling in 2D and 3D approaches for the improvement of the recycled water supply systems of large energy complexes based on reservoirs-coolers. Int. J. Heat Mass Transf. 2019, 140, 897–908. [Google Scholar] [CrossRef]
- Faulkner, A.; Bulgin, C.E.; Merchant, C.J. Coastal Tidal Effects on Industrial Thermal Plumes in Satellite Imagery. Remote Sens. 2019, 11, 2132. [Google Scholar] [CrossRef] [Green Version]
- Pivato, M.; Carniello, L.; Viero, D.P.; Soranzo, C.; Defina, A.; Silvestri, S. Remote Sensing for Optimal Estimation of Water Temperature Dynamics in Shallow Tidal Environments. Remote Sens. 2020, 12, 51. [Google Scholar] [CrossRef] [Green Version]
- Vreugdenhil, C.B. Numerical methods for shallow-water flow. In Water Science and Technology Library; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; Volume 13. [Google Scholar]
- Reference Manual “RiverFlow2D Two-Dimensional River Dynamics Model” August, 2016, Hydronia LLC. Available online: http://www.hydronia.com/riverflow2d (accessed on 4 May 2020).
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK; New York, NY, USA, 1972; 169p. [Google Scholar]
- Wu, J. Wind stress and surface roughness at sea interface. J. Geophys. Res. 1969, 74, 444–453. [Google Scholar] [CrossRef] [Green Version]





| Value | Month | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Cp. T, °C | −13,0 | −9,6 | −3,0 | 2,6 | 10,4 | 14,8 | 16,7 | 15,6 | 9,5 | 1,7 | −6,0 | −9,7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyubimova, T.; Parshakova, Y.; Lepikhin, A.; Lyakhin, Y.; Tiunov, A. The Effect of Unsteady Water Discharge through Dams of Hydroelectric Power Plants on Hydrodynamic Regimes of the Upper Pools of Waterworks. Water 2020, 12, 1336. https://doi.org/10.3390/w12051336
Lyubimova T, Parshakova Y, Lepikhin A, Lyakhin Y, Tiunov A. The Effect of Unsteady Water Discharge through Dams of Hydroelectric Power Plants on Hydrodynamic Regimes of the Upper Pools of Waterworks. Water. 2020; 12(5):1336. https://doi.org/10.3390/w12051336
Chicago/Turabian StyleLyubimova, Tatyana, Yanina Parshakova, Anatoly Lepikhin, Yury Lyakhin, and Alexey Tiunov. 2020. "The Effect of Unsteady Water Discharge through Dams of Hydroelectric Power Plants on Hydrodynamic Regimes of the Upper Pools of Waterworks" Water 12, no. 5: 1336. https://doi.org/10.3390/w12051336
APA StyleLyubimova, T., Parshakova, Y., Lepikhin, A., Lyakhin, Y., & Tiunov, A. (2020). The Effect of Unsteady Water Discharge through Dams of Hydroelectric Power Plants on Hydrodynamic Regimes of the Upper Pools of Waterworks. Water, 12(5), 1336. https://doi.org/10.3390/w12051336





