Consistent Boundary Conditions for Age Calculations
Abstract
1. Introduction
2. The Age Distribution Function and Its First Two Moments
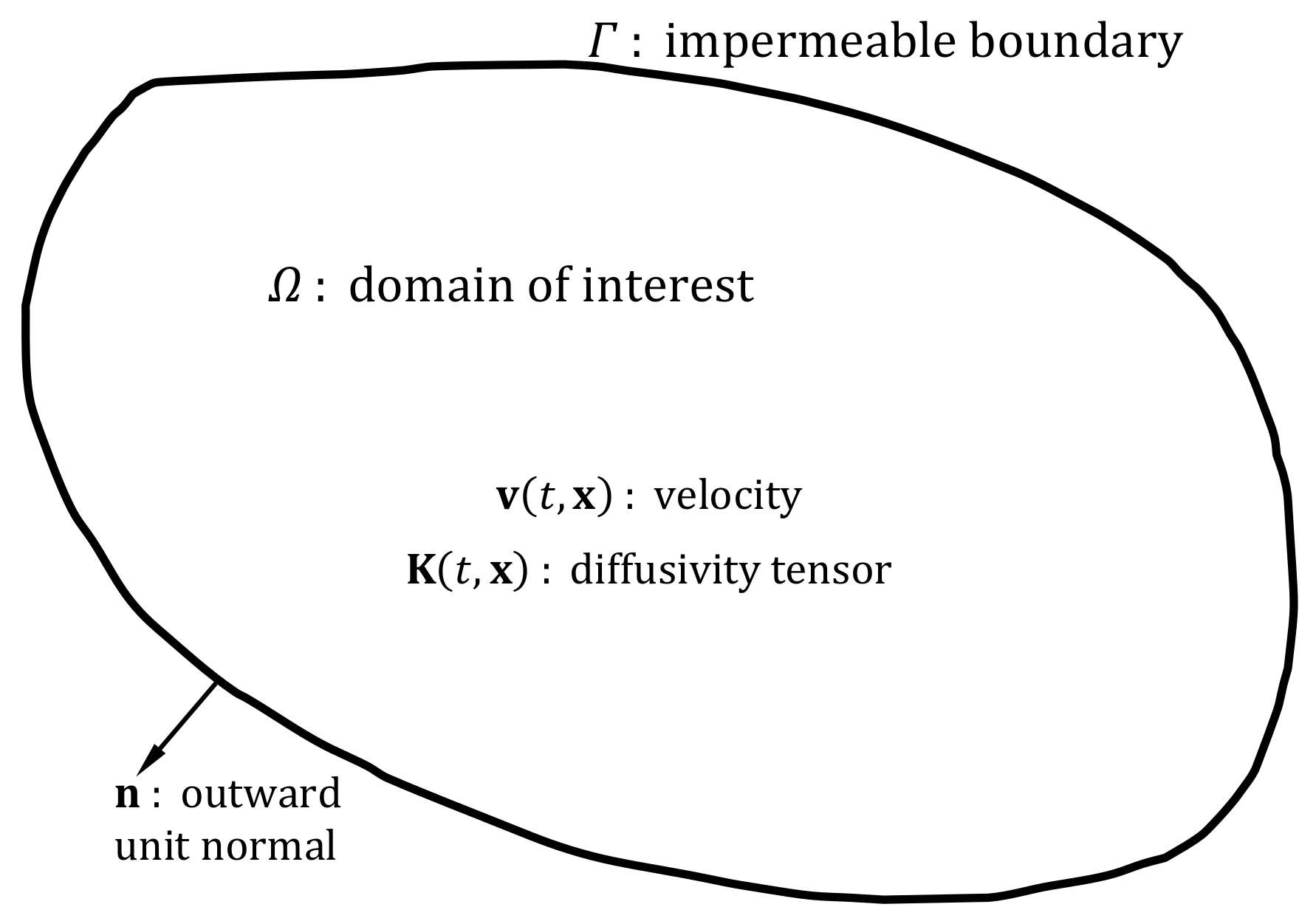
3. Consistent Insulating, Departure, and Arrival Boundary Conditions
3.1. Insulating Boundary
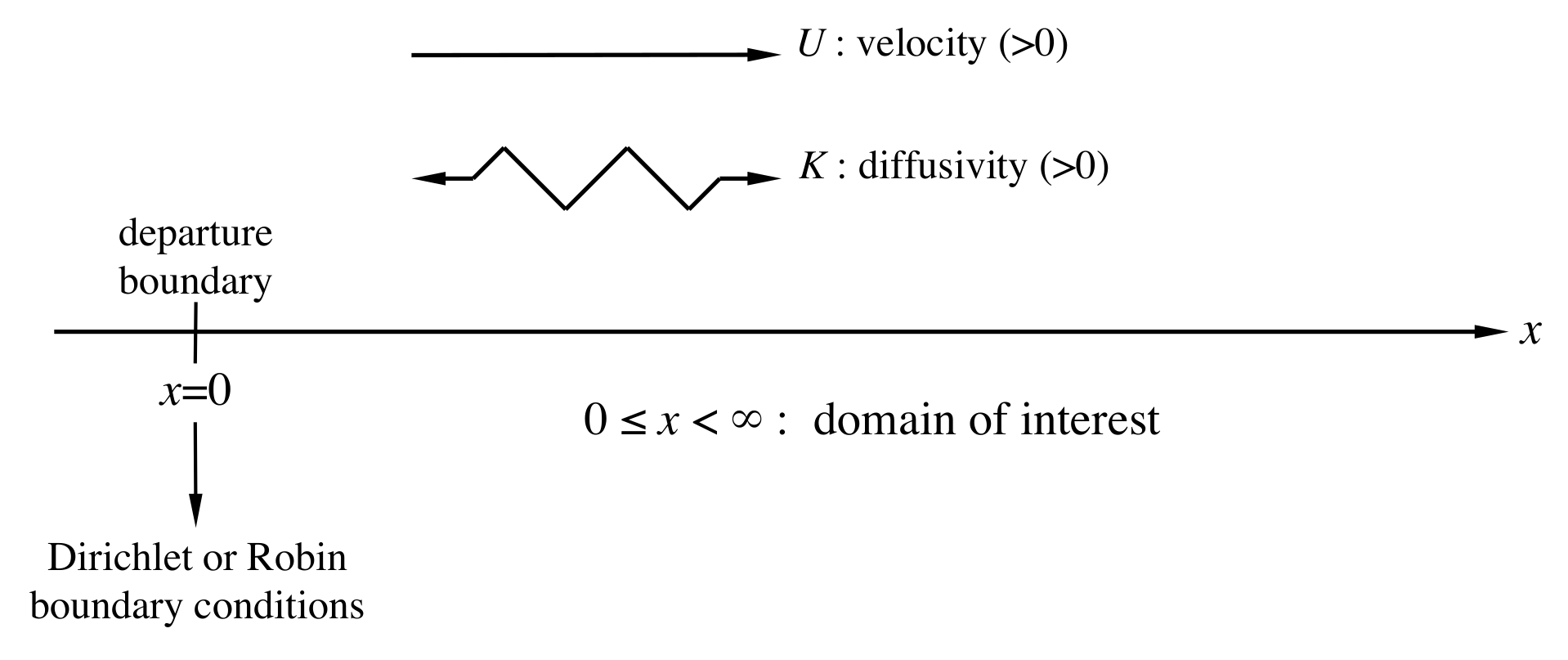
3.2. Departure Boundary
3.3. Departure Boundary: An Alternative Approach
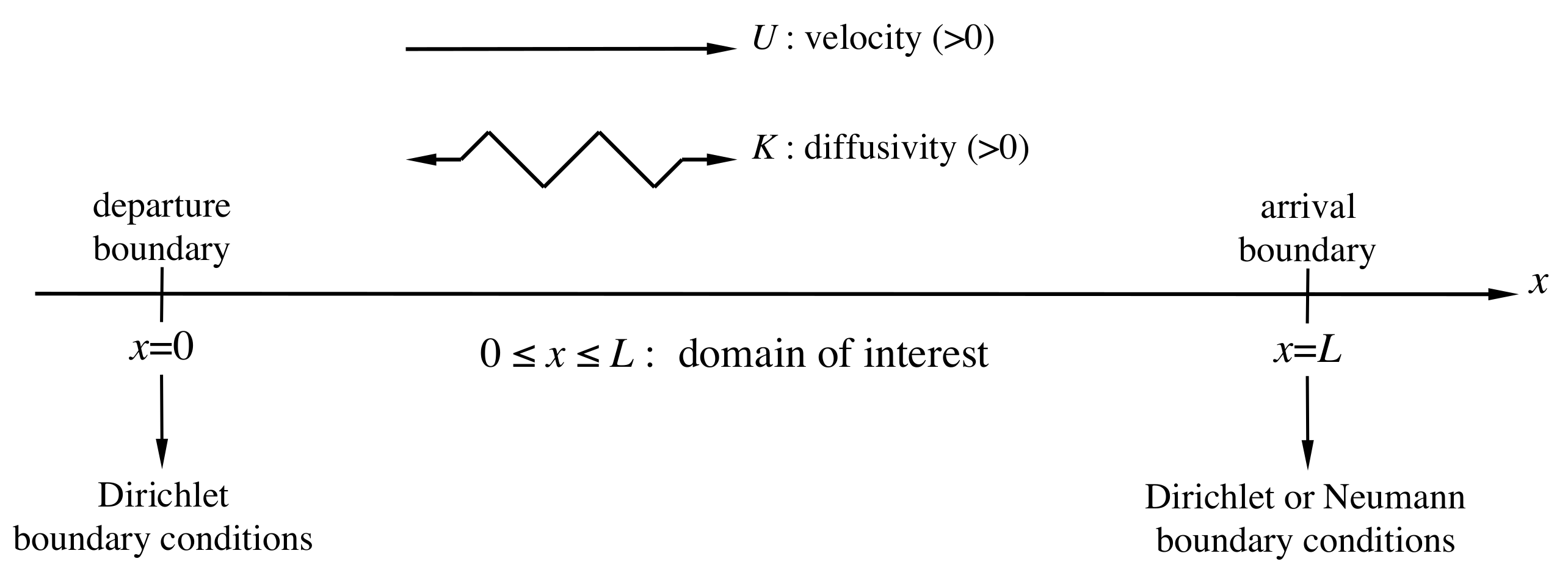
3.4. Arrival Boundary
3.5. Arrival Boundary: An Alternative Approach
3.6. Gas Exchanges through the Water–air Interface
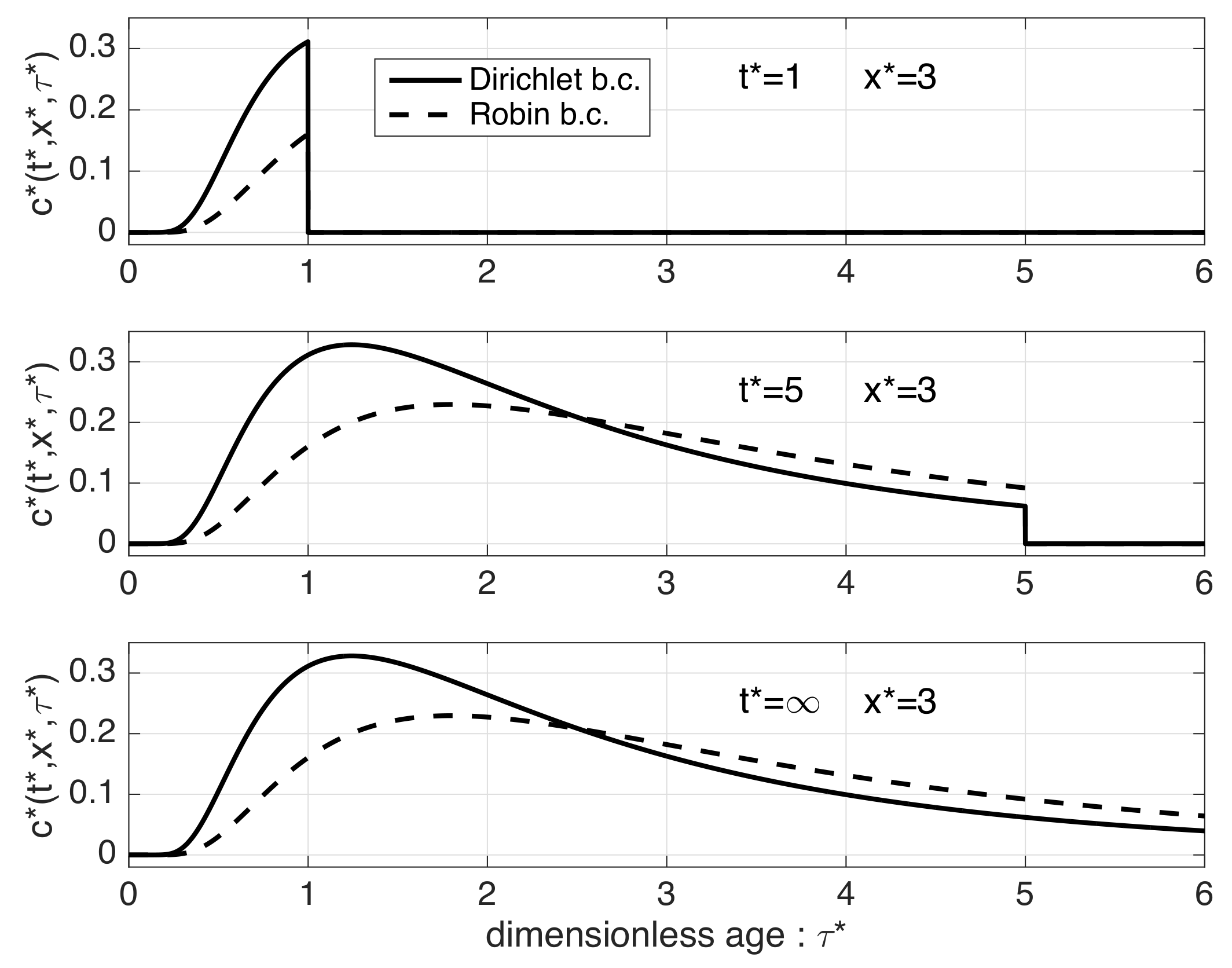
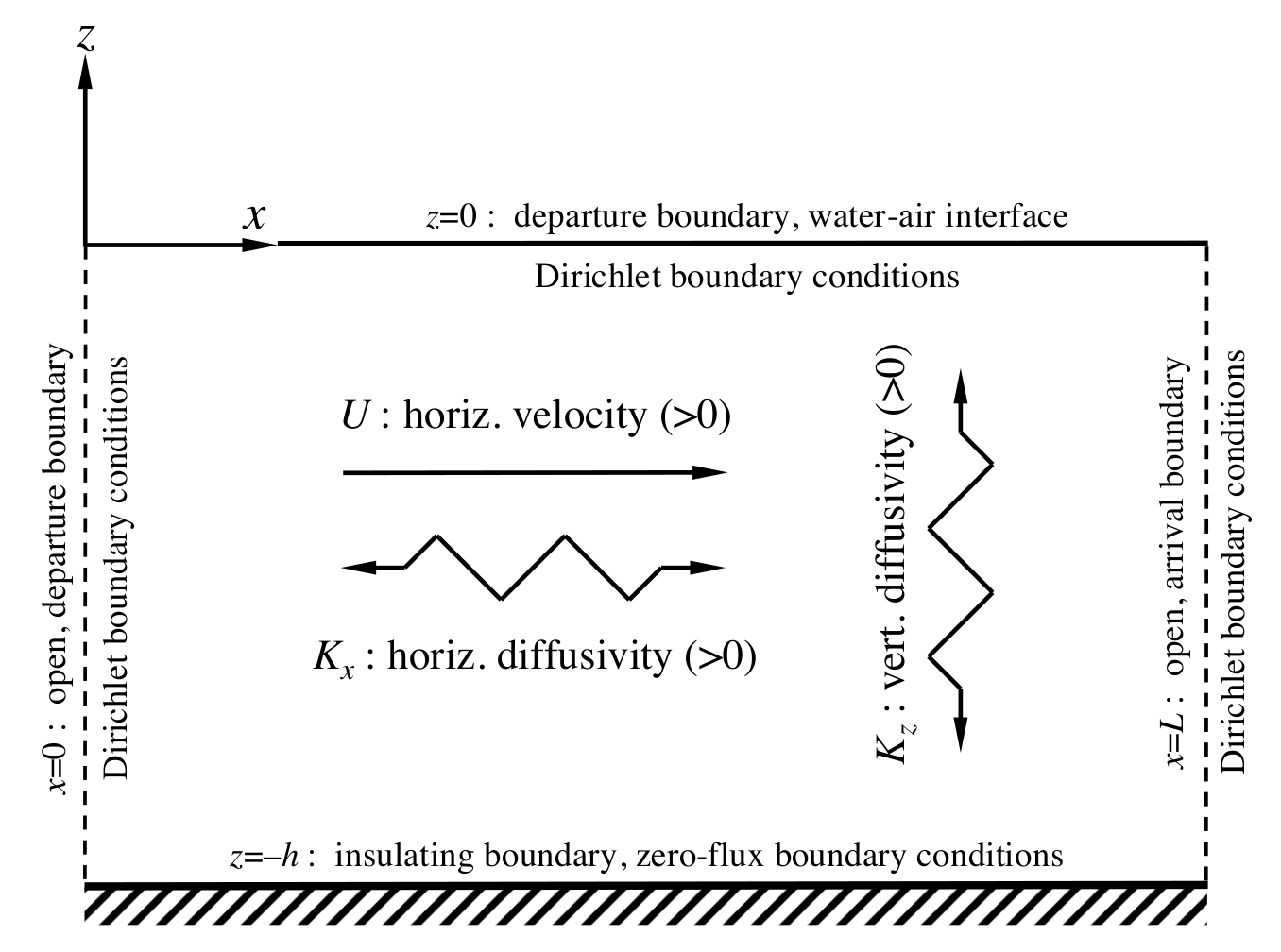
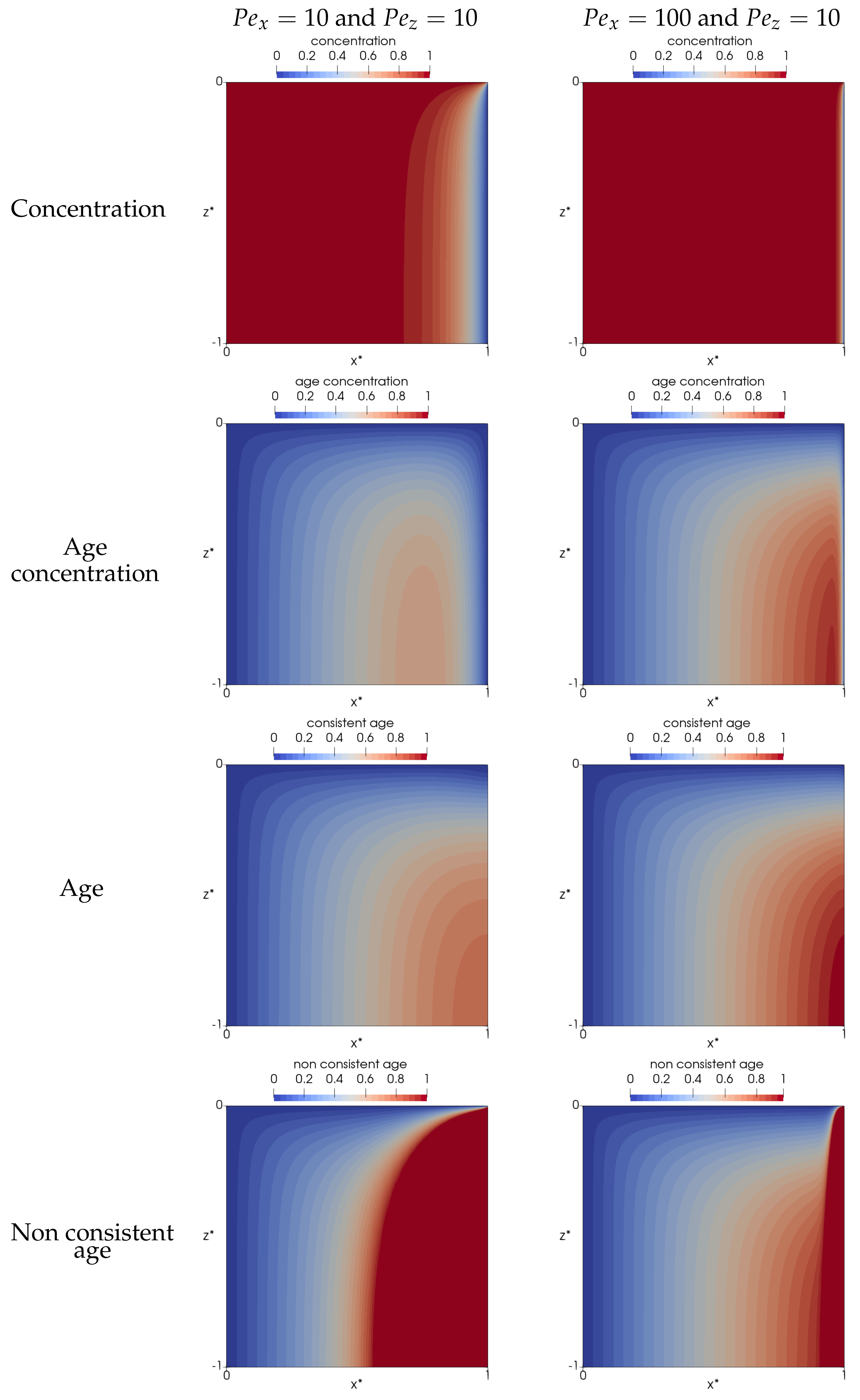
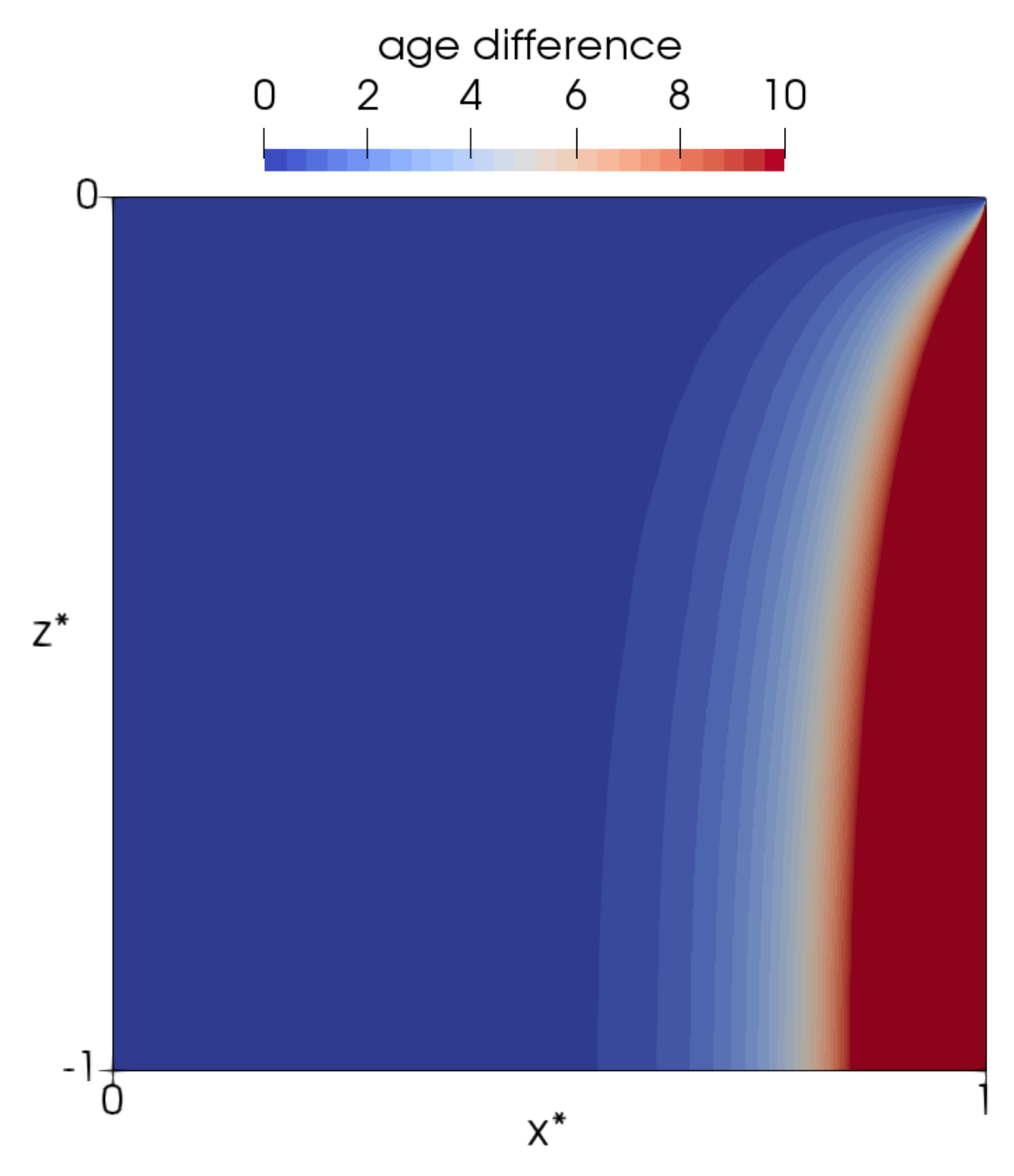
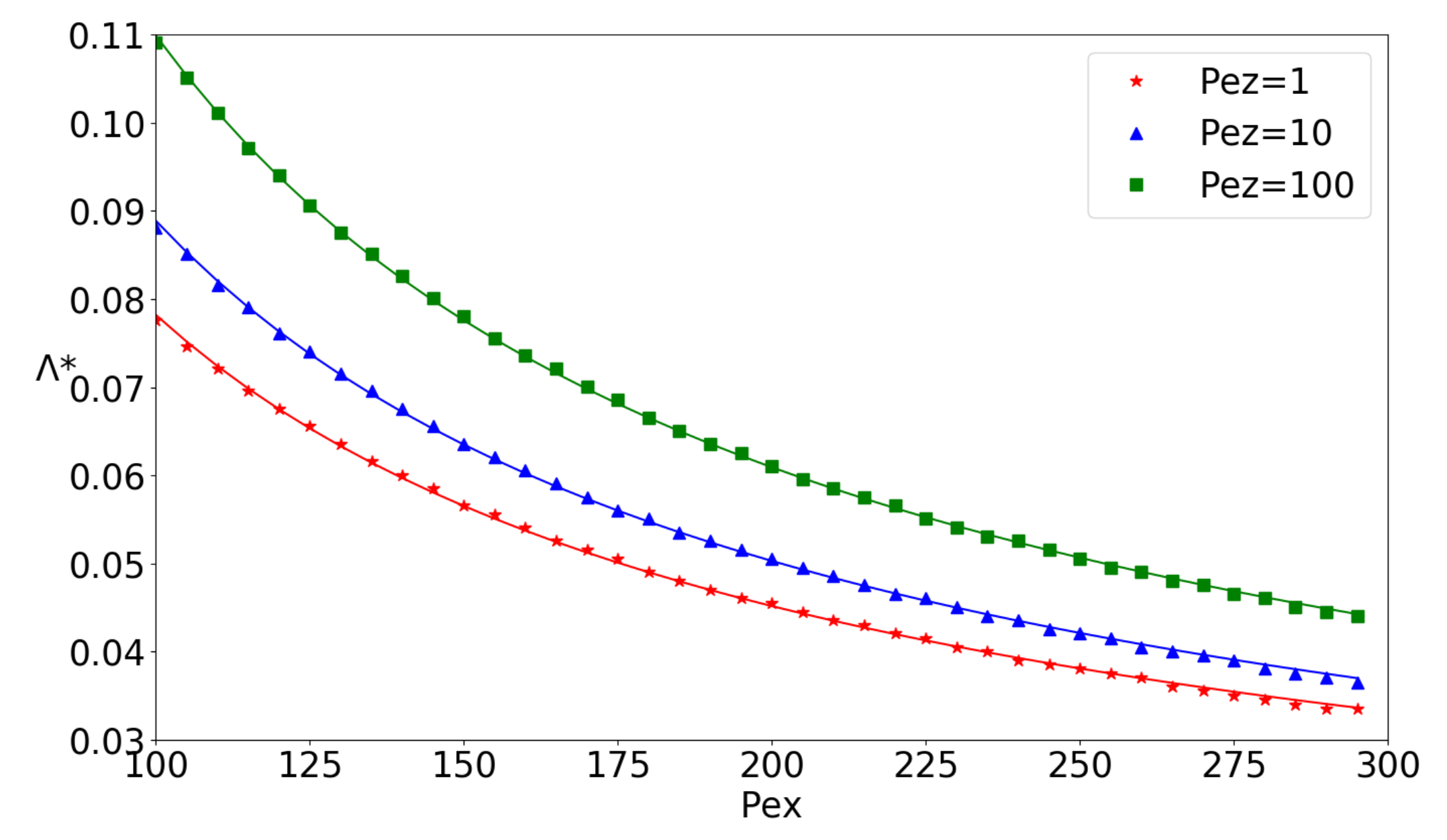
4. A Simple Ventilation Assessment Problem
5. Discussion and Conclusions
- Set out the reasons why the age, rather than other timescales (or diagnoses of another nature), is likely to be of use to help interpret the aquatic processes under consideration;
- Select the constituent whose (mean) age is to be evaluated and explain the rationale of this choice;
- Define the age, especially where and when the age of a particle of the constituent under study is to set or reset to zero, as well as where, when, and how this particle will cease to be taken into consideration;
- Build the boundary conditions for the age distribution function in accordance with the outcome of the previous three steps;
- Derive consistent boundary conditions for the concentration and age concentration using the methodology developed in this article (see also Appendix D).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Hall, T.M.; Plumb, R.A. Age as a diagnostic of stratospheric transport. J. Geophys. Res. Atmos. 1994, 99, 1059–1070. [Google Scholar] [CrossRef]
- Holzer, M.; Hall, T.M. Transit-time and tracer-age distributions in geophysical flows. J. Atmos. Sci. 2000, 57, 3539–3558. [Google Scholar] [CrossRef]
- Waugh, D.W.; Hall, T.M. Age of stratospheric air: Theory, observations, and models. Rev. Geophys. 2002, 40, 1010. [Google Scholar] [CrossRef]
- Orbe, C.; Waugh, D.W.; Newman, P.A.; Steenrod, S. The transit-time distribution from the Northern Hemisphere midlatitude surface. J. Atmos. Sci. 2016, 73, 3785–3802. [Google Scholar] [CrossRef]
- Dronkers, J.; Zimmerman, J.T.F. Some principles of mixing in tidal lagoons. In Proceedings of the Oceanologica Acta, N° SP, Actes Symposium International sur les lagunes côtières, SCOR/IABO/UNESCO, Bordeaux, France, 8–14 September 1982; pp. 107–117. [Google Scholar]
- Helder, W.; Ruardij, P. A one-dimensional mixing and flushing model of the Ems-Dollard estuary: calculation of time scales at different river discharges. Neth. J. Sea Res. 1982, 15, 293–312. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. Estuarine Residence Times. Hydrodynamics of Estuaries; Kjerfve, B., Ed.; CRC Press: Boca Raton, FL, USA, 1988; Volume I, pp. 75–84. [Google Scholar]
- Delesalle, B.; Sournia, A. Residence time of water and phytoplankton biomass in coral reef lagoons. Cont. Shelf Res. 1992, 12, 939–949. [Google Scholar] [CrossRef]
- Salomon, J.C.; Breton, M.; Guegueniat, P. A 2D long term advection—dispersion model for the Channel and southern North Sea Part B: Transit time and transfer function from Cap de La Hague. J. Mar. Syst. 1995, 6, 515–527. [Google Scholar] [CrossRef]
- Oliveira, A.; Baptista, A.M. Diagnostic modeling of residence times in estuaries. Water Resour. Res. 1997, 33, 1935–1946. [Google Scholar] [CrossRef]
- Jenkins, W.J. Studying subtropical thermocline ventilation and circulation using tritium and 3He. J. Geophys. Res. Ocean. 1998, 103, 15817–15831. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Wang, J.; Mooers, C.N.K. A two-compartment model for understanding the simulated three-dimensional circulation in Prince William Sound, Alaska. Cont. Shelf Res. 1998, 18, 279–287. [Google Scholar] [CrossRef][Green Version]
- Campin, J.M.; Fichefet, T.; Duplessy, J.C. Problems with using radiocarbon to infer ocean ventilation rates for past and present climates. Earth Planet. Sci. Lett. 1999, 165, 17–24. [Google Scholar] [CrossRef]
- Andréfouët, S.; Pagès, J.; Tartinville, B. Water renewal time for classification of atoll lagoons in the Tuamotu Archipelago (French Polynesia). Coral Reefs 2001, 20, 399–408. [Google Scholar] [CrossRef]
- Haine, T.W.N.; Hall, T.M. A generalized transport theory: Water-mass composition and age. J. Phys. Oceanogr. 2002, 32, 1932–1946. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Waugh, D.W.; Vollmer, M.K.; Weiss, R.F.; Haine, T.W.N.; Hall, T.M. Transit time distributions in Lake Issyk-Kul. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Braunschweig, F.; Martins, F.; Chambel, P.; Neves, R. A methodology to estimate renewal time scales in estuaries: the Tagus Estuary case. Ocean. Dyn. 2003, 53, 137–145. [Google Scholar] [CrossRef]
- Waugh, D.W.; Hall, T.M.; Haine, T.W.N. Relationships among tracer ages. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Andrejev, O.; Myrberg, K.; Lundberg, P.A. Age and renewal time of water masses in a semi-enclosed basin—Application to the Gulf of Finland. Tellus Dyn. Meteorol. Oceanogr. 2004, 56, 548–558. [Google Scholar]
- Abdelrhman, M.A. Simplified modeling of flushing and residence times in 42 embayments in New England, USA, with special attention to Greenwich Bay, Rhode Island. Estuar. Coast. Shelf Sci. 2005, 62, 339–351. [Google Scholar] [CrossRef]
- Gao, Y.; Drange, H.; Bentsen, M.; Johannessen, O.M. Tracer-derived transit time of the waters in the eastern Nordic Seas. Tellus Chem. Phys. Meteorol. 2005, 57, 332–340. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective–dispersive systems: 1. Generalized reservoir theory. Adv. Water Resour. 2006, 29, 1267–1291. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective–dispersive systems; 2. Reservoir theory for sub-drainage basins. Adv. Water Resour. 2006, 29, 1292–1305. [Google Scholar] [CrossRef]
- Cucco, A.; Perilli, A.; De Falco, G.; Ghezzo, M.; Umgiesser, G. Water circulation and transport timescales in the Gulf of Oristano. Chem. Ecol. 2006, 22, S307–S331. [Google Scholar] [CrossRef]
- Holzer, M.; Primeau, F. The diffusive ocean conveyor. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Jouon, A.; Douillet, P.; Ouillon, S.; Fraunié, P. Calculations of hydrodynamic time parameters in a semi-opened coastal zone using a 3D hydrodynamic model. Cont. Shelf Res. 2006, 26, 1395–1415. [Google Scholar] [CrossRef]
- Kazemi, G.H.; Lehr, J.H.; Perrochet, P. Groundwater Age; Wiley: Hoboken, NJ, USA, 2006; p. 325. [Google Scholar]
- Orre, S.; Gao, Y.; Drange, H.; Nilsen, J.E.Ø. A reassessment of the dispersion properties of 99Tc in the North Sea and the Norwegian Sea. J. Mar. Syst. 2007, 68, 24–38. [Google Scholar] [CrossRef]
- Torréton, J.P.; Rochelle-Newall, E.; Jouon, A.; Faure, V.; Jacquet, S.; Douillet, P. Correspondence between the distribution of hydrodynamic time parameters and the distribution of biological and chemical variables in a semi-enclosed coral reef lagoon. Estuar. Coast. Shelf Sci. 2007, 74, 766–776. [Google Scholar] [CrossRef]
- Cucco, A.; Umgiesser, G.; Ferrarin, C.; Perilli, A.; Canu, D.M.; Solidoro, C. Eulerian and lagrangian transport time scales of a tidal active coastal basin. Ecol. Model. 2009, 220, 913–922. [Google Scholar] [CrossRef]
- Plus, M.; Dumas, F.; Stanisière, J.Y.; Maurer, D. Hydrodynamic characterization of the Arcachon Bay, using model-derived descriptors. Cont. Shelf Res. 2009, 29, 1008–1013. [Google Scholar] [CrossRef]
- Lucas, L.V. Implications of estuarine transport for water quality. Contemp. Issues Estuar. Phys. 2010, 273–303. [Google Scholar]
- Maltrud, M.; Bryan, F.; Peacock, S. Boundary impulse response functions in a century-long eddying global ocean simulation. Environ. Fluid Mech. 2010, 10, 275–295. [Google Scholar] [CrossRef][Green Version]
- Cavalcante, G.H.; Kjerfve, B.; Feary, D.A. Examination of residence time and its relevance to water quality within a coastal mega-structure: The Palm Jumeirah Lagoon. J. Hydrol. 2012, 468, 111–119. [Google Scholar] [CrossRef]
- Mouchet, A.; Deleersnijder, E.; Primeau, F. The leaky funnel model revisited. Tellus Dyn. Meteorol. Oceanogr. 2012, 64, 19131. [Google Scholar] [CrossRef]
- Grifoll, M.; Del Campo, A.; Espino, M.; Mader, J.; González, M.; Borja, Á. Water renewal and risk assessment of water pollution in semi-enclosed domains: Application to Bilbao Harbour (Bay of Biscay). J. Mar. Syst. 2013, 109, S241–S251. [Google Scholar] [CrossRef]
- Andutta, F.P.; Ridd, P.V.; Deleersnijder, E.; Prandle, D. Contaminant exchange rates in estuaries–New formulae accounting for advection and dispersion. Prog. Oceanogr. 2014, 120, 139–153. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Wolk, F. Diagnosis of the transport of adsorbed material in the Scheldt estuary: A proof of concept. J. Mar. Syst. 2013, 128, 17–26. [Google Scholar] [CrossRef]
- Rinaldo, A.; Benettin, P.; Harman, C.J.; Hrachowitz, M.; McGuire, K.J.; Van Der Velde, Y.; Bertuzzo, E.; Botter, G. Storage selection functions: A coherent framework for quantifying how catchments store and release water and solutes. Water Resour. Res. 2015, 51, 4840–4847. [Google Scholar] [CrossRef]
- Viero, D.P.; Defina, A. Renewal Time Scales in Tidal Basins: Climbing the Tower of Babel. Sustainable Hydraulics in the Era of Global Change; Erpicum, S., Ed.; Taylor & Francis Group: Abingdon, UK, 2016; pp. 338–345. [Google Scholar]
- Viero, D.P.; Defina, A. Water age, exposure time, and local flushing time in semi-enclosed, tidal basins with negligible freshwater inflow. J. Mar. Syst. 2016, 156, 16–29. [Google Scholar] [CrossRef]
- Hiatt, M.; Castañeda-Moya, E.; Twilley, R.; Hodges, B.R.; Passalacqua, P. Channel-island connectivity affects water exposure time distributions in a coastal river delta. Water Resour. Res. 2018, 54, 2212–2232. [Google Scholar] [CrossRef]
- Cheng, Y.; Mu, Z.; Wang, H.; Zhao, F.; Li, Y.; Lin, L. Water Residence Time in a Typical Tributary Bay of the Three Gorges Reservoir. Water 2019, 11, 1585. [Google Scholar] [CrossRef]
- Dippner, J.W.; Bartl, I.; Chrysagi, E.; Holtermann, P.L.; Kremp, A.; Thoms, F.; Voss, M. Lagrangian Residence Time in the Bay of Gdansk, Baltic Sea. Front. Mar. Sci. 2019, 6, 725. [Google Scholar] [CrossRef]
- Drouzy, M.; Douillet, P.; Fernandez, J.M.; Pinazo, C. Hydrodynamic time parameters response to meteorological and physical forcings: toward a stagnation risk assessment device in coastal areas. Ocean. Dyn. 2019, 69, 967–987. [Google Scholar] [CrossRef]
- Gross, E.; Andrews, S.; Bergamaschi, B.; Downing, B.; Holleman, R.; Burdick, S.; Durand, J. The Use of Stable Isotope-Based Water Age to Evaluate a Hydrodynamic Model. Water 2019, 11, 2207. [Google Scholar] [CrossRef]
- Huguet, J.R.; Brenon, I.; Coulombier, T. Characterisation of the Water Renewal in a Macro-Tidal Marina Using Several Transport Timescales. Water 2019, 11, 2050. [Google Scholar] [CrossRef]
- Jiang, L.; Soetaert, K.; Gerkema, T. Decomposing the intra-annual variability of flushing characteristics in a tidal bay along the North Sea. J. Sea Res. 2019, 155, 101821. [Google Scholar] [CrossRef]
- Mercier, C.; Delhez, E.J.M. Diagnosis of the sediment transport in the Belgian Coastal Zone. Estuar. Coast. Shelf Sci. 2007, 74, 670–683. [Google Scholar] [CrossRef]
- Gong, W.; Shen, J. A model diagnostic study of age of river-borne sediment transport in the tidal York River Estuary. Environ. Fluid Mech. 2010, 10, 177–196. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R. Sediment transport time scales and trapping efficiency in a tidal river. J. Geophys. Res. Earth Surf. 2017, 122, 2042–2063. [Google Scholar] [CrossRef]
- Delhez, E.J.M. On the concept of exposure time. Cont. Shelf Res. 2013, 71, 27–36. [Google Scholar] [CrossRef]
- Zimmerman, J.T.F. Mixing and flushing of tidal embayments in the western Dutch Wadden Sea part I: Distribution of salinity and calculation of mixing time scales. Neth. J. Sea Res. 1976, 10, 149–191. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Thiele, G.; Sarmiento, J.L. Tracer dating and ocean ventilation. J. Geophys. Res. Ocean. 1990, 95, 9377–9391. [Google Scholar] [CrossRef]
- England, M.H. The age of water and ventilation timescales in a Global Ocean model. J. Phys. Oceanogr. 1995, 25, 2756–2777. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Campin, J.M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean. Model. 1999, 1, 17–27. [Google Scholar] [CrossRef]
- Hirst, A.C. Determination of water component age in ocean models: Application to the fate of North Atlantic Deep Water. Ocean. Model. 1999, 1, 81–94. [Google Scholar] [CrossRef]
- Deleersnijder, E. On the Timescales Relevant to a Linear Transport-Decay Reservoir Model; Technical Report; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2019; Available online: http://hdl.handle.net/2078.1/219115 (accessed on 29 April 2020).
- de Brye, B.; de Brauwere, A.; Gourgue, O.; Delhez, E.J.M.; Deleersnijder, E. Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2012, 94, 74–86. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Lacroix, G.; Deleersnijder, E. The age as a diagnostic of the dynamics of marine ecosystem models. Ocean. Dyn. 2004, 54, 221–231. [Google Scholar] [CrossRef]
- White, L.; Deleersnijder, E. Diagnoses of vertical transport in a three-dimensional finite element model of the tidal circulation around an island. Estuar. Coast. Shelf Sci. 2007, 74, 655–669. [Google Scholar] [CrossRef]
- Bendtsen, J.; Gustafsson, K.E.; Söderkvist, J.; Hansen, J.L. Ventilation of bottom water in the North Sea–Baltic Sea transition zone. J. Mar. Syst. 2009, 75, 138–149. [Google Scholar] [CrossRef]
- Shah, S.H.A.M.; Primeau, F.; Deleersnijder, E.; Heemink, A. Tracing the ventilation pathways of the deep North Pacific Ocean using Lagrangian particles and Eulerian tracers. J. Phys. Oceanogr. 2017, 47, 1261–1280. [Google Scholar] [CrossRef]
- Sun, J.; Liu, L.; Lin, J.; Lin, B.; Zhao, H. Vertical water renewal in a large estuary and implications for water quality. Sci. Total Environ. 2019, 135593. [Google Scholar] [CrossRef] [PubMed]
- Van Sebille, E.; Griffies, S.M.; Abernathey, R.; Adams, T.P.; Berloff, P.; Biastoch, A.; Blanke, B.; Chassignet, E.P.; Cheng, Y.; Cotter, C.J.; et al. Lagrangian ocean analysis: Fundamentals and practices. Ocean. Model. 2018, 121, 49–75. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Campin, J.M.; Delhez, E.J. The concept of age in marine modelling: I. Theory and preliminary model results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Mouchet, A.; Delhez, E.J.M.; Beckers, J.M. Transient behaviour of water ages in the World Ocean. Math. Comput. Model. 2002, 36, 121–127. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E. The concept of age in marine modelling: II. Concentration distribution function in the English Channel and the North Sea. J. Mar. Syst. 2002, 31, 279–297. [Google Scholar] [CrossRef]
- Garabedian, P. Partial Differential Equations; Chelsea Publishing Company: New York, NY, USA, 1964; 672p. [Google Scholar]
- Shen, J.; Haas, L. Calculating age and residence time in the tidal York River using three-dimensional model experiments. Estuar. Coast. Shelf Sci. 2004, 61, 449–461. [Google Scholar] [CrossRef]
- Shen, J.; Lin, J. Modeling study of the influences of tide and stratification on age of water in the tidal James River. Estuar. Coast. Shelf Sci. 2006, 68, 101–112. [Google Scholar] [CrossRef]
- Meier, H.E.M. Modeling the pathways and ages of inflowing salt-and freshwater in the Baltic Sea. Estuar. Coast. Shelf Sci. 2007, 74, 610–627. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Guo, X.; Wang, Q.; Gao, H. The age of Yellow River water in the Bohai Sea. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Radtke, H.; Neumann, T.; Voss, M.; Fennel, W. Modeling pathways of riverine nitrogen and phosphorus in the Baltic Sea. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Bendtsen, J.; Mortensen, J.; Rysgaard, S. Seasonal surface layer dynamics and sensitivity to runoff in a high Arctic fjord (Young Sound/Tyrolerfjord, 74 N). J. Geophys. Res. Ocean. 2014, 119, 6461–6478. [Google Scholar] [CrossRef]
- Kärnä, T.; Baptista, A.M. Water age in the Columbia River estuary. Estuar. Coast. Shelf Sci. 2016, 183, 249–259. [Google Scholar] [CrossRef]
- Rayson, M.D.; Gross, E.S.; Hetland, R.D.; Fringer, O.B. Time scales in Galveston Bay: An unsteady estuary. J. Geophys. Res. Ocean. 2016, 121, 2268–2285. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, X.; Liang, B.; Xin, L.; Zhao, Y. Numerical Study on the Influences of Hydrodynamic Factors on Water Age in the Liao River Estuary, China. J. Coast. Res. 2017, 80, 98–107. [Google Scholar] [CrossRef]
- Du, J.; Park, K.; Shen, J.; Dzwonkowski, B.; Yu, X.; Yoon, B.I. Role of baroclinic processes on flushing characteristics in a highly stratified estuarine system, Mobile Bay, Alabama. J. Geophys. Res. 2018, 123, 4518–4537. [Google Scholar] [CrossRef]
- Gao, Q.; He, G.; Fang, H.; Bai, S.; Huang, L. Numerical simulation of water age and its potential effects on the water quality in Xiangxi Bay of Three Gorges Reservoir. J. Hydrol. 2018, 566, 484–499. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, W.; Zhang, H.; Qiao, J.; Liu, J.; Shi, Z.; Gong, W. Evaluation of the total maximum allocated load of dissolved inorganic nitrogen using a watershed—Coastal ocean coupled model. Sci. Total Environ. 2019, 673, 734–749. [Google Scholar] [CrossRef]
- Grosse, F.; Fennel, K.; Laurent, A. Quantifying the relative importance of riverine and open-ocean nitrogen sources for hypoxia formation in the northern Gulf of Mexico. J. Geophys. Res. 2019, 124, 5451–5467. [Google Scholar] [CrossRef]
- Li, Y.; Feng, H.; Zhang, H.; Sun, J.; Yuan, D.; Guo, L.; Nie, J.; Du, J. Hydrodynamics and water circulation in the New York/New Jersey Harbor: A study from the perspective of water age. J. Mar. Syst. 2019, 199, 103219. [Google Scholar] [CrossRef]
- Shang, J.; Sun, J.; Tao, L.; Li, Y.; Nie, Z.; Liu, H.; Chen, R.; Yuan, D. Combined Effect of Tides and Wind on Water Exchange in a Semi-Enclosed Shallow Sea. Water 2019, 11, 1762. [Google Scholar] [CrossRef]
- Yang, J.; Kong, J.; Tao, J. Modeling the Water-Flushing Properties of the Yangtze Estuary and Adjacent Waters. J. Ocean. Univ. China 2019, 18, 93–107. [Google Scholar] [CrossRef]
- Beckers, J.M.; Delhez, E.; Deleersnijder, E. Some properties of generalized age-distribution equations in fluid dynamics. SIAM J. Appl. Math. 2001, 61, 1526–1544. [Google Scholar]
- Deleersnijders, E.; Delhez, E.J.M.; Crucifix, M.; Beckers, J.M. On the symmetry of the age field of a passive tracer released into a one-dimensional fluid flow by a point-source. Bull. de la Soc. R. des Sci. de Liège 2001, 70, 5–21. Available online: https://popups.uliege.be/0037-9565/index.php?id=1392 (accessed on 29 April 2020).
- Deleersnijder, E. Water Renewal of a Region of Freshwater Influence (ROFI): Mathematical Properties of Some of the Relevant Diagnostic Variables; Technical Report; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2019; Available online: http://hdl.handle.net/2078.1/220841 (accessed on 29 April 2020).
- Deleersnijder, E.; Delhez, E.J.M. Symmetry and asymmetry of water ages in a one-dimensional flow. J. Mar. Syst. 2004, 48, 61–66. [Google Scholar] [CrossRef]
- Hall, T.M.; Haine, T.W.N. Tracer age symmetry in advective–diffusive flows. J. Mar. Syst. 2004, 48, 51–59. [Google Scholar] [CrossRef]
- Cox, M.D. An idealized model of the world ocean. Part I: The global-scale water masses. J. Phys. Oceanogr. 1989, 19, 1730–1752. [Google Scholar] [CrossRef]
- Goosse, H.; Campin, J.M.; Tartinville, B. The sources of Antarctic bottom water in a global ice–ocean model. Ocean. Model. 2001, 3, 51–65. [Google Scholar] [CrossRef]
- Cornaton, F.J. Transient water age distributions in environmental flow systems: The time-marching Laplace transform solution technique. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Deleersnijder, E.; Mouchet, A.; Beckers, J.M. A note on the age of radioactive tracers. J. Mar. Syst. 2003, 38, 277–286. [Google Scholar] [CrossRef]
- Delhez, É.J.; Deleersnijder, É. The boundary layer of the residence time field. Ocean. Dyn. 2006, 56, 139–150. [Google Scholar] [CrossRef]
- Deleersnijder, E. A Conjecture about Age Inequalities; Technical Report; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2019; Available online: http://hdl.handle.net/2078.1/227647 (accessed on 29 April 2020).
- Beckers, J.M. YAAI: Yet Another Age Inequality; Technical Report; Université de Liège: Liège, Belgium, 2020; Available online: http://hdl.handle.net/2268/245381 (accessed on 29 April 2020).
- Liss, P.S. Gas Transfer: Experiments and Geochemical Implications. In Air-Sea Exchange of Gases and Particles; NATO ASI Series (Series C: Mathematical and Physical Sciences); Liss, P.S., Slinn, W.G.N., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 241–298. [Google Scholar]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. Ocean. 1992, 97, 7373–7382. [Google Scholar] [CrossRef]
- Jähne, B.; Haußecker, H. Air-water gas exchange. Annu. Rev. Fluid Mech. 1998, 30, 443–468. [Google Scholar] [CrossRef]
- Haine, T.W.N. On tracer boundary conditions for geophysical reservoirs: How to find the boundary concentration from a mixed condition. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef]
- Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 2014, 12, 351–362. [Google Scholar] [CrossRef]
- Deleersnijder, E. On the Impact of the Atmosphere on the Time-Varying Age of a Passive Tracer in the Ocean; Technical Report; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2017; Available online: http://hdl.handle.net/2078.1/184324 (accessed on 29 April 2020).
- Hong, B.; Gong, W.; Peng, S.; Xie, Q.; Wang, D.; Li, H.; Xu, H. Characteristics of vertical exchange process in the Pearl River estuary. Aquat. Ecosyst. Health Manag. 2016, 19, 286–295. [Google Scholar] [CrossRef]
- Kärnä, T.; Legat, V.; Deleersnijder, E. A baroclinic discontinuous Galerkin finite element model for coastal flows. Ocean. Model. 2013, 61, 1–20. [Google Scholar] [CrossRef]
- Vallaeys, V.; Kärnä, T.; Delandmeter, P.; Lambrechts, J.; Baptista, A.M.; Deleersnijder, E.; Hanert, E. Discontinuous Galerkin modeling of the Columbia River’s coupled estuary-plume dynamics. Ocean. Model. 2018, 124, 111–124. [Google Scholar] [CrossRef]
- Delandmeter, P.; Lambrechts, J.; Legat, V.; Vallaeys, V.; Naithani, J.; Thiery, W.; Remacle, J.F.; Deleersnijder, E. A fully consistent and conservative vertically adaptive coordinate system for SLIM 3D v0. 4 with an application to the thermocline oscillations of Lake Tanganyika. Geosci. Model Dev. 2018, 11, 1161–1179. [Google Scholar] [CrossRef]
- Delhez, É.J.; de Brye, B.; de Brauwere, A.; Deleersnijder, E. Residence time vs influence time. J. Mar. Syst. 2014, 132, 185–195. [Google Scholar] [CrossRef]
- Mouchet, A.; Cornaton, F.; Deleersnijder, E.; Delhez, E.J. Partial ages: diagnosing transport processes by means of multiple clocks. Ocean. Dyn. 2016, 66, 367–386. [Google Scholar] [CrossRef]
- Orlanski, I. A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 1976, 21, 251–269. [Google Scholar] [CrossRef]
- Israeli, M.; Orszag, S.A. Approximation of radiation boundary conditions. J. Comput. Phys. 1981, 41, 115–135. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Kantha, L.H. Open boundary condition for circulation models. J. Hydraul. Eng. 1985, 111, 237–255. [Google Scholar] [CrossRef]
- Oddo, P.; Pinardi, N. Lateral open boundary conditions for nested limited area models: A scale selective approach. Ocean. Model. 2008, 20, 134–156. [Google Scholar] [CrossRef]
- Martinsen, E.A.; Engedahl, H. Implementation and testing of a lateral boundary scheme as an open boundary condition in a barotropic ocean model. Coast. Eng. 1987, 11, 603–627. [Google Scholar] [CrossRef]
- Lavelle, J.; Thacker, W. A pretty good sponge: Dealing with open boundaries in limited-area ocean models. Ocean. Model. 2008, 20, 270–292. [Google Scholar] [CrossRef]
- Blayo, E.; Debreu, L. Revisiting open boundary conditions from the point of view of characteristic variables. Ocean. Model. 2005, 9, 231–252. [Google Scholar] [CrossRef]
- Pham Van, C.; De Brye, B.; De Brauwere, A.; Hoitink, A.; Soares-Frazao, S.; Deleersnijder, E. Numerical Simulation of Water Renewal Timescales in the Mahakam Delta, Indonesia. Water 2020, 12, 1017. [Google Scholar] [CrossRef]
- Gräwe, U.; Wolff, J.O. Suspended particulate matter dynamics in a particle framework. Environ. Fluid Mech. 2010, 10, 21–39. [Google Scholar] [CrossRef]
- Gräwe, U.; Deleersnijder, E.; Shah, S.H.A.M.; Heemink, A.W. Why the Euler scheme in particle tracking is not enough: the shallow-sea pycnocline test case. Ocean. Dyn. 2012, 62, 501–514. [Google Scholar] [CrossRef]
- Wunsch, C. Oceanic age and transient tracers: Analytical and numerical solutions. J. Geophys. Res. Ocean. 2002, 107, 1. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959; 510p. [Google Scholar]
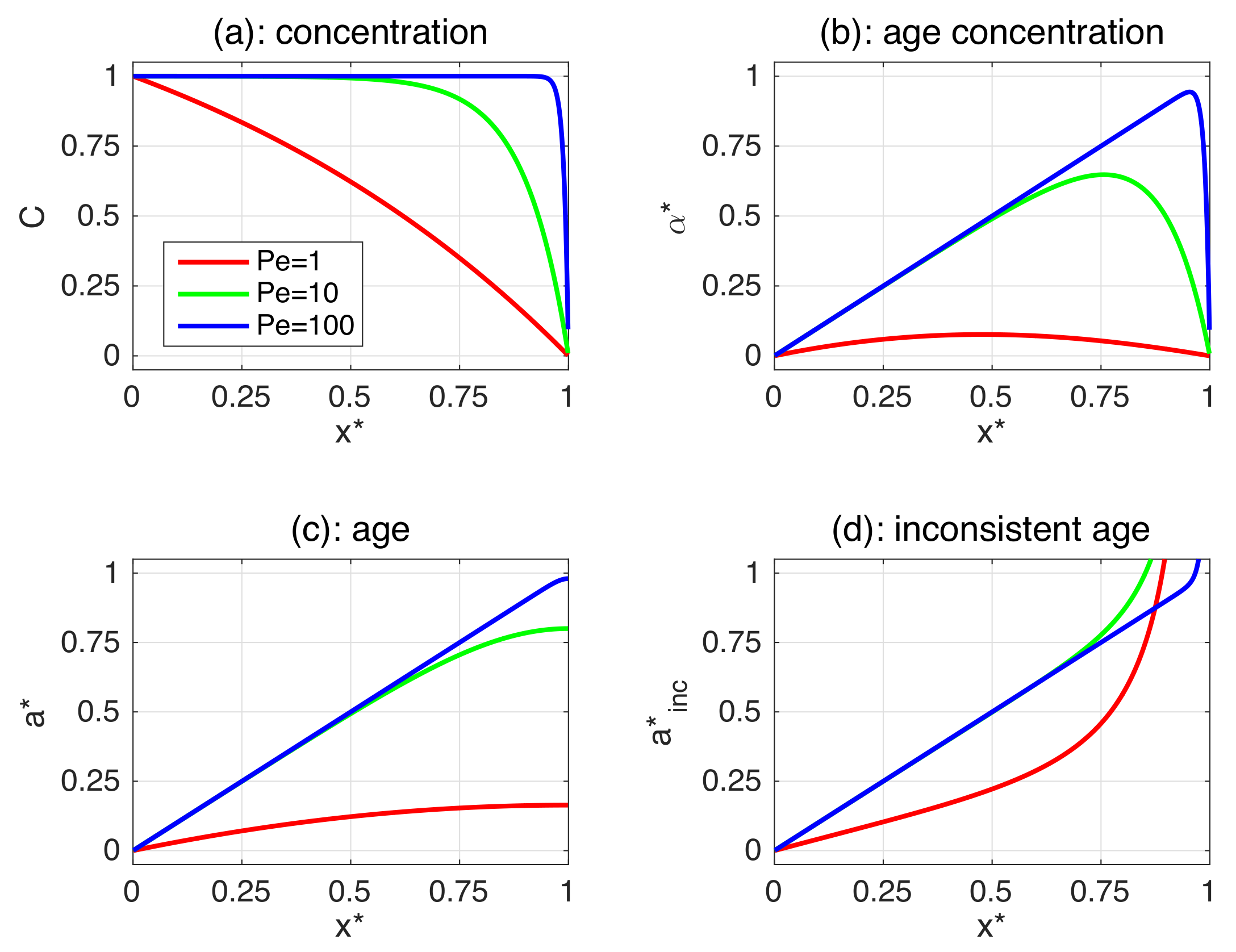
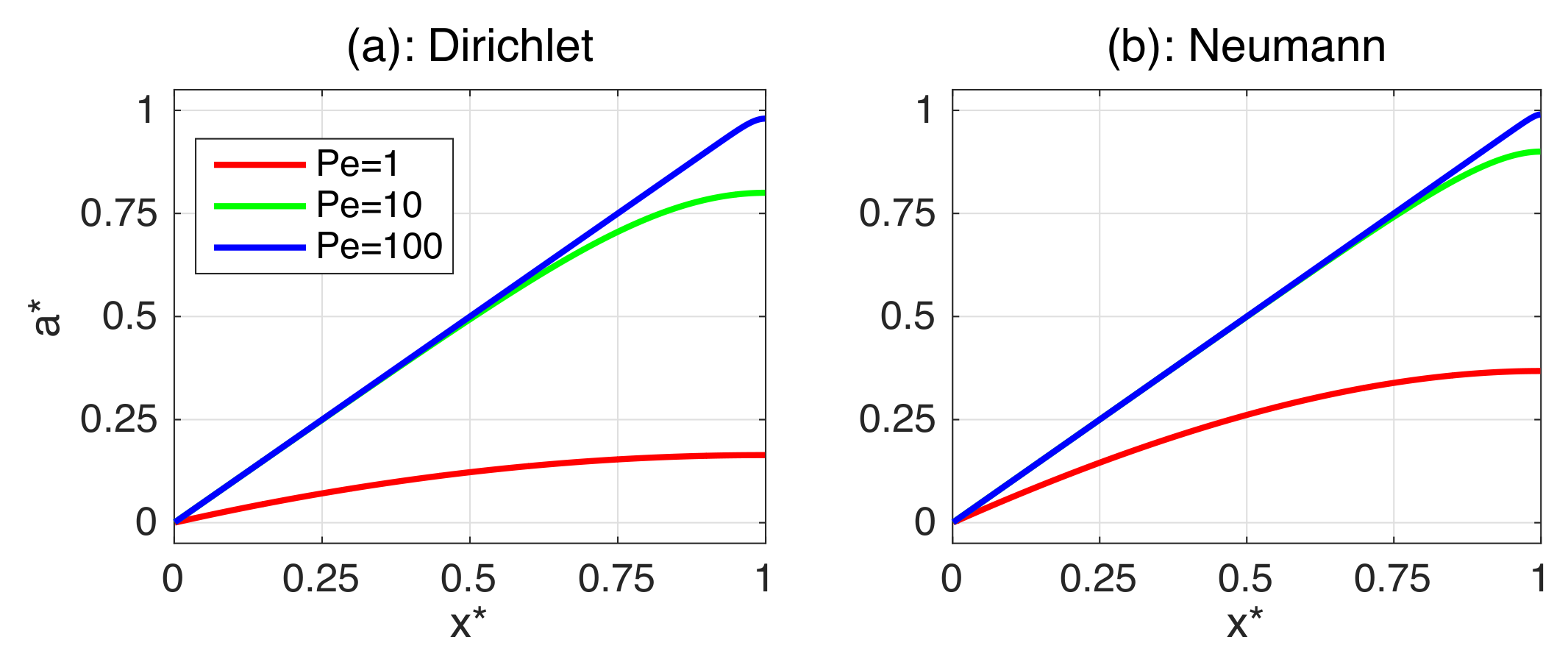
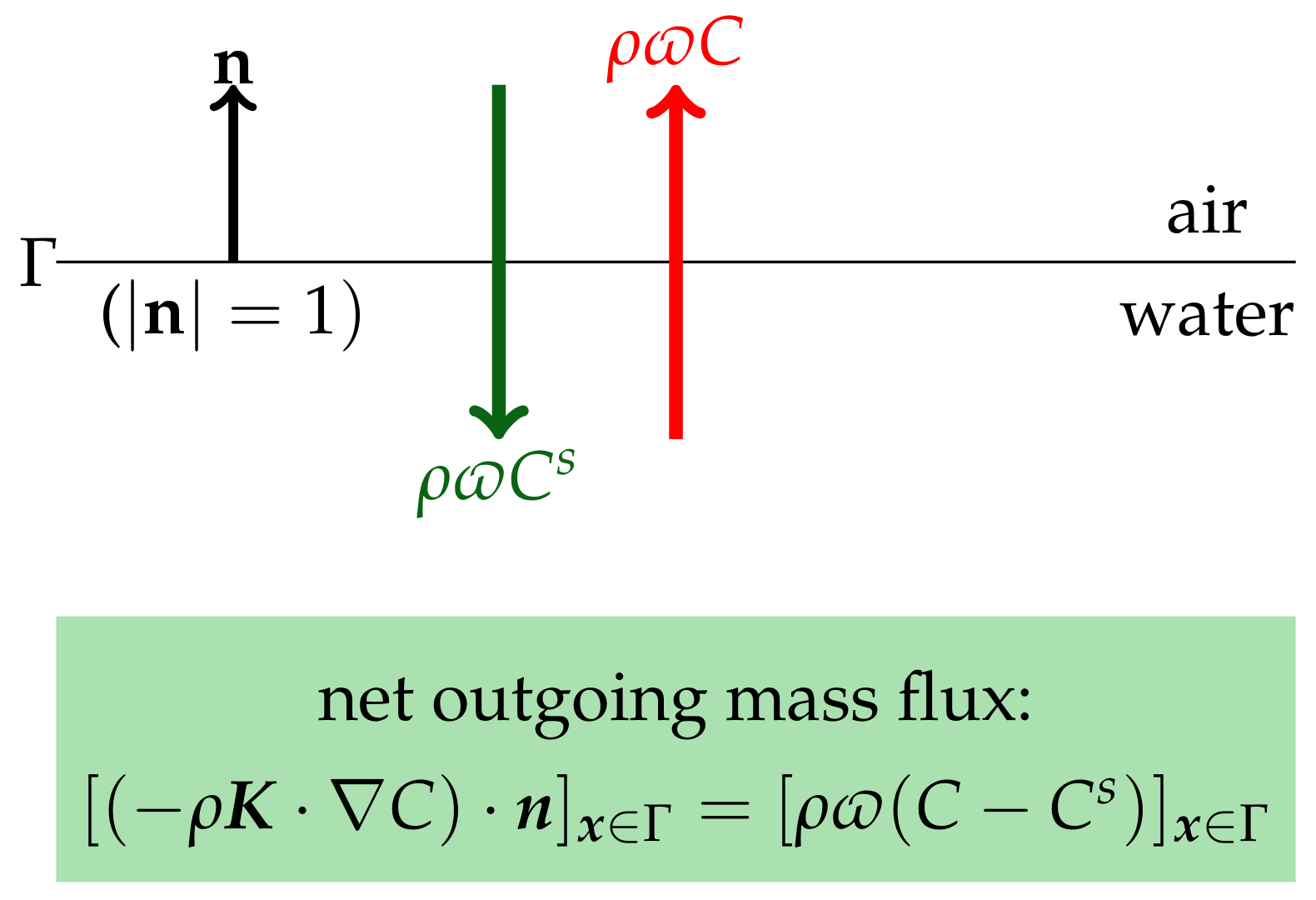
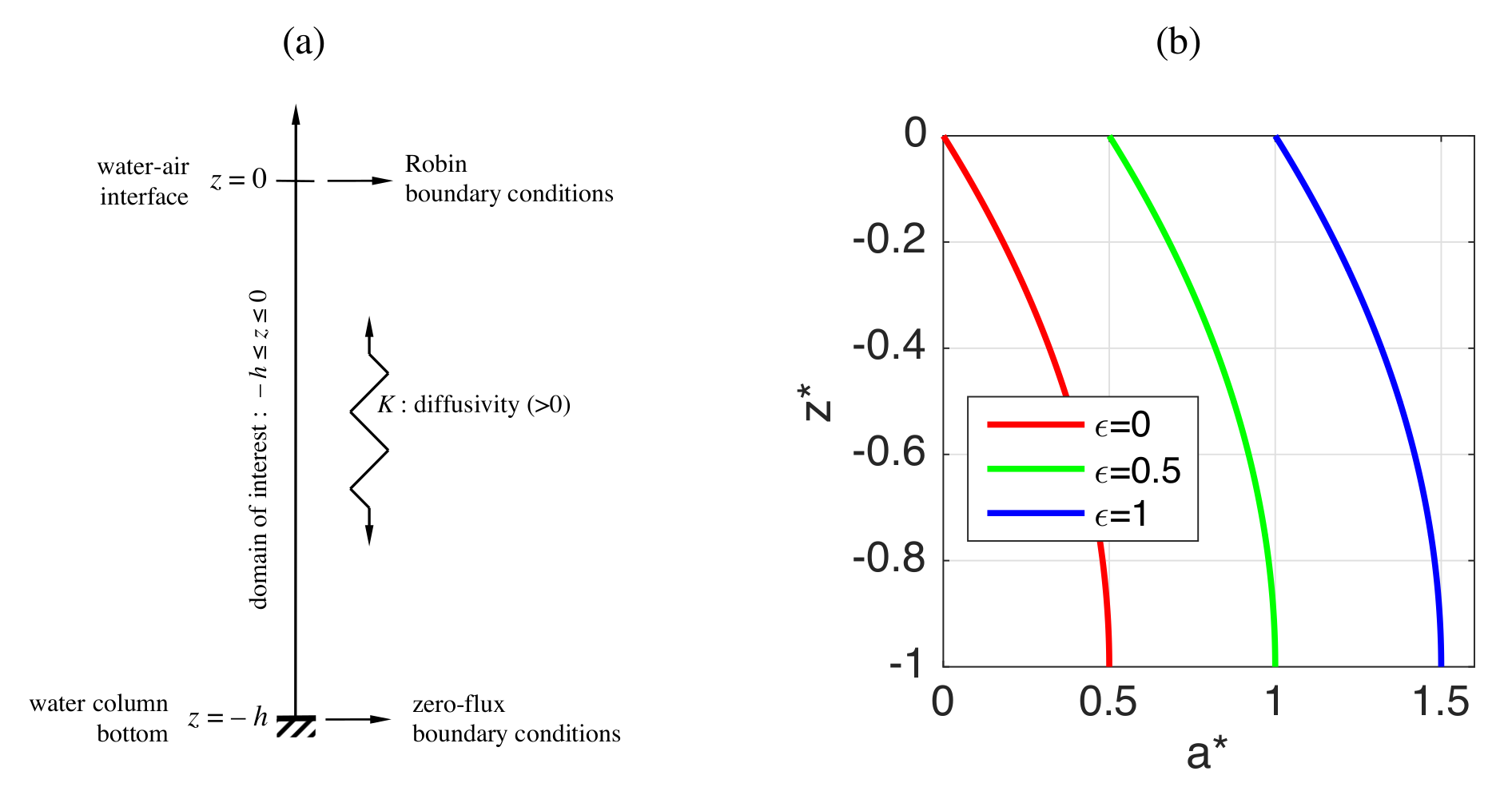
| Variable | Outgoing (Upward) | Incoming (Downward) Specific Flux | ||
|---|---|---|---|---|
| Specific Flux | General Expression | |||
| age distribution function | ||||
| concentration | ||||
| age concentration | 0 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deleersnijder, E.; Draoui, I.; Lambrechts, J.; Legat, V.; Mouchet, A. Consistent Boundary Conditions for Age Calculations. Water 2020, 12, 1274. https://doi.org/10.3390/w12051274
Deleersnijder E, Draoui I, Lambrechts J, Legat V, Mouchet A. Consistent Boundary Conditions for Age Calculations. Water. 2020; 12(5):1274. https://doi.org/10.3390/w12051274
Chicago/Turabian StyleDeleersnijder, Eric, Insaf Draoui, Jonathan Lambrechts, Vincent Legat, and Anne Mouchet. 2020. "Consistent Boundary Conditions for Age Calculations" Water 12, no. 5: 1274. https://doi.org/10.3390/w12051274
APA StyleDeleersnijder, E., Draoui, I., Lambrechts, J., Legat, V., & Mouchet, A. (2020). Consistent Boundary Conditions for Age Calculations. Water, 12(5), 1274. https://doi.org/10.3390/w12051274







