Abstract
As the third largest fresh water lake in China, Taihu Lake is suffering from serious eutrophication, where nutrient loading from tributary and surrounding river networks is one of the main contributors. In this study, water age is used to investigate the impacts of tributary discharge and wind influence on nutrient status in Taihu Lake, quantitatively. On the base of sub-basins of upstream catchments and boundary conditions of the lake, multiple inflow tributaries are categorized into three groups. For each group, the water age has been computed accordingly. A well-calibrated and validated three-dimensional Delft3D model is used to investigate both spatial and temporal heterogeneity of water age. Changes in wind direction lead to changes in both the average value and spatial pattern of water age, while the impact of wind speed differs in each tributary group. Water age decreases with higher inflow discharge from tributaries; however, discharge effects are less significant than that of wind. Wind speed decline, such as that induced by climate change, has negative effects on both internal and external nutrient source release, and results in water quality deterioration. Water age is proved to be an effective indicator of water exchange efficiency, which may help decision-makers to carry out integrated water management at a complex basin scale.
1. Introduction
Located in the southeastern part of China, Taihu Lake is the third largest fresh water lake in China. Like most large shallow lakes all over the world and as a typical shallow lake around the middle and lower reaches of the Yangtze River, Taihu Lake is suffering from the threat of eutrophication [1,2,3]. Considering the multi-functionality of Taihu Lake, both as an economic resource (such as supplying drinking water, and providing flood control, irrigation, water transport, and recreation) and as a valuable ecological resource, the water quality issue and consequential algae bloom problem have caused, and are still causing huge losses to this regional industrial and economic center, ever since 1987 [4,5,6,7].
The formation of the algae bloom happens when the concentration of algae is high at a particular spot. The growth of the algae population requires proper temperature, light availability, and essential nutrients, such as Nitrogen (N) and Phosphorus (P) [8]. The local government has made many attempts to mitigate the algae bloom, including wetland restoration, water transfer from the Yangtze River, and environmental dredging [9,10,11]. However, these treatments have not achieved the expected goal. Research has suggested applying a nutrient input reduction strategy for Taihu Lake’s water quality and ecology restoration [12,13,14,15,16].
Nutrients are released into the lake’s water body from two types of sources—namely, internal sources from sediment resuspension, and external sources from the connected river network. The previously mentioned studies of input nutrient reduction considered the external sources of nutrient release, which are significantly correlated to the local urbanization around the lake [17]. The lake-connected river networks accumulate nutrients from various sources (such as the diffuse sources of agriculture runoff, atmospheric deposition, or point sources of industry waste water and domestic sewage) and transport these into the lake [18,19,20,21]. Nutrient distribution in Taihu Lake varies both spatially and temporally, partially because the nutrients from the inflow tributaries vary due to local economic structure differences [22,23]. In turn, the uneven distribution has caused an inter-annual difference in the location of algae bloom in the lake. During the summer, algae bloom happens in the northern part of the lake, while in the early summer, autumn, and sometimes early winter, the algae bloom happens along the southwestern lake region [24]. However, these studies usually consider the lake as a whole black-box model or as several separate regions for a roughly spatially averaged evaluation, without considering the hydrodynamics. Thus, little attention has been paid to the spatial and temporal variations of nutrient distribution inside the waterbody of the lake resulting from the influence of the difference in both external input and physical factors, such as meteorological conditions, and the lake’s intrinsic characters before and after the input reduction. Besides, based on hydrodynamic studies, more attention should be paid to the effectiveness of stand-alone input nutrient reduction in different sub-basins upstream of Taihu Lake.
To quantitatively study the influence of the external nutrient input, a time scale is considered valuable, since a certain time is required for the nutrient to transport to a given location, and this amount of time is correlated to the hydrodynamics of the lake system [25]. Considering the nutrient transport from the connected river tributaries into Taihu Lake as point sources, the concept of water age is introduced here as an index to describe the time taken for the transport of nutrients within the lake. Water age is widely used in marine and fresh water systems to effectively reflect the nutrient transport and mixing process of nutrients, and to provide the spatial and temporal heterogeneity of these processes [26,27,28]. Studies have shown a strong correlation of in situ measured Chl-a concentration and water age distribution of external discharge into shallow lakes, which proves the significance of the existing hydrodynamics [29].
In this study, a three-dimensional Delft3D numerical model has been set up and used to investigate the transport and mixing of dissolved nutrients in Taihu Lake using the concept of water age. The purpose of this study was to answer the following questions: (1) Whether it is possible to quantitatively compare the nutrient load from different parts of the catchment river networks to Taihu Lake using the concept of water age; and (2) how the meteorological factor wind, which is the largest influencing factor for lake hydrodynamics, impacts the transport of nutrients from all over the catchment inside the lake.
This chapter is organized as follows. Section 2 is the theoretical background describing the water age theory. In the methodology Section 3, a detailed description of the geographical area, and Delft3D numerical modelling is introduced. In Section 4, the hydrodynamic results and water age distribution in various scenarios are provided. Then, in Section 5, our discussion and further extensions of this study are shown. Section 6 is the conclusion section.
2. Theoretical Background
Several transport time scales are frequently utilized in hydrodynamic, biological, and water environmental studies for multiple topics, like pollution transport tracking and water mass renewal [30]. These time scales include, for example, water age, flushing time, residence time or transit time, turnover time, and exposure time. Each of the transport time scales works within the scope of a certain application [31]. In this study, considering the complicated hydrodynamic condition and spatial heterogeneity, the concept of water age (WA) has been chosen.
The most common definition of water age is given as “the time that has elapsed since the particle under consideration left the region in which its age is prescribed as being zero” [32,33]. Thus, particularly in this study, WA is defined as the time elapsed since the tributary water with dissolved nutrients entered the lake water body, with WA being equal to zero at the boundary between the connected river network and the lake water.
Research on WA includes theoretical study, field observation, and numerical modelling [34,35,36,37,38,39]. Considering the applicability and accuracy, a numerical modelling study of WA is suitable under realistic bathymetry and hydrodynamic conditions [26,40]. There are two widely used numerical approaches for WA calculation in numerical models, namely, the Particle-Tracking Method (PTM) [41], and the Constituent-oriented Age and Residence time Theory (CART) [34,42,43]. PTM is based on a Lagrangian approach by releasing a large amount of numerical particle tracers and calculating WA from the concentration spectrum. The disadvantage is the high computational cost. While CART is based on the Eulerian method, and thus no numerical particle tracer is required, the actual transport trajectory is not provided in the model result [44]. The governing equation for the evolution of the WA concentration distribution function in CART is
where is concentration, t is time, is velocity, is water age number, and are source and sink terms, is the eddy diffusivity tensor, and is the diffusive flux. Thus, the mean age at a given location is calculated with Equation (2) based on the assumption that the mean age of a set of water parcels is mass-weighted, and thus, arithmetically averaged.
A numerical WA simulation based on PTM usually combines the hydrodynamic model with a random-walk model of horizontal eddy diffusion for the statistical treatment of turbulent mixing.
The position of a random particle is described by the following function:
where is the particle’s position at time t, is the time step, is the velocity vector, is the eddy diffusion tensor from a hydrodynamic model, and is the normally distributed random vector with unit standard deviation and zero average value.
3. Methodology
3.1. Study Area
Taihu Lake is located in the lower part of Yangtze River Delta in the southeastern part of China, between and and between and . [27]. As a typical large shallow lake, Taihu Lake has an average depth of 1.9 m and maximum depth of no more than 3 m, while the total surface area is 2338 km. The Taihu Lake Basin, with an area of 36,900 km, has a typical subtropical monsoon climate, with a mean annual precipitation around 1200 mm, concentrated mainly in the monsoon season between May and September. The dominant prevailing wind direction is southeasterly in summer and reverses in winter, with the average wind speed ranging from 3.5 m/s to 5 m/s. [45]
Around Taihu Lake, there are over 150 tributaries connecting to the adjacent river networks, some of which are very seasonal. The altitude to the northwest of Taihu Lake is higher than the south and the east, thus water normally flows from the northwest to the southeast. However, since Taihu Lake is located at a very developed area, many artificial hydraulic structures have been constructed. Thus, the discharge and flow direction near the river inlet have been remarkably altered by human interventions.
3.2. Numerical Model Description
Delft3D, an integrated open-source modelling software developed by Deltares (Delft, The Netherlands), is used to simulate the hydrodynamics of Taihu Lake and the temporal and spatial varying water age (WA) distribution in this study. In particular, its hydrodynamic (FLOW) and water quality (WAQ) modules are applied. Delft3D-WAQ is a multi-dimensional water quality model framework, which solves the advection-diffusion-reaction equation on a predefined computational grid for a wide range of model sub-stances. Delft3D-WAQ simulation includes large numbers of substances and processes. Applications of Delft3D-WAQ include, amongst others, the eutrophication of lakes and reservoirs, dissolved oxygen depletion in stratified systems, the impact of a sewage outfall on nutrient concentrations and primary production, transport of heavy metals through an estuary, accumulation of organic micro-pollutants in fresh water basins, and the emission of greenhouse gases from reservoirs. Hydrodynamic information has been derived from the Delft3D-FLOW model [46].
The mass balance equation in Delft3D-WAQ is:
where is the mass at the beginning of time step t; represents the mass changes by transport, including both advective and dispersive transport; represents the mass changes by physical, (bio)chemical, or biological processes; and represents the mass changes by sources (e.g., waste loads, river discharges).
Mass transport by advection and dispersion in Delft3D-WAQ is:
where is the concentration gradient, is the dispersion coefficient in the x direction, and is the velocity in the x direction.
3.3. Age Calculation in Delft3D
In the Delft3D model, WA calculation is similar to CART based on the mass concentration ratio of two kinds of tracers, namely, the conservative tracer and decayable tracer. The mass of the conservative tracer remains the same amount as at the released time, while the mass of the decayable tracer will decay with time at a given decay rate. The decayable tracers do not need to necessarily exist or be released into the real world—they are a reference to compute the water age in numerical modelling. The mechanism is that the two kinds of tracers will be released at the same time, and since they participate in the advection and diffusion process at the same time, the ratio of their concentration will remain the same at a fixed time. With the decay rate, the water age can be easily achieved. For the conservative tracer, the time derivative of concentration is
while for the decayable tracer, it is
where K is the decay rate. The formulation used to calculate water age in this study is:
where is the age of the tracer ; is the concentration of the conservative tracer ; is the concentration of the decayable tracer ; is the first-order decay rate constant for the decayable tracer ; and is flux for the decayable tracer .
3.4. Model Setup
The hydrodynamic section of the Taihu Lake model was developed by [45] with Delft3D. This model uses a rectangular grid with a grid resolution of 1000 m horizontally, and five vertical sigma layers uniformly defined in depth. The model is driven by tributary discharge boundaries and meteorological conditions, like surface wind, evaporation, and precipitation. Over 150 tributaries have been arranged into 21 groups for simplicity. The simulation time is during the entire year of 2008, with a time step of 10 min. Detailed physical and numerical parameter sets are listed in the paper [45].
Based on upstream catchment sub-basins [22] and the boundary condition of the hydrodynamic model [45], inflow tributary boundaries have been categorized into three groups for the WA simulation (Figure 1). For each group of boundaries, a set of conservative and decayable tracers are continuously released, with the decay rate of the decayable tracers set to be 0.01/day. The northern and northwestern boundaries mainly represent the discharges from Jiangsu province (WA1), while the southern and southwestern boundaries include mountainous river discharges and tributaries from Zhejiang province (WA2). Northeastern boundaries mainly account for water transfer from the Yangtze River (WA3). The WA simulation time step is the same as in the hydrodynamic model, and the model result is recorded at every 6 h of model time. Note, both inflow and outflow occur in the above-mentioned boundaries throughout the year. Tracers released with the outflow boundary condition will be transported out of the model domain and not be included in the WA calculation. Based on Taihu Lake’s geometry and hydrological features, the lake is divided into seven sub-basins. For each sub-basin, an observation point is set to monitor the WA distribution (Figure 1).
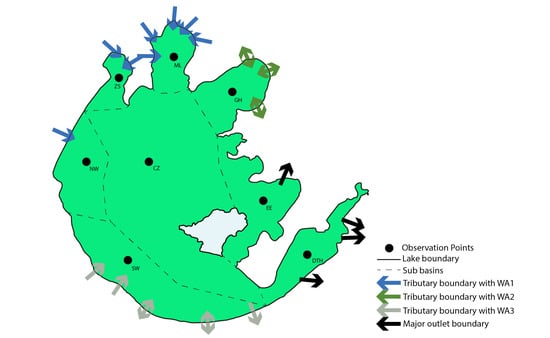
Figure 1.
Tributary discharge, observation points, and sub-basins of Taihu Lake. Directions of arrows imply the major inflow/outflow direction of tributary discharge. Abbreviations stand for names of sub-basins, namely, ML: Meiliang Bay; GH: Gonghu Bay; EE: East Epigeal; DTH: Dongtaihu Bay; SW: Southwest Zone; NW: Northwest Zone; ZS: Zhushan Bay; CZ: Central Zone.
3.5. Scenarios
The calibrated hydrodynamic model was used to quantitatively investigate the influence from the surrounding river network and wind, focusing on tributary discharges, wind direction, and wind speed. A series of numerical scenarios were conducted (Table 1). A reference scenario was set up to represent the real tributary discharge and the wind record in 2008 (Scenario 1). With the actual boundary discharge conditions and wind directions, wind speed in 2008 downscaled with a ratio 0.5 and 0 (Scenario 2, 3). The other cases were designed to investigate the influence of the prevailing wind and the magnitude of inflow boundary discharge (Scenarios 4–11). Further, the influence of all wind directions was studied (Scenarios 12–18). For the constant tributary discharge case, the same amount of water is flowing out of the model domain through the major outlet boundary as the inflow of water.

Table 1.
Scenarios.
4. Results
4.1. Spatial and Temporal Distribution of WA
Influenced by the time-varying wind field and hydrodynamics, WA distribution for all three groups of tracers changed both spatially and temporally. Bottom and surface WA1 distribution at the last time-step of Scenario 1 is shown in Figure 2. Little WA1 vertical difference (∼0.01 day) between the surface and bottom layer is observed from the model result, as well as in WA2 and WA3. The consistency in vertical WA distribution implies that, although surface and bottom horizontal flow velocity fields differ hugely [45], WA is fully mixed in vertically within each time step.
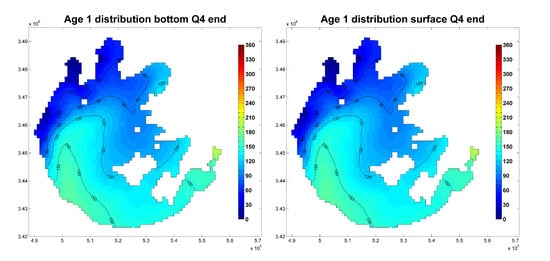
Figure 2.
WA1 distribution of Scenario 1 at the last time step. (Unit: days).
WA distribution varies spatially for WA1; the highest WA1 is over 200 days in Dongtaihu Bay, while the lowest WA1 is less than 30 days in Zhushan Bay. The phenomenon could be explained by the difference in distance from the inflow WA1 tributaries. WA1 values near the northern and western part of Taihu Lake (∼30–90 days at Zhushan Bay, Meiliang Bay, Gonghu Bay, and the northern part of the Central Zone) are significantly smaller than the values of the southern and eastern part of the lake (∼120–200 days at the Northwestern Zone and Dongtaihu Bay), since the WA1 tributary boundary is located in the northern and western part of the lake.
High temporal heterogeneity is also observed in the model results for WA1 distribution after each quarter of the year in Scenario 1 (Figure 3). As time passes since the model’s starting time, the maximum WA1 increases. By definition, this value will not exceed the model time passed, but the location with the value varies. At the end of Q1, the maximum value (∼90 days) is located at the eastern part of the lake; one quarter later, the maximum value (∼120 days) moves to the northeastern part in Gonghu Bay, and the northwestern part at Dongtaihu Bay; after another quarter, the maximum value (∼180 days) occurs only in Gonghu Bay in the northeast, and at the end of year, the peak value (∼200 days) lies in Dongtaihu Bay. In contrast, the lowest WA1 value occurs near the WA1 tributary boundary throughout the whole year.
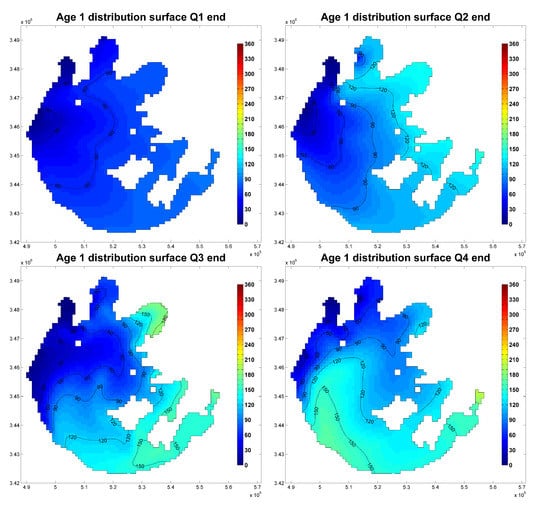
Figure 3.
WA1 distribution at the end of each quarter. (Unit: days).
Since the tributary boundaries for each WA are located at different locations around Taihu Lake, the distribution of each WA also varies, both spatially and temporally. WA distributions of the final time step in Scenario 1 are shown in Figure 4. For WA1, the northern sub-basins (Zhushan Bay, Meiliang Bay, Gonghu Bay, and the northern part of the Central Zone and East Epigeal) have a lower WA1, while the Southwestern Zone and Dongtaihu Bay have a higher WA1. For WA2, WA in the western half of the lake is higher than 240days, implying that hardly any water from the WA2 boundary has reached this part of lake; while for WA3, small WA occurs near the western margin of the lake.
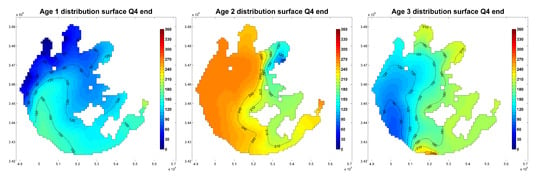
Figure 4.
Water age (WA) distribution for Scenario 1 at the end of the year. (Unit: days).
Besides the distance to the tributary boundaries, the variance in WA distribution could be explained by the value of total discharge through the tributary boundary for each WA group (Figure 5).
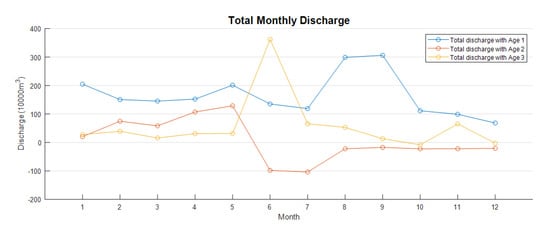
Figure 5.
Total discharge for each WA discharge.
Total discharge for WA2 peaks in June then becomes almost zero for the next 5 months, which could explain the extreme high WA2 in the western half of the lake, since water from WA2 barely enters this area. While total discharge for WA1 is always positive and larger than around 100 m/s, lower WA1 occurs in around half the area of the lake. For WA3, discharge remains negative since June, but since two inflow boundaries among WA3 boundaries still have positive discharge from the mountainous area, the area near the western margin of the lake still has a smaller WA3. However, for all three WA, larger values occur in Dongtaihu Bay, suggesting that less inflow tributary water enters this sub-basin. This is possibly due to the narrow entrance and elongated geometry of Dongtaihu Bay.
In general, under the influence of time-varying inflow discharge, WA distributions show heterogeneity both spatially and temporally.
4.2. Wind Speed and Direction Effects
Wind influence on WA is studied by comparing the WA value at the last time step of each steady wind scenario with tributary discharge at 10 m/s. The WA of steady wind for each observation point differs at both the average and range values. This difference could be explained by the influence from hydrodynamics. With steady wind, the horizontal circulation patterns of Taihu Lake differ with the wind direction, which in turn influence the advection and mixing processes of inflow tributary discharge. Thus, the corresponding range and average of the WA value varies. For example, WA1 distribution within the Southwestern Zone ranges from the highest in an east wind condition (∼190 days) to the lowest with a south wind condition (∼120 days) with the average WA1 being around 140 days; while for WA3, the situation is different, and the highest WA3 is with a southwestern wind (∼120 days) and the lowest WA is with a north wind (∼70 days), with the lowest WA being around 100 days (Figure 6).
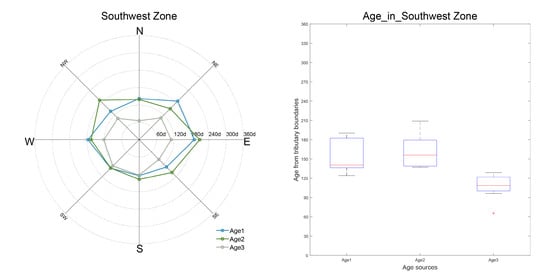
Figure 6.
WA for the Southwestern Zone observation point with eight wind scenarios.
Moreover, in some sub-basins where inflow tributary discharge is nearby, the wind influence is relatively low, such as in Gonghu Bay, where WA2 boundaries are adjacent. With eight wind directions, the range of WA2 is less than 30 days, while at the same location the difference between the maximum WA1 and lowest WA1 is larger than 100 days (Figure 7). The bias in WA implies that WA2 tributary inflow contributes more to the water retention in Gonghu Bay than WA1 and WA3 tributary discharges.
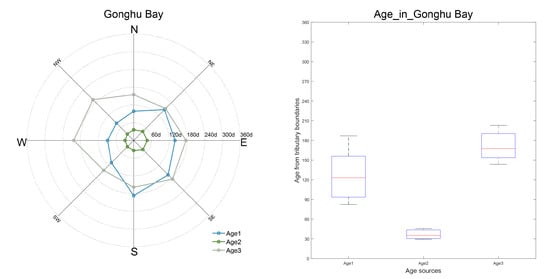
Figure 7.
WA for the Gonghu Bay observation point with eight wind scenarios.
Beside wind directions, wind speed is also an important factor influencing WA distribution. In Scenario 2, the wind speed of the entire simulation is half the wind speed in scenario, which is from the real 2008 wind data. As illustrated in the comparison of the model result (Figure 8), differences occur for all three WA distributions. However, the increase or decrease of WA is site-specific and WA-specific. For the Northwestern Zone, with half wind, WA1 decreases while WA2 and WA3 increases. However, for Gonghu Bay, with half wind, all three WA values increase.
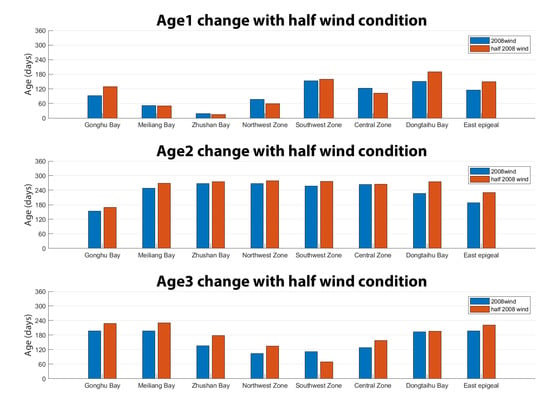
Figure 8.
Water age comparison between the 2008 real wind data scenario and half wind speed scenario.
In general, wind direction and wind speed do influence WA distribution over the whole Taihu Lake. The influence is spatially heterogeneous. Change of wind direction would lead to a change in both the average value and the range of WA, while wind speed difference induces a site-specific and age-specific change of the WA value.
4.3. Discharge Effects
Discharge influence is studied by comparing scenarios with the same wind condition, but using a different inflow discharge rate. Flow discharge in Scenario 4 and Scenario 6 are 10 m/s and 20 m/s in each WA inflow tributary, respectively, while the outflow discharge at the remaining boundaries are calculated to ensure a mass balance between inflow and outflow. For both scenarios, a steady southeastern wind with 3.5 m/s wind speed is set.
The WA for all three WAs of all observation points decreases with a rising tributary inflow discharge (Figure 9), which could be explained by the enhancing hydrodynamics due to more momentum input through the tributary boundaries. The largest WA difference is the WA2 change in East Epigeal (45 days), while the smallest WA difference is the WA1 change in Zhushan Bay (13 days). Again, changes in WA show spatial heterogeneity, and that it is WA-specific.
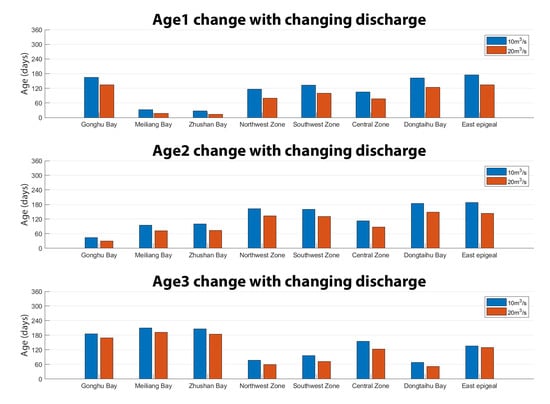
Figure 9.
Water age comparison between the 2008 real wind data scenario and half wind speed scenario.
Comparing with the impact of wind speed and wind direction change, the influence of discharge on WA is smaller, partially because it is easier to dampen the increasing momentum from tributary discharge when it has penetrated farther into the lake, while wind momentum input through surface shear stress is continuous all over the lake.
5. Discussion
5.1. Various Transport Time Scales
Transport time scales are frequently adopted in describing the hydrodynamic processes, which transport water and the constituents. Water age is one of the most favorable transport time scales, while the usage of flushing time and residence time is also very common. To extensively adopt transport time scales in large shallow lake studies, understanding the definition and limitations of these time scales is crucial.
Residence time is the time spent by a water parcel or a pollutant to leave the given water body [47]. By definition, resident time is a location-specific value, such as water age, and serves as a complement to water age, since water age is the duration for a water parcel from the inflow boundary to a given spot, while residence time is the duration from this particular location to the outflow boundary [30]. Residence time is commonly used to evaluate the inflow nutrient’s further influence inside the water body [48].
Flushing time, on the other hand, is a bulk parameter to describe the exchange of water body. Flushing time is defined as the time it takes to replace all the water in a basin [32]. Flushing time could be seen as the sum of water age and residence time. This concept is frequently used in estuary and lagoon research, and early studies can be traced back to the 1950s [49]. The original method to get flushing time is the “tidal prism method”—that is, flushing time is calculated as the ratio of the mass of a scalar to the rate of renewal of the scalar, with the assumption of an instantaneous release of inflow and thorough mixing inside the water body. Another approach considering salt balance has also been adopted in previous studies [30,50]. Further studies have improved the “tidal prism method” to mitigate underestimation due to the idealized assumptions; however, the thoroughly mixing assumption is still adopted [51].
Beside residence time and flushing time, some terminologies like transit time and turn-over time are also found in literature. By definition, turn-over time is identical to flushing time, and transit time is the average residence time [32].
Based on the definition of these transport time scales, the application of these time scales are purpose-oriented. Water age is more suitable when considering the spatial distribution of influence from tributary discharge into the large shallow lake as in this study, while residence time could help to study the dilution of pollution already inside the lake. Flushing time, as the sum of water age and residence time, could be used to indicate the temporal extent and the efficiency of diluted fresh water from the external waterbody.
5.2. Radio-Age
In this study, water age is calculated with a concentration of both conservative and decayable tracers, as described in Section 3.4. In previous studies, it is usually referred to as “radio-age” [52]. However, theoretically, the value is between the water age of passive tracers (or water parcels) and of radioactive tracers. A 10% bias with water age larger than 7 years has also been reported [52]. Choice of decay rate is crucial for the modelled radio age value, and with a smaller decay rate, the difference between radio-age and water age of passive tracers is small (Equation (9)).
where is the decay rate, is the calculated radio- age, and is the age of the passive tracers.
To verify this further, the modelled water age averaged over the whole lake after 1 year of simulation was investigated with additional numerical tests using five decay rates, ranging from to (Figure 10). The age value is almost identical with a decay rate less than and the difference is less than days, while the largest difference in mean water age with and is around 20 days.
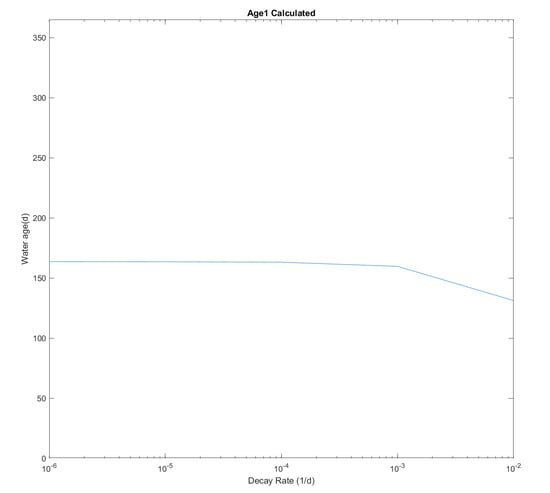
Figure 10.
Water age modelled with various decay rates.
This model’s results are similar to that in Figure 1 by Delhez et al. (2003) [52], where the curve of radio-age is asymptotic to the line representing the passive tracers. With a small decay rate, the value of radio-age is close to the age of passive tracers. Thus, we believe that with a smaller decay rate (say, less than ), the radio-age distribution gives a similar indication on water horizontal circulation as the age of radioactive tracers do.
Radio age results provide diagnoses consistent with the model results interpretation, that the relative importance of water injection from tributaries in this study could be compared. Furthermore, the advantage of the Eulerian approach is that numerical results are easier to obtain than in the Lagrangian formalism [52].
5.3. Wind Change Due to Climate Change
Terrestrial near-surface wind speed has been reported to decrease due to climate change. During the last 30 years, 73% of terrestrial stations record average wind speed decline across most of the northern mid-latitudes [53,54,55]. For large shallow lakes like Taihu Lake, where wind influences not only the hydrodynamic conditions [45] but also the ecological statues [6,7], climate change-induced wind condition variation and its consequences should be granted more attention.
Nutrient loads in shallow water mainly come from two sources, namely, the internal sources and the external sources. Albeit low wind speed causes low waves and low corresponding bottom shear stresses, hampering sediment resuspension which is crucial for the release of internal nutrient sources, it promotes hypoxia in the bottom layer of the water column, and in turn, enhances nutrient release from sediment and counteracts the effect of declining resuspension, stimulating algae growth and finally leading to more severe eutrophication. More effort should be spent on this with numerical models.
The combination of summer water level increase and wind speed decrease, [14,56], is expected to change the distribution of nutrients from external sources in shallow lakes. To illustrate the actual influence of a change in wind speed, a comparison of model results with a steady southeastern wind but changing wind speed (Scenario and Scenario ) is illustrated (Figure 11).
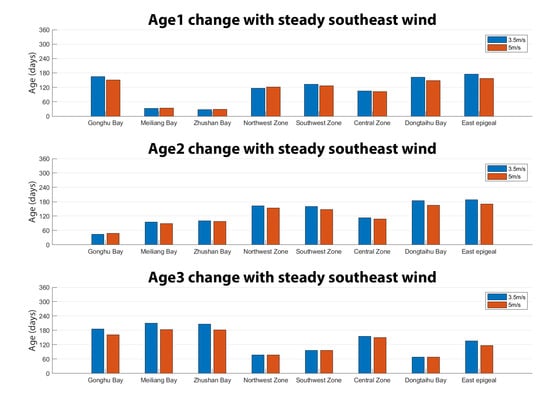
Figure 11.
WA change with 3.5 m/s and 5 m/s southeastern wind.
For most observation points, wind speed decline causes an increase in WA values for all three WAs. Since less wind speed weakens the wind-induced hydrodynamics in most parts of the lake, the advection and mixing processes of incoming water is attenuated. Moreover, increased WA means that external nutrient input would stay longer in the lake, increasing the chances for cyanobacteria to capture more nutrients and to form an algae bloom [57].
Thus, less wind speed will encourage the release of inner sources and cause a longer duration of outer source nutrient inflow, both of which will induce more severe algae bloom and deterioration of water quality.
5.4. Implication of Water Age on Shallow Lake Management
The initial water age study mainly has two applications: (a) To assess the ventilation rate of semi-closed basins; (b) to infer the horizontal circulation, which focuses more on estuaries and lagoons [34]. Further studies in broader aqua systems have paid more attention to water quality issues, such as the efficiency of water transfer [27]. With climate change and a more complicated nutrient control policy, water age is able to provide more assistance in integrated water quality management of shallow lakes, such as Taihu Lake.
Firstly, water age analysis would provide help when a critical toxin leakage condition happens. With numerical models and meteorological forecasts, water age distribution maps could be generated in minutes. Thus, the spatial and temporal spread information of inflow toxins could be provided, and further measures could be decided based on that.
Secondly, water age analysis would provide information on the tributary discharge influence of critical spots, assisting the governance of water quality in a complicated management condition. In this study, three water age groups have been chosen corresponding to inflow tributary discharge from three municipalities. Situations become complicated when nutrient control and wastewater treatment involves more stakeholders. Water age analysis could also provide essential information to divide the responsibility and help improve the master plan of Taihu Basin’s water quality management.
6. Conclusions
The impact of tributary discharge inflow from river discharge around Taihu Lake, the third largest fresh water lake in China, has been investigated using the concept of water age. The main purposes of this study were to provide quantitative comparison of nutrient loads from different parts of the catchment river networks and to investigate the meteorological influences on the advection and mixing process of nutrients from tributary discharge inside the lake body. In this study, the inflow tributaries were divided into three groups based on upstream catchment sub-basins and the boundary condition of the hydrodynamic model. Water age was computed using the three-dimensional Delft3D model with FLOW and WAQ module.
Model results show both spatial and temporal heterogeneity occurred in all three water age groups, which was influenced by both the distance to the tributary boundaries and total discharge through tributary boundaries for each water-age group. The influence of wind on water age was also analyzed. Change of wind direction would lead to changes in both the average value and range of water age, while wind speed difference would induce site-specific and group-specific changes of WA value. Water age decreases with rising of tributaries inflow discharge; however, the influence of discharge is less significant than that of a change of wind.
Various time scales, such as residence time and flushing time, have been discussed for clearer understanding. Wind speed decline induced by climate change was analyzed on the effect on both internal and external nutrient source release, and influences on both sources would cause water quality to be deteriorated. Lastly, further application of water age is suggested for more complicated integrated water management on a lake basin scale.
Author Contributions
Funding acquisition, S.W.; Methodology, S.L. and Q.Y.; Writing—original draft, S.L.; Writing—review and editing, Q.Y., S.W. and M.J.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Chinese national key research and development program (2018YFC0407200), China Scholarship Council (CSC) (201407720008) and Het Lamminga Fonds.
Acknowledgments
The authors would like to thank TBA for providing tributary discharge data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Y.; Fan, C.; Teubner, K.; Dokulil, M. Changes of nutrients and phytoplankton chlorophyll-a in a large shallow lake, Taihu, China: An 8-year investigation. Hydrobiologia 2003, 506–509, 273–279. [Google Scholar] [CrossRef]
- Janssen, A.B.; Teurlincx, S.; An, S.; Janse, J.H.; Paerl, H.W.; Mooij, W.M. Alternative stable states in large shallow lakes? J. Great Lakes Res. 2014, 40, 813–826. [Google Scholar] [CrossRef]
- Jin, X. Analysis of eutrophication state and trend for lakes in China. J. Limnol. 2003, 62, 60. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, X.; Kong, F.; Zhang, S.; Kong, W.; Hao, J.; Shang, L. Two-Decade Reconstruction of Algal Blooms in China’s Lake Taihu. Environ. Sci. Technol. 2009, 43, 3522–3528. [Google Scholar] [CrossRef]
- Guo, L. ECOLOGY: Doing Battle With the Green Monster of Taihu Lake. Science 2007, 317, 1166. [Google Scholar] [CrossRef]
- Paerl, H.W.; Hall, N.S.; Calandrino, E.S. Controlling harmful cyanobacterial blooms in a world experiencing anthropogenic and climatic-induced change. Sci. Total Environ. 2011, 409, 1739–1745. [Google Scholar] [CrossRef]
- Qin, B.; Zhu, G.; Gao, G.; Zhang, Y.; Li, W.; Paerl, H.W.; Carmichael, W.W. A Drinking Water Crisis in Lake Taihu, China: Linkage to Climatic Variability and Lake Management. Environ. Manag. 2010, 45, 105–112. [Google Scholar] [CrossRef]
- McGowan, S. Algal Blooms. In Biological and Environmental Hazards, Risks, and Disasters; Elsevier: Amsterdam, The Netherlands, 2016; pp. 5–43. [Google Scholar] [CrossRef]
- He, W.; Shang, J.; Lu, X.; Fan, C. Effects of sludge dredging on the prevention and control of algae-caused black bloom in Taihu Lake, China. J. Environ. Sci. 2013, 25, 430–440. [Google Scholar] [CrossRef]
- Li, Y.; Tang, C.; Wang, C.; Anim, D.O.; Yu, Z.; Acharya, K. Improved Yangtze River Diversions: Are they helping to solve algal bloom problems in Lake Taihu, China? Ecol. Eng. 2013, 51, 104–116. [Google Scholar] [CrossRef]
- Sun, X.; Xiong, S.; Zhu, X.; Zhu, X.; Li, Y.; Li, B.L. A new indices system for evaluating ecological-economic- social performances of wetland restorations and its application to Taihu Lake Basin, China. Ecol. Model. 2015, 295, 216–226. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, H.; Deng, J.; Qin, B.; He, Y. Impact of nutrient loading on phytoplankton: A mesocosm experiment in the eutrophic Lake Taihu, China. Hydrobiologia 2019, 829, 167–187. [Google Scholar] [CrossRef]
- Janssen, A.B.; de Jager, V.C.; Janse, J.H.; Kong, X.; Liu, S.; Ye, Q.; Mooij, W.M. Spatial identification of critical nutrient loads of large shallow lakes: Implications for Lake Taihu (China). Water Res. 2017, 119, 276–287. [Google Scholar] [CrossRef] [PubMed]
- Ke, Z.; Xie, P.; Guo, L. Ecological restoration and factors regulating phytoplankton community in a hypertrophic shallow lake, Lake Taihu, China. Acta Ecol. Sin. 2018, 39, 81–88. [Google Scholar] [CrossRef]
- Paerl, H.W.; Xu, H.; McCarthy, M.J.; Zhu, G.; Qin, B.; Li, Y.; Gardner, W.S. Controlling harmful cyanobacterial blooms in a hyper-eutrophic lake (Lake Taihu, China): The need for a dual nutrient (N & P) management strategy. Water Res. 2011, 45, 1973–1983. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Fujibayashi, M.; Nomura, M.; Nishimura, O.; Li, X. Asymmetric response of sedimentary pool to surface water in organics from a shallow hypereutrophic lake: The role of animal consumption and microbial utilization. Ecol. Indic. 2015, 58, 346–355. [Google Scholar] [CrossRef]
- Deng, X.; Xu, Y.; Han, L.; Song, S.; Yang, L.; Li, G.; Wang, Y. Impacts of Urbanization on River Systems in the Taihu Region, China. Water 2015, 7, 1340–1358. [Google Scholar] [CrossRef]
- Bozelli, R.L.; Caliman, A.; Guariento, R.D.; Carneiro, L.S.; Santangelo, J.M.; Figueiredo-Barros, M.P.; Leal, J.J.; Rocha, A.M.; Quesado, L.B.; Lopes, P.M.; et al. Interactive effects of environmental variability and human impacts on the long-term dynamics of an Amazonian floodplain lake and a South Atlantic coastal lagoon. Limnologica 2009, 39, 306–313. [Google Scholar] [CrossRef]
- Chen, C.; Zhong, J.C.; Yu, J.H.; Shen, Q.S.; Fan, C.X.; Kong, F.X. Optimum dredging time for inhibition and prevention of algae-induced black blooms in Lake Taihu, China. Environ. Sci. Pollut. Res. 2016, 23, 14636–14645. [Google Scholar] [CrossRef]
- Huang, K.; Guo, H.; Liu, Y.; Zhou, F.; Yu, Y.; Wang, Z. Water environmental planning and management at the watershed scale: A case study of Lake Qilu, China. Front. Environ. Sci. Eng. China 2008, 2, 157–162. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Zheng, L.; Liu, B.; Liu, J.; Wang, X. Assessment of Heavy Metal Pollution in the Sediment of the Main Tributaries of Dongting Lake, China. Water 2018, 10, 1060. [Google Scholar] [CrossRef]
- Wang, M.; Strokal, M.; Burek, P.; Kroeze, C.; Ma, L.; Janssen, A.B. Excess nutrient loads to Lake Taihu: Opportunities for nutrient reduction. Sci. Total Environ. 2019, 664, 865–873. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Xue, B.; Lai, G.; Gui, F.; Liu, X. A 200-year historical modeling of catchment nutrient changes in Taihu basin, China. Hydrobiologia 2007, 581, 79–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, S.; Qian, X.; Wang, Q.; Qian, Y.; Liu, J.; Ge, Y. Temporal and spatial variability of chlorophyll a concentration in Lake Taihu using MODIS time-series data. Hydrobiologia 2011, 661, 235–250. [Google Scholar] [CrossRef]
- Shen, J.; Yuan, H.; Liu, E.; Wang, J.; Wang, Y. Spatial distribution and stratigraphic characteristics of surface sediments in Taihu Lake, China. Chin. Sci. Bull. 2011, 56, 179–187. [Google Scholar] [CrossRef]
- de Brye, B.; de Brauwere, A.; Gourgue, O.; Delhez, E.J.; Deleersnijder, E. Reprint of Water renewal timescales in the Scheldt Estuary. J. Mar. Syst. 2013, 128, 3–16. [Google Scholar] [CrossRef]
- Li, Y.; Acharya, K.; Yu, Z. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China. Ecol. Eng. 2011, 37, 325–334. [Google Scholar] [CrossRef]
- Qi, H.; Lu, J.; Chen, X.; Sauvage, S.; Sanchez-Pérez, J.M. Water age prediction and its potential impacts on water quality using a hydrodynamic model for Poyang Lake, China. Environ. Sci. Pollut. Res. 2016, 23, 13327–13341. [Google Scholar] [CrossRef]
- Wu, Z.; Lai, X.; Zhang, L.; Cai, Y.; Chen, Y. Phytoplankton chlorophyll a in Lake Poyang and its tributaries during dry, mid-dry and wet seasons: A 4-year study. Knowl. Manag. Aquat. Ecosyst. 2014, 412, 6. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Delhez, É.J.M.; de Brye, B.; de Brauwere, A.; Deleersnijder, É. Residence time vs influence time. J. Mar. Syst. 2014, 132, 185–195. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Delhez, E.J.; Campin, J.M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean Model. 1999, 1, 17–27. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Campin, J.M.; Delhez, E.J. The concept of age in marine modelling I. Theory and preliminary model results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- Jenkins, W.; Clarke, W. The distribution of 3He in the western Atlantic ocean. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 481–494. [Google Scholar] [CrossRef]
- Johnston, C.; Cook, P.; Frape, S.; Plummer, L.; Busenberg, E.; Blackport, R. Ground Water Age and Nitrate Distribution Within a Glacial Aquifer Beneath a Thick Unsaturated Zone. Ground Water 1998, 36, 171–180. [Google Scholar] [CrossRef]
- Karstensen, J.; Tomczak, M. Age determination of mixed water masses using CFC and oxygen data. J. Geophys. Res. Oceans 1998, 103, 18599–18609. [Google Scholar] [CrossRef]
- Pangle, L.A.; Klaus, J.; Berman, E.S.F.; Gupta, M.; McDonnell, J.J. A new multisource and high-frequency approach to measuring δ 2 H and δ 18 O in hydrological field studies. Water Resour. Res. 2013, 49, 7797–7803. [Google Scholar] [CrossRef]
- Wunsch, C. Oceanic age and transient tracers: Analytical and numerical solutions. J. Geophys. Res. 2002, 107, 3048. [Google Scholar] [CrossRef]
- Li, Y.; Tang, C.; Wang, C.; Tian, W.; Pan, B.; Hua, L.; Lau, J.; Yu, Z.; Acharya, K. Assessing and modeling impacts of different inter-basin water transfer routes on Lake Taihu and the Yangtze River, China. Ecol. Eng. 2013, 60, 399–413. [Google Scholar] [CrossRef]
- Zhang, X.Y. Ocean Outfall Modeling–Interfacing Near and Far Field Models with Particle Tracking Method. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1995. [Google Scholar]
- Chen, X. A laterally averaged two-dimensional trajectory model for estimating transport time scales in the Alafia River estuary, Florida. Estuar. Coast. Shelf Sci. 2007, 75, 358–370. [Google Scholar] [CrossRef]
- Liu, W.C.; Chen, W.B.; Hsu, M.H. Using a three-dimensional particle-tracking model to estimate the residence time and age of water in a tidal estuary. Comput. Geosci. 2011, 37, 1148–1161. [Google Scholar] [CrossRef]
- Wang, H.; Guo, X.; Liu, Z.; Gao, H. A comparative study of CART and PTM for modelling water age. J. Ocean Univ. China 2015, 14, 47–58. [Google Scholar] [CrossRef]
- Liu, S.; Ye, Q.; Wu, S.; Stive, M. Horizontal Circulation Patterns in a Large Shallow Lake: Taihu Lake, China. Water 2018, 10, 792. [Google Scholar] [CrossRef]
- Deltares. Delft3D-WAQ Users Manual; Technical Report; Deltares: Delft, The Netherlands, 2005. [Google Scholar]
- Delhez, É.J.; Heemink, A.W.; Deleersnijder, É. Residence time in a semi-enclosed domain from the solution of an adjoint problem. Estuar. Coast. Shelf Sci. 2004, 61, 691–702. [Google Scholar] [CrossRef]
- Rueda, F.J.; Cowen, E.A. Residence time of a freshwater embayment connected to a large lake. Limnol. Oceanogr. 2005, 50, 1638–1653. [Google Scholar] [CrossRef]
- Choi, K.W.; Lee, J.H. Numerical determination of flushing time for stratified water bodies. J. Mar. Syst. 2004, 50, 263–281. [Google Scholar] [CrossRef]
- Miller, R.L.; McPherson, B.F. Estimating estuarine flushing and residence times in Charlotte Harbor, Florida. via salt balance and a box model. Limnol. Oceanogr. 1991, 36, 602–612. [Google Scholar] [CrossRef]
- Luketina, D. Simple Tidal Prism Models Revisited. Estuar. Coast. Shelf Sci. 1998, 46, 77–84. [Google Scholar] [CrossRef]
- Delhez, É.J.; Deleersnijder, É.; Mouchet, A.; Beckers, J.M. A note on the age of radioactive tracers. J. Mar. Syst. 2003, 38, 277–286. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M.; et al. Climate Change 2013—The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Vautard, R.; Cattiaux, J.; Yiou, P.; Thépaut, J.N.; Ciais, P. Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nat. Geosci. 2010, 3, 756–761. [Google Scholar] [CrossRef]
- Deng, J.; Paerl, H.W.; Qin, B.; Zhang, Y.; Zhu, G.; Jeppesen, E.; Cai, Y.; Xu, H. Climatically-modulated decline in wind speed may strongly affect eutrophication in shallow lakes. Sci. Total Environ. 2018, 645, 1361–1370. [Google Scholar] [CrossRef] [PubMed]
- Ji, Z.G. Hydrodynamics and Water Quality; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).