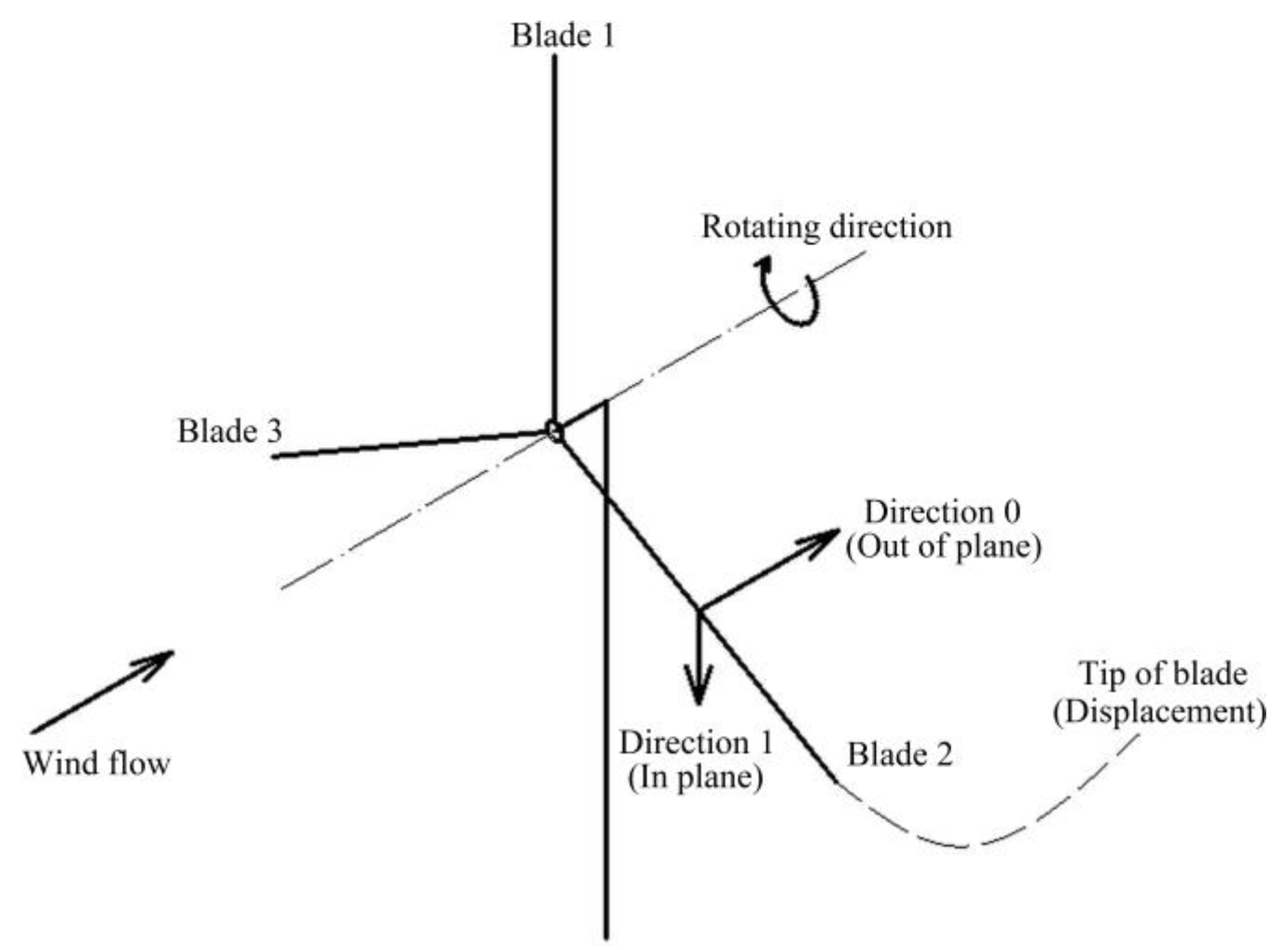
Figure 1.
Blades represented by actuator line and discretized into actuator sections.
Figure 1.
Blades represented by actuator line and discretized into actuator sections.
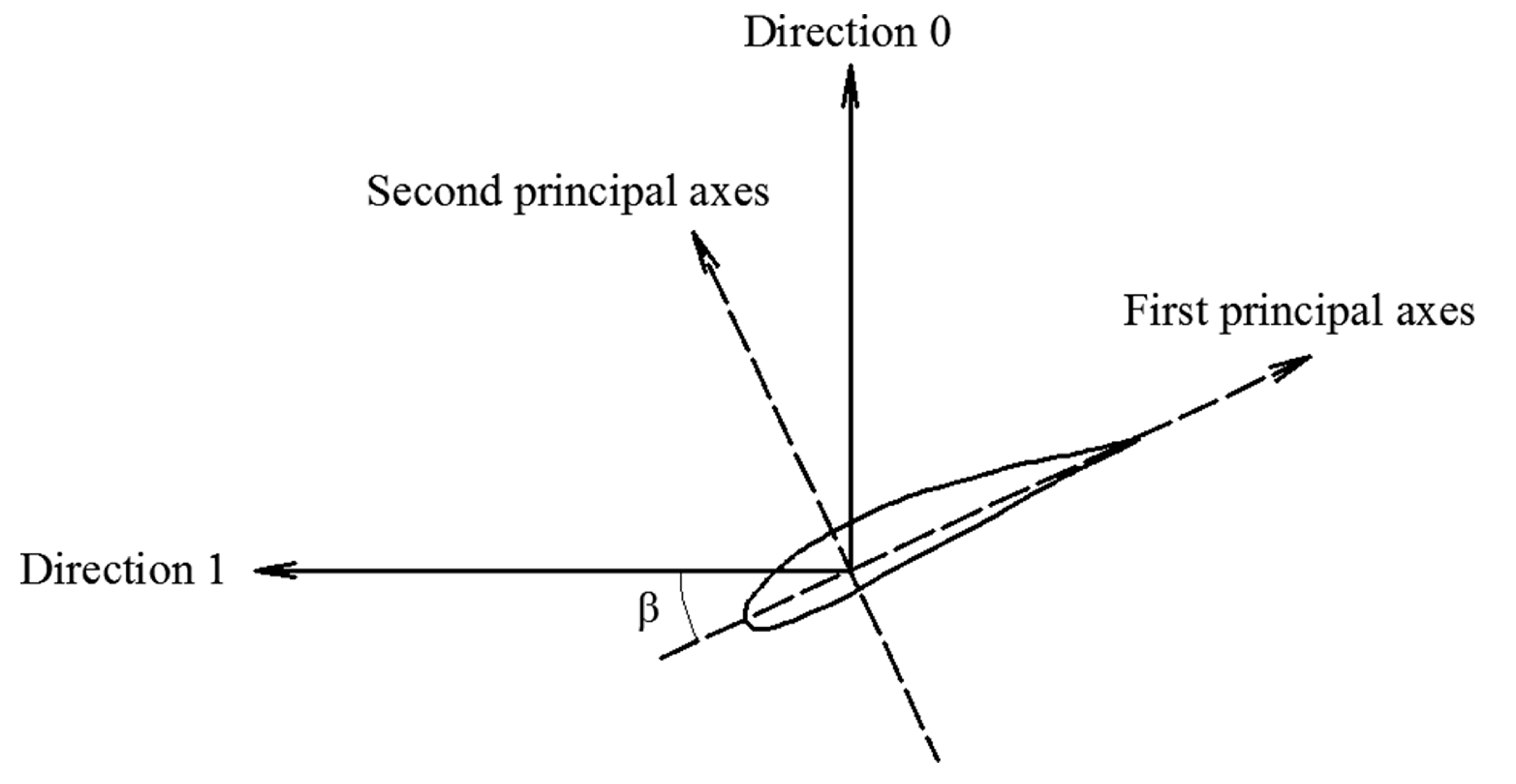
Figure 2.
Coordinate system of the blade deflection.
Figure 2.
Coordinate system of the blade deflection.
Figure 3.
The diagrammatic sketch of the forces on the cantilever beam.
Figure 3.
The diagrammatic sketch of the forces on the cantilever beam.
Figure 4.
The blade element in the local coordinate system.
Figure 4.
The blade element in the local coordinate system.
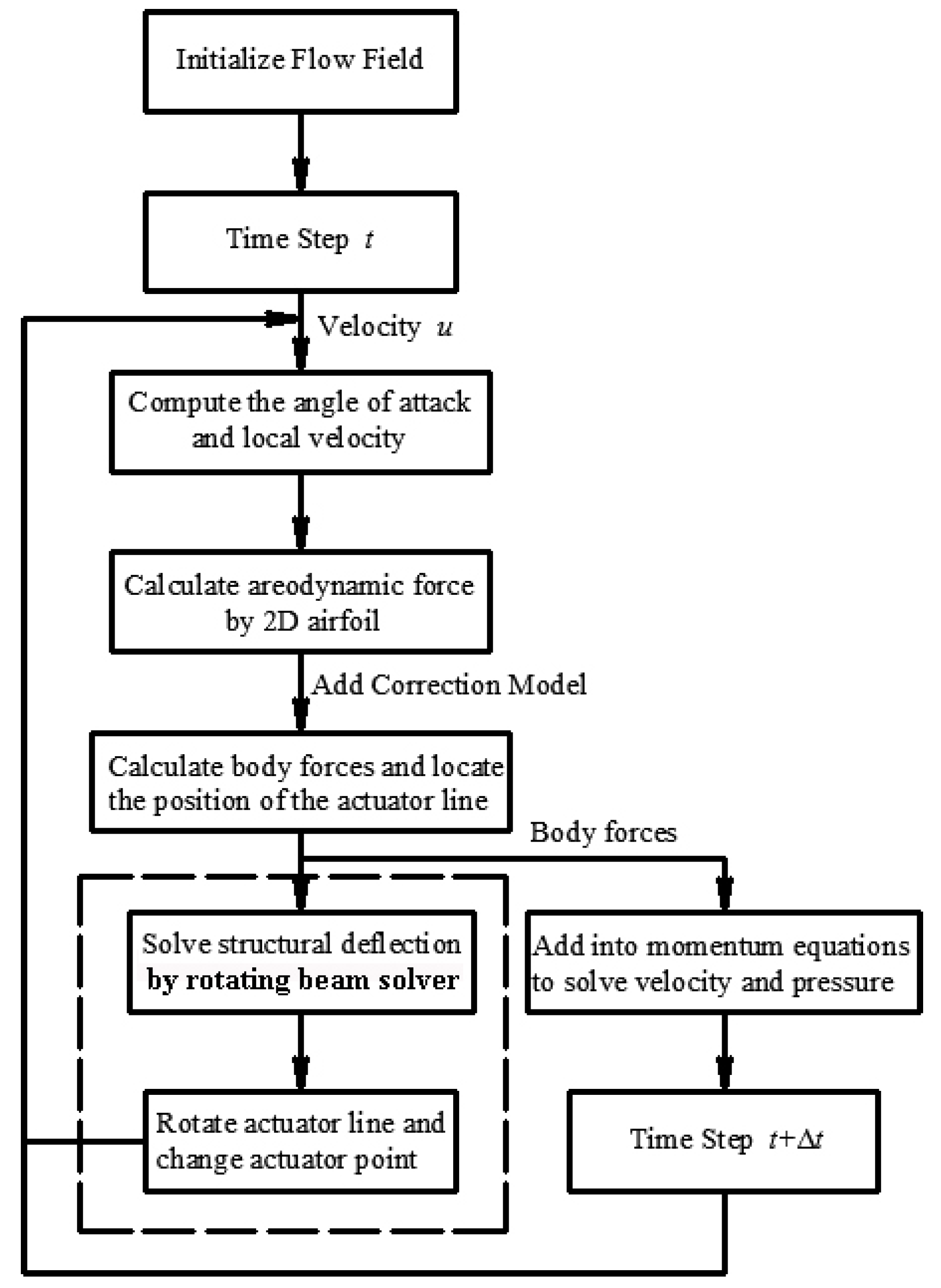
Figure 5.
The computational flow chart of new elastic actuator line model.
Figure 5.
The computational flow chart of new elastic actuator line model.
Figure 6.
The simulation domain of single wind turbine.
Figure 6.
The simulation domain of single wind turbine.
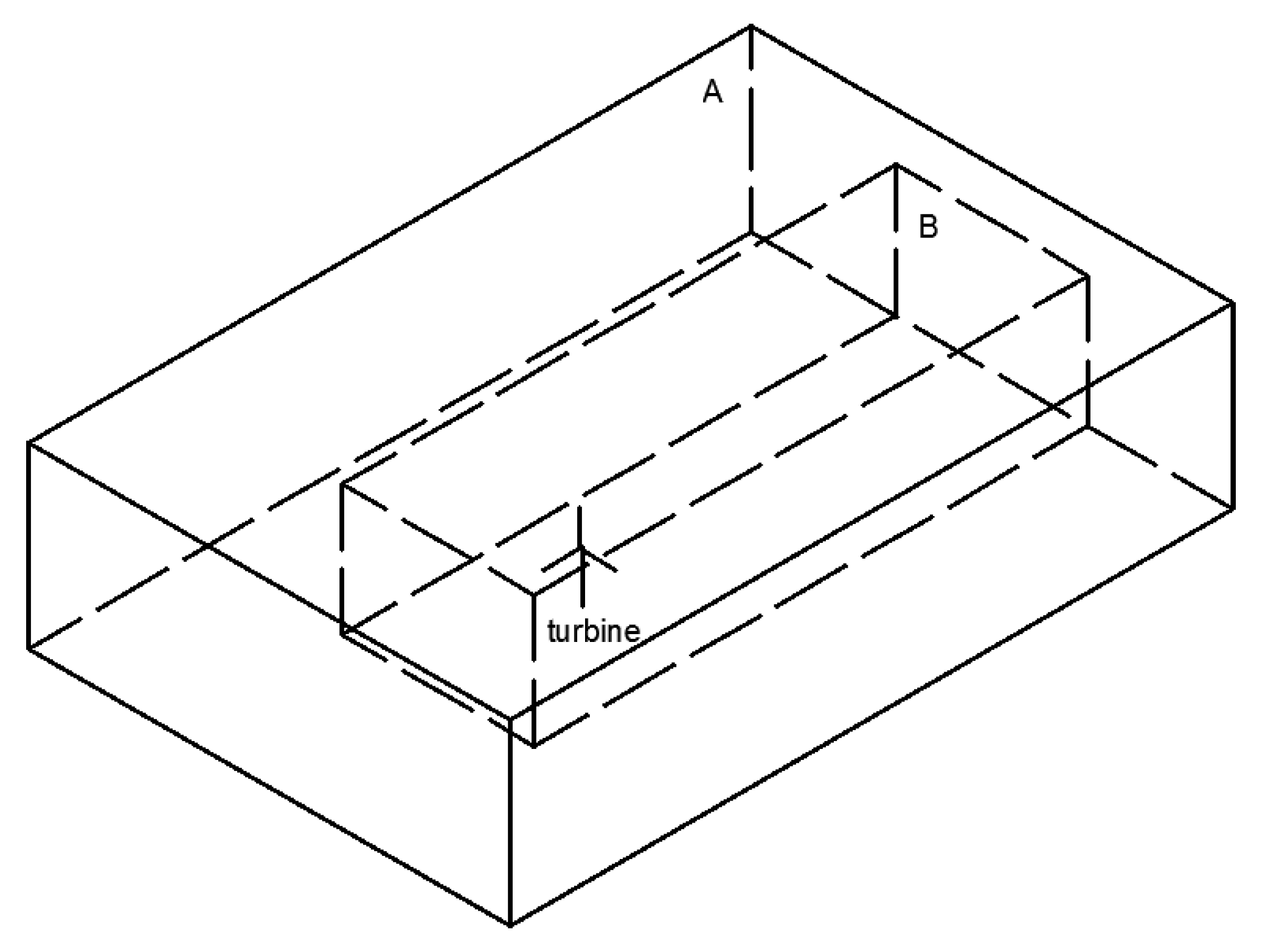
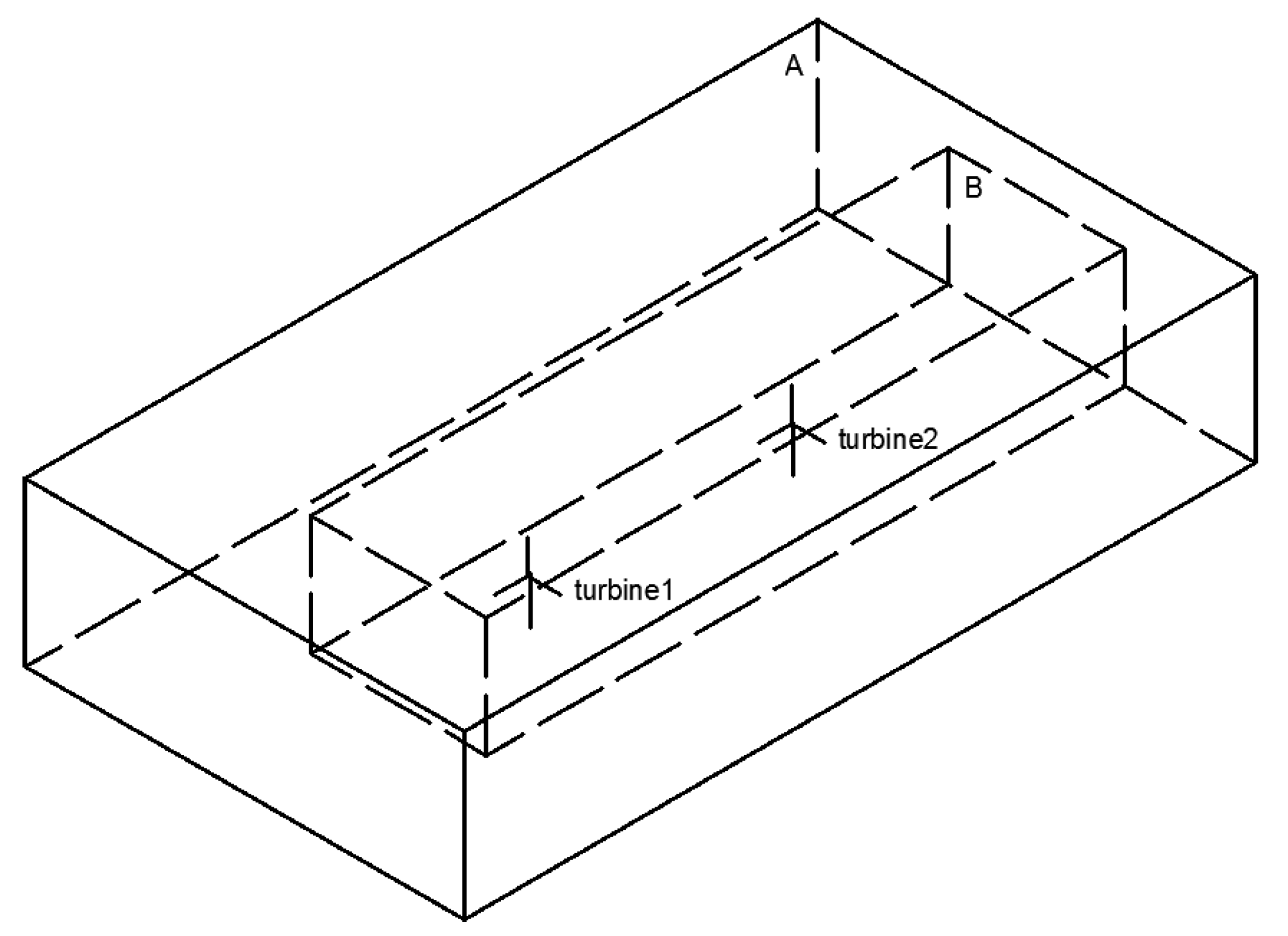
Figure 7.
The simulation domain of double wind turbines.
Figure 7.
The simulation domain of double wind turbines.
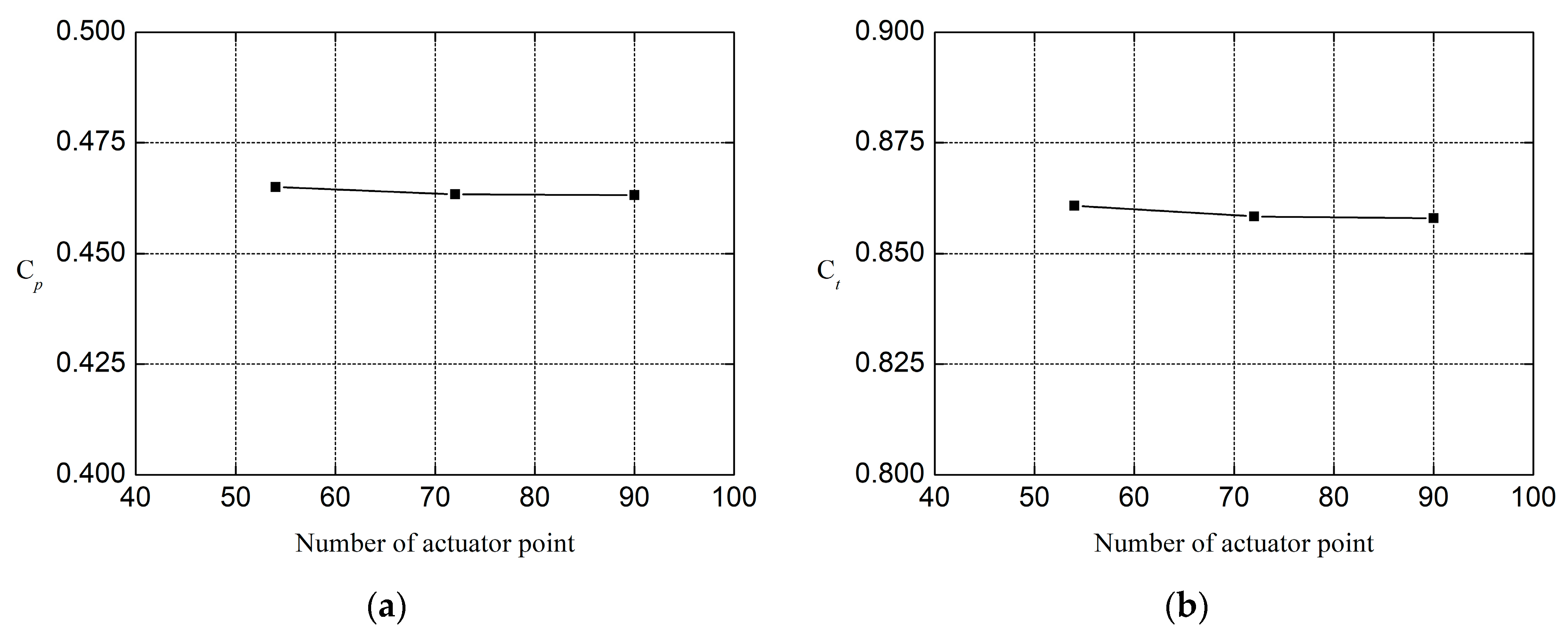
Figure 8.
Relationship between actuator point number and aerodynamic coefficient, (a) power coefficient, and (b) thrust coefficient.
Figure 8.
Relationship between actuator point number and aerodynamic coefficient, (a) power coefficient, and (b) thrust coefficient.
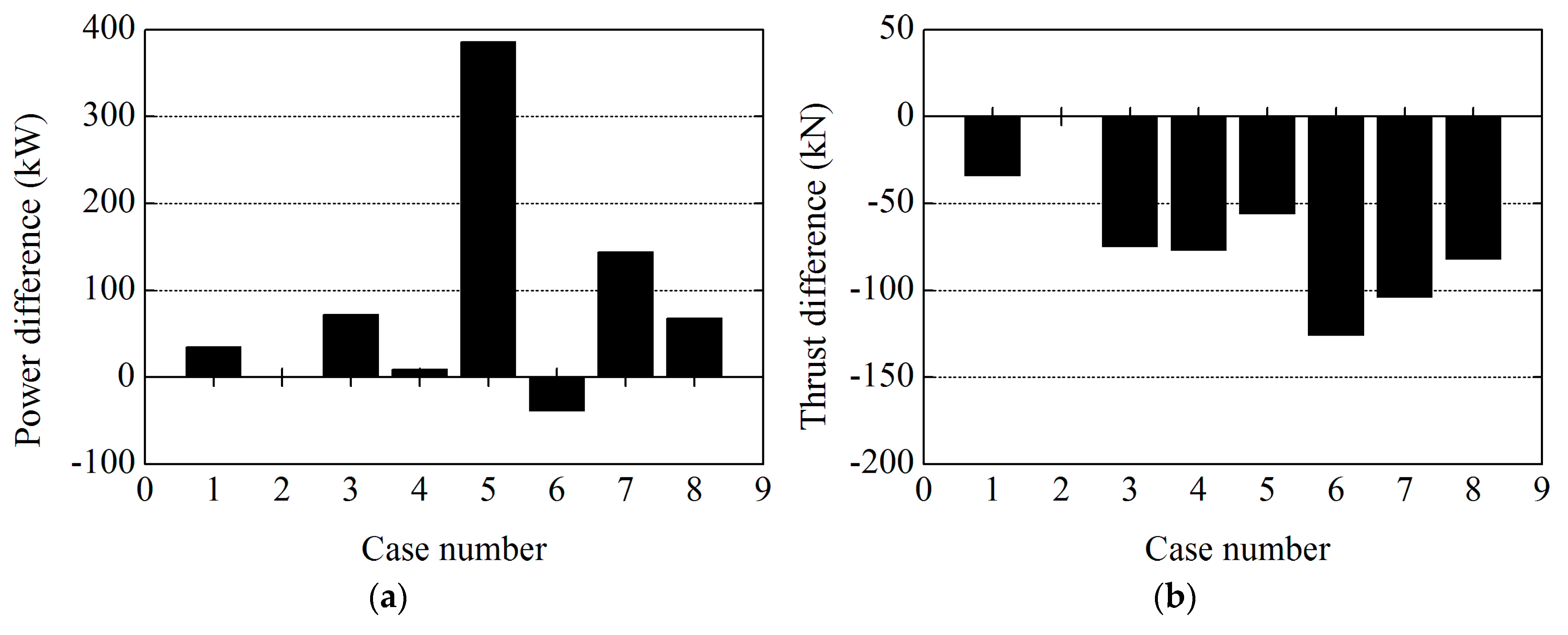
Figure 9.
Comparison of different cases results in 8 m/s: (
a) power; and (
b) thrust Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: Horizontal Axis Wind turbine simulation Code 2nd generation results; Case 4: research by Li et al. [
17]; Case 5: research by Jeong et al. [
30]; Case 6: research by Ponta et al. [
31]; Case 7: research by Yu et al. [
32,
33]; Case 8: research by Ma et al. [
13].
Figure 9.
Comparison of different cases results in 8 m/s: (
a) power; and (
b) thrust Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: Horizontal Axis Wind turbine simulation Code 2nd generation results; Case 4: research by Li et al. [
17]; Case 5: research by Jeong et al. [
30]; Case 6: research by Ponta et al. [
31]; Case 7: research by Yu et al. [
32,
33]; Case 8: research by Ma et al. [
13].
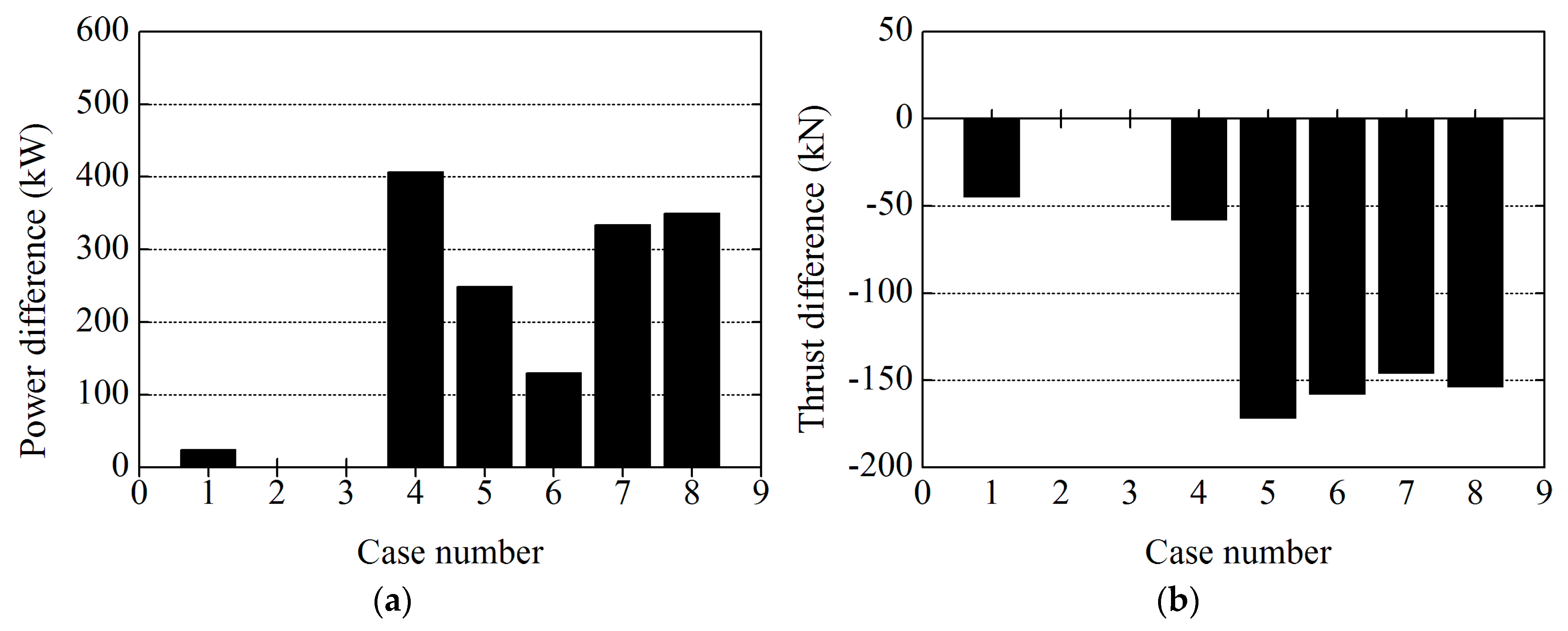
Figure 10.
Comparison of different cases results in 11.4 m/s: (
a) power; and (
b) thrust Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: Horizontal Axis Wind turbine simulation Code 2nd generation results; Case4: research by Li et al. [
17]; Case 5: research by Jeong et al. [
30]; Case 6: research by Ponta et al. [
31]; Case 7: research by Yu et al. [
32,
33]; Case 8: research by Ma et al. [
13].
Figure 10.
Comparison of different cases results in 11.4 m/s: (
a) power; and (
b) thrust Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: Horizontal Axis Wind turbine simulation Code 2nd generation results; Case4: research by Li et al. [
17]; Case 5: research by Jeong et al. [
30]; Case 6: research by Ponta et al. [
31]; Case 7: research by Yu et al. [
32,
33]; Case 8: research by Ma et al. [
13].
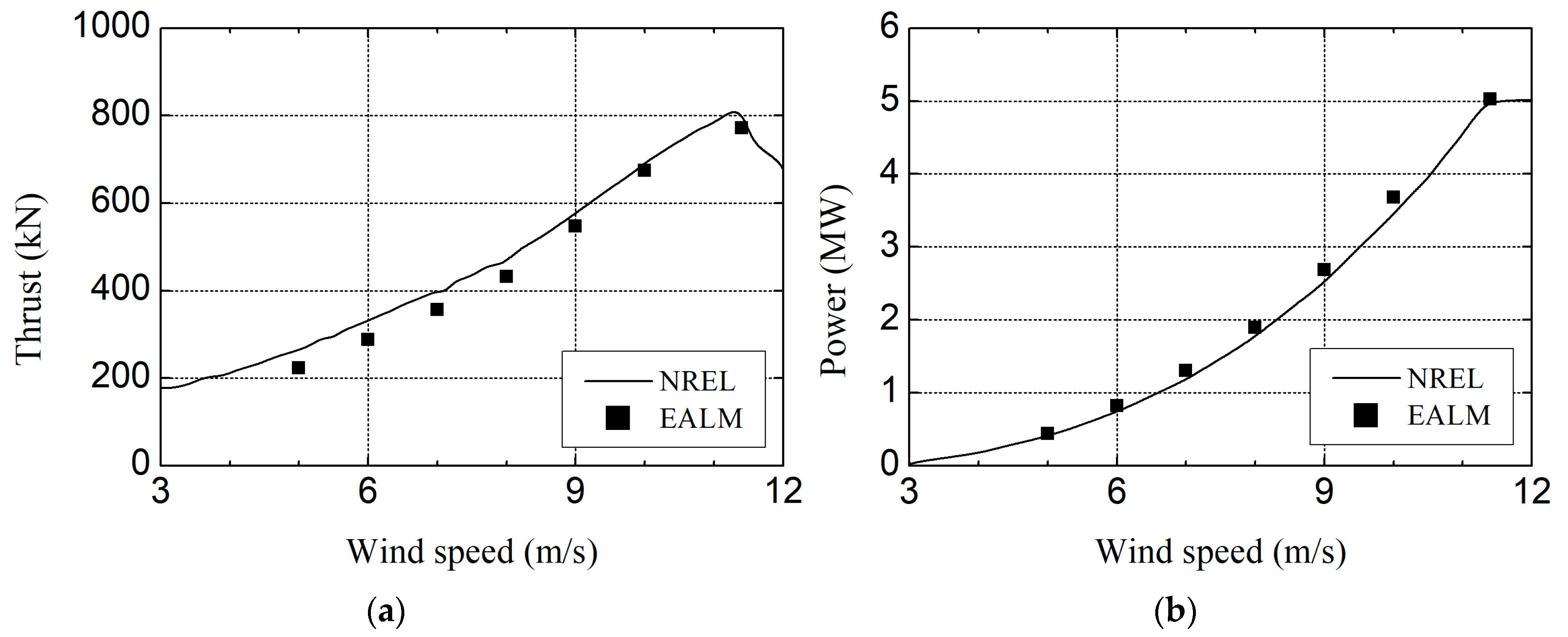
Figure 11.
Comparisons of the aerodynamic performance results between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds: (a) thrust; and (b) power.
Figure 11.
Comparisons of the aerodynamic performance results between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds: (a) thrust; and (b) power.
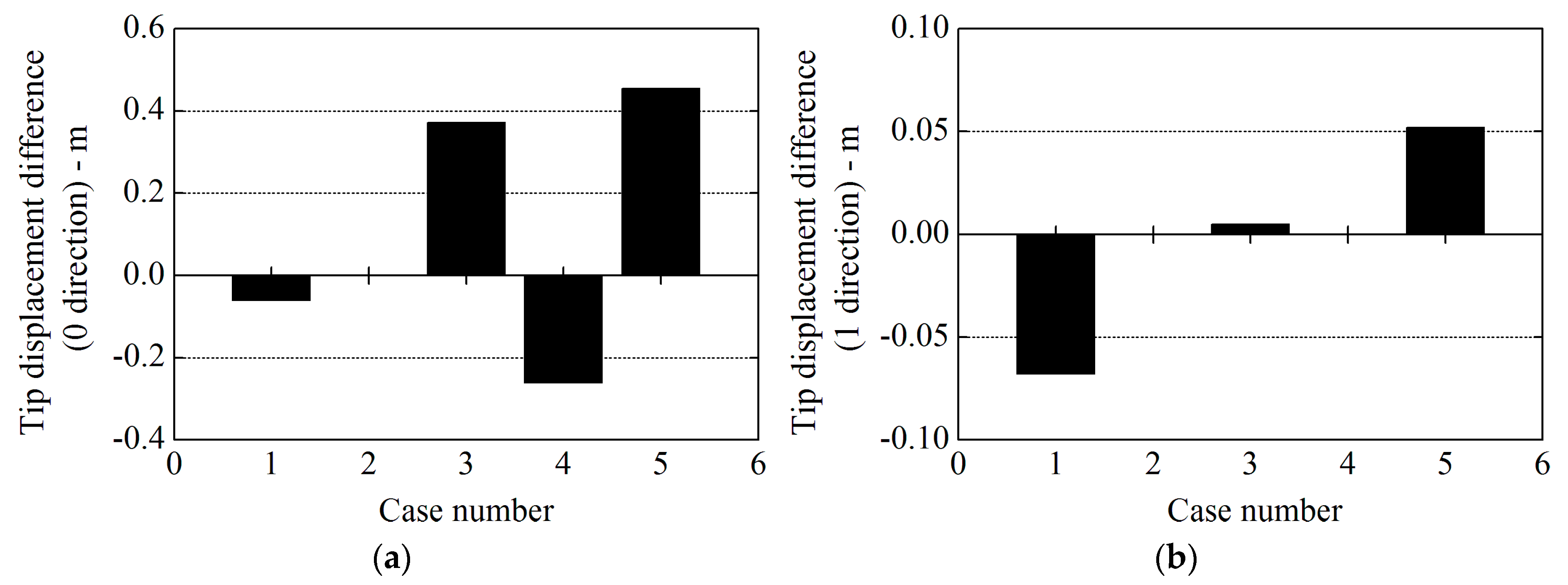
Figure 12.
Comparison of different cases tip displacement results in 8 m/s: (
a) 0 direction; and (
b) 1 direction Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: research by Li et al. [
17]; Case 4: research by Yu et al. [
32,
33]; Case 5: research by Ma et al. [
13].
Figure 12.
Comparison of different cases tip displacement results in 8 m/s: (
a) 0 direction; and (
b) 1 direction Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: research by Li et al. [
17]; Case 4: research by Yu et al. [
32,
33]; Case 5: research by Ma et al. [
13].
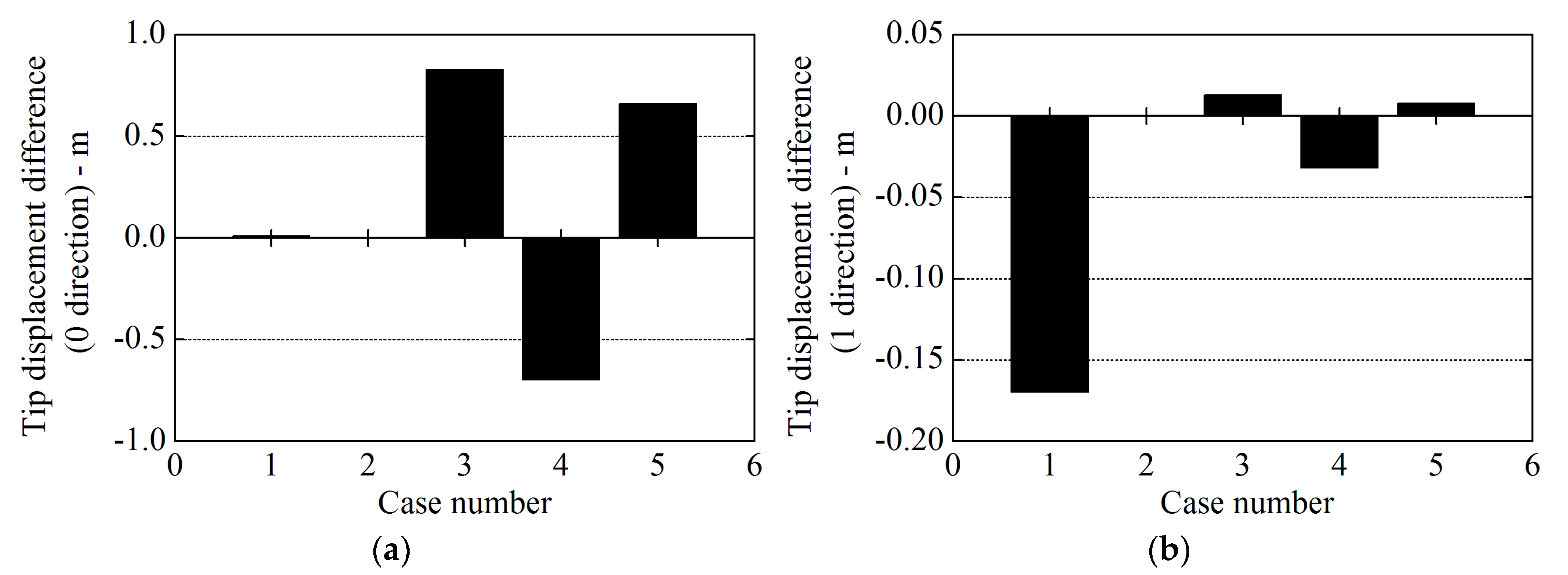
Figure 13.
Comparison of different tip displacement results in 11.4 m/s: (
a) 0 direction; and (
b) 1 direction Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: research by Li et al. [
17]; Case 4: research by Yu et al. [
32,
33]; Case 5: research by Ma et al. [
13].
Figure 13.
Comparison of different tip displacement results in 11.4 m/s: (
a) 0 direction; and (
b) 1 direction Case 1: Elastic Actuator Line Model (present study); Case 2: NREL’s FAST code; Case 3: research by Li et al. [
17]; Case 4: research by Yu et al. [
32,
33]; Case 5: research by Ma et al. [
13].
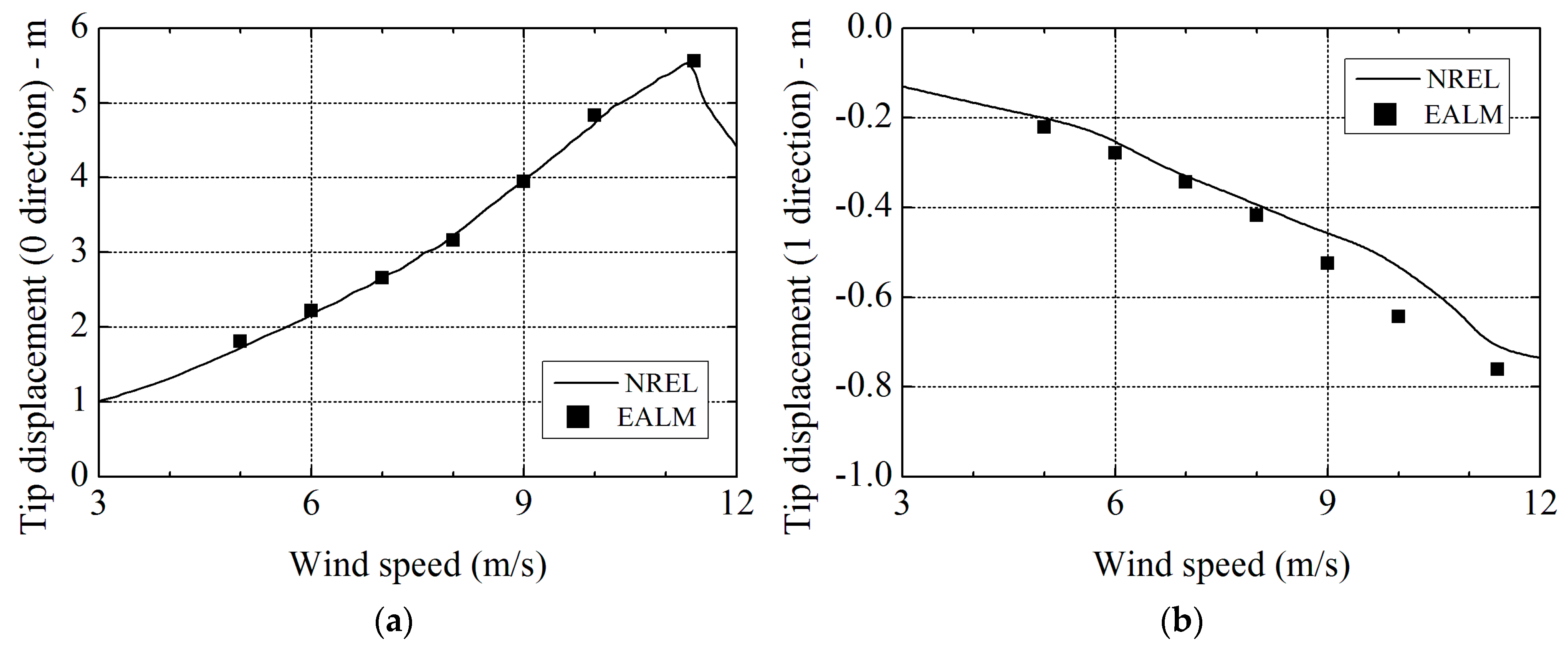
Figure 14.
Comparison of the tip displacement results between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds: (a) in 0 direction; and (b) in 1 direction.
Figure 14.
Comparison of the tip displacement results between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds: (a) in 0 direction; and (b) in 1 direction.
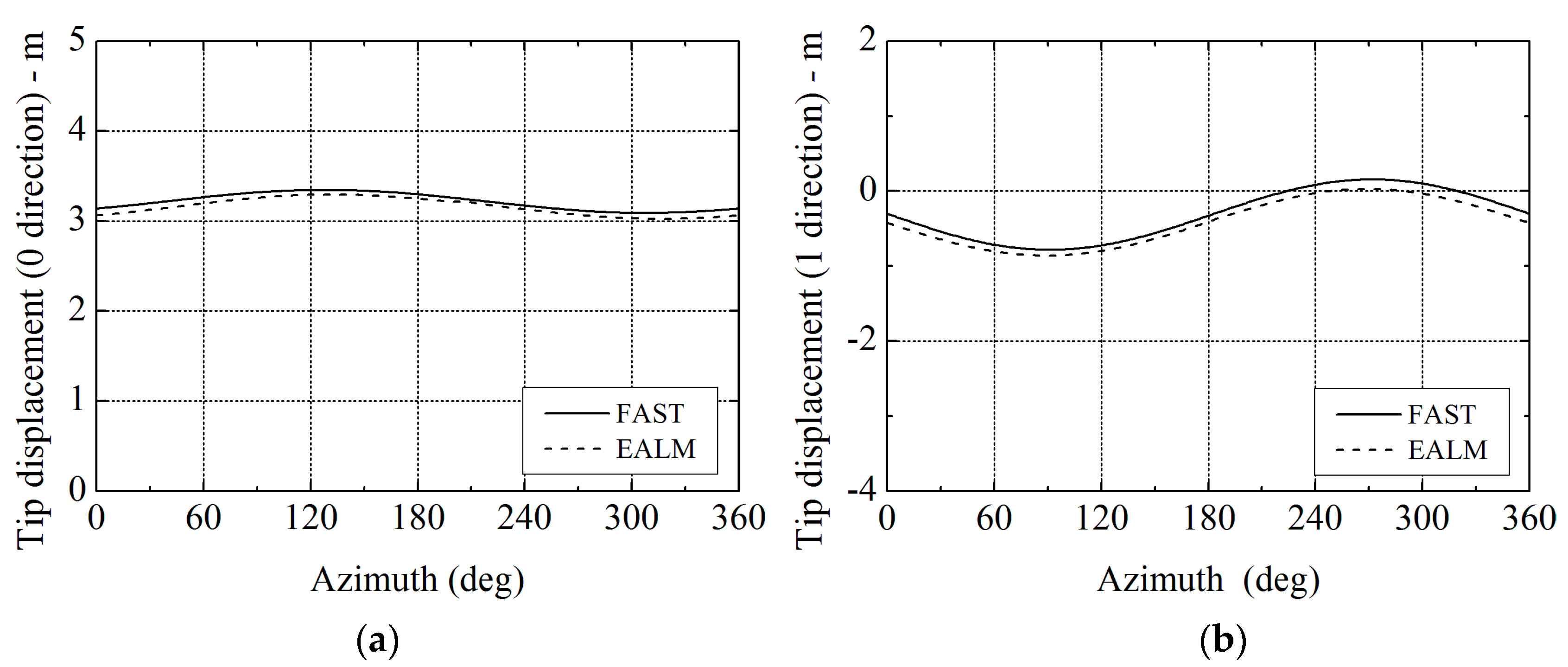
Figure 15.
Comparison of azimuthal variations of blade tip deformations between elastic actuator line model (EALM) and NREL’s FAST code at 8 m/s: (a) in 0 direction; and (b) in 1 direction.
Figure 15.
Comparison of azimuthal variations of blade tip deformations between elastic actuator line model (EALM) and NREL’s FAST code at 8 m/s: (a) in 0 direction; and (b) in 1 direction.
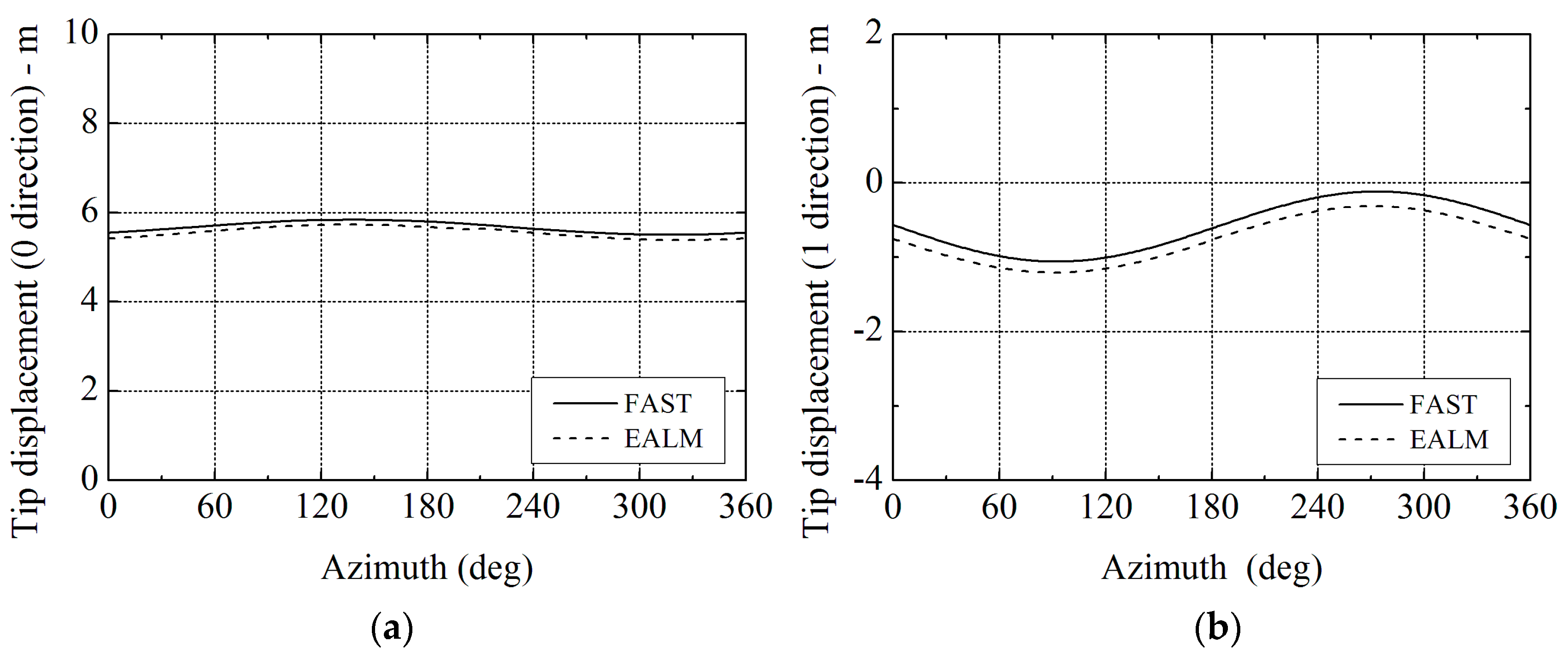
Figure 16.
Comparison of azimuthal variations of blade tip deformations between elastic actuator line model (EALM) and NREL’s FAST code at 11.4 m/s: (a) in 0 direction; and (b) in 1 direction.
Figure 16.
Comparison of azimuthal variations of blade tip deformations between elastic actuator line model (EALM) and NREL’s FAST code at 11.4 m/s: (a) in 0 direction; and (b) in 1 direction.
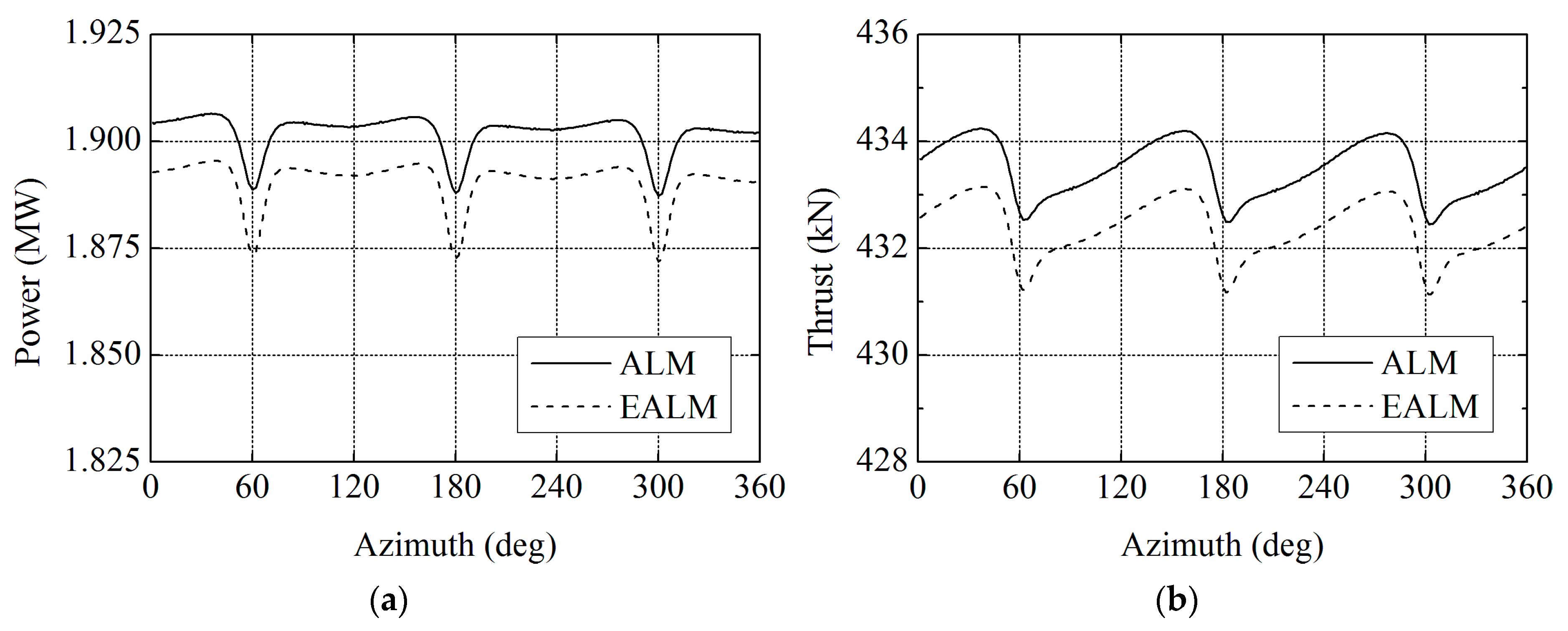
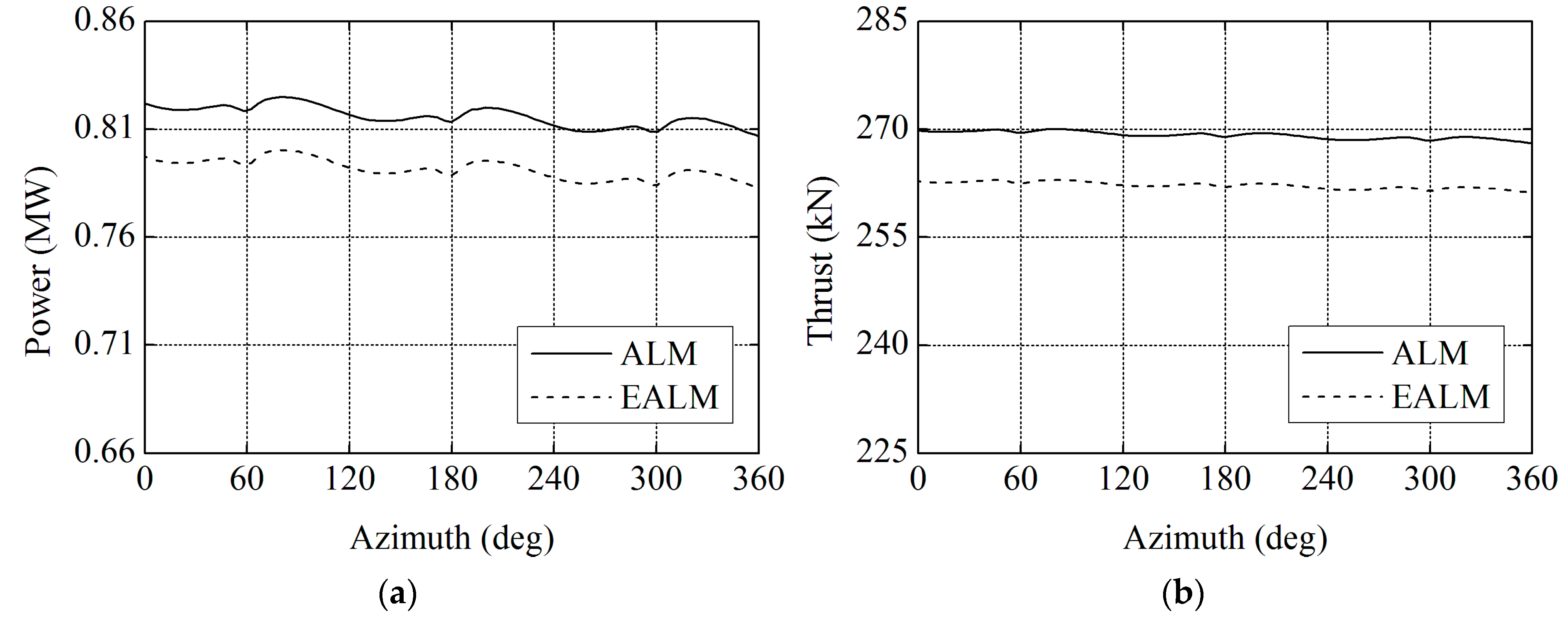
Figure 17.
Comparisons of the aerodynamic performance results between traditional actuator line model (ALM) and elastic actuator line model (EALM) at 8 m/s: (a) power; and (b) thrust.
Figure 17.
Comparisons of the aerodynamic performance results between traditional actuator line model (ALM) and elastic actuator line model (EALM) at 8 m/s: (a) power; and (b) thrust.
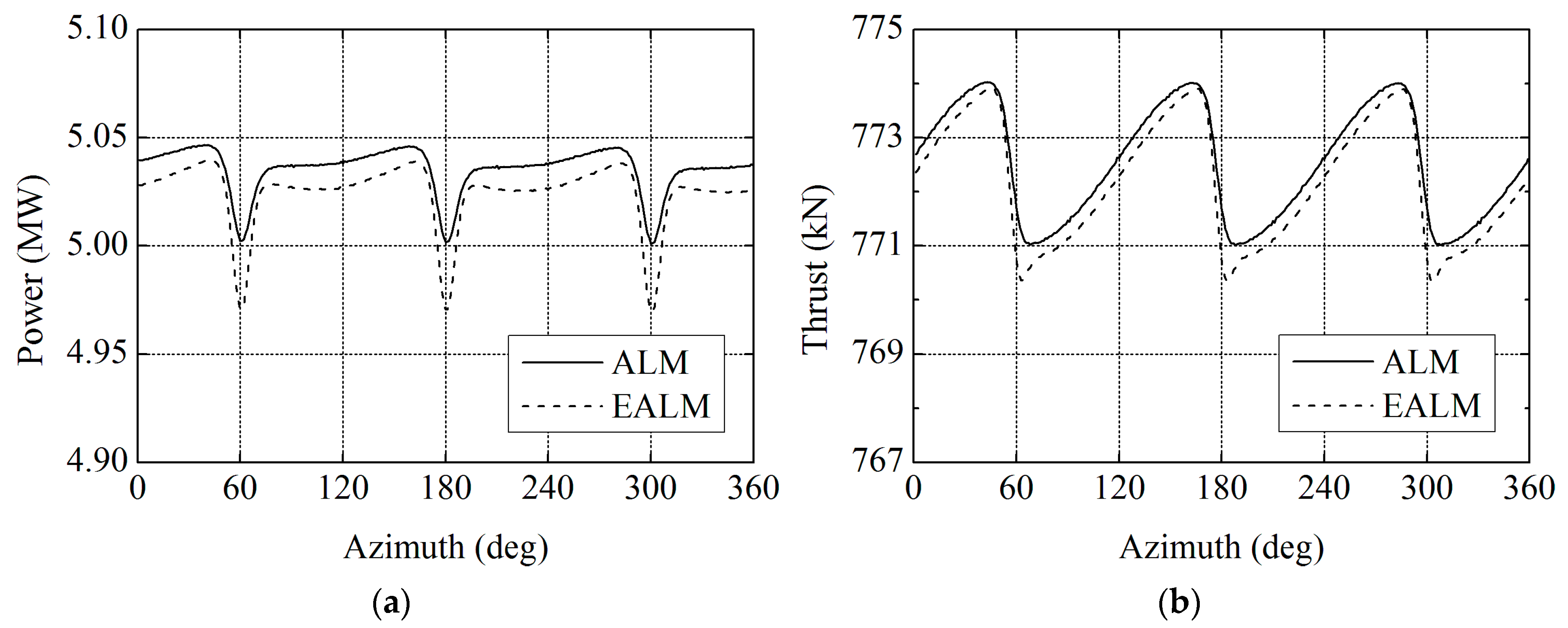
Figure 18.
Comparisons of the aerodynamic performance results between traditional actuator line model (ALM) and elastic actuator line model (EALM) at 11.4 m/s: (a) power; and (b) thrust.
Figure 18.
Comparisons of the aerodynamic performance results between traditional actuator line model (ALM) and elastic actuator line model (EALM) at 11.4 m/s: (a) power; and (b) thrust.
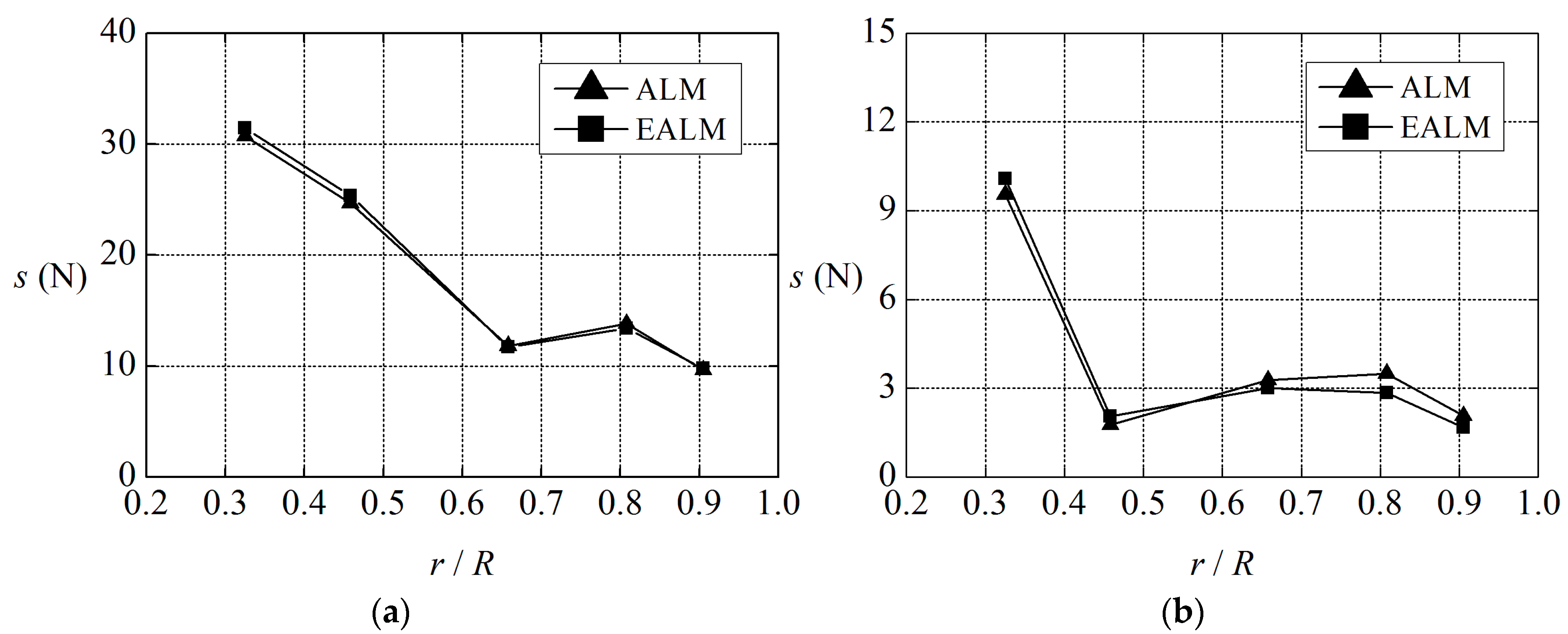
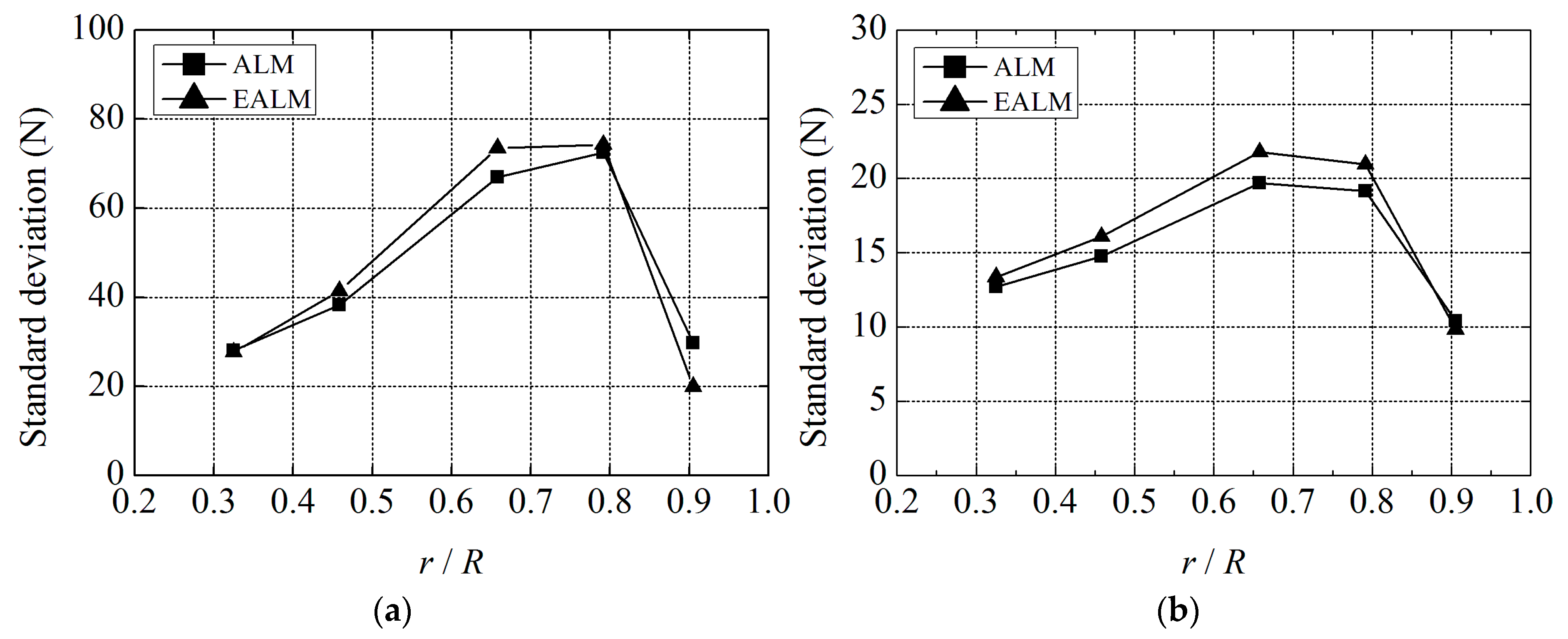
Figure 19.
Stabilization of forces on blade: (a) normal force; and (b) tangential force.
Figure 19.
Stabilization of forces on blade: (a) normal force; and (b) tangential force.
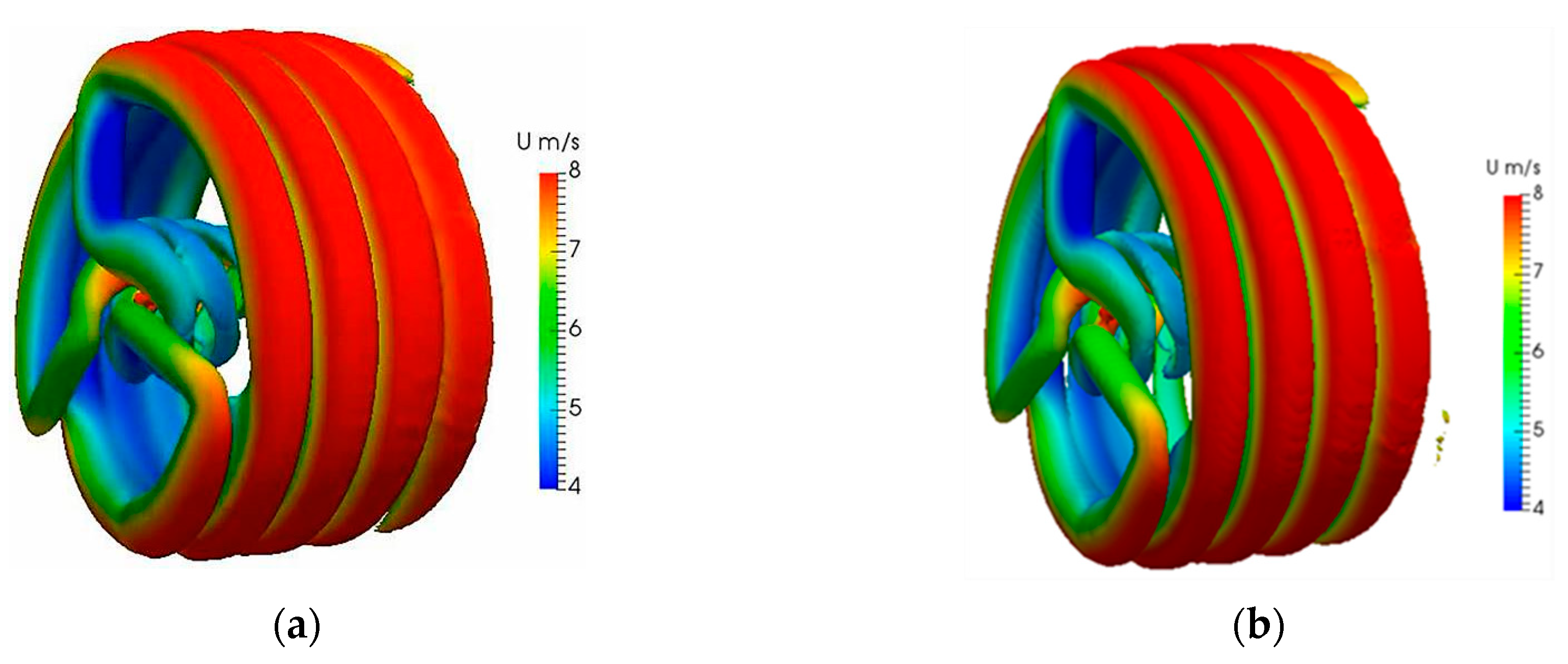
Figure 20.
The wake structures in terms of Q field at 8 m/s: (a) by EALM; and (b) by ALM.
Figure 20.
The wake structures in terms of Q field at 8 m/s: (a) by EALM; and (b) by ALM.
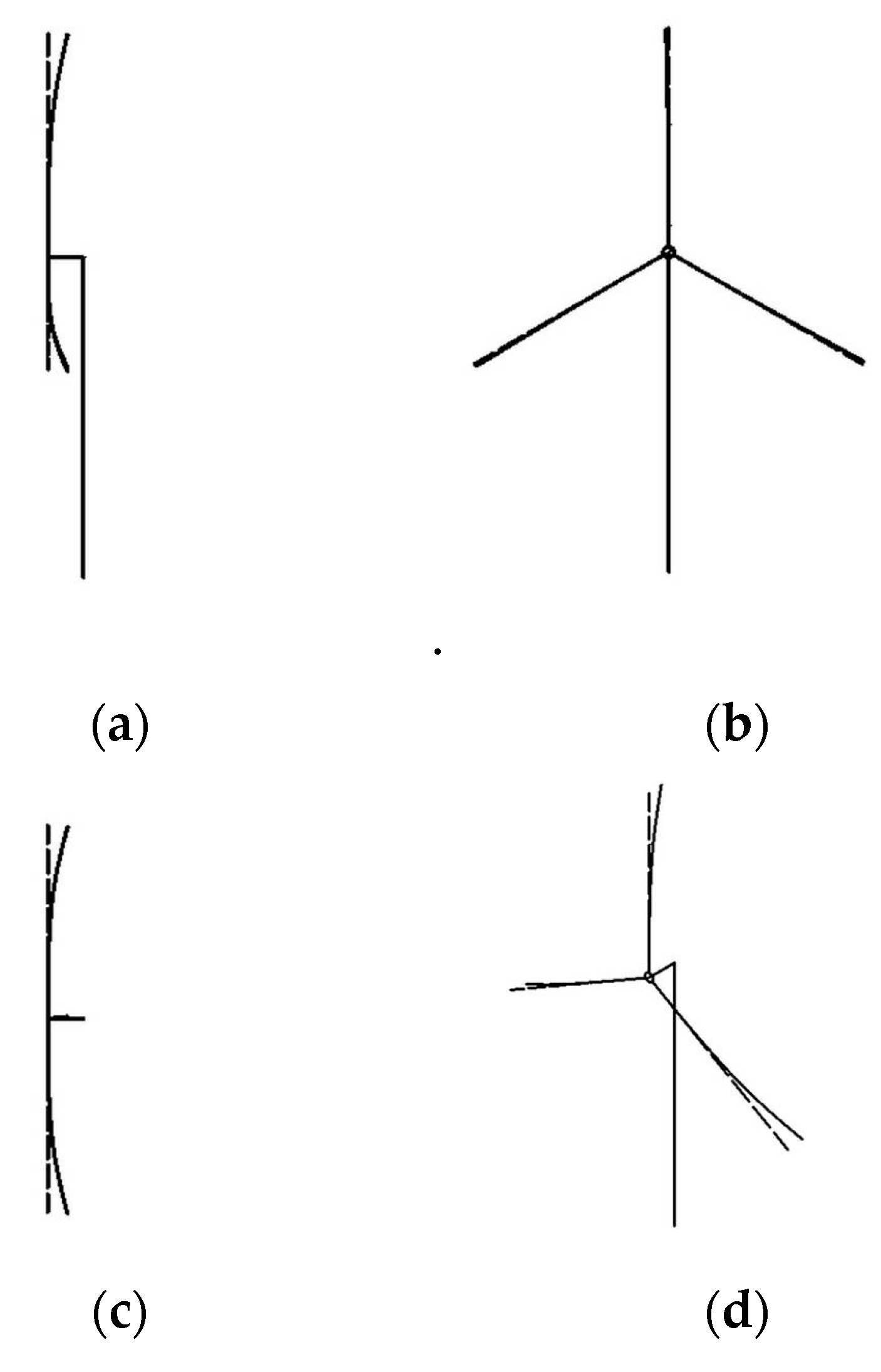
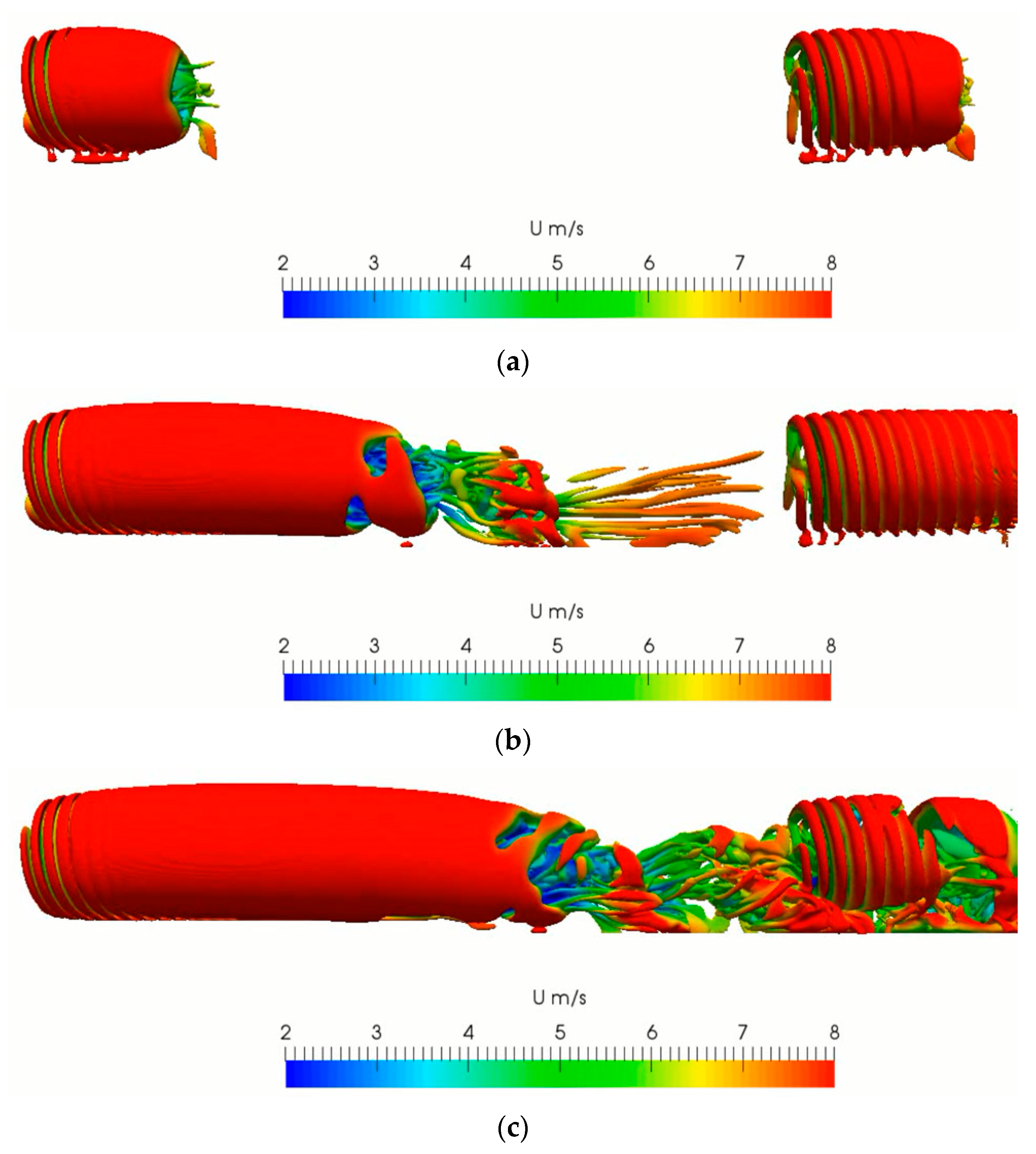
Figure 21.
The abbreviated sketches of blade deflection: (a) front side view; (b) left side view; (c) vertical side view; and (d) southwest isometric side view.
Figure 21.
The abbreviated sketches of blade deflection: (a) front side view; (b) left side view; (c) vertical side view; and (d) southwest isometric side view.
Figure 22.
Comparison of downstream wind turbine aerodynamic performance results between
Table 8. m/s: (
a) power; and (
b) thrust.
Figure 22.
Comparison of downstream wind turbine aerodynamic performance results between
Table 8. m/s: (
a) power; and (
b) thrust.
Figure 23.
Stabilization of forces on downstream wind turbine blades: (a) normal force; and (b) tangential force.
Figure 23.
Stabilization of forces on downstream wind turbine blades: (a) normal force; and (b) tangential force.
Figure 24.
The wake structure development of double wind turbine aligned: (a) initial status without disturb; (b) developing status; and (c) interference status.
Figure 24.
The wake structure development of double wind turbine aligned: (a) initial status without disturb; (b) developing status; and (c) interference status.
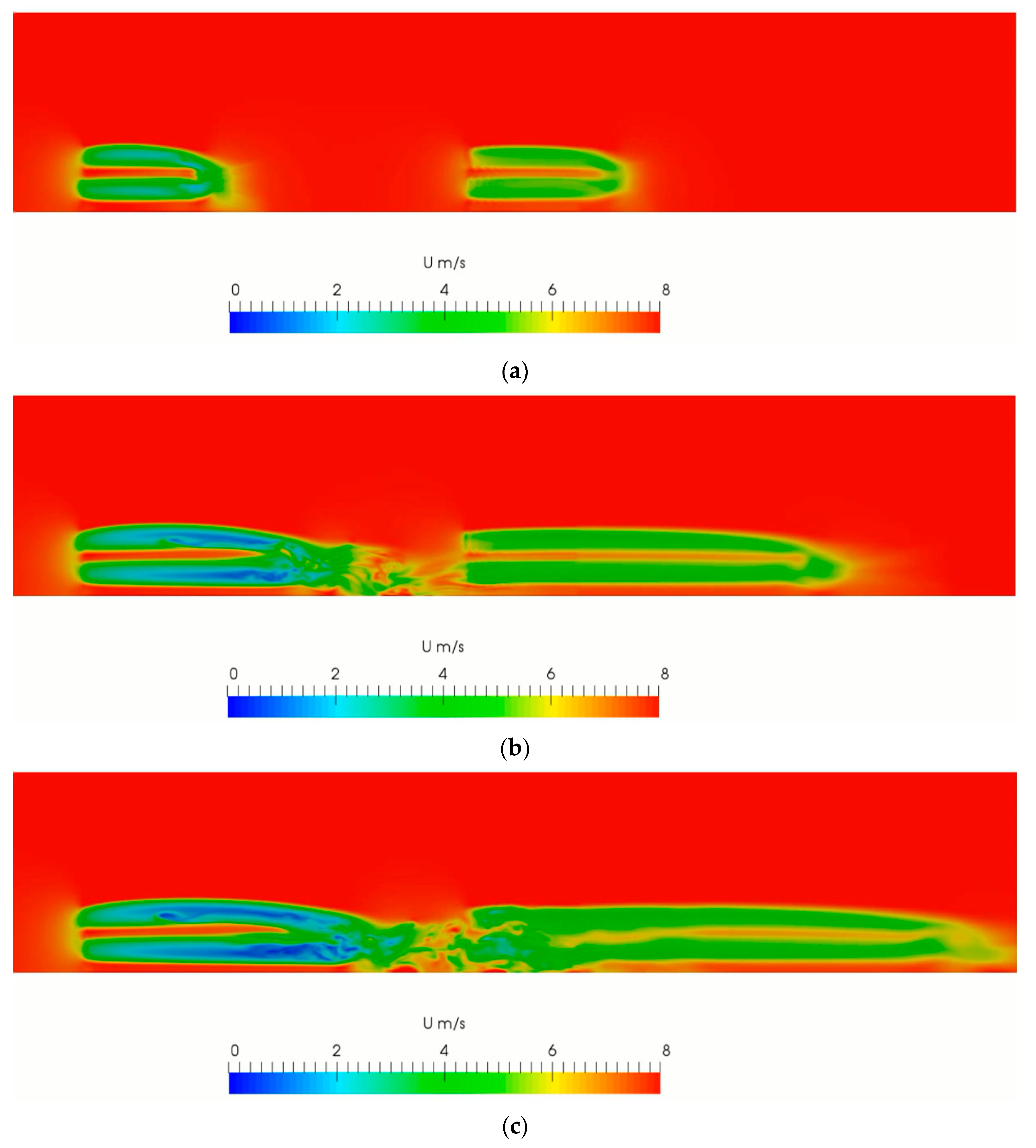
Figure 25.
The wake velocity field development of double wind turbine aligned: (a) initial status without disturb; (b) developing status; and (c) interference status.
Figure 25.
The wake velocity field development of double wind turbine aligned: (a) initial status without disturb; (b) developing status; and (c) interference status.
Table 1.
Properties of NREL 5 MW baseline wind turbine (NREL: National Renewable Energy Laboratory).
Table 1.
Properties of NREL 5 MW baseline wind turbine (NREL: National Renewable Energy Laboratory).
| Properties | Content |
|---|
| Rotor orientation | Upwind |
| Rotor configuration | Three blades |
| Rotor diameter | 126 m |
| Hub diameter | 3 m |
| Hub height | 90 m |
| Shaft tilt angle | 5° |
| Rotor mass | 110,000 kg |
| Rated power | 5 MW |
| Rated wind speed | 11.4 m/s |
| Rated rotor speed | 12.1 rpm |
Table 2.
Mesh independence test of power and thrust coefficient.
Table 2.
Mesh independence test of power and thrust coefficient.
| Grid Level | Number of Cell | Size of Wake Region Cell (m) | Cp | Ct |
|---|
| 1 | 0.38 M | 2.5 | 0.4678 | 0.8665 |
| 2 | 0.75 M | 2.0 | 0.4642 | 0.8599 |
| 3 | 2.90 M | 1.5 | 0.4634 | 0.8584 |
| 4 | 5.96 M | 1.0 | 0.4627 | 0.8572 |
Table 3.
Relationship between actuator point number and aerodynamic coefficients.
Table 3.
Relationship between actuator point number and aerodynamic coefficients.
| Level | Actuator Point Number | Cp | Ct |
|---|
| 1 | 54 | 0.4650 | 0.8608 |
| 2 | 72 | 0.4634 | 0.8584 |
| 3 | 90 | 0.4632 | 0.8580 |
Table 4.
Comparison of the computational cost between actuator line method (ALM) and computational fluid dynamics (CFD) method.
Table 4.
Comparison of the computational cost between actuator line method (ALM) and computational fluid dynamics (CFD) method.
| Method | Software | Number of Cell | Simulated Time | Power |
|---|
| ALM | OpenFOAM | 1.49 M | 9.2 h | 5.036 MW |
| CFD | Star CCM+ | 5.01 M | 82.0 h | 5.050 MW |
Table 5.
Detailed information about the solved method on the aerodynamic performance and the structural responses in different cases.
Table 5.
Detailed information about the solved method on the aerodynamic performance and the structural responses in different cases.
| Case Number | Aerodynamic Method | Elastic Dynamics Method | Studying Contents |
|---|
| 1 | ALM | Rotating beam solver | Variation in wake flow |
| 2 | BEM | Modal approach | Blade response and aerodynamics |
| 3 | BEM | MBD | Blade response and aerodynamics |
| 4 | CFD | MBD | Influence of wind turbulence |
| 5 | BEM | Geometric nonlinearity beam model | Optimal yaw and pitch angle |
| 6 | BEM | Dynamic rotor deformation model | Rotor structure deformation |
| 7 | CFD | FEM-based CSD beam solver | Yaw and wind shear |
| 8 | ALM | Finite-element beam method | Wake behavior |
Table 6.
Comparison of the power and the thrust with different research.
Table 6.
Comparison of the power and the thrust with different research.
| Case Number | 8 m/s | 11.4 m/s |
|---|
| Power (MW) | Thrust (kN) | Power (MW) | Thrust (kN) |
|---|
| 1 | 1.891 | 432 | 5.024 | 772 |
| 2 | 1.856 | 466 | 5.000 | 817 |
| 3 | 1.928 | 391 | No data | No data |
| 4 | 1.865 | 389 | 5.407 | 759 |
| 5 | 2.242 | 410 | 5.249 | 645 |
| 6 | 1.817 | 340 | 5.130 | 659 |
| 7 | 2.000 | 362 | 5.334 | 671 |
| 8 | 1.924 | 384 | 5.350 | 663 |
Table 7.
Comparisons of the power and the thrust relative error between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds.
Table 7.
Comparisons of the power and the thrust relative error between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds.
| Wind Speed (m/s) | Power (MW) | Error | Thrust (kN) | Error |
|---|
| 5.0 | 0.4355 | 2.828% | 222.6153 | 15.965% |
| 6.0 | 0.8194 | 7.080% | 287.8339 | 13.253% |
| 7.0 | 1.2986 | 6.099% | 356.5589 | 10.233% |
| 8.0 | 1.8906 | 3.856% | 432.3593 | 7.543% |
| 9.0 | 2.6880 | 3.564% | 546.8937 | 5.374% |
| 10.0 | 3.6799 | 3.405% | 674.6184 | 2.392% |
| 11.4 | 5.0241 | 0.482% | 772.1718 | 3.948% |
Table 8.
Comparison of tip deflection with different research.
Table 8.
Comparison of tip deflection with different research.
| Case Number | 8 m/s | 11.4 m/s |
|---|
| Out of Plane Tip Displacement (m) | In Plane Tip Displacement (m) | Out of Plane Tip Displacement (m) | In Plane Tip Displacement (m) |
|---|
| 1 | 3.159 | −0.418 | 5.560 | −0.762 |
| 2 | 3.220 | −0.350 | 5.550 | −0.592 |
| 3 | 3.592 | −0.345 | 6.379 | −0.579 |
| 4 | 2.958 | No data | 4.851 | −0.624 |
| 5 | 3.675 | −0.298 | 6.212 | −0.584 |
Table 9.
Comparison of the tip displacement relative errors between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds.
Table 9.
Comparison of the tip displacement relative errors between elastic actuator line model (EALM) and NREL’s FAST code at different wind speeds.
| Wind Speed (m/s) | Out of Plane Tip Displacement (m) | Error | In Plane Tip Displacement (m) | Error |
|---|
| 5.0 | 1.8092 | 5.340% | −0.2215 | −10.536% |
| 6.0 | 2.2194 | 2.598% | −0.2793 | −8.828% |
| 7.0 | 2.6592 | 0.345% | −0.3437 | −3.692% |
| 8.0 | 3.1594 | 2.090% | −0.4177 | −4.895% |
| 9.0 | 3.9490 | 0.596% | −0.5247 | −14.135% |
| 10.0 | 4.8308 | 2.069% | −0.6441 | −20.776% |
| 11.4 | 5.5591 | 2.545% | −0.7616 | −3.225% |
Table 10.
Comparison of blade tip displacement Pearson simplified correlation coefficient between elastic actuator line model (EALM) and NREL’s FAST code.
Table 10.
Comparison of blade tip displacement Pearson simplified correlation coefficient between elastic actuator line model (EALM) and NREL’s FAST code.
| Wind Speed (m/s) | Direction | R |
|---|
| 8.0 | 0 | 99.18% |
| 1 | 99.91% |
| 11.4 | 0 | 99.40% |
| 1 | 99.97% |
Table 11.
Comparisons of mean output power with Jha et al. [
34].
Table 11.
Comparisons of mean output power with Jha et al. [
34].
| Research | Mean Power of Upstream Wind Turbine (MW) | Difference with Jha et al. [34] | Mean Power of Downstream Wind Turbine (MW) | Difference with Jha et al. [34] |
|---|
| EALM | 2.0231 | 5.28% | 0.7943 | 8.11% |
| ALM | 2.0345 | 5.87% | 0.8089 | 6.42% |
| Jha et al. [34] | 1.9217 | - | 0.8644 | - |