Abstract
This review paper addresses the structure of the mean flow and key turbulence quantities in free-surface flows with emergent vegetation. Emergent vegetation in open channel flow affects turbulence, flow patterns, flow resistance, sediment transport, and morphological changes. The last 15 years have witnessed significant advances in field, laboratory, and numerical investigations of turbulent flows within reaches of different types of emergent vegetation, such as rigid stems, flexible stems, with foliage or without foliage, and combinations of these. The influence of stem diameter, volume fraction, frontal area of stems, staggered and non-staggered arrangements of stems, and arrangement of stems in patches on mean flow and turbulence has been quantified in different research contexts using different instrumentation and numerical strategies. In this paper, a summary of key findings on emergent vegetation flows is offered, with particular emphasis on: (1) vertical structure of flow field, (2) velocity distribution, 2nd order moments, and distribution of turbulent kinetic energy (TKE) in horizontal plane, (3) horizontal structures which includes wake and shear flows and, (4) drag effect of emergent vegetation on the flow. It can be concluded that the drag coefficient of an emergent vegetation patch is proportional to the solid volume fraction and average drag of an individual vegetation stem is a linear function of the stem Reynolds number. The distribution of TKE in a horizontal plane demonstrates that the production of TKE is mostly associated with vortex shedding from individual stems. Production and dissipation of TKE are not in equilibrium, resulting in strong fluxes of TKE directed outward the near wake of each stem. In addition to Kelvin–Helmholtz and von Kármán vortices, the ejections and sweeps have profound influence on sediment dynamics in the emergent vegetated flows.
1. Introduction
Vegetation is ubiquitous in rivers, estuaries, lake shores and some coastal areas [1]. It can be of different types including submerged, floating and emergent, whose incidence in a channel is schematized in Figure 1. Plants having varied stiffness, density, flexibility and height influence the water flow in different ways [2,3]. Its spatial distribution is seldom uniform [4]. Vegetation is frequently arranged in patches [5,6]. The presence of vegetation in water bodies has major impacts on flow hydrodynamics, including mean flow and variables describing turbulence. Certain important features like flow rate, changes in the bed and sediment carrying capacity of the stream are influenced by riparian plantation and its interactions with hydrodynamics.
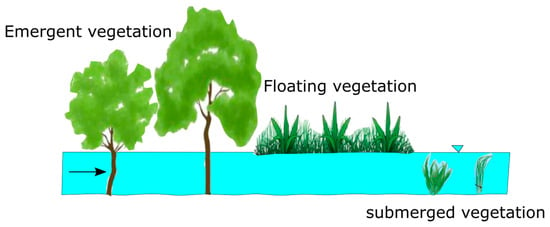
Figure 1.
Different types of vegetation in open channel flow.
Parameters such as increased length, density and height of vegetation result in increased roughness, increased water levels and decreased velocities. In some cases vegetation offers protection against bank erosion, tsunamis and high waves. Experimental results show that the presence of vegetation leads to the generation of turbulence and additional drag forces. It is well known that the vertical distribution of flow velocity depends on the density of vegetation. The increase in stem density decreases the flow velocity through the interior of vegetation and increases the velocity in the regions without vegetation. Lichtenstein [7] classified aquatic plants into four types: algae, floating-leaved plants, submerged plants and emerged plants as shown in Figure 2a.
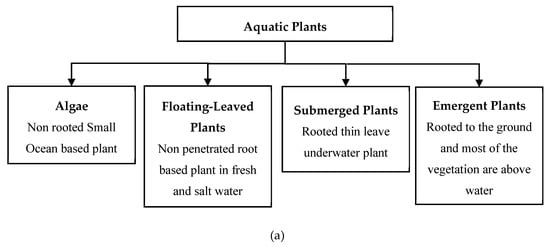
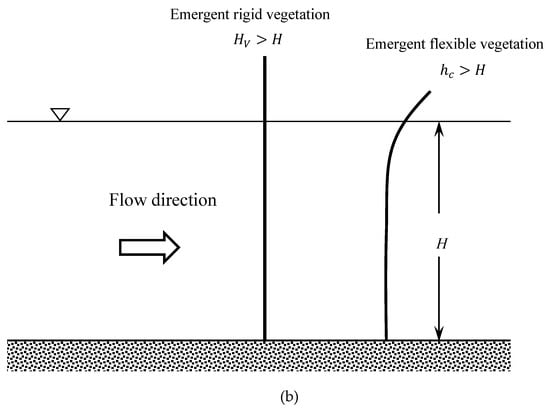
Figure 2.
(a) Classification of aquatic plants; (b) emergent vegetation types based on plant stiffness.
Vegetation may be broadly divided into rigid and flexible, as shown in Figure 2b. The effect of flexible vegetation is quite different from that of rigid vegetation. The rigid vegetation causes the flow to produce separation, wakes and eddies which in turn dissipate the flow energy [8]. Figure 2 shows definition of emergent, rigid and flexible vegetations, in which, = height of rigid vegetation, = height of bent vegetation and = water depth.
Given the complexity of emergent vegetated flows with ecological, geomorphologic and hydrodynamic effects, a great deal of research work including sophisticated field, laboratory and numerical studies have been undertaken to understand it. Significant advances have been achieved in the field of emergent vegetation hydrodynamics with respect to horizontal and vertical structures, [3,4,8,9,10,11,12,13], drag and frictional characteristics, [9,10,14,15,16,17,18,19]. Furthermore, with increasing computer power and improvements in numerical modelling, impressive advances were made in the study of the origin and development of coherent structures in the emergent vegetated flows [11,12]. These numerous investigations require a consolidated review to help researchers working on the hydrodynamics of emergent vegetated flows for deeper understanding. Therefore, the aim and scope of the paper is to make a synthesis of the state of the art relevant research works on the hydrodynamics of emergent vegetated flows, with emphasis on mean flow, turbulence and drag. In line with these objectives, present review highlights important research contributions of emergent vegetation hydrodynamics including complex interactions between turbulence and vortex structures.
The review of research findings on open channel flows with emergent vegetation is further divided into: (i) vertical structure of flow field (ii) velocity distribution, 2nd order moments, and distribution of turbulent kinetic energy (TKE) in the horizontal plane, (iii) horizontal features which include wake and shear flows and (iv) drag effect of vegetation on the flow. In addition, future directions are deliberated for researchers working on the emergent vegetated flows, and finally conclusions of the paper are presented at the end.
2. Hydrodynamics of Emergent Vegetated Flows
Vegetation extending from the bed all the way beyond the free surface is called emergent vegetation. Good examples of emergent vegetation include jute plantations, mangroves, and often partially submerged trunks of palm trees in flood water. Studying emergent vegetation is sought after because it modifies velocity vertical profiles and turbulence intensities. Commonly, emergent vegetation consists of relatively stiff stems, which are usually circular in cross section and without leaves below the water surface [3]. Therefore, emergent rigid cylindrical stems have been extensively employed in research works as a proxy for natural stems.
In unbounded open channels, the mean flow through groups of emergent vegetation is decreased. The emergent canopy has a significant role on coherent structures and accompanying mass and momentum fluxes at the boundary between emergent vegetation and open channel. In particular, emergent canopy patch density in the open channel flow affects mass and momentum transfer, roughness, sedimentation, velocity of flow, bed shear, turbulence quantities, biological processes and aquatic life within the canopy. Additionally, characteristics of flow through emergent vegetation consist of significant velocity gradients (in transverse, stream wise and vertical directions) and drag discontinuity at the interface resulting in the formation of a shear layer between the vegetation stems and the flow exterior of the vegetation. The shear layer in turn generates large coherent vertical structures due to Kelvin–Helmholtz instability. These coherent structures grow downstream due to creation of vortex-street, vortex pairing and eventually dissipate into the flow.
2.1. Vertical Structure
The vertical structure of flows within the stems of emergent vegetation is divided in three layers: (i) the reach close to the bottom, where the flow is highly 3D due to interaction with the bed; (ii) the layer close to the free surface, which is affected by the oscillations of the free surface; and (iii) the intermediate layer, sufficiently away from the bed and from the free surface, where the flow is controlled by the vertical stems and the flow properties are approximately constant in the vertical direction [9,10,11,20] as shown in Figure 3.
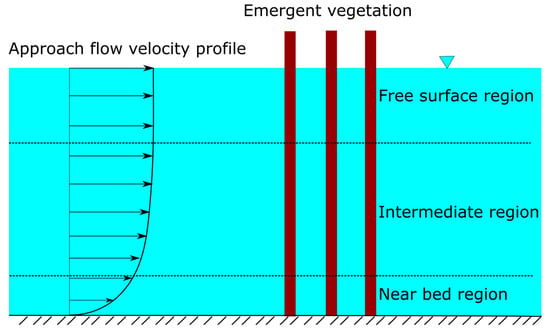
Figure 3.
Vertical structure of flow in emergent vegetation.
Stoesser et al. [11] numerically studied three types of spacing between cylinders on the flow field. Very small vertical velocities are observed in the large spacing cases except just behind the cylinder where relatively large values of vertical velocity indicates considerable upward movement of fluid observed just behind the cylinder. However, upward and downward movement of fluid is observed in the case of low spacing between the cylinders. Contours of the time-averaged streamwise velocity and streamlines at about half depth for the three different vegetation densities are investigated. Flow separation occurs at approximately 95° and a relatively large recirculation region comprising two counteracting vortices that are about the size of the cylinder diameter are observed in low and medium vegetation densities. In high vegetation density, flow separates considerably later and the recirculation region behind the cylinder is much smaller.
Ricardo et al. [3] addressed the influence of the longitudinal variation of the stem areal number density on the spatial distribution of the turbulent flow variables at the inter-stem scale. They concluded that Reynolds stresses are not sensitive to local spatial gradients of the stem distribution, being determined by the local number of stems per unit area. However, form-induced stresses depend on the local number of stems and its spatial distribution. Ricardo et al. [4] identified a spatial memory of the flow manifested by the upstream generated complexity of the flow that subsists further downstream and is combined with the complexity locally generated, resulting in the increased spatial variability relative to that of a flow with a uniform stem distribution.
Chang and Constantinescu [12] numerically investigated the flow and turbulence structure interior and exterior of a circular array of emergent rigid vegetation patch by varying the solid volume fractions and relative cylinder diameter arrays. These studies were performed without considering a different bedforms effect, which could be a crucial factor in flows through natural bedforms as studied by Pu et al. [21]. The flow was found to be highly three dimensional in the array when solid volume fraction (SVF) was more than 0.1 and this effect was relatively small when the magnitude of SVF was less than 0.025. Von Kármán vortex streets were developed for cylinder Reynolds number greater than 10,000. Furthermore, Chang and Constantinescu [12] found that at sufficiently high SVFs such as 0.2, von Kármán wake cylinder interactions become important resulting in the formation of von Kármán vortex street. In low SVFs such as 0.023, wake and cylinder interactions were weak and flow advects through the cylinders without a vortex street. However, shear layers are observed irrespective of formation of von Kármán vortex streets. For larger values of SVF, cylinders in the downstream imped the formation of strong vortices.
Liu and Shan [22] used an analytical model to predict longitudinal profile of depth averaged streamwise velocity for simulated emergent cylindrical vegetation and used an experimental setup to validate the proposed model for short and long arrays of vegetation. Tong et al. [23] investigated the effect of emergent rigid vegetation in a shaped confluence channel and concluded that non submerged vegetation is responsible for changing the flow structure. Due to the vegetation, middle of the non-vegetated area in the vicinity of tributaries showed existence of high velocity region, and the disappearance of the secondary flow. The flow in non-vegetated areas was more intense and turbulent kinetic energy of the non-vegetated area was lesser than the vegetated area.
2.2. Mean Flow and Distribution of Turbulent Kinetic Energy (TKE) in the Horizontal Plan
Ricardo et al. [8] carried out a laboratory work simulating rigid and emergent cylinders, with longitudinally varying density where 2D instantaneous velocity maps were measured with a Particle Image Velocimetry (PIV) aiming at characterizing the mean flow field at the inter-cylinder and patch scales. Figure 4a,b exemplifies a horizontal map of longitudinal velocity and out-of-plane vorticity map for a patch of 1200 cylinders/m2 in a 3.5 m-long reach populated with rigid cylinders and with longitudinally varying density of cylinders.
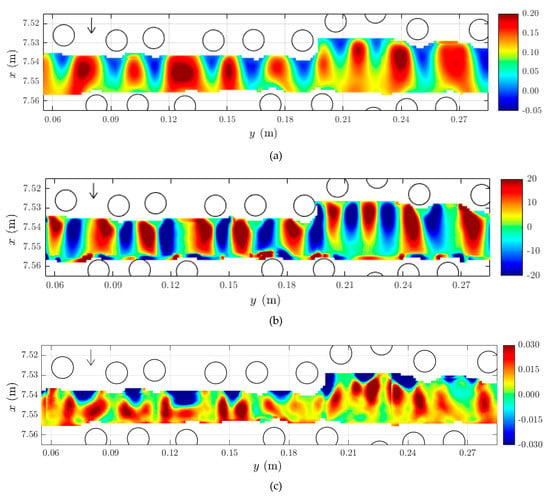
Figure 4.
(a) Time-averaged longitudinal velocity map (m/s); (b) out-of-plane vorticity map (m−1); (c) rate of production of TKE (m2 s−3), at longitudinal position P8 and at 3.1 cm above the bed corresponding to 60% of the flow depth. (Source: Ricardo et al., 2014).
The mean flow field within vegetation covered areas is heterogeneous at large scales, as reach or patch scales, with zones of low longitudinal velocity at the vegetation elements wake alternated by high longitudinal velocity zones between those elements [8,24]. These low/high velocity patterns are observed independently of the density and distribution of the vegetation elements.
Relative to the vorticity distribution, a repeating pattern of paired vortexes caused by the unsteady separation of the flow on the cylinders is observed. These quasi-symmetric high vorticity patterns behind the cylinders identify von Kármán vortex streets. Comparing vorticity maps for the different density of cylinders, the conclusion is that the cylinders induce a regular structure of vortex patterns independently space between cylinders. The main difference is that the space necessary to fully develop the vortex pattern is strongly reduced at smaller distances between cylinders. At higher cylinder densities, the vortex pattern is forced to compress due to the proximity of the next cylinder, while at positions with lower cylinder density cases the vortex pattern has space to develop a vortex street.
Ricardo et al. [8] performed laboratory experiments on rigid emergent vegetation aimed at the characterization of the key terms of the TKE equation. Three dimensional laser doppler anemometry (LDA) and two dimensional particle image velocimetry (PIV) measurements have been employed. They characterized the spatial distribution of turbulent production, convective rate of change of TKE and turbulent diffusion and the dissipation rate of TKE was also computed. They observed that the production of TKE is mostly associated with vortex shedding from individual stems (Figure 4c). The magnitude of the rate of production is higher in the wake region and negative production of TKE was identified between close cylinders, associated with strong local accelerations in the flow field. Turbulent transport is particularly important along the von Kármán vortex street and convective rate of change of TKE and pressure diffusion are most relevant in the vicinity of the cylinders. The rate of dissipation was found to increase with the stem areal number density. Ricardo et al. [8] observed that the rates of production and dissipation are not in equilibrium in the inter-stem space, revealing important interactions of turbulence with mean flow and pressure field and turbulent transport of TKE. The cumulative effect of convection and turbulent transport of TKE is the generation of background turbulence, i.e., non-locally generated turbulence.
Ricardo et al. [4] investigated the impact of the background turbulence caused by randomly placed cylinders on the vortex shedding regime. The strong background turbulence, generated by the randomly placed cylinders in the array, causes a premature vortex detachment increasing the shedding frequency. It was concluded that the background turbulence acts on the faster loss of vortex coherence as they travel downstream. Furthermore, Ricardo et al. [4] observed that the impact of the background turbulence on decay of the longitudinal vorticity flux is small, the latter is mainly caused by the vorticity cancellation imposed by the local distribution of neighbouring cylinders.
2.3. Horizontal Structure
Density, shape and arrangement of the stems in the emergent vegetation patch have a dominant role on the mean flow and turbulence structures in the interior and exterior of the patch in horizontal direction.
The mean flow is largely dominated by the wakes which tend to reduce the flow between the bodies and this effect is larger than the inviscid kinematic effect of the bodies blocking the flow. The difference between Lagrangian and Eularian velocities with different void ratios is one of the aspects of horizontal structure. At the upstream of the array of cylinders, the flow is irrotational and slows down due to the blocking effect of the entire patch and the drag force from the cylinders. The flow bleeds through the vegetation with low velocity and high velocity flow takes through the region without vegetation. Shear layers form on either sides of the vegetation patch as shown in Figure 5. At what distances upstream and downstream of the flow is influenced by the array of cylinders is a function of vegetation density, width of the patch, Reynolds and Froude numbers.
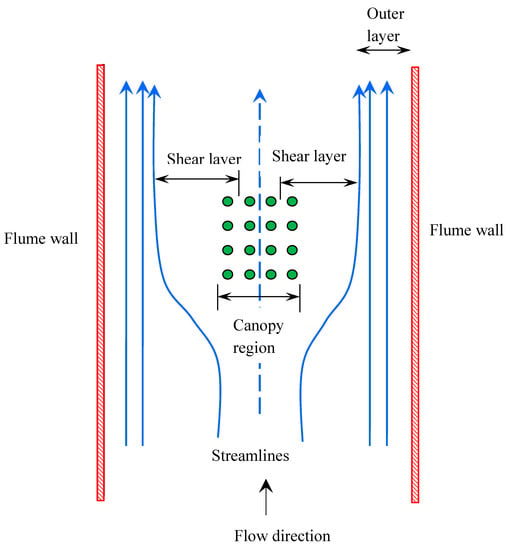
Figure 5.
Horizontal structure of the flow through a vegetation patch.
Stoesser et al. [11] carried out large eddy simulations (LES) of flow through the canopies with solid volume fractions 0.016, 0.063 and 0.251. In their analysis, the streamwise turbulence intensity profiles were significantly different from unobstructed channel flow not only in shape but also in magnitude. Higher streamwise turbulence intensities were observed in high vegetation density cases. Similarly, normalized vertical turbulence intensities have higher magnitudes for higher density vegetation. The turbulence in the high vegetation density case is rather generated by high streamwise velocity gradients, while von Kármán vortex shedding occurs in low density cases [11].
Nicolle and Eames [25] studied the effects of the patch of emergent and rigid cylinders on the flow field in a uniform air flow using direct numerical simulations (DNS). Nicolle and Eames [25] found that the von Kármán vortex-street behind the circular cylinder array is similar to that of flow past a single cylinder. The most obvious limitation of their study is the implementation of 2D model to study the 3D flow field where additional drag is caused by vortex stretching.
Nepf [26] concluded that emergent vegetation develops two different types of turbulent scales i.e., canopy scale turbulence and stem scale turbulence in which canopy scale vortices control the high level of turbulent diffusion in the exchange zone. In general, the turbulence in the interior of emergent vegetation is less than that of the outside the vegetation in free surface flows. However, the decrease in turbulence due to decreased mean velocity near the bed is too small as compared to the additional turbulence generated by stem vortices. White and Nepf [13] and White and Nepf [27] considered horizontal flow structure and studied the momentum transfer at the interface between the flow inside the emergent vegetation and the region outside the vegetation. Shear layer is created due to the drag discontinuity at the interface and coherent vortices are generated in the shear layer due to Kelvin–Helmholtz instability. The exchange of fluxes between the open channel flow through the vegetation and the region outside the vegetation is dominated by the energetic shear layer vortices. Vortices in the shear layer are found to be continuously growing in the downstream direction predominantly through vortex pairing. In addition a quasi-coherent vortical structure with two times the spacing of the shear layer vortices is generated by the interaction of paired shear layer vortices.
Meftah and Mossa [28] studied channel partially obstructed by emergent vegetation with an emphasis to understand the effect of contraction ratio. They observed the formation of a shear layer immediately next to the interface, followed by an adjacent free stream region of full velocity flow. In addition, the transversal flow velocity profile at the obstructed and unobstructed interface was analyzed. The experimental results demonstrated that the contraction ratio significantly affects the flow hydrodynamic structure. Finally, a general modified log-law was proposed to describe the typical transversal profile of the mean velocity and its application was in good agreement with analytical solutions.
Naot et al. [29] used computational fluid dynamics (CFD) with the model to simulate hydrodynamic behaviour of compound channel with rigid and emergent vegetation on the flood plain, they found that flow behaviour depends on shading factor and reference length of the vegetation. A two dimensional LES model was used by Ikeda et al. [30] to get a relation between the square of flow velocity and the waving motion of a flexible emergent (where plant height is equal to water depth) plant. The interesting observation in this study is the motion of the plant increases the frequency of vortices whereas increased strength of vortices increases the motion of plants.
Stoesser et al. [11], and Kim and Stoesser [31] concluded that von Kármán-type vortices, Kelvin–Helmholtz instability and vortex shedding are clearly visible in sparse vegetation. As the vegetation density increases, the influence of vortices that are shed from upstream cylinders affects more irregular shedding behavior of downstream cylinders. Increase in vegetation patch density increases the vorticity magnitude which is accompanied by the linear increase of vertical vorticity. Furthermore, the frequency of vortex shedding increases as the patch density increase.
Chang and Constantinescu [12] numerically found that coherent structures formed in the separated shear layer (SSL) are larger with SVF = 0.2 as compared to SVF = 1.0. For low SVF values, the separated shear layer (SSL) was found to be longer and eddies in the SSL have more energy as compared to that of the SSL in high SVF patch. Furthermore, the behaviour of eddies in SSL of low SVF patch resembles that of a mixing layer. Von Kármán Street was formed only in flows with SVF values higher than 0.2 and in which vortical structures were impeded and, therefore, not producing the regular wake vortices. For SVF values less than 0.05, shedding of wake vortices behind a cylinder was strongly disturbed by the vortices shedding from other cylinders in the vicinity. Chang and Constantinescu [12] concluded that for SVF = 0.023, shedding behind an individual cylinder in the patch is similar to that of an isolated cylinder in the flow.
Anjum and Tanaka [32] used discontinuous and vertically doubled layered patches and simulated it numerically for varying vegetable density and patches. Large-scale turbulence followed by saw-tooth distribution within the patches and low turbulence in the non-vegetation regions was observed. Maximum of 13% turbulence intensity for dense vegetation arrangements and maximum of 9% turbulence intensity for sparse vegetation was observed. They concluded the presence of non-uniform flow through discontinuous and double layered vegetation patches. Yamasaki et al. [33] studied the hydrodynamics of flow-vegetation interactions using a computational fluid dynamics model.
2.4. Drag and Frictional Characteristics
In open channel flows without vegetation, streamwise velocity distribution along the depth is a function of Reynolds shear stress, whereas velocity vertical profile in the vegetated channel is a function of frictional drag imposed by the vegetation since the vegetation drag is far greater than the frictional drag at the bed in high-density vegetated flows [10,34]. The drag force exerted by the flow on emergent vegetation can be estimated based on the available knowledge of flow around a circular cylinder.
Many studies are available in the literature to predict or measure frictional resistance in emergent vegetation conditions [9,10,11,14,15,16,35,36]. To compute the flow resistance in a vegetated channel, the drag caused by a single stem and the addition of individual drags of all the stems in that canopy, the blockage effect of the canopy in addition to the already existing bed roughness must be considered. Fathi-Maghadam and Kouwen [16] were among the first researchers who studied emergent flexible vegetation effect on the drag coefficient and in-turn on Manning’s roughness coefficient. Fathi-Maghadam and Kouwen [16] experimentally analysed the effect of proposed non-dimensional variables on and concluded that (i) Manning’s roughness proportionally increases with an increase in the square root of flow depth and increase in density of vegetation, and (ii) Manning’s roughness inversely proportional to the average flow velocity and vegetation flexibility.
In the riverine environment, however, canopies occur in finite patches and make a random angle with the direction of flow; for example, patches of mangroves in Purna River, India and Daintree River Queensland, Australia as shown in Figure 6. In these scenarios, flow is divided into flow passing through interior and exterior of the vegetation. According to Mitul et al. [18], mangroves are the densest canopies in coastal water with stem diameters between 4 cm to 9 cm and their solid volume fraction is around 0.55.
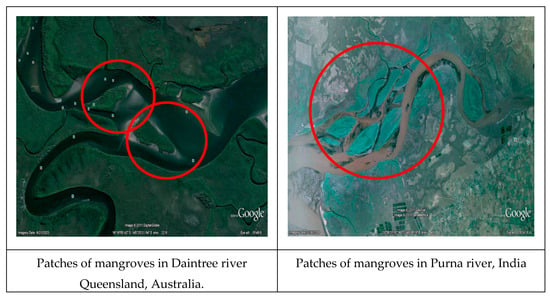
Figure 6.
Patches of vegetation (highlighted in circles) present in the river systems (Background image is sourced from Google Earth).
Maji et.al. [37] investigated the turbulence characteristics in open channel flow with an emergent, sparse and rigid vegetation patch. They observed that the nature of time-averaged velocities along streamwise, lateral and vertical directions are not consistent upto half the length of the patch from its leading edge; however, velocity profile becomes uniform after that length and their results are similar to various un-obstructed uniform and non-uniform flows studied by Pu et al. [38]. Inside the patch, the magnitude of vertical normal stress is small as compared to the streamwise and lateral normal stresses and Reynolds shear stress decreases along the centreline of the patch in the downstream. Furthermore, flow velocity decreases within the vegetation, which can lead to deposition of sediment which accelerates with the time and acts like a catalyst to the larger morphological changes in the river [37,39].
Heidari et al. [40] studied the drag created by a slender emergent cylinder in open channel flow and proposed that wake stability parameter significantly affects the drag on the cylinder away from the bed. Kothyari et al. [41] developed a drag model applicable to emergent plants in which drag coefficient decreases as the stem Reynolds number increases. Luna et al. [42] defined a term called ‘global flow resistance’ similar to Chezy’s coefficient, however the global flow resistance is a combination of bed shear stress and vegetation drag on the flow. Luna et al. [42] assessed various global flow resistance models for emergent vegetation and found that Baptist [43] model accomplishes the bestfit. Takemura and Tanaka [44] investigated the fluid structures in a colony type of emergent vegetation and coefficient of drag was experimentally measured. Their results restated that vortex patterns, strouhal number and drag coefficient of colony are function of where is cross stream spacing between neighboring cylinders and is cylinder diameter. Takemura and Tanaka [44] termed a von Kármán vortex-street behind an individual cylinder as primitive von Kármán vortex street (PKV) and its instability governs large scale vortical structures.
Tanino and Nepf [9] examined the canopy drag as a function of (, where = double averaged pore velocity, is kinematic viscosity and is stem diameter) which is in the range of 25–685 and solid volume fraction ranging from 0.091 to 0.35. They found that the value of a canopy patch is inversely proportional to and proportional to solid volume fraction. Average drag per unit cylinder length non-dimensionalized by the product of and dynamic viscosity is found to be a linear function of . This linear relation was further investigated by Ferreira et al. [10], who proposed that the increase of the solid fraction generates a momentum sink observed as an increase in the gradients of dispersive stresses. This may justify the increase of the drag coefficient with the increase of solid fraction at intermediate values of the latter. Liu and Zeng [45], however, suggest that, in general, the drag coefficient decreases with the solid fraction. Another important observation is that the drag of an individual cylinder is not a function of solid volume fraction. Chen et al. [17] studied the wake region behind a circular vegetation patch and found that for low flow blockages sediment deposition occurs, whereas for high flow blockages erosion takes place in the wake region.
Musleh and Cruise [36] combined the effects of flow depth, velocity, stem diameter, lateral spacing and longitudinal spacing into a non-dimensional variable called relative density ratio (ratio of total surface area of the vegetation to bed cross-sectional area) that is linearly related to Darcy’s friction factor and mannings coefficient. Musleh and Cruise [36] explained that for rigid vegetation, flow resistance of vegetation non-linearly increases with increasing flow depth especially when vegetation density is high, whereas flow resistance found to be nonlinearly decreasing with increasing mean flow velocity for flexible emergent vegetation flows. In addition, they found that the arrangement of rigid emergent cylinders plays an important role on the flow resistance and friction factor linearly varies with the relative density ratio. Musleh and Cruise [36] found that lateral spacing and stem diameter of cylinders have a more significant effect on the flow resistance as compared to the streamwise spacing of cylinders for a given stem density. The important observation in this experimental study is the drag effect of stem diameter is more than the transverse and streamwise spacings of cylinders. Furthermore, Musleh and Cruise [36] found that lateral spacing between the rods significantly affects the drag on rods. Wu et al. [19] experimentally found that the drag coefficient of emergent rigid vegetation increases with the increasing flow Reynolds number.
Chen et al. [14] used a tapered emergent flexible vegetation plant model to derive an analytical solution for flow resistance, bending behaviour and potential rupture locations. In this method, power law was used to determine the velocity distribution which is responsible for drag force on the rigid as well as flexible stems. Analytically computed deflections were validated with experimentally measured deflections. Finally, Chen et al. [14] concluded that the location of rupture depends on the tapering angle and the base diameter of the stem. Their results were consistent with earlier research that drag is inversely proportional to the average flow velocity.
Stoesser et al. [11] found that value of is linearly proportional to canopy density. In highly dense canopies, the downstream cylinders experience a drag force which is slightly smaller than for an isolated cylinder, but the lift force is much larger than the isolated cylinder because downstream cylinders are sitting in the wakes of two upstream cylinders [25]. In sparse canopies (SVF ≪ 1.0) upstream cylinders experience a drag force similar to that of an isolated cylinder but the lift force, while still relatively small is determined by the position of the cylinders in downstream. Cylinders located in the wake of other cylinders experience larger drag and lift forces as a result of the accelerated flow induced between the upstream cylinders. For intermediate void fractions, the force on the individual cylinders is steady and the lift force acting on the whole patch is negligible. The aggregate drag force on the canopy is dominated by the contributions from the upstream rows of cylinders, which experience a drag force comparable to that of a single cylinder. For high void fractions, the lift forces are significant and are mainly induced by the wake of the whole array. The effect of increasing void fraction leads to a slight increase in the scatter of the forces on the upstream cylinders and significantly increases the magnitude of the wake forces on the downstream cylinders.
Stoesser et al. [11] also studied the forces on cylindrical stems in a canopy and derived the following conclusions. Pressure drag, friction drag components are high and bed shear is low on the single cylinder in high patch density as compared to low patch density. In general the drag forces, pressure drag constitutes about 90% and remaining forces are only 10% (frictional drag is around 7% and bed shear is around 3%). Bed shear stress decreases with increasing patch density. The friction drag is almost constant regardless of vegetation density. Chang and Constantinescu [12] found that for numerical simulations, drag coefficient of a cylinder in the array is a very important parameter. They have also added that combined drag parameter for porous cylinders increases as frontal area per unit volume of patch increases.
Rooijen et al. [46] used an isolated emergent cylinder to assess canopy drag and obtained good agreement in drag computation by their proposed analytical model. In the case of a submerged cylinder, the authors suggested that their results are consistent with isolated cylinder theory. Wang et al. [47] used an experimental model to investigate the drag coefficient due to rainfall over vegetation. Experiments were conducted with varying stem density and applied water to obtain a link between friction slope and local kinetic energy head induced by steady non uniform flow. Spatial variation of drag coefficient exhibited a monotonic reduction during rain or non-monotonic hump formation when rain was absent.
Shan et al. [48] examined the effect on the change of drag force and velocity inside mangrove forest model for different vegetation stem arrangements. They found that the force at root is most dominant, randomly distributed branches inside a tree may experience more or less same force, and however, drag force increases with tree density. Razmi et al. [49] used a field scale large eddy simulation model by using distributed-drag approach and velocity-dependent models to study the effect of canopy reconfiguration on canopy posture and canopy drag. This model removed the flaws in the previous research of not capturing vertical spread in peak Reynold stress that is associated with the movement of the canopy interface.
2.5. Vegetation in Bank Protection and Sediment Transport
The effect of riparian vegetation on river morphology is well documented [50,51]. The role of vegetation density on improved riverbank stability is an emerging topic and important for further research [52]. River bankside vegetation can effectively improve bank strength and stability by mechanical, hydrologic, and hydraulic effects [53,54,55] and hence it may be considered essential to plant vegetation at erosion-prone locations on the riverbank [56]. Mechanical method comprised of root reinforcement along with flow resistance increment [53,57,58,59]. Hydrologic method protects the river bank from current induced erosion by reduction of soil moisture and pore water pressure, and increasing the root-induced compaction [60]. By contrast, the hydraulic method causes increase in hydraulic roughness and toe erosion reduction [61,62,63]. Interconnection between soil and root by apparent cohesion can increase bank stability [64]. But plant root can also negatively affect stability if extra weight of the vegetation increases downward force causing bank failure [58,65]. In addition, vegetal cover can reduce the danger of river course change and braid formation, which helps in maintaining river morphology [59,66,67,68,69,70]. Yu et al. [71] used the bank stability and toe erosion model (BSTEM) to find the effects of different root conditions on channel bank strength and verified that roots are good at reinforcing the unconsolidated banks and erosion control, hence proving the effectiveness of riverbank vegetation.
Yang and Nepf [72] proposed that near bed turbulent kinetic energy is better than bed shear stress for indicating bed load transport in vegetated flows. They proposed a turbulent kinetic energy based Einstein–Brown equation and satisfactorily compared the bed load transport with experimental results. Armanini and Cavedon [73] used a probabilistic/deterministic model to estimate the flow field changes induced by vegetation and associated bed load transport by refining their previous bed load model [74] and recalibrating [75] parameters. Their model shows good resemblance with experimental observations.
3. Further Research Prospects
Most of the research studies available are based on using rigid cylinders as vegetation stems, but real vegetation has a different shape, roughness and bending stiffness, and therefore laboratory experiments may not substitute the field investigations and this could be the focus in the future. In fact, a few researchers are working towards this achievement. Plant morphological studies were conducted with real vegetation for uniformly vegetated flow [2,76,77,78,79]. But there is a lack of dedicated study for partly vegetated flow with real vegetation. Caroppi et al. [80] are carrying out pioneering research by using naturally grown plants in an open channel for the study of reconfiguration and mixing effect of flow. In the real channels, aquatic seeds grow into aquatic plants and further experimental studies are required to study the transient flow field during aquatic plants growing stage. Similarly, capabilities of numerical simulations must be extended to field plants and scenarios. The feedback between flow field and sediment dynamics in the interior and exterior of the vegetation is beginning to be recognized as vital. Such research now provides an outstanding background for beginning to address areas of greater complexity that will enable a better understanding of these important natural features. In this context, studies conducted by [81,82,83] on threshold magnitude of velocity fluctuations and duration of velocity fluctuations for particle entrainment from the bed are useful for developing new sediment transport theories based on the energy approach in emergent vegetated flows. It is recognized that sweep events play a dominant role in dislodging bed particles. Flow conditions and the solid volume fraction of emergent vegetation affect the individual contributions of sweep and ejection coherent structures in the interior and wake regions. Therefore, the direct relation between the sediment transport and instantaneous coherent flow structures in vegetated flows are to be probed further. The effect of patch size of aquatic plants has not yet been fully investigated and elaborated clearly. As per the authors’ knowledge, the effect of changing the size of the patch in hydrodynamics and sediment transport through vegetation was studied only by [84] and gave an idea of the minimum size of a patch for triggering the flow interaction but it required the study of detailed turbulence characteristics for further investigation.
4. Conclusions
The additional drag created by vegetation resulting in a decrease in discharge in irrigation channels across the world has prompted researchers to characterize and quantify the effect of emergent vegetation on the flow field. Furthermore, the advent of accurate invasive and non-invasive velocity-measuring devices has accelerated the research in this area since early 2000. It was well accepted that the presence of emergent vegetation in the rivers and open channel flows has a significant role on mean velocity, turbulence levels, coherent structures and the accompanying mass and momentum fluxes at the boundary between emergent vegetation and an open channel. Decreased flow velocity within the vegetation leads to the deposition of sediment which accelerates with the time and acts like a catalyst to the larger morphological changes in the river. Another important and consistent research finding is that universal logarithmic law is not applicable for spatially and time averaged velocity vertical profile within the flow region of emergent vegetation.
Experimental evidence shows that the magnitude of vertical normal stress is small as compared to the streamwise and lateral normal stresses within the vegetation patch. The streamwise and vertical turbulence intensities, vorticity and vortex shedding have higher magnitudes for higher solid volume fraction of the vegetation. Investigation of spatial distribution of the turbulent flow variables at the inter-stem scale demonstrated that Reynolds stresses are not sensitive to local spatial gradients of the stem distribution, whereas form-induced stresses depend on the local number of stems and its spatial distribution. The production of TKE is mostly associated with vortex shedding from individual stems and therefore the magnitude of the rate of TKE production is higher in the wake region. Another important and consistent research finding is that the rate of TKE production and dissipation is found to be increasing with the increasing stem areal density. Few researchers studied the momentum transfer at the interface between the flow region inside and outside the emergent vegetation and observed the formation of coherent vortices in the shear layer due to Kelvin–Helmholtz instability. Researchers found the motion of the flexible emergent plant increases the frequency of vortices whereas the increased strength of vortices increases the motion of plants.
The coefficient of drag of the emergent vegetation patch was found to be inversely proportional to the cylinder Reynolds number, flow velocity and vegetation flexibility. However, the coefficient of drag was found to be proportional to the solid volume fraction, flow depth, and bed slope. It was also established that for low flow blockages, Kelvin–Helmholtz vortices are dominant, whereas for high flow blockages in which the vegetation patch acts like a bluff body von Kármán vortices are dominant. It was established that stem diameter of cylinders has a more significant effect on the flow resistance as compared to the streamwise and lateral spacing of cylinders for a given stem density.
Author Contributions
S.M.: writing—original draft preparation, funding acquisition; P.R.H.: writing—review and editing, project administration; R.B.: writing—review and editing, data curation; J.H.P.: writing—review and editing, supervision; A.M.R.: writing—review and editing; R.M.L.F.: writing—review and editing. All authors contributed to the work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yager, E.M.; Schmeeckle, M.W. The influence of vegetation on turbulence and bed load transport. J. Geophys. Res. Earth Surf. 2013, 118, 1585–1601. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- O’Hare, M.T. Aquatic vegetation—A primer for hydrodynamic specialists. J. Hydraul. Res. 2015, 53, 687–698. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Franca, M.J.; Ferreira, R.M.L. Turbulent flows within random arrays of rigid and emergent cylinders with varying distribution. J. Hydraul. Eng. 2016, 142, 4016022. [Google Scholar] [CrossRef]
- Schoelynck, J.; De Groote, T.; Bal, K.; Vandenbruwaene, W.; Meire, P.; Temmerman, S. Self-organised patchiness and scale-dependent bio-geomorphic feedbacks in aquatic river vegetation. Ecography 2012, 35, 760–768. [Google Scholar] [CrossRef]
- Meire, D.W.S.A.; Kondziolka, J.M. Nepf, H.M. Interaction between neighboring vegetation patches: Impact on flow and deposition. Water Resour. Res. 2014, 50, 3809–3825. [Google Scholar] [CrossRef]
- Lichtenstein, D. Types of Aquatic Plants Sciencing.com. Available online: https://sciencing.com/types-of-aquatic-plants-12003789.html (accessed on 9 January 2020).
- Ricardo, A.M.; Koll, K.; Franca, M.J.; Schleiss, A.J.; Ferreira, R.M.L. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res. 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Ferreira, R.M.L.; Ricardo, A.M.; Franca, M.J. Discussion of “Laboratory Investigation of Mean Drag in a Random Array of Rigid, Emergent Cylinders” by Yukie Tanino and Heidi M. Nepf. J. Hydraul. Eng. 2009, 135, 690–693. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Chang, K.; Constantinescu, G. Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 2015, 776, 161–199. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 2007, 593, 1–32. [Google Scholar] [CrossRef]
- Chen, L.; Stone, M.C.; Acharya, K.; Steinhaus, K.A. Mechanical analysis for emergent vegetation in flowing fluids. J. Hydraul. Res. 2011, 49, 766–774. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Cowen, E.A. The direct and indirect measurement of boundary stress and drag on individual and complex arrays of elements. Exp. Fluid. 2013, 54, 1–16. [Google Scholar] [CrossRef]
- Fathi-Maghadam, M.; Kouwen, N.; Nonsubmerged, N. Vegetative Roughness on Floodplains. J. Hydraul. Eng. 1997, 123, 51–57. [Google Scholar] [CrossRef]
- Chen, Z.; Ortiz, A.; Zong, L.; Nepf, H.M. The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 2012, 48, W09517. [Google Scholar] [CrossRef]
- Mitul, L.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 2008, 8, 423–439. [Google Scholar] [CrossRef]
- Wu, F.-C.; Shen, H.W.; Chou, Y.-J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, 1–16. [Google Scholar] [CrossRef]
- Pu, J.H.; Wei, J.; Huang, Y. Velocity Distribution and 3D Turbulence Characteristic Analysis for Flow over Water-Worked Rough Bed. Water 2017, 9, 668. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Analytical model for predicting the longitudinal profiles of velocities in a channel with a model vegetation patch. J. Hydrol. 2019, 576, 561–574. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Yang, T.; Hua, Z.; Wang, Z.; Liu, J.; Li, R. Hydraulic Features of Flow through Local Non-Submerged Rigid Vegetation in the Y-Shaped Confluence Channel. Water 2019, 11, 146. [Google Scholar] [CrossRef]
- Heidari, M. Wake Characteristics of Single and Tandem Emergent Cylinders in Shallow Open Channel Flow. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2016. [Google Scholar]
- Nicolle, A.; Eames, I. Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 2011, 679, 1–31. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, WR005651. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M. Partially obstructed channel: Contraction ratio effect on the flow hydrodynamic structure and prediction of the transversal mean velocity profile. J. Hydrol. 2016, 542, 87–100. [Google Scholar] [CrossRef]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic Behavior of Partly Vegetated Open Channels. J. Hydraul. Eng. 1996, 122, 625–633. [Google Scholar] [CrossRef]
- Ikeda, S.; Yamada, T.; Toda, Y. Numerical study on turbulent flow and honami in and above flexible plant canopy. Int. J. Heat Fluid Flow 2001, 22, 252–258. [Google Scholar] [CrossRef]
- Kim, S.J.; Stoesser, T. Closure modelling and direct simulation of vegetation drag in flow through emergent vegetation. Water Resour. Res. 2011, 47, W10511. [Google Scholar] [CrossRef]
- Anjum, N.; Tanaka, N. Study on the flow structure around discontinued vertically layered vegetation in an open channel. J. Hydrodyn. 2019. [Google Scholar] [CrossRef]
- Yamasaki, T.N.; de Lima, P.H.; Silva, D.F.; Cristiane, G.D.A.; Janzen, J.G.; Johannes, G.; Nepf, H.M. From patch to channel scale: The evolution of emergent vegetation in a channel. Adv. Water Res. 2019, 129, 131–145. [Google Scholar] [CrossRef]
- Pu, J.H.; Hussain, A.; Guo, Y.; Vardakastanis, N.; Hanmaiahgari, R.; Lam, D. Submerged Flexible Vegetation Impact toward Open Channel Flow Velocity Distribution: An Analytical Modelling Study on Drag and Friction. Water Sci. Eng. 2019, 12, 121–128. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, Turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Musleh, F.; Cruise, J. Functional Relationships of Resistance in Wide Flood Plains with Rigid Unsubmerged Vegetation. J. Hydraul. Eng. 2006, 132, 163–171. [Google Scholar] [CrossRef]
- Maji, S.; Pal, D.; Hanmaiahgari, P.R.; Pu, J.H. Phenomenological Features of Turbulent Hydrodynamics in Sparsely Vegetated Open Channel Flow. J. Appl. Fluid Mech. 2016, 9, 2865–2875. [Google Scholar] [CrossRef]
- Pu, J.H.; Tait, S.; Guo, Y.; Huang, Y.; Hanmaiahgari, R. Dominant Features in Three-Dimensional Turbulence Structure: Comparison of Non-Uniform Accelerating and Decelerating Flows. Environ. Fluid Mech. 2018, 18, 395–416. [Google Scholar] [CrossRef]
- Maji, S.; Pal, D.; Hanmaiahgari, R.; Gupta, U. Hydrodynamics and turbulence in emergent and sparsely vegetated open channel flow. Environ. Fluid Mech. 2017, 17, 853–877. [Google Scholar] [CrossRef]
- Heidari, M.; Balachandar, R.; Roussinova, V.; Barron, R.M. Characteristics of flow past a slender, emergent cylinder in shallow open channels. Phys. Fluid. 2017, 29, 065111. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hashimoto, H.; Hayashi, K. Effect of tall vegetation on sediment transport by channel flows. J. Hydraul. Res. 2009, 47, 700–710. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth. Surf. Proc. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Baptist, M.J. Modelling Floodplain Biogeomorphology. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 2017, 17, 1035–1050. [Google Scholar] [CrossRef]
- Van Rooijen, A.; Lowe, R.; Ghisalberti, M.; Conde-Frias, M.; Tan, L. Predicting Current-Induced Drag in Emergent and Submerged Aquatic Vegetation Canopies. Front. Mar. Sci. 2018, 5, 449. [Google Scholar] [CrossRef]
- Wang, W.J.; Huaia, W.X.; Thompson, S.; Peng, W.Q.; Katul, G.G. Drag coefficient estimation using flume experiments in shallow non-uniform water flow within emergent vegetation during rainfall. Ecol. Indic. 2018, 92, 367–378. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, C.; Nepf, H. Comparison of drag and velocity in model mangrove forests with random and in-line tree distributions. J. Hydrol. 2019, 568, 735–746. [Google Scholar] [CrossRef]
- Razmi, A.; Chamecki, M.; Nepf, H.M. Efficient numerical representation of the impacts of flexible plant reconfiguration on canopy posture and hydrodynamic drag. J. Hydraul. Res. 2019. [Google Scholar] [CrossRef]
- Perucca, E.; Camporeale, C.; Ridolfi, L. Significance of the riparian vegetation dynamics on meandering river morphodynamics. Water Resour. Res. 2007, 43, W03430. [Google Scholar] [CrossRef]
- Motta, D.; Langendoen, E.J.; Abad, J.D.; García, M.H. Modification of meander migration by bank failures. J. Geophys. Res. Earth Surf. 2014, 119, 1026–1042. [Google Scholar] [CrossRef]
- Liu, D.; Valyrakis, M.; Williams, R. Flow Hydrodynamics across Open Channel Flows with Riparian Zones: Implications for Riverbank Stability. Water 2017, 9, 720. [Google Scholar] [CrossRef]
- Thorne, C.R. Effects of vegetation on riverbank erosion and stability. In Vegetation and Erosion; Thorne, J.B., Ed.; John Wiley and Sons: Chichester, UK, 1990; pp. 125–144. [Google Scholar]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth. Surf. Proc. Landf. 2010, 27, 527–546. [Google Scholar] [CrossRef]
- Hopkinson, L.; Wynn, T. Vegetation impacts on near bank flow. Ecohydrology 2009, 2, 404–418. [Google Scholar] [CrossRef]
- Baets, S.D.; Poesen, J.; Reubensm, B.; Wemans, J.; Baerdemaeker, D.; Muys, B. Root tensile strength and root distribution of typical Mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The effect of riparian tree roots on the mass-stability of riverbanks. Earth. Surf. Proc. Landf. J. Br. Geomorphol. Res. Group 2000, 25, 921–937. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Tal, M.; Paola, C. Effects of vegetation on channel morphodynamics: Results and insights from laboratory experiments. Earth. Surf. Proc. Landf. 2010, 35, 1014–1028. [Google Scholar] [CrossRef]
- Krzeminska, D.; Kerkhof, T.; Skaalsveen, K.; Stolte, J. Effect of riparian vegetation on stream bank stability in small agricultural catchments. Catena 2019, 172, 87–96. [Google Scholar] [CrossRef]
- Hupp, C.R.; Osterkamp, W.R. Riparian vegetation and fluvial geomorphic processes. Geomorphology 1996, 14, 277–295. [Google Scholar] [CrossRef]
- Tooth, S.; Nanson, G.C. The role of vegetation in the formation of anabranching channels in an ephemeral river, Northern Plains, arid central Australia. Hydrol. Process. 2000, 14, 3099–3117. [Google Scholar] [CrossRef]
- Micheli, E.R.; Kirchner, J.W.; Larsen, E.W. Quantifying the effect of riparian forest versus agricultural vegetation on river meander migration rates, central Sacramento river, California, USA. River Res. Appl. 2010, 20, 537–548. [Google Scholar] [CrossRef]
- Hickin, E.J. Vegetation and river channel dynamics. Can. Geogr. 1984, 28, 111–126. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A.; Collision, A.J.C. Advances in assessing the mechanical and hydrologic effect of riparian vegetation on streambank stability. Riparian Veg. Fluv. Geomorphol. 2004, 8, 125–139. [Google Scholar]
- Graf, W.L. Fluvial Processes in Dryland Rivers; Springer: Berlin, Germany, 1988. [Google Scholar]
- Birken, A.S.; Cooper, D.J. Processes of Tamarix invasion and floodplain development along the lower Green River Utah. Ecol. Appl. 2006, 16, 1103–1120. [Google Scholar] [CrossRef]
- Braudrick, C.A.; Dietrich, W.E.; Leverich, G.T.; Sklar, L.S. Experimental evidence for the conditions necessary to sustain meandering in coarse bedded rivers. Proc. Natl. Acad. Sci. USA 2009, 106, 16936–16941. [Google Scholar] [CrossRef] [PubMed]
- Camporeale, C.; Perucca, E.; Ridolfi, L.; Gurnell, A.M. Modeling the interactions between river morphodynamics and riparian vegetation. Rev. Geophys. 2013, 51, 379–414. [Google Scholar] [CrossRef]
- Gran, K.; Wartman, E.D. Co-evolution of riparian vegetation and channel dynamics in an aggrading braided river system, Mount Pinatubo. Philippines. Earth Surf. Proc. Landf. 2015, 40, 1101–1115. [Google Scholar] [CrossRef]
- Yu, M.-H.; Wei, H.-Y.; Wu, S.-B. Experimental study on the bank erosion and interaction with near-bank bed evolution due to fluvial hydraulic force. Int. J. Sediment Res. 2015, 30, 81–89. [Google Scholar] [CrossRef]
- Yang, J.Q.; Nepf, H.M. A turbulence-based bed-load transport model for bare and vegetated channels. Geophys. Res. Lett. 2018, 45, 10428–10436. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V. Bed-load through emergent vegetation. Adv. Water Resour. 2019, 129, 250–259. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V.; Righetti, M. A probabilistic/deterministic approach for the prediction of the sediment transport rate. Adv. Water Res. 2015, 81, 10–18. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; Technical Report No. 1026; U.S. Department of Agriculture: Washington, DC, USA, 1950.
- Rowiński, M.; Kubrak, J. A mixing-length model for predicting vertical velocity distribution in flows through emergent vegetation. Hydrol. Sci. J. 2002, 47, 893–904. [Google Scholar] [CrossRef]
- Rubol, S.; Ling, B.; Battiato, I. Universal scaling-law for flow resistance over canopies with complex morphology. Sci. Rep. 2018, 8, 4430. [Google Scholar] [CrossRef] [PubMed]
- Siniscalchi, F.; Nikora, V.I.; Aberle, J. Plant patch hydrodynamics in streams: Mean flow, turbulence, and drag forces. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Modeling the flow resistance of woody vegetation using physically based properties of the foliage and stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Rowiński, M.; Giugni, M. Turbulence at water-vegetation interface in open channel flow: Experiments with natural-like plants. Adv. Water Resour. 2019, 127, 180–191. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res. Earth Surf. 2013, 118, 42–53. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, C.L.; Dancey, K.; Greer, K.; Celik, A.O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef]
- Licci, S.; Nepf, H.M.; Delolme, C.; Marmonier, P.; Bouma, T.J.; Puijalon, S. The role of patch size in ecosystem engineering capacity: A case study of aquatic vegetation. Aquat. Sci. 2019, 81. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).