The Costs of Sea-Level Rise: Coastal Adaptation Investments vs. Inaction in Iberian Coastal Cities
Abstract
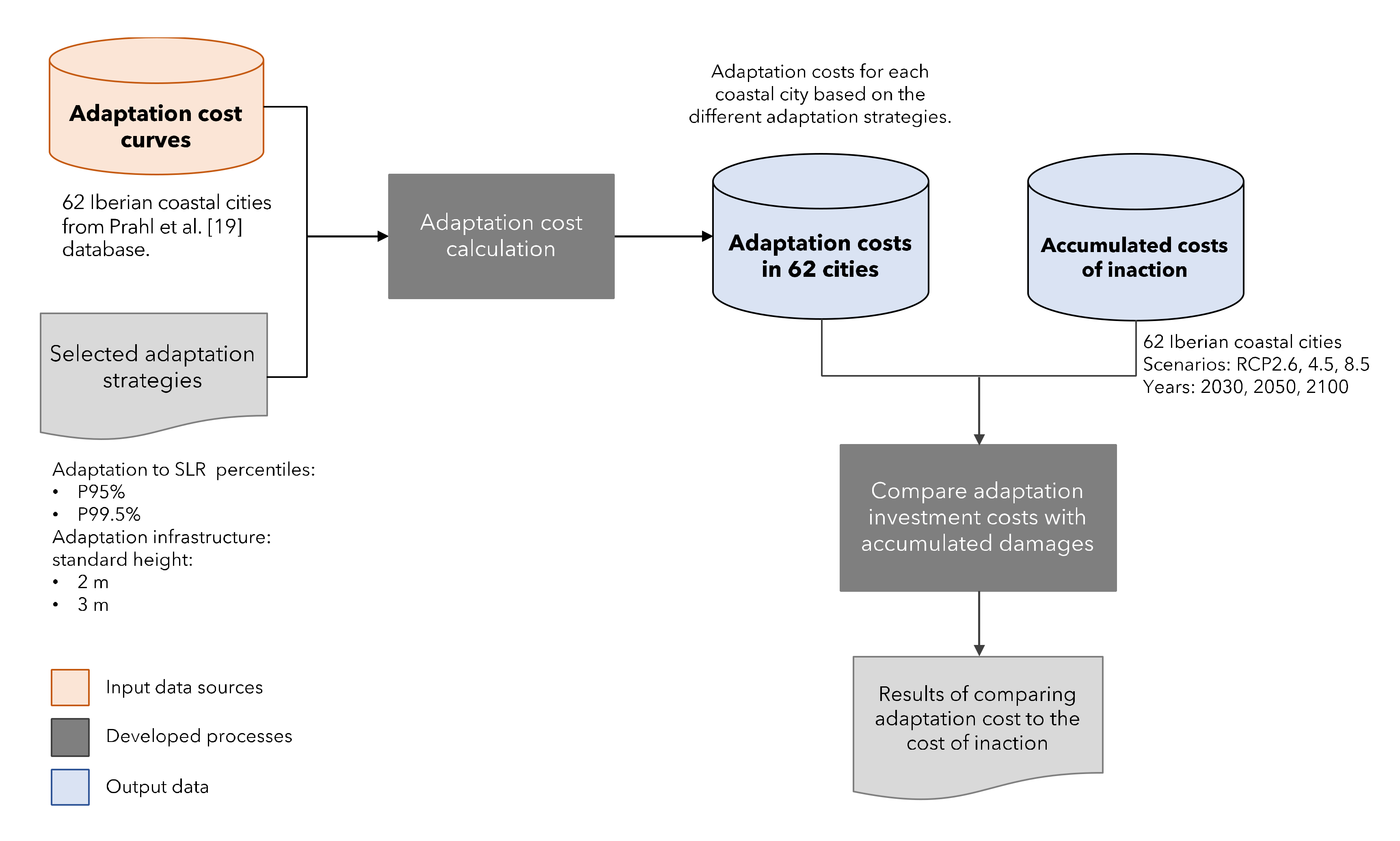
:1. Introduction
2. The Impacts of and Adaptation to Sea-Level Rise in the Iberian Peninsula
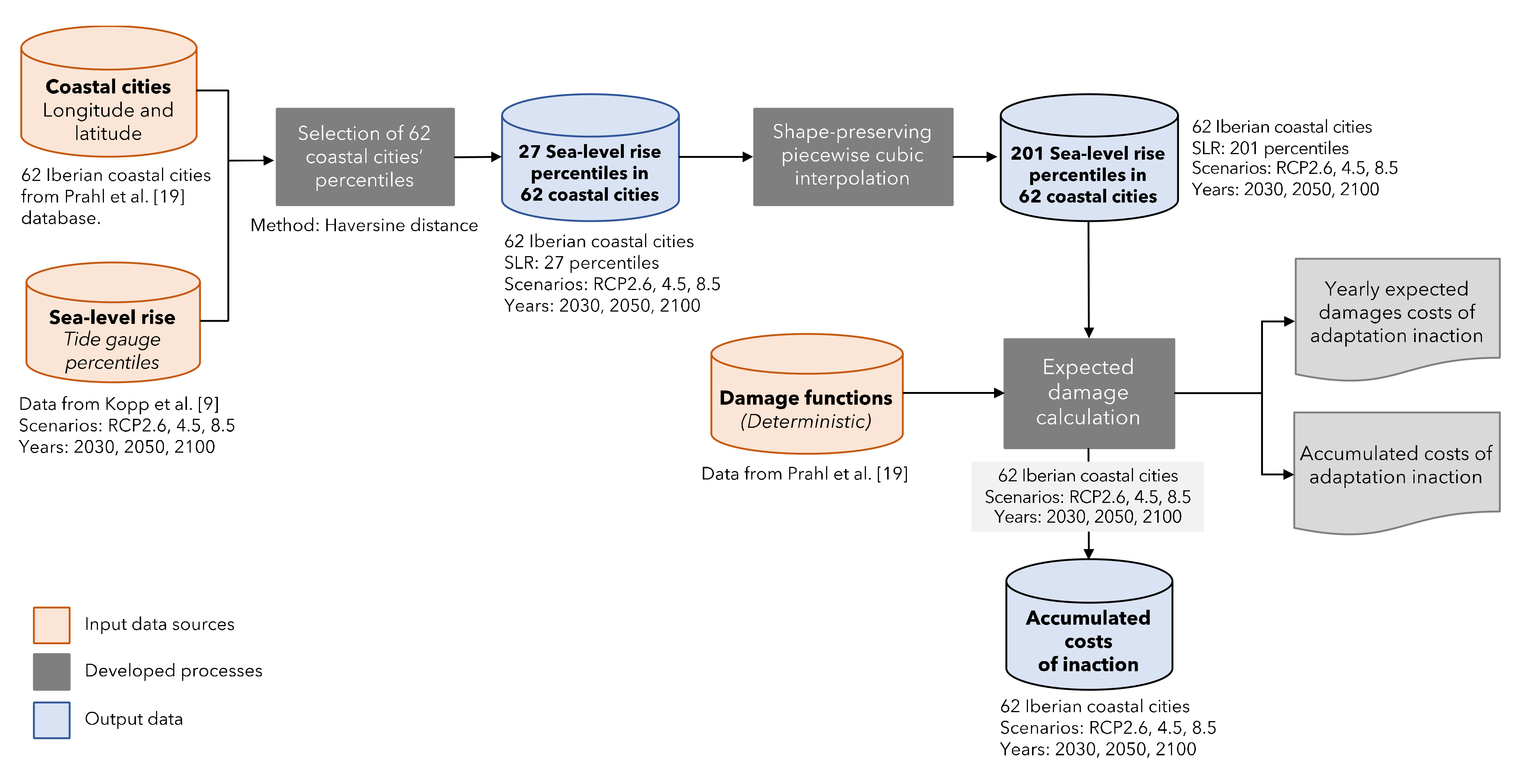
3. Materials and Methods
3.1. Estimating the Costs of Adaptation Inaction
3.1.1. Modelling Projected Sea-Level Rise in Each City
3.1.2. Estimation of Economic Damage
3.2. Measuring the Investment Costs of Adaptation
- The first strategy aims at reducing climate change risk, for example by building a defence that can only be overcome in a certain percentage of the cases by a given year under one of the RCP scenarios. In this case we have defined 5% and 0.5% of the cases by the year 2100 under RCP 8.5. In other words, this option requires building an infrastructure to protect from sea-level rise percentiles 95th and 99.5th. We have named this strategy as “risk tailoring”.
- The second strategy consists of building defences of standard height (e.g., 2 m or 3 m) and comparing the protection level and costs with the “risk tailoring” strategy.
4. Results
4.1. Local Sea-Level Rise and the Costs of Inaction
4.2. Adaptation Strategies and Investment Costs
4.2.1. Adapting to the Risk of Sea-Level Rise or “Risk Tailoring”
4.2.2. Adapting by Fixing a Certain Height
5. Discussion
5.1. The Economic Damage of Sea-Level Rise
5.2. Comparing the Costs of Inaction to Protection Investment Costs
5.3. Policy Implications
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. IPCC Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Church, J.A.; White, N.J.; Aarup, T.; Wilson, W.S.; Woodworth, P.L.; Domingues, C.M.; Hunter, J.R.; Lambeck, K. Understanding global sea levels: Past, present and future. Sustain. Sci. 2008, 3, 9–22. [Google Scholar] [CrossRef] [Green Version]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Sun, W.; Heki, K.; Qian, A. An increase in the rate of global mean sea level rise since 2010. Geophys. Res. Lett. 2015, 42, 3998–4006. [Google Scholar] [CrossRef] [Green Version]
- Hardy, R.D.; Nuse, B.L. Global sea-level rise: Weighing country responsibility and risk. Clim. Change 2016, 137, 333–345. [Google Scholar] [CrossRef]
- Hamlington, B.D.; Fasullo, J.T.; Nerem, R.S.; Kim, K.-Y.; Landerer, F.W. Uncovering the Pattern of Forced Sea Level Rise in the Satellite Altimeter Record. Geophys. Res. Lett. 2019, 46, 4844–4853. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Carson, M.; Katsman, C.A.; Wal, R.S.W.; van de Köhl, A.; Vermeersen, L.L.A.; Stammer, D. Projecting twenty-first century regional sea-level changes. Clim. Chang. 2014, 124, 317–332. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earths Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Grinsted, A.; Jevrejeva, S.; Riva, R.; Dahl-Jensen, D. Sea level rise projections for northern Europe under RCP8.5. Clim. Res. 2015, 64, 15–23. [Google Scholar] [CrossRef] [Green Version]
- Jackson, L.P.; Jevrejeva, S. A probabilistic approach to 21st century regional sea-level projections using RCP and High-end scenarios. Glob. Planet. Chang. 2016, 146, 179–189. [Google Scholar] [CrossRef] [Green Version]
- Nauels, A.; Gütschow, J.; Mengel, M.; Meinshausen, M.; Clark, P.U.; Schleussner, C.-F. Attributing long-term sea-level rise to Paris Agreement emission pledges. Proc. Natl. Acad. Sci. USA 2019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bamber, J.L.; Oppenheimer, M.; Kopp, R.E.; Aspinall, W.P.; Cooke, R.M. Ice sheet contributions to future sea-level rise from structured expert judgment. Proc. Natl. Acad. Sci. USA 2019, 116, 11195–11200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- IPCC. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Mintenbeck, K., Nicolai, M., Okem, A., Petzold, J., Rama, B., et al., Eds.; IPCC: Geneva, Switzerland, 2019; In press. [Google Scholar]
- Ciscar, J.C.; Ibarreta, D.; Soria, A.; Dosio, A.; Toreti, A.; Ceglar, A.; Fumagalli, D.; Dentener, F.; Lecerf, R.; Zucchini, A.; et al. Climate Impacts in Europe: Final Report of the JRC PESETA III Project; European Commission: Luxenbourg, 2018; p. 95. [Google Scholar]
- Wong, P.P.; Losada, I.J.; Gattuso, J.P.; Hinkel, J.; Khattabi, A.; McInnes, K.L.; Saito, Y.; Sallenger, A. Coastal systems and low-lying areas. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 361–409. [Google Scholar]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Bianchi, A.; Dottori, F.; Feyen, L. Climatic and socioeconomic controls of future coastal flood risk in Europe. Nat. Clim. Chang. 2018, 8, 776–780. [Google Scholar] [CrossRef]
- Sánchez-Arcilla, A.; García-León, M.; Gracia, V.; Devoy, R.; Stanica, A.; Gault, J. Managing coastal environments under climate change: Pathways to adaptation. Sci. Total Environ. 2016, 572, 1336–1352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prahl, B.F.; Boettle, M.; Costa, L.; Kropp, J.P.; Rybski, D. Damage and protection cost curves for coastal floods within the 600 largest European cities. Sci. Data 2018, 5, 180034. [Google Scholar] [CrossRef]
- Weitzman, M.L. A precautionary tale of uncertain tail fattening. Environ. Resour. Econ. 2013, 55, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Hinkel, J.; Jaeger, C.; Nicholls, R.J.; Lowe, J.; Renn, O.; Peijun, S. Sea-level rise scenarios and coastal risk management. Nat. Clim. Chang. 2015, 5, 188–190. [Google Scholar] [CrossRef]
- Thiéblemont, R.; Le Cozannet, G.; Toimil, A.; Meyssignac, B.; Losada, I.J. Likely and High-End Impacts of Regional Sea-Level Rise on the Shoreline Change of European Sandy Coasts Under a High Greenhouse Gas Emissions Scenario. Water 2019, 11, 2607. [Google Scholar] [CrossRef] [Green Version]
- Abadie, L.M.; Galarraga, I.; Sainz de Murieta, E. Understanding risks in the light of uncertainty: Low-probability, high-impact coastal events in cities. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Abadie, L.M.; Sainz de Murieta, E.; Galarraga, I. Investing in adaptation: Flood risk and real option application to Bilbao. Environ. Model. Softw. 2017, 95, 76–89. [Google Scholar] [CrossRef] [Green Version]
- Galarraga, I.; Sainz de Murieta, E.; Markandya, A.; Abadie, L.M. Addendum to Understanding risks in the light of uncertainty: Low-probability, high-impact coastal events in cities. Environ. Res. Lett. 2018, 13, 029401. [Google Scholar] [CrossRef]
- Losada, I.J.; Toimil, A.; Muñoz, A.; Garcia-Fletcher, A.P.; Diaz-Simal, P. A planning strategy for the adaptation of coastal areas to climate change: The Spanish case. Ocean. Coast. Manag. 2019, 104983. [Google Scholar] [CrossRef]
- Galarraga, I.; Osés, N.; Markandya, A.; Chiabai, A.; Khatun, K. Aportaciones desde la economía de la adaptación a la toma de decisiones sobre Cambio Climático: Un ejemplo para la Comunidad Autónoma del País Vasco. Econ. Agrar. Recur. Nat. 2011, 11, 113–142. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Morales, A.; Gil-Guirado, S.; Olcina-Cantos, J. Housing bubbles and the increase of flood exposure. Failures in flood risk management on the Spanish south-eastern coast (1975–2013): Housing bubbles and increase of flood risk in Spain. J. Flood Risk Manag. 2015, 11, S302–S313. [Google Scholar] [CrossRef]
- Satta, A.; Puddu, M.; Venturini, S.; Giupponi, C. Assessment of coastal risks to climate change related impacts at the regional scale: The case of the Mediterranean region. Int. J. Disaster Risk Reduct. 2017, 24, 284–296. [Google Scholar] [CrossRef]
- Losada, I.J.; Izaguirre, C.; Díaz, P. Cambio Climático en la Costa Española; Oficina Española de Cambio Climático, Ministerio de Agricultura, Alimentación y Medio Ambiente: Madrid, Spain, 2014; p. 133. [Google Scholar]
- Mendoza, E.T.; Jimenez, J.A.; Mateo, J. A coastal storms intensity scale for the Catalan sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef] [Green Version]
- Freitas, M.C.; Andrade, C.; Cachado, C.; Cardoso, A.C.; Monteiro, J.H.; Brito, P.; Rebelo, L. Coastal land-loss associated with sea-level rise assessed by aerial Videotape-Assisted Vulnerability Analysis—The case of mainland Portugal. J. Coast. Res. 2006, 1310–1315. [Google Scholar]
- Gornitz, V. Global coastal hazards from future sea level rise. Glob. Planet. Change 1991, 3, 379–398. [Google Scholar] [CrossRef]
- Pereira, C.; Coelho, C. Mapping erosion risk under different scenarios of climate change for Aveiro coast, Portugal. Nat. Hazards 2013, 69, 1033–1050. [Google Scholar] [CrossRef]
- Ferreira, O.; Viavattene, C.; Jiménez, J.; Bole, A.; Plomaritis, T.; Costas, S.; Smets, S. CRAF Phase 1, a framework to identify coastal hotspots to storm impacts. E3S Web Conf. 2016, 7, 11008. [Google Scholar] [CrossRef] [Green Version]
- Viavattene, C.; Jiménez, J.A.; Ferreira, O.; Priest, S.; Owen, D.; McCall, R. Selecting coastal hotspots to storm impacts at the regional scale: A Coastal Risk Assessment Framework. Coast. Eng. 2018, 134, 33–47. [Google Scholar] [CrossRef]
- Rocha, C.; Antunes, C.; Catita, C. Coastal Vulnerability Assessment Due to Sea Level Rise: The Case Study of the Atlantic Coast of Mainland Portugal. Water 2020, 12, 360. [Google Scholar] [CrossRef] [Green Version]
- Antunes, C. Assessment of Sea Level Rise at West Coast of Portugal Mainland and Its Projection for the 21st Century. J. Mar. Sci. Eng. 2019, 7, 61. [Google Scholar] [CrossRef] [Green Version]
- Semeoshenkova, V.; Newton, A. Overview of erosion and beach quality issues in three Southern European countries: Portugal, Spain and Italy. Ocean. Coast. Manag. 2015, 118, 12–21. [Google Scholar] [CrossRef]
- Abadie, L.M.; Galarraga, I.; Markandya, A.; Sainz de Murieta, E. Risk measures and the distribution of damage curves for 600 European coastal cities. Environ. Res. Lett. 2019, 14, 064021. [Google Scholar] [CrossRef]
- Huizinga, J.; De Moel, H.; Szewczyk, W. Global Flood Depth-Damage Functions. Methodology and the Database with Guidelines; European Commission: Luxembourg, 2017; p. 114. [Google Scholar]
- Abadie, L.M.; Chamorro, J.M. Income risk of EU coal-fired power plants after Kyoto. Energy Policy 2009, 37, 5304–5316. [Google Scholar] [CrossRef] [Green Version]
- Weitzman, M.L. On modeling and interpreting the economics of catastrophic climate change. Rev. Econ. Stat. 2009, 91, 1–19. [Google Scholar] [CrossRef]
- Stern, N. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Gollier, C. Pricing the Planet’s Future: The Economics of Discounting in an Uncertain World; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Groom, B. Discounting. In Routledge Handbook of the Economics of Climate Change Adaptation; Markandya, A., Galarraga, I., Sainz de Murieta, E., Eds.; Routledge International Handbooks: Oxon, UK; New York, NY, USA, 2014; pp. 138–168. ISBN 978-0-415-63311-6. [Google Scholar]
- Drupp, M.A.; Freeman, M.C.; Groom, B.; Nesje, F. Discounting Disentangled. Am. Econ. J. Econ. Policy 2018, 10, 109–134. [Google Scholar] [CrossRef] [Green Version]
- Markanday, A.; Galarraga, I.; Chiabai, A.; Sainz de Murieta, E.; Lliso, B.; Markandya, A. Determining discount rates for the evaluation of natural assets in land-use planning: An application of the Equivalency Principle. J. Clean. Prod. 2019, 230, 672–684. [Google Scholar] [CrossRef]
- Abadie, L.M. Sea level damage risk with probabilistic weighting of IPCC scenarios: An application to major coastal cities. J. Clean. Prod. 2018, 175, 582–598. [Google Scholar] [CrossRef]
- TEEB. The Economics of Ecosystems and Biodiversity: Ecological and Economic Foundations; Kumar, P., Ed.; Earthscan: London, UK, 2010; ISBN 978-1-84971-212-5. [Google Scholar]
- Costanza, R.; de Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Lima, M.; Coelho, C.; Veloso-Gomes, F.; Roebeling, P. An integrated physical and cost-benefit approach to assess groins as a coastal erosion mitigation strategy. Coast. Eng. 2020, 156, 103614. [Google Scholar] [CrossRef]
- Coelho, C.; Cruz, T.; Roebeling, P. Longitudinal revetments to mitigate overtopping and flooding: Effectiveness, costs and benefits. Ocean. Coast. Manag. 2016, 134, 93–102. [Google Scholar] [CrossRef]
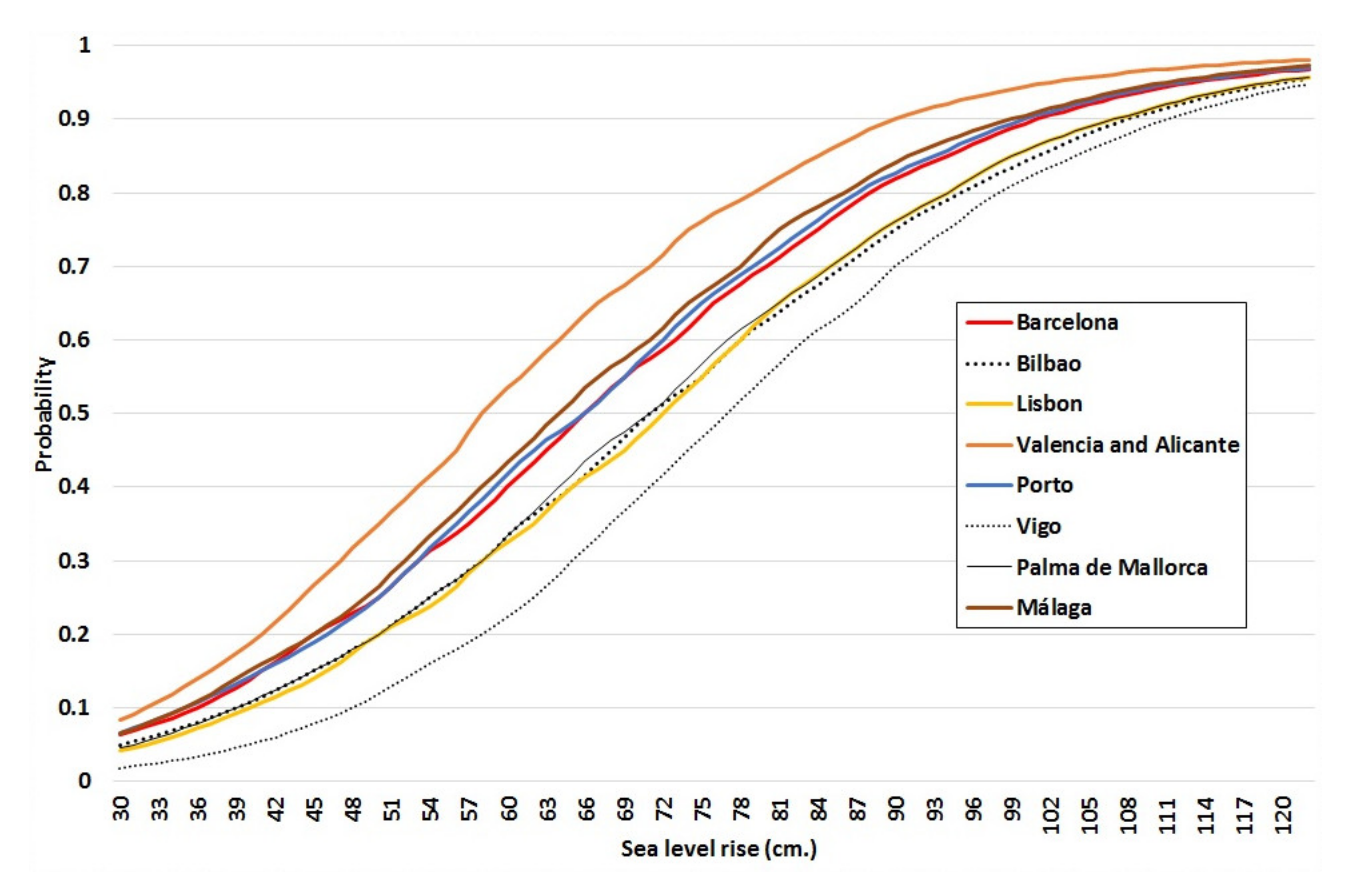
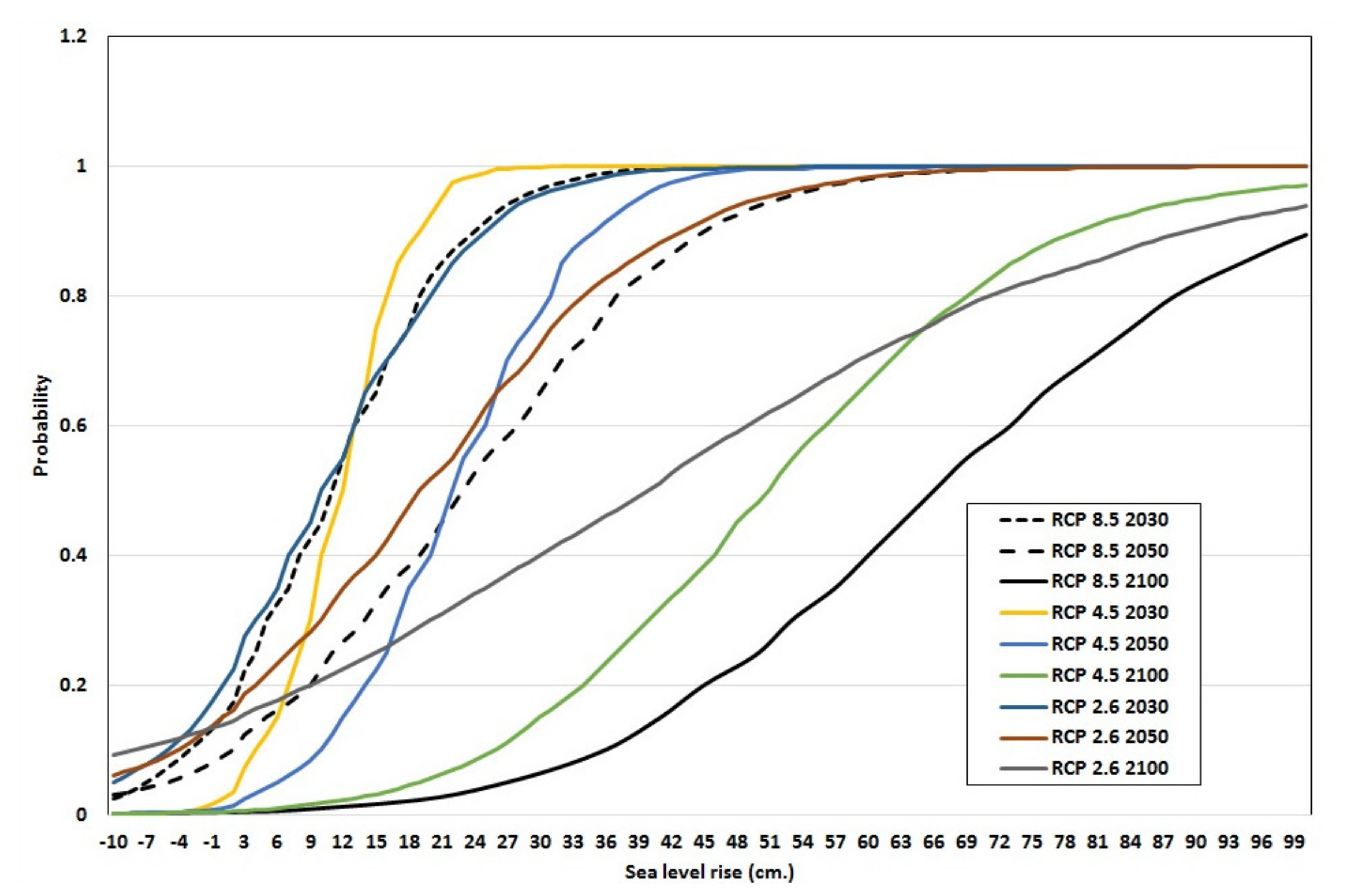


| City | Year | P50 (cm) | P95 (cm) | P99.5 (cm) | Damage (million EUR) |
|---|---|---|---|---|---|
| Barcelona | 2030 | 11 | 28 | 39 | 75.8 |
| Lisbon | 2030 | 13 | 21 | 26 | 34.5 |
| Valencia | 2030 | 10 | 18 | 24 | 79.4 |
| Porto | 2030 | 12 | 20 | 24 | 22.1 |
| Bilbao | 2030 | 14 | 23 | 29 | 177.0 |
| Málaga | 2030 | 11 | 20 | 25 | 28.3 |
| Palma de Mallorca | 2030 | 12 | 30 | 41 | 48.0 |
| Alicante | 2030 | 10 | 18 | 24 | 32.3 |
| Vigo | 2030 | 15 | 23 | 27 | 21.3 |
| Gijón | 2030 | 14 | 23 | 30 | 35.4 |
| Barcelona | 2050 | 23 | 52 | 71 | 343.1 |
| Lisbon | 2050 | 26 | 42 | 53 | 150.0 |
| Valencia | 2050 | 21 | 36 | 47 | 365.8 |
| Porto | 2050 | 24 | 39 | 51 | 98.8 |
| Bilbao | 2050 | 27 | 45 | 57 | 806.4 |
| Málaga | 2050 | 23 | 38 | 50 | 132.8 |
| Palma de Mallorca | 2050 | 25 | 52 | 70 | 201.1 |
| Alicante | 2050 | 21 | 36 | 47 | 159.2 |
| Vigo | 2050 | 30 | 45 | 56 | 89.4 |
| Gijón | 2050 | 27 | 45 | 58 | 155.8 |
| Barcelona | 2100 | 66 | 113 | 171 | 2059.5 |
| Lisbon | 2100 | 72 | 119 | 181 | 946.3 |
| Valencia | 2100 | 58 | 102 | 161 | 2504.3 |
| Porto | 2100 | 66 | 112 | 174 | 601.7 |
| Bilbao | 2100 | 71 | 120 | 180 | 4592.3 |
| Málaga | 2100 | 64 | 111 | 168 | 831.9 |
| Palma de Mallorca | 2100 | 71 | 119 | 176 | 1288.4 |
| Alicante | 2100 | 58 | 102 | 161 | 991.2 |
| Vigo | 2100 | 77 | 123 | 184 | 550.9 |
| Gijón | 2100 | 72 | 122 | 182 | 944.9 |
| City | Values | 2030 | 2050 | 2100 |
|---|---|---|---|---|
| Barcelona | Expected damage (A) | 8.76 | 18.00 | 52.93 |
| Damage using 50th percentile (B) | 8.25 | 17.24 | 49.00 | |
| Difference in damage (A−B) | 0.52 | 0.75 | 3.93 | |
| Skewness | −0.03 | 0.00 | 3.67 | |
| Lisbon | Expected damage (A) | 3.84 | 7.81 | 25.36 |
| Damage using 50th percentile (B) | 3.79 | 7.58 | 23.23 | |
| Difference in damage (A−B) | 0.05 | 0.23 | 2.13 | |
| Skewness | −0.09 | 0.65 | 3.88 | |
| Valencia | Expected damage (A) | 9.05 | 19.94 | 70.54 |
| Damage using 50th percentile (B) | 9.33 | 19.58 | 58.53 | |
| Difference in damage (A−B) | −0.28 | 0.36 | 12.01 | |
| Skewness | −0.06 | 0.62 | 4.41 | |
| Porto | Expected damage (A) | 2.53 | 5.16 | 15.55 |
| Damage using 50th percentile (B) | 2.54 | 5.09 | 14.55 | |
| Difference in damage (A−B) | −0.01 | 0.07 | 1.00 | |
| Skewness | 0.01 | 0.73 | 4.05 | |
| Bilbao | Expected damage (A) | 20.78 | 41.82 | 110.93 |
| Damage using 50th percentile (B) | 21.41 | 41.28 | 105.04 | |
| Difference in damage (A−B) | −0.63 | 0.54 | 5.89 | |
| Skewness | −0.18 | 0.38 | 3.47 |
| Country | Scenario | 2030 | 2050 | 2100 |
|---|---|---|---|---|
| Total Iberian | RCP 8.5 | 1764 | 8100 | 50,476 |
| Spain | 1574 | 7261 | 45,342 | |
| Portugal | 189 | 839 | 5133 | |
| Total Iberian | RCP 4.5 | 1718 | 7588 | 41,261 |
| Spain | 1536 | 6796 | 37,044 | |
| Portugal | 183 | 792 | 4216 | |
| Total Iberian | RCP 2.6 | 1732 | 7474 | 36,895 |
| Spain | 1545 | 6684 | 33,089 | |
| Portugal | 188 | 789 | 3806 |
| City | Accumulated Damage | Sea-Level Rise (cm) | Adaptation costs | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Average | |||||||
| P95 | P99.5 | P95 | P99.5 | P95 | P99.5 | P95 | P99.5 | ||
| Barcelona | 2060 | 113 | 171 | 318 | 595 | 459 | 859 | 388 | 727 |
| Lisbon | 946 | 119 | 181 | 223 | 425 | 323 | 614 | 273 | 520 |
| Valencia | 2504 | 102 | 161 | 326 | 645 | 472 | 932 | 399 | 788 |
| Porto | 602 | 112 | 174 | 87 | 164 | 126 | 236 | 106 | 200 |
| Bilbao | 4592 | 120 | 180 | 424 | 702 | 613 | 1,015 | 518 | 858 |
| Málaga | 832 | 111 | 168 | 127 | 221 | 184 | 319 | 155 | 270 |
| Palma de Mallorca | 1288 | 119 | 176 | 240 | 531 | 347 | 767 | 293 | 649 |
| Alicante | 991 | 102 | 161 | 164 | 289 | 237 | 417 | 200 | 353 |
| Vigo | 551 | 123 | 184 | 154 | 283 | 223 | 409 | 189 | 346 |
| Gijón | 945 | 122 | 182 | 211 | 348 | 305 | 503 | 258 | 425 |
| City | Accumulated Damage | Adaptation costs | |||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Average | |||||
| 2 m | 3 m | 2 m | 3 m | 2 m | 3 m | ||
| Barcelona | 2060 | 758 | 1434 | 1096 | 2072 | 927 | 1753 |
| Lisbon | 946 | 491 | 947 | 710 | 1369 | 601 | 1158 |
| Valencia | 2504 | 873 | 1638 | 1262 | 2368 | 1067 | 2003 |
| Porto | 602 | 201 | 404 | 291 | 584 | 246 | 494 |
| Bilbao | 4592 | 799 | 1343 | 1156 | 1942 | 978 | 1642 |
| Málaga | 832 | 279 | 496 | 404 | 717 | 341 | 607 |
| Palma de Mallorca | 1288 | 712 | 1342 | 1029 | 1940 | 870 | 1641 |
| Alicante | 991 | 378 | 644 | 547 | 931 | 463 | 787 |
| Vigo | 551 | 319 | 614 | 461 | 888 | 390 | 751 |
| Gijón | 945 | 391 | 660 | 565 | 955 | 478 | 808 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abadie, L.M.; Sainz de Murieta, E.; Galarraga, I. The Costs of Sea-Level Rise: Coastal Adaptation Investments vs. Inaction in Iberian Coastal Cities. Water 2020, 12, 1220. https://doi.org/10.3390/w12041220
Abadie LM, Sainz de Murieta E, Galarraga I. The Costs of Sea-Level Rise: Coastal Adaptation Investments vs. Inaction in Iberian Coastal Cities. Water. 2020; 12(4):1220. https://doi.org/10.3390/w12041220
Chicago/Turabian StyleAbadie, Luis Maria, Elisa Sainz de Murieta, and Ibon Galarraga. 2020. "The Costs of Sea-Level Rise: Coastal Adaptation Investments vs. Inaction in Iberian Coastal Cities" Water 12, no. 4: 1220. https://doi.org/10.3390/w12041220
APA StyleAbadie, L. M., Sainz de Murieta, E., & Galarraga, I. (2020). The Costs of Sea-Level Rise: Coastal Adaptation Investments vs. Inaction in Iberian Coastal Cities. Water, 12(4), 1220. https://doi.org/10.3390/w12041220







