Abstract
Modelling of hydrological extremes and drought modelling in particular has received much attention over recent decades. The main aim of this study is to apply a statistical model for drought estimation (in this case deficit volume) using extreme value theory and the index-flood method and to reduce the uncertainties in estimation of drought event return levels. Deficit volumes for 133 catchments in the Czech Republic (1901–2015) were simulated by hydrological model BILAN. The validation of severity, intensity and length of simulated drought events revealed good match with the available observed data. To estimate return levels of the deficit volumes, it is assumed (in accord with the index-flood method), that the deficit volumes within a homogeneous region are identically distributed after scaling with a site-specific factor. The parameters of the scaled regional distribution are estimated using L-moments. The goodness-of-fit of the statistical model is assessed by Anderson–Darling test. For the estimation of critical values, sampling methods allowing for handling of years without drought were used. It is shown, that the index-flood model with a Generalized Pareto distribution performs well and substantially reduces the uncertainty related to the estimation of the shape parameter and of the large deficit volume quantiles.
1. Introduction
Central Europe recently experienced a number severe drought events (e.g., 2000, 2003, 2015, 2018; e.g., [1,2,3]). These events attracted public, media and scientific attention as well as stimulated drought research, development of drought legislation and adaptation strategies. Many of these activities require assessment of drought characteristics (like severity, intensity, duration and frequency). While these characteristics are routinely estimated for heavy precipitation events and floods (e.g., [4,5,6,7]), the applications in the drought context are less common.
This could be at least partly attributed to the vague definition of drought potentially leading to contradicting assessments. A common definition of such drought is the deficit of water with respect to variable of interest or specific water use.
Drought can be identified and quantified using various drought indices, which use different variables for its estimation. The most widely used are the Palmer Drought Severity Index (PDSI) [8,9], with temperature and precipitation as an input; the Standardized Precipitation Index (SPI) [10] using only precipitation; the Standardized Precipitation Evapotranspiration index (SPEI) [11] facilitating both the sensitivity of PDSI and the simplicity of the SPI calculation; and the Reconnaissance Drought Index (RDI) [12] incorporating directly potential evapotranspiration. Ref. [13] compared the ten most widely used meteorological drought indices and tracked the indicated effect of drought on streamflow.
Here we are focusing on hydrological drought. Ref. [14] distinguished streamflow droughts and low flows; low flows are normally experienced during a drought, but they feature only one element of the drought, i.e., drought intensity. However, other characteristics of a drought event, such as cumulative deficit volume of an event or event duration, are also of interest for water management.
Another modification of SPI was made by [15], introducing an analogous approach for streamflow and thus capturing the hydrological droughts. One of the first studies modelling hydrological droughts via deficit volumes was made by [16]. Ref. [17] offered a review of multiple climatological and hydrological parameters concerning drought and summarized drought modelling methods in [18]. Ref. [19] performed streamflow and hydrological drought trend analysis using Streamflow Drought Index (SDI) [15]. Ref. [20] used Generalized Extreme Value distribution, Generalized Pareto, three-parameter lognormal and Pearson type III distributions to describe drought durations and deficit volumes. This study did not add much in the context of different drought indices discussed here, but it is important for the discussion of which distribution function to use to estimate large quantiles of said variables.
Since drought is a phenomenon that needs a long period of time to evolve and is an intermittent process, another limitation is usually short length of available observed data [21]. Due to the rarity of extreme events, modelling of drought extremes is related to large uncertainties. One possible way how to prolong the study period is the use reconstructed climate fields or climate models to obtain sufficient period length, this may however introduce new uncertainty. To cope with the uncertainty issue, it is desirable to employ methods such as regional frequency analysis [22].
Regional frequency analysis (RFA) uses spatial pooling of data from a homogeneous region to reduce the standard error of the estimates, i.e., it trades time for space. The vast majority of its applications is for runoff (e.g., [23,24]), precipitation (e.g., [25,26,27]) or temperature maxima (e.g., [28]), while the applications in the drought context are rare. Some noteworthy exceptions are [29] who carried out RFA of deficit runoff volumes, or [30] who presented regional analysis of low flows over South China. The RFA method based on L-moments was carried out by [31] and [32].
Here we show the application of an (RFA) model based on L-moments for estimation of drought characteristics, more specifically the distribution of maximum deficit volumes for the period 1900–2015 over the Czech Republic. The model aims at reduction of uncertainty in the estimated return levels, in the periods of drought events and in the parameters of the extremal model. The goodness-of-fit of the model is evaluated through discordance analysis, as well as the Anderson–Darling test, with the critical values estimated by a bootstrap procedure.
2. Study Area—Czech Republic
Although Czech Republic is a small country in central Europe, weather conditions differs markedly among its various regions. The variability of the weather is strongly driven by the unstable location and magnitude of two main pressure centres. In particular during the warm period of the year, the expansion of the high pressure projection into Czech Republic causes warmer temperatures and dry weather, whereas the Icelandic Low manifests itself with a greater number of atmospheric fronts bringing more clouds and precipitation.
The average air temperature is strongly dependent on the altitude and ranges from 0.4 °C on the highest elevation point (mountain Sněžka; 1603 m) to almost 10 °C in the lowlands of southeast Moravia. The annual rainfall is also strongly dependent on the altitude and orography. The wettest areas are the mountain ranges with steep slopes facing northwest in Jizerské hory (Jizera Mountains) with average total rainfall exceeding 1700 millimetres. On the other hand, the driest regions are the lowlands in southeast Moravia and northwest Bohemia receiving approximately 400 mm on average (the latter is influenced by rain shadow east of the Krušné hory (Ore Mountains) Figure 1 left.
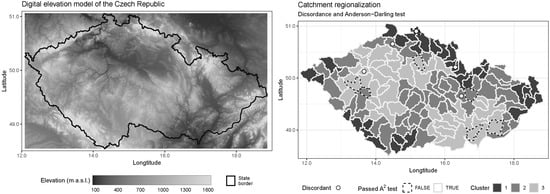
Figure 1.
(Left panel): Digital Elevation model of the Czech Republic; (Right panel): Resulting clusters, discordance measure and results of at-site A2 test.
For the purpose of the study we considered all of the 133 catchments defined by [33] covering the entirety of the Czech Republic (Figure 1 right) with respective areas ranging from 154 to 1928 km2. The catchments are based on hydrological division of the Czech Republic as provided by the Czech Hydrometeorological Institute, which is also considered in the application of water management policies.
3. Data and Methods
3.1. Data
Since 80 out of the 133 catchments over the study area are ungauged, we used the BILAN hydrological model [34,35,36,37] to estimate runoff from each catchment. BILAN has been frequently applied in various hydrological studies, as well as for the assessment of possible climate change impacts on water resources in the Czech Republic [38,39,40,41]. It is a lumped hydrological model for assessment of water balance components in monthly or daily step. The catchment is schematized as a system of reservoirs and flows, with catchment precipitation, air temperature and relative air humidity as inputs and total streamflow as output.
Precipitation and air temperature from the HadCRU-TS3.21 [42] dataset was used for the period 1900–1960 and the gridded data-set of precipitation and temperature provided by [43] for the period 1961–2015. The latter is derived from a larger number of stations and therefore the HadCRU-TS3.21 dataset was adjusted to have same monthly mean over the period 1961–2015. The gridded data were transferred to the river catchment areas using a weighted average, with weights proportional to the area of the intersection between the catchment and grid boxes.
Since the spatial resolution of the gridded data set used for derivation of catchment precipitation and temperature might be too coarse for smaller catchments with large altitude differences, the mean monthly catchment precipitation and temperature were finally corrected for error in long-term mean (1980–2010) by comparing the long-term average of the derived catchment data with long-term average precipitation and temperature calculated from fine-scale (1 km) gridded product provided by Czech Hydrometeorological Institute [44].
The BILAN model simulates water balance at three vertical levels: on the land surface, in the soil layer and in groundwater aquifer. The three water balance algorithms that are applied were developed for winter conditions, snow melting and summer conditions. Surface water balance depends on evapotranspiration, which is derived using temperature based empirical formula derived by [45]. Excess water (precipitation minus evapotranspiration) forms direct runoff or infiltrates to a deeper zone, where it is divided into interflow and groundwater recharge [38].
To estimate water balance at ungauged catchments, we used a database of calibrated BILAN models available for more than 300 catchments in the Czech Republic. For each catchment of interest we transferred models from catchments intersecting the catchment area. The simulated runoff for the catchment of interest was calculated as a weighted average of runoff from transferred models. The weights were proportional to the area of intersection between the catchment of interest and the transferred model. Thus, for each catchment a time series for the period 1900–2015 was obtained.
Drought Definition
To analyze drought characteristics, a cumulative deficit volume below a pre-selected threshold is considered [46,47,48]. The volume was first developed by [49] and later extended and summarized by [50]. An early application in hydrology includes [51], where the method is based on the statistical theory of runs for analyzing a sequential time series.
The threshold level is either representing a certain water demand, e.g., power plants or water supply, or the boundary between normal and unusually low stream flow conditions. The threshold level can be fixed or varying over the year to reflect seasonal variability of hydrological regime or water demands, and can be chosen in a number of ways.
In the present study a varying monthly 80% quantile of the flow exceedance curve was chosen, similarly to [52] or [53]. Basic characteristics describing the deficit event include:
- event severity (deficit volume), D [mm or m3];
- event length, L [months];
- event intensity, [mm/month or m3/month];
- relative severity (i.e., deficit volume to monthly runoff ratio), [-];
- relative event intensity, [t−1].
While we used all of the above mentioned characteristics for the evaluation of the simulation of hydrological model, for the extreme value analysis we considered annual maximum event severity (deficit volume).
3.2. Statistical Model
The RFA approach based on L-moments [54] was applied in order to estimate quantiles of the distribution of maximum deficit volumes.
RFA uses data from a number of measuring sites. A “region” is a group of sites each of which is assumed to have data drawn from the same frequency distribution [55]. The RFA consists of two steps. In the first one the homogeneous regions are identified. The second establishes a regional frequency distribution curve for each region. A region is considered to be homogeneous when the sites belonging to it exhibit a similar behavior when the non-dimensional local frequency distribution curves have similar shapes within a sampling error.
A convenient way of pooling summary statistics for RFA from different data samples is the index-flood technique [4]. The term “index-flood” was coined because early applications of the pooling algorithm were to flood data in hydrology. The application of the method to low flows was termed “regional frequency analysis” [34] and “index low flow method” [56]. The method assumes that the variables within a homogeneous region are identically distributed after scaling with a site-specific factor (the index-flood). A consequence of the index-flood assumption is that the coefficient of variation of a given variable should be constant over the region of interest. Of all the stages in RFA, the identification of homogeneous regions is usually the most difficult and requires the greatest amount of subjective judgment [54].
In our study, the Hartigan–Wong k-means algorithm [57] was used to identify the homogeneous regions. K-means algorithm identifies k number of centroids, and then allocates every data point to the nearest centroid, while keeping the clusters as small as possible. The input to the algorithm is a set of points defined by the coordinates in the n-dimensional space, and the number k, defining the number of clusters. The cluster analysis was carried out with scaled data of runoff minus potential evapotranspiration.
The parameters of the regional distribution are estimated using the L-moments method [58]. The at-site L-moments for annual maximum deficit volumes were estimated using the algorithm developed by [59]. For a random variable X, the rth population L-moment is described by [54] as
where denotes the jth order statistic in an independent sample of size n from the distribution of X and E denotes expected value.
Four probability distributions were used for comparison of the estimated empirical L-moments—L-skewness () and L-kurtosis () to the theoretical ratios: Generalized Pareto Distribution (GPD), Generalized Extreme Value distribution (GEV), Generalized normal distribution, Log-normal distribution.
GPD is a family of continuous probability distributions, which has been often used to model the tails of another distribution (e.g., [60]). Although it is defined by three parameters: location, scale and shape parameters [54,61], it has been shown that can be defined by only scale and shape or just by its shape parameter [62]. The three-parameter GPD is formulated as [54]
where is location, scale and shape parameter with range of x: if and if .
According to [54], the relation between and for GPD is
The regional GPD parameters were estimated using the index-flood method. The key assumption here is that the frequency distributions at all sites belonging to the same (homogeneous) region are identical, except for a scale factor (the so-called index flood) e.g., [63,64]. In our case, the at-site values were used as the scaling factor. Scaling is performed as follows: first two at-site moments and are divided by the corresponding mean (), after scaling equals 1 and becomes coefficient of L-variation ().
Regional L-moments ratios (denoted ) were obtained by following the algorithm described by [54]:
where N is the number of sites and n the record length.
Then the three regional GPD parameters are given by
When selecting the distribution, attention has to be paid to the choice of the distribution bounds. Lower bound of the distribution has to be zero - since years with no drought event are necessary to be taken into account. Therefore, we used mixed distribution as suggested by [65], having the form
where is the probability of a zero value (years with no drought event occurring) and is the cumulative distribution function of the nonzero values.
3.3. Model Assessment
3.3.1. Ratio Diagrams and Gumbel Plot
Two ways of assessing the model visually are Ratio diagrams and Gumbel plots. The ratio diagrams ere constructed by plotting the estimated sample L-moment ratios versus the theoretical L-moment ratio curves for the candidate distributions. Gumbel plot is a quantile function with transformed Gumbel variate () instead of probability (F) on the horizontal axis. This transformation is done in order to better visualize values with high return periods. Then, F, which is cumulative probability P of non exceedance of the mth value in n order ranked observations, was calculated by the plotting position
where m is the rank from the smallest to the largest observation and n is the number of observations.
3.3.2. Discordance
A discordance analysis was performed in order to assess whether the distributions of at-site deficit volumes within each cluster were acceptably similar. The discordance measure [55] compares L-moment ratios of a site with those of the pooling group as a whole, identifying sites with L-moment ratios that are unusually relative to the pooling group.
A formal definition of discordance [22] for N sites is as follows:
is the group average with is transpose vector containing values of L-moment ratios , and for site i,
is matrix of sums of squares and cross-products and
is discordance measure D for site i. The criterion for discordance is an increasing function of the number of sites in the region. This is because large regions are more likely to contain sites with large values of D. However it is recommended to regard any site with as discordant, since such sites have the L-moment ratios that are markedly different from the average for the other sites in the region [54].
3.3.3. Anderson–Darling Test
Anderson–Darling (A2) test was chosen over goodness-of-fit framework within [22] based on the findings presented by [66] which specifically compares the Anderson–Darling test with methods used in [22] in order to make recommendations for test selection based on the assumed skewness of the data.
Anderson–Darling (A2) test is a modification of the Cramér–von Mises test [67,68,69]. It differs from the Cramér–von Mises test in such a way that it gives more weight to the tails of the distribution [70]. A2 is the most powerful empirical distribution function test [71]. The Anderson–Darling test statistic belongs to the quadratic class of the empirical distribution function statistic in which it is based on the squared difference .
Ref. [72] defined the statistic test as
where F is theoretical cumulative distribution function under the null hypothesis and is empirical cumulative distribution function.
Critical values for Anderson–Darling statistic A2, are based on bootstrap resampling as suggested by [73] and used by [74].
Let be the value of A2 calculated from the deficit volumes at catchment and let be the value of A2 from bootstrap sample b for this catchment. For a chosen significance level , the local critical values are obtained for each catchment as the kth smallest value of the , where .
The determination of the global critical values of the requires simulation from the model under the null hypothesis. In particular, the preservation of spatial dependence is important. This is done by bootstraping the data for a certain year simultaneously, rather than bootstrapping the data of the catchments individually [75,76]. Let be the local critical values that we get if bootstrap sample b is excluded. The bootstrap estimate of the global error rate is obtained as
where is the number of b for which is true. This error rate can be calculated using the fact that bootstrap sample b fulfills the condition if and only if rank for at least one s. Thus, if the values of are stored in a matrix with stations in columns and bootstrap samples in rows, then we first calculate the columnwise ranks and subsequently the proportion of rows in which the maximum rank is greater than or equal to k. The value of k is chosen such that is as close as possible to the desired global significance level.
The bootstrapping method used here is described by [74] in steps as:
- Fit the statistical model to the original sample.
- Calculate standard normal residuals with the parameter estimates from step using quantile mapping.
- Calculate the average correlation of the standard normal residuals.
- Generate a sample of S equicorrelated standard normal variables with correlation .
- Transform the sample from step 4 back to the original scale using the parameter estimates from step 1.
- Fit the statistical model again.
- Calculate the A2 statistics.
- Repeat steps 4–7 until the desired number of bootstrap samples is obtained.
4. Results and Discussion
The characteristics of simulated deficit events in four successive 30-year (climatic) periods starting in 1901 are given in Table 1. The average values of event severity (D), intensity (I), length (L), relative severity (rD) and relative intensity (rI) are varying over the periods with largest values of event severity in the periods 1931–1960 and 1961–1990. These periods are in good agreement with the extreme droughts that manifested in 1947, 1953–1954, 1959, 1963–1964, 1973–1974, 1983 [77,78,79,80,81].

Table 1.
Average values of severity (D), intensity (I), length (L), relative severity (rD) and relative intensity (rI) of deficit events derived from simulated data.
The relatively lower values of all variables in the last period might be linked with the rather wet conditions that prevailed in Central Europe [82]. In addition, the current dry period over the Czech Republic spans the years 2014–2018, so considerable part is not considered here. A steady decrease in soil moisture has been reported for the same period [83], due to the increasing temperature and consequently to the rising evapotranspiration. The latter can be also seen in the drought representation by the SPEI index [84].
In the 53 gauged catchments, the properties of simulated deficit volumes for the period 1980–2010 were compared to the observational records. The validation showed that the characteristics of simulated deficit volumes correspond well to those based on observed data, as shown in Figure 2 and Table 2. In Figure 2, the simulated event severities and lengths are well represented through the median, as well as through the confidence interval in all ranges. The simulated low event intensities correspond quite well to the observed ones, despite the overestimation of the high intensities by the model. The simulated relative severity and intensity are slightly overestimated in the whole range, due to the cumulative effect in their computation. This overestimation pattern is well shown in Table 2 through the average of the individual variables.
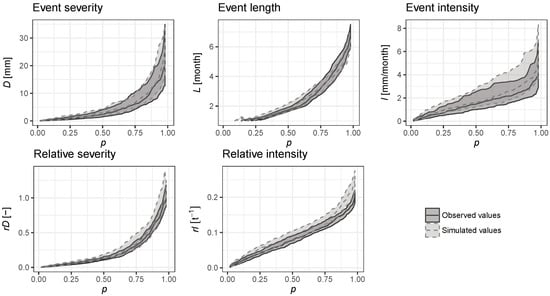
Figure 2.
Comparison of drought characteristics for observed and simulated runoff. The empirical quantiles of the individual characteristics are indicated on the horizontal axis, the vertical axis shows values of drought characteristics, the polygons correspond to interquartile range.

Table 2.
Validation of simulated deficit volumes. D: severity, I: intensity, L: length, rD: relative severity and rI: relative intensity.
4.1. Spatial Pooling
The input to K-means algorithm was mean runoff and mean potential evapotranspiration for each catchment which resulted in three clusters of catchments. The algorithm ran ten times, each time starting with cluster centres in a different random position. Within fifty iterations, each run converged to a locally-optimal solution. Cluster 1 represents the catchments at high elevations with a lot of precipitation (see Table 3 for average precipitation for individual clusters), low land dry catchments with limited precipitation form cluster 3, while cluster 2 is a transition between the low drought risk cluster 1 and severe drought event risk cluster 3. Table 3 reports also the probability of year without drought. It may be surprising that the low-risk cluster 1 has the lowest probability of year without drought (0.3), while this probability is 0.49 for severe drought event risk cluster 3. However, it has to be noted (and is demonstrated further) that the tail of the distribution of deficit volume is much heavier in cluster 3 than in cluster 1 (see, e.g., parameter in Table 4 or the quantile functions in Figure 3).

Table 3.
Mean values of annual precipitation sum (P[mm]) for each cluster, average deficit volumes DV [mm] for each cluster and probabilities p0 of year without drought event per cluster.

Table 4.
Fitted regional parameters with estimated regional A2 critical values.
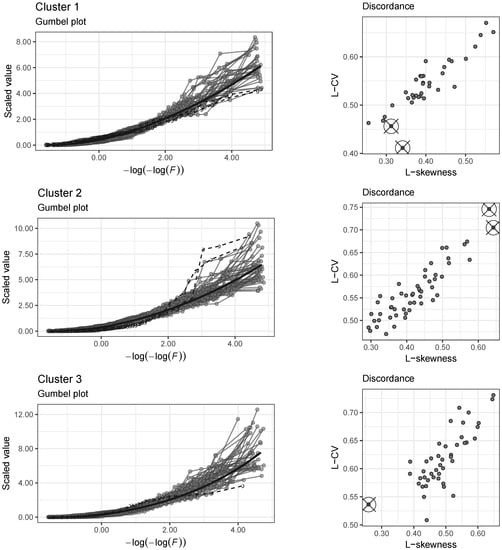
Figure 3.
Left panels: Gumbel plot—Continuous black lines represent fitted regional quantile functions, grey points with lines are scaled deficit volumes with probabilities calculated using plotting position, dashed lines highlight discordant catchments; Right panels: Discordance measure showing ratio between coefficient of L-variation and L-skewness, discordant ratios lie outside the notional ellipsis (critical value) that would be drawn around the concordant values.
At-site distributions were chosen on the basis of L-moment ratio diagrams and at-site Anderson–Darling (A2) tests. The diagrams were constructed by plotting the estimated sample L-moment ratios versus the theoretical L-moment ratio curves for the candidate distributions (Figure 4). From the considered distributions, the estimated L-moment ratios for deficit volumes correspond best to those of the Generalized Pareto Distribution (GPD). In addition, the Anderson–Darling test at the significance level = 0.05 rejected the GPD only at six out of 133 catchments, which is very close to the nominal level of the test.
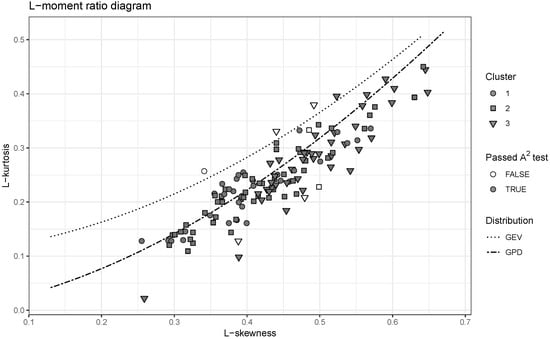
Figure 4.
L-moment ratio diagram with highlighted clusters and results of at-site Anderson–Darling test. The dashed lines show the theoretical L-moment ratio for Generalized Pareto Distribution (GPD) and Generalized Extreme Value distribution (GEV) and the points the L-moment ratios for each catchment.
For each cluster a stationary index flood model for scaled deficit volumes was developed. The scaling was performed by the at-site first L-moment, with the scaling factors varying between 1.94 and 23.5 mm. The fitted regional parameters of the model are presented in Table 4. It is evident that the cluster 3 (dry catchments) exhibits quite different behaviour than the other two clusters. In particular, the low value of the shape parameter indicates heavy tail. In addition, the smaller scale parameter also points towards dry regime prone to heavy extremes.
The goodness-of-fit was assessed using Gumbel plots, discordance measure and regional Anderson–Darling test (Figure 3). It is clear that the regional model fits the deficit volumes scaled by the first L-moment well. The same figure, highlights 1–2 catchments in every cluster demonstrating different behaviour than the rest of the cluster (discordant catchments). Regions were checked for within-cluster discordance based on a critical value set at 3 with a 10% significance level as defined by [54], and five catchments in total were found discordant. In the Anderson–Darling test, the regional critical values were estimated using the methods described above with 3000 bootstrap samples for each region (Table 4). All clusters passed the regional Anderson–Darling test for significance level = 0.10.
4.2. Choice of the At-Site Distribution
The annual maximum deficit volumes analyzed in the present paper cannot be regarded as standard block maxima, since there is often only one drought event (and only seldom more than two) for individual year and catchment. Therefore the annual maximum deficit volume are not theoretically expected to follow Generalized Extreme Value distribution. Indeed, the results suggest that for most stations the Generalized Pareto Distribution is appropriate for the description of the distribution of the annual maximum deficit volume (though generalized normal and generalized extreme value distributions could be also good candidates for stations that did not pass the Anderson–Darling or are being an outliers in Figure 4).
Similar results can be seen in [20], where annual deficit volumes were fitted to various distributions and GPD presented the best results. However, no spatial pooling was employed in this study. In another study that employed RFA for deficit volumes [29] the Generalized Exponential Distribution was used, which is a reparameterization of the Generalized Pareto Distribution.
In addition, the analyses conducted within searching for the optimal at-site distribution revealed that Generalized Extreme Value distribution cannot be used to characterize the distribution of deficit volumes, although it is very often found appropriate for maximum discharges or heavy precipitation indices. This result can be, at least partly, region-specific, therefore the at-site distribution should be always checked prior the regional frequency analysis.
4.3. Drought Definition
In contrast to extreme precipitation or runoff, the definition of drought is not straightforward and various definitions do exist. In the present paper, we considered deficit volume, due to its clear physical interpretation. On the other hand, one may also consider drought indices, based on cumulative deviation from the mean, e.g., Drought Severity Index [85] or indices inspired by the Standardized Precipitation Index (SPI). The use of the latter within regional frequency analysis, however, is complex since often the temporal dimension of drought is characterized by different time-scales for which the SPI is calculated.
Moreover, even the definition of deficit volume allows for several subjective choices like threshold level, form of the threshold (variable or fixed within a year), number of days/months needed for the discharge to be above threshold to end the drought event etc. This increases the uncertainty in the estimation of drought characteristics.
4.4. Reduction of Uncertainty
Statistical modelling of extremes is related to large uncertainties due to the rarity of extreme events or problems with their measurement. This especially applies to droughts since they do not occur every year and thus the length of series typically available for hydrological analysis provides only limited information. This can be, at least partly, overcome by “trading space for time”, i.e., combining data from several sites over homogeneous regions. The effect of adding sites/catchments is maximal when the data are independent. This is seldom true, however, thus the real reduction of uncertainty not only depends on the number of data but also on the dependence structure of the analyzed data.
To assess the increase in precision of the parameter estimates owing to spatial pooling, GPD parameters were fitted for each individual catchment and the 25th and 75th percentiles of the parameter estimates were calculated using 500 bootstrap samples. Then, for each region and each parameter the average interquartile range was obtained as the difference between the average 75th and 25th percentile of the estimates. These average interquartile ranges were compared with those of the regional model. Results are shown in Table 5.

Table 5.
Percentage decrease in uncertainties in parameter and return level estimation.
Increase in precision for the return levels was calculated by substituting the estimated parameters of the bootstrap sample to GPD quantile function with corresponding probability p, , where T is the return period in years. The estimated return levels for each cluster together with calculated confidence intervals can be seen in Figure 5.
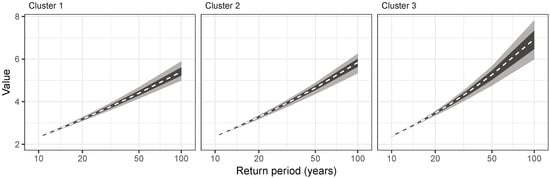
Figure 5.
Estimated return periods of deficit volumes. Dashed line shows regional quantile function, darker area the 25th and 75th, light area 5th and 95th percent quantile calculated from the bootstrap samples.
Another option how to increase the sample size is to consider reconstructed climate data (e.g., [86]) in combination with a hydrological model. This introduces additional sources of uncertainty, though, through the reconstructed climate fields and the parameterization of the hydrological model. On the other hand, the spatial and temporal scales relevant for drought may allow to obtain reliable information even based on data with limited spatial coverage.
4.5. Identification of Homogeneous Regions
Identification of the homogeneous regions requires the greatest amount of subjective judgment of all stages of regional frequency analysis. When using K-mean clustering, methods uncertainties stem from the choice of the number of clusters, which can actually be mitigated by using methods like gap statistics [87,88]. However in this study we had a predefined number of clusters from the very beginning since the initial idea was to classify the catchments into three groups based on the level of threat by drought. Another ways to proceed with spatial pooling would be by using self-organizing maps [89,90], dimensionality reduction technique [91], or pooling methods first suggested by [92] and [93] with subsequent implementation of the method referred to as the region of influence approach by [5].
Although we used unsupervised clustering algorithm it is worth noting that the resulting regions used for regional frequency analysis shown in Figure 1, correspond well with the distribution of hydroclimatic variables relevant to drought such as aridity index [44], which supports the relevance of the clustering algorithm.
5. Summary and Concluding Remarks
Statistical model using index-flood method based on L-moments was used on simulated runoff series for the period 1900–2015 for 133 catchments in the Czech Republic. Goodness-of-fit of the model was assessed using Gumbel plots and Anderson–Darling statistical test. Critical values of the test were estimated by bootstrap resampling, which also provided the estimate of the confidence intervals allowing for calculation of the reduction in uncertainties of the regional parameter and return level estimation.
The main conclusions that can be drawn are:
- Regional frequency analysis reduces uncertainty of estimated drought characteristics and parameters of its distribution.
- Use of Generalized Pareto Distribution is appropriate to describe the deficit volumes on majority of catchments, which is not the case for Generalized Extreme Value distribution. However, it is not clear to what extent this result depends on characteristics of the area under study and other parameters of the analysis like the threshold defining drought.
- The most subjective part of the regional frequency analysis is the definition of homogeneous regions—methods such as region of influence or Self Organizing maps could be considered to minimize the subjective decisions within the regional frequency analysis.
Author Contributions
Conceptualization, M.H. and P.M.; methodology, M.H. and F.S.; software, F.S., J.M. and M.S.; validation, F.S. and V.M.; formal analysis, F.S.; writing—original draft preparation, F.S., V.M.; writing—review and editing, P.M., M.H. and Y.M.; visualization, F.S.; supervision, M.H. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Czech Science Foundation (grant no. 19-24089J), Internal Grant Agency of The Faculty of Environmental Sciences CZU (grant no. 20164230 and no. 20174227) and The Faculty of Economics and Management CZU (grant. no. 20151038).
Acknowledgments
All calculations and visualization was done in R Project for Statistical Computing [94].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fink, A.H.; Brücher, T.; Krüger, A.; Leckebusch, G.C.; Pinto, J.G.; Ulbrich, U. The 2003 European summer heatwaves and drought–synoptic diagnosis and impacts. Weather 2004, 59, 209–216. [Google Scholar] [CrossRef]
- Laaha, G.; Gauster, T.; Tallaksen, L.; Vidal, J.P.; Stahl, K.; Prudhomme, C.; Heudorfer, B.; Vlnas, R.; Ionita, M.; Van Lanen, H.A.; et al. The European 2015 drought from a hydrological perspective. Hydrol. Earth Syst. Sci. 2016, 21, 3001–3024. [Google Scholar] [CrossRef]
- Ionita, M.; Tallaksen, L.; Kingston, D.; Stagge, J.; Laaha, G.; Van Lanen, H.; Scholz, P.; Chelcea, S.; Haslinger, K. The European 2015 drought from a climatological perspective. Hydrol. Earth Syst. Sci. 2017, 21, 1397–1419. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual Of Hydrology: Part 3; Technical Report; USGPO: Washington, DC, USA, 1960. [Google Scholar]
- Burn, D.H. Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Blazkov, S.; Beven, K. Flood frequency prediction for data limited catchments in the Czech Republic using a stochastic rainfall model and TOPMODEL. J. Hydrol. 1997, 195, 256–278. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best fit and selection of theoretical flood frequency distributions based on different runoff generation mechanisms. Water 2010, 2, 239–256. [Google Scholar] [CrossRef]
- Wayne, C.P. Meteorological Drought; US Weather Bureau Research Paper; US Weather Bureau: Silver Spring, MD, USA, 1965. [Google Scholar]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9, 3–11. [Google Scholar]
- Myronidis, D.; Fotakis, D.; Ioannou, K.; Sgouropoulou, K. Comparison of ten notable meteorological drought indices on tracking the effect of drought on streamflow. Hydrol. Sci. J. 2018, 63, 2005–2019. [Google Scholar] [CrossRef]
- Beran, M.A.; Rodier, J.A. Hydrological Aspects of Drought: A Contribution to the International Hydrological Programme; Unesco: Paris, France, 1985; Volume 39. [Google Scholar]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Zelenhasić, E.; Salvai, A. A method of streamflow drought analysis. Water Resour. Res. 1987, 23, 156–168. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K.; Fotakis, D.; Dörflinger, G. Streamflow and hydrological drought trend analysis and forecasting in Cyprus. Water Resour. Manag. 2018, 32, 1759–1776. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Hisdal, H. Regional analysis of extreme streamflow drought duration and deficit volume. IAHS Publ. 1997, 246, 141–150. [Google Scholar]
- Fekete, B.; Vörösmarty, C.; Grabs, W. Global Composite Runoff Data Set (v1. 0); Complex Systems Research Center, University of New Hampshire: Durham, NH, USA, 2000. [Google Scholar]
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Clausen, B.; Pearson, C. Regional frequency analysis of annual maximum streamflow drought. J. Hydrol. 1995, 173, 111–130. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-moments approach for regional flood frequency analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Fowler, H.; Kilsby, C. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Modarres, R. Regional dry spells frequency analysis by L-moment and multivariate analysis. Water Resour. Manag. 2010, 24, 2365–2380. [Google Scholar] [CrossRef]
- Santos, J.F.; Portela, M.M.; Pulido-Calvo, I. Regional frequency analysis of droughts in Portugal. Water Resour. Manag. 2011, 25, 3537. [Google Scholar] [CrossRef]
- Brown, B.G.; Katz, R.W. Regional analysis of temperature extremes: Spatial analog for climate change? J. Clim. 1995, 8, 108–119. [Google Scholar] [CrossRef]
- Madsen, H.; Rosbjerg, D. A regional Bayesian method for estimation of extreme streamflow droughts. In Statistical and Bayesian Methods in Hydrological Sciences; UNESCO: Paris, France, 1998; pp. 327–340. [Google Scholar]
- Chen, Y.D.; Huang, G.; Shao, Q.; Xu, C.Y. Regional analysis of low flow using L-moments for Dongjiang basin, South China. Hydrol. Sci. J. 2006, 51, 1051–1064. [Google Scholar] [CrossRef]
- Núnez, J.H.; Verbist, K.; Wallis, J.R.; Schaefer, M.G.; Morales, L.; Cornelis, W. Regional frequency analysis for mapping drought events in north-central Chile. J. Hydrol. 2011, 405, 352–366. [Google Scholar] [CrossRef]
- Abdi, A.; Hassanzadeh, Y.; Talatahari, S.; Fakheri-Fard, A.; Mirabbasi, R. Regional drought frequency analysis using L-moments and adjusted charged system search. J. Hydroinform. 2017, 19, 426–442. [Google Scholar] [CrossRef]
- Zítek, J. Hydrologické Poměry ČSSR; Hydrometeorologický ústav: Praha, ČSSR, 1965. [Google Scholar]
- Tallaksen, L.M.; Van Lanen, H.A. Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004; Volume 48. [Google Scholar]
- Horáček, S.; Rakovec, O.; Kašpárek, L.; Vizina, A. Development of the hydrological balance model BILAN. Water Manag. Tech. Econ. Inf. J. 2009, 51, 2–5. [Google Scholar]
- Vizina, A.; Horáček, S.; Hanel, M. Recent developments of the BILAN model. Water Manag. Tech. Econ. Inf. J. 2015, 57, 7–10. [Google Scholar]
- Kašpárek, L.; Hanel, M.; Horáček, S.; Máca, P.; Vizina, A. Bilan Water Balance Model, R package version 2016-10-20. 2016.
- Horáček, S.; Kašpárek, L.; Novický, O. Estimation of Climate Change Impact on Water Resources by Using Bilan Water Balance Model; IOP conference series: Earth and environmental science; IOP Publishing: Bristol, UK, 2008; Volume 4, p. 012023. [Google Scholar]
- Hanel, M.; Mrkvičková, M.; Máca, P.; Vizina, A.; Pech, P. Evaluation of simple statistical downscaling methods for monthly regional climate model simulations with respect to the estimated changes in runoff in the Czech Republic. Water Resour. Manag. 2013, 27, 5261–5279. [Google Scholar] [CrossRef]
- Beran, A.; Hanel, M. Identification of regions vulnerable to deficits in water resources in the Czech Republic. Water Manag. Tech. Econ. Inf. J. 2015, 57, 23–26. [Google Scholar]
- Beran, A.; Hanel, M.; Nesládková, M. Changes in the hydrological balance caused by climate change impacts in the Karlovy Vary district. Water Manag. Tech. Econ. Inf. J. 2016, 58, 20–25. [Google Scholar]
- Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Štěpánek, P.; Zahradníček, P.; Huth, R. Interpolation techniques used for data quality control and calculation of technical series: An example of a Central European daily time series. Idojaras 2011, 115, 87–98. [Google Scholar]
- Tolasz, R.; Brázdil, R.; Bulíř, O.; Dobrovolnỳ, P.; Dubrovskỳ, M.; Hájková, L.; Halásková, O.; Hostỳnek, J.; Janouch, M.; Kohut, M.; et al. Atlas podnebí Česka. 1. vydání; Českỳ hydrometeorologickỳ ústav: Praha, Czech Republic; Universita Palackého: Olomouc, Czech Republic, 2007. [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Tallaksen, L.M. Streamflow drought frequency analysis. In Drought and Drought Mitigation in Europe; Springer: Berlin/Heidelberg, Germany, 2000; pp. 103–117. [Google Scholar]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Luo, L.; Apps, D.; Arcand, S.; Xu, H.; Pan, M.; Hoerling, M. Contribution of temperature and precipitation anomalies to the California drought during 2012–2015. Geophys. Res. Lett. 2017, 44, 3184–3192. [Google Scholar] [CrossRef]
- Rice, S.O. Mathematical analysis of random noise. Bell Syst. Tech. J. 1945, 24, 46–156. [Google Scholar] [CrossRef]
- Cramér, H.; Leadbetter, M.R. Stationary and Related Stochastic Processes; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Yevjevich, V.M. An objective approach to definitions and investigations of continental hydrologic droughts. In Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1967. [Google Scholar]
- Hisdal, H.; Tallaksen, L.; Peters, E.; Stahl, K.; Zaidman, M. Drought event definition. ARIDE Tech. Rep. 2000, 6, 15. [Google Scholar]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. Discuss. 2006, 10, 535–552. [Google Scholar] [CrossRef]
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Hosking, J.; Wallis, J. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Savenije, H.; Viglione, A. Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Hosking, J. L-Moments, R Package, Version 2.8; 2019. Available online: https://CRAN.R-project.org/package=lmom (accessed on 24 April 2020).
- Papalexiou, S.; Koutsoyiannis, D.; Makropoulos, C. How extreme is extreme? An assessment of daily rainfall distribution tails. Hydrol. Earth Syst. Sci. 2013, 17, 851–862. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Hosking, J.; Wallis, J. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Grover, P.L.; Burn, D.H.; Cunderlik, J.M. A comparison of index flood estimation procedures for ungauged catchments. Can. J. Civ. Eng. 2002, 29, 734–741. [Google Scholar] [CrossRef]
- Bocchiola, D.; De Michele, C.; Rosso, R. Review of recent advances in index flood estimation. Hydrol. Earth Syst. Sci. Discuss. 2003, 7, 283–296. [Google Scholar] [CrossRef]
- Engeland, K.; Hisdal, H.; Frigessi, A. Practical extreme value modelling of hydrological floods and droughts: A case study. Extremes 2004, 7, 5–30. [Google Scholar] [CrossRef]
- Viglione, A.; Laio, F.; Claps, P. A comparison of homogeneity tests for regional frequency analysis. Water Resour. Res. 2007, 43, W03428. [Google Scholar] [CrossRef]
- Cramér, H. On the composition of elementary errors: First paper: Mathematical deductions. Scand. Actuar. J. 1928, 1928, 13–74. [Google Scholar] [CrossRef]
- Von Mises, R. Vorlesungen aus dem Gebiete der Angewandten Mathematik: Wahrscheinlichkeitsrechnung und ihre Anwendung in der Statistik und Theoretischen Physik; F. Deuticke: Vienna, Austria, 1931. [Google Scholar]
- Smirnov, N.V. Sur la distribution de w2. Comp. Rend. Acad. Sci. 1936, 202, 449–452. [Google Scholar]
- Farrell, P.J.; Rogers-Stewart, K. Comprehensive study of tests for normality and symmetry: Extending the Spiegelhalter test. J. Stat. Comput. Simul. 2006, 76, 803–816. [Google Scholar] [CrossRef]
- Masqat, O. Anderson Darling and modified Anderson Darling tests for generalized Pareto distribution. Pak. J. Appl. Sci. 2003, 3, 85–88. [Google Scholar]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge university press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Hanel, M.; Buishand, T.A.; Ferro, C.A. A nonstationary index flood model for precipitation extremes in transient regional climate model simulations. J. Geophys. Res. Atmos. (1984–2012) 2009, 114, D15107. [Google Scholar] [CrossRef]
- Faulkner, D.; Jones, D. The FORGEX method of rainfall growth estimation III: Examples and confidence intervals. Hydrol. Earth Syst. Sci. Discuss. 1999, 3, 205–212. [Google Scholar] [CrossRef][Green Version]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2007, 20, 1419–1444. [Google Scholar] [CrossRef]
- Blinka, P. Climatological evaluation of drought and dry periods on the territory of Czech Republic in the years 1876-2002. Meteorol. Bull. 2005, 58, 10–18. [Google Scholar]
- Treml, P. The largest droughts in the Czech Republic in the period 1875–2010. Meteorol. Bull. 2011, 64, 168–176. [Google Scholar]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Brázdil, R.; Trnka, M.; Zahradníček, P.; Dobrovolný, P.; Řezníčková, L.; Treml, P.; Stachoň, Z. The Central European drought of 1947: Causes and consequences, with particular reference to the Czech Lands. Clim. Res. 2016, 70, 161–178. [Google Scholar] [CrossRef]
- Hanel, M.; Rakovec, O.; Markonis, Y.; Máca, P.; Samaniego, L.; Kyselý, J.; Kumar, R. Revisiting the recent European droughts from a long-term perspective. Sci. Rep. 2018, 8, 9499. [Google Scholar] [CrossRef] [PubMed]
- Markonis, Y.; Hanel, M.; Máca, P.; Kyselý, J.; Cook, E. Persistent multi-scale fluctuations shift European hydroclimate to its millennial boundaries. Nat. Commun. 2018, 9, 1767. [Google Scholar] [CrossRef] [PubMed]
- Trnka, M.; Brázdil, R.; Možný, M.; Štěpánek, P.; Dobrovolný, P.; Zahradníček, P.; Balek, J.; Semerádová, D.; Dubrovský, M.; Hlavinka, P.; et al. Soil moisture trends in the Czech Republic between 1961 and 2012. Int. J. Climatol. 2015, 35, 3733–3747. [Google Scholar] [CrossRef]
- Potopova, V.; Boroneanţ, C.; Možný, M.; Štěpánek, P.; Skalák, P. Observed spatiotemporal characteristics of drought on various time scales over the Czech Republic. Theor. Appl. Climatol. 2014, 115, 563–581. [Google Scholar] [CrossRef]
- Phillips, I.D.; McGregor, G.R. The utility of a drought index for assessing the drought hazard in Devon and Cornwall, South West England. Meteorol. Appl. 1998, 5, 359–372. [Google Scholar] [CrossRef]
- Dobrovolný, P.; Brázdil, R.; Trnka, M.; Kotyza, O.; Valášek, H. Precipitation reconstruction for the Czech Lands, AD 1501-2010. Int. J. Climatol. 2015, 35, 1–14. [Google Scholar] [CrossRef]
- Yan, M.; Ye, K. Determining the number of clusters using the weighted gap statistic. Biometrics 2007, 63, 1031–1037. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. Identification of homogeneous regions for regional frequency analysis using the self-organizing map. J. Hydrol. 2006, 324, 1–9. [Google Scholar] [CrossRef]
- Kraemer, G.; Reichstein, M.; Mahecha, M.D. dimRed and coRanking—unifying dimensionality reduction in R. R J. 2018, 10, 342–358. [Google Scholar] [CrossRef]
- Acreman, M.; Wiltshire, S. Identification of regions for regional flood frequency analysis. Eos 1987, 68, 1262. [Google Scholar]
- Acreman, M. Regional Flood Frequency Analysis in the UK: Recent Research-New Ideas; Institute of Hydrology: Wallingford, UK, 1987. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).