A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels
Abstract
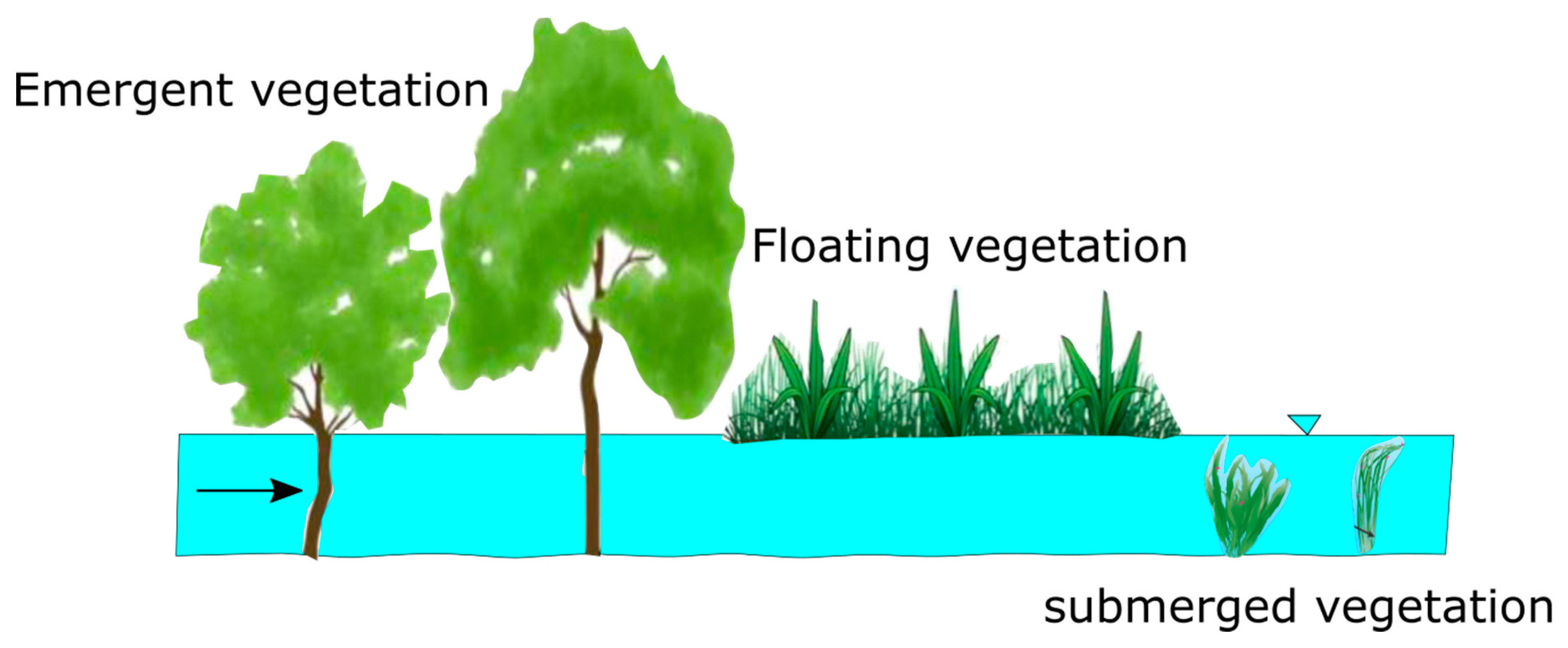
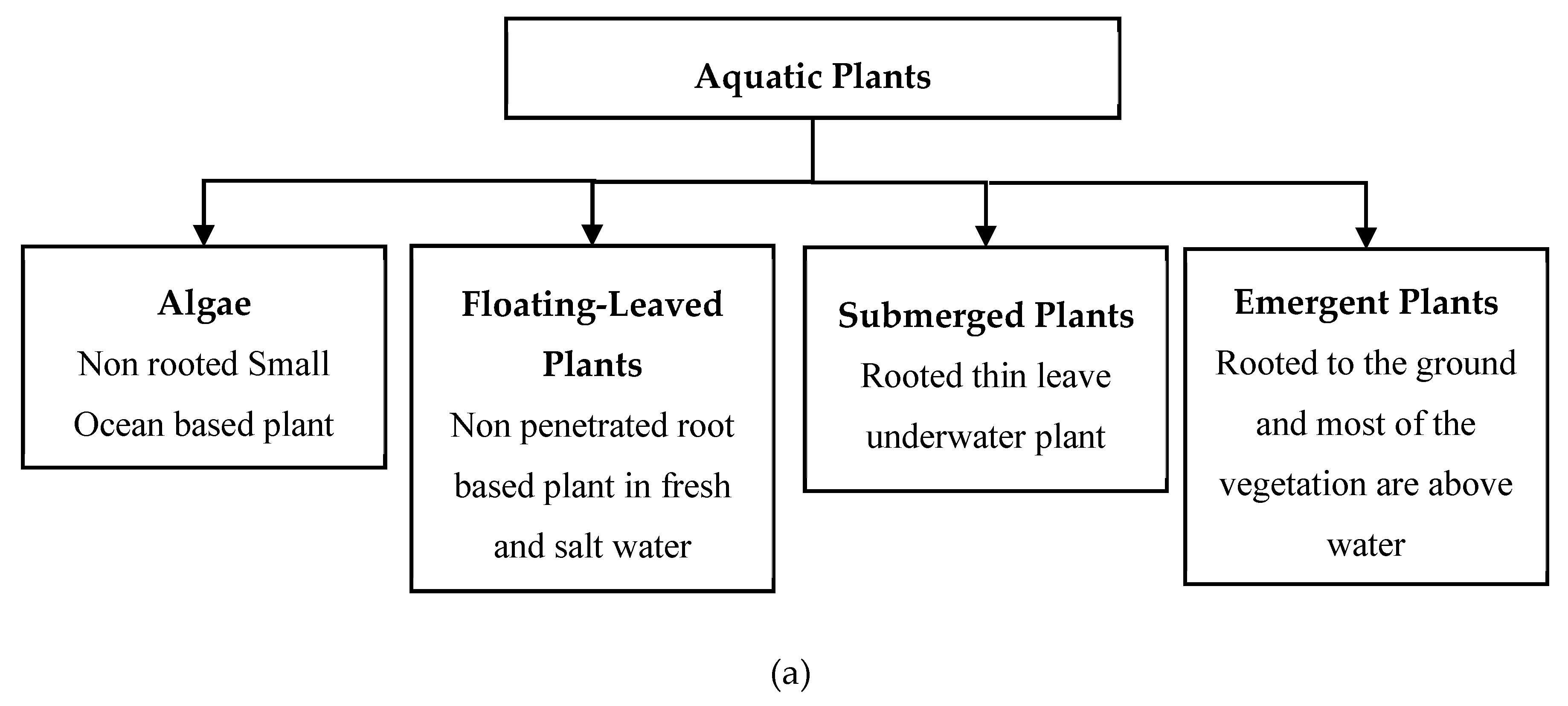
1. Introduction
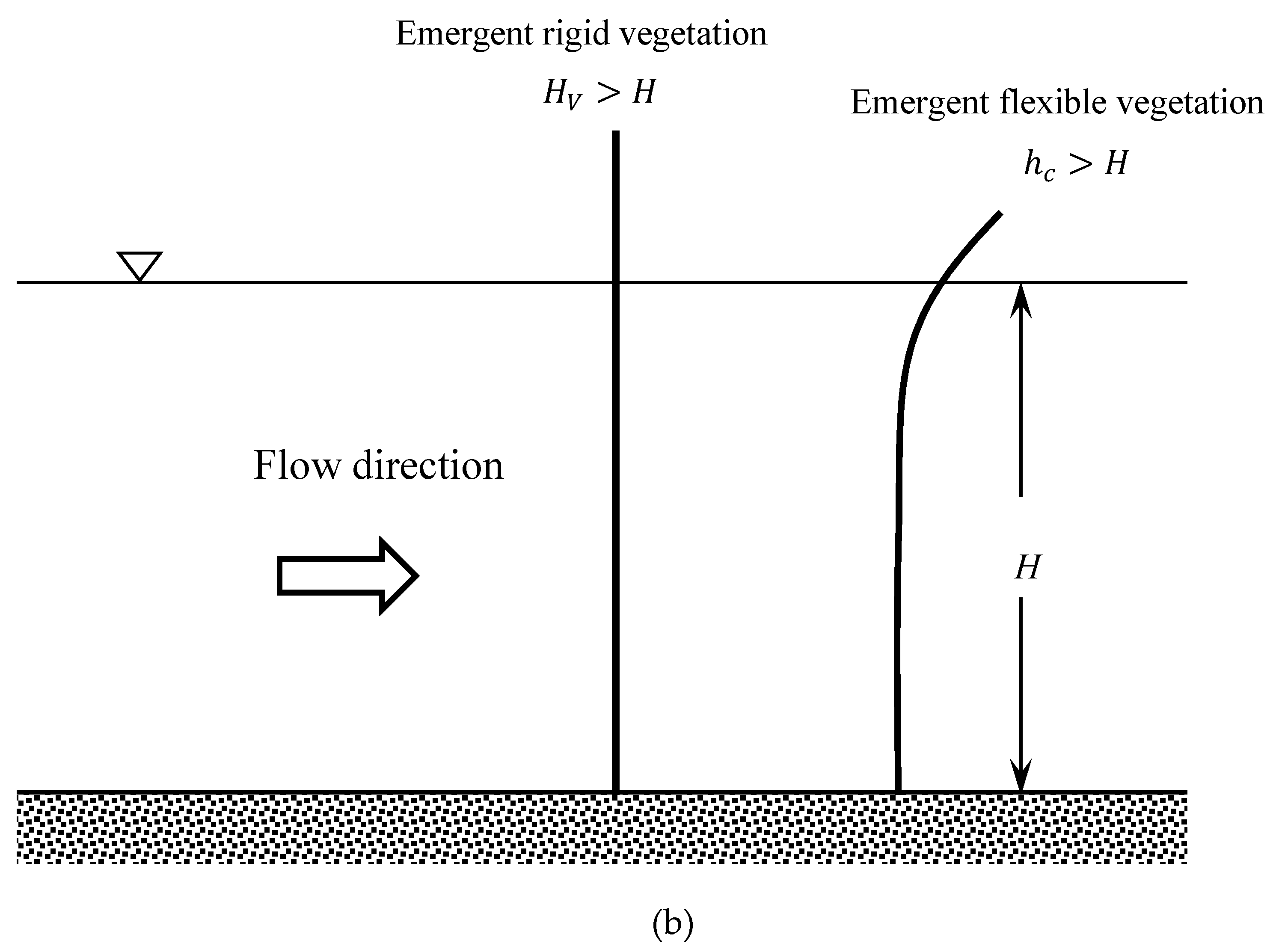
2. Hydrodynamics of Emergent Vegetated Flows
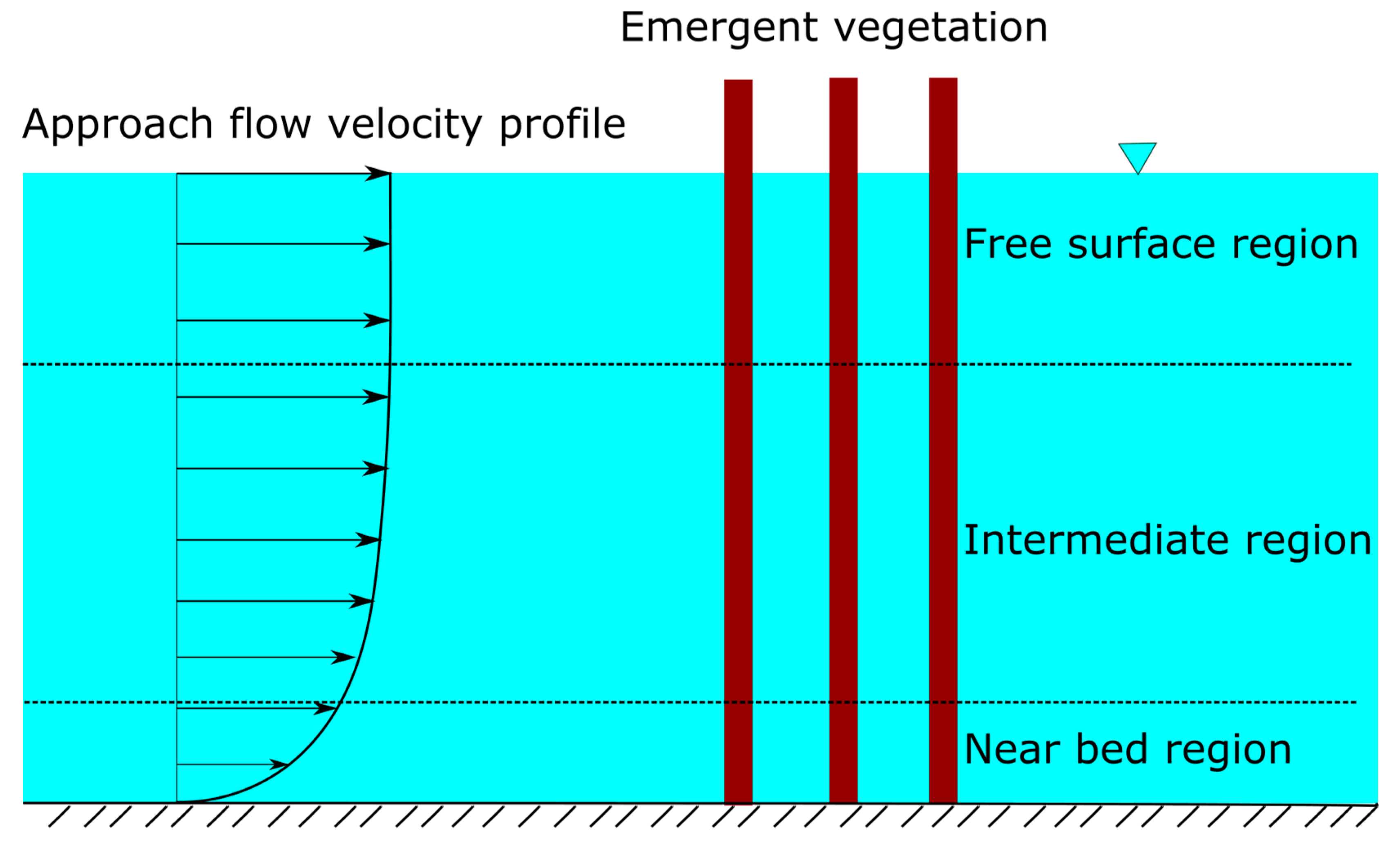
2.1. Vertical Structure
2.2. Mean Flow and Distribution of Turbulent Kinetic Energy (TKE) in the Horizontal Plan
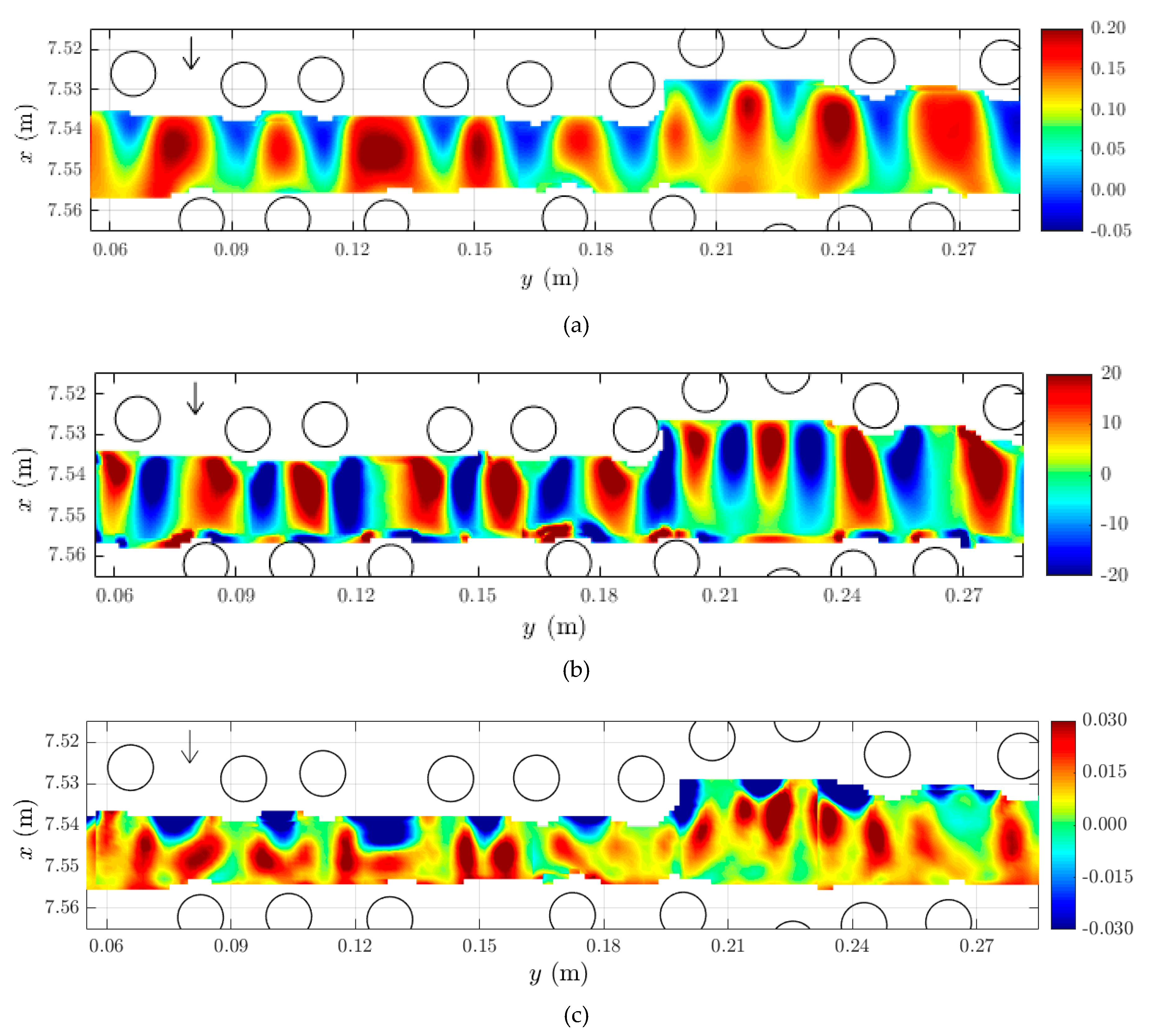
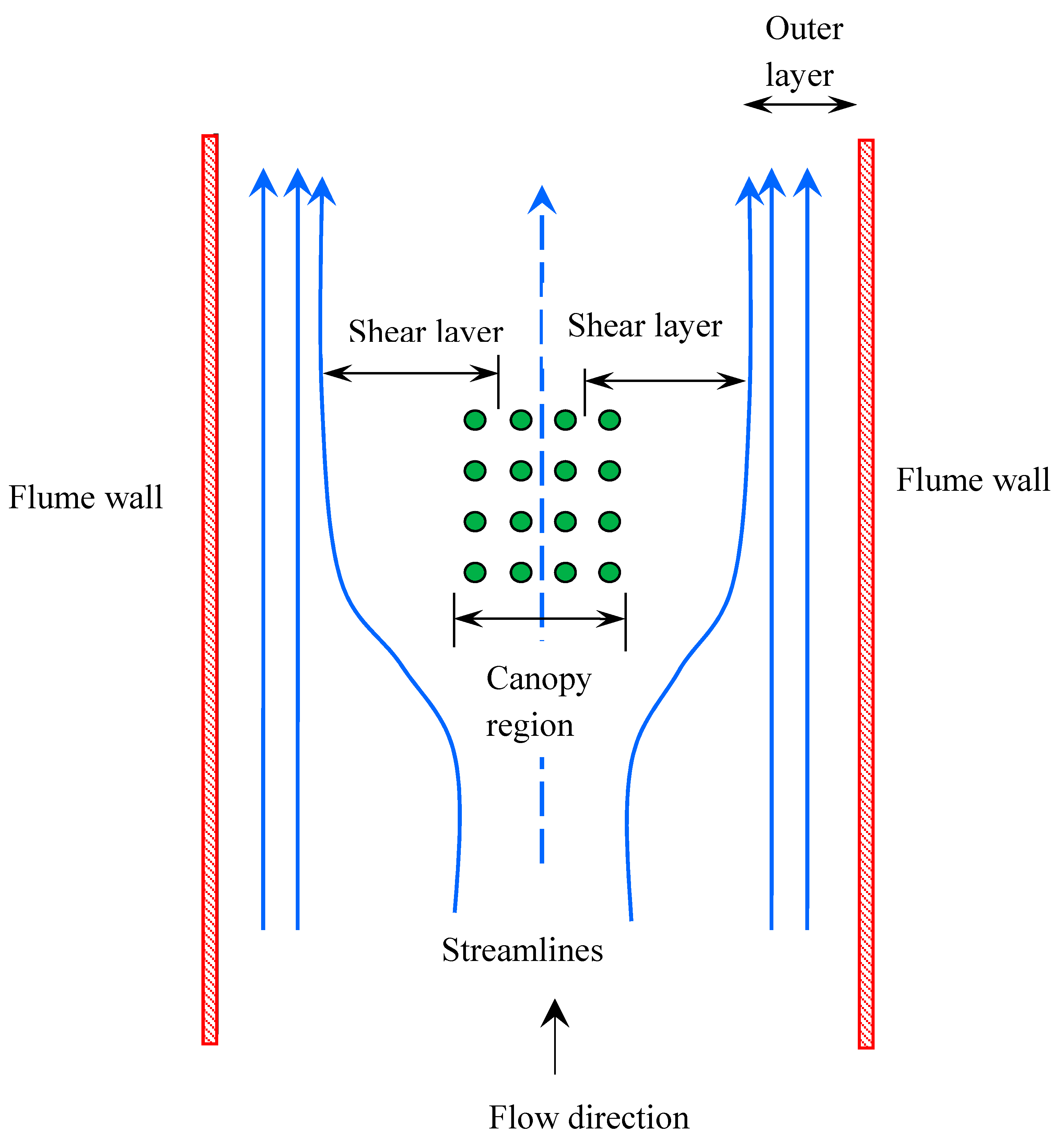
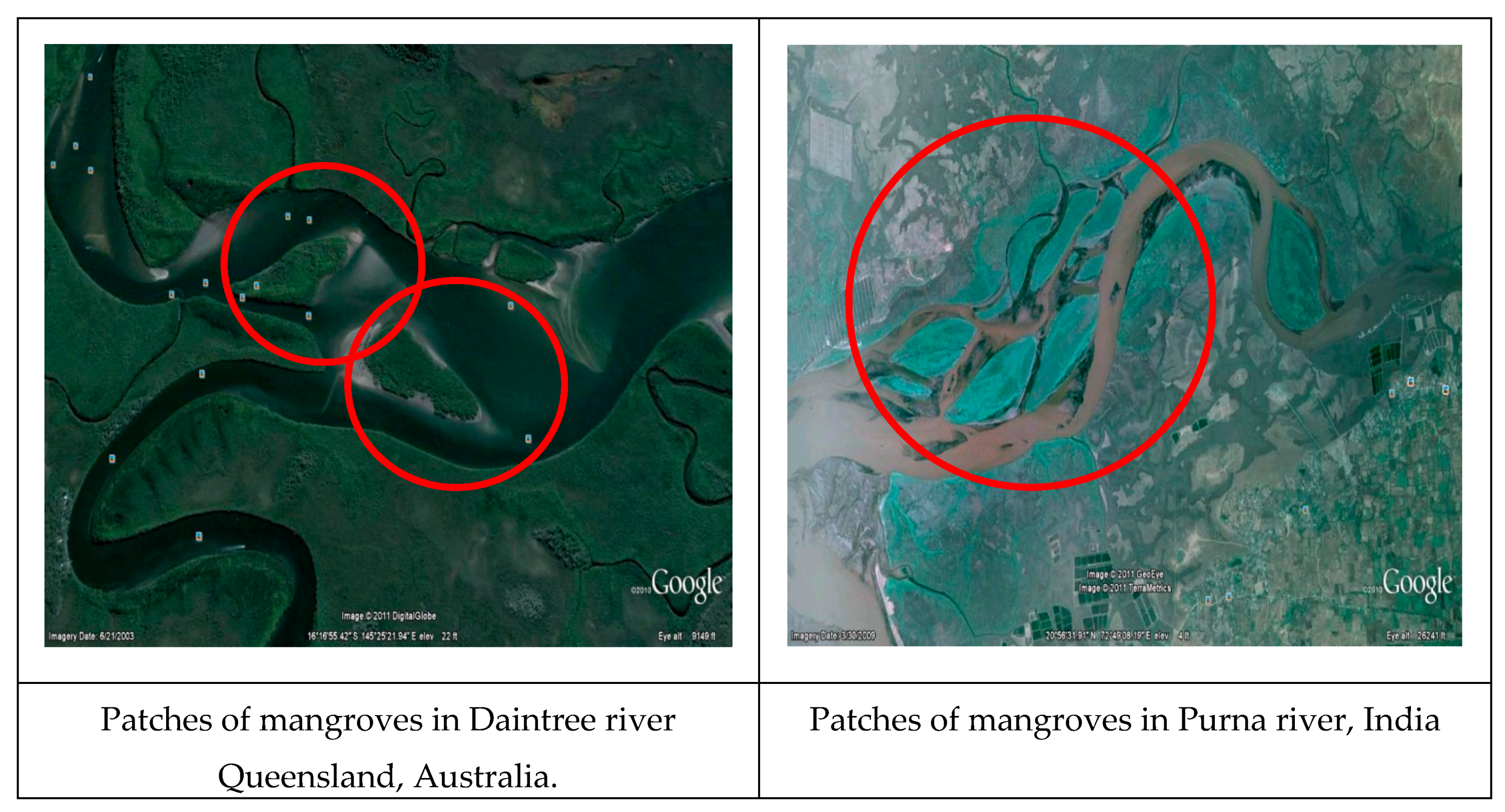
2.3. Horizontal Structure
2.4. Drag and Frictional Characteristics
2.5. Vegetation in Bank Protection and Sediment Transport
3. Further Research Prospects
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yager, E.M.; Schmeeckle, M.W. The influence of vegetation on turbulence and bed load transport. J. Geophys. Res. Earth Surf. 2013, 118, 1585–1601. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- O’Hare, M.T. Aquatic vegetation—A primer for hydrodynamic specialists. J. Hydraul. Res. 2015, 53, 687–698. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Franca, M.J.; Ferreira, R.M.L. Turbulent flows within random arrays of rigid and emergent cylinders with varying distribution. J. Hydraul. Eng. 2016, 142, 4016022. [Google Scholar] [CrossRef]
- Schoelynck, J.; De Groote, T.; Bal, K.; Vandenbruwaene, W.; Meire, P.; Temmerman, S. Self-organised patchiness and scale-dependent bio-geomorphic feedbacks in aquatic river vegetation. Ecography 2012, 35, 760–768. [Google Scholar] [CrossRef]
- Meire, D.W.S.A.; Kondziolka, J.M. Nepf, H.M. Interaction between neighboring vegetation patches: Impact on flow and deposition. Water Resour. Res. 2014, 50, 3809–3825. [Google Scholar] [CrossRef]
- Lichtenstein, D. Types of Aquatic Plants Sciencing.com. Available online: https://sciencing.com/types-of-aquatic-plants-12003789.html (accessed on 9 January 2020).
- Ricardo, A.M.; Koll, K.; Franca, M.J.; Schleiss, A.J.; Ferreira, R.M.L. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res. 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Ferreira, R.M.L.; Ricardo, A.M.; Franca, M.J. Discussion of “Laboratory Investigation of Mean Drag in a Random Array of Rigid, Emergent Cylinders” by Yukie Tanino and Heidi M. Nepf. J. Hydraul. Eng. 2009, 135, 690–693. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent flow through idealized emergent vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Chang, K.; Constantinescu, G. Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 2015, 776, 161–199. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 2007, 593, 1–32. [Google Scholar] [CrossRef]
- Chen, L.; Stone, M.C.; Acharya, K.; Steinhaus, K.A. Mechanical analysis for emergent vegetation in flowing fluids. J. Hydraul. Res. 2011, 49, 766–774. [Google Scholar] [CrossRef]
- Tinoco, R.O.; Cowen, E.A. The direct and indirect measurement of boundary stress and drag on individual and complex arrays of elements. Exp. Fluid. 2013, 54, 1–16. [Google Scholar] [CrossRef]
- Fathi-Maghadam, M.; Kouwen, N.; Nonsubmerged, N. Vegetative Roughness on Floodplains. J. Hydraul. Eng. 1997, 123, 51–57. [Google Scholar] [CrossRef]
- Chen, Z.; Ortiz, A.; Zong, L.; Nepf, H.M. The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 2012, 48, W09517. [Google Scholar] [CrossRef]
- Mitul, L.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 2008, 8, 423–439. [Google Scholar] [CrossRef]
- Wu, F.-C.; Shen, H.W.; Chou, Y.-J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, 1–16. [Google Scholar] [CrossRef]
- Pu, J.H.; Wei, J.; Huang, Y. Velocity Distribution and 3D Turbulence Characteristic Analysis for Flow over Water-Worked Rough Bed. Water 2017, 9, 668. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Analytical model for predicting the longitudinal profiles of velocities in a channel with a model vegetation patch. J. Hydrol. 2019, 576, 561–574. [Google Scholar] [CrossRef]
- Tong, X.; Liu, X.; Yang, T.; Hua, Z.; Wang, Z.; Liu, J.; Li, R. Hydraulic Features of Flow through Local Non-Submerged Rigid Vegetation in the Y-Shaped Confluence Channel. Water 2019, 11, 146. [Google Scholar] [CrossRef]
- Heidari, M. Wake Characteristics of Single and Tandem Emergent Cylinders in Shallow Open Channel Flow. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2016. [Google Scholar]
- Nicolle, A.; Eames, I. Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 2011, 679, 1–31. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, WR005651. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M. Partially obstructed channel: Contraction ratio effect on the flow hydrodynamic structure and prediction of the transversal mean velocity profile. J. Hydrol. 2016, 542, 87–100. [Google Scholar] [CrossRef]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic Behavior of Partly Vegetated Open Channels. J. Hydraul. Eng. 1996, 122, 625–633. [Google Scholar] [CrossRef]
- Ikeda, S.; Yamada, T.; Toda, Y. Numerical study on turbulent flow and honami in and above flexible plant canopy. Int. J. Heat Fluid Flow 2001, 22, 252–258. [Google Scholar] [CrossRef]
- Kim, S.J.; Stoesser, T. Closure modelling and direct simulation of vegetation drag in flow through emergent vegetation. Water Resour. Res. 2011, 47, W10511. [Google Scholar] [CrossRef]
- Anjum, N.; Tanaka, N. Study on the flow structure around discontinued vertically layered vegetation in an open channel. J. Hydrodyn. 2019. [Google Scholar] [CrossRef]
- Yamasaki, T.N.; de Lima, P.H.; Silva, D.F.; Cristiane, G.D.A.; Janzen, J.G.; Johannes, G.; Nepf, H.M. From patch to channel scale: The evolution of emergent vegetation in a channel. Adv. Water Res. 2019, 129, 131–145. [Google Scholar] [CrossRef]
- Pu, J.H.; Hussain, A.; Guo, Y.; Vardakastanis, N.; Hanmaiahgari, R.; Lam, D. Submerged Flexible Vegetation Impact toward Open Channel Flow Velocity Distribution: An Analytical Modelling Study on Drag and Friction. Water Sci. Eng. 2019, 12, 121–128. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, Turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Musleh, F.; Cruise, J. Functional Relationships of Resistance in Wide Flood Plains with Rigid Unsubmerged Vegetation. J. Hydraul. Eng. 2006, 132, 163–171. [Google Scholar] [CrossRef]
- Maji, S.; Pal, D.; Hanmaiahgari, P.R.; Pu, J.H. Phenomenological Features of Turbulent Hydrodynamics in Sparsely Vegetated Open Channel Flow. J. Appl. Fluid Mech. 2016, 9, 2865–2875. [Google Scholar] [CrossRef]
- Pu, J.H.; Tait, S.; Guo, Y.; Huang, Y.; Hanmaiahgari, R. Dominant Features in Three-Dimensional Turbulence Structure: Comparison of Non-Uniform Accelerating and Decelerating Flows. Environ. Fluid Mech. 2018, 18, 395–416. [Google Scholar] [CrossRef]
- Maji, S.; Pal, D.; Hanmaiahgari, R.; Gupta, U. Hydrodynamics and turbulence in emergent and sparsely vegetated open channel flow. Environ. Fluid Mech. 2017, 17, 853–877. [Google Scholar] [CrossRef]
- Heidari, M.; Balachandar, R.; Roussinova, V.; Barron, R.M. Characteristics of flow past a slender, emergent cylinder in shallow open channels. Phys. Fluid. 2017, 29, 065111. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hashimoto, H.; Hayashi, K. Effect of tall vegetation on sediment transport by channel flows. J. Hydraul. Res. 2009, 47, 700–710. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Crosato, A.; Uijttewaal, W.S.J. Effects of vegetation on flow and sediment transport: Comparative analyses and validation of predicting models. Earth. Surf. Proc. Landf. 2015, 40, 157–176. [Google Scholar] [CrossRef]
- Baptist, M.J. Modelling Floodplain Biogeomorphology. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, Y. Drag coefficient for rigid vegetation in subcritical open-channel flow. Environ. Fluid Mech. 2017, 17, 1035–1050. [Google Scholar] [CrossRef]
- Van Rooijen, A.; Lowe, R.; Ghisalberti, M.; Conde-Frias, M.; Tan, L. Predicting Current-Induced Drag in Emergent and Submerged Aquatic Vegetation Canopies. Front. Mar. Sci. 2018, 5, 449. [Google Scholar] [CrossRef]
- Wang, W.J.; Huaia, W.X.; Thompson, S.; Peng, W.Q.; Katul, G.G. Drag coefficient estimation using flume experiments in shallow non-uniform water flow within emergent vegetation during rainfall. Ecol. Indic. 2018, 92, 367–378. [Google Scholar] [CrossRef]
- Shan, Y.; Liu, C.; Nepf, H. Comparison of drag and velocity in model mangrove forests with random and in-line tree distributions. J. Hydrol. 2019, 568, 735–746. [Google Scholar] [CrossRef]
- Razmi, A.; Chamecki, M.; Nepf, H.M. Efficient numerical representation of the impacts of flexible plant reconfiguration on canopy posture and hydrodynamic drag. J. Hydraul. Res. 2019. [Google Scholar] [CrossRef]
- Perucca, E.; Camporeale, C.; Ridolfi, L. Significance of the riparian vegetation dynamics on meandering river morphodynamics. Water Resour. Res. 2007, 43, W03430. [Google Scholar] [CrossRef]
- Motta, D.; Langendoen, E.J.; Abad, J.D.; García, M.H. Modification of meander migration by bank failures. J. Geophys. Res. Earth Surf. 2014, 119, 1026–1042. [Google Scholar] [CrossRef]
- Liu, D.; Valyrakis, M.; Williams, R. Flow Hydrodynamics across Open Channel Flows with Riparian Zones: Implications for Riverbank Stability. Water 2017, 9, 720. [Google Scholar] [CrossRef]
- Thorne, C.R. Effects of vegetation on riverbank erosion and stability. In Vegetation and Erosion; Thorne, J.B., Ed.; John Wiley and Sons: Chichester, UK, 1990; pp. 125–144. [Google Scholar]
- Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability. Earth. Surf. Proc. Landf. 2010, 27, 527–546. [Google Scholar] [CrossRef]
- Hopkinson, L.; Wynn, T. Vegetation impacts on near bank flow. Ecohydrology 2009, 2, 404–418. [Google Scholar] [CrossRef]
- Baets, S.D.; Poesen, J.; Reubensm, B.; Wemans, J.; Baerdemaeker, D.; Muys, B. Root tensile strength and root distribution of typical Mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The effect of riparian tree roots on the mass-stability of riverbanks. Earth. Surf. Proc. Landf. J. Br. Geomorphol. Res. Group 2000, 25, 921–937. [Google Scholar] [CrossRef]
- Pollen, N. Temporal and spatial variability in root reinforcement of streambanks: Accounting for soil shear strength and moisture. Catena 2007, 69, 197–205. [Google Scholar] [CrossRef]
- Tal, M.; Paola, C. Effects of vegetation on channel morphodynamics: Results and insights from laboratory experiments. Earth. Surf. Proc. Landf. 2010, 35, 1014–1028. [Google Scholar] [CrossRef]
- Krzeminska, D.; Kerkhof, T.; Skaalsveen, K.; Stolte, J. Effect of riparian vegetation on stream bank stability in small agricultural catchments. Catena 2019, 172, 87–96. [Google Scholar] [CrossRef]
- Hupp, C.R.; Osterkamp, W.R. Riparian vegetation and fluvial geomorphic processes. Geomorphology 1996, 14, 277–295. [Google Scholar] [CrossRef]
- Tooth, S.; Nanson, G.C. The role of vegetation in the formation of anabranching channels in an ephemeral river, Northern Plains, arid central Australia. Hydrol. Process. 2000, 14, 3099–3117. [Google Scholar] [CrossRef]
- Micheli, E.R.; Kirchner, J.W.; Larsen, E.W. Quantifying the effect of riparian forest versus agricultural vegetation on river meander migration rates, central Sacramento river, California, USA. River Res. Appl. 2010, 20, 537–548. [Google Scholar] [CrossRef]
- Hickin, E.J. Vegetation and river channel dynamics. Can. Geogr. 1984, 28, 111–126. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A.; Collision, A.J.C. Advances in assessing the mechanical and hydrologic effect of riparian vegetation on streambank stability. Riparian Veg. Fluv. Geomorphol. 2004, 8, 125–139. [Google Scholar]
- Graf, W.L. Fluvial Processes in Dryland Rivers; Springer: Berlin, Germany, 1988. [Google Scholar]
- Birken, A.S.; Cooper, D.J. Processes of Tamarix invasion and floodplain development along the lower Green River Utah. Ecol. Appl. 2006, 16, 1103–1120. [Google Scholar] [CrossRef]
- Braudrick, C.A.; Dietrich, W.E.; Leverich, G.T.; Sklar, L.S. Experimental evidence for the conditions necessary to sustain meandering in coarse bedded rivers. Proc. Natl. Acad. Sci. USA 2009, 106, 16936–16941. [Google Scholar] [CrossRef] [PubMed]
- Camporeale, C.; Perucca, E.; Ridolfi, L.; Gurnell, A.M. Modeling the interactions between river morphodynamics and riparian vegetation. Rev. Geophys. 2013, 51, 379–414. [Google Scholar] [CrossRef]
- Gran, K.; Wartman, E.D. Co-evolution of riparian vegetation and channel dynamics in an aggrading braided river system, Mount Pinatubo. Philippines. Earth Surf. Proc. Landf. 2015, 40, 1101–1115. [Google Scholar] [CrossRef]
- Yu, M.-H.; Wei, H.-Y.; Wu, S.-B. Experimental study on the bank erosion and interaction with near-bank bed evolution due to fluvial hydraulic force. Int. J. Sediment Res. 2015, 30, 81–89. [Google Scholar] [CrossRef]
- Yang, J.Q.; Nepf, H.M. A turbulence-based bed-load transport model for bare and vegetated channels. Geophys. Res. Lett. 2018, 45, 10428–10436. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V. Bed-load through emergent vegetation. Adv. Water Resour. 2019, 129, 250–259. [Google Scholar] [CrossRef]
- Armanini, A.; Cavedon, V.; Righetti, M. A probabilistic/deterministic approach for the prediction of the sediment transport rate. Adv. Water Res. 2015, 81, 10–18. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; Technical Report No. 1026; U.S. Department of Agriculture: Washington, DC, USA, 1950.
- Rowiński, M.; Kubrak, J. A mixing-length model for predicting vertical velocity distribution in flows through emergent vegetation. Hydrol. Sci. J. 2002, 47, 893–904. [Google Scholar] [CrossRef]
- Rubol, S.; Ling, B.; Battiato, I. Universal scaling-law for flow resistance over canopies with complex morphology. Sci. Rep. 2018, 8, 4430. [Google Scholar] [CrossRef] [PubMed]
- Siniscalchi, F.; Nikora, V.I.; Aberle, J. Plant patch hydrodynamics in streams: Mean flow, turbulence, and drag forces. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
- Västilä, K.; Järvelä, J. Modeling the flow resistance of woody vegetation using physically based properties of the foliage and stem. Water Resour. Res. 2014, 50, 229–245. [Google Scholar] [CrossRef]
- Caroppi, G.; Västilä, K.; Järvelä, J.; Rowiński, M.; Giugni, M. Turbulence at water-vegetation interface in open channel flow: Experiments with natural-like plants. Adv. Water Resour. 2019, 127, 180–191. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res. Earth Surf. 2013, 118, 42–53. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, C.L.; Dancey, K.; Greer, K.; Celik, A.O. Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef]
- Licci, S.; Nepf, H.M.; Delolme, C.; Marmonier, P.; Bouma, T.J.; Puijalon, S. The role of patch size in ecosystem engineering capacity: A case study of aquatic vegetation. Aquat. Sci. 2019, 81. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maji, S.; Hanmaiahgari, P.R.; Balachandar, R.; Pu, J.H.; Ricardo, A.M.; Ferreira, R.M.L. A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels. Water 2020, 12, 1218. https://doi.org/10.3390/w12041218
Maji S, Hanmaiahgari PR, Balachandar R, Pu JH, Ricardo AM, Ferreira RML. A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels. Water. 2020; 12(4):1218. https://doi.org/10.3390/w12041218
Chicago/Turabian StyleMaji, Soumen, Prashanth Reddy Hanmaiahgari, Ram Balachandar, Jaan H. Pu, Ana M. Ricardo, and Rui M.L. Ferreira. 2020. "A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels" Water 12, no. 4: 1218. https://doi.org/10.3390/w12041218
APA StyleMaji, S., Hanmaiahgari, P. R., Balachandar, R., Pu, J. H., Ricardo, A. M., & Ferreira, R. M. L. (2020). A Review on Hydrodynamics of Free Surface Flows in Emergent Vegetated Channels. Water, 12(4), 1218. https://doi.org/10.3390/w12041218







