SPH Simulation of Interior and Exterior Flow Field Characteristics of Porous Media
Abstract
1. Introduction
2. Smooth Particle Hydrodynamics (SPH) Methodology
3. SPH Model
3.1. Equations for Flow Field Porous Media
3.2. Numerical Model Solving Process
3.3. Boundary Conditions
3.3.1. Free Surface Boundary
3.3.2. Fluid-Structure Coupling Boundary
3.3.3. Impermeable/Fixed Solid Wall Boundary
3.3.4. Periodic Inflow and Outflow Boundaries Accompanied with a Damping Zone
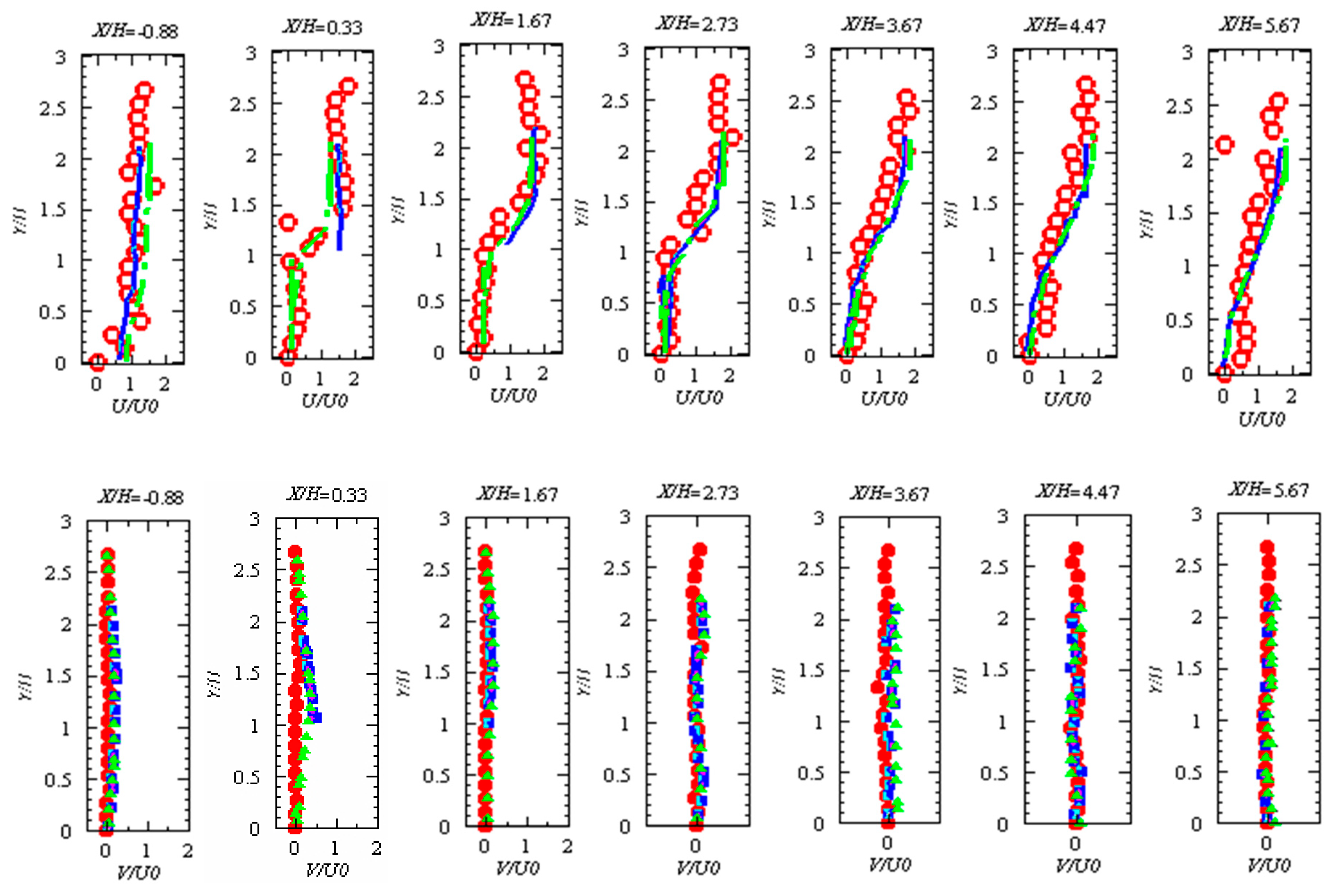
4. Model Verification
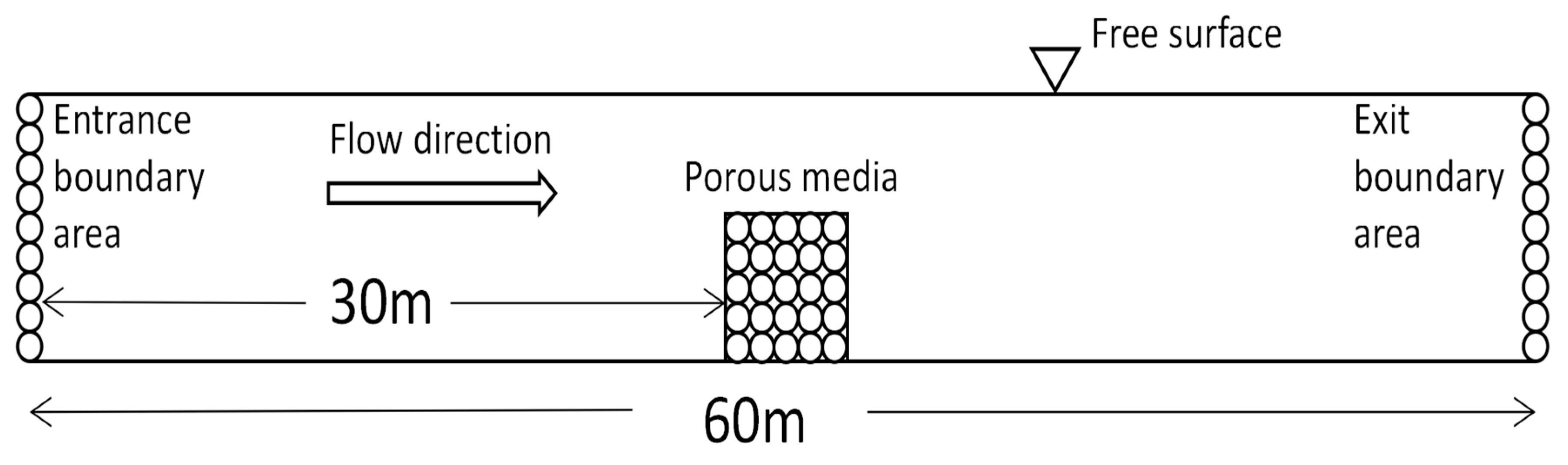
5. Model Application
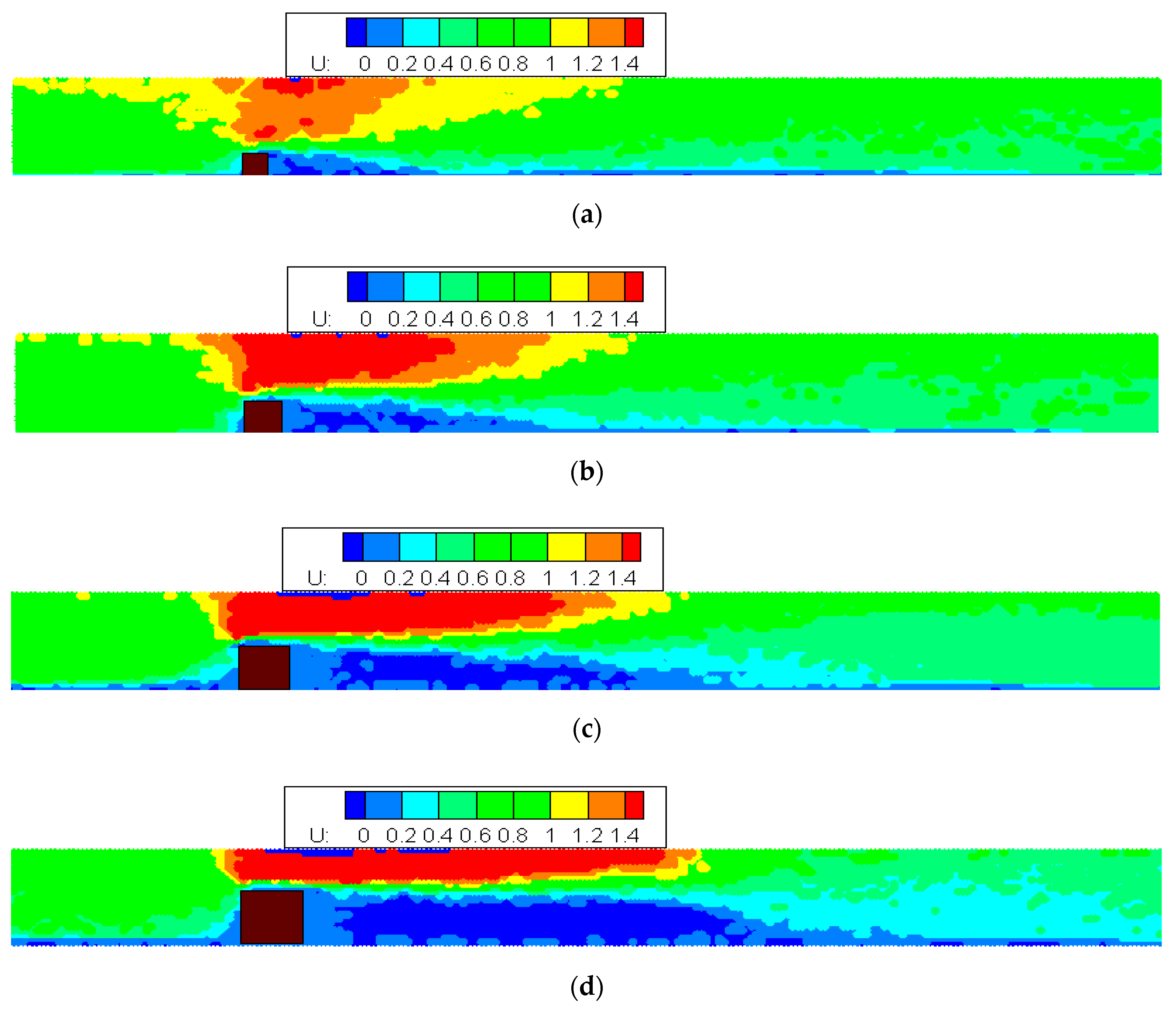
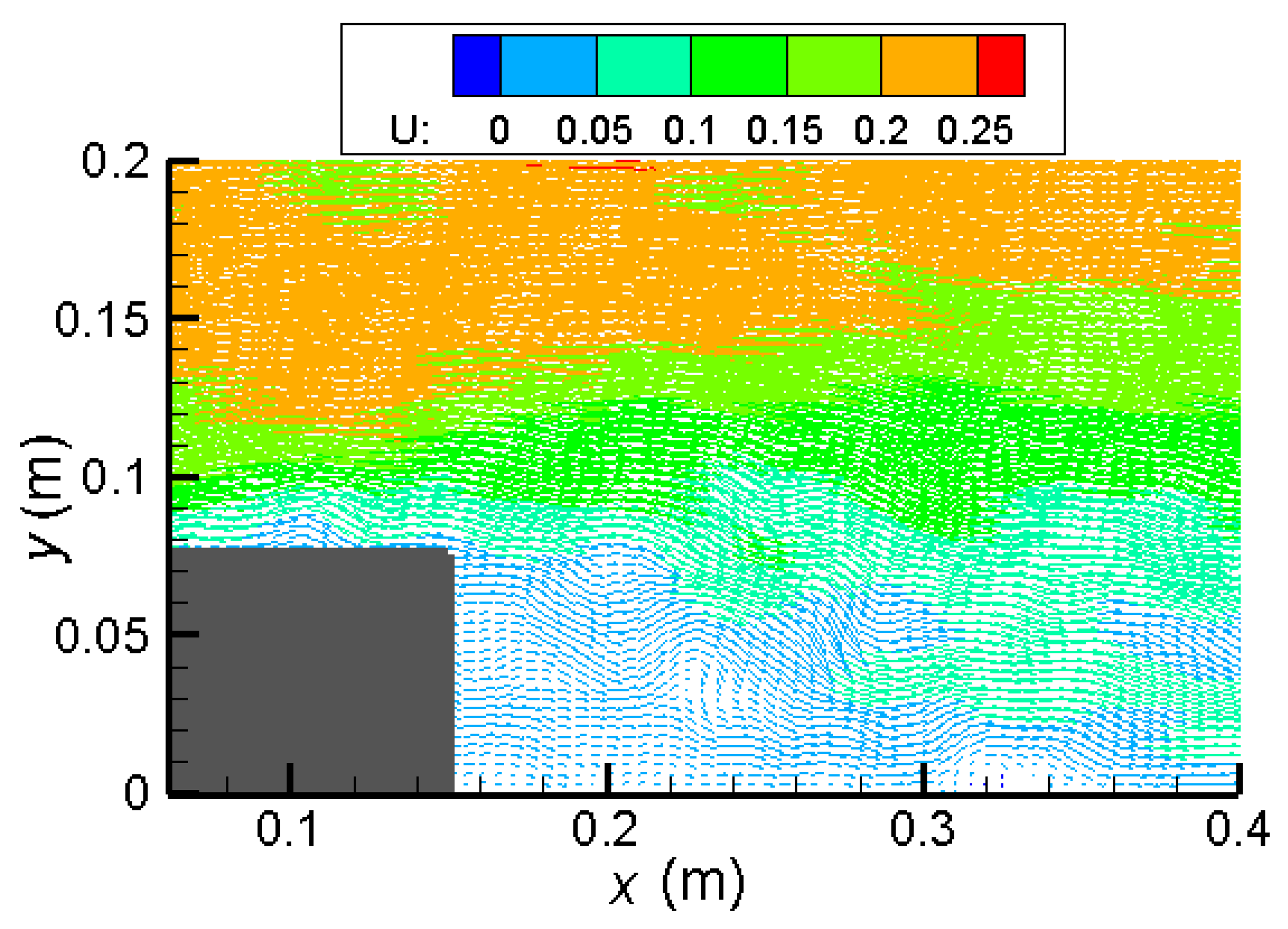
5.1. Flow Field Velocity Distribution Diagram of Different Volumes of Porous Media
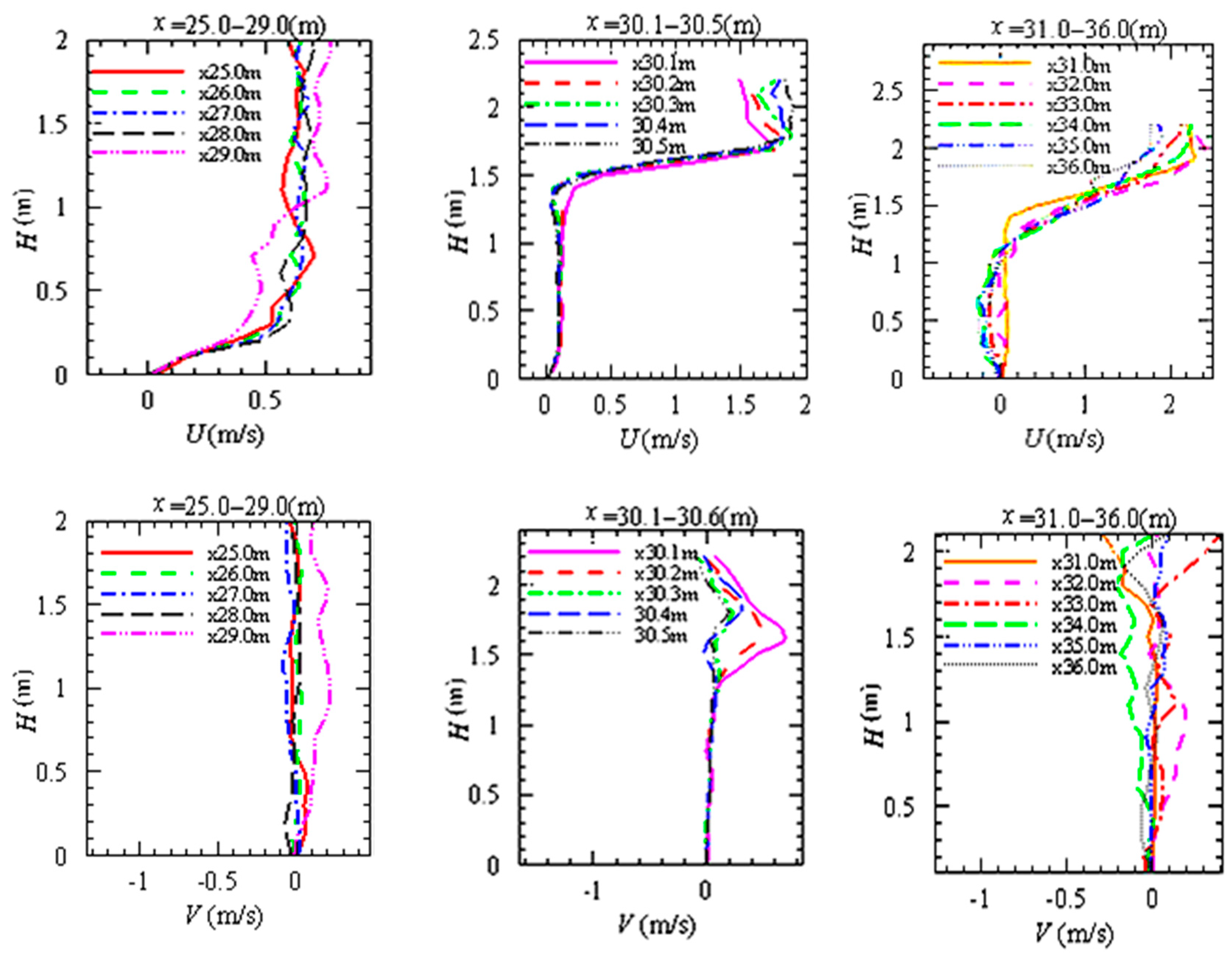
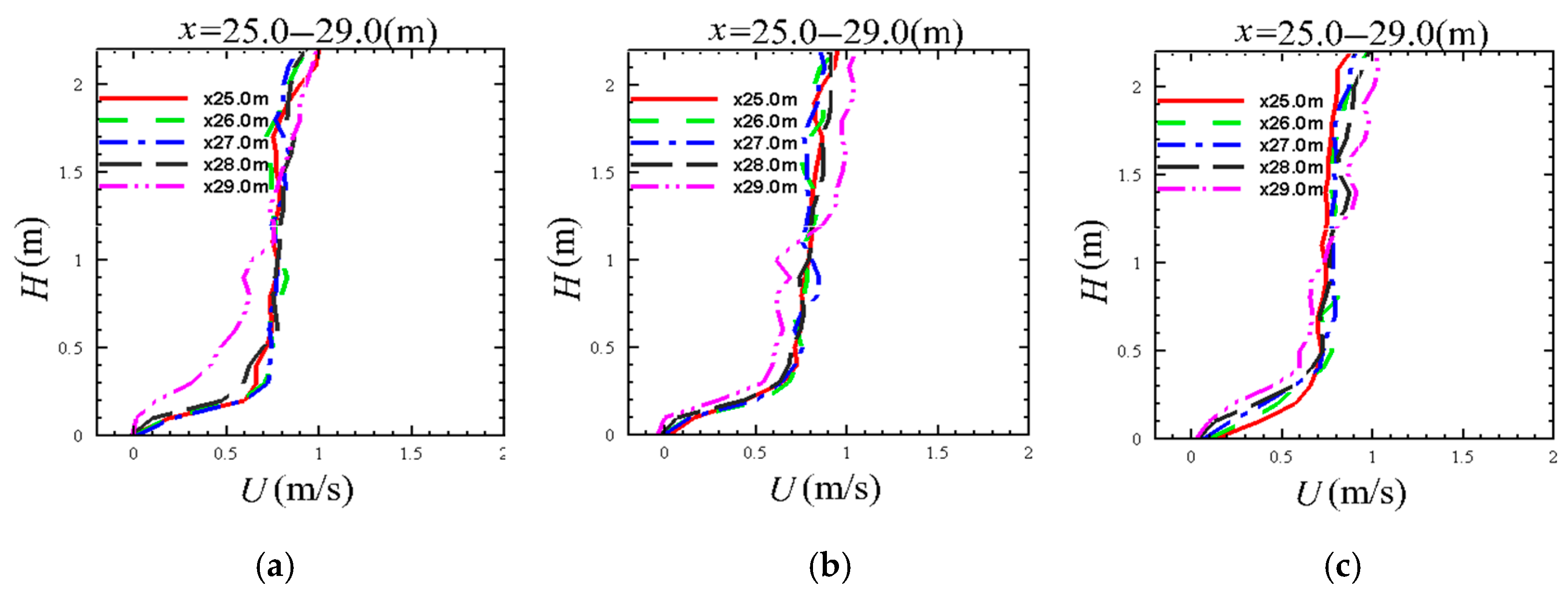
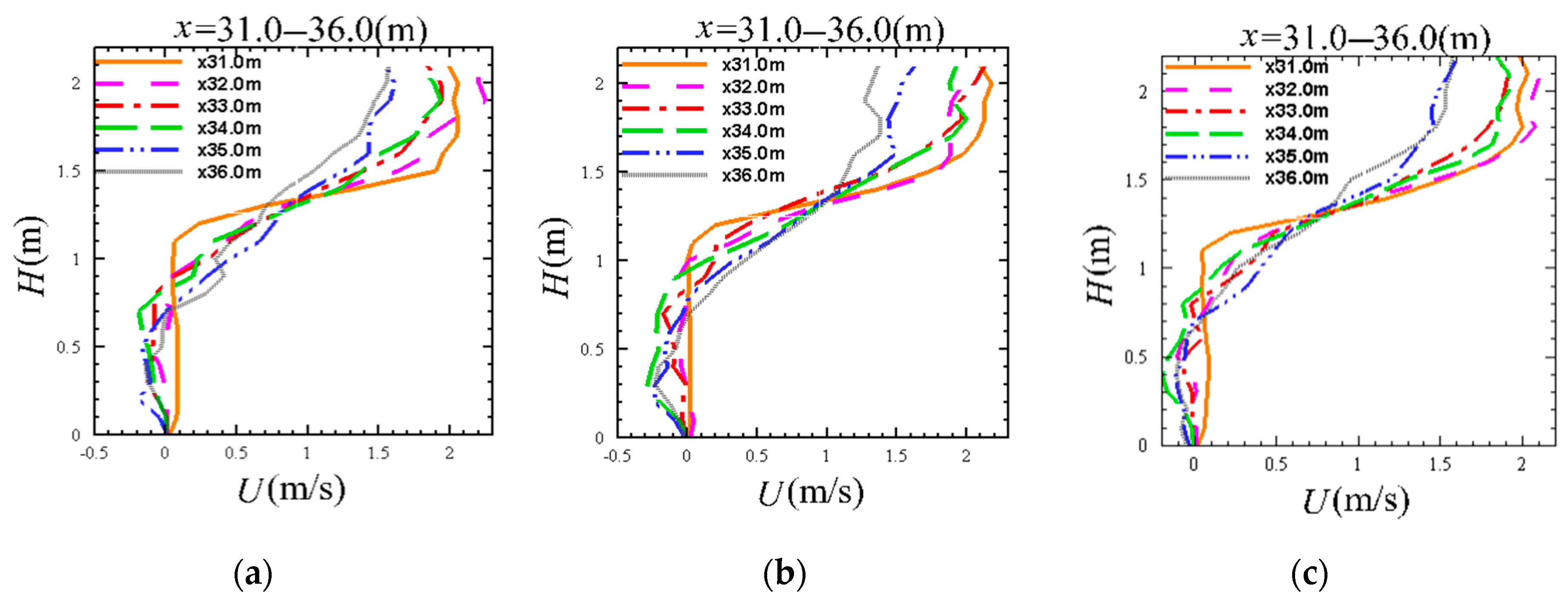
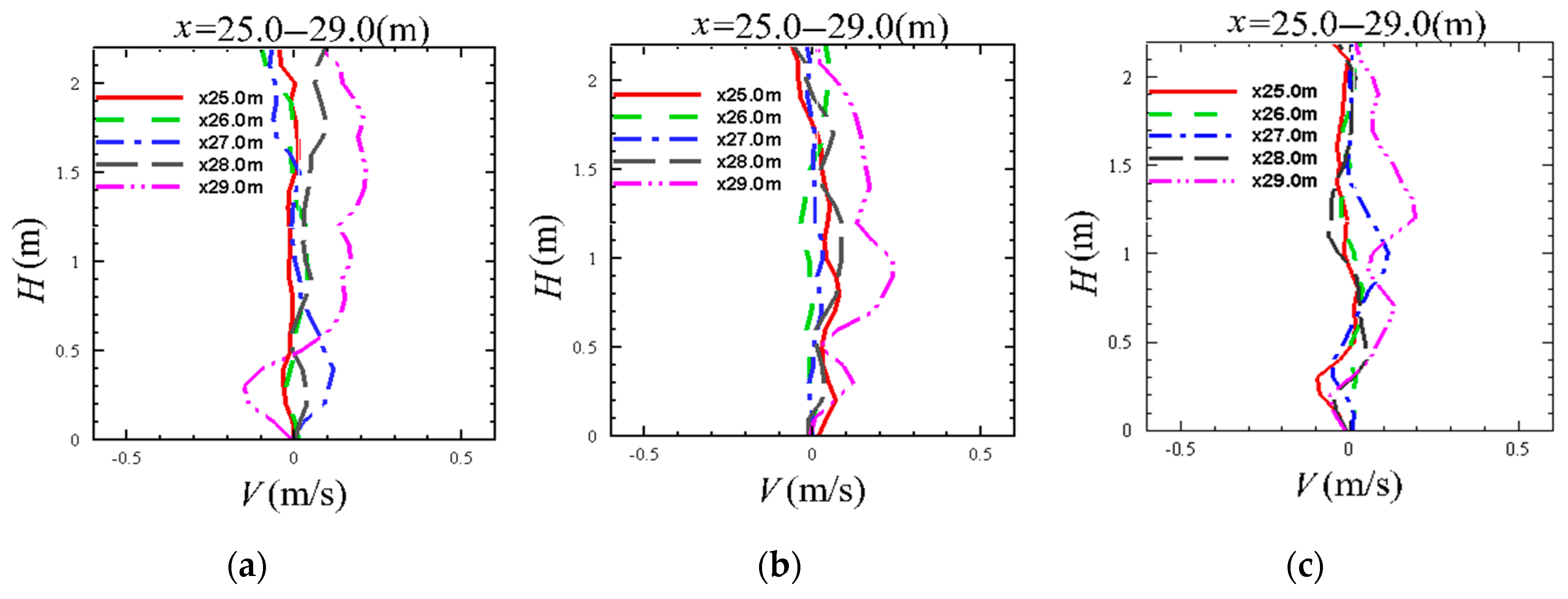
5.2. Analysis of Flow Field Inside and Outside the Porous Media
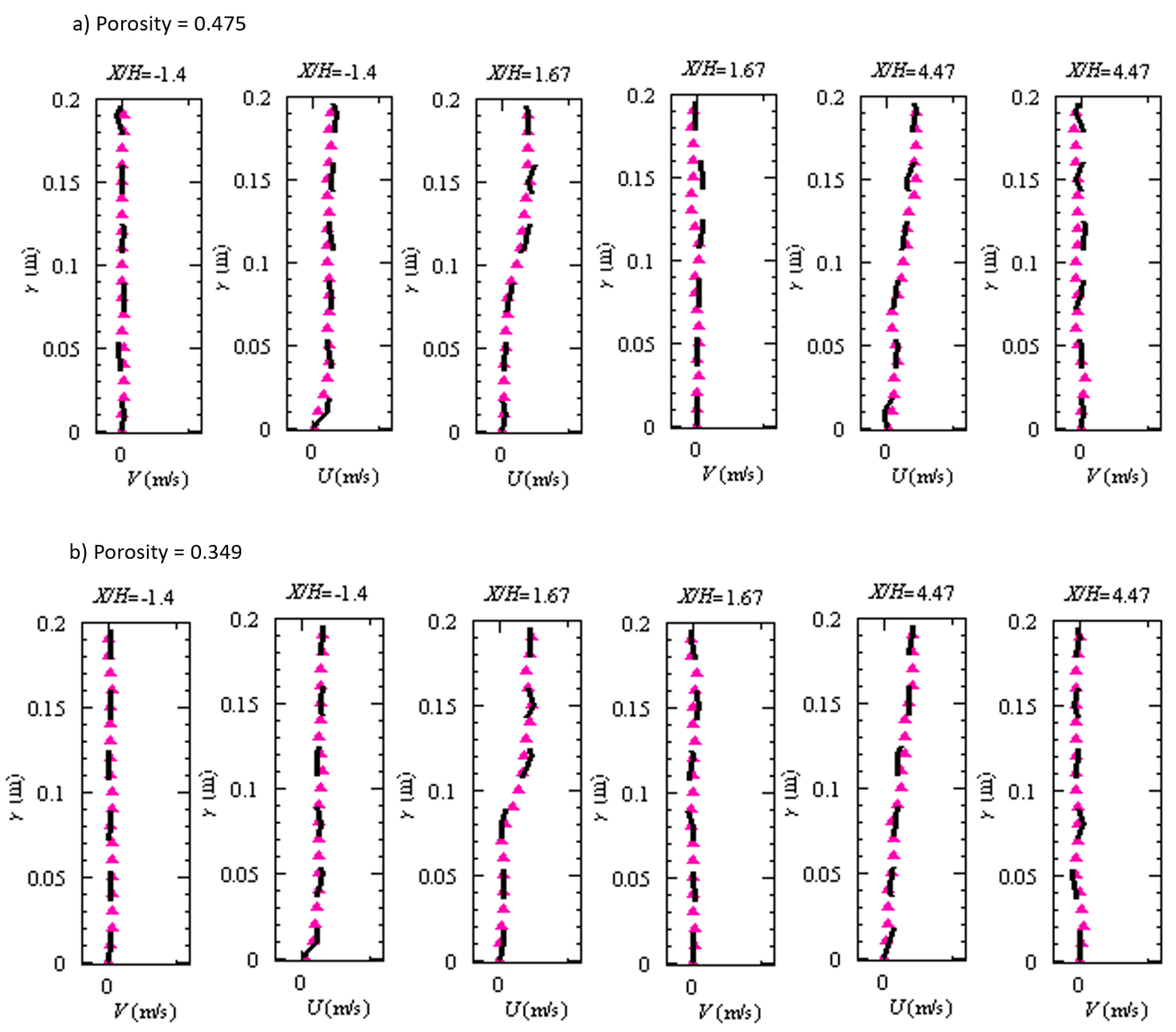
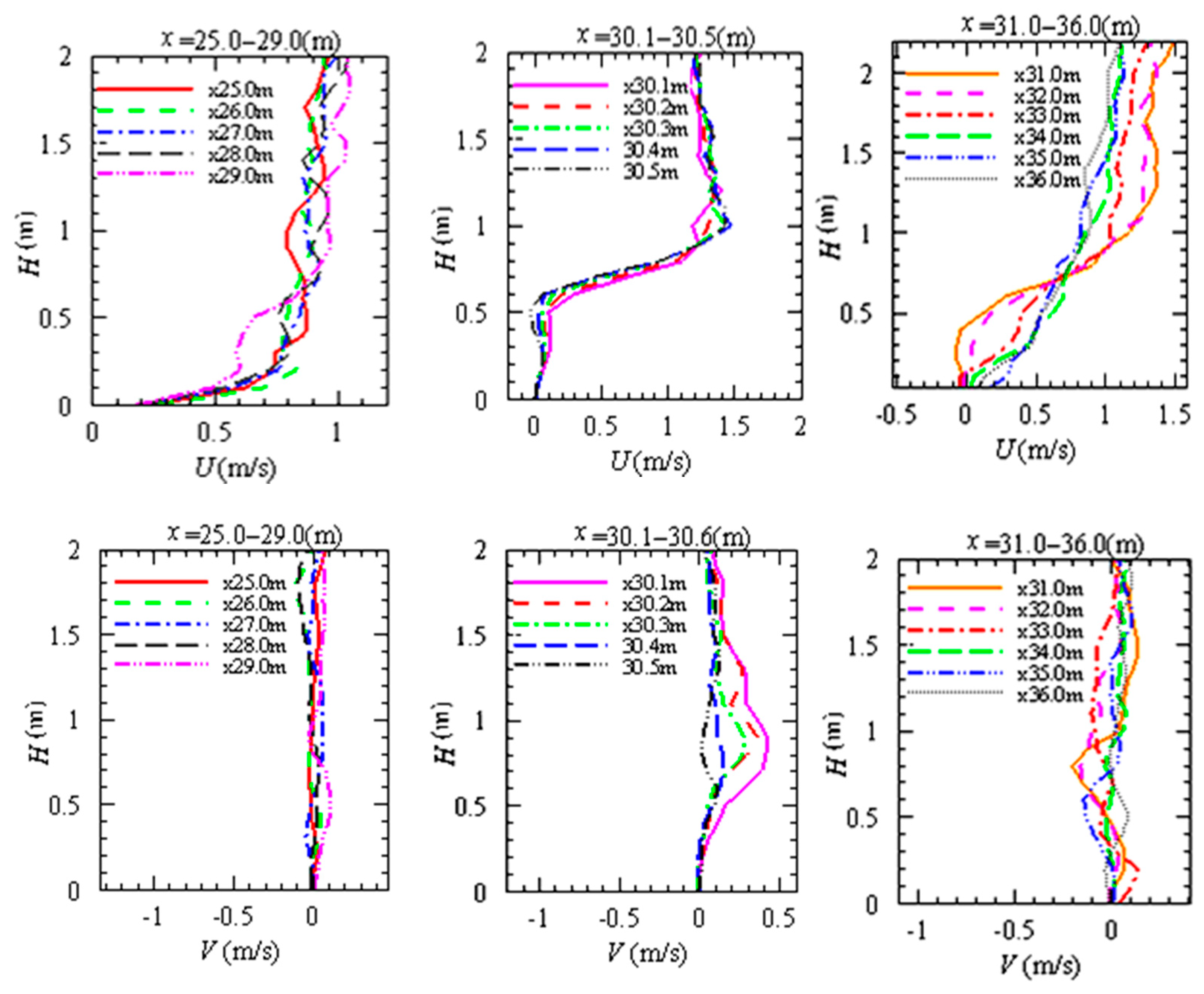
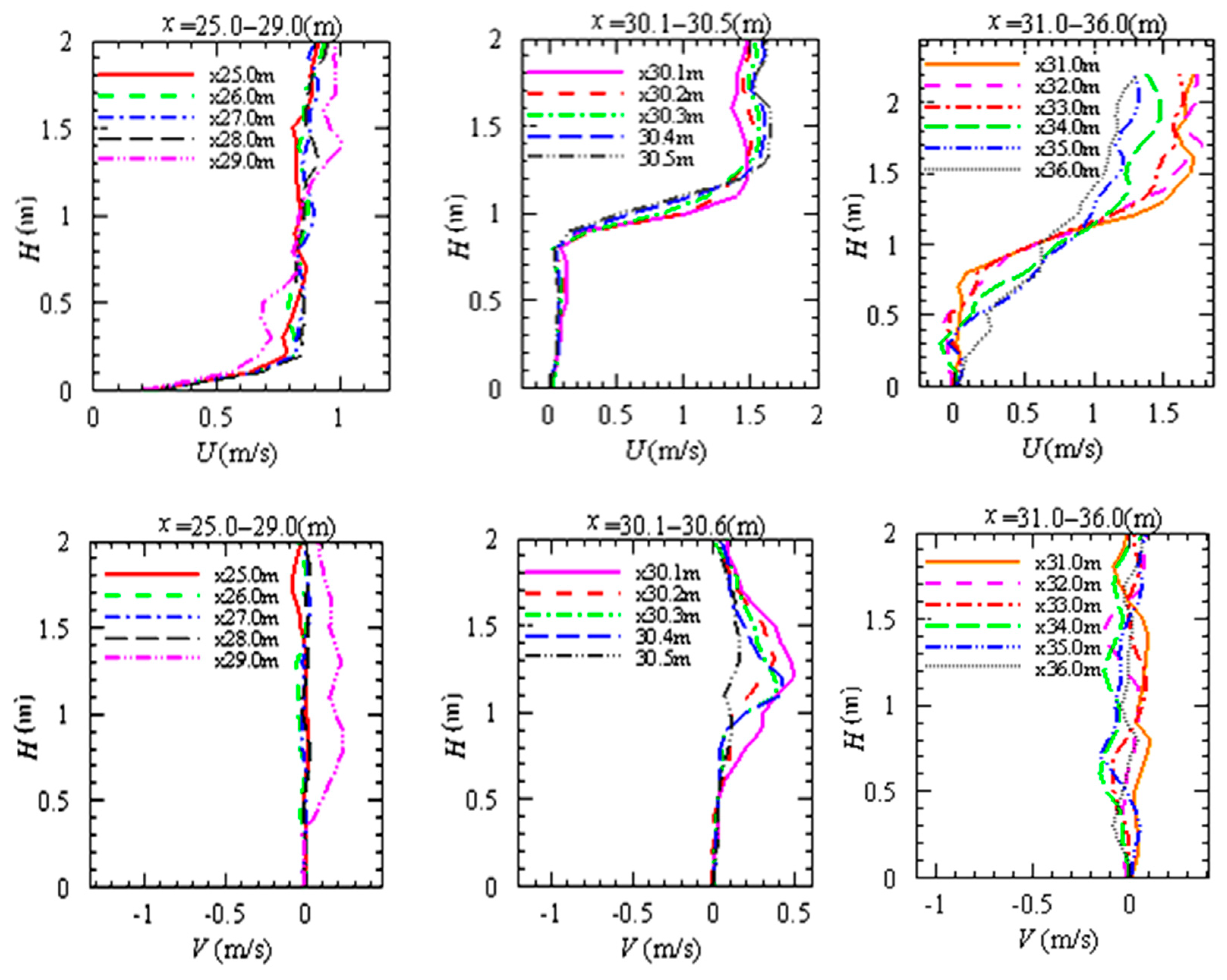
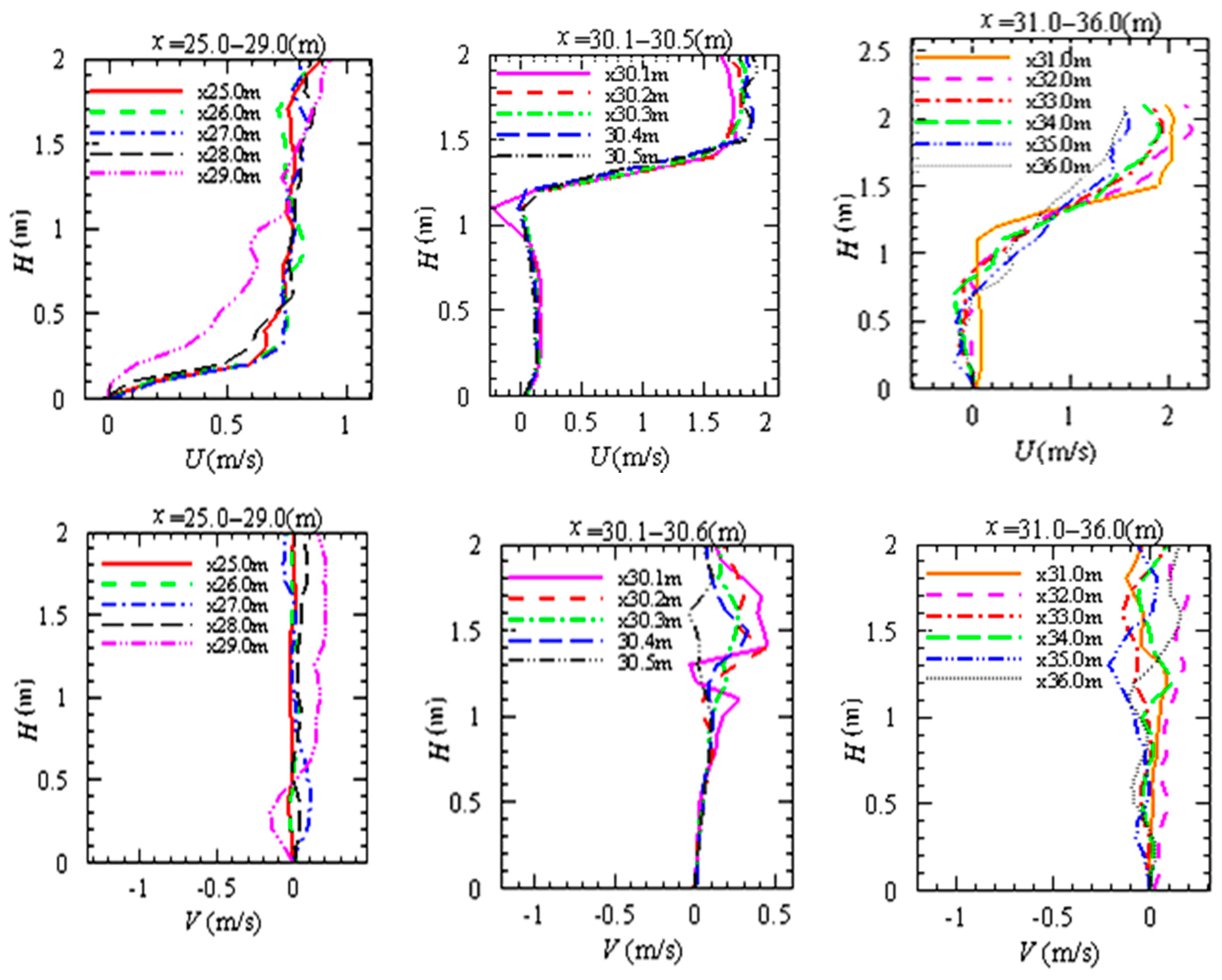
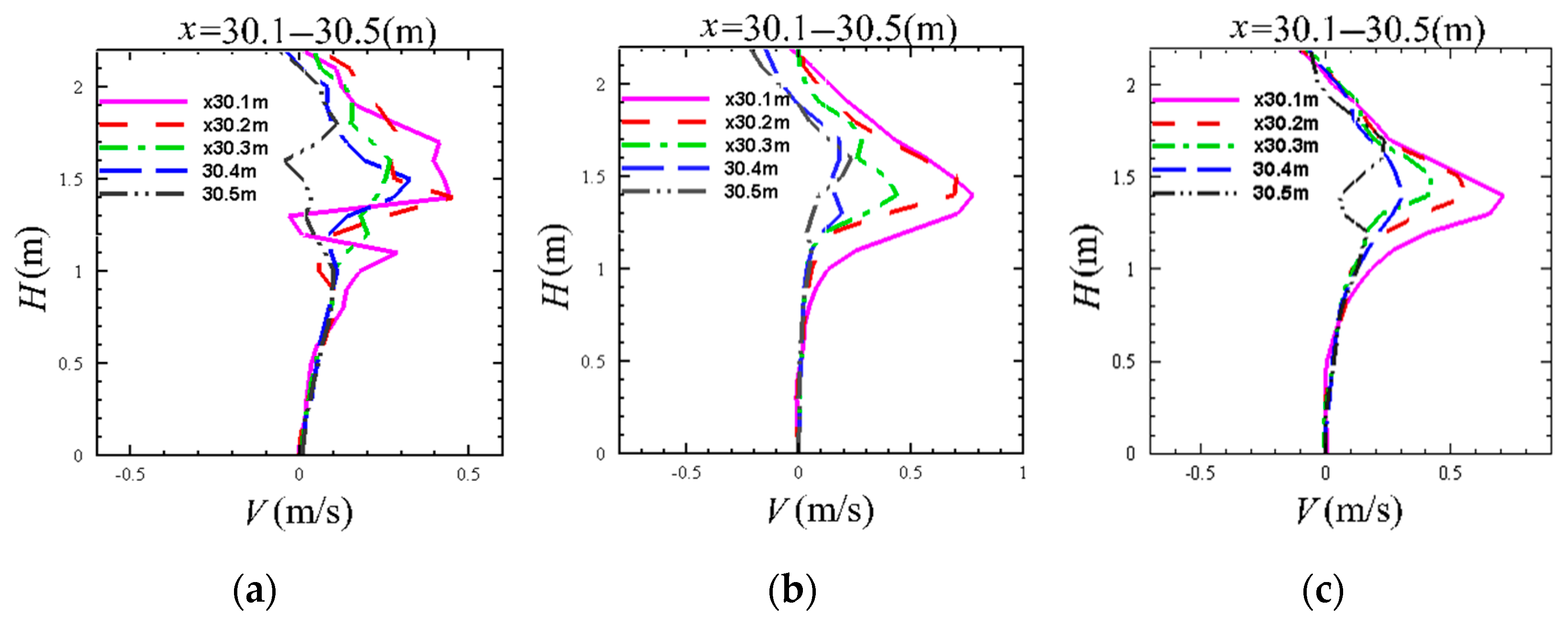
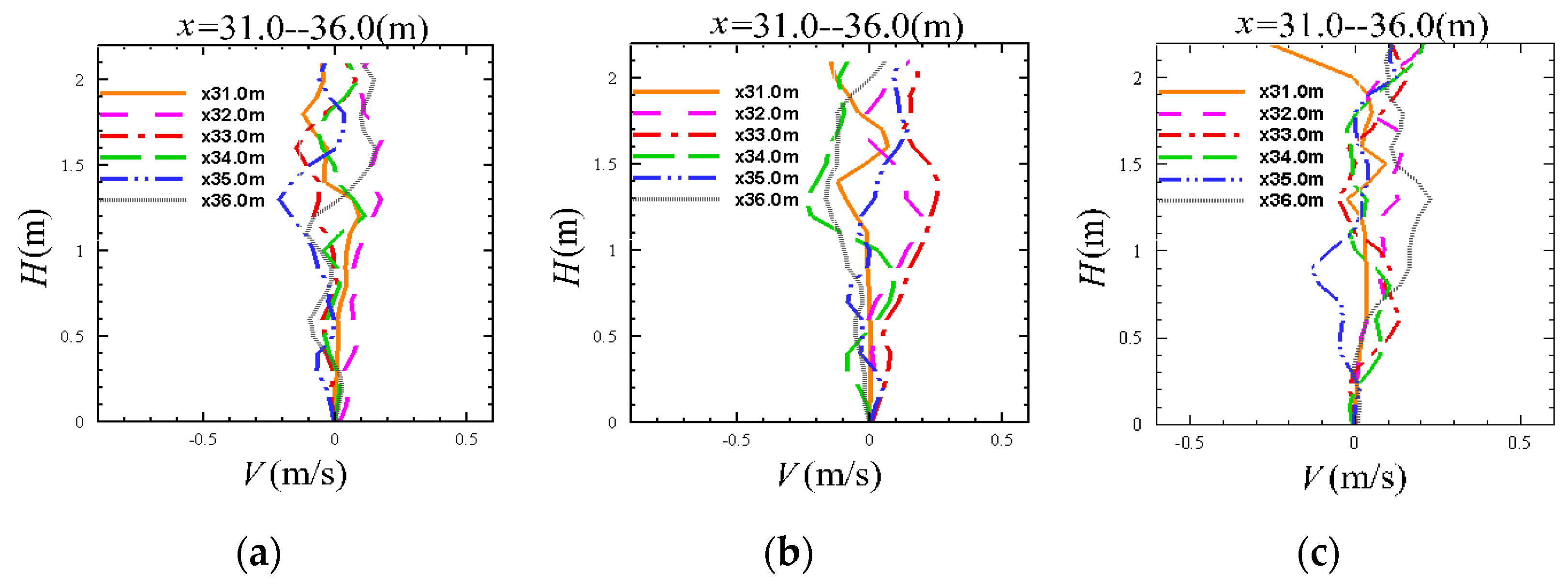
5.3. Longitudinal and Vertical Flow Field Distribution under Different Porosity
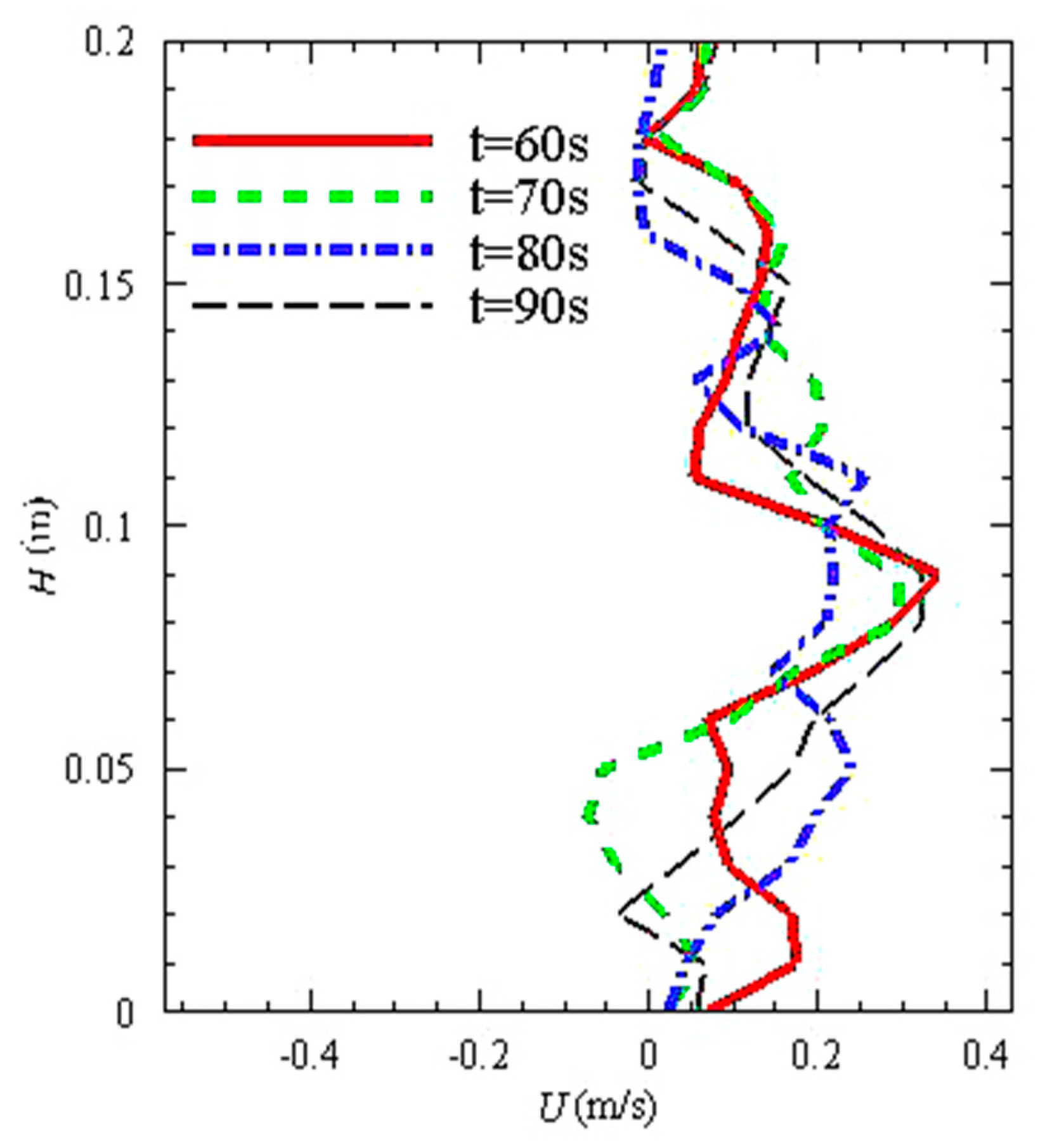
5.4. Convergence Verification of Pore Logistics Field Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Espinoza-Andaluz, M.; Velasco-Galarza, V.; Romero-Vera, A. On hydraulic tortuosity variations due to morphological considerations in 2D porous media by using the Lattice Boltzmann method. Math. Comput. Simul. 2020, 169, 74–87. [Google Scholar] [CrossRef]
- Akbari, H. Modified moving particle method for modeling wave interaction with multi layered porous structures. Coast. Eng. 2014, 89, 1–19. [Google Scholar] [CrossRef]
- Houreh, N.B.; Shokouhmand, H.; Afshari, E. Effect of inserting obstacles in flow field on a membrane humidifier performance for PEMFC application: A CFD model. Int. J. Hydrog. Energy 2019, 44, 30420–30439. [Google Scholar] [CrossRef]
- Mei, T.-L.; Zhang, T.; Candries, M.; Lataire, E.; Zou, Z.-J. Comparative study on ship motions in waves based on two time domain boundary element methods. Eng. Anal. Bound. Elem. 2020, 111, 9–21. [Google Scholar] [CrossRef]
- Basser, H.; Rudman, M.; Daly, E. SPH modelling of multi-fluid lock-exchange over and within porous media. Adv. Water Resour. 2017, 108, 15–28. [Google Scholar] [CrossRef]
- Aganetti, R.; Lamorlette, A.; Thorpe, G.R. The relationship between external and internal flow in a porous body using the penalisation method. Int. J. Heat Fluid Flow 2017, 66, 185–196. [Google Scholar] [CrossRef]
- Chan, H.C.; Leu, J.M.; Lai, C.J. Velocity and turbulence field around permeable structure:Comparisons between laboratory and numerical experiments. J. Hydraul. Res. 2007, 45, 216–226. [Google Scholar] [CrossRef]
- Gui, Q.; Dong, P.; Shao, S.; Chen, Y. Incompressible SPH simulation of wave interaction with porous structure. Ocean Eng. 2015, 110, 126–139. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shimizu, Y.; Gotoh, K.; Falahaty, H.; Shao, S. Development of a projection-based SPH method for numerical wave flume with porous media of variable porosity. Coast. Eng. 2018, 140, 1–22. [Google Scholar] [CrossRef]
- Vanneste, D.; Troch, P. 2D numerical simulation of large-scale physical model tests of wave interaction with a rubble-mound breakwater. Coast. Eng. 2015, 103, 22–41. [Google Scholar] [CrossRef]
- Shao, S. Incompressible SPH flow model for wave interactions with porous media. Coast. Eng. 2010, 57, 304–316. [Google Scholar] [CrossRef]
- Gnanasekaran, B.; Liu, G.-R.; Fu, Y.; Wang, G.; Niu, W.; Lin, T. A Smoothed Particle Hydrodynamics (SPH) procedure for simulating cold spray process—A study using particles. Surf. Coat. Technol. 2019, 377, 124812. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touze, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial appliactions: Motivations, current state and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Niu, X.; Zhao, J.; Wang, B. Application of smooth particle hydrodynamics (SPH) method in gravity casting shrinkage activity prediction. Comput. Part. Mech. 2019, 6, 803–810. [Google Scholar] [CrossRef]
- Yin, J.P.; Shi, Z.X.; Chen, J.; Chang, B.H.; Yi, J.Y. Smooth particle hydrodynamics-based characteristics of a shaped jet from different materials. Strength Mater. 2019, 51, 85–94. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Chiogna, G.; Bellin, A. An alternative smooth particle hydrodynamics formulation to simulate chemotaxis in porous media. J. Math. Biol. 2017, 74, 1037–1058. [Google Scholar] [CrossRef]
- Eghtesad, A.; Knezevic, M. A new approach to fluid–structure interaction within graphics hardware accelerated smooth particle hydrodynamics considering heterogeneous particle size distribution. Comput. Part. Mech. 2018, 5, 387–409. [Google Scholar] [CrossRef]
- Yang, H.X.; Li, R.; Lin, P.Z.; Wan, H.; Feng, J. Two-phase smooth particle hydrodynamics modeling of air-water interface in aerated flows. Sci. China Technol. Sci. 2017, 60, 479–490. [Google Scholar] [CrossRef]
- Shao, S. Incompressible smoothed particle hydrodynamics simulation of multifluid flows. Int. J. Numer. Methods Fluids 2011, 69, 11. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Shao, S.D. Corrected incompressible SPH method for accurate water-surface tracking in breaking waves. Coast. Eng. 2008, 55, 236–250. [Google Scholar] [CrossRef]
- Shao, S.; Gotoh, H. Turbulence particle models for tracking free surfaces. J. Hydraul. Res. 2010, 43, 276–289. [Google Scholar] [CrossRef]
- Wang, S.; Shu, A.; Rubinato, M.; Wang, M.; Qin, J. Numerical Simulation of Non-Homogeneous Viscous Debris-Flows based on the Smoothed Particle Hydrodynamics (SPH) Method. Water 2019, 11, 2314. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y.M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Huang, C.-J.; Chang, H.-H.; Hwung, H.-H. Structural permeability effects on the interaction of a solitary wave and a submerged breakwater. Coast. Eng. 2003, 49, 1–24. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. Comput. Phys. Commun. 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Sun, P.N.; Colagrossi, A.; Le Touze, D.; Zhang, A.M. Extension of the δ-plus-SPH model for simulating vortex-induced-vibration problems. J. Fluids. Struct. 2019, 90, 19–42. [Google Scholar] [CrossRef]
- Rubinato, M.; Martins, R.; Kesserwani, G.; Leandro, J.; Djordjevic, S.; Shucksmith, J. Experimental investigation of the influence of manhole grates on drainage flows in urban flooding conditions. In Proceedings of the 14th IWA/IAHR International Conference on Urban Drainage, Prague, Czech Republic, 10–15 September 2017. [Google Scholar]
- Rubinato, M.; Martins, R.; Kesserwani, G.; Leandro, J.; Djordjevic, S.; Shucksmith, J. Experimental calibration and validation of sewer/surface flow exchange equations in steady and unsteady flow conditions. J. Hydrol. 2017, 552, 421–432. [Google Scholar] [CrossRef]
- Rubinato, M.; Lee, S.; Martins, R.; Shucksmith, J. Surface to sewer flow exchange through circular inlets during urban flood conditions. J. Hydroinform. 2018, 20, 564–576. [Google Scholar] [CrossRef]
- Martins, R.; Rubinato, M.; Kesserwani, G.; Leandro, J.; Djordjević, S.; Shucksmith, J.D. On the Characteristics of Velocities Fields in the Vicinity of Manhole Inlet Grates During Flood Events. Water Resour. Res. 2018, 54, 6408–6422. [Google Scholar] [CrossRef]
- Nichols, A.; Rubinato, M. Remote sensing of environmental processes via low-cost 3D free-surface mapping. In Proceedings of the 4th IHAR Europe Congress, Liege, Belgium, 27–29 July 2016. [Google Scholar]
- Lopes, P.; Shucksmith, J.; Leandro, J.; de Fernandes Carvalho, R.; Rubinato, M. Velocities profiles and air-entrainment characterization in a scaled circular manhole. In Proceedings of the 13th ICUD, Sawarak, Malaysia, 7–12 September 2014. [Google Scholar]
- Rojas Arques, S.; Rubinato, M.; Nichols, A.; Shucksmith, J.D. Cost effective measuring technique to simultaneously quantify 2D velocity fields and depth-averaged solute concentrations in shallow water flows. Flow Meas. Instrum. 2018, 64, 213–223. [Google Scholar] [CrossRef]
- Beg, M.N.A.; Carvalho, R.F.; Tait, S.; Brevis, W.; Rubinato, M.; Schellart, A.; Leandro, J. A comparative study of manhole hydraulics using stereoscopic PIV and different RANS models. Water Sci. Tech. 2018, 2017, 87–98. [Google Scholar] [CrossRef]
- Cavelan, A.; Boussafir, M.; Rozenbaum, O.; Laggoun-Défarge, F. Organic petrography and pore structure characterization of low-mature and gas-mature marine organic-rich mudstones: Insights into porosity controls in gas shale systems. Mar. Pet. Geol. 2019, 103, 331–350. [Google Scholar] [CrossRef]
- Zheng, X.; Ma, Q.; Shao, S.; Khayyer, A. Modelling of Violent Water Wave Propagation and Impact by Incompressible SPH with First-Order Consistent Kernel Interpolation Scheme. Water 2017, 9, 400. [Google Scholar] [CrossRef]
- Lo, E.Y.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean. Res. 2002, 24, 275–286. [Google Scholar]







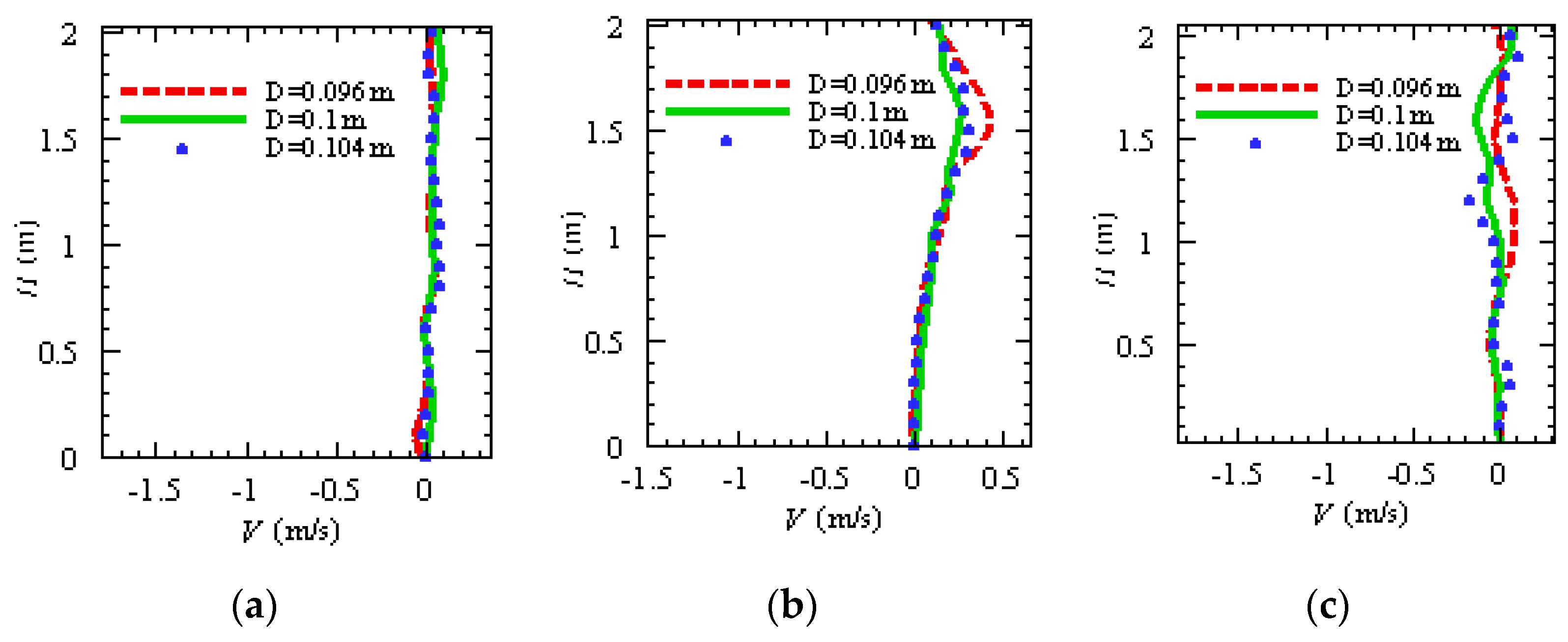

| Particle Size D (m) | Total Number of Particles | Total Physical Simulation Time (s) | CPU Time | CPU Cores |
|---|---|---|---|---|
| 0.0104 | 13,914 | 100 | 27 h 05 min | 4 |
| 0.01 | 15,000 | 100 | 27 h 14 min | 4 |
| 0.096 | 16,225 | 100 | 8 h 28 min | 20 |
| 0.1 | 15,000 | 100 | 8 h 23 min | 20 |
| 0.104 | 13,914 | 100 | 8 h 18 min | 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Rubinato, M.; Gui, Q. SPH Simulation of Interior and Exterior Flow Field Characteristics of Porous Media. Water 2020, 12, 918. https://doi.org/10.3390/w12030918
Wu S, Rubinato M, Gui Q. SPH Simulation of Interior and Exterior Flow Field Characteristics of Porous Media. Water. 2020; 12(3):918. https://doi.org/10.3390/w12030918
Chicago/Turabian StyleWu, Shijie, Matteo Rubinato, and Qinqin Gui. 2020. "SPH Simulation of Interior and Exterior Flow Field Characteristics of Porous Media" Water 12, no. 3: 918. https://doi.org/10.3390/w12030918
APA StyleWu, S., Rubinato, M., & Gui, Q. (2020). SPH Simulation of Interior and Exterior Flow Field Characteristics of Porous Media. Water, 12(3), 918. https://doi.org/10.3390/w12030918






