Investigating Atrazine Concentrations in the Zwischenscholle Aquifer Using MODFLOW with the HYDRUS-1D Package and MT3DMS
Abstract
:1. Introduction
2. Materials and Methods
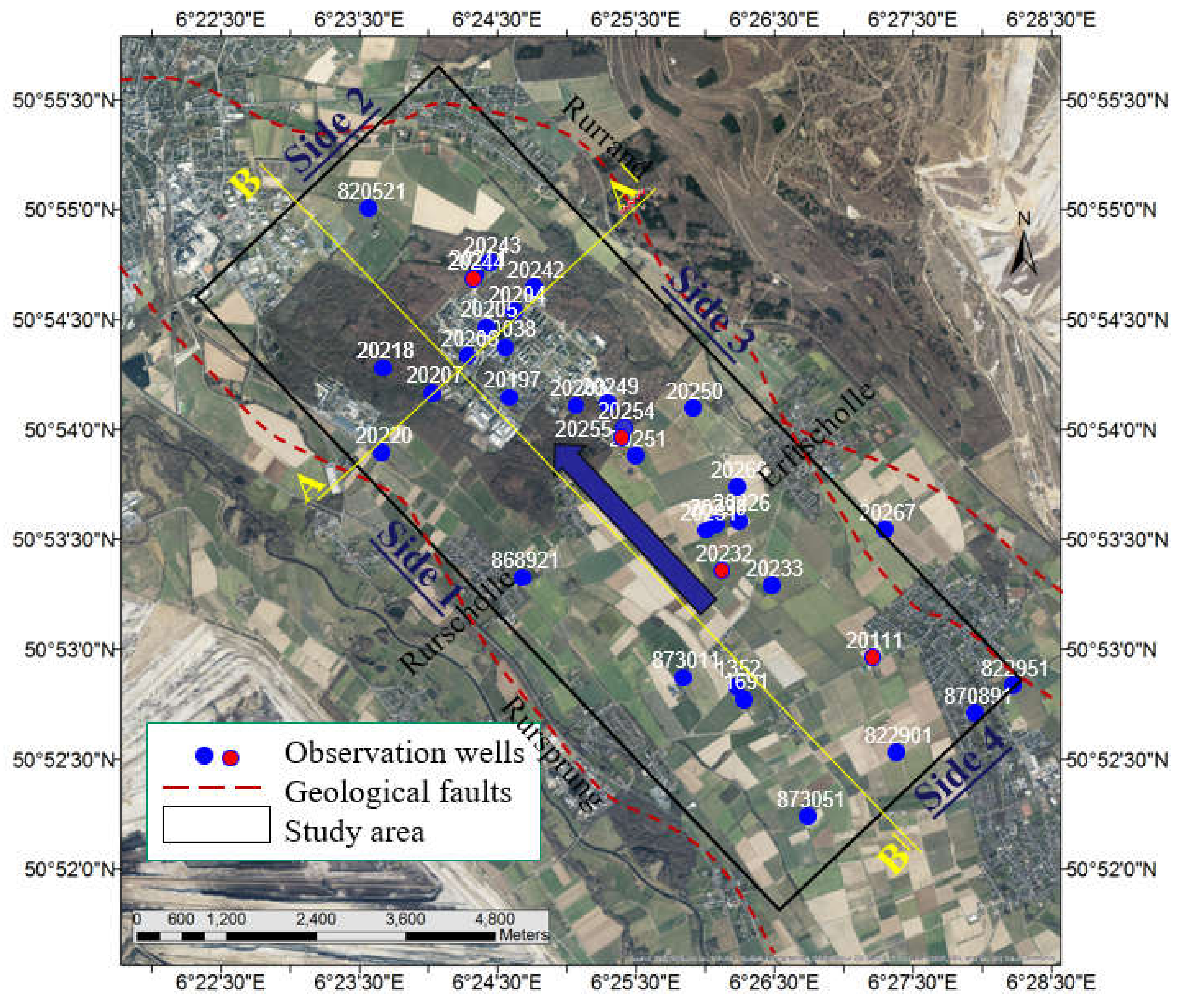
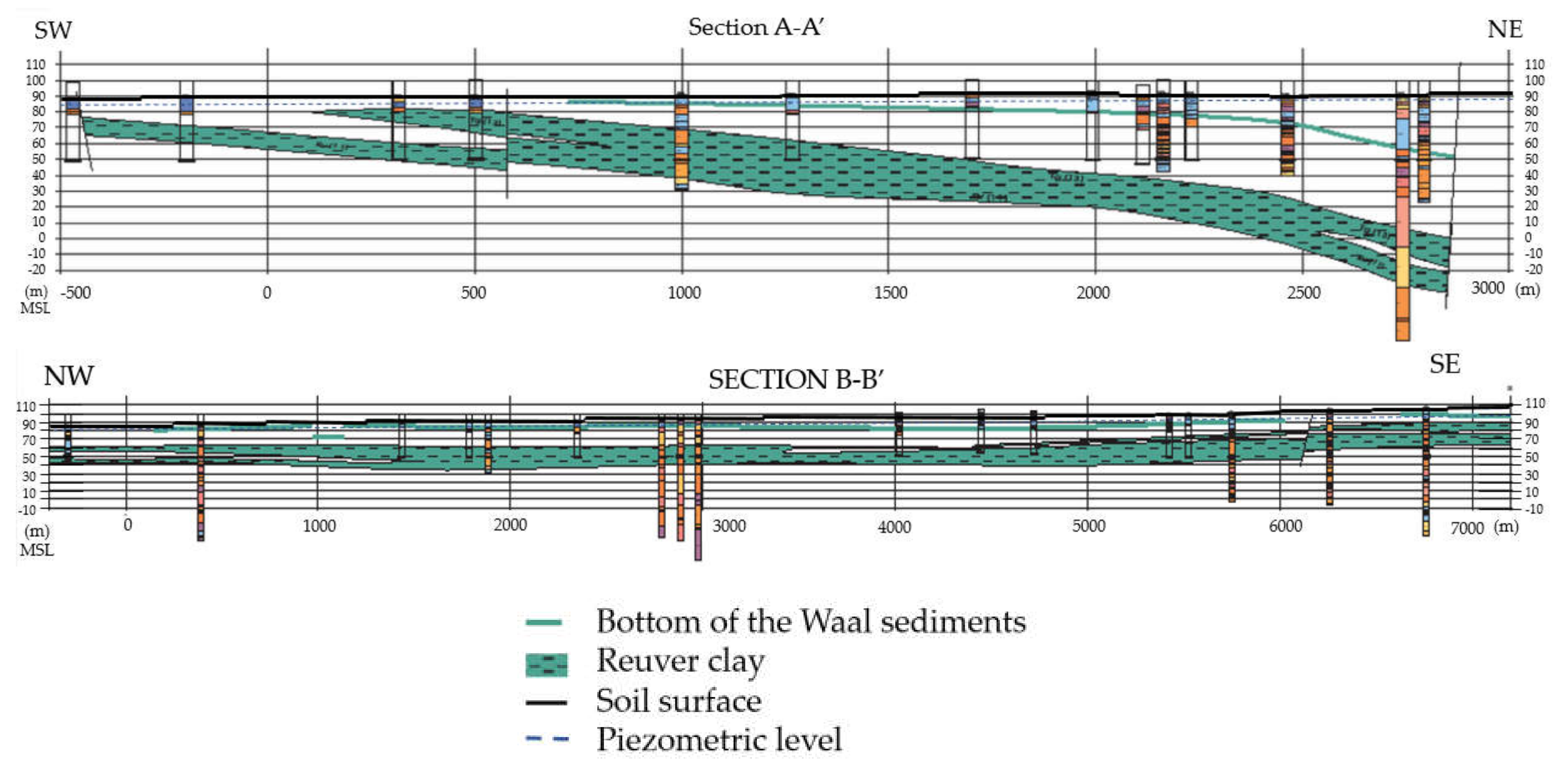
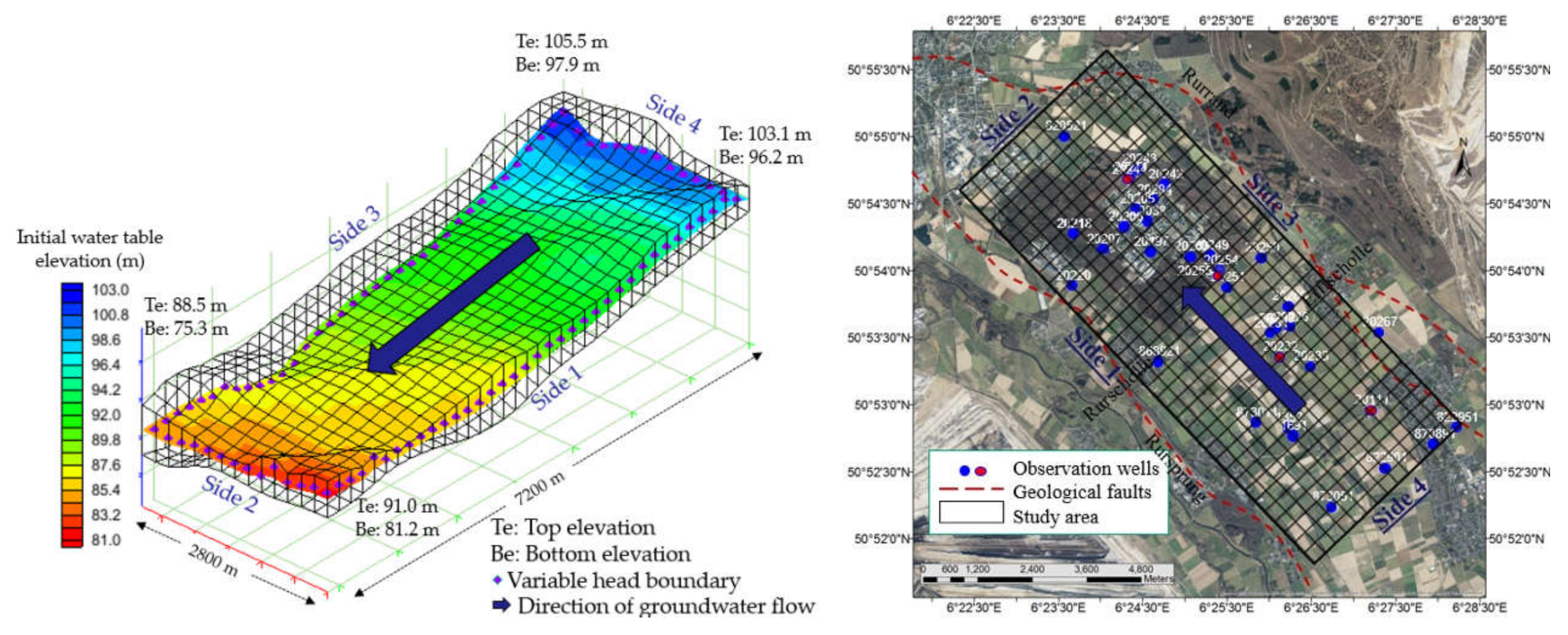
2.1. Study Area: Zwischenscholle Aquifer
2.2. MODFLOW with the HYDRUS-1D Package and MT3DMS
2.3. Data Available for Modeling
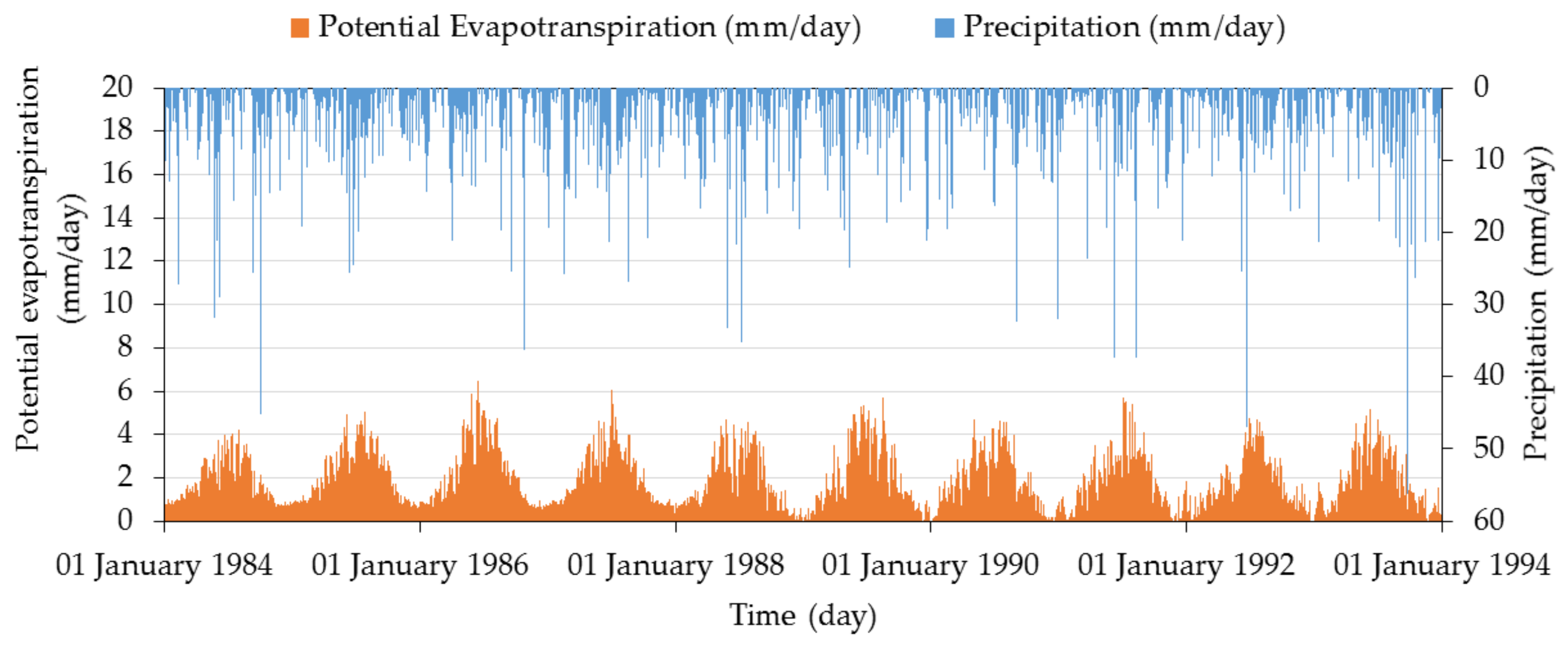
2.3.1. Climate Data
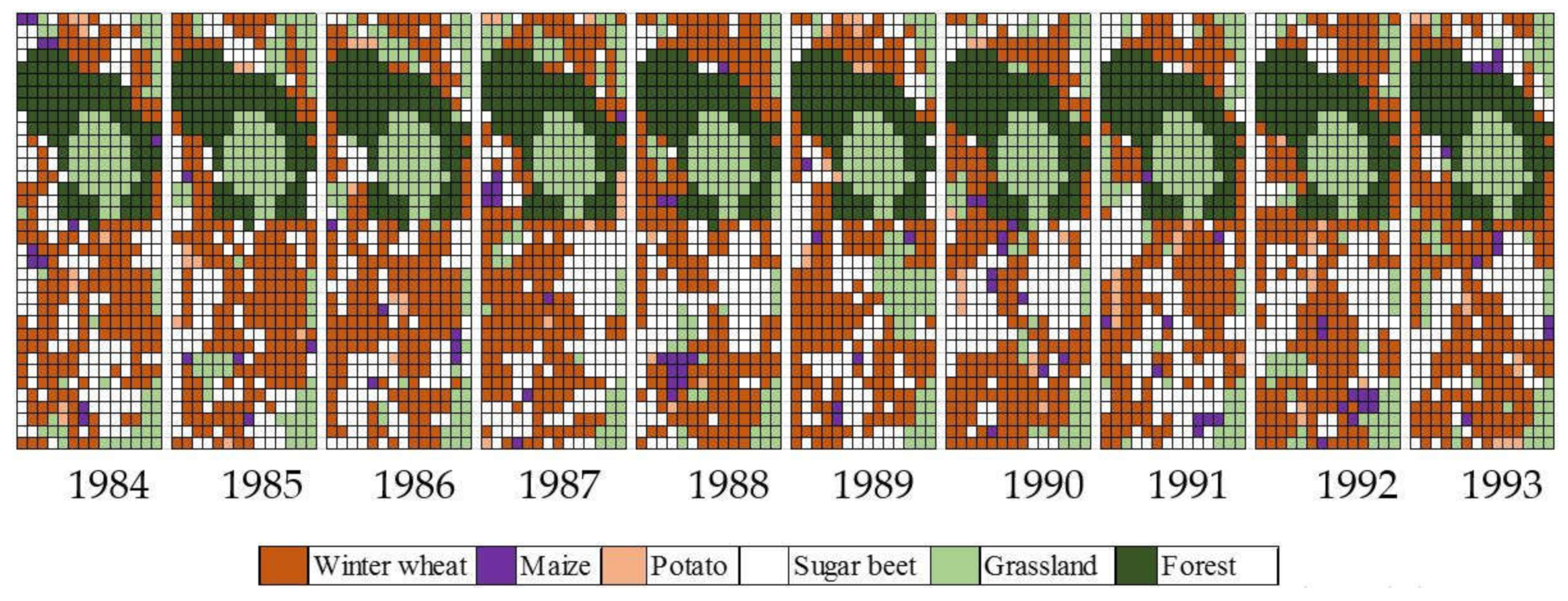
2.3.2. Land Use and Information about Atrazine Applications
2.3.3. Soil Types and Soil Hydraulic Properties
2.3.4. Simulation of Crop Transpiration and Root Water Uptake
2.3.5. Solute Transport Parameters
2.4. Model Setup
2.4.1. Spatial and Temporal Discretizations
2.4.2. Initial and Boundary Conditions
2.4.3. Model Settings for Analyzing the Long-Term Atrazine Concentrations in Groundwater
2.4.4. Looping Boundary Condition
3. Results and Discussion
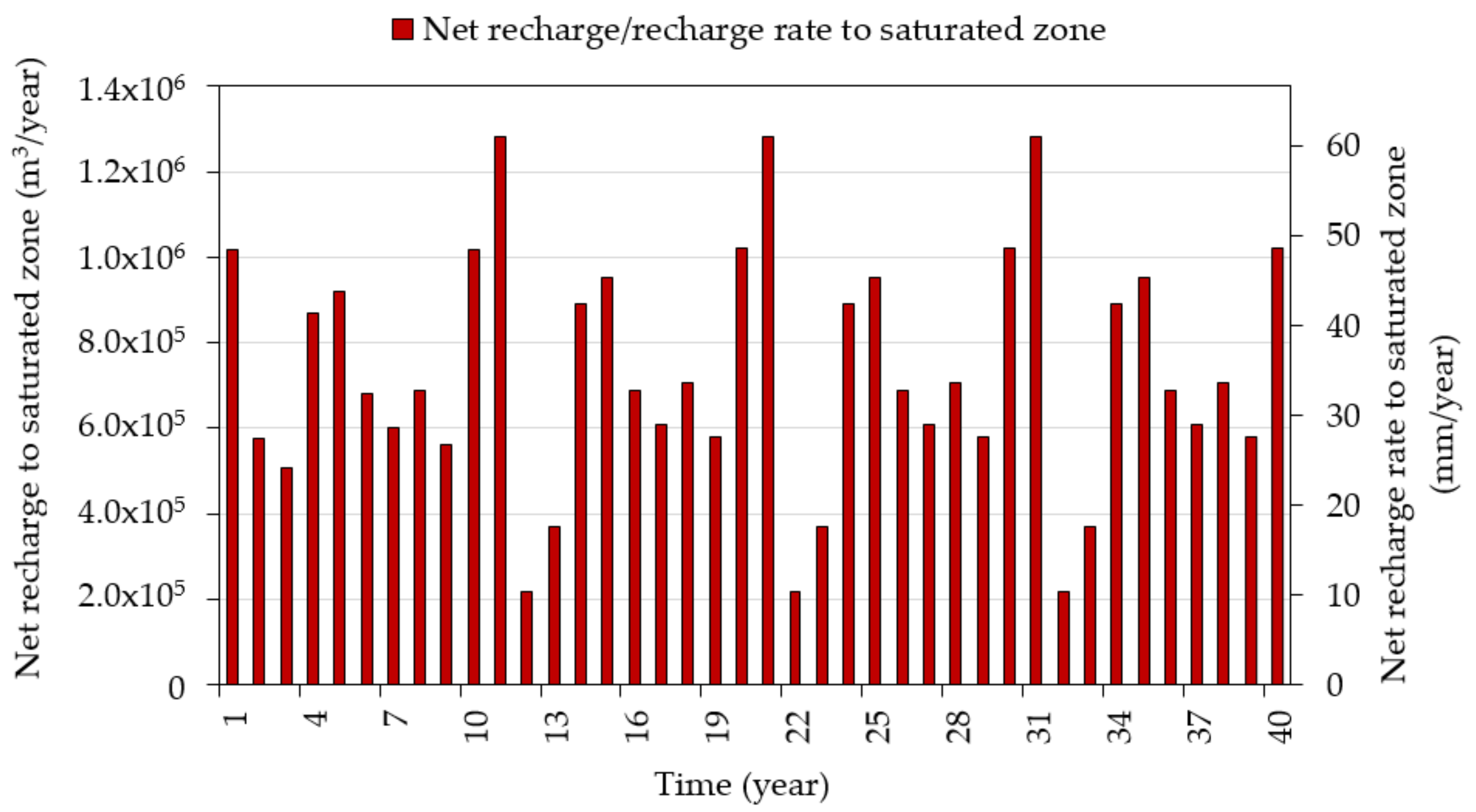
3.1. Water Flow Modeling Using MODFLOW with the HYDRUS-1D Package
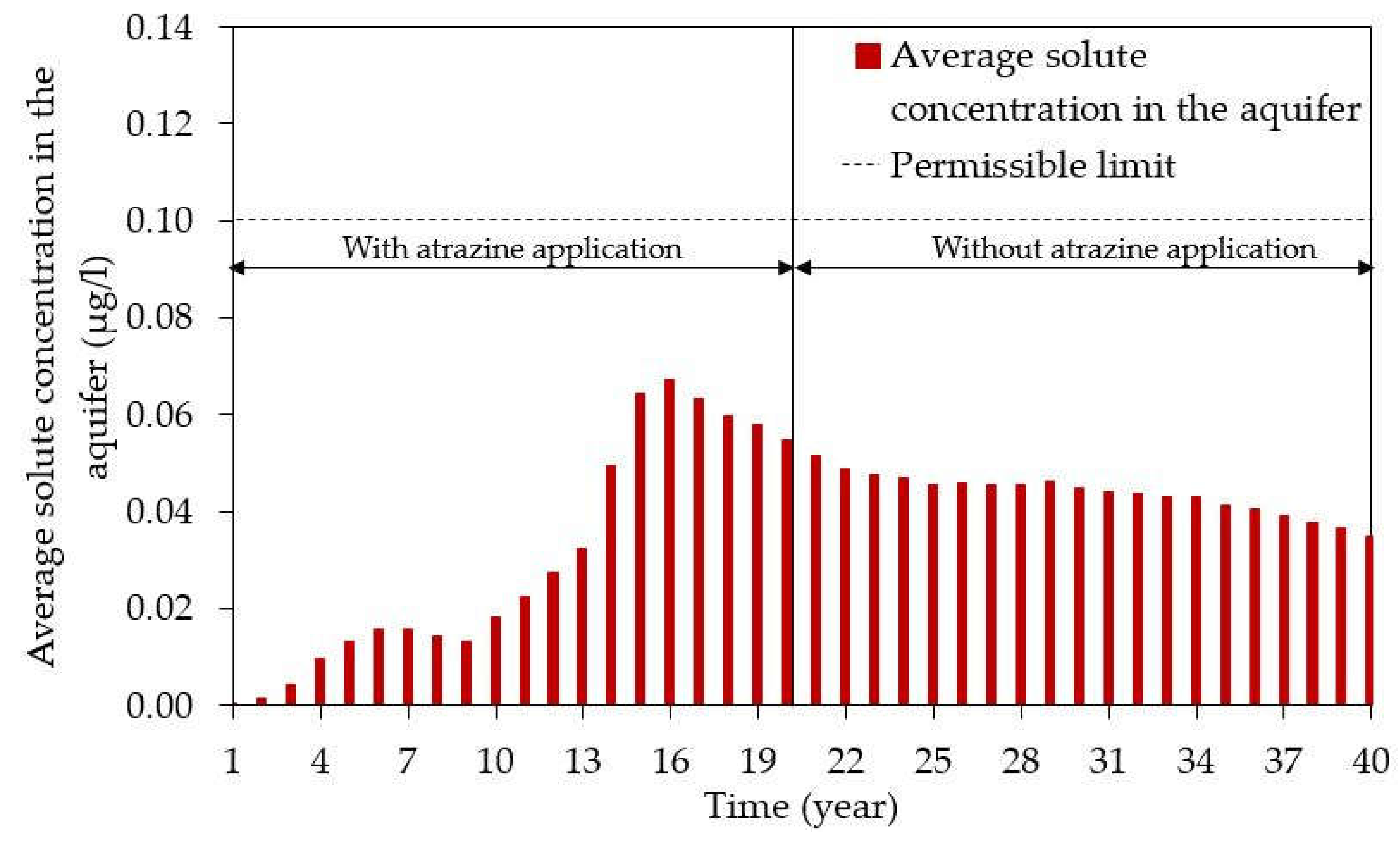
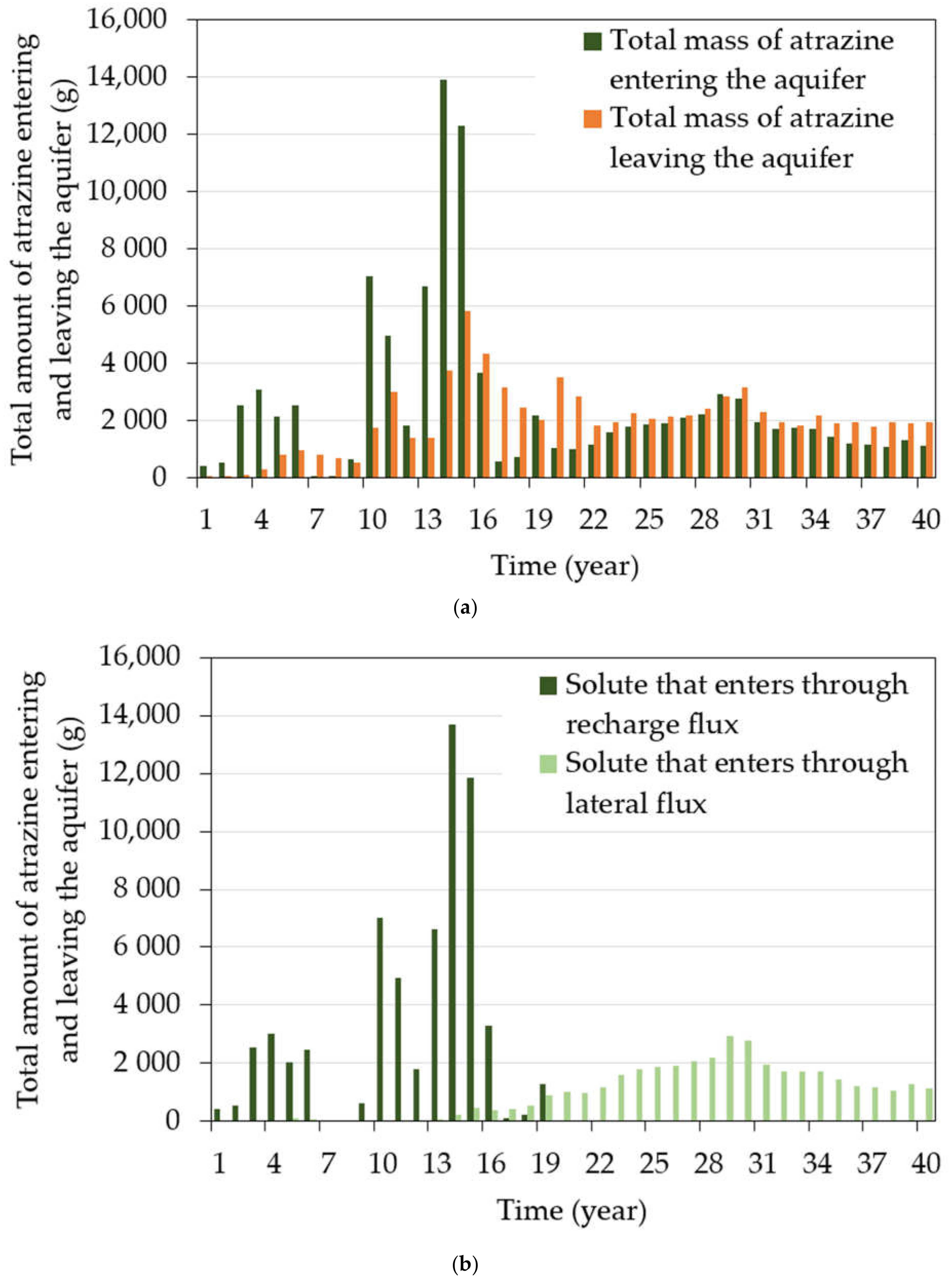
3.2. Atrazine Concentrations in Groundwater
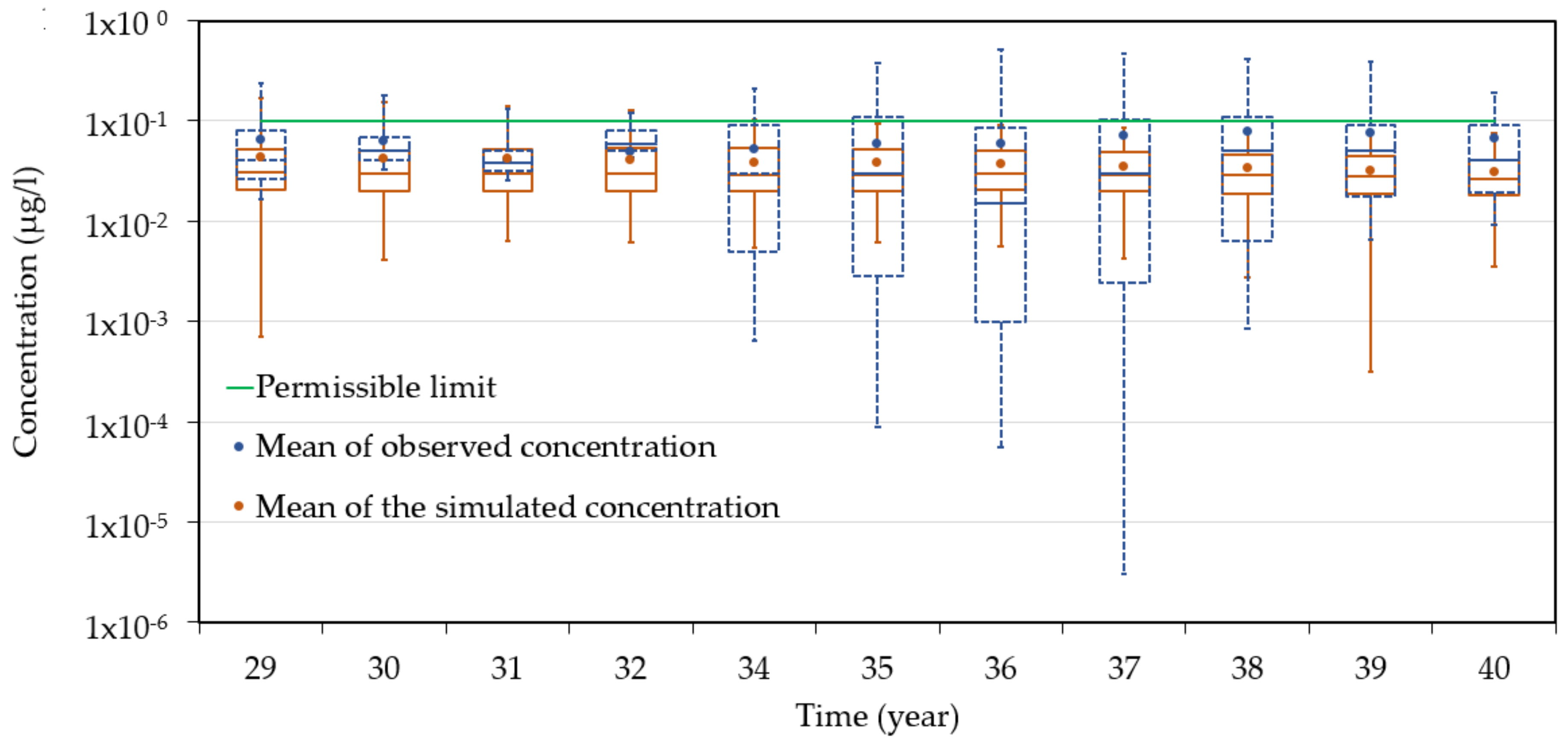
3.3. Comparison of Observed and Model-Simulated Average Annual Atrazine Concentrations
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, F.; Li, Z.; Zhang, C.; Habumugisha, T.; Liu, F.; Luo, X. Pesticides in the typical agricultural groundwater in Songnen plain, northeast China: Occurrence, spatial distribution and health risks. Environ. Geochem. Health 2019, 41, 2681–2695. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.; Khan, S.; Ur Rahman, I.; Muhammad, S. Human health risk assessment through consumption of organophosphate pesticide-contaminated water of Peshawar basin, Pakistan. Expo. Health 2018, 10, 259–272. [Google Scholar] [CrossRef]
- Gupta, S.D.; Mukherjee, A.; Bhattacharya, J.; Bhattacharya, A. An overview of agricultural pollutants and organic contaminants in groundwater of India. In Groundwater of South Asia; Springer: Singapore, 2018; pp. 247–255. [Google Scholar]
- El Alfy, M.; Faraj, T. Spatial distribution and health risk assessment for groundwater contamination from intensive pesticide use in arid areas. Environ. Geochem. Health 2017, 39, 231–253. [Google Scholar] [CrossRef] [PubMed]
- Chaza, C.; Sopheak, N.; Mariam, H.; David, D.; Baghdad, O.; Moomen, B. Assessment of pesticide contamination in Akkar groundwater, northern Lebanon. Environ. Sci. Pollut. Res. 2018, 25, 14302–14312. [Google Scholar] [CrossRef]
- Pan, H.; Lei, H.; He, X.; Xi, B.; Han, Y.; Xu, Q. Levels and distributions of organochlorine pesticides in the soil–groundwater system of vegetable planting area in Tianjin City, Northern China. Environ. Geochem. Health 2017, 39, 417–429. [Google Scholar] [CrossRef]
- Sieczka, A.; Bujakowski, F.; Falkowski, T.; Koda, E. Morphogenesis of a floodplain as a criterion for assessing the susceptibility to water pollution in an agriculturally rich valley of a lowland river. Water 2018, 10, 399. [Google Scholar] [CrossRef] [Green Version]
- Segerson, K. Liability for groundwater contamination from pesticides. Econ. Water Qual. 2018, 19, 227–243. [Google Scholar]
- Srivastav, A.L. Chemical fertilizers and pesticides: Role in groundwater contamination. In Agrochemicals Detection, Treatment and Remediation; Elsevier: Amsterdam, The Netherlands, 2020; pp. 143–159. [Google Scholar]
- Worrall, F.; Besien, T. The vulnerability of groundwater to pesticide contamination estimated directly from observations of presence or absence in wells. J. Hydrol. 2005, 303, 92–107. [Google Scholar] [CrossRef]
- Thapinta, A.; Hudak, P.F. Use of geographic information systems for assessing groundwater pollution potential by pesticides in Central Thailand. Environ. Int. 2003, 29, 87–93. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulou-Mourkidou, E.; Karpouzas, D.G.; Patsias, J.; Kotopoulou, A.; Milothridou, A.; Kintzikoglou, K.; Vlachou, P. The potential of pesticides to contaminate the groundwater resources of the Axios river basin in Macedonia, Northern Greece. Part I. Monitoring study in the north part of the basin. Sci. Total Environ. 2004, 321, 127–146. [Google Scholar] [CrossRef]
- Leterme, B.; Vanclooster, M.; Rounsevell, M.D.A.; Bogaert, P. Discriminating between point and non-point sources of atrazine contamination of a sandy aquifer. Sci. Total Environ. 2006, 362, 124–142. [Google Scholar] [CrossRef] [PubMed]
- Tiktak, A.; De Nie, D.S.; Garcet, J.D.P.; Jones, A.O.; Vanclooster, M. Assessment of the pesticide leaching risk at the Pan-European level. The EuroPEARL approach. J. Hydrol. 2004, 289, 222–238. [Google Scholar] [CrossRef]
- Loague, K.; Soutter, L.A. Desperately seeking a cause for hotspots in regional-scale groundwater plumes resulting from non-point source pesticide applications. Vadose Zone J. 2006, 5, 204–221. [Google Scholar] [CrossRef]
- Franke, H.-J.; Teutsch, G. Stochastic simulation of the regional pesticide transport including the unsaturated and the saturated zone. Ecol. Model. 1994, 75, 529–539. [Google Scholar] [CrossRef]
- Kupfersberger, H.; Klammler, G.; Schumann, A.; Brückner, L.; Kah, M. Modeling subsurface fate of s-metolachlor and metolachlor ethane sulfonic acid in the Westliches Leibnitzer Feld aquifer. Vadose Zone J. 2018, 17, 170030. [Google Scholar] [CrossRef] [Green Version]
- Honeycutt, R. Mechanisms of Pesticide Movement into Ground Water; CRC Press: Boca Raton, FL, USA, 2018; ISBN 1351082795. [Google Scholar]
- Jones, R.L. Modeling the degradation and movement of agricultural chemicals in ground water. In Mechanisms of Pesticide Movement into Ground Water; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Vonberg, D.; Vanderborght, J.; Cremer, N.; Pütz, T.; Herbst, M.; Vereecken, H. 20 years of long-term atrazine monitoring in a shallow aquifer in western Germany. Water Res. 2014, 50, 294–306. [Google Scholar] [CrossRef]
- Vonberg, D.; Hofmann, D.; Vanderborght, J.; Lelickens, A.; Köppchen, S.; Pütz, T.; Burauel, P.; Vereecken, H. Atrazine soil core residue analysis from an agricultural field 21 years after its ban. J. Environ. Qual. 2014, 43, 1450. [Google Scholar] [CrossRef]
- Farlin, J.; Drouet, L.; Gallé, T.; Pittois, D.; Bayerle, M.; Braun, C.; Maloszewski, P.; Vanderborght, J.; Elsner, M.; Kies, A. Delineating spring recharge areas in a fractured sandstone aquifer (Luxembourg) based on pesticide mass balance. Hydrogeol. J. 2013, 21, 799–812. [Google Scholar] [CrossRef]
- Gutierrez, A.; Baran, N. Long-term transfer of diffuse pollution at catchment scale: Respective roles of soil, and the unsaturated and saturated zones (Brévilles, France). J. Hydrol. 2009, 369, 381–391. [Google Scholar] [CrossRef]
- Tappe, W.; Groeneweg, J.; Jantsch, B. Diffuse atrazine pollution in German aquifers. Biodegradation 2002, 13, 3–10. [Google Scholar] [CrossRef]
- Dunlap, K.; Brown, A. Atrazine Levels in Water, Sediment, and Amphibian Tissue Samples from Selected Ponds in Westernmost Kentucky; Murray State University: Murray, KY, USA, 2018. [Google Scholar]
- Guzzella, L.; Pozzoni, F.; Giuliano, G. Herbicide contamination of surficial groundwater in Northern Italy. Environ. Pollut. 2006, 142, 344–353. [Google Scholar] [CrossRef] [PubMed]
- Jayachandran, K.; Steinheimer, T.R.; Somasundaram, L.; Moorman, T.B.; Kanwar, R.S.; Coats, J.R. Occurrence of atrazine and degradates as contaminants of subsurface drainage and shallow groundwater. J. Environ. Qual. 1994, 23, 311–319. [Google Scholar] [CrossRef] [Green Version]
- Wehtje, G.; Leavitt, J.R.C.; Spalding, R.F.; Mielke, L.N.; Schepers, J.S. Atrazine contamination of groundwater in the Platte Valley of Nebraska from non-point sources. Sci. Total Environ. 1981, 21, 47–51. [Google Scholar] [CrossRef]
- Regulation, E.U. Council Directive 98/83/EC of 3 November 1998 on the quality of water intended for human consumption. Off. J. Eur. Commun. 1998, 41, 32–54. [Google Scholar]
- Herbst, M.; Hardelauf, H.; Harms, R.; Vanderborght, J.; Vereecken, H. Pesticide fate at regional scale: Development of an integrated model approach and application. Phys. Chem. Earth Parts A/B/C 2005, 30, 542–549. [Google Scholar] [CrossRef]
- Mouvet, C.; Baran, N.; Thiery, D.; Gutierrez, A.; Darsy, C.; Dubus, I.G.; Falkiewicz, W.; Ritsema, C.; Dekker, L.; Normand, B. Pesticides in European groundwaters: Detailed study of representative aquifers and simulation of possible evolution scenarios (PEGASE). In Proceedings of the EU Workshop: The Functioning and Management of the Water-Soil-System at River-Basin Scale: Diffuse Polltuion and Point Sources, Orléans, France, 26–28 November 2003; pp. 248–263. [Google Scholar]
- Suffet, I.H.; Gibs, J.; Coyle, J.A.; Chrobak, R.S.; Yohe, T.L. Applying analytical techniques to solve groundwater contamination problems. J. Am. Water Works Assoc. 1985, 77, 65–72. [Google Scholar] [CrossRef]
- Walton, W.C. Analytical Groundwater Modeling Flow and Contaminant Migration; Lewis Publishers: Chelsea, MI, USA, 1989. [Google Scholar]
- Aller, L. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings; Robert, S., Ed.; Kerr Environmental Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Washington, DC, USA, 1985. [Google Scholar]
- Bartzas, G.; Tinivella, F.; Medini, L.; Zaharaki, D.; Komnitsas, K. Assessment of groundwater contamination risk in an agricultural area in north Italy. Inf. Process. Agric. 2015, 2, 109–129. [Google Scholar] [CrossRef] [Green Version]
- Djoudi, S.; Boulabiez, F.; Pistre, S.; Houha, B. Assessing Groundwater Vulnerability to Contamination in a Semi-Arid Environment Using DRASTIC and GOD Models, Case of F’kirina Plain, North of Algeria. IOSR J. Environ. Sci., Toxicol. Food Technol. 2019, 13, 39–44. [Google Scholar]
- Al-Adamat, R.; Al-Shabeeb, A.A.-R. A simplified method for the assessment of groundwater vulnerability to contamination. J. Water Resour. Protect. 2017, 9, 305. [Google Scholar] [CrossRef] [Green Version]
- Civita, M.; De Maio, M.; Ubertini, L. Valutazione e cartografia automatica della vulnerabilità degli acquiferi all’inquinamento con il sistema parametrico Sintacs R5: A new parametric system for the assessment and automatic mapping of ground water vulnerability to contamination; Pitagora: Bologna, Italy, 2000; ISBN 8837112319. [Google Scholar]
- Fusco, F.; Allocca, V.; Coda, S.; Cusano, D.; Tufano, R.; De Vita, P. Quantitative assessment of specific vulnerability to nitrate pollution of shallow alluvial aquifers by process-based and empirical approaches. Water 2020, 12, 269. [Google Scholar] [CrossRef] [Green Version]
- Michalak, A.M.; Shlomi, S. A geostatistical data assimilation approach for estimating groundwater plume distributions from multiple monitoring events. Geophys. Monogr. Am. Geophys. Union 2007, 171, 73. [Google Scholar]
- McLean, M.I.; Evers, L.; Bowman, A.W.; Bonte, M.; Jones, W.R. Statistical modelling of groundwater contamination monitoring data: A comparison of spatial and spatiotemporal methods. Sci. Total Environ. 2019, 652, 1339–1346. [Google Scholar] [CrossRef] [PubMed]
- Lappala, E.G.; Healy, R.W.; Weeks, E.P. Documentation of Computer Program VS2D to Solve the Equations of Fluid Flow in Variably Saturated Porous Media; Department of the Interior, US Geological Survey: Reston, VA, USA, 1987; p. 83. [Google Scholar]
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; Alabama University: Tuscaloosa, AL, USA, 1999. [Google Scholar]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT: A New Code of the TOUGH Family for Non-Isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geologic Media; University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Healy, R.W. Simulation of Solute Transport Invariably Saturated Porous Media with Supplemental Information on Modifications to the US Geological Survey’s Computer Program VS2D; Department of the Interior, US Geological Survey: Reston, VA, USA, 1990; p. 90. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. The HYDRUS-1D software package for simulating the one-dimensional movement of water, heat, and multiple solutes in variably-saturated media. Univ. Calif. Riverside Res. Rep. 2005, 3, 1–240. [Google Scholar]
- Šimůnek, J.; Bradford, S.A. Vadose zone modeling: Introduction and importance. Vadose Zone J. 2008, 7, 581–586. [Google Scholar] [CrossRef]
- Refsgaard, J.; Storm, B. Computer models of watershed hydrology, MIKE SHE. Water Resour. Publ. 1995, 809–846. [Google Scholar]
- Twarakavi, N.K.C.; Simunek, J.; Seo, S. Evaluating interactions between groundwater and vadose zone using the HYDRUS-based flow package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar] [CrossRef] [Green Version]
- Brunner, P.; Simmons, C.T. HydroGeoSphere: A fully integrated, physically based hydrological model. Groundwater 2012, 50, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Kalbacher, T.; Delfs, J.O.; Shao, H.; Wang, W.; Walther, M.; Samaniego, L.; Schneider, C.; Kumar, R.; Musolff, A.; Centler, F.; et al. The IWAS-ToolBox: Software coupling for an integrated water resources management. Environ. Earth Sci. 2012, 65, 1367–1380. [Google Scholar] [CrossRef]
- Morway, E.D.; Niswonger, R.G.; Langevin, C.D.; Bailey, R.T.; Healy, R.W. Modeling variably saturated subsurface solute transport with MODFLOW-UZF and MT3DMS. GroundWater 2013, 51, 237–251. [Google Scholar] [CrossRef]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Implementation of solute transport in the vadose zone into the “HYDRUS Package for MODFLOW. ” Groundwater 2019, 57, 392–408. [Google Scholar] [CrossRef] [Green Version]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.P.; Nambi, I.M. Updating the coupling algorithm between HYDRUS and MODFLOW in the HYDRUS Package for MODFLOW. Vadose Zone J. 2018, 17, 180034. [Google Scholar] [CrossRef] [Green Version]
- Mouvet, C.; Albrechtsen, H.J.; Baran, N.; Chen, T.; Clausen, L.; Darsy, C. PEGASE. Pesticides in European Groundwaters: Detailed Study of Representative Aquifers and Simulation of possible Evolution Scenarios; Final Report of the European Project; UW Umweltwirtschaft GmbH: Stuttgart, Germany, 2004. [Google Scholar]
- Lahmeyer Site appraisal of geology, hydrogeology and soil mechanics (Standortgutachten Geologie, Hydrogeologie und Bodenmechanik). Unpublished work. 1984.
- Seo, H.S.; Šimůnek, J.; Poeter, E.P. Documentation of the HYDRUS Package for MODFLOW -2000, the US Geological Survey Modular Ground Water Model. GWMI 2007-01, IGWMC-International Ground Water Modeling Center; Colorado School of Mines: Golden, CO, USA, 2007; p. 96. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; Mcdonald, M.G. MODFLOW-2000, the US Geological Survey modular ground-water model: User guide to modularization concepts and the ground-water flow process. USA Geol. Surv. 2000, 1–92. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; van Genuchten, M.T. Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef] [Green Version]
- Bogena, H. MOSYRUR: Water Balance Analysis in the Rur Basin; Heye Bogena, Forschungszentrum, Zentralbibliothek: Julich, Germany, 2005. [Google Scholar]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Spitters, C.J.T.; Van Keulen, H.; Van Kraalingen, D.W.G. A simple and universal crop growth simulator: SUCROS87. In Simulation and Systems Management in Crop Protection; Rabbinge, R., Ward, S.A., van Laar, H.H., Eds.; Pudoc: Wageningen, The Netherlands, 1989; pp. 147–181. ISBN 9022008991. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Crop Water Requirements. FAO Irrigation and Drainage Paper 24; Land and Water Development Division; FAO: Rome, Italy, 1977; p. 144. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Rakowski, P.; Knowling, M.J. Heretaunga Aquifer Groundwater Model: Development Report; HBRC Report No RM18-14-4997; Hawke’s Bay Regional Council: Napier, New Zealand, 2018. [Google Scholar]
- Nachabe, M.H. Analytical expressions for transient specific yield and shallow water table drainage. Water Resour. Res. 2002, 38, 11. [Google Scholar] [CrossRef] [Green Version]
- Said, A.; Nachabe, M.; Ross, M.; Vomacka, J. Methodology for estimating specific yield in shallow water environment using continuous soil moisture data. J. Irrig. Drain. Eng. 2005, 131, 533–538. [Google Scholar] [CrossRef]
- Jablonowski, N.D.; Köppchen, S.; Hofmann, D.; Schäffer, A.; Burauel, P. Persistence of 14C-labeled atrazine and its residues in a field lysimeter soil after 22 years. Environ. Pollut. 2009, 157, 2126–2131. [Google Scholar] [CrossRef] [Green Version]



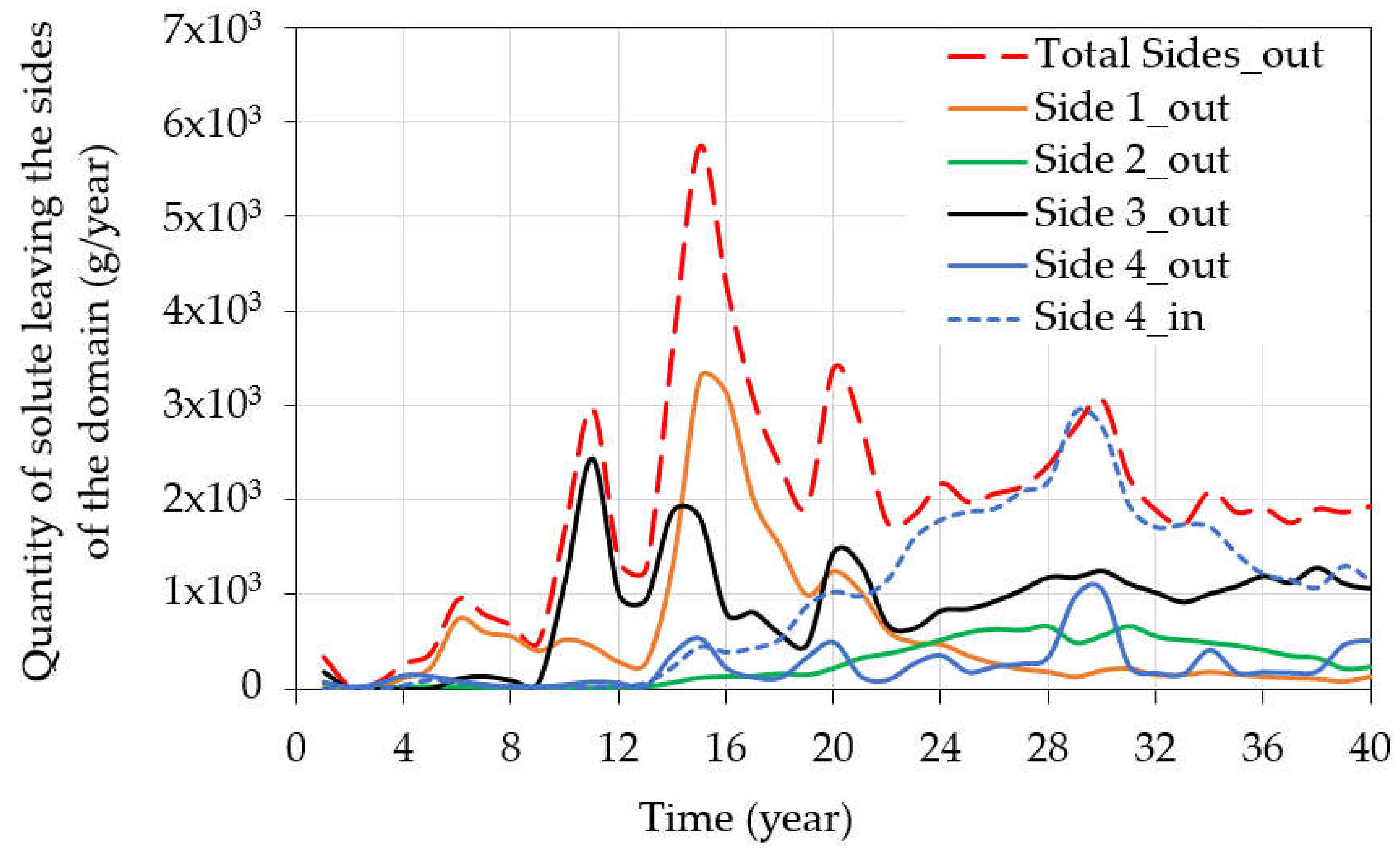
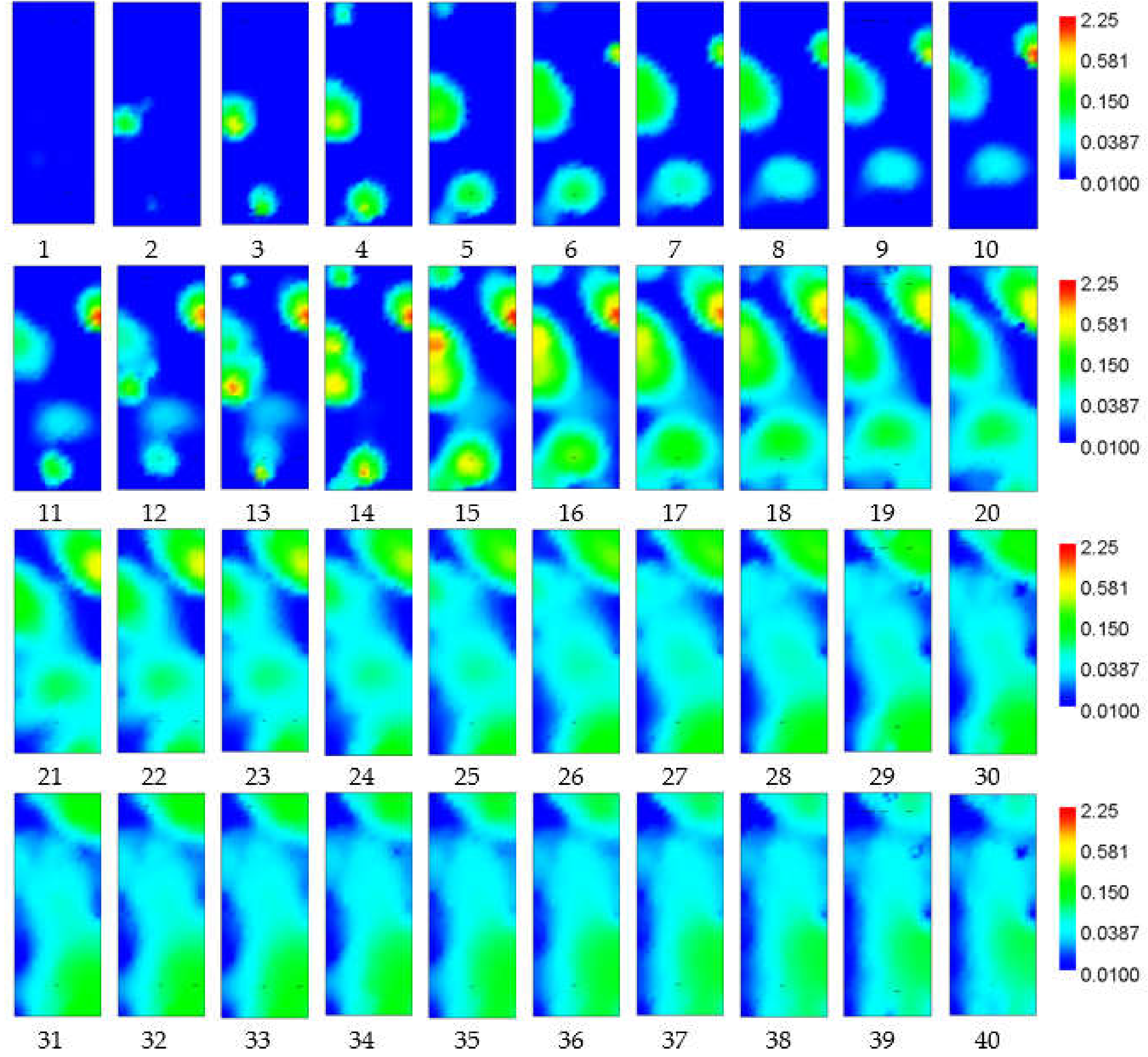
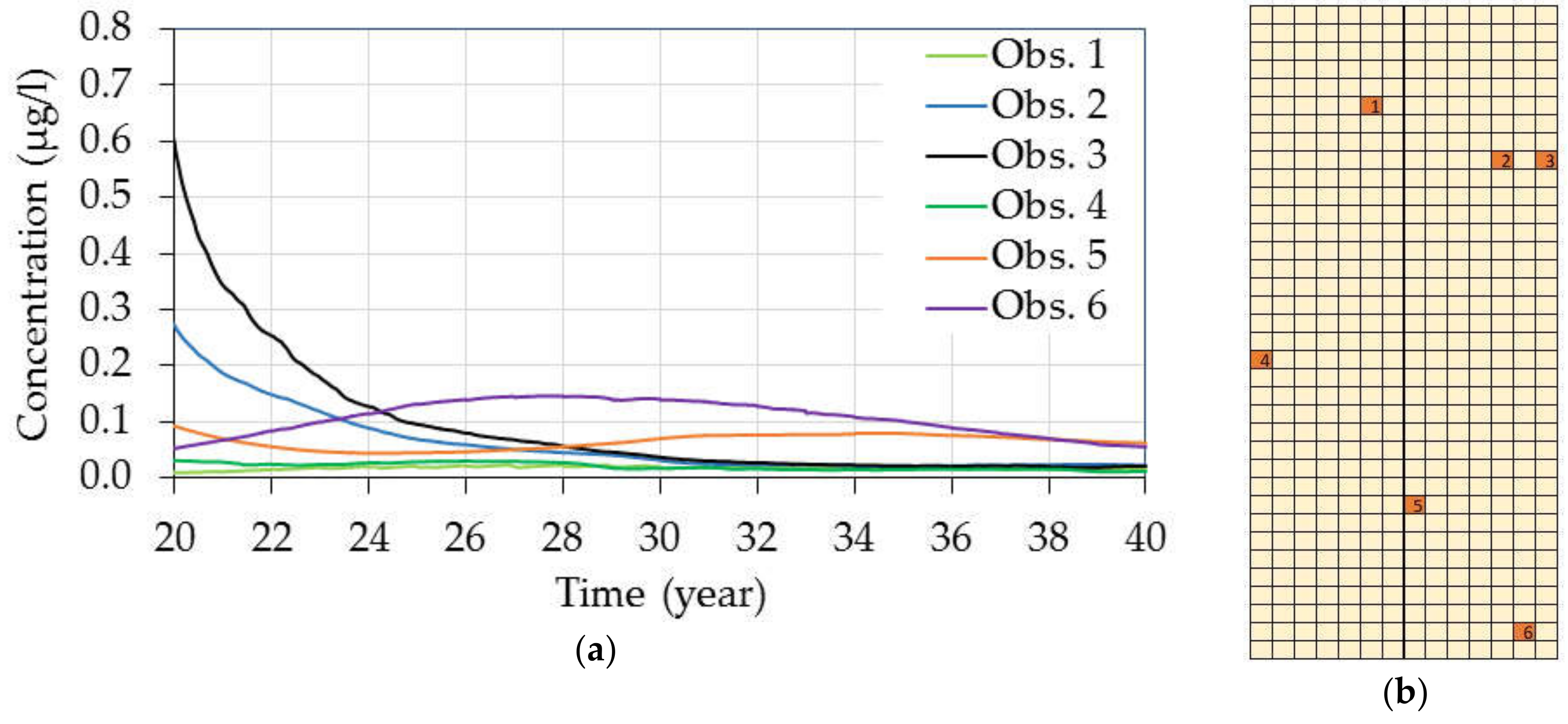
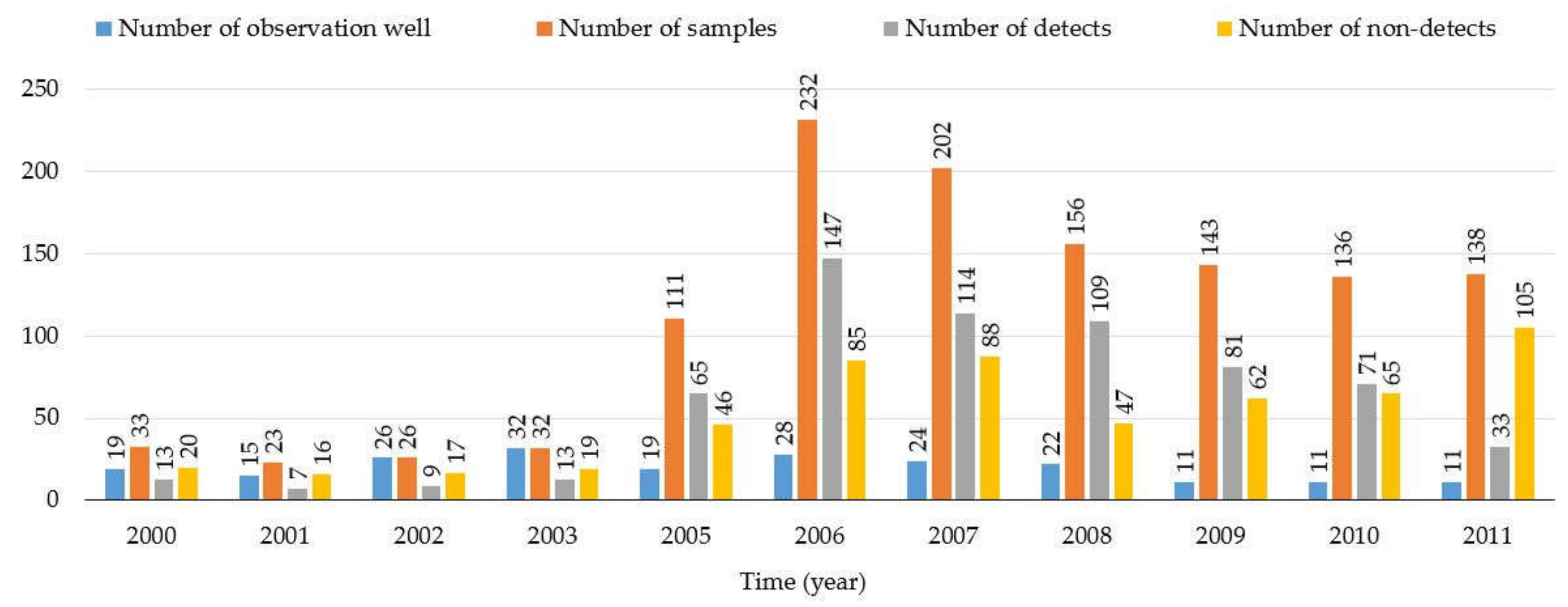
| Soil Type | Layers | Thickness (m) | Residual Water Content, θr (-) | Saturated Water Content, θs (-) | Parameter α in the Soil Water Retention Function, (m−1) | Parameter n in the Soil Water Retention Function, (-) | Saturated Hydraulic Conductivity, Ks (m day−1) | Tortuosity Parameter l in the Conductivity Function (-) |
|---|---|---|---|---|---|---|---|---|
| Silt loam | 1 | 0.23 | 0.045 | 0.463 | 2.16 | 1.35 | 0.080 | 0.5 |
| 2 | 0.28 | 0.041 | 0.392 | 1.60 | 1.35 | 0.032 | 0.5 | |
| 3 | 1.35 | 0.074 | 0.359 | 1.42 | 1.30 | 0.017 | 0.5 | |
| Sandy loam | 1 | 0.25 | 0.056 | 0.382 | 11.2 | 1.35 | 1.38 | 0.5 |
| 2 | 0.30 | 0.053 | 0.314 | 9.33 | 1.40 | 0.891 | 0.5 | |
| Loam 1 | 1 | 0.06 | 0.048 | 0.461 | 2.10 | 1.34 | 0.074 | 0.5 |
| 2 | 1.00 | 0.082 | 0.358 | 4.32 | 1.33 | 0.067 | 0.5 | |
| Loam 2 | 1 | 0.20 | 0.044 | 0.395 | 2.04 | 1.34 | 0.049 | 0.5 |
| 2 | 1.00 | 0.069 | 0.298 | 4.16 | 1.33 | 0.110 | 0.5 | |
| Aquifer | - | Variable | 0.001 | 0.184 | 10.0 | 2.10 | 134. | 0.5 |
| Crop | P0 (m) | POpt (m) | P2H (m) | P2L (m) | P3 (m) | Maximum Rooting Depth (m) |
|---|---|---|---|---|---|---|
| Winter wheat | 0.000 | −0.010 | −5.00 | −9 | −160 | 0.95 |
| Maize | −0.150 | −0.300 | −3.25 | −6 | −80 | 1.15 |
| Potato | −0.100 | −0.250 | −3.20 | −6 | −160 | 0.74 |
| Sugar beet | −0.100 | −0.250 | −3.20 | −6 | −160 | 1.15 |
| Grassland | −0.001 | −0.025 | −2.00 | −8 | −80 | 0.75 |
| Forest | 1000.001 | 1000 | −4.25 | −8 | −160 | 1.50 |
| Relative Rooting Depth (-) | Root Density; Value Characterizing the Depth Distribution of Root Water Uptake (m−1) | |||||
|---|---|---|---|---|---|---|
| Winter Wheat | Maize | Potato | Sugar Beet | Grassland | Forest | |
| 0.0 | 0.26 | 1.05 | 1.00 | 0.97 | 1.05 | 0.30 |
| 0.1 | 0.16 | 0.76 | 0.94 | 0.92 | 0.76 | 0.60 |
| 0.2 | 0.10 | 0.55 | 0.89 | 0.86 | 0.55 | 0.90 |
| 0.3 | 0.06 | 0.39 | 0.84 | 0.80 | 0.39 | 0.95 |
| 0.4 | 0.04 | 0.28 | 0.78 | 0.74 | 0.28 | 0.90 |
| 0.5 | 0.02 | 0.20 | 0.73 | 0.69 | 0.20 | 0.80 |
| 0.6 | 0.01 | 0.15 | 0.68 | 0.63 | 0.15 | 0.70 |
| 0.7 | 0.01 | 0.10 | 0.62 | 0.57 | 0.10 | 0.60 |
| 0.8 | 0.00 | 0.07 | 0.57 | 0.51 | 0.07 | 0.50 |
| 0.9 | 0.00 | 0.05 | 0.52 | 0.46 | 0.05 | 0.40 |
| 1.0 | 0.00 | 0.04 | 0.47 | 0.40 | 0.04 | 0.30 |
| Soil Type | Layers | Porosity (-) | Longitudinal Dispersivity, αL (m) | Transverse Dispersivity, αT (m) | Bulk Density, (kg/m3) | Adsorption Coefficient, Kd (m3/kg) | First-order Degradation Rate, λ (day−1) |
|---|---|---|---|---|---|---|---|
| Silt loam | 1 | 0.509 | 0.045 | 0.0045 | 1350 | 1.42 × 10−3 | 3.47 × 10−3 |
| 2 | 0.434 | 0.045 | 0.0045 | 1375 | 3.26 × 10−4 | 1.73 × 10−3 | |
| 3 | 0.434 | 0.045 | 0.0045 | 1375 | 1.63 × 10−4 | 1.04 × 10−3 | |
| Sandy loam | 1 | 0.509 | 0.045 | 0.0045 | 1350 | 1.42 × 10−3 | 3.47 × 10−3 |
| 2 | 0.434 | 0.045 | 0.0045 | 1375 | 3.26 × 10−4 | 1.73 × 10−3 | |
| Loam 1 | 1 | 0.510 | 0.045 | 0.0045 | 1350 | 6.91 × 10−3 | 3.47 × 10−3 |
| 2 | 0.440 | 0.045 | 0.0045 | 1375 | 6.52 × 10−4 | 1.73 × 10−3 | |
| Loam 2 | 1 | 0.509 | 0.045 | 0.0045 | 1350 | 1.42 × 10−3 | 3.47 × 10−3 |
| 2 | 0.434 | 0.045 | 0.0045 | 1375 | 3.26 × 10−4 | 1.04 × 10−3 | |
| Aquifer | - | 0.184 | 15.4 | 1.54 | 1400 | 3.55 × 10−4 | 3.47 × 10−10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beegum, S.; Vanderborght, J.; Šimůnek, J.; Herbst, M.; Sudheer, K.P.; Nambi, I.M. Investigating Atrazine Concentrations in the Zwischenscholle Aquifer Using MODFLOW with the HYDRUS-1D Package and MT3DMS. Water 2020, 12, 1019. https://doi.org/10.3390/w12041019
Beegum S, Vanderborght J, Šimůnek J, Herbst M, Sudheer KP, Nambi IM. Investigating Atrazine Concentrations in the Zwischenscholle Aquifer Using MODFLOW with the HYDRUS-1D Package and MT3DMS. Water. 2020; 12(4):1019. https://doi.org/10.3390/w12041019
Chicago/Turabian StyleBeegum, Sahila, Jan Vanderborght, Jiří Šimůnek, Michael Herbst, K. P. Sudheer, and Indumathi M Nambi. 2020. "Investigating Atrazine Concentrations in the Zwischenscholle Aquifer Using MODFLOW with the HYDRUS-1D Package and MT3DMS" Water 12, no. 4: 1019. https://doi.org/10.3390/w12041019





