Abstract
Urbanization typically results in increased imperviousness which alters suspended sediment yield and impacts geomorphic and ecological processes within urban streams. Therefore, there is an increasing interest in the ability to predict suspended sediment yield. This study assesses the combined impact of urban development and increased precipitation on suspended sediment yield in the Cuyahoga River using statistical modeling. Historical satellite-based land-cover data was combined with precipitation and suspended sediment yield data to create a Multiple Linear Regression (MLR) model for the Cuyahoga watershed. An R2 value of 0.71 was obtained for the comparison between the observed and predicted results based on limited land-use and land-cover data. The model also shows that every 1 mm increase in the mean annual precipitation has the potential to increase the mean annual suspended sediment yield by 860 tons/day. Further, a 1 km2 increase in developed land area has the potential to increase mean annual suspended sediment yield by 0.9 tons/day. The framework proposed in this study provides decision makers with a measure for assessing the potential impacts of future development and climate alteration on water quality in the watershed and implications for stream stability, dam and flood management, and in-stream and near-stream infrastructure life.
Keywords:
urbanization; suspended sediment; hydrology; water quality; remote sensing; Cuyahoga River 1. Introduction
As the population living near natural waters increases, there is an increased global interest in water security and the impacts of development on water resource quantity and quality. Urban developments (e.g., construction of roads, buildings, and parking lots) alter watershed characteristics such as land-use and land-cover (LULC) and total impervious area. Changes in LULC ultimately impact water resources and the ecology of the streams and, therefore, such changes are of a great concern not only to watershed managers but also to all levels of stakeholders in areas around these features [1,2,3].
In recent decades, many studies have demonstrated the impacts of watershed development on streams, deepening our understanding of fluvial geomorphology, river channel dynamics, and sediment transport [4,5]. Urbanizing watersheds often have a larger total sediment yield compared with unurbanized and fully developed watersheds, even for watersheds with small and widely scattered areas of exposed soil [6,7]. Hillslope erosion is largely responsible for the increased sediment supply during the construction or urbanizing phase [7,8]. For urbanized watersheds, hillslope sediment supply is decreased, but bankfull flows are increased due to imperviousness as a result of the reduction in infiltration rates [1]. This results in bank erosion, as the urban stream attempts to adjust itself to receive larger discharge [8]. Imperviousness leads to a reduction in infiltration rates and increase in runoff [1]. Studies by Wolman and Schick [6], Leopold [7] and Paul and Meyer [8] all emphasize the importance of land development on suspended sediment yield in urban areas. While the total sediment load decreases in urban areas, the suspended load often increases [9].
Precipitation is a key factor for surface erosion and driving suspended sediment transport through waterways for a given watershed [10,11,12]. Surface erosion within a watershed is often intensified by a combination of rain events with high intensity and substantial LULC changes towards development [13,14]. Additionally, storm water in a developed area may transport considerable amounts of nutrients and suspended sediment [12,15,16,17]. The suspended sediment concentration is closely correlated with water quality [18] and is, therefore, factored into stormwater regulation as it is of great concern to watershed managers and residents. Although changes in precipitation may alter the suspended sediment concentration within the stream, the relationship between the two is difficult to establish. Sediment discharge is not solely dependent on precipitation and usually varies nonlinearly during an event [18,19]. Further, different rain patterns generate completely different patterns of surface erosion [20,21], resulting in alteration in the sediment yield delivered downstream. For example, in a study of rivers fed by runoff from the Himalaya mountains using over a decade of data [21], it was reported that only two out of eight peaks of suspended sediment discharges coincided with peaks in precipitation. The other six peaks coincided with moderate–low rain. This suggests that other control factors such as substantial erosions within the streams and banks, a potentially significant source of suspended sediment, may be responsible for the peaks [22,23,24].
Land-cover type significantly influences suspended sediment yield [25,26,27]. Exposure of soil to stormwater runoff is the principal consequence of land use on sediment yield in a developing watershed [7,17]. Land development and watershed surface alterations have the potential to substantially alter suspended sediment yield in streams [15,28,29]. Despite numerous studies on the effects of land-cover types on water resources, the relationship between land development and suspended sediment is not fully understood. For instance, land-use changes in a watershed may cause an increase in sediment yield, while a similar change in another watershed may decrease the yield [30,31]. Variations in sediment yield are assumed to be related to watershed physiography [32] and the system of sediment delivery in the watershed [33,34]. Schilling [34] reported that for a case study in Iowa, changing the LULC of a watershed from agriculture to native prairie did not cause significant change in sediment yield due to an increase in channel erosion. In this case, a substantial amount of the eroded sediment may originate from within a river’s channels and banks [1,35]. Local changes in a watershed such as urban construction, dams, new patterns of agriculture, mining, and tree felling can alter the erosion and deposition regime [25]. Sediment yield in a small watershed (<103 km2) is more sensitive to LULC change [35,36]. In larger watersheds, the eroded sediment is more likely to settle in the basin before reaching the outlet [35]. These factors highlight the need for individual case studies of watersheds to quantify the effects of urban development on sediment yield.
Remote sensing techniques and satellite imagery are useful tools for assessing Earth’s surface features, providing valuable information for water resource analysis [37]. Landsat satellite images provide the world’s longest continuous Earth surface data and have been used extensively for land type classification and surface change detection. Landsat images continue to play an important role in many water resource applications, such as the classification of isolated wetlands in Cuyahoga County, Ohio [38].
There are few studies on land type changes and their effects on sediment yield for the Cuyahoga Watershed. One study [39] analyzed trapped sediment behind the Gorge Dam on the Cuyahoga River and concluded that from 1926 to 1978, sediment yield had doubled due to urbanization in the watershed. The study also showed that there was no substantial increase in total sediment yield until 2004 and then an increase from 2004 to 2008 and in 2011. To the best of the authors’ knowledge, there is currently no model for predicting suspended sediment yield within the Cuyahoga River. Suspended sediment transport modeling is traditionally based on an understanding of the hydraulics of particle transport [40,41]. Advancements in computational power over recent decades, however, has resulted in the creation of innovative techniques for estimating sediment load such as machine learning algorithms that can estimate suspended sediment yield without solving the governing hydraulic equations [42,43]. In addition to these methods, empirical models such as the Soil Water Assessment Tool (SWAT), which is based on the Universal Soil Loss Equation (USLE) [44,45], and physically based models such as the Water Erosion Prediction Project (WEPP) model [46,47] have also been used. However, most of these existing models require either substantial amounts of data or training in order to properly utilize them. There is no known study which utilizes limited historical satellite image and precipitation data to create a simplified Multiple Linear Regression (MLR) model for predicting suspended sediment yield.
In contrast to existing models for estimating suspended sediment yield, this study introduces a new framework for suspended sediment yield estimation by combining remote sensing techniques with limited historical data to establish and quantify the combined effect of land development and precipitation on suspended sediment yield in the Cuyahoga Watershed. This unique approach simplifies the process of suspended sediment yield estimation by taking advantage of readily available historical satellite image and precipitation data. The period of 1991–2011 was chosen for this study because it contains continuous satellite image data for the Cuyahoga Watershed. A major advantage of this simplified statistical method for modeling suspended sediment yield is that this framework can be easily replicated in other watersheds, particularly with the growing availability of satellite and precipitation data. The outcome of this research provides decision makers with a means for assessing the impacts of future development and climate alteration on stream total suspended solids (TSS) for a given watershed, as well as implications for stream stability, fluvial infrastructure stainability, and flood management.
2. Study Area
The study area for this research is the Cuyahoga River watershed in northeast Ohio (Figure 1). The watershed area is 2105 km2—of which, 51% is covered by forest, shrub, grassland, pasture, cultivated crops and wetlands, and 46% is classified as developed land based on National Land Cover Database 2011 [48], following two decades of substantial development. The average terrain slope for the whole watershed is 3.8%, with an elevation change from 160 to 395 m [48]. The relatively steep slopes of the Cuyahoga River banks and its tributaries’ banks cause frequent river bank failures in the watershed [49]. The watershed is U-shaped, with its origins in northeast Ohio. It flows southwards to Cuyahoga Falls, where it redirects northward towards Cleveland and finally empties into Lake Erie. Compared with the western segment, the eastern segment is less urbanized, with more wetlands and more channelized tributaries. The degree of development within the watershed increases from Summit County toward Lake Erie, reaching peak industrial development in the Cleveland area [50]. The soil of the watershed ranges from organic to clay, silt and sand, with an estimated average sediment yield of 5 to 100 tons per acre per year [49]. There are five major dams along the main stem of the Cuyahoga River and several smaller dams on many of its tributaries.
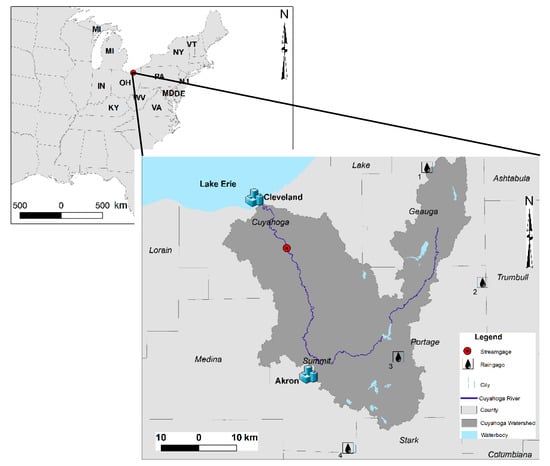
Figure 1.
The Cuyahoga watershed and study area. (Map data from Ohio Department of Natural Resources, United States Census Bureau, United States Geological Survey, National Oceanic and Atmospheric Administration.)
3. Materials and Methods
3.1. Data Integration
Table 1 summarizes the data utilized for this study. This includes both hydrologic and geographic information system (GIS) spatial data types, such as vector and raster datasets.

Table 1.
Summary of data used in study.
3.1.1. Precipitation
Daily precipitation data was obtained from National Oceanic and Atmospheric Administration (NOAA) gage stations located at (1) Chardon (USC00331458), (2) Hiram (USC00333780), (3) Ravenna (USW0001485), and (4) Akron-Canton (USW00014895) as shown in Figure 1. Daily precipitation data at each gage station was averaged over each year from 1991 to 2011 to obtain an annual average. Figure 2 plots the annual precipitation of individual gages and the annual mean areal precipitation of the entire watershed computed using the Thiessen weighted average method.
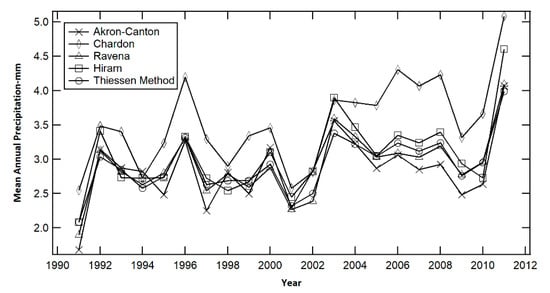
Figure 2.
Mean annual precipitation measured across the watershed. The Thiessen method is used to estimate the average precipitation from the four gages.
3.1.2. Suspended Sediment Yield
Mean daily suspended sediment yield data was obtained from the USGS stream gage at Independence, Ohio, and averaged for each year. It is important to note that suspended sediment data was available only from 1950 to 2002. For the purpose of this study, a sediment rating curve was developed to estimate suspended sediment yield from 2003 to 2011 (Figure 3). The rating curve takes the form of a power function expressed as
where is the discharge, is the suspended sediment yield, and and are coefficients [58,59]. All the discharge values from 2003 to 2011 were within the limits of the rating curve, and hence there was no extrapolation beyond those limits.
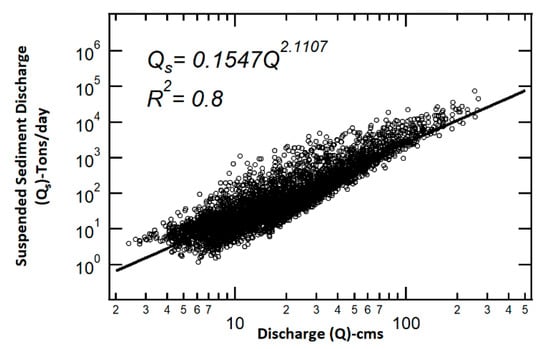
Figure 3.
Suspended sediment rating curve created from data from 1950 to 2002 at the Independence stream gage.
3.1.3. Satellite Images
Landsat provides accurate Earth surface images [60] and has been widely used in various studies including water TSS monitoring, ecosystem mapping, flood evaluations, and detecting land-use change [61]. The Landsat images used in this study were obtained from the USGS Global Visualization Viewer website [53]. The images used in this study are captured by the Landsat 5 Thematic Mapper Sensor [62] and are radiometrically and geometrically corrected. The images had a 30 m by 30 m spatial resolution taken at sixteen day intervals. Satellite data often have varying percentages of cloud coverage, depending on the time of day and year the data was collected. The selected images were limited to data collected between April and September to minimize cloud coverage. In addition, visual inspections were performed to exclude images with high cloud or shadow coverage. The majority of the images used had a cloud cover of less than twenty percent. In cases of higher cloud cover, pixels in the clouded area were replaced with matching pixels from the subsequent year as suggested by [63]. This step allowed for the estimation of the full extent of annual land-cover change.
3.2. Land Classification
To detect land development changes within the watershed from 1991 to 2011, a supervised image classification was performed using Environment for Visualizing Images (ENVI) [64], a software for geospatial imagery processing. Additional post-processing was performed using the ArcGIS [65] software application. The images were classified into three categories: developed, undeveloped and open water. The developed category included rooftops, roads, parking lots and other impervious surfaces. Agricultural land, forests, bare soil and other pervious surfaces were classified as undeveloped land. Lakes, rivers and all other water bodies were grouped under open water.
Pre-processing of the images was performed to improve the outcome of the image classification. The pre-processing began with a calibration using ENVI to compensate for satellite sensor errors due to variations in scan angle and system noise. Noise within the images resulting from light scattering was minimized using an image correction procedure known as dark subtraction [66].
After the calibration and dark subtraction, each image was classified into three categories. To perform the classification, training samples were first created using on-screen selection polygons. A minimum of 50 training samples were defined for each class. The minimum-distance-to-means classification algorithm [62] was then used to classify each pixel as either developed, undeveloped or open water.
3.3. MLR Model
Regression models have been used extensively in the field of water resources and environmental engineering for predicting, forecasting and interpolating data [67]. The MLR model developed in this study was used to establish the statistical relationship among mean annual suspended sediment yield Qsavg, mean annual precipitation (Pavg), and total area of developed land in each year (Dev). Qsavg was treated as the response variable (dependent variable), while Pavg and Dev were modeled as predictor variables (independent variables). Summary statistics for the MLR variables are presented in Table 2.

Table 2.
Summary statistics of the Multiple Linear Regression (MLR) variables.
Each variable (Qsavg, Pavg, and Dev), was standardized as
where is the variable, is the standardized variable, is the mean of the variable and is the standard deviation of the variable. Standardizing the variables is an important step for regression modeling, as it results in a standard normal random variable with a mean of zero and a standard deviation of unity. This enhances the understanding between the dependent and independent variables and helps in determining which variables are most important for the MLR model.
To develop the model, the suitability of a variety of variables was evaluated. This evaluation assessed the inter-dependency of the variables using correlation coefficients (Table 3). In addition to Qsavg, Pavg, and Dev, the suitability of the mean annual discharge (Qavg) for the statistical model was also considered.

Table 3.
Correlation coefficient among variables.
The strongest correlation was observed between Pavg and Qsavg. There was also a strong correlation between Qsavg and Qavg as well as between Pavg and Qavg. However, due to the inter-dependency between Pavg and Qavg, only was included in the MLR model. There was also a weak inverse correlation between and Qsavg. To this end, Qsavg may be modeled as a function of Dev and Pavg that is . Using MLR analysis, the holistic understanding of the combined impact of both and on suspended sediment yield is expressed as:
where is the expected value of the standardized suspended sediment yield (non-dimensional), expressed as a function of Dev (non-dimensional) and Pavg (non-dimensional). The values of are the intercept and slopes of the fitted MLR model, respectively. The first ten years of data (1991 to 2000) was used to create the MLR model. The remaining eleven years of data was used to verify the model.
4. Results and Discussion
4.1. Assessing the Effect of Land Development on Suspended Sediment Yield
The results of the geospatial imagery analysis (Figure 4) indicate a steady increase in developed land area within the Cuyahoga watershed between 1991 and 2001. There is also a corresponding decrease in the percentage of undeveloped land, which reduces from 75% in 1991 to 53% in 2001. The rate of urbanization reduces significantly after 2001 and remains nearly flat for another decade. The area covered by water bodies did not change significantly over the period of the study. The percentage of area covered in water remain steadily at an average of 2% during the study period which implies that there was no significant change in total surface area of water bodies within the watershed during the period of study.
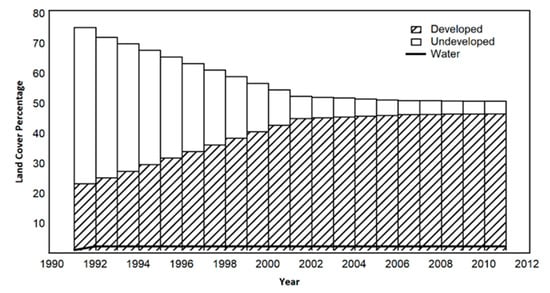
Figure 4.
Time series trend of land-cover change within the Cuyahoga watershed.
The direct consequence of urbanization on suspended sediment is often difficult to quantify due to the nonlinear relationship that exists between the two variables. In the case of the Cuyahoga watershed, the relationship is equally difficult to establish. However, based on the overall trend of both variables (Figure 5), while land development showed an increasing trend throughout the period of study, the mean annual suspended sediment only increased from 1991 to 1996. Further, with the exception of the unusually high suspended sediment yield in 2011, the suspended sediment yield has an overall decreasing trend over the two decades studied.
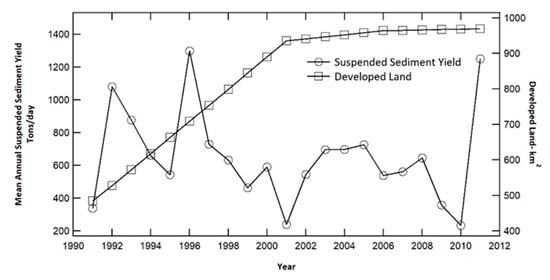
Figure 5.
Variation in suspended sediment yield and land development.
It can be inferred from Figure 6 that the majority of the land development in the Cuyahoga watershed during the first decade of the study period (1991–2001) occurred within the western segment of the watershed between Akron in the south and Cleveland in the northwest. Developed land (rooftops, roads, parking lots and other impervious surfaces) for the entire watershed constituted 23% in 1991, 45% in 2001 and 47% in 2011. Despite this increasing trend in land development, the mean annual suspended sediment only increased from 1991 to 1996, as seen in Figure 5, and this indicates that there may be other geomorphic drivers which make this watershed respond differently to land development, hence the need for this type of study.
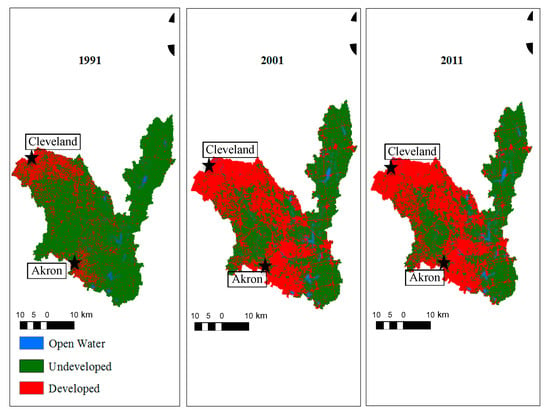
Figure 6.
Land classification showing land change from 1991 to 2011.
4.2. Assessing the Effect of Precipitation on Suspended Sediment Yield
The relationship between mean annual precipitation and mean annual suspended sediment yield was also assessed. As shown in Figure 7, except for 1992 and 1996, the annual mean suspended sediment yield and annual mean precipitation generally followed a similar annual trend. The discrepancies may be the result of the combined effects of changes in developed land area or other activity, such as an in-stream construction within the watershed, forcing an alteration to the instream sediment transport.
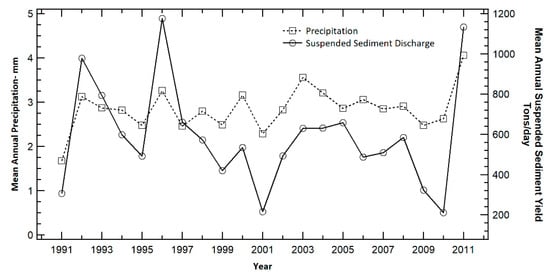
Figure 7.
Variation in suspended sediment yield and precipitation.
4.3. MLR Model Results
The significance F-value for the regression model was 0.0008, suggesting that this is a valid MLR model. A summary of the MLR coefficient estimates, their standard errors and p-values are presented in Table 4. The p-value for the coefficients and are both significant at a 95% confidence level, suggesting that both variables (developed land area and mean annual precipitation) are relevant for the MLR. The p-value for the intercept (α) is not significant at a 95% confidence level, suggesting that the model’s intercept is not significantly different from zero.

Table 4.
MLR model coefficient estimates, standard errors and p-values.
The goodness-of-fit statistics presented in Table 5 demonstrate an acceptable fit between the data and the regression model. In particular, the strong R-squared (0.87) and adjusted R-squared (0.83) values of the fitted model confirm the model’s ability to explain the variance within the data and hence the appropriateness of this model for the given data.

Table 5.
Statistics on the goodness-of-fit of the MLR model.
The MLR for the Cuyahoga watershed can thus be expressed as
in which, is the standardized mean annual suspended sediment yield (non-dimensional), is the standardized developed area (non-dimensional), and is the standardized mean annual precipitation (non-dimensional).
The coefficient estimates of the MLR are also a measure of the sensitivity of the model to changes in the predictor variables. Therefore, based on this model, every 1 standard deviation increase in developed land area (167 km2) could result in potential 0.52 standard deviations of reduction in mean annual suspended sediment yield (149 tons/day), i.e., a 1 km2 increase in developed land area will result in a 0.9 tons/day decrease in the mean annual suspended sediment yield. Conversely, a 1 mm increase in annual mean precipitation could result in an 860 tons/day increase in the mean annual suspended sediment yield assuming the mean annual precipitation is constant. This suggests that the model is much more sensitive to changes in precipitation than it is to changes in developed land area.
The MLR model was then used to predict suspended sediment yield from 2001 to 2011. As shown in Figure 8, the model prediction tracks well with the trend in observed suspended sediment yield. This is also consistent with the correlation coefficient (0.8) estimated for the comparison between observed and predicted suspended sediment yield. Given the limited amount of data used in developing the MLR model, this result can be considered as acceptable. The accuracy of the model may be improved with additional satellite, precipitation and suspended sediment data.
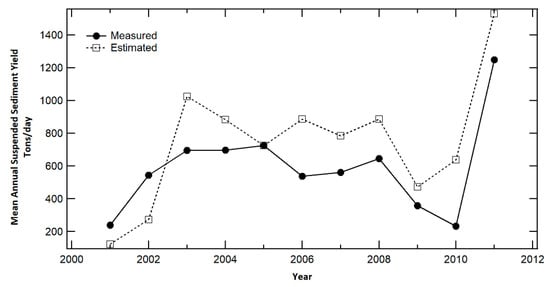
Figure 8.
Comparison of estimated and measured suspended sediment yield.
4.4. Model Verification and Uncertainty
Typical with regression-based models, the MLR model developed in this study has some uncertainty. Model verification and uncertainty assessments were performed to enhance the understanding of potential limitations of the model’s application. To verify the results of the model, the observed and predicted mean annual suspended sediment yields were compared (Figure 9). The estimated R-squared for the comparison between predicted and observed data was 0.71. Based on the Model Performance Rating suggested by Ayele et al. [68], this MLR model can be considered as “good” to “very good”. Comparatively, published studies involving sediment load prediction with other regression models such as Sinnakaudan et al. [69] yielded an R-squared value of 0.67.
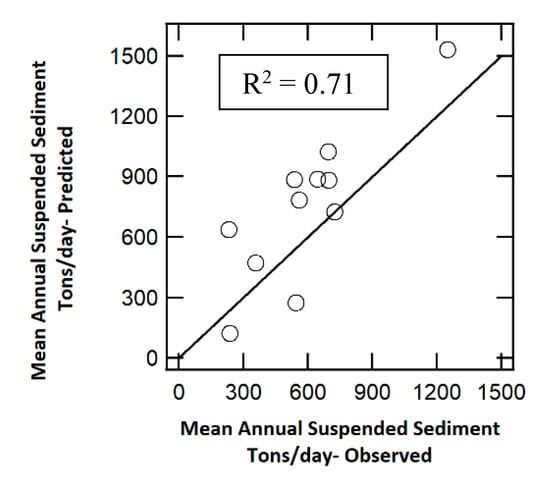
Figure 9.
Observed and predicted suspended sediment yield.
In addition to the R-squared value, several statistical parameters were estimated to provide a broader understanding of the model’s performance. An examination of the mean and standard deviation of the observed and predicted annual mean suspended sediment yield (Table 6) shows that the MLR developed in this study generally overpredicts the suspended sediment yield. This may be influenced by a number of reasons including the fact that only 10 years of data was used to train the MLR model. Some of the uncertainties in the sediment data itself may also account for underprediction or over prediction in some of the years. It is also important to note that suspended sediment measurements themselves are inherently prone to some level of uncertainty. For example, Yen et al. [70] reported suspended sediment measurement uncertainty as high as 117%.

Table 6.
Statistics for observed and predicted annual mean suspended sediment yield.
The closeness of the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE) is an indication of low variance in the differences between the observed and the predicted values. The strong Pearson’s Correlation Coefficient (0.8) also demonstrates the model’s ability to replicate the trend within the observed annual mean suspended sediment yield data. It is important to note, however, that although the Index of Agreement is high (0.8), and it is significantly greater than the Modified Index of Agreement. This is an indication that the results of this MLR may have been influenced more by the larger values within the independent variables (developed land area and mean annual precipitation) as explained by Legates and McCabe [71].
The uncertainty within the MLR model results was further assessed by computing the 95% confidence interval (Figure 10). This interval indicates that there is a 95% chance that the estimated suspended sediment yield will be contained within the confidence bound shown. It is interesting to note that seven out of the eleven observed values (2003, 2004, 2005, 2007, 2008, 2009, and 2011) fall within the confidence bound. This is an indication that there is a 63% chance that the observed suspended sediment yield falls within the confidence interval of this MLR model.
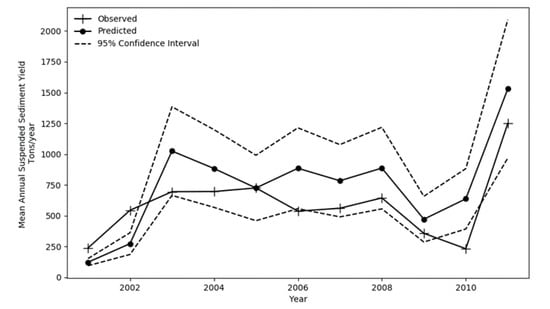
Figure 10.
95% Confidence interval for suspended sediment yield by MLR model.
4.5. Validation of the MLR Assumptions
For the regression model to be valid, all underlying assumptions of an MLR must be correct. The first assumption in an MLR is that the relationship between the independent and dependent variables is linear. Although the correlation between the developed land area and mean annual suspended sediment yield was weak, there was a general linear trend within the data (Figure 11a). Linearity was also verified for mean annual precipitation and mean annual suspended sediment as presented in Figure 11b. The linearity among the variables indicates that they are appropriate for the MLR model.
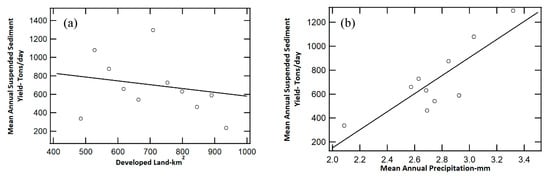
Figure 11.
Relationship between (a) developed land area and mean annual suspended sediment yield, and (b) mean annual precipitation and mean annual suspended sediment yield.
The second key assumption of a regression model is that all variables are multivariate normal. To test this assumption, the quantiles of each variable is plotted against that of a standard normal distribution. Based on Figure 12, all three variables were normally distributed. Hence, the normality assumption has been satisfied and, therefore, precipitation, suspended sediment yield and developed land area are appropriate for this MLR model.
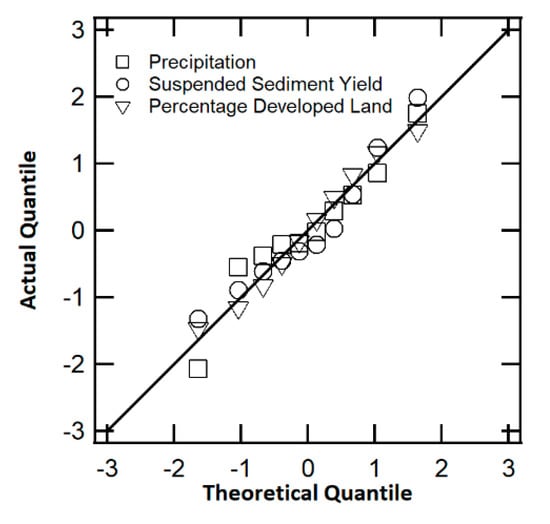
Figure 12.
The Quantile–Quantile plot shows that variables are multivariate.
Further, a regression model assumes that there is no multicollinearity among the variables. For this assumption to be correct, the Variance Inflation Factor (VIF) of the independent variables must be less than 10. A VIF of 0.00008 was computed for both and . This low VIF indicates the absence of a linear relation between the developed land area and precipitation and, therefore, validates the use of these variables in the MLR model.
Finally, the homoscedasticity assumption must be satisfied for the MLR to be valid. Homoscedasticity represents the variance of the model residuals around the regression line. The evenly spread out residuals around the regression line in Figure 13 indicates that on the average, the random disturbance in the relationship between the suspended sediment yield (dependent variable), developed land area and precipitation (independent variables) is similar across all values of the independent variables. The presence of homoscedasticity among the dependent and independent variables makes them valid inputs for the MLR model.
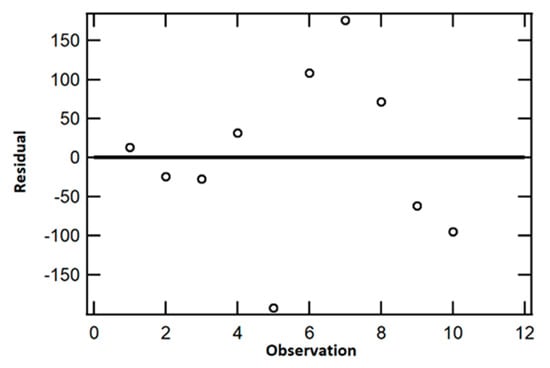
Figure 13.
Residual plot confirms homoscedasticity assumption.
5. Conclusions
Land-use and land-cover characteristics along with precipitation are some of the most important factors influencing the suspended sediment yield in a watershed. The relation between those variables is site specific and important for watershed managers, as it provides them with a tool to predict potential impacts to water quality and also evaluate possible implications for stream stability, dam and flood management, and in-stream and near-stream infrastructure life.
This study aimed to develop a framework for establishing the relation between land developments, mean annual precipitation, and mean annual suspended sediment yield in Cuyahoga River, OH by combining remote sensing techniques with limited data. To do that, remote sensing techniques were employed to classify land cover of the Cuyahoga watershed from 1991 to 2011 with historical satellite imagery. Then, a statistical model was developed to find the relation between measured mean annual precipitation, land development and measured mean annual suspended sediment yield. The geospatial imagery analysis showed that nearly all the urbanization within the Cuyahoga watershed between 1991 and 2011 occurred within the first decade. This rapid urbanization, however, did not directly result in an increase in suspended sediment yield within the Cuyahoga River. It is, therefore, possible that within the period of study, urbanization was not the most dominant geomorphic driver for suspended sediment yield. This study also found that within the Cuyahoga watershed, precipitation was more correlated to the suspended sediment yield than the rate of urbanization. This is demonstrated by the similarity in trends between mean annual precipitation and mean annual suspended sediment yield. It is worth noting, however, that the highest mean annual precipitation measurement did not coincide with the years with the highest mean annual suspended sediment yield, an additional indication that there may be some other factors influencing suspended sediment yield. This finding is consistent with findings from previous studies such as Wulf [21].
Using an MLR model, this research predicted the suspended sediment yield from 2001 to 2011 moderately well. Given the limited amount of data used in developing the model, this result is acceptable and can be improved with additional data. The study has produced a tool for estimating the potential changes in suspended sediment yield in the Cuyahoga River resulting from alterations in the land-use and land-cover as well as climatic effects on this watershed. The outcome of this research can provide decision makers with a measure for assessing the impacts of future development and climate alteration on Total Suspended Solids (TSS), and ultimately water quality in the watershed and may have implications for stream stability, dam and flood management as well as infrastructure life. With the increasing availability of satellite and precipitation data, this method has the potential to be a viable alternative to other data-intensive and sophisticated models for predicting suspended sediment yield especially for watersheds with limited data.
Overall, the performance of the model presented in this study was acceptable, as demonstrated by an estimated R-squared value of 0.7 based on the comparison between predicted and observed mean annual suspended sediment yield. However, it is important to note that typical with regression-based studies, this model has some uncertainty which was investigated and discussed. Based on the uncertainty analysis, there is a 63% chance that the observed suspended sediment of the Cuyahoga River falls within the 95% confidence interval of this model. Some of the uncertainty around the model’s predictions is due to the size of dataset used to develop the model. Further, there are inherent uncertainties with data, such as suspended sediment yield measurements in general, which may impact the performance of any suspended sediment yield model.
Author Contributions
Conceptualization, R.A., H.H., L.Z., K.S.-L., and V.S.; methodology, R.A., H.H., L.Z., and V.S.; software, R.A., H.H.; validation, R.A., H.H., L.Z., K.S.-L., and V.S.; formal analysis, R.A. and H.H., resources, L.Z., K.S.-L., and V.S.; writing—original draft preparation, R.A. and H.H., writing—review and editing, R.A., H.H., L.Z., K.S.-L., and V.S.; visualization, R.A. and H.H., supervision, L.Z., K.S.-L., and V.S.; project administration, L.Z., K.S.-L., and V.S.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding and was funded by the University of Akron.
Acknowledgments
The authors would like to thank Ward Barnes for sharing his insight with us during the creation of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Ngo, T.S.; Shrestha, R.P.N.D.B. Effect of Land Use Change on Runoff and Sediment Yield in Da River Basin of Hoa Binh Province, Noorthwest Vietnam. J. Mt. Sci. 2015, 12, 1051–1064. [Google Scholar] [CrossRef]
- Hosseiny, H.; Crimmins, M.; Smith, V.; Kremer, P. A Generalized Automated Framework for Urban Runoff Modeling and Its Application at a Citywide Landscape. Water 2020, 12, 357. [Google Scholar] [CrossRef]
- Zarzar, C.M.; Hosseiny, H.; Siddique, R.; Gomez, M.; Smith, V.; Mejia, A.; Dyer, J. A Hydraulic MultiModel Ensemble Framework for Visualizing Flood Inundation Uncertainty. JAWRA J. Am. Water Resour. Assoc. 2018. [Google Scholar] [CrossRef]
- Chin, A. Urban Transformation of River Landscapes in a Global Context. Geomorphology 2006, 79, 460–487. [Google Scholar] [CrossRef]
- Wolman, M.G. A Cycle of Sedimentation and Erosion in Urban River Channels. Geogr. Ann. 1967, 49, 385–395. [Google Scholar] [CrossRef]
- Wolman, M.G.; Schick, A.P. Effects of Construction on Fluvial Sediment, Urban and Suburban Areas of Maryland. Water Resour. Res. 1967, 3, 451–464. [Google Scholar] [CrossRef]
- Leopold, L. Hydrology for Urban Land Planning—A Guidebook on the Hydrologic Effects of Urban Land Use. Geol. Surv. Circ. 1968, 554, 1–21. [Google Scholar]
- Paul, M.J.; Meyer, J.L. Streams in the Urban Landscape. Annu. Rev. Ecol. Syst. 2001, 32, 333–365. [Google Scholar] [CrossRef]
- Chen, H.J.; Chang, H. Response of Discharge, TSS, and E. Coli to Rainfall Events in Urban, Suburban, and Rural Watersheds. Environ. Sci. Process. Impacts 2014, 16, 2313–2324. [Google Scholar] [CrossRef]
- Reiners, P.W.; Ehlers, T.A.; Mitchell, S.G.; Montgomery, D.R. Coupled Spatial Variations in Precipitation and Long-Term Erosion Rates across the Washington Cascades. Nature 2003, 426, 645–647. [Google Scholar] [CrossRef]
- Bookhagen, B.; Thiede, R.C.; Strecker, M.R. Abnormal Monsoon Years and Their Control on Erosion and Sediment Flux in the High, Arid Northwest Himalaya. Earth Planet. Sci. Lett. 2005, 231, 131–146. [Google Scholar] [CrossRef]
- Krajewski, A.; Sikorska, A.E.; Banasik, K. Modeling Suspended Sediment Concentration in the Stormwater Outflow from a Small Detention Pond. J. Environ. Eng. 2017, 143, 1–11. [Google Scholar] [CrossRef]
- Fiener, P.; Neuhaus, P.; Botschek, J. Long-Term Trends in Rainfall Erosivity-Analysis of High Resolution Precipitation Time Series (1937–2007) from Western Germany. Agric. For. Meteorol. 2013, 171, 115–123. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Badwaik, M.R.; Rajeevan, M. Analysis of the Daily Rainfall Events over India Using a New Long Period (1901–2010) High Resolution (0.25° × 0.25°) Gridded Rainfall Data Set. Clim. Dyn. 2015, 45, 755–776. [Google Scholar] [CrossRef]
- Frick, E.A.; Buell, G.R. Relation of Land Use to Nutrient and Suspended-Sediment Concentrations, Loads, and Yields in the Upper Chattahoochee River Basin, Georgia, 1993–1998. In Proceedings of the Georgia Water Resources Conference, Athens, Georgia, 30–31 March 1999; pp. 170–179. [Google Scholar]
- Chichakly, K.J.; Bowden, W.B.; Eppstein, M.J. Minimization of Cost, Sediment Load, and Sensitivity to Climate Change in a Watershed Management Application. Environ. Model. Softw. 2013, 50, 158–168. [Google Scholar] [CrossRef]
- Franz, C.; Makeschin, F.; Weiß, H.; Lorz, C. Sediments in Urban River Basins: Identification of Sediment Sources within the Lago Paranoá Catchment, Brasilia DF, Brazil—Using the Fingerprint Approach. Sci. Total Environ. 2014, 466, 513–523. [Google Scholar] [CrossRef]
- Marttila, H.; Nieminen, M.L.; Arje, J.; Meissner, K.; Tuukkanen, T.; Saukkoriipi, J.; Klove, B. Dynamics and Temporal Changes in Suspended Sediment Transport in Northern Finland: Transport of Very Fine Particulate Matter. Boreal Environ. Res. 2016, 21, 541–555. [Google Scholar]
- Morris, G.L.; FAN, J. Reservoir Sedimentation Handbook; McGraw-Hill Book Co.: New York, NY, USA, 1998. [Google Scholar]
- Smith, V.B.; David, C.H.; Cardenas, M.B.; Yang, Z.L. Climate, River Network, and Vegetation Cover Relationships across a Climate Gradient and Their Potential for Predicting Effects of Decadal-Scale Climate Change. J. Hydrol. 2013, 488, 101–109. [Google Scholar] [CrossRef]
- Wulf, H.; Bookhagen, B.; Scherler, D. Seasonal Precipitation Gradients and Their Impact on Fluvial Sediment Flux in the Northwest Himalaya. Geomorphology 2010, 118, 13–21. [Google Scholar] [CrossRef]
- Trimble, S.W. Contribution of Stream Channel Erosion to Sediment Yield from an Urbanizing Watershed. Science 1997, 278, 1442–1444. [Google Scholar] [CrossRef]
- Banasik, K.; Popek, Z.I.E.W.; Hejduk, L. Estimating the Annual Sediment Yield of a Small Agricultural Catchment in Central Poland. Eros. Sediment Yields Chang. Environ. 2012, 11–15, 267–275. [Google Scholar]
- Hosseiny, H.; Smith, V. Two Dimensional Model for Backwater Geomorphology: Darby Creek, PA. Water 2019, 11, 2204. [Google Scholar] [CrossRef]
- Nelson, E.J.; Booth, D.B. Sediment Sources in an Urbanizing, Mixed Land-Use Watershed. J. Hydrol. 2002, 264, 51–68. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Vorosmarty, C.J.; Kettner, A.J.; Green, P. Impacts of Humans on the Flux of Terrestrial Sediment to the Global Coastal Ocean. Res. Artic. 2005, 308, 376–380. [Google Scholar] [CrossRef]
- Stenberg, L.; Tuukkanen, T.; Finér, L.; Marttila, H.; Piirainen, S.; Kløve, B.; Koivusalo, H. Ditch Erosion Processes and Sediment Transport in a Drained Peatland Forest. Ecol. Eng. 2015, 75, 421–433. [Google Scholar] [CrossRef]
- Hart, H.M. Effect of Land Use on Total Suspended Solids and Turbidity in the Little River Watershed, Blount County, Tennessee. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 2006. [Google Scholar]
- Zhang, X.; Cao, W.; Guo, Q.; Wu, S. Effects of Landuse Change on Surface Runoff and Sediment Yield at Different Watershed Scales on the Loess Plateau. Int. J. Sediment Res. 2010, 25, 283–293. [Google Scholar] [CrossRef]
- Overland, H.; Kleenberg, H.B. Influence of Land Use Change on Discharge and Sediment Transport Floods. Sediment Stream Water Qual. Chang. Environ. Trends Explan. 1991, 83–92. [Google Scholar]
- Dutton, C.L.; Subalusky, A.L.; Anisfeld, S.C.; Njoroge, L.; Rosi, E.J.; Post, D.M. The Influence of a Semi-Arid Sub-Catchment on Suspended Sediments in the Mara River, Kenya. PLoS ONE 2018, 13, 1–19. [Google Scholar] [CrossRef]
- Odhiambo, B.K.; Boss, S.K. Watershed Physiography, Land Use, and Sediment Yield: A Case Study from Northwest Arkansas, USA. J. Spat. Hydrol. 2006, 6, 29–51. [Google Scholar]
- Walling, D.E. Linking Land Use, Erosion and Sediments Yields in River Basins. Hydrobiologia 1999, 410, 223–240. [Google Scholar] [CrossRef]
- Schilling, K.E.; Isenhart, T.M.; Palmer, J.A.; Wolter, C.F.; Spooner, J. Impacts of Land-Cover Change on Suspended Sediment Transport in Two Agricultural Watersheds. J. Am. Water Resour. Assoc. 2011, 47, 672–686. [Google Scholar] [CrossRef]
- Kithiia, S.M.; Mutua, F.M. Impacts of Land-Use Changes on Sediment Yields and Water Quality within the Nairobi River Sub-Basins, Kenya. In Sediment Dynamics and the Hydromorphology of Fluvial Systems; IAHS: Wallingford, UK, 2006; pp. 582–588. [Google Scholar]
- Dearing, J.A.; Jones, R.T. Coupling Temporal and Spatial Dimensions of Global Sediment Flux through Lake and Marine Sediment Records. Glob. Planet. Chang. 2003, 39, 147–168. [Google Scholar] [CrossRef]
- Hamidi, S.A.; Hosseiny, H.; Ekhtari, N.; Khazaei, B. Using MODIS Remote Sensing Data for Mapping the Spatio-Temporal Variability of Water Quality and River Turbid Plume. J. Coast. Conserv. 2017, 21, 939–950. [Google Scholar] [CrossRef]
- Frohn, R.C.; D’amico, E.; Lane, C.; Autrey, B.; Rhodus, J.; Liu, H. Multi-Temporal Sub-Pixel Landsat ETM+ Classification of Isolated Wetlands in Cuyahoga County, OHIO, USA. Wetlands 2012, 32, 289–299. [Google Scholar] [CrossRef]
- Mann, K.C.; Peck, J.A.; Peck, M.C. Assessing Dam Pool Sediment for Understanding Past, Present and Future Watershed Dynamics: An Example from the Cuyahoga River, Ohio. Anthropocene 2013, 2, 76–88. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport: Bed Load Transport. J. Hydraul. Eng. ASCE 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Peter, A.; William, W. Sediment Transport: New Approach and Analysis. J. Hydraul. Div. 1973, 99, 2041–2060. [Google Scholar]
- Kisi, O.; Ozkan, C.; Akay, B. Modeling Discharge-Sediment Relationship Using Neural Networks with Artificial Bee Colony Algorithm. J. Hydrol. 2012, 428, 94–103. [Google Scholar] [CrossRef]
- Aytek, A.; Kişi, Ö. A Genetic Programming Approach to Suspended Sediment Modelling. J. Hydrol. 2008, 351, 288–298. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Wang, J. Predicting Sediment Yield and Transport Dynamics of a Cold Climate Region Watershed in Changing Climate. Sci. Total Environ. 2018, 625, 1030–1045. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Leta, O.T.; De Fraine, B.; van Griensven, A.; Bauwens, W. OpenMI-Based Integrated Sediment Transport Modelling of the River Zenne, Belgium. Environ. Model. Softw. 2013, 47, 193–206. [Google Scholar] [CrossRef]
- Elliot, W.J. Erosion Processes and Prediction with Wepp Technology in Forests in the Northwestern U.S. Trans. ASABE 2013, 56, 563–579. [Google Scholar] [CrossRef]
- Ramsankaran, R.; Kothyari, U.C.; Rawat, J.S. Simulation of Surface Runoff and Sediment Yield Using the Water Erosion Prediction Project (WEPP) Model: A Study in Kaneli Watershed, Himalaya, India. Hydrol. Sci. J. 2009, 54, 513–525. [Google Scholar] [CrossRef]
- WikiWatershed. Available online: https://wikiwatershed.org/ (accessed on 20 November 2018).
- Nandi, A.; Shakoor, A. Application of Logistic Regression Model for Slope Instability Prediction in Cuyahoga River Watershed, Ohio, USA. Georisk 2008, 2, 16–27. [Google Scholar] [CrossRef]
- Rice, C.P.; Schmitz-Afonso, I.; Loyo-Rosales, J.E.; Link, E.; Thoma, R.; Fay, L.; Altfater, D.; Camp, M.J. Alkylphenol and Alkylphenol-Ethoxylates in Carp, Water, and Sediment from the Cuyahoga River, Ohio. Environ. Sci. Technol. 2003, 37, 3747–3754. [Google Scholar] [CrossRef] [PubMed]
- NOAA. Land-Based Station Data. Available online: https://www.ncdc.noaa.gov/data-access/land-based-station-data (accessed on 20 November 2018).
- USGS. Water Resources of the United States. Available online: https://maps.waterdata.usgs.gov/mapper/index.html (accessed on 20 November 2018).
- U.S. Geological Survey. Global Visualization Viewer. Available online: https://glovis.usgs.gov/ (accessed on 20 November 2018).
- ODNR. Ohio Department of Natural Resources, GIS Applications. Available online: http://water.ohiodnr.gov/ (accessed on 20 November 2018).
- US Census Bureau. Available online: https://www.census.gov/data.html (accessed on 20 November 2018).
- USGS NHD. National Hydrography Dataset. Available online: https://www.usgs.gov/core-science-systems/ngp/national-hydrography/national-hydrography-dataset?qt-science_support_page_related_con=0#qt-science_support_page_related_con (accessed on 20 November 2018).
- US EPA. Green Infrastructure BMP Design. Available online: https://www.epa.gov/snecwrp/providence-ri-green-infrastructure-project (accessed on 10 September 2019).
- Strom, K.; Hosseiny, H.; Wang, K.H. Sediment Sampling, Characterization, and Analysis on the Guadalupe River in the Coastal Plain of Texas; University of Houston, Department of Civil and Environmental Engineering: Houston, TX, USA, 2015. [Google Scholar]
- Strom, K.; Hosseiny, H. Suspended Sediment Sampling and Annual Sediment Yield on the Middle Trinity River; University of Houston, Department of Civil and Environmental Engineering: Houston, TX, USA, 2015. [Google Scholar]
- Klein, I.; Gessner, U.; Dietz, A.J.; Kuenzer, C. Global WaterPack—A 250 m Resolution Dataset Revealing the Daily Dynamics of Global Inland Water Bodies. Remote Sens. Environ. 2017, 198, 345–362. [Google Scholar] [CrossRef]
- Landsat Science Data. Available online: https://landsat.gsfc.nasa.gov/data/ (accessed on 15 June 2013).
- Jensen, J.R. Introductory Digital Image Processing, a Remote Sensing Perspective; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Cai, Z.; Ho, A.T.S. Cloud Detection in Satellite Images for Tropical Regions. In Proceedings of the Multispectral Imaging for Terrestrial Applications, International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 4 November 1996; pp. 1174–1177. [Google Scholar] [CrossRef]
- Exelis Visual Information Solutions. ENVI Version 4.2 User Guide; Exelis Visual Information Solutions: Boulder, CO, USA, 2008. [Google Scholar]
- Environmental Systems Research Institute. ArcGIS Release 10.1; Environmental Systems Research Institute: Redlands, CA, USA, 2012. [Google Scholar]
- Bodhinayake, W.; Si, B.C. Near-Saturated Surface Soil Hydraulic Properties under Different Land Uses in the St Denis National Wildlife Area, Saskatchewan, Canada. Hydrol. Process. 2004, 18, 2835–2850. [Google Scholar] [CrossRef]
- Araghinejad, S. Data-Driven Modeling: Using MATLAB in Water Resources and Environmental Engineering. In Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2014; Volume 67, p. 3. [Google Scholar]
- Ayele, G.T.; Teshale, E.Z.; Yu, B.; Rutherfurd, I.D.; Jeong, J. Streamflow and Sediment Yield Prediction for Watershed Prioritization in the Upper Blue Nile River Basin, Ethiopia. Water 2017, 9. [Google Scholar] [CrossRef]
- Sinnakaudan, S.K.; Ghani2, A.A.; Ahmad, M.S.S.; Zakaria, N.A. Multiple Linear Regression Model for Total Bed Material Load Prediction. XI Jorn. Españolas Presas 2006, 132, 521–528. [Google Scholar] [CrossRef]
- Yen, H.; Lu, S.; Feng, Q.; Wang, R.; Gao, J.; Brady, D.M.; Sharifi, A.; Ahn, J.; Chen, S.T.; Jeong, J.; et al. Assessment of Optional Sediment Transport Functions via the Complex Watershed Simulation Model SWAT. Water 2017, 9. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “goodness-of-fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).