Quantitative Estimation of Soil Salinization in an Arid Region of the Keriya Oasis Based on Multidimensional Modeling
Abstract
1. Introduction
2. Materials and Methods
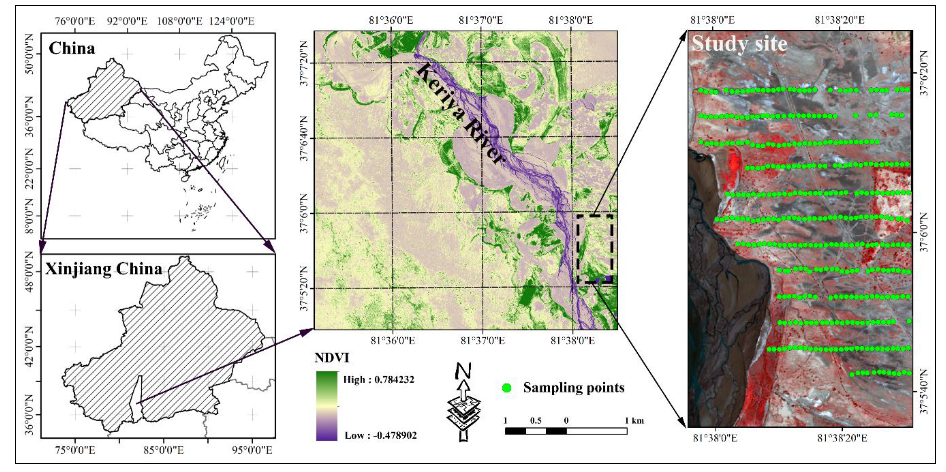
2.1. Study Area
2.2. Field Measurement
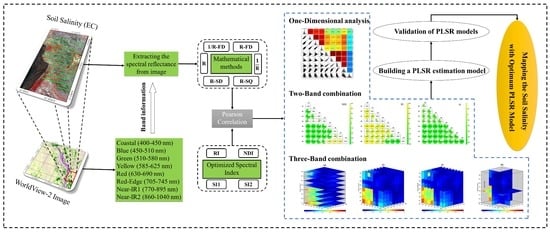
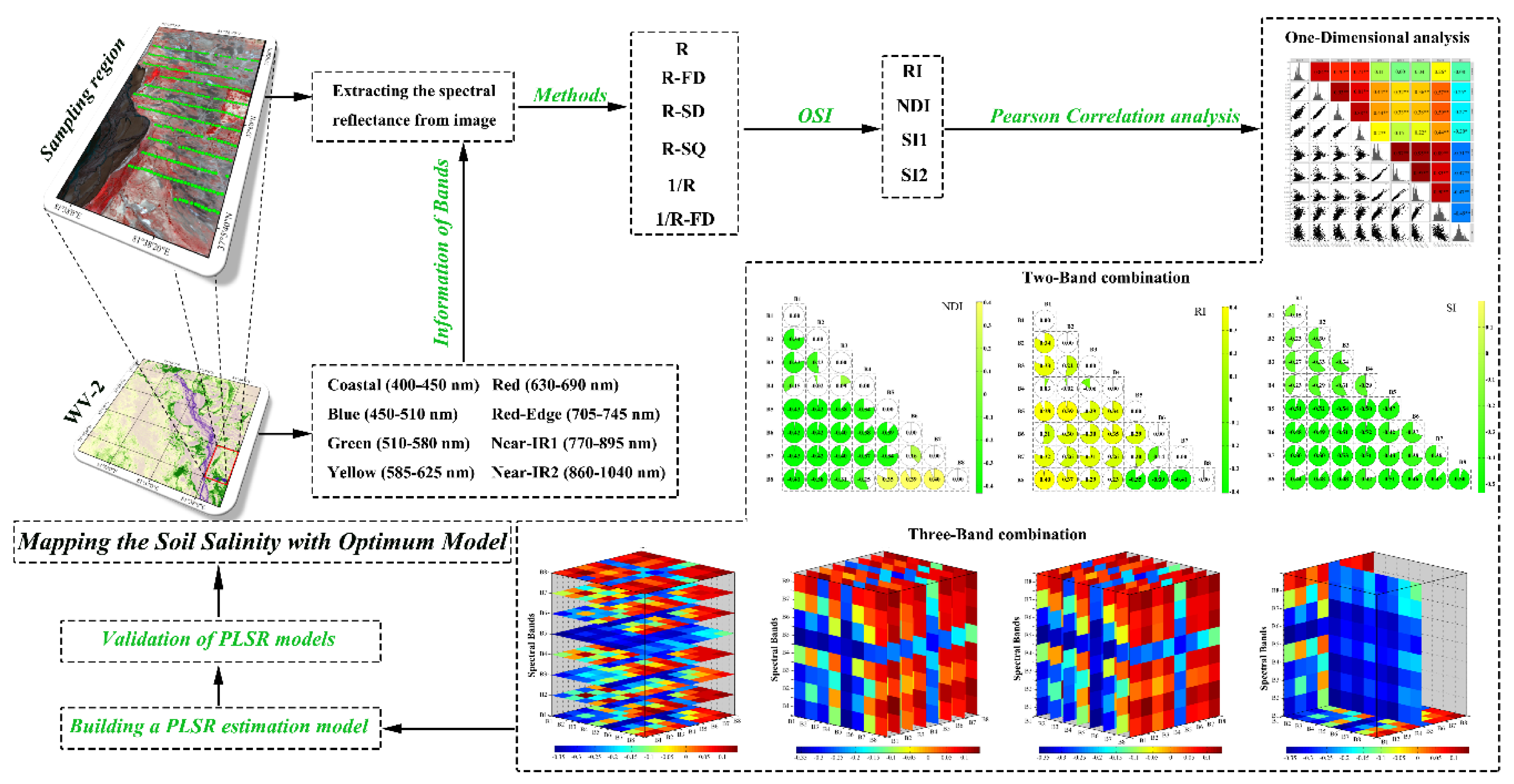
2.3. Selection of Spectral Indices and Sensitive Bands
- (1)
- (2)
- Spectral radiometric calibration and atmospheric and Geometric corrections were performed on the WV-2 [21].
- (3)
- The FLAASH model was used to eliminate atmospheric and adjacency effects for images using the Environmental for Visualizing Images (ENVI 5.3, EXELIS VIS) software package® [22]. The WV-2 image was resampled into 2-m resolution, and the River channel with water bodies was clipped out due to the inaccessibility for sampling.
2.4. Model Generation and Data Analysis
2.5. Partial Least-Squares Regression
2.6. Model Evaluation
- (1)
- A high coefficient of determination (R2), indicating a strong linear relationship.
- (2)
- Low Root Mean Square Errors (RMSE) of the model’s variables, indicating that the low error between measured and predicted data were calculated by the equation listed in Table 3.
- (3)
- Relative Percent Deviation (RPD), indicating the predictive ability of the model. Its computation process is the ratio between standard deviation (SD) and standard error of prediction (SEP). According to the predictive ability of the model, the RPD is divided into three categories: (1) The value of RPD exceeds 2.0, indicating a model with better predictive ability. (2) The RPD values ranging from 1.4 to 2.0 represent a model with general predictive ability. (3) The RPD value is less than 1.4, indicating that it has poor predictive ability.
3. Results and Analysis
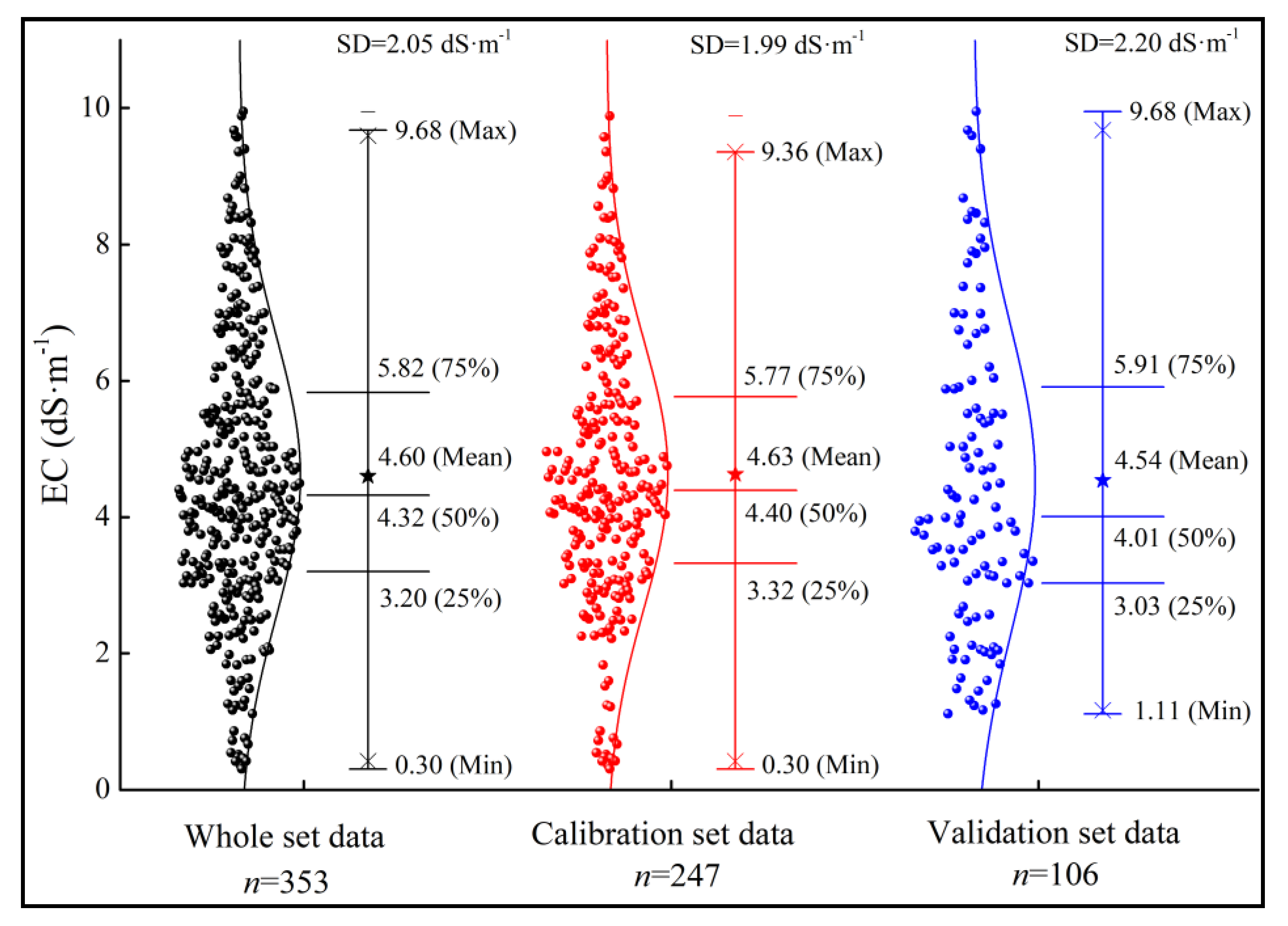
3.1. Statistical Characteristics of the Sampling Data
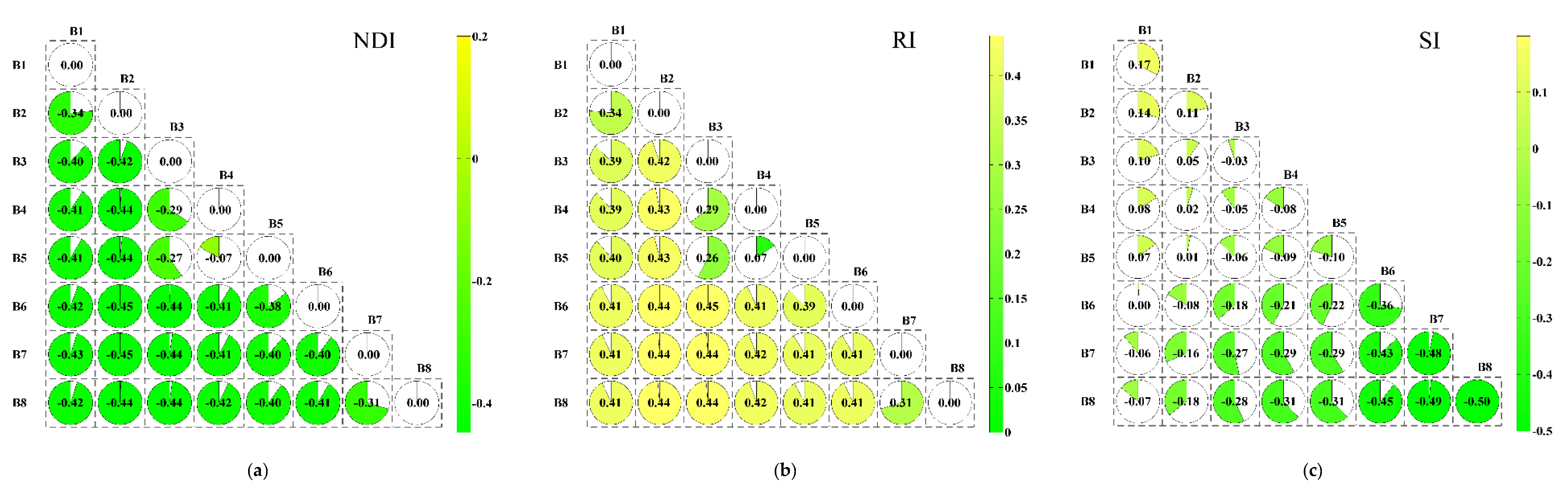
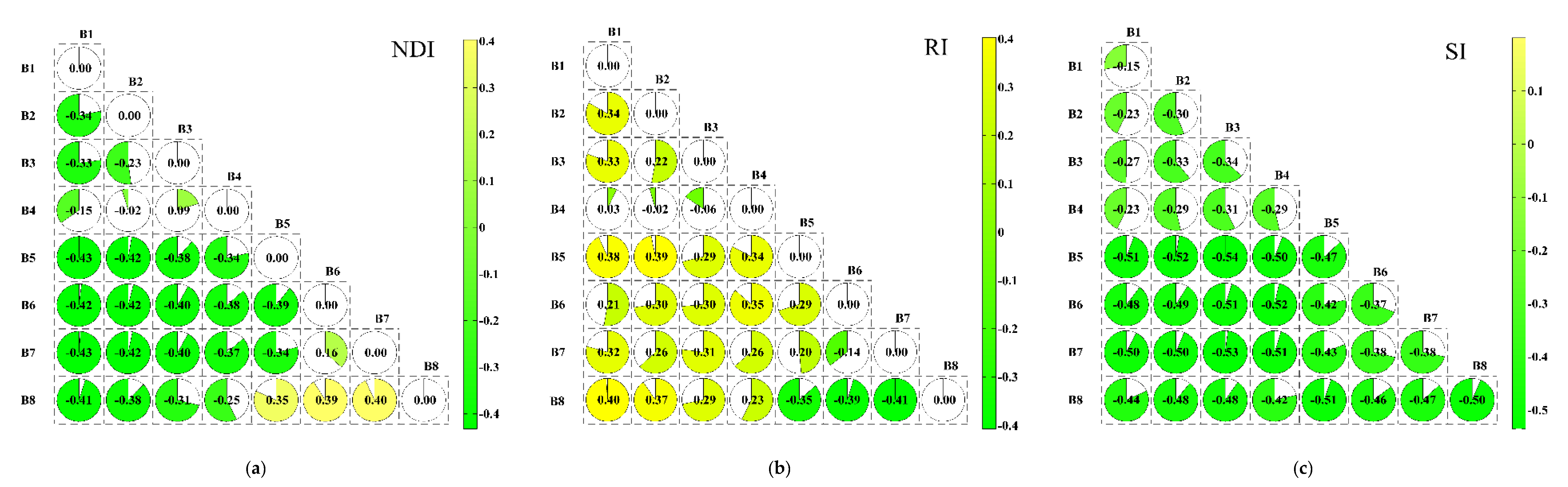
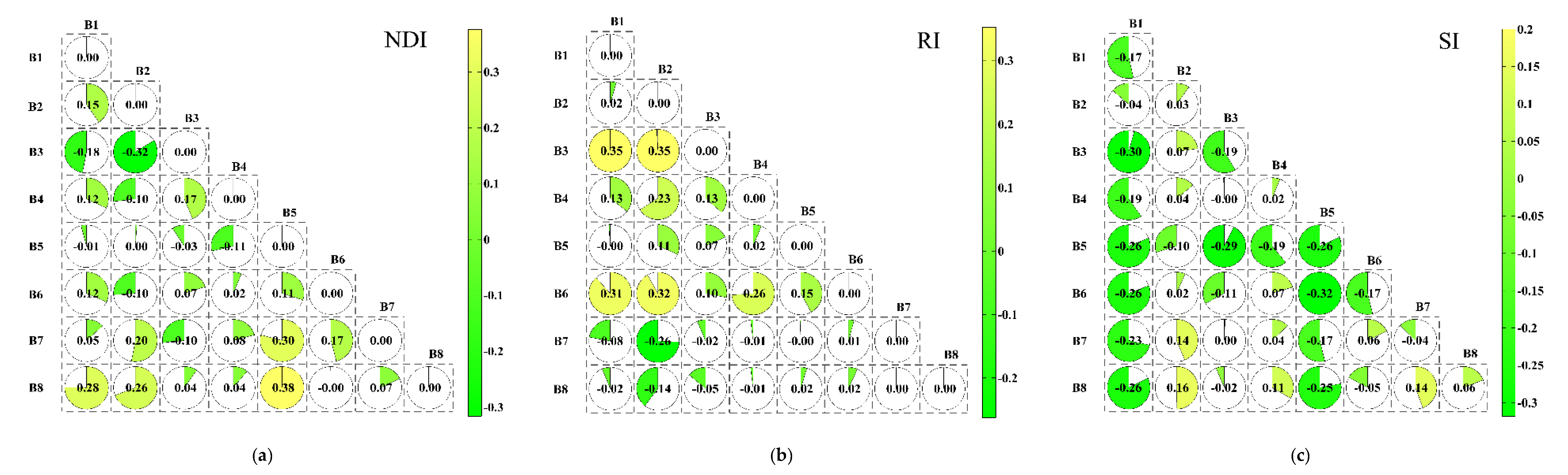
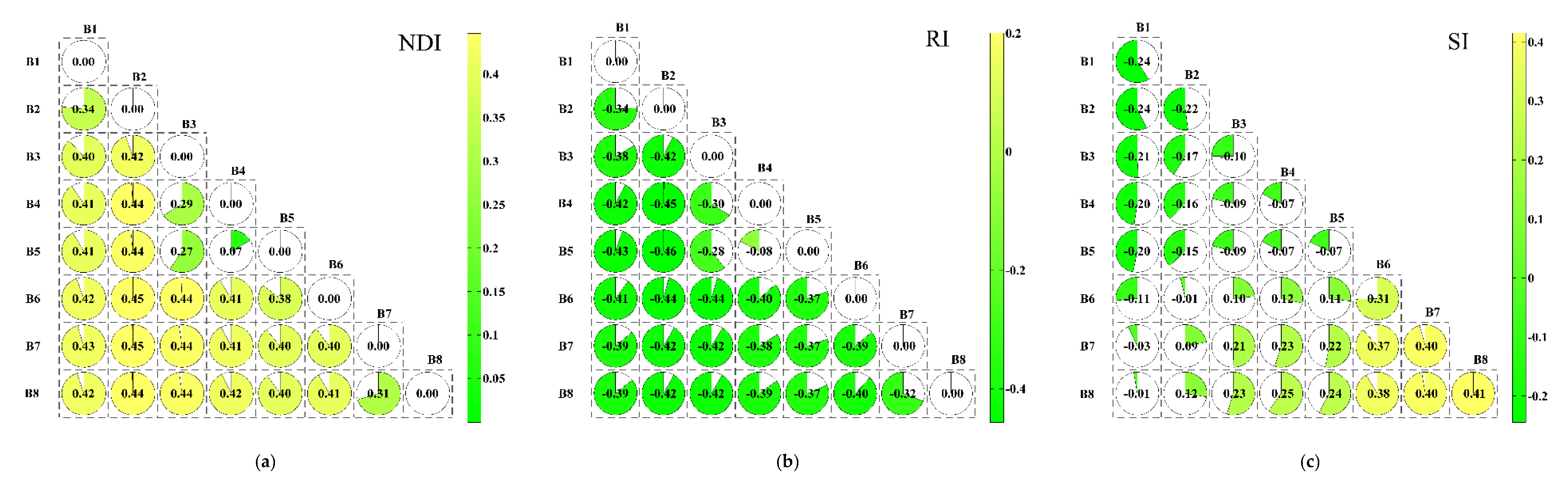
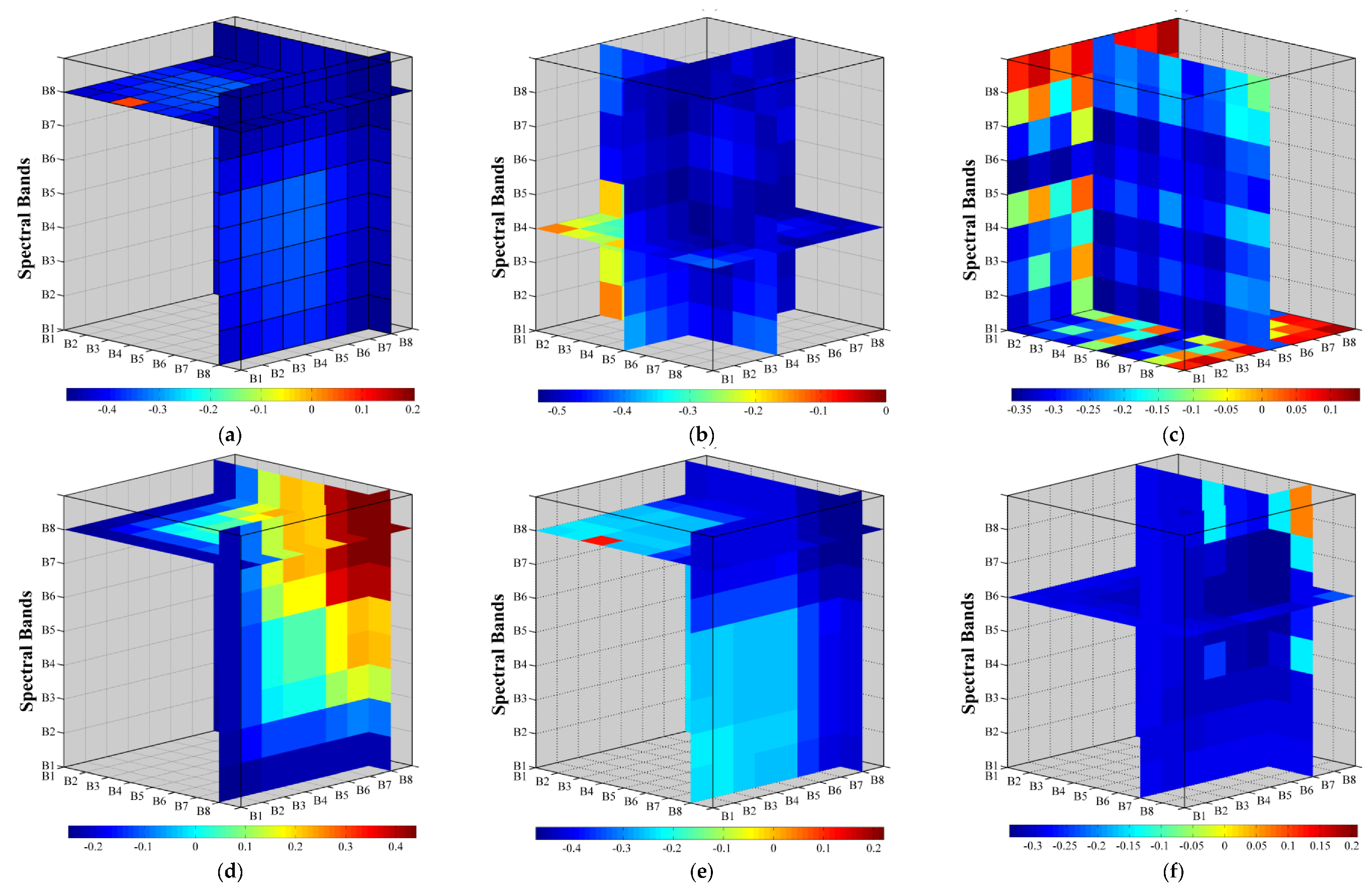
3.2. Analysis Correlation between EC and Bands of Worldview2-Images
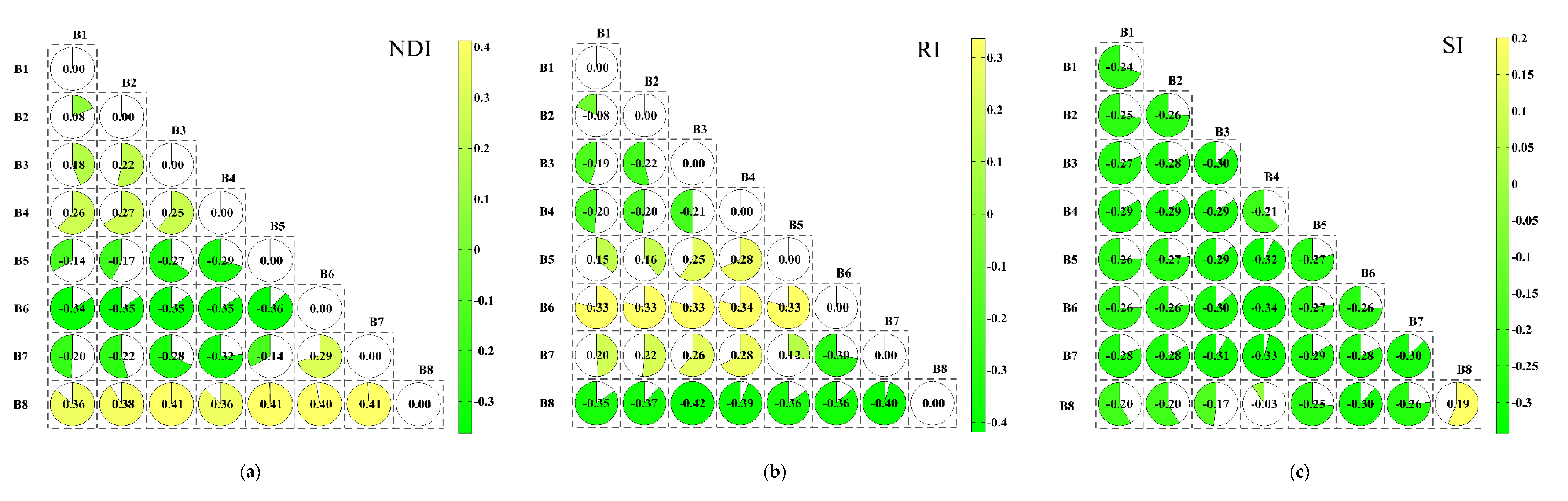
3.3. Analysis Correlation between EC and Optimized Spectral Index
3.3.1. Two-Dimensional Correlation Analysis
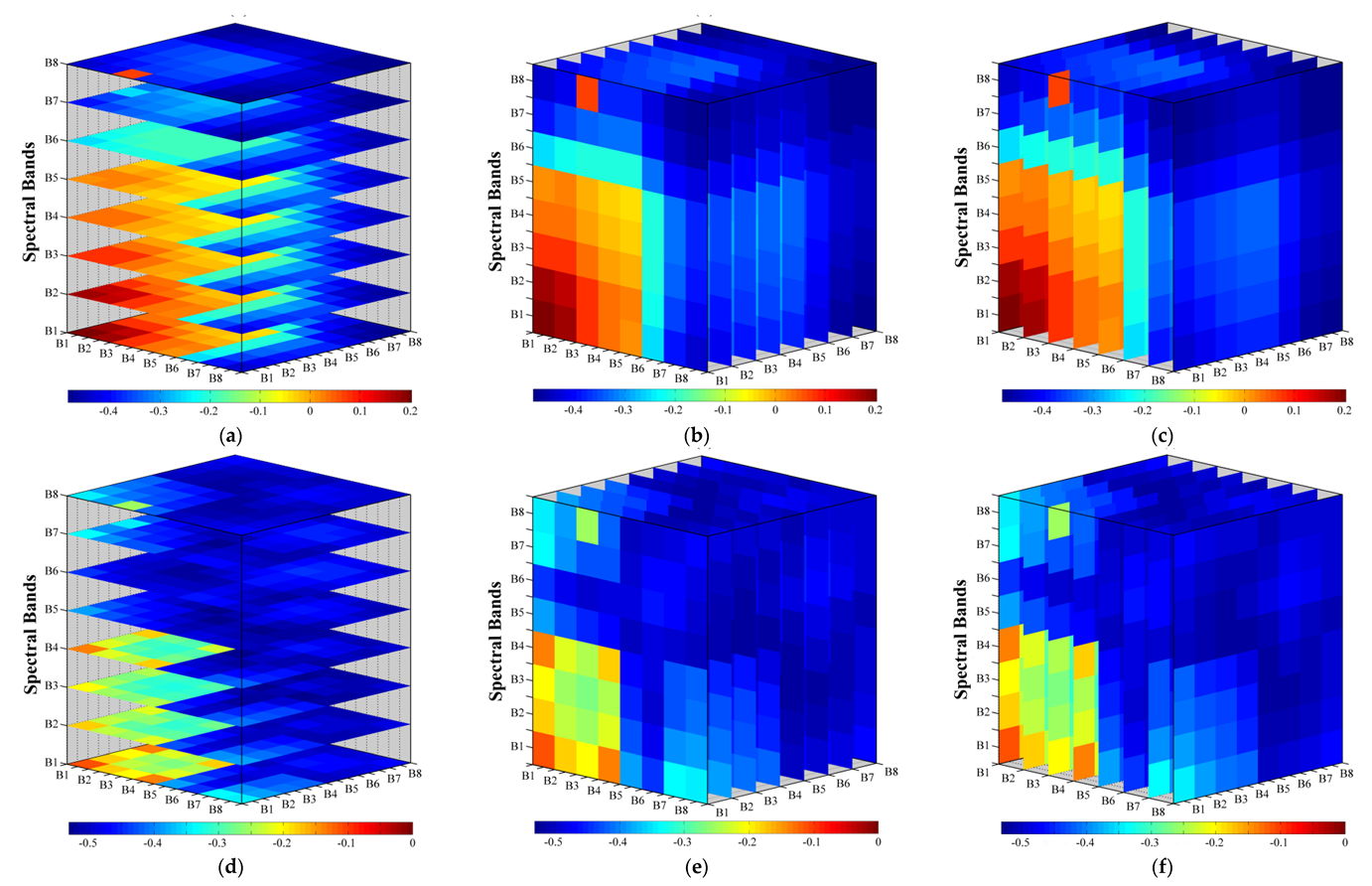
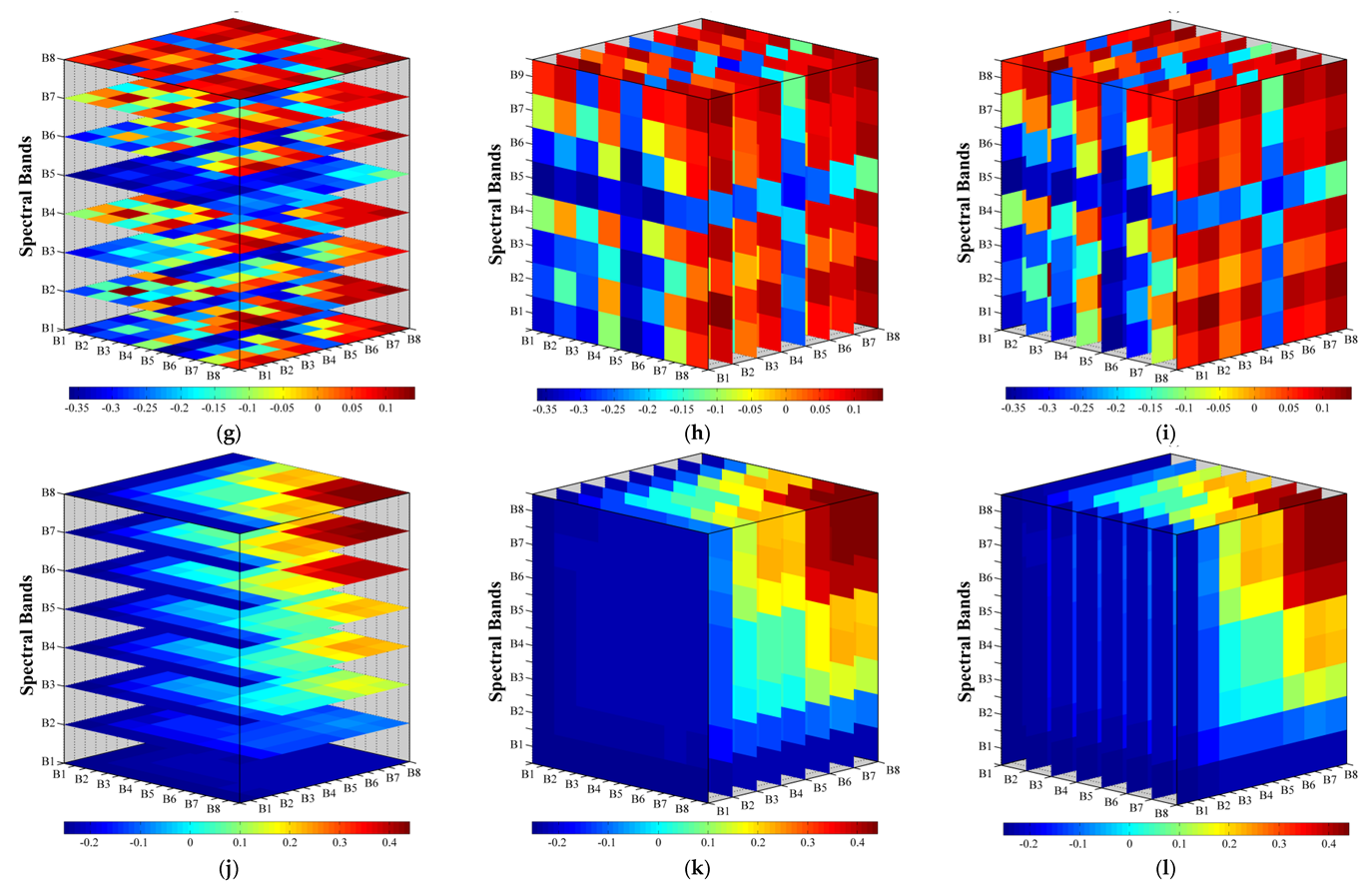
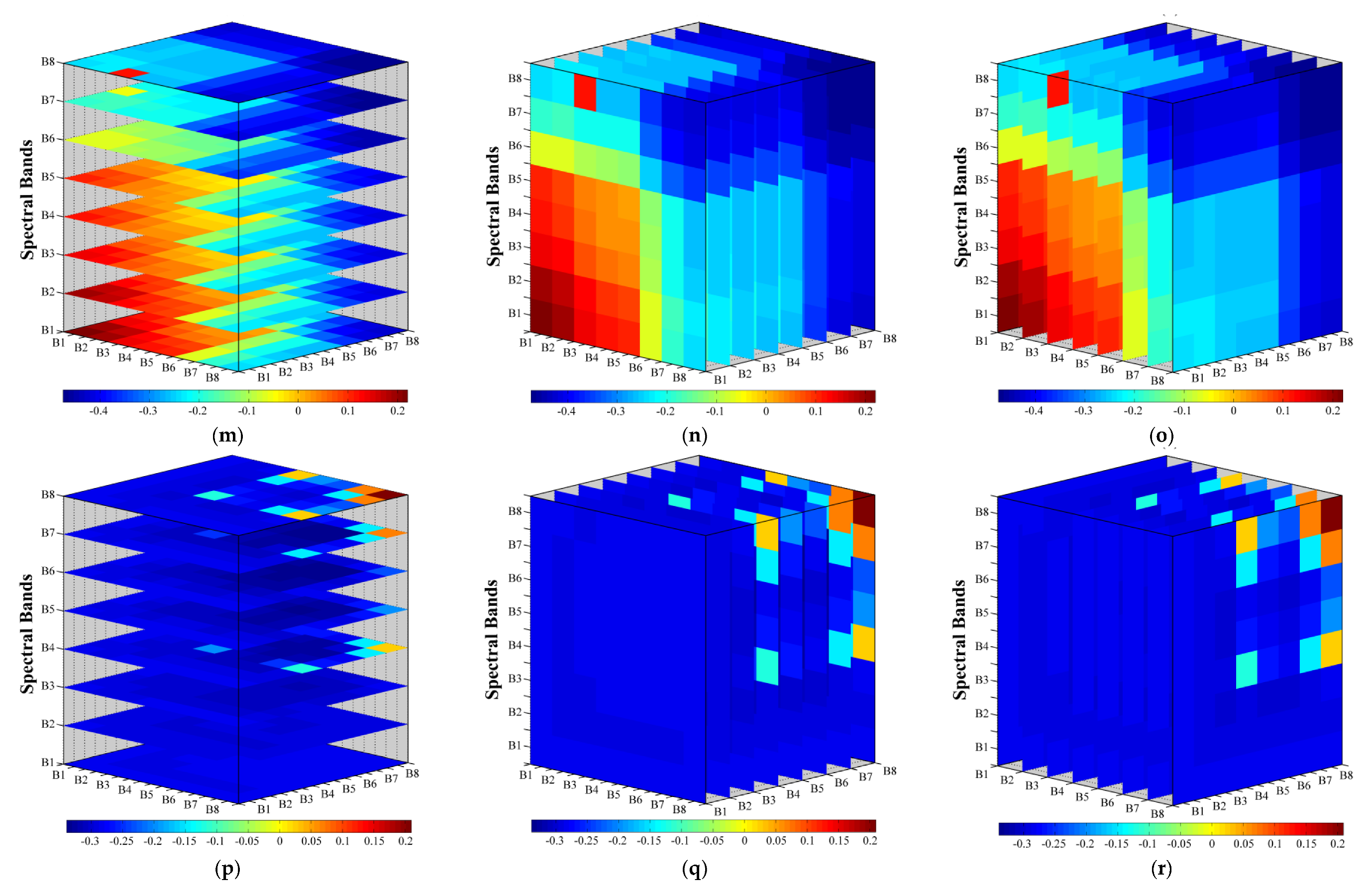
3.3.2. Three-Dimensional Correlation Analysis
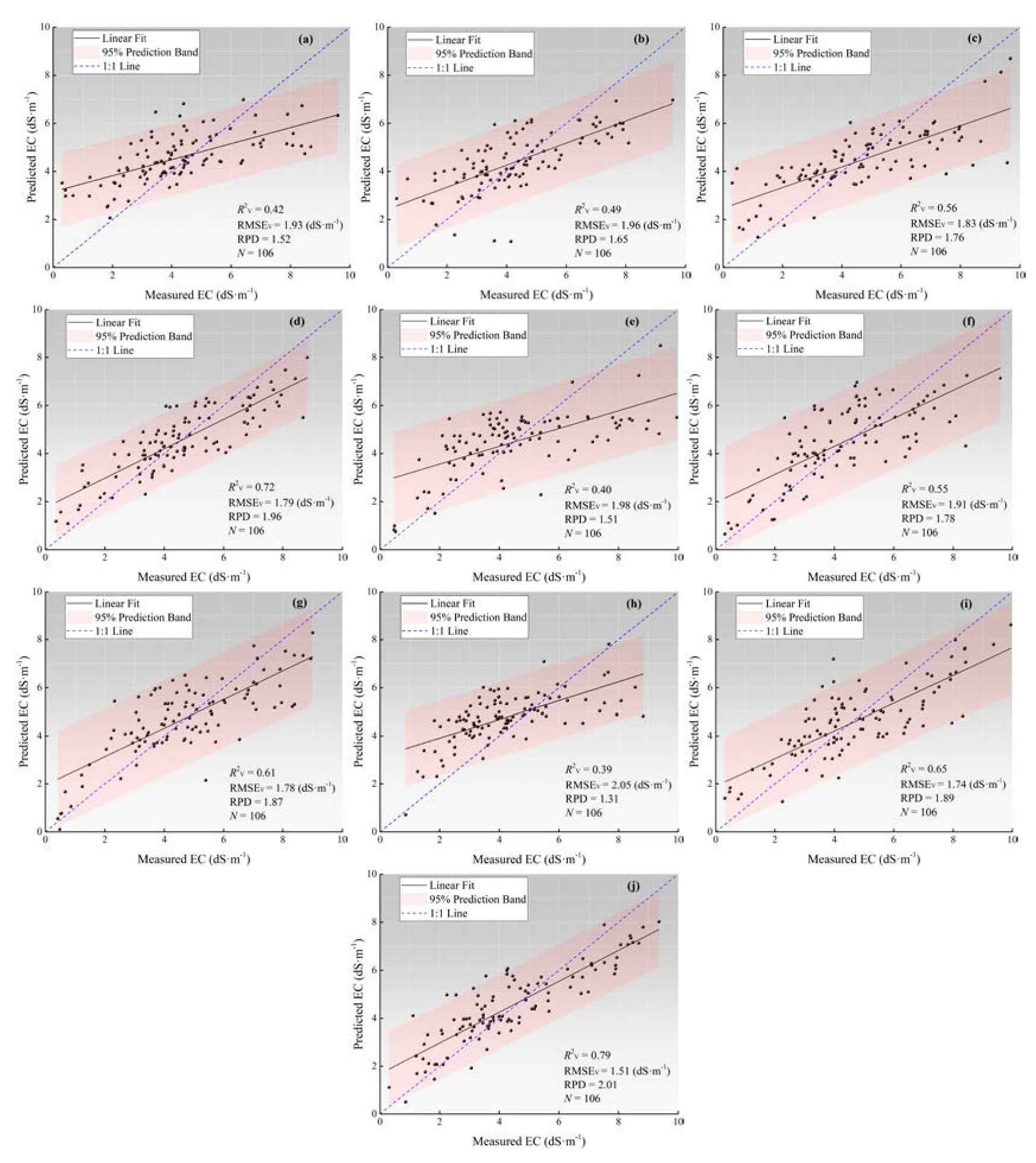
3.4. Estimation PLSR Models and Evaluation
3.5. Soil Salinity Maps with EC Data
4. Discussion
4.1. Application of Multidimensional Modeling with Different Algorithm
4.2. Estimation of Salt-Affected Land in Arid and Semiarid Regions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bot, A.J.; Nachtergaele, F.O.; Young, A. Land resource potential and constraints at regional and country levels. World Soil Resour. Rep. 2000, 90, 1–114. [Google Scholar] [CrossRef]
- Wicke, B.; Sikkema, R.; Dornburg, V.; Faaij, A. Exploring land use changes and the role of palm oil production in Indonesia and Malaysia. J. Land Use Policy 2011, 28, 193–206. [Google Scholar] [CrossRef]
- Abbas, A.; Khan, S.; Hussain, N.; Hanjra, M.A.; Akbar, S. Characterizing soil salinity in irrigated agriculture using a remote sensing approach. J. Phys. Chem. Earth Parts A/B/C 2013, 55–57, 43–52. [Google Scholar] [CrossRef]
- Peng, J.; Biswas, A.; Jiang, Q.; Zhao, R.; Hu, J.; Hu, B.; Shi, Z. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China. J. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Douaoui, A.E.K.; Nicolas, H.; Walter, C. Detecting salinity hazards within a semiarid context by means of combining soil and remote-sensing data. J. Geoderma 2006, 134, 217–230. [Google Scholar] [CrossRef]
- Ma, L.; Yang, S.; Simayi, Z.; Gu, Q.; Li, J.; Yang, X.; Ding, J. Modeling variations in soil salinity in the oasis of Junggar Basin, China. J. Land Degrad. Dev. 2018, 29, 551–562. [Google Scholar] [CrossRef]
- Aldabaa, A.A.A.; Weindorf, D.C.; Chakraborty, S.; Sharma, A.; Li, B. Combination of proximal and remote sensing methods for rapid soil salinity quantification. J. Geoderma 2015, 239–240, 34–46. [Google Scholar] [CrossRef]
- Bannari, A.; El-Battay, A.; Bannari, R.; Rhinane, H. Sentinel-MSI VNIR and SWIR bands sensitivity analysis for soil salinity discrimination in an arid landscape. J. Remote Sens. 2018, 10, 855. [Google Scholar] [CrossRef]
- Peng, J.; Xiang, H.; Guo, Y.; Shi, Z. Comparative study on hyperspectral inversion accuracy of soil salt content and electrical conductivity. J. Spectrosc. Spectr. Anal. 2014, 34, 510–514. [Google Scholar]
- Ge, X.; Wang, J.; Ding, J.; Cao, X.; Zhang, Z.; Liu, J.; Li, X. Combining UAV-based hyperspectral imagery and machine learning algorithms for soil moisture content monitoring. J. PeerJ 2019, 7, e6926. [Google Scholar] [CrossRef]
- Khan, N.M.; Rastoskuev, V.V.; Sato, Y.; Shiozawa, S. Assessment of hydrosaline land degradation by using a simple approach of remote sensing indicators. J. Agric. Water Manag. 2005, 77, 96–109. [Google Scholar] [CrossRef]
- Kallel, A.; Ksibi, M.; Dhia, H.B.; Khélifi, N. Erratum to: Recent Advances in Environmental Science from the Euro-Mediterranean and Surrounding Regions. In Euro-Mediterranean Conference for Environmental Integration; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Allbed, A.; Kumar, L.; Aldakheel, Y.Y. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region. J. Geoderma 2014, 230–231, 1–8. [Google Scholar] [CrossRef]
- Triki Fourati, H.; Bouaziz, M.; Benzina, M.; Bouaziz, S. Modeling of soil salinity within a semi-arid region using spectral analysis. Arab. J. Geosci. 2015, 8, 11175–11182. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; Onus, A. Spatial analysis of soil salinity and soil structural stability in a semiarid region of new south wales, Australia. J. Environ. Manag. 2008, 42, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Ghulam, A.; Qin, Q.; Zhu, L.; Abdrahman, P. Satellite remote sensing of groundwater: Quantitative modelling and uncertainty reduction using 6s atmospheric simulations. Int. J. Remote Sens. 2004, 25, 5509–5524. [Google Scholar] [CrossRef]
- Kasim, N.; Tiyip, T.; Abliz, A.; Nurmemet, I.; Sawut, R.; Maihemuti, B. Mapping and modeling of soil salinity using worldview-2 data and em38-km2 in an arid region of the keriya river, China. J. Photogramm. Eng. Remote Sens. 2018, 12, 43–52. [Google Scholar] [CrossRef]
- Abdulla, A.; Abduwasit, G.; Ümüt, H.; Jian-li, D.; Mamat, S.; Fei, Z.; Ilyas, N.; Abdugheni, A. Effects of shallow groundwater table and salinity on soil salt dynamics in the Keriya Oasis, Northwestern China. J. Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar]
- Wang, F.; Yang, S.; Yang, W.; Yang, X.; Jianli, D. Comparison of machine learning algorithms for soil salinity predictions in three dryland oases located in xinjiang uyghur autonomous region (Xjuar) of China. Eur. J. Remote Sens. 2020, 52, 256–276. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M.; Oster, J.D.; Kaffka, S.R. Short-term sustainability of drainage water reuse: Spatio-temporal impacts on soil chemical properties. J. Environ. Qual. 2008, 37, S8–S24. [Google Scholar] [CrossRef]
- Sidike, A.; Zhao, S.; Wen, Y. Estimating soil salinity in pingluo county of China using quickbird data and soil reflectance spectra. Internat. J. Appl. Earth Obser. Geoinformat. 2014, 26, 156–175. [Google Scholar] [CrossRef]
- Guo, S.; Ruan, B.; Chen, H.; Guan, X.; Wang, S.; Xu, N. Characterizing the spatiotemporal evolution of soil salinization in hetao irrigation district (China) using a remote sensing approach. Int. J. Remote Sens. 2018, 39, 6805–6825. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses: 2. Application to simulated and glass spectral data. Anal. Chem. 1988, 60, 1202–1208. [Google Scholar] [CrossRef]
- Kahaer, Y.; Tashpolat, N. Estimating Salt Concentrations Based on Optimized Spectral Indices in Soils with Regional Heterogeneity. J. Spectrosc. 2019, 2019, 15. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A. Early detection of plant physiological responses to different levels of water stress using reflectance spectroscopy. J. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Li, S.; Shi, Z.; Chen, S.; Ji, W.; Zhou, L.; Yu, W. In situ measurements of organic carbon in soil profiles using vis-nir spectroscopy on the qinghai–tibet plateau. Environ. Sci. Technol. 2015, 49, 4980–4987. [Google Scholar] [CrossRef]
- Karunaratne, S.B.; Bishop, T.F.A.; Baldock, J.A.; Odeh, I.O.A. Catchment scale mapping of measurable soil organic carbon fractions. J. Geoderma 2014, S219-220, 14–23. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J. Digital mapping of soil properties using multivariate statistical analysis and aster data in an arid region. J. Remote Sens. 2015, 7, 1181–1205. [Google Scholar] [CrossRef]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy–principal components regression analyses of soil properties. SSSA 2000, 65, 480–490. [Google Scholar] [CrossRef]
- Williams, B.; Walker, J.; Anderson, J. Spatial variability of regolith leaching and salinity in relation to whole farm planning. Aust. J. Exp. Agric. 2006, 46, 1271–1277. [Google Scholar] [CrossRef]
- Farifteh, J.; Meer, F.V.D.; Atzberger, C.; Carranza, E.J.M. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). J. Remote Sens. Environ. 2007, 110, 59–78. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. J. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Ding, J.; Yu, D. Monitoring and evaluating spatial variability of soil salinity in dry and wet seasons in the Werigan–Kuqa Oasis, China, using remote sensing and electromagnetic induction instruments. J. Geoderma 2014, 235–236, 316–322. [Google Scholar] [CrossRef]
- Gorji, T.; Tanik, A.; Sertel, E. Soil salinity prediction, monitoring and mapping using modern technologies. J. Procedia Earth Planet. Sci. 2015, 15, 507–512. [Google Scholar] [CrossRef]
- Hu, J.; Peng, J.; Zhou, Y.; Xu, D.; Zhao, R.; Jiang, Q.; Fu, T.; Wang, F.; Shi, Z. Quantitative estimation of soil salinity using UAV-borne hyperspectral and satellite multispectral images. J. Remote Sens. 2019, 11, 736. [Google Scholar] [CrossRef]
- Doolittle, J.A.; Brevik, E.C. The use of electromagnetic induction techniques in soils studies. J. Geoderma 2014, 223–225, 33–45. [Google Scholar] [CrossRef]



| Bands | Wavelength (nm) | Resolution |
|---|---|---|
| Coastal | 400–450 | Multispectral: 1.85 m GSD at nadir, 2.07 m GSD at 20° off-nadir. |
| Blue | 450–510 | |
| Green | 510–580 | |
| Yellow | 585–625 | |
| Red | 630–690 | |
| Red Edge | 705–745 | Panchromatic: 0.46 m GSD at nadir, 0.52 m GSD at 20° off-nadir. |
| Near-IR1 | 770–895 | |
| Near-IR2 | 860–1040 |
| Optimized Spectral Index | Abbreviation | Equation | Reference |
|---|---|---|---|
| Ratio index | RI | Rλ1/Rλ2 | [23] |
| Normalized difference index | NDI | (Rλ1 − Rλ2)/(Rλ1 − Rλ2) | |
| Soil salinization index1 | SI1 | Sqrt (Rλ12 × Rλ22) | |
| Soil salinization index2 | SI2 | Sqrt (Rλ12 +Rλ22 + Rλ32) | [11] |
| Index | Equation |
|---|---|
| Coefficient of Determination | R2 = |
| Root Mean Square Error | RMSE = |
| Relative Percent Deviation | RPD = SD/SEP |
| Type | Acronym | Parameters | R2c | RMSEc | R2v | RMSEv | RPD |
|---|---|---|---|---|---|---|---|
| OD | Raw-I-PLSR | 4 | 0.45 | 1.81 | 0.42 | 1.93 | 1.52 |
| Raw-II-PLSR | 3 | 0.49 | 1.84 | 0.49 | 1.96 | 1.65 | |
| 2D | I-PLSR | 3 | 0.58 | 1.74 | 0.56 | 1.83 | 1.76 |
| II-PLSR | 0.76 | 1.76 | 0.72 | 1.79 | 1.96 | ||
| III-PLSR | 0.42 | 1.82 | 0.40 | 1.98 | 1.51 | ||
| IV-PLSR | 0.58 | 1.82 | 0.55 | 1.91 | 1.78 | ||
| V-PLSR | 0.63 | 1.75 | 0.61 | 1.78 | 1.87 | ||
| VI-PLSR | 0.43 | 1.97 | 0.39 | 2.05 | 1.31 | ||
| 3D | α-PLSR | 4 | 0.69 | 1.73 | 0.65 | 1.74 | 1.89 |
| β-PLSR | 3 | 0.80 | 1.40 | 0.79 | 1.51 | 2.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasim, N.; Maihemuti, B.; Sawut, R.; Abliz, A.; Dong, C.; Abdumutallip, M. Quantitative Estimation of Soil Salinization in an Arid Region of the Keriya Oasis Based on Multidimensional Modeling. Water 2020, 12, 880. https://doi.org/10.3390/w12030880
Kasim N, Maihemuti B, Sawut R, Abliz A, Dong C, Abdumutallip M. Quantitative Estimation of Soil Salinization in an Arid Region of the Keriya Oasis Based on Multidimensional Modeling. Water. 2020; 12(3):880. https://doi.org/10.3390/w12030880
Chicago/Turabian StyleKasim, Nijat, Balati Maihemuti, Rukeya Sawut, Abdugheni Abliz, Cui Dong, and Munira Abdumutallip. 2020. "Quantitative Estimation of Soil Salinization in an Arid Region of the Keriya Oasis Based on Multidimensional Modeling" Water 12, no. 3: 880. https://doi.org/10.3390/w12030880
APA StyleKasim, N., Maihemuti, B., Sawut, R., Abliz, A., Dong, C., & Abdumutallip, M. (2020). Quantitative Estimation of Soil Salinization in an Arid Region of the Keriya Oasis Based on Multidimensional Modeling. Water, 12(3), 880. https://doi.org/10.3390/w12030880