Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China
Abstract
1. Introduction
2. Materials and Methods
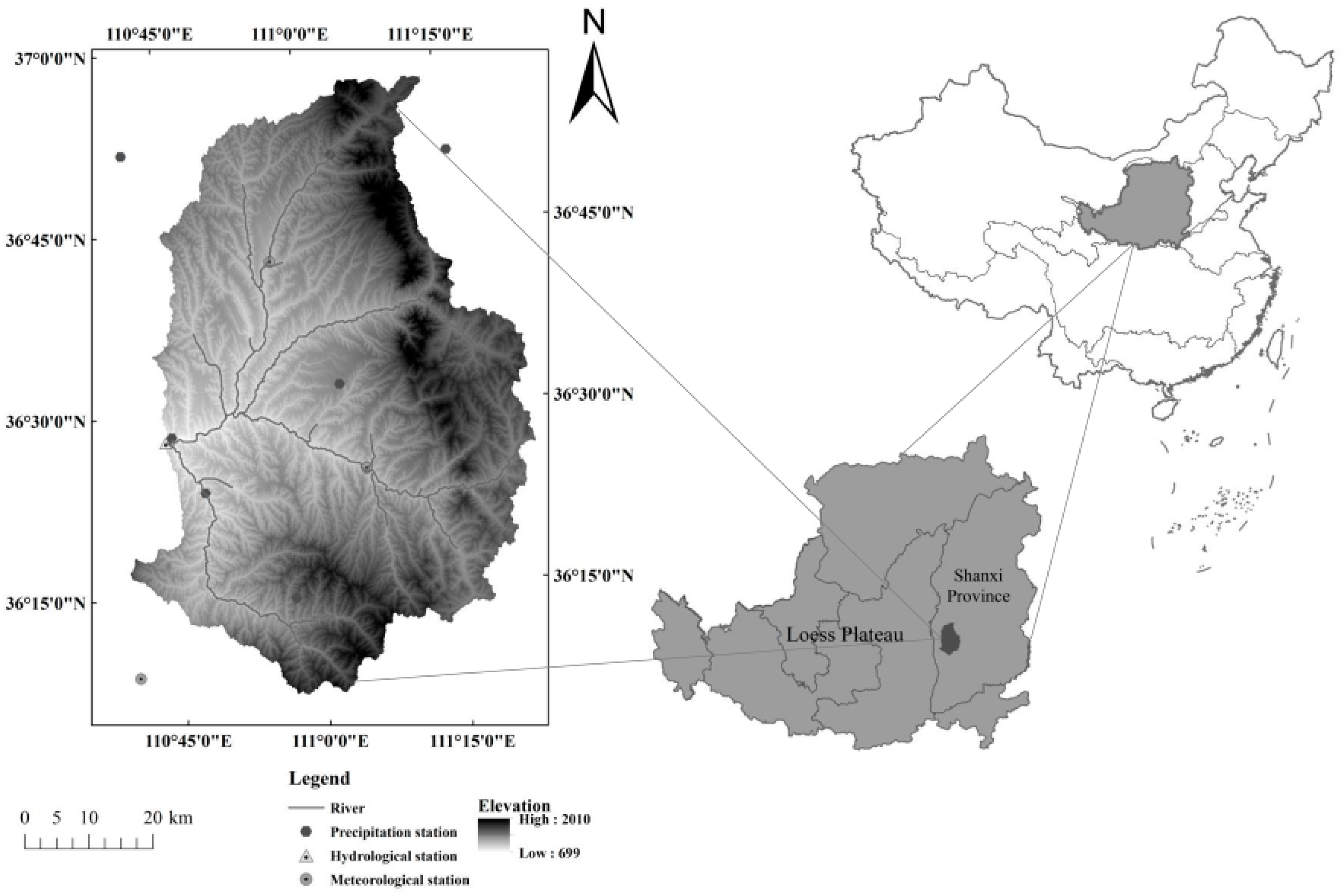
2.1. Study Area
2.2. SWAT Structure
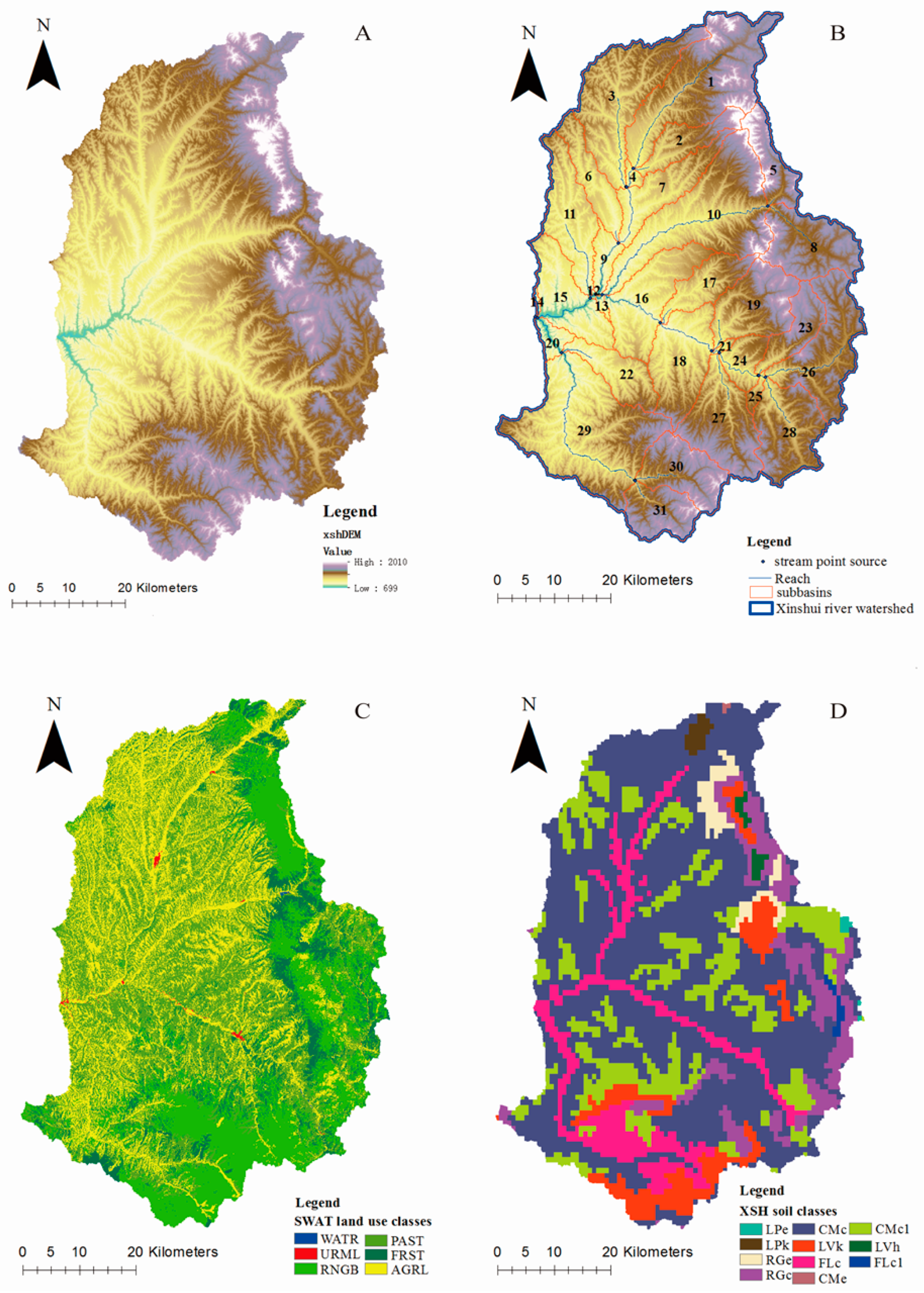
2.3. Data Preparation and Model Construction
2.4. SUFI-2 Method Description
2.4.1. Sensitivity Analysis
2.4.2. Uncertainty Analysis
2.4.3. Calibration and Validation
2.4.4. Model Performance Evaluation
3. Results
3.1. Sensitivity Analysis
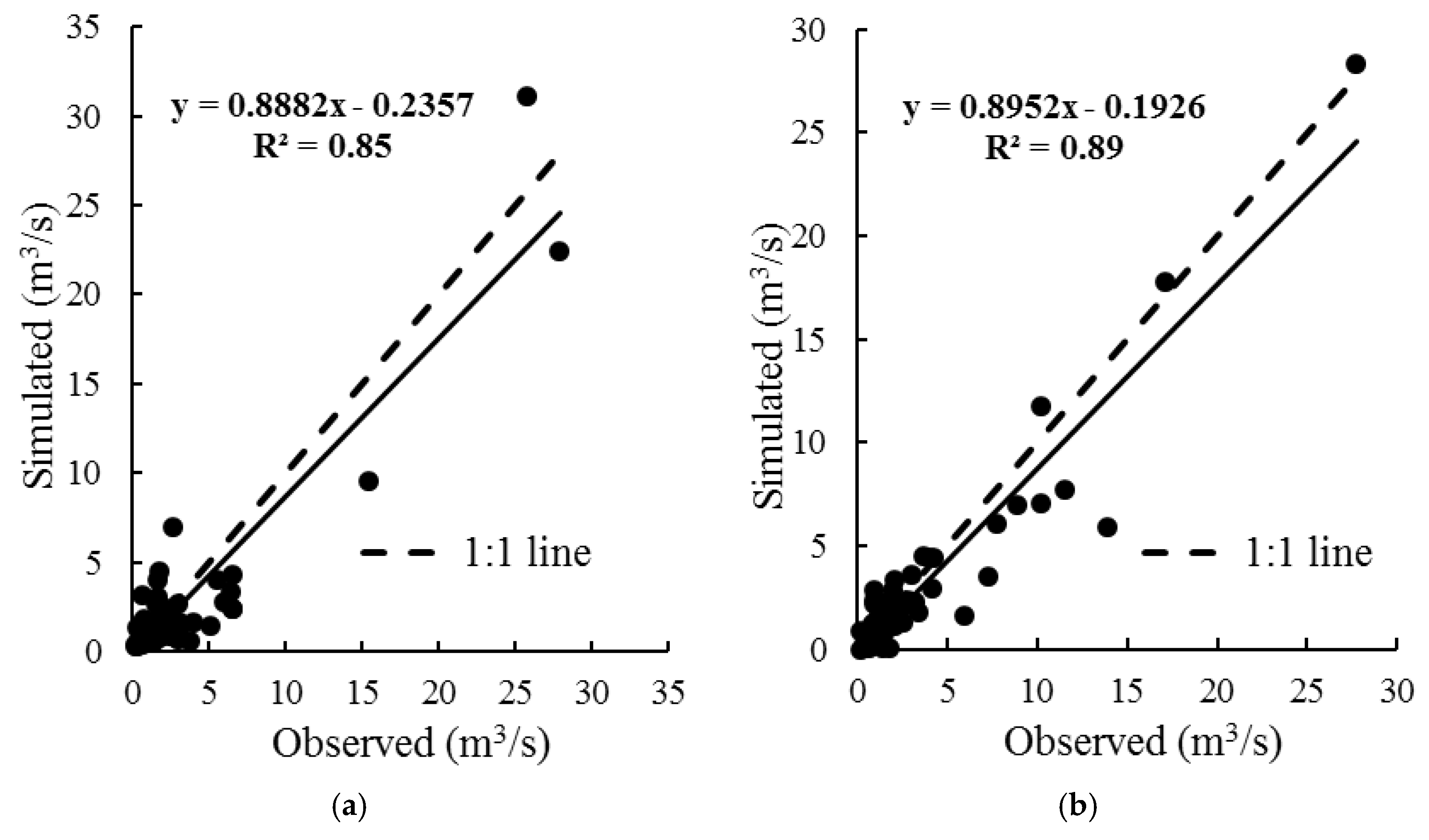
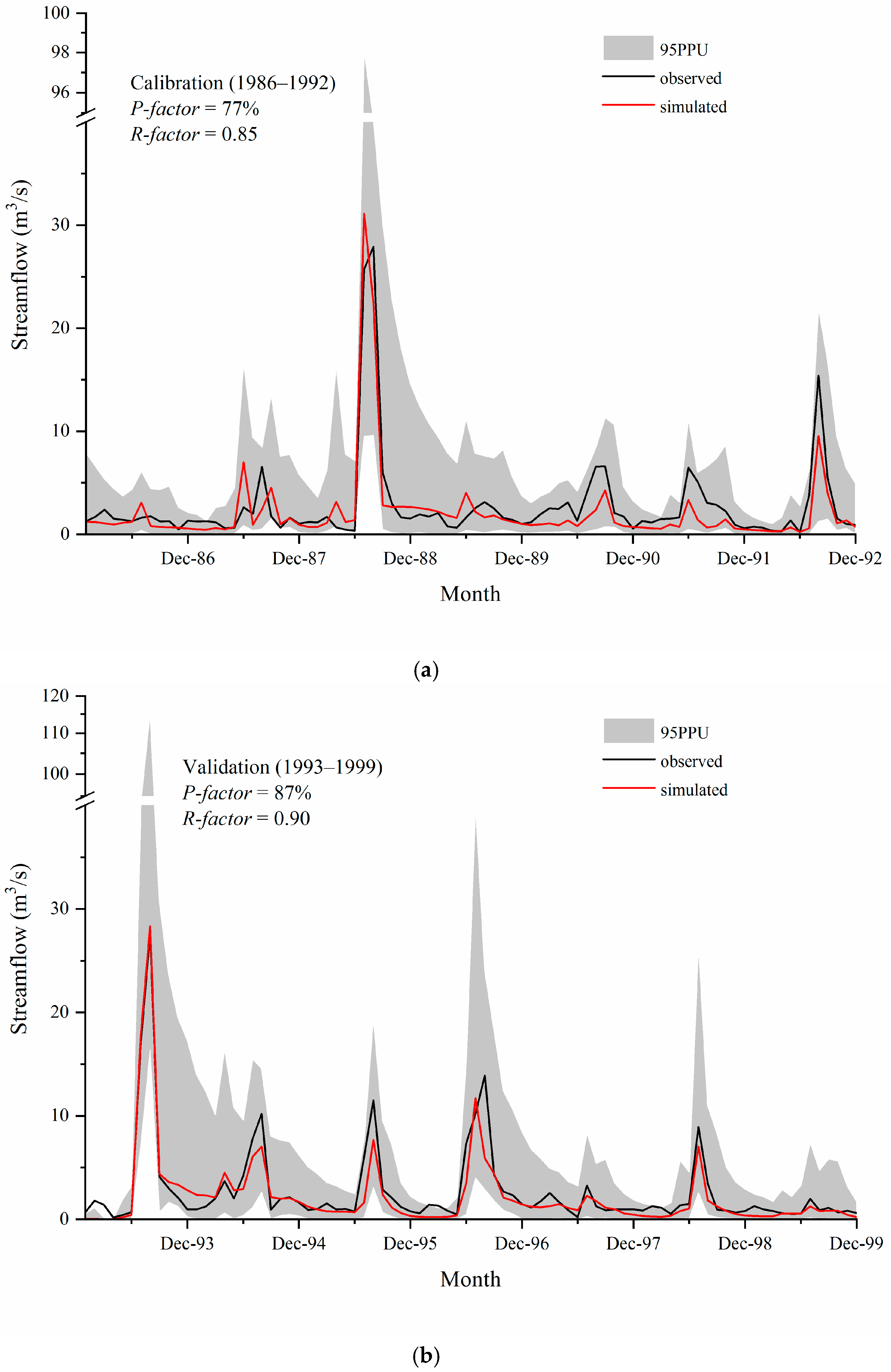
3.2. Model Calibration and Validation
3.3. Uncertainty Analysis
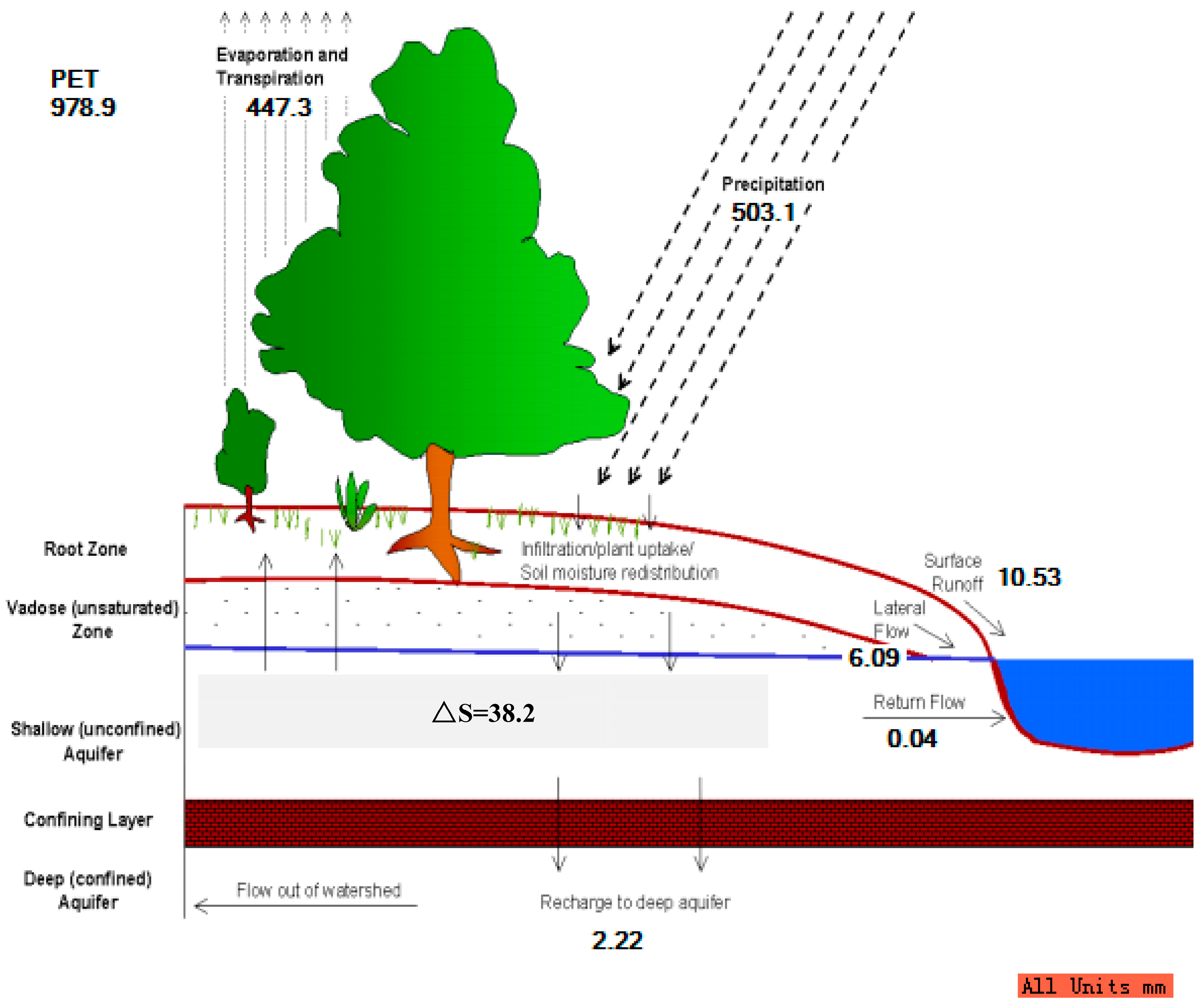
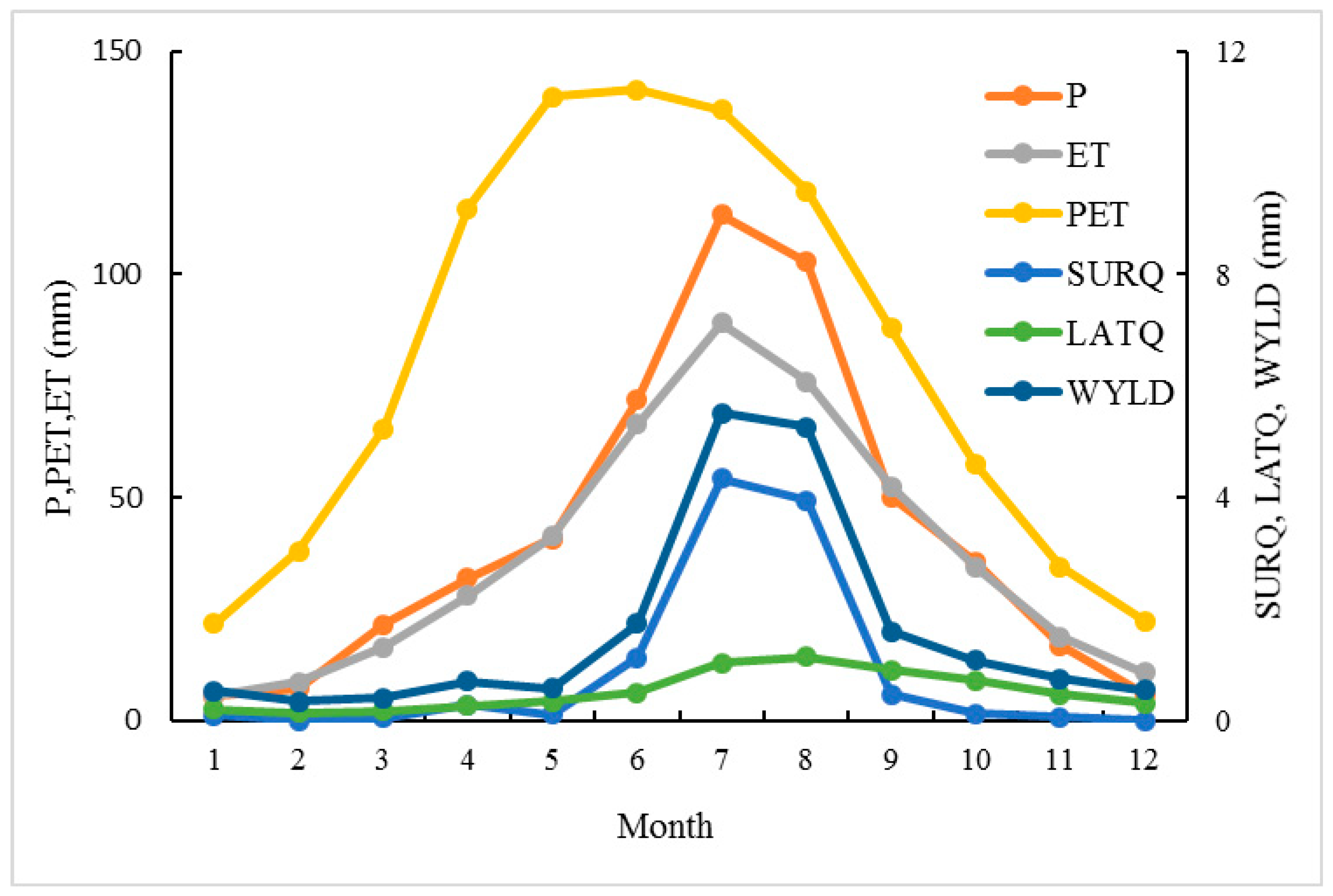
3.4. Water Balances
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zuo, D.; Xu, Z.; Yao, W.; Jin, S.; Xiao, P.; Ran, D. Assessing the effects of changes in land use and climate on runoff and sediment yields from a watershed in the Loess Plateau of China. Sci. Total Environ. 2016, 544, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, Y.; Fu, G. Uncertainties in SWAT extreme flow simulation under climate change. J. Hydrol. 2014, 515, 205–222. [Google Scholar] [CrossRef]
- Zhao, A.; Zhu, X.; Liu, X.; Pan, Y.; Zuo, D. Impacts of land use change and climate variability on green and blue water resources in the Weihe River Basin of northwest China. Catena 2015, 137, 318–327. [Google Scholar] [CrossRef]
- Malagó, A.; Bouraoui, F.; Vigiak, O.; Grizzetti, B.; Pastori, M. Modelling water and nutrient fluxes in the Danube River Basin with SWAT. Sci. Total Environ. 2017, 603–604, 196–218. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Q.; Xu, F.; Men, C.; Guo, L. Impacts of manure application on SWAT model outputs in the Xiangxi River watershed. J. Hydrol. 2017, 555, 479–488. [Google Scholar] [CrossRef]
- Jung, C.G.; Kim, S.J. Assessment of the water cycle impact by the Budyko curve on watershed hydrology using SWAT and CO2concentrations derived from Terra MODIS GPP. Ecol. Eng. 2018, 118, 179–190. [Google Scholar] [CrossRef]
- Zhao, Q.; Ye, B.; Ding, Y.; Zhang, S.; Yi, S.; Wang, J.; Shangguan, D.; Zhao, C.; Han, H. Coupling a glacier melt model to the Variable Infiltration Capacity (VIC) model for hydrological modeling in north-western China. Environ. Earth Sci. 2013, 68, 87–101. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Sun, G.; McNulty, S.G.; Zhang, H.; Li, J.; Zhang, M.; Klaghofer, E.; Strauss, P. Evaluation of the MIKE SHE model for application in the Loess Plateau, China. J. Am. Water Resour. Assoc. 2008, 44, 1108–1120. [Google Scholar] [CrossRef]
- Qin, N.; Wang, J.; Chen, X.; Yang, G.; Liang, H. Impacts of climate change on regional hydrological regimes of the Wujiang River watershed in the Karst area, Southwest China. Geoenvironmental Disasters 2015, 2, 1–18. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; VanLiew, M.W.; et al. Swat: Model Use, Calibration, and Validation. Asabe 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Her, Y.; Yoo, S.H.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in hydrological analysis of climate change: Multi-parameter vs. multi-GCM ensemble predictions. Sci. Rep. 2019, 9, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of calibrated parameters and water resource estimates on different objective functions and optimization algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Chen, L.; Chen, T. Analysis of parameter uncertainty in hydrological and sediment modeling using GLUE method: A case study of SWAT model applied to Three Gorges Reservoir Region, China. Hydrol. Earth Syst. Sci. 2012, 16, 121–132. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Guo, H.; He, D. Combining the SWAT model with sequential uncertainty fitting algorithm for stream flow prediction and uncertainty analysis for the Lake Dianchi Basin, China. Hydrol. Process. 2014, 28, 521–533. [Google Scholar] [CrossRef]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Thavhana, M.P.; Savage, M.J.; Moeletsi, M.E. SWAT model uncertainty analysis, calibration and validation for runoff simulation in the Luvuvhu River catchment, South Africa. Phys. Chem. Earth 2018, 105, 115–124. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter uncertainty analysis of the SWAT model in a mountain-loess transitional watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute Science and Technology, Eawag: Duebendorf, Switzerland, 2015. [Google Scholar]
- Yin, J.; He, F.; Jiu Xiong, Y.; Yu Qiu, G. Effects of land use/land cover and climate changes on surface runoff in a semi-humid and semi-arid transition zone in northwest China. Hydrol. Earth Syst. Sci. 2017, 21, 183–196. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Hornberger, G.M. How much complexity is warranted in a rainfall-runoff model? Water Resour. Res. 1993, 29, 2637–2649. [Google Scholar] [CrossRef]
- Meaurio, M.; Zabaleta, A.; Angel, J.; Srinivasan, R.; Antigüedad, I. Evaluation of SWAT models performance to simulate streamflow spatial origin. The case of a small forested watershed. J. Hydrol. 2015, 525, 326–334. [Google Scholar] [CrossRef]
- Guse, B.; Pfannerstill, M.; Strauch, M.; Reusser, D.E.; Lüdtke, S.; Volk, M.; Gupta, H.; Fohrer, N. On characterizing the temporal dominance patterns of model parameters and processes. Hydrol. Process. 2016, 30, 2255–2270. [Google Scholar] [CrossRef]
- Romagnoli, M.; Portapila, M.; Rigalli, A.; Maydana, G.; Burgués, M.; García, C.M. Assessment of the SWAT model to simulate a watershed with limited available data in the Pampas region, Argentina. Sci. Total Environ. 2017, 596–597, 437–450. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Xie, H.; Lian, Y. Uncertainty-based evaluation and comparison of SWAT and HSPF applications to the Illinois River Basin. J. Hydrol. 2013, 481, 119–131. [Google Scholar] [CrossRef]
- Yang, K.; Lu, C. Evaluation of land-use change effects on runoff and soil erosion of a hilly basin-the Yanhe River in the Chinese Loess Plateau. L. Degrad. Dev. 2018, 29, 1211–1221. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F. Impacts of land use change and climate variability on hydrology in an agricultural catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Chen, L.; Chen, S.; Li, S.; Shen, Z. Temporal and spatial scaling effects of parameter sensitivity in relation to non-point source pollution simulation. J. Hydrol. 2019, 571, 36–49. [Google Scholar] [CrossRef]
- Gong, J.; Li, Z.; Li, P.; Ren, Z. Spatial distribution of runoff erosion power based on SWAT Model in Yanhe River Basin. Trans. Chinese Soc. Agric. Eng. 2017, 33, 120–126. [Google Scholar]
- Zhu, T.X.; Cai, Q.G.; Zeng, B.Q. Runoff generation on a semi-arid agricultural catchment: Field and experimental studies. J. Hydrol. 1997, 196, 99–118. [Google Scholar] [CrossRef]
- Liu, D.; Tian, F.; Hu, H.; Hu, H. The role of run-on for overland flow and the characteristics of runoff generation in the Loess Plateau, China. Hydrol. Sci. J. 2012, 57, 1107–1117. [Google Scholar] [CrossRef]
- Yu, Y.; Wei, W.; Chen, L.; Feng, T.; Stefani, D. Quantifying the effects of precipitation, vegetation, and land preparation techniques on runoff and soil erosion in a Loess watershed of China. Sci. Total Environ. 2019, 652, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Paul, M.; Negahban-Azar, M. Sensitivity and uncertainty analysis for streamflow prediction using multiple optimization algorithms and objective functions: San Joaquin Watershed, California. Model. Earth Syst. Environ. 2018, 4, 1509–1525. [Google Scholar] [CrossRef]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Juston, J.M.; Kauffeldt, A.; Montano, B.Q.; Seibert, J.; Beven, K.J.; Westerberg, I.K. Smiling in the rain: Seven reasons to be positive about uncertainty in hydrological modelling. Hydrol. Process. 2013, 27, 1117–1122. [Google Scholar] [CrossRef]
- Xie, H.; Shen, Z.; Chen, L.; Lai, X.; Qiu, J.; Wei, G.; Dong, J.; Peng, Y.; Chen, X. Parameter Estimation and Uncertainty Analysis: A Comparison between Continuous and Event-Based Modeling of Streamflow Based on the Hydrological Simulation Program–Fortran (HSPF) Model. Water 2019, 11, 171. [Google Scholar] [CrossRef]
- Gao, G.; Fu, B.; Zhang, J.; Ma, Y.; Sivapalan, M. Multiscale temporal variability of flow-sediment relationships during the 1950s–2014 in the Loess Plateau, China. J. Hydrol. 2018, 563, 609–619. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in China’s Loess Plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019–1022. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Kushwaha, A.; Jain, M.K. Hydrological Simulation in a Forest Dominated Watershed in Himalayan Region using SWAT Model. Water Resour. Manag. 2013, 27, 3005–3023. [Google Scholar] [CrossRef]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface For SWAT2012: User’s Guide; Blackland Research Center, Texas Agricultural Experiment Station and Grassland, Soil and Water Research Laboratory, USDA Agricultural Research Service: Temple, TX, USA, 2013.
- Farmer, D.; Sivapalan, M.; Jothityangkoon, C. Climate, soil, and vegetation controls upon the variability of water balance in temperate and semiarid landscapes: Downward approach to water balance analysis. Water Resour. Res. 2003, 39, 1–21. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Yan, R.; Zhang, X.; Yan, S.; Zhang, J.; Chen, H. Spatial patterns of hydrological responses to land use/cover change in a catchment on the Loess Plateau, China. Ecol. Indic. 2018, 92, 151–160. [Google Scholar] [CrossRef]
- Nash, E.; Sutcliffe, V. River flow forecasting through conceptual models Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Tamm, O.; Maasikamäe, S.; Padari, A.; Tamm, T. Modelling the effects of land use and climate change on the water resources in the eastern Baltic Sea region using the SWAT model. Catena 2018, 167, 78–89. [Google Scholar] [CrossRef]
- Du, J.; Rui, H.; Zuo, T.; Li, Q.; Zheng, D.; Chen, A.; Xu, Y.; Xu, C.Y. Hydrological Simulation by SWAT Model with Fixed and Varied Parameterization Approaches Under Land Use Change. Water Resour. Manag. 2013, 27, 2823–2838. [Google Scholar] [CrossRef]
- Li, Z.; Wu, P.; Feng, H.; Zhao, X.; Huang, J.; Zhuang, W. Simulated experiment on effect of soil bulk density on soil infiltration capacity. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2009, 25, 40–45. [Google Scholar]
- Fu, Z.; Wang, Y. Spatio-temporal characteristics of soil bulk density and saturated hydraulic conductivity at small watershed scale on Loess Plateau. Trans. Chinese Soc. Agric. Eng. (Trans. CSAE) 2015, 31, 128–134. [Google Scholar]
- Qiu, L.; Wu, Y.; Wang, L.; Lei, X.; Liao, W.; Hui, Y.; Meng, X. Spatiotemporal response of the water cycle to land use conversions in a typical hilly-gully basin on the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2017, 21, 6485–6499. [Google Scholar] [CrossRef]
- Ozdemir, A.; Leloglu, U.M. A fast and automated hydrologic calibration tool for SWAT. Water Environ. J. 2018, 0, 1–11. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Li, Q.; Xing, Z.; Bourque, C.P.A.; Meng, F.R. A new soil-temperature module for SWAT application in regions with seasonal snow cover. J. Hydrol. 2016, 538, 863–877. [Google Scholar] [CrossRef]
- Qi, J.; Zhang, X.; Wang, Q. Improving hydrological simulation in the Upper Mississippi River Basin through enhanced freeze-thaw cycle representation. J. Hydrol. 2019, 571, 605–618. [Google Scholar] [CrossRef]
- Bai, M.; Mo, X.; Liu, S.; Hu, S. Contributions of climate change and vegetation greening to evapotranspiration trend in a typical hilly-gully basin on the Loess Plateau, China. Sci. Total Environ. 2019, 657, 325–339. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, Z.; Chen, L.; Leng, M.; Yang, F. Baseflow variation and driving factors for the last six decades in a watershed on the Loess Plateau, Northern China. J. Nat. Resour. 2019, 34, 563–572. [Google Scholar]
| No. | Parameter | Name | Hydrological Component | Range |
|---|---|---|---|---|
| 1 | SCS runoff curve number | CN2 | Surface runoff | −0.2~0.2 |
| 2 | Manning’s “n” value of overland flow | OV_N | 0.01~30 | |
| 3 | Lag time of surface runoff | SURLAG | 0.05~24 | |
| 4 | Length of average slope | SLSUBBSN | 10~150 | |
| 5 | Manning’s “n” value of the main channel | CH_N2 | channel flow | 0~0.3 |
| 6 | Effective hydraulic conductivity | CH_K2 | 5~130 | |
| 7 | Critical depth of water required for return flow to occur in the shallow aquifer | GWQMN | Groundwater | 0~5000 |
| 8 | Groundwater delay | GW_DELAY | 30~450 | |
| 9 | Baseflow alpha factor | ALPHA_BF | 0~1 | |
| 10 | Baseflow alpha factor of bank storage | ALPHA_BNK | 0~1 | |
| 11 | Deep aquifer percolation fraction | RCHRG_DP | 0~1 | |
| 12 | Moist bulk density | SOL_BD | Soil water | −0.5~0.6 |
| 13 | Saturated hydraulic conductivity | SOL_K | −0.8~0.8 | |
| 14 | Available water capacity | SOL_AWC | −0.2~0.4 | |
| 15 | Moist soil albedo | SOL_ALB | 0~0.25 | |
| 16 | Average slope steepness | HRU_SLP | Later flow | 0~0.2 |
| 17 | Lateral flow travel time | LAT_TTIME | 0~180 | |
| 18 | Snow maximum melt rate | SMFMX | Snow | 0~20 |
| 19 | Base temperature of snow melt | SMTMP | −20~20 | |
| 20 | Snowfall temperature | SFTMP | −20~20 | |
| 21 | Snow minimum melt rate | SMFMN | 0~20 | |
| 22 | Soil evaporation compensation factor | ESCO | Evapotranspiration | 0–1 |
| 23 | Critical depth of water for “revap” to occur in the shallow aquifer | REVAPMN | 0–500 | |
| 24 | “Revap” coefficient of groundwater | GW_REVAP | 0.02–0.2 |
| Parameter Name | Ranking | t-Stat | p-Value |
|---|---|---|---|
| R__SOL_BD.sol | 1 | 14.26 | 0.00 |
| V__RCHRG_DP.gw | 2 | −12.16 | 0.00 |
| V__GWQMN.gw | 3 | 8.73 | 0.00 |
| V__ESCO.hru | 4 | 8.59 | 0.00 |
| R__CN2.mgt | 5 | −5.71 | 0.00 |
| V__SLSUBBSN.hru | 6 | 3.69 | 0.00 |
| V__OV_N.hru | 7 | 3.27 | 0.00 |
| V__GW_DELAY.gw | 8 | 2.59 | 0.01 |
| V__ALPHA_BNK.rte | 9 | 2.55 | 0.01 |
| V__CH_N2.rte | 10 | −2.49 | 0.01 |
| R__SOL_K.sol | 11 | 2.23 | 0.03 |
| V__SFTMP.bsn | 12 | −1.91 | 0.06 |
| R__SOL_AWC.sol | 13 | 1.46 | 0.14 |
| R__HRU_SLP.hru | 14 | −1.31 | 0.19 |
| V__LAT_TTIME.hru | 15 | −1.17 | 0.24 |
| V__CH_K2.rte | 16 | −1.11 | 0.27 |
| V__ALPHA_BF.gw | 17 | −0.98 | 0.33 |
| V__GW_REVAP.gw | 18 | 0.80 | 0.43 |
| V__SURLAG.hru | 19 | −0.72 | 0.47 |
| V__SMTMP.bsn | 20 | 0.59 | 0.56 |
| V__SMFMX.bsn | 21 | −0.45 | 0.65 |
| V__REVAPMN.gw | 22 | 0.44 | 0.66 |
| R__SOL_ALB.sol | 23 | −0.26 | 0.79 |
| V__SMFMN.bsn | 24 | 0.05 | 0.96 |
| Parameter Name | Ranking | Min-Value | Max-Value | Fitted_Value |
|---|---|---|---|---|
| R__SOL_BD.sol | 1 | −0.63 | 0.19 | −0.2195 |
| V__RCHRG_DP.gw | 2 | −0.31 | 0.56 | 0.125 |
| V__GWQMN.gw | 3 | 156.57 | 3393.43 | 1775 |
| V__ESCO.hru | 4 | 0.84 | 0.95 | 0.891 |
| R__CN2.mgt | 5 | −0.05 | 0.25 | 0.098 |
| V__SLSUBBSN.hru | 6 | 14.36 | 105.04 | 59.7 |
| V__OV_N.hru | 7 | 3.20 | 21.11 | 12.15 |
| V__GW_DELAY.gw | 8 | −38.72 | 287.72 | 124.499 |
| V__ALPHA_BNK.rte | 9 | 0.21 | 0.74 | 0.475 |
| V__CH_N2.rte | 10 | 0.13 | 0.39 | 0.2565 |
| R__SOL_K.sol | 11 | −0.61 | 0.33 | −0.136 |
| V__SFTMP.bsn | 12 | −6.94 | 1.04 | −2.95 |
| R__SOL_AWC.sol | 13 | 0.01 | 0.43 | 0.217 |
| R__HRU_SLP.hru | 14 | −0.01 | 0.13 | 0.059 |
| V__LAT_TTIME.hru | 15 | −34.86 | 108.66 | 36.89 |
| V__CH_K2.rte | 16 | −54.83 | 68.58 | 6.875 |
| V__ALPHA_BF.gw | 17 | 0.26 | 0.79 | 0.525 |
| V__GW_REVAP.gw | 18 | −0.01 | 0.13 | 0.059 |
| V__SURLAG.hru | 19 | 0.80 | 16.30 | 8.55 |
| Period | Number | R2 | NS | PBIAS | RSR | P-Factor | R-Factor |
|---|---|---|---|---|---|---|---|
| Calibrations | 11 | 0.7 | 0.66 | 32.30% | 0.58 | 65% | 0.58 |
| 12 | 0.7 | 0.66 | 32.30% | 0.58 | 65% | 0.58 | |
| 13 | 0.7 | 0.66 | 32.30% | 0.58 | 65% | 0.58 | |
| 14 | 0.72 | 0.69 | −27.90% | 0.56 | 74% | 0.76 | |
| 15 | 0.7 | 0.66 | 32.10% | 0.58 | 56% | 0.46 | |
| 16 | 0.72 | 0.65 | 40.70% | 0.59 | 57% | 0.58 | |
| 17 | 0.72 | 0.65 | 40.70% | 0.59 | 57% | 0.58 | |
| 18 | 0.72 | 0.65 | 40.70% | 0.59 | 56% | 0.51 | |
| 19 | 0.85 | 0.83 a | 20% c | 0.41 a | 77% | 0.85 | |
| Validation | 19 | 0.89 | 0.88 a | 17.6% c | 0.35 a | 87% | 0.9 |
| Calibration without SOL_BD | 18 | 0.75 | 0.72 | 15.8 | 0.53 | - | - |
| Validation without SOL_BD | 18 | 0.82 | 0.81 | 9.8 | 0.43 | - | - |
| Year | P (mm) | SURQ (mm) | PERC (mm) | LATQ (mm) | ET (mm) | △S (mm) | Relative Error (%) |
|---|---|---|---|---|---|---|---|
| 1986 | 314.82 | 1.5 | 0.08 | 3.21 | 359.29 | −49.7 | 0.14 |
| 1987 | 576.47 | 4.75 | 16.2 | 6.27 | 499.08 | 59.44 | −1.61 |
| 1988 | 682.85 | 34.98 | 170.02 | 10 | 493.14 | −22.63 | −0.39 |
| 1989 | 494.87 | 2.29 | 3.36 | 5.38 | 459.58 | 15.47 | 1.78 |
| 1990 | 566.38 | 5.22 | 34.74 | 6.53 | 507.47 | 11.34 | 0.19 |
| 1991 | 474.13 | 3.23 | 12.67 | 5.25 | 492.76 | −40.81 | 0.22 |
| 1992 | 550.86 | 7.37 | 30.53 | 6.44 | 461.36 | 55.69 | −1.91 |
| 1993 | 703.09 | 40.98 | 160.3 | 9.79 | 466.22 | 10.52 | 2.17 |
| 1994 | 504.63 | 10.31 | 35.74 | 6.73 | 471.19 | −21.19 | 0.37 |
| 1995 | 406.64 | 8.62 | 9.3 | 4.82 | 423.8 | −30.72 | −2.26 |
| 1996 | 599.94 | 19.14 | 87.61 | 7.77 | 454.62 | 27.76 | 0.51 |
| 1997 | 305.52 | 1.81 | 0.48 | 3.54 | 368.13 | −62.58 | −1.92 |
| 1998 | 480.47 | 6.96 | 30.31 | 5.69 | 433.83 | 0.34 | 0.70 |
| 1999 | 383.28 | 0.33 | 0.27 | 3.89 | 371.47 | 8.87 | −0.40 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, M.; Yu, Y.; Wang, S.; Zhang, Z. Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China. Water 2020, 12, 878. https://doi.org/10.3390/w12030878
Leng M, Yu Y, Wang S, Zhang Z. Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China. Water. 2020; 12(3):878. https://doi.org/10.3390/w12030878
Chicago/Turabian StyleLeng, Manman, Yang Yu, Shengping Wang, and Zhiqiang Zhang. 2020. "Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China" Water 12, no. 3: 878. https://doi.org/10.3390/w12030878
APA StyleLeng, M., Yu, Y., Wang, S., & Zhang, Z. (2020). Simulating the Hydrological Processes of a Meso-Scale Watershed on the Loess Plateau, China. Water, 12(3), 878. https://doi.org/10.3390/w12030878





