Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil
Abstract
1. Introduction
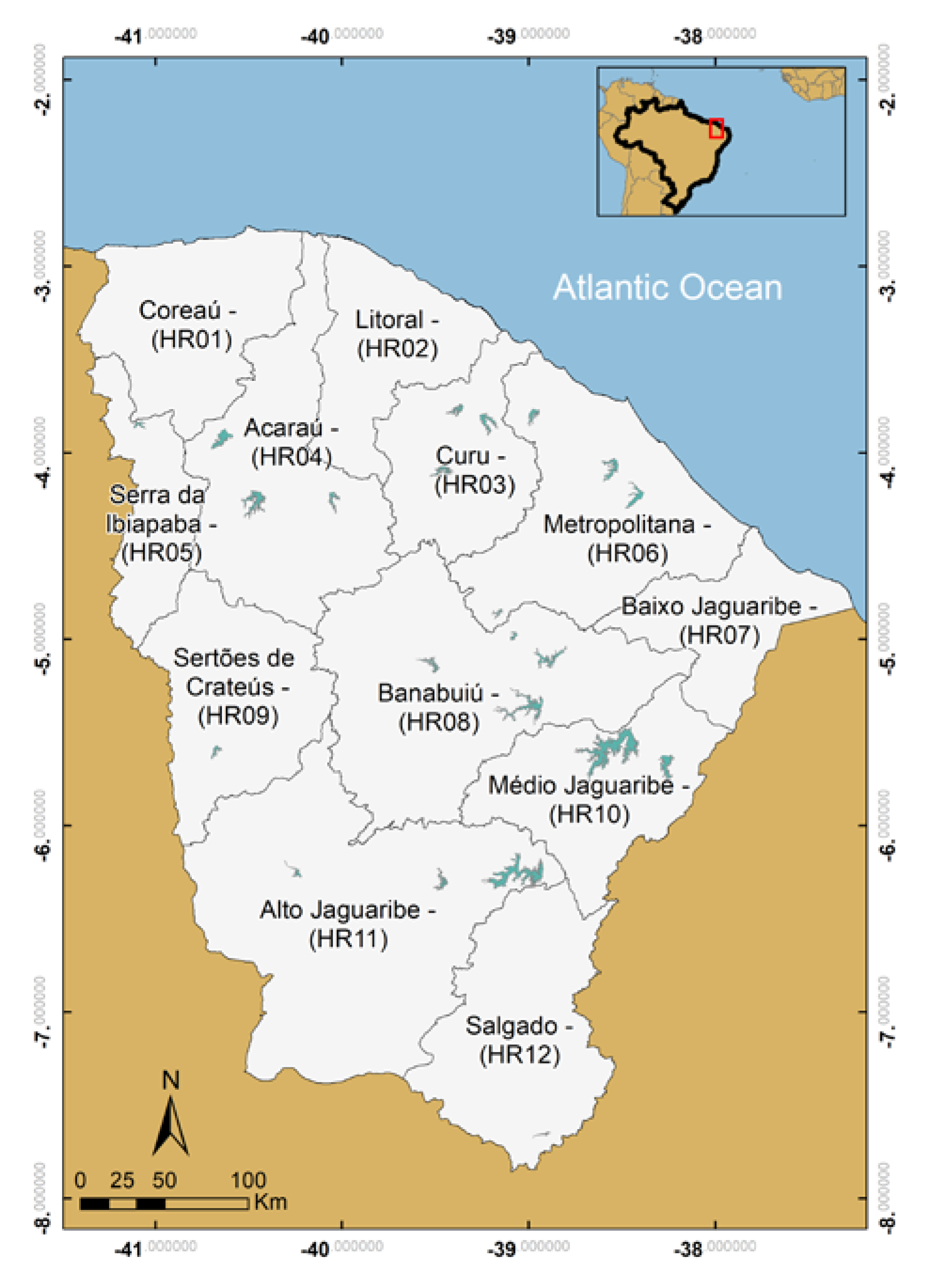
2. Study Area
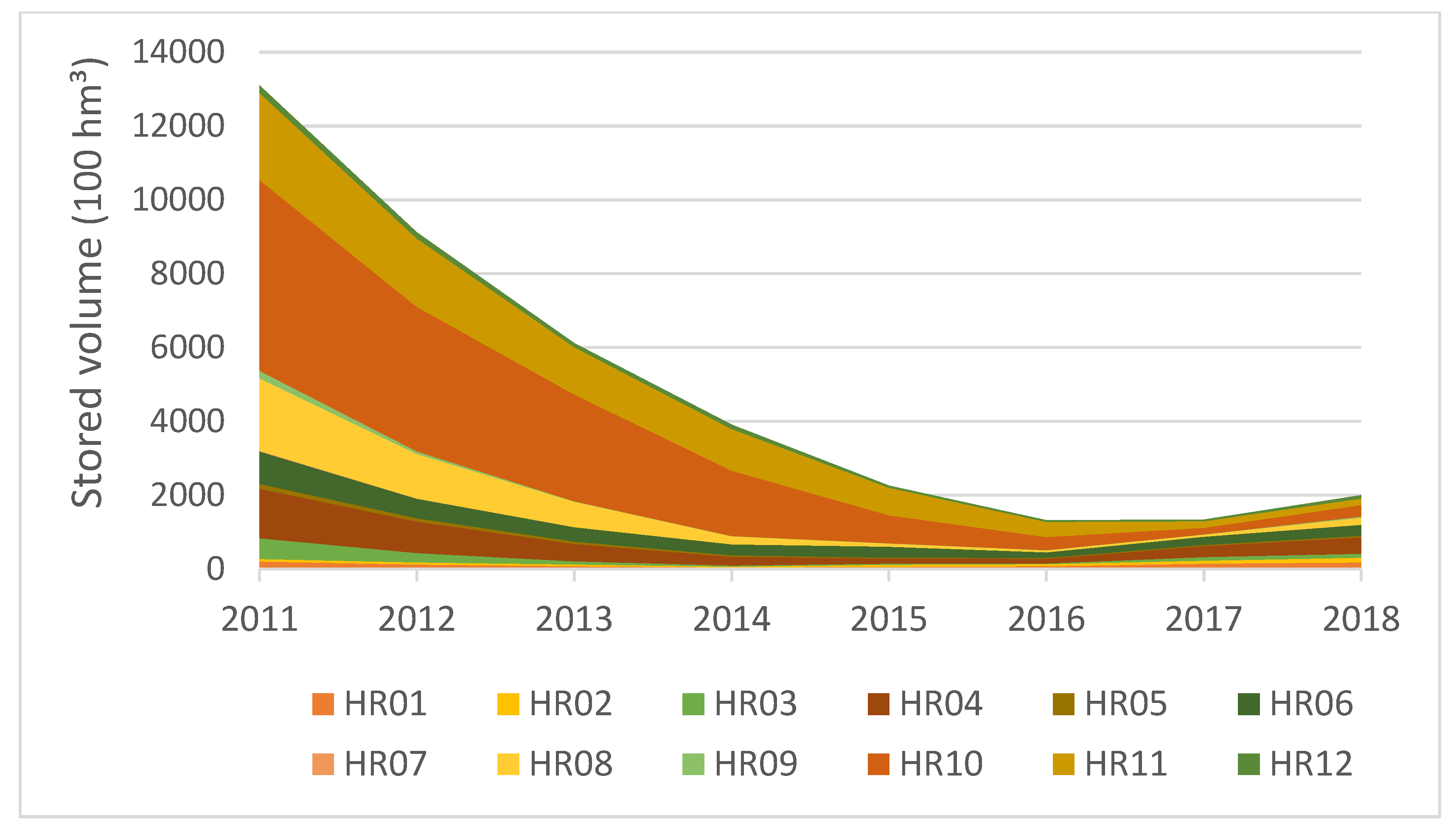
3. The 2012–2018 Drought
4. Data and Methods
4.1. Data
4.2. Drought Analysis
4.3. Statistical Inference
| Clayton | (3) | |
| Frank | (4) | |
| Gumbel | (5) | |
| Gaussian | (6) | |
| t-Student | (7) |
4.4. Frequency Analysis
4.4.1. Univariate Return Period
4.4.2. Bivariate Return Period
5. Results
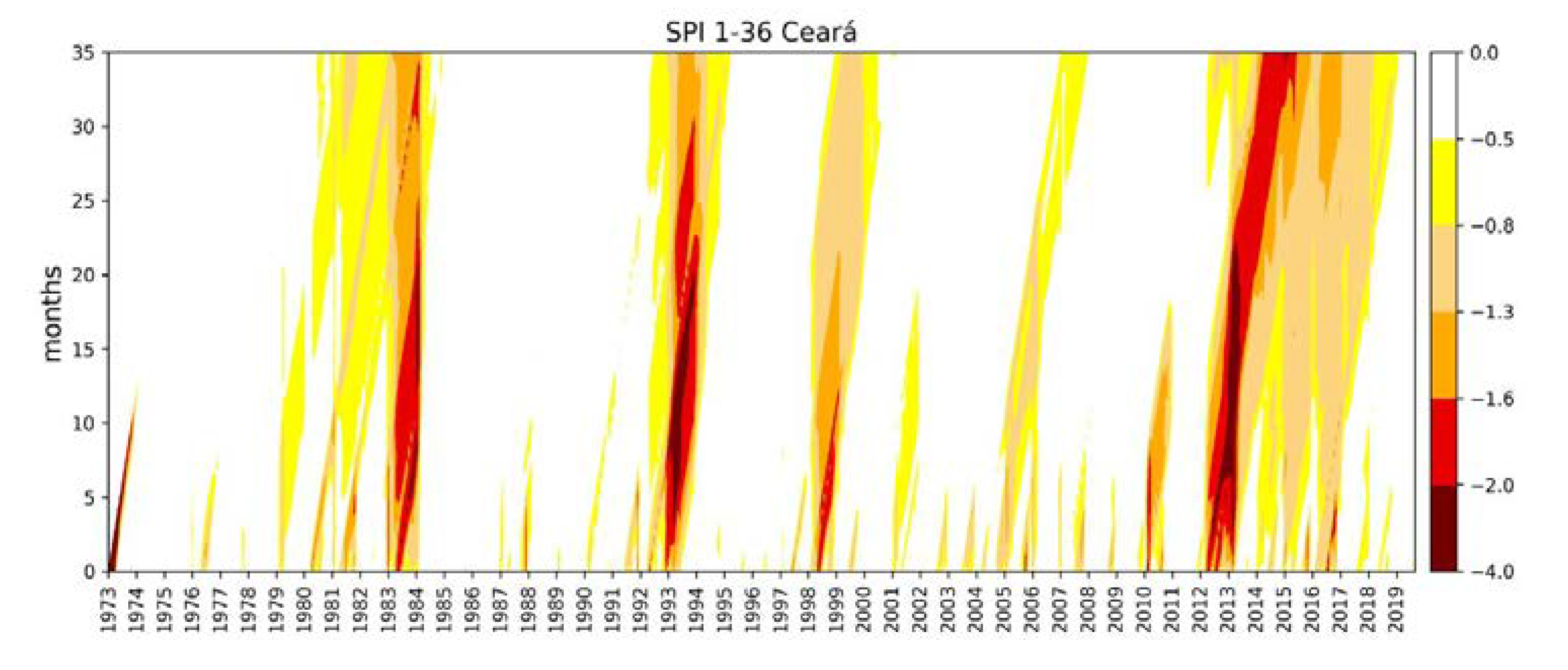
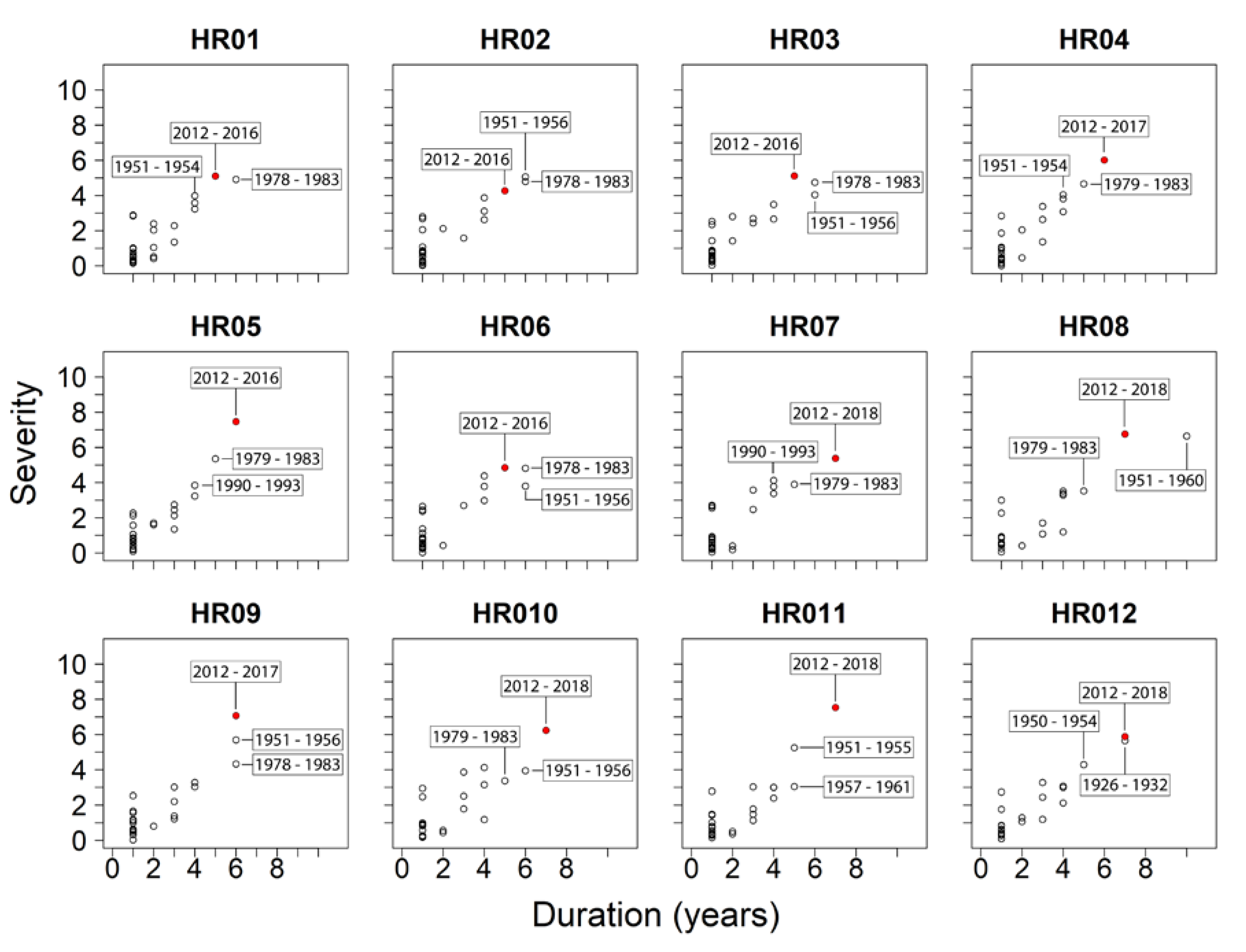
5.1. Drought Analysis
5.2. Frequency Analysis
6. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gutiérrez, A.P.A.; Engle, N.L.; De Nys, E.; Molejón, C.; Martins, E.S. Drought preparedness in Brazil. Weather Clim. Extrem. 2014, 3, 95–106. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Alvala, R.C.; Cunha, A.P.; Brito, S.; Moraes, O.L.L. Climatic characteristics of the 2010-2016 drought in the semiarid Northeast Brazil region. Acad. Bras. Cienc. 2017, 90, 1973–1985. [Google Scholar] [CrossRef]
- Martins, E.S.P.R.; Magalhães, A.R.; Fontenele, D. A seca plurianual de 2010–2017 no Nordeste e seus impactos. Parcerias Estratégicas 2017, 22, 17–40. [Google Scholar]
- De Azevedo, S.C.; Cardim, G.P.; Puga, F.; Singh, R.P.; Da Silva, E.A. Analysis of the 2012-2016 drought in the northeast Brazil and its impacts on the Sobradinho water reservoir. Remote Sens Lett. 2018, 9, 438–446. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Tomasella, J.; Ribeiro-Neto, G.G.; Brown, M.; Garcia, S.R.; Brito, S.B. Changes in the spatial–temporal patterns of droughts in the Brazilian Northeast. Atmos. Sci. Lett. 2018, 19, 1–8. [Google Scholar] [CrossRef]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the Semiarid Northeast Brazil region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Vieira, R.M.S.P.; Tomasella, J.; Alvalá, R.C.S.; Sestini, M.F.; Affonso, A.G.; Rodriguez, D.A. Identifying areas susceptible to desertification in the Brazilian northeast. Solid Earth 2015, 6, 347–360. [Google Scholar] [CrossRef]
- Marengo, J.A.; Cunha, A.P.; Alves, L.M. A seca de 2012-15 no semiárido do Nordeste do Brasil no contexto histórico. Rev. Climanálise 2016, 4, 49–54. [Google Scholar]
- Cunha, A.P.M.; Alvalá, R.C.; Nobre, C.A.; Carvalho, M.A. Monitoring vegetative drought dynamics in the Brazilian semiarid region. Agric. For. Meteorol. 2015, 214–215, 494–505. [Google Scholar] [CrossRef]
- Martins, E.S.P.R.; Coelho, C.A.S.; Haarsma, R.; Otto, F.E.L.; King, A.D.; Jan van Oldenborgh, G. A Multimethod Attribution Analysis of the Prolonged Northeast Brazil Hydrometeorological Drought (2012–16). Bull. Am. Meteorol. Soc. 2018, 99, S65–S69. [Google Scholar] [CrossRef]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—past, present, and future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
- Campos, J.N.B. Paradigms and Public Policies on Drought in Northeast Brazil: A Historical Perspective. Environ. Manag. 2015, 55, 1052–1063. [Google Scholar] [CrossRef] [PubMed]
- Silva, B.K.N.; Amorim, A.C.B.; Silva, C.M.S.; Lucio, P.S.; Barbosa, L.M. Rainfall-related natural disasters in the Northeast of Brazil as a response to ocean-atmosphere interaction. Theor. Appl. Climatol. 2019. [Google Scholar] [CrossRef]
- Hastenrath, S. Exploring the climate problems of Brazil’s Nordeste: A review. Clim. Chang. 2012, 112, 243–251. [Google Scholar] [CrossRef]
- Andreoli, R.V.; Kayano, M.T. ENSO-related rainfall anomalies in South America and associated circulation features during warm and cold Pacific decadal oscillation regimes. Int. J. Climatol. 2005, 25, 2017–2030. [Google Scholar] [CrossRef]
- Souza Filho, F.A.; Lall, U. Seasonal to interannual ensemble streamflow forecasts for Ceara, Brazil: Applications of a multivariate, semiparametric algorithm. Water Resour Res. 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Lall, U.; Souza Filho, F.A.; Sharma, A. Improved water allocation utilizing probabilistic climate forecasts: Short-term water contracts in a risk management framework. Water Resour. Res. 2009, 45, 1–18. [Google Scholar] [CrossRef]
- Delgado, J.M.; Voß, S.; Bürger, G.; Vormoor, K.; Murawski, A.; Pereira, J.M.R. Seasonal drought prediction for semiarid northeastern Brazil: Verification of six hydro-meteorological forecast products. Hydrol. Earth Syst. Sci. 2018, 22, 5041–5056. [Google Scholar] [CrossRef]
- Formiga-Johnsson, R.M.; Kemper, K.E. Institutional and Policy Analysis of River Basin Management; World Bank Policy Research Working Paper; World Bank: New York, NY, USA, 2005; pp. 1–40. [Google Scholar]
- Haan, C.T. Statistical Methods in Hydrology, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2002. [Google Scholar]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Pontes Filho, J.D.; Portela, M.M.; Marinho de Carvalho Studart, T.; Souza Filho, F.D.A. A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas. Water 2019, 11, 1925. [Google Scholar] [CrossRef]
- Alidoost, F.; Su, Z.; Stein, A. Evaluating the effects of climate extremes on crop yield, production and price using multivariate distributions: A new copula application. Weather Clim. Extrem. 2019, 26, 100227. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Nelsen, R.B. An. Introduction to Copulas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–656. [Google Scholar]
- Genest, C.; Favre, A.-C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Mishra, A.K.; Guo, J. Drought Analysis Using Copulas. J. Hydrol. Eng. 2013, 18, 797–808. [Google Scholar] [CrossRef]
- Lazoglou, G.; Anagnostopoulou, C. Joint distribution of temperature and precipitation in the Mediterranean, using the Copula method. Theor. Appl. Climatol. 2018, 1–13. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch Environ. Res. Risk Assess. 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kisi, O. Joint modelling of annual maximum drought severity and corresponding duration. J. Hydrol. 2016, 543, 406–422. [Google Scholar] [CrossRef]
- Kim, J.E.; Yoo, J.; Chung, G.H.; Kim, T.W. Hydrologic Risk Assessment of Future Extreme Drought in South Korea Using Bivariate Frequency Analysis. Water 2019, 11, 2052. [Google Scholar] [CrossRef]
- Tu, X.; Singh, V.P.; Chen, X.; Ma, M.; Zhang, Q.; Zhao, Y. Uncertainty and variability in bivariate modeling of hydrological droughts. Stoch Environ. Res. Risk Assess. 2016. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B.; Rezaie, H. New approach in bivariate drought duration and severity analysis. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P. Uncertainty evaluation of copula analysis of hydrological droughts in the East River basin, China. Glob. Planet. Chang. 2015. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S.; Javed, T.; Yao, N. Probabilistic modelling of drought events in China via 2-dimensional joint copula. J. Hydrol. 2018, 559, 373–391. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S. Multivariate Drought Frequency Analysis using Four-Variate Symmetric and Asymmetric Archimedean Copula Functions. Water Resour. Manag. 2019, 33, 103–127. [Google Scholar] [CrossRef]
- Ribeiro, A.F.S.; Russo, A.; Gouveia, C.M.; Pascoa, P.; Pires, C.A.L. Probabilistic modelling of the dependence between rainfed crops and drought hazard. Nat. Hazards Earth Syst. Sci. 2019, 19, 2795–2809. [Google Scholar] [CrossRef]
- Ribeiro, A.F.S.; Russo, A.; Gouveia, C.M.; Páscoa, P. Copula-based agricultural drought risk of rainfed cropping systems. Agric. Water Manag. 2019, 223, 105689. [Google Scholar] [CrossRef]
- Espinosa, L.A.; Portela, M.M.; Pontes Filho, J.D.; Studart, T.M.D.C.; Santos, J.F.; Rodrigues, R. Jointly modeling drought characteristics with smoothed regionalized SPI series for a small island. Water 2019, 11, 2489. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of droughts in Portugal. Water Resour. Res. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Gimeno, L.; Nieto, R.; Trigo, R.M.; Vicente-Serrano, S.M.; López-Moreno, J.I. Where Does the Iberian Peninsula Moisture Come From? An Answer Based on a Lagrangian Approach. J. Hydrometeorol. 2010, 11, 421–436. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; González-Hidalgo, J.C.; de Luis, M.; Raventós, J. Drought patterns in the Mediterranean area: The Valencia region (eastern Spain). Clim. Res. 2004, 26, 5–15. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Can, I. Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey. Nat. Hazards 2016. [Google Scholar] [CrossRef]
- Uvo, C.B.; Repelli, C.A.; Zebiak, S.E.; Kushnir, Y. The Relationships between Tropical Pacific and Atlantic SST andNortheast Brazil Monthly Precipitation. J. Clim. 1998, 551–562. [Google Scholar] [CrossRef]
- Hastenrath, S.; Heller, L. Dynamics of climatic hazards in northeast Brazil. Q. J. R. Meteorol. Soc. 1977, 103, 77–92. [Google Scholar] [CrossRef]
- Moura, A.D.; Shukla, J. On the Dynamics of Droughts in Northeast Brazil: Observations, Theory and Numerical Experiments with a General Circulation Model. J. Atmos. Sci. 1981, 38, 2653–2675. [Google Scholar] [CrossRef]
- Kayano, M.T.; Andreoli, R.V. Decadal variability of northern northeast Brazil rainfall and its relation to tropical sea surface temperature and global sea level pressure anomalies. J. Geophys. Res. Ocean. 2004, 109, 1–8. [Google Scholar] [CrossRef]
- Nobre, P.; Shukla, J. Variatons of Sea Surface Temperature, Wind Stress, and Rainfall Over the Tropical Atlantic and South America. J. Clim. 1996, 9. [Google Scholar] [CrossRef]
- Hounsou-Gbo, G.A.; Servain, J.; Araujo, M.; Caniaux, G.; Bourlès, B.; Fontenele, D. SST indexes in the tropical South Atlantic for forecasting rainy seasons in Northeast Brazil. Atmosphere (Basel) 2019, 10, 335. [Google Scholar] [CrossRef]
- Hounsou-Gbo, G.A.; Servain, J.; Araujo, M.; Martins, E.S.; Bourlès, B.; Caniaux, G. Oceanic Indices for Forecasting Seasonal Rainfall over the Northern Part of Brazilian Northeast. Am. J. Clim. Chang. 2016, 5, 261–274. [Google Scholar] [CrossRef]
- Kerr, R.A. A North Atlantic Climate Pacemaker for the Centuries. Science 2000, 288, 1984–1985. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Kayano, M.T.; Capistrano, V.B. How the Atlantic multidecadal oscillation (AMO) modifies the ENSO influence on the South American rainfall. Int. J. Climatol. 2014, 34, 162–178. [Google Scholar] [CrossRef]
- Knight, J.R.; Folland, C.K.; Scaife, A.A. Climate impacts of the Atlantic multidecadal oscillation. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar] [CrossRef]
- Kayano, M.T.; Andreoli, R.V.; Garcia, S.R.; de Souza, R.A.F. How the two nodes of the tropical Atlantic sea surface temperature dipole relate the climate of the surrounding regions during austral autumn. Int. J. Climatol. 2018, 38, 3927–3941. [Google Scholar] [CrossRef]
- Jones, C.; Carvalho, L.M.V. The influence of the Atlantic multidecadal oscillation on the eastern Andes low-level jet and precipitation in South America. Clim. Atmos. Sci. 2018, 1, 1–7. [Google Scholar] [CrossRef]
- Lucena, D.B.; Servain, J.; Filho, M.F.G. Rainfall response in Northeast Brazil from ocean climate variability during the second half of the twentieth century. J. Clim. 2011, 24, 6174–6184. [Google Scholar] [CrossRef]
- Rocha, R.V.; Souza Filho, F.A.; de Silva, S.M.O. Análise da Relação entre a Precipitação Média do Reservatório Orós, Brasil—Ceará, e os índices PDO e AMO Através da Análise de Changepoints e Transformada de Ondeletas. Rev. Bras. Meteorol. 2019, 34, 139–149. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; McPhaden, M.J. Why did the 2011–2012 La Niña cause a severe drought in the Brazilian Northeast? Geophys Res. Lett. 2014, 41, 1012–1018. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A.; Camargo, H.; Riveros, M.P. Two Contrasting Severe Seasonal Extremes in Tropical South America in 2012: Flood in Amazonia and Drought in Northeast Brazil. J. Clim. 2013, 26, 9137–9154. [Google Scholar] [CrossRef]
- Nobre, C.A.; Marengo, J.A.; Seluchi, M.E.; Cuartas, L.A.; Alves, L.M. Some Characteristics and Impacts of the Drought and Water Crisis in Southeastern Brazil during 2014 and 2015. J. Water Resour. Prot. 2016, 8, 252–262. [Google Scholar] [CrossRef]
- Ceará, E. Decreto no 23.068, de 11 de fevereiro de 1994; Governo do Estado do Ceará: Fortaleza, Brasil, 1994.
- Santos, J.A.; Marins, R.V.; Aguiar, J.E.; Chalar, G.; Silva, F.A.T.F.; Lacerda, L.D. Hydrochemistry and trophic state change in a large reservoir in the Brazilian northeast region under intense drought conditions. J. Limnol. 2017, 76, 41–51. [Google Scholar] [CrossRef][Green Version]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. AMS Conf. Appl. Climatol. 1993, 17, 179–184. Available online: http://ccc.atmos.colostate.edu/relationshipofdroughtfrequency.pdf (accessed on 16 October 2018).
- Silva, S.M.; Souza Filho, F.A.; Araújo, L.M., Jr. Mecanismo financeiro projetado com índices de seca como instrumento de gestão de risco em recursos hídricos. Rev. Bras. Recur Hídricos. 2015, 20, 320–330. [Google Scholar] [CrossRef]
- Yevjevich, V.I.J. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Colorado State Univesrsity: Fort Collins, CO, USA, 1967. [Google Scholar]
- Kwon, H.-H.; Lall, U. A copula-based nonstationary frequency analysis for the 2012-2015 drought in California. Water Resour Res. 2016, 52, 5662–5675. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Brechmann, E.C.; Schepsmeier, U. Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Shiau, J.-T.; Shen, H.W. Recurrence Analysis of Hydrologic Droughts of Differing Severity. J. Water Resour Plan. Manag. 2001, 127, 30–40. [Google Scholar] [CrossRef]
- Awange, J.L.; Mpelasoka, F.; Goncalves, R.M. When every drop counts: Analysis of Droughts in Brazil for the 1901-2013 period. Sci. Total Environ. 2016, 566–567, 1472–1488. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econom Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin, Ed.; Springer: London, UK, 1975. [Google Scholar]
- Pan, T.; Chen, J.; Liu, Y. Spatial and Temporal Pattern of Drought Hazard under Different RCP Scenarios for China in the 21st century. Nat. Hazards Earth Syst. Sci. Discuss. 2018, 1–18. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought and Water Crises; Wilhite, D.A., Ed.; CRC Press: Boca Raton, FL, USA, 2005; p. 406. [Google Scholar]
- Portela, M.M.; dos Santos, J.F.; Silva, A.T.; Benitez, J.B.; Frank, C.; Reichert, J.M. Drought analysis in southern Paraguay, Brazil and northern Argentina: Regionalization, occurrence rate and rainfall thresholds. Hydrol. Res. 2015, 46, 792–810. [Google Scholar] [CrossRef]



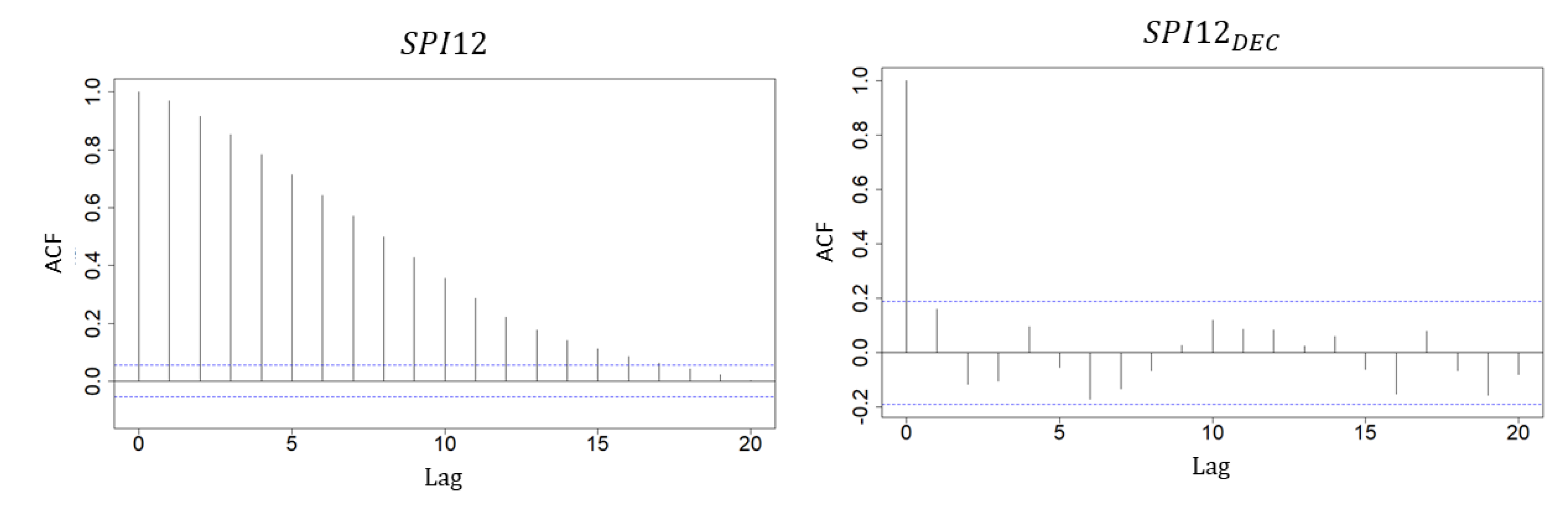

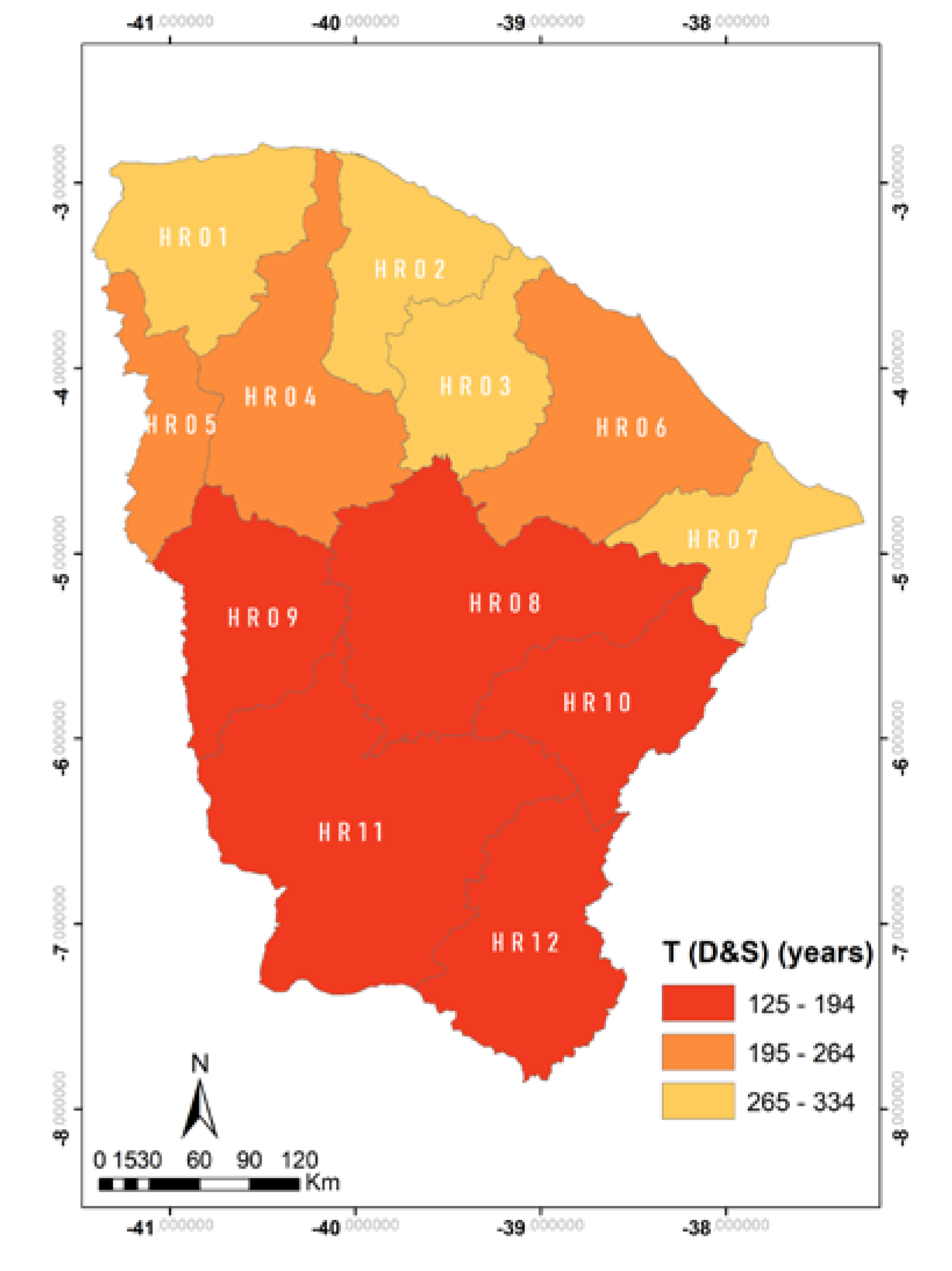
| Region | No. Drought Events | Inter- Arrival Time | Duration (Years) | Severity | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | 2012–2018 Drought | Mean | CV | Max | 2012–2018 Drought | Mean | CV | |||
| HR01 | 25 | 4.32 | 6 | 5 | 2.08 | 0.71 | 5.10 | 5.10 | 1.69 | 0.91 |
| HR02 | 26 | 4.15 | 6 | 5 | 2.00 | 0.85 | 5.06 | 4.27 | 1.65 | 0.93 |
| HR03 | 26 | 4.15 | 6 | 5 | 2.00 | 0.82 | 5.11 | 5.11 | 1.64 | 0.91 |
| HR04 | 25 | 4.32 | 6 | 6 | 2.04 | 0.74 | 6.01 | 6.01 | 1.73 | 0.95 |
| HR05 | 24 | 4.5 | 6 | 6 | 2.04 | 0.73 | 7.47 | 7.47 | 1.85 | 0.95 |
| HR06 | 26 | 4.15 | 6 | 5 | 2.00 | 0.85 | 4.85 | 4.85 | 1.69 | 0.93 |
| HR07 | 26 | 4.15 | 7 | 7 | 1.96 | 0.82 | 5.38 | 5.38 | 1.62 | 0.98 |
| HR08 | 22 | 4.91 | 10 | 7 | 2.64 | 0.90 | 6.76 | 6.76 | 1.92 | 1.01 |
| HR09 | 22 | 4.91 | 6 | 6 | 2.36 | 0.77 | 7.07 | 7.07 | 1.99 | 0.91 |
| HR010 | 23 | 4.7 | 7 | 7 | 2.39 | 0.76 | 6.24 | 6.24 | 1.85 | 0.89 |
| HR011 | 23 | 4.7 | 7 | 7 | 2.43 | 0.71 | 7.54 | 7.54 | 1.85 | 0.97 |
| HR012 | 23 | 4.7 | 7 | 7 | 2.43 | 0.79 | 5.88 | 5.88 | 1.83 | 0.94 |
| Hydrographic Region | Duration | Severity | Copula |
|---|---|---|---|
| HR01 | Log-normal | Exponential | Gumbel |
| (µ = 0.53, σ = 0.61) | (λ = 0.59) | (θ = 2.26, τ = 0.56) | |
| HR02 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.43, σ = 0.67) | (λ = 0.61) | (θ = 1.78, τ = 0.47) | |
| HR03 | Log-normal | Exponential | Gumbel |
| (µ = 0.44, σ = 0.65) | (λ = 0.61) | (θ = 2.38, τ = 0.58) | |
| HR04 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.49, σ = 0.64) | (λ = 0.58) | (θ = 2.56, τ = 0.56) | |
| HR05 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.50, σ = 0.63) | (λ = 0.54) | (θ = 2.28, τ = 0.56) | |
| HR06 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.43, σ = 0.67) | (λ = 0.59) | (θ = 1.70, τ = 0.46) | |
| HR07 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.43, σ = 0.64) | (λ = 0.62) | (θ = 1.56, τ = 0.44) | |
| HR08 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.65, σ = 0.77) | (λ = 0.52) | (θ = 2.32, τ = 0.54) | |
| HR09 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.60, σ = 0.7) | (λ = 0.50) | (θ = 2.33, τ = 0.54) | |
| HR010 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.62, σ = 0.70) | (λ = 0.54) | (θ = 1.90, τ = 0.49) | |
| HR011 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.66, σ = 0.68) | (λ = 0.54) | (θ = 2.23, τ = 0.53) | |
| HR012 | Log-normal | Exponential | Survival Clayton |
| (µ = 0.62, σ = 0.71) | (λ = 0.55) | (θ = 3.20, τ = 0.62) |
| Hydrographic Region | Drought Period | Rank in the Set of Events | ||||||
|---|---|---|---|---|---|---|---|---|
| Duration | Severity | Joint | ||||||
| HR01 | 2012–2016 | 113 | 88 | 72 | 155 | 2 | 1 | 2 |
| HR02 | 2012–2016 | 106 | 56 | 52 | 124 | 3 | 3 | 3 |
| HR03 | 2012–2016 | 115 | 94 | 77 | 157 | 3 | 1 | 3 |
| HR04 | 2012–2017 | 206 | 141 | 131 | 234 | 1 | 1 | 1 |
| HR05 | 2012–2017 | 223 | 254 | 191 | 313 | 1 | 1 | 1 |
| HR06 | 2012–2016 | 106 | 73 | 63 | 136 | 3 | 1 | 3 |
| HR07 | 2012–2018 | 465 | 117 | 115 | 499 | 1 | 1 | 1 |
| HR08 | 2012–2018 | 106 | 165 | 98 | 188 | 2 | 1 | 2 |
| HR09 | 2012–2017 | 111 | 168 | 102 | 193 | 1 | 1 | 1 |
| HR010 | 2012–2018 | 161 | 136 | 112 | 215 | 1 | 1 | 1 |
| HR011 | 2012–2018 | 160 | 275 | 150 | 309 | 1 | 1 | 1 |
| HR012 | 2012–2018 | 152 | 119 | 110 | 171 | 1 | 1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pontes Filho, J.D.; Souza Filho, F.d.A.; Martins, E.S.P.R.; Studart, T.M.d.C. Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil. Water 2020, 12, 834. https://doi.org/10.3390/w12030834
Pontes Filho JD, Souza Filho FdA, Martins ESPR, Studart TMdC. Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil. Water. 2020; 12(3):834. https://doi.org/10.3390/w12030834
Chicago/Turabian StylePontes Filho, João Dehon, Francisco de Assis Souza Filho, Eduardo Sávio Passos Rodrigues Martins, and Ticiana Marinho de Carvalho Studart. 2020. "Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil" Water 12, no. 3: 834. https://doi.org/10.3390/w12030834
APA StylePontes Filho, J. D., Souza Filho, F. d. A., Martins, E. S. P. R., & Studart, T. M. d. C. (2020). Copula-Based Multivariate Frequency Analysis of the 2012–2018 Drought in Northeast Brazil. Water, 12(3), 834. https://doi.org/10.3390/w12030834






