Study on the Nearshore Evolution of Regular Waves under Steady Wind
Abstract
1. Introduction
2. Numerical Methods
2.1. Governing Equations
2.2. Turbulence Model
2.3. Boundary Conditions
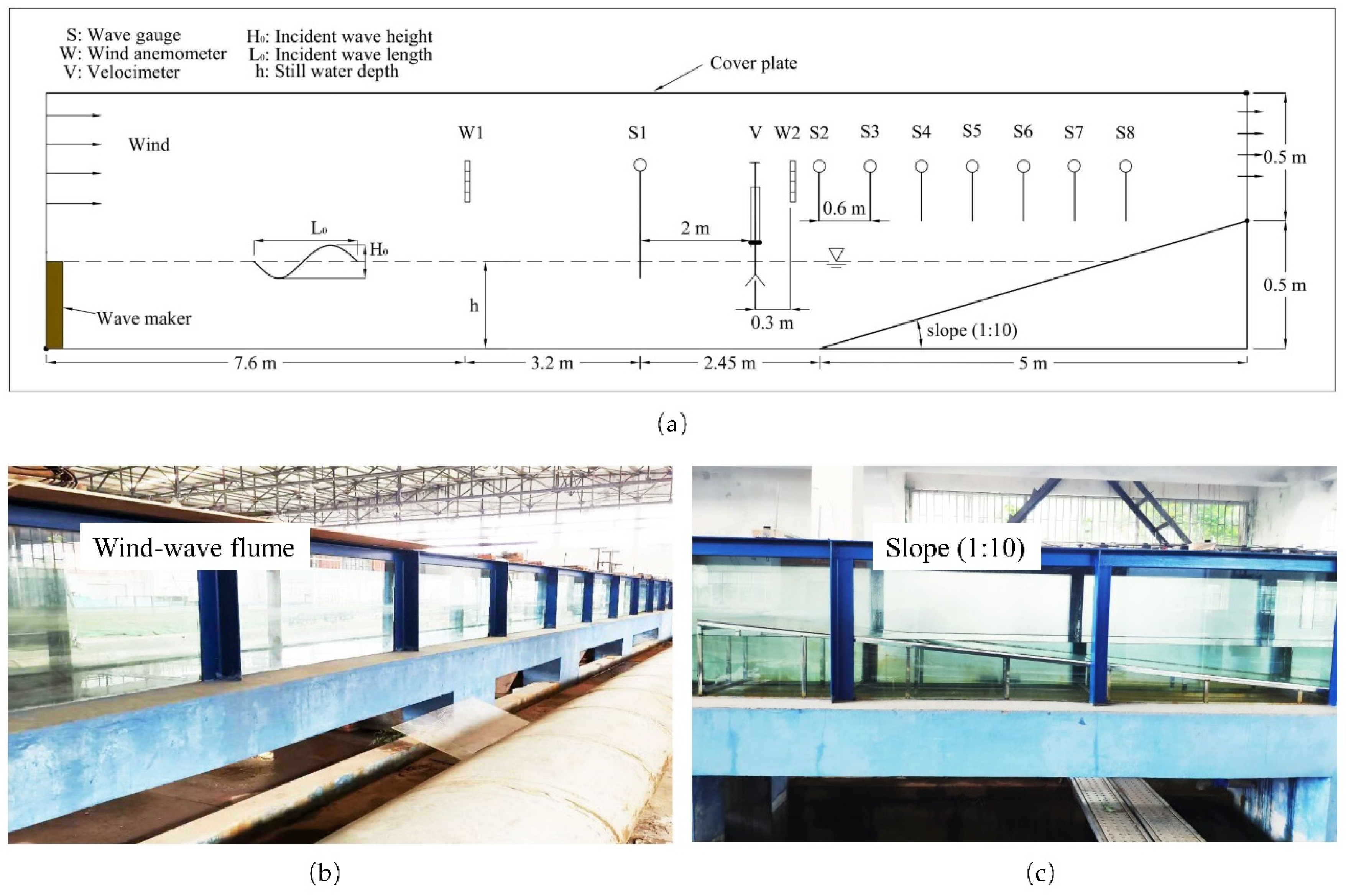
3. Experimental and Numerical Setup
3.1. Experimental Setup
3.2. Numerical Setup
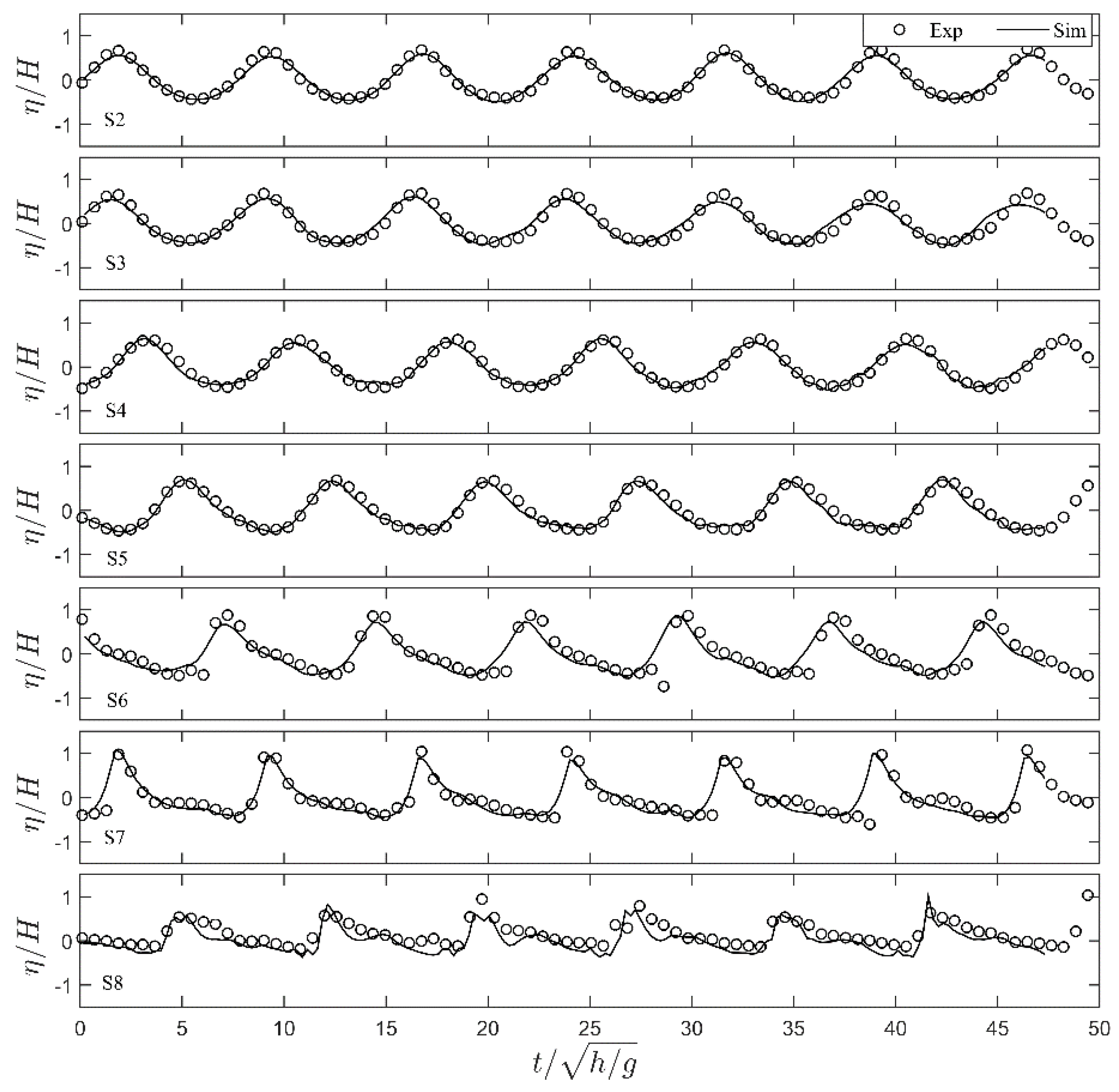
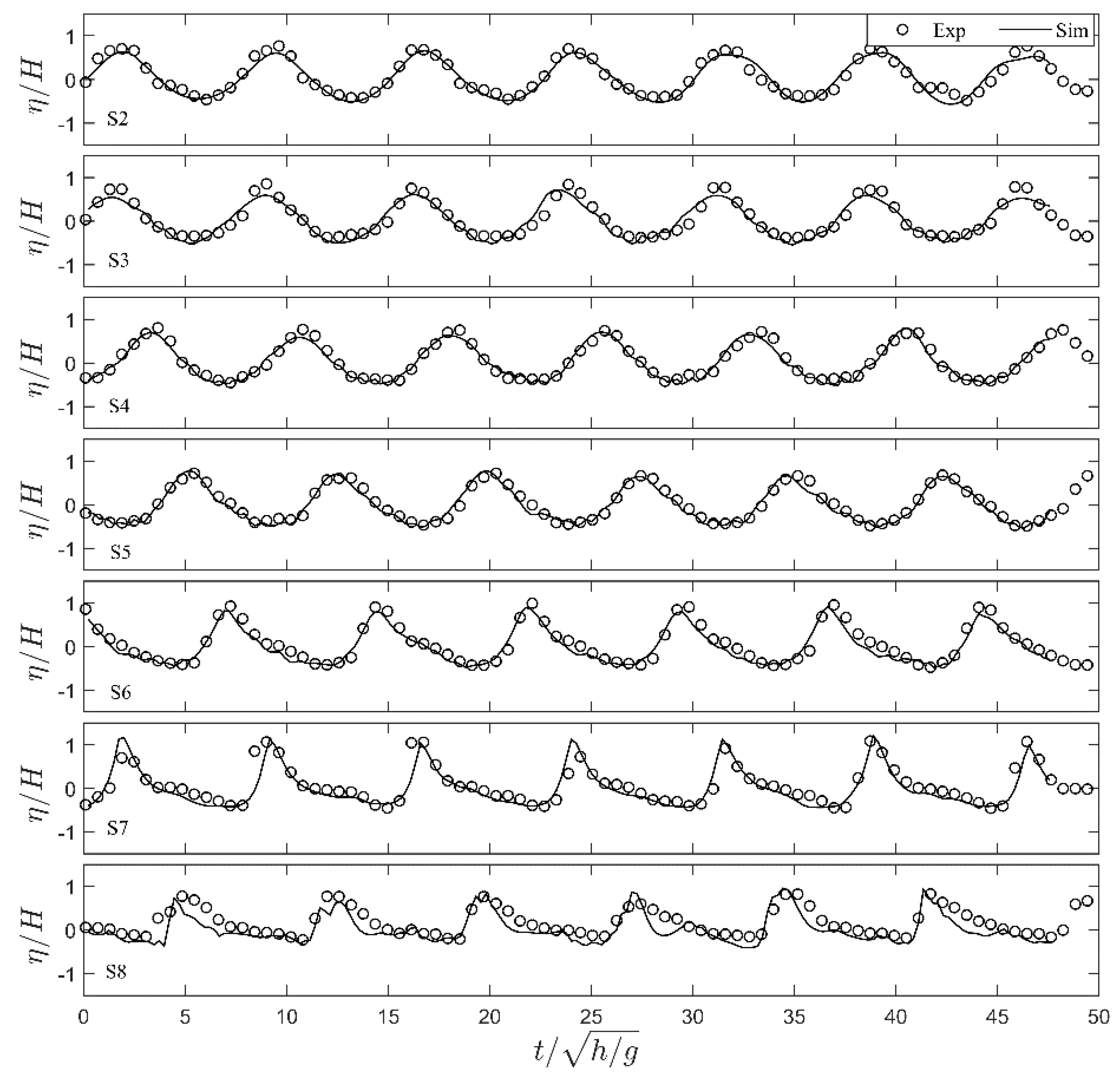
4. Model Validation
5. Results and Discussions
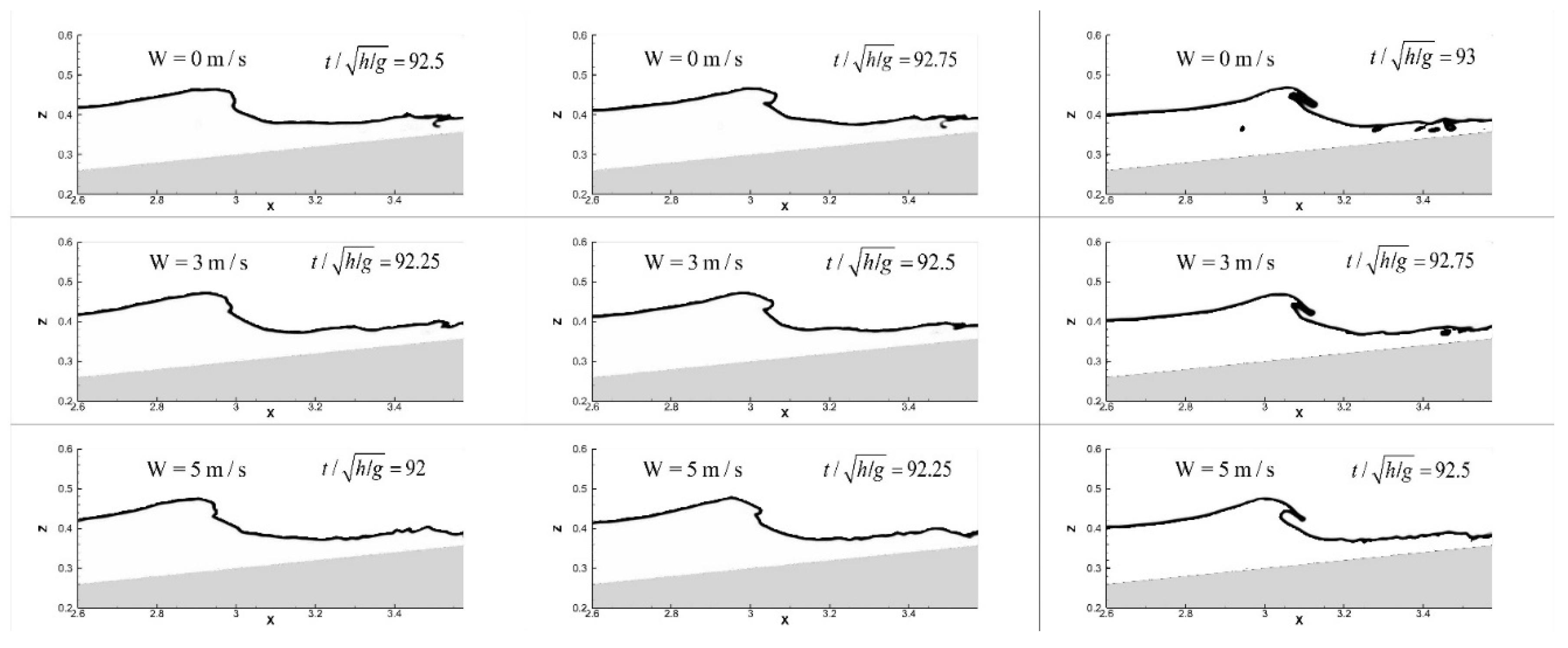
5.1. Wave Breaking
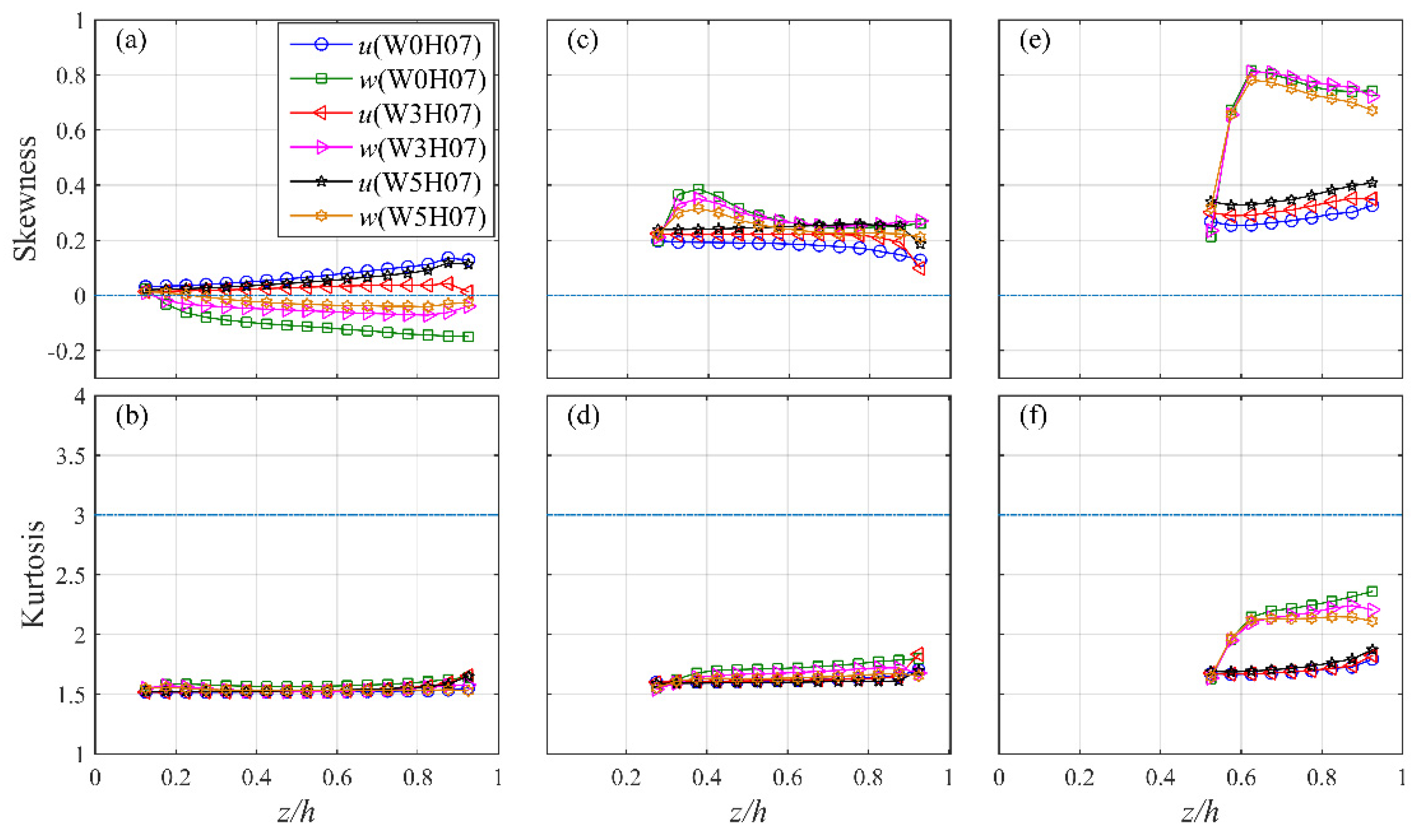
5.2. Turbulent Flow
5.3. Undertow
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observation of the directional spectrum of sea waves using the motion of a floating buoy. In Proceedings of the Ocean Wave Spectra, Easton, MD, USA, 1–4 May 1961; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1963; pp. 113–136. [Google Scholar]
- Gilchrist, A.W.R. The directional spectrum of ocean waves: An experimental investigation of certain prediction of the Miles-Phillps theory of wave generation. J. Fluid Mech. 1966, 25, 795–816. [Google Scholar] [CrossRef]
- Fujinawa, Y. Measurements of Directional Spectrum of Wind Waves using an Array of Wave Detectors Part II. Field Observation. J. Oceanogr. Soc. Jpn. 1975, 31, 25–42. [Google Scholar] [CrossRef]
- Jeffreys, H. On the formation of water waves by wind. R. Soc. 1925, 107, 189–206. [Google Scholar]
- Miles, J.W. On the generation of surface waves by shear flows. J. Fluid Mech. 1957, 3, 185–204. [Google Scholar] [CrossRef]
- Mei, C.C.; Liu, P.L. Surface waves and coastal dynamics. Annu. Rev. Fluid Mech. 1993, 25, 215–240. [Google Scholar] [CrossRef]
- Peter, J. The Interaction of Ocean Waves and Wind; Cambridge University Press: Cambridge, UK, 2004; pp. 74–167. [Google Scholar]
- Toba, Y. Drop production by bursting of air bubbles on the sea surface. III. Study by use of a wind flume. J. Oceanogr. Soc. Jpn. 1961, 40, 63–64. [Google Scholar]
- Kuninshi, H. An experimental study on the generation and growth of wind waves. Bull. Disaster Prev. Res. Inst. Kyoto Univ. 1963, 61, 1–41. [Google Scholar]
- Wu, J. Laboratory studies of wind-wave interactions. J. Fluid Mech. 1968, 34, 99–111. [Google Scholar] [CrossRef]
- Wu, T. On the formation of streaks on wind-driven water surfaces. Geophys. Res. Lett. 2001, 28, 3959–3962. [Google Scholar]
- Lin, M.Y.; Moeng, C.H.; Tsai, W.T.; Sullivan, P.P.; Belcher, S.E. Direct numerical simulation of wind-wave generation processes. J. Fluid Mech. 2008, 616, 1–30. [Google Scholar] [CrossRef]
- Longo, S. Wind-generated water waves in a wind tunnel: Free surface statistics, wind friction and mean air flow properties. Coast. Eng. 2012, 61, 27–41. [Google Scholar] [CrossRef]
- Longo, S. Turbulent flow structure in experimental laboratory wind-generated gravity waves. Coast. Eng. 2012, 64, 1–15. [Google Scholar] [CrossRef]
- Longo, S. Study of the turbulence in the air-side and water-side boundary layers in experimental laboratory wind induced surface waves. Coast. Eng. 2012, 69, 67–81. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, J.; Jiang, C.; Liu, X.; Deng, B.; Qu, K.; He, Z.; Xie, Z. Numerical investigation of Typhoon Kai-tak (1213) using a mesoscale coupled WRF-ROMS model—Part Ⅱ: Wave effects. Ocean Eng. 2020, 196, 106805. [Google Scholar] [CrossRef]
- Sibul, O.J.; Tickner, E.G. Model Study of Overtopping of Wind Generated Waves on Levees with Slopes 1:3 and 1:6. U.S. Beach Eros. Board Tech. Memo. 1956, 80, 1–27. [Google Scholar]
- Kinsman, B. Wind Waves: Their Generation and Propagation on the Ocean Surface; Prentice-Hall: Englewood Cliffs, NJ, USA, 1965; pp. 543–575. [Google Scholar]
- Walker, J.R. Recreational Surf Parameters; Technical Report; Look Laboratory of Oceanographic Engineering, Hawaii University: Honolulu, HI, USA, 1974; pp. 73–130. [Google Scholar]
- Kawata, Y. Wave Breaking under Storm Condition. Coast. Eng. 1995, 36, 330–339. [Google Scholar]
- Galloway, J.S.; Collins, M.B.; Moran, A.D. Onshore/offshore wind influence on breaking waves: An empirical study. Coast. Eng. 1989, 13, 305–323. [Google Scholar] [CrossRef]
- Douglass, S.L. Influence of wind on breaking waves. J. Waterw. Port Coast. Ocean Eng. 1990, 116, 651–663. [Google Scholar] [CrossRef]
- King, D.M.; Baker, C.J. Changes to wave parameters in the surf zone due to wind effects. J. Hydraul. Res. 1996, 34, 55–76. [Google Scholar] [CrossRef]
- Feddersen, F.; Veron, F. Wind effects on shoaling wave shape. J. Phys. Oceanogr. 2005, 35, 1223–1228. [Google Scholar] [CrossRef]
- Kharif, C.; Giovanangeli, J.P.; Touboul, J.; Grare, L.; Pelinovsky, E. Influence of wind on extreme wave events: Experimental and numerical approaches. J. Fluid Mech. 2008, 594, 209–247. [Google Scholar] [CrossRef]
- Tian, Z.; Choi, W. Evolution of deep-water waves under wind forcing and wave breaking effects: Numerical simulations and experimental assessment. Eur. J. Mech. B Fluid 2013, 41, 11–22. [Google Scholar] [CrossRef]
- Liu, K. Modeling Wind Effects on Shallow Water Waves. J. Waterw. Port Coast. Ocean Eng. 2016, 142, 1–8. [Google Scholar] [CrossRef]
- Hasan, S.A. Numerical modelling of wind-modified focused waves in a numerical wave tank. Ocean Eng. 2018, 160, 276–300. [Google Scholar] [CrossRef]
- Xie, Z. Numerical modelling of wind effects on breaking waves in the surf zone. Ocean Dyn. 2017, 67, 1251–1261. [Google Scholar] [CrossRef]
- Chen, H. Transformation of Nonlinear Waves in the Presence of Wind, Current, and Vegetation. Ph.D. Thesis, Maine University, Orono, ME, USA, 2017. [Google Scholar]
- Lafrati, A. Effects of the wind on the breaking of modulated wave trains. Eur. J. Mech. B Fluid 2018, 73, 1–17. [Google Scholar]
- Zou, Q.; Chen, H. Numerical simulation of wind effects on the evolution of freak waves. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Yang, D.; Shen, L. Direct-simulation-based study of turbulent flow over various waving boundaries. J. Fluid Mech. 2010, 650, 131–180. [Google Scholar] [CrossRef]
- Lakehal, D.; Meier, M.; Fulgosi, M. Interface tracking towards the direct simulation of heat and mass transfer in multiphase flows. Int. J. Heat Fluid Flow 2002, 23, 242–257. [Google Scholar] [CrossRef]
- Fulgosi, M.; Lakehal, D.; Banerjee, S.; De Angelis, V. Direct numerical simulation of turbulence in a sheared air–water flow with a deformable interface. J. Fluid Mech. 2003, 482, 319–345. [Google Scholar] [CrossRef]
- Lubin, P.; Vincent, S.; Abadie, S. Three-dimensional Large Eddy Simulation of air entrainment under plunging breaking waves. Coast. Eng. 2006, 53, 631–655. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Sethian, J.A.; Smereka, P. Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.; Greaves, D.; Reeve, D.; Hunt-Raby, A.; Graham, D.; Lv, X. A level set immersed boundary method for water entry and exit. Commun. Comput. Phys. 2010, 8, 265–288. [Google Scholar] [CrossRef]
- Hansen, J. A theoretical and experimental study of undertow. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984. [Google Scholar]
- Ting, F.; Kirby, J. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Ting, F.; Kirby, J. Dynamics of surf zone turbulence in a strong plunging breaker. Coast. Eng. 1995, 24, 177–204. [Google Scholar] [CrossRef]
- Bakhtyar, R. Numerical simulation of surf–swash zone motions and turbulent flow. Adv. Water Resour. 2009, 32, 250–263. [Google Scholar] [CrossRef]
- Cavallaro, L.; Scandura, P.; Foti, E. Turbulence-induced steady streaming in an oscillating boundary layer: On the reliability of turbulence closure models. Coast. Eng. 2011, 58, 290–304. [Google Scholar] [CrossRef]
- Kranenburg, W.M.; Ribberink, J.S.; Uittenbogaard, R.E.; Hulscher, S.J.M.H. Net currents in the wave bottom boundary layer: On waveshape streaming and progressive wave streaming. J. Geophys. Res. Earth 2012, 117, F03005. [Google Scholar] [CrossRef]
- Blondeaux, P.; Vittori, G.; Porcile, G. Modeling the turbulent boundary layer at the bottom of sea wave. Coast. Eng. 2018, 141, 12–23. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College, London, UK, 2002. [Google Scholar]
- Bogey, C. Large eddy simulations of round free jets using explicit filtering with/without dynamic Smagorinsky model. Int. J. Heat Fluid Flow 2006, 27, 603–610. [Google Scholar] [CrossRef]
- Higurea, P.; Lara, J.L.; Losada, I.J. Realistic wave generation and active wave absorbtion for Navior-Stokes models. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf similarity. In Proceedings of the 14th International Conference on Coastal Engineering, Honolulu, HI, USA, 24–28 June 1974. [Google Scholar]
- Inami, T. Study on Wave Reflection Coefficient and Wave Runup Height on a Slope. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Wu, J. Froude number scaling of wind-stress coefficients. J. Atmos. Sci. 1969, 26, 408–413. [Google Scholar] [CrossRef]
- Collins, J.I.; Weir, W. Probabilities of Breaking Wave Characteristics in the surf zone. In Proceedings of the 12th International Conference on Coastal Engineering, Pasadena, CA, USA, 13–18 September 1970. [Google Scholar]
- Le Mehhaute, B. On the breaking of waves arriving at an angle to the shore. J. Hydraul Res. 1967, 5, 67–80. [Google Scholar] [CrossRef]
- Galvin, C.J. Breaker type classification of three laboratory beaches. J. Geophys. Res. Atmos. 1968, 73, 3651–3659. [Google Scholar] [CrossRef]
- Komori, S.; Nagaosa, R.; Murakami, Y. Turbulence structure and mass transfer across a sheared air-water interface in wind-driven turbulence. J. Fluid Mech. 1993, 249, 161–183. [Google Scholar] [CrossRef]
- William, K.G. Lectures in Turbulence for the 21st Century; Chalmers University of Technology: Gothenburg, Sweden, 2013; pp. 59–64. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Christensen, E.D.; Walstra, D.J.; Emarat, N. Vertical variation of the flow across the surf zone. Coast. Eng. 2002, 45, 169–198. [Google Scholar] [CrossRef]



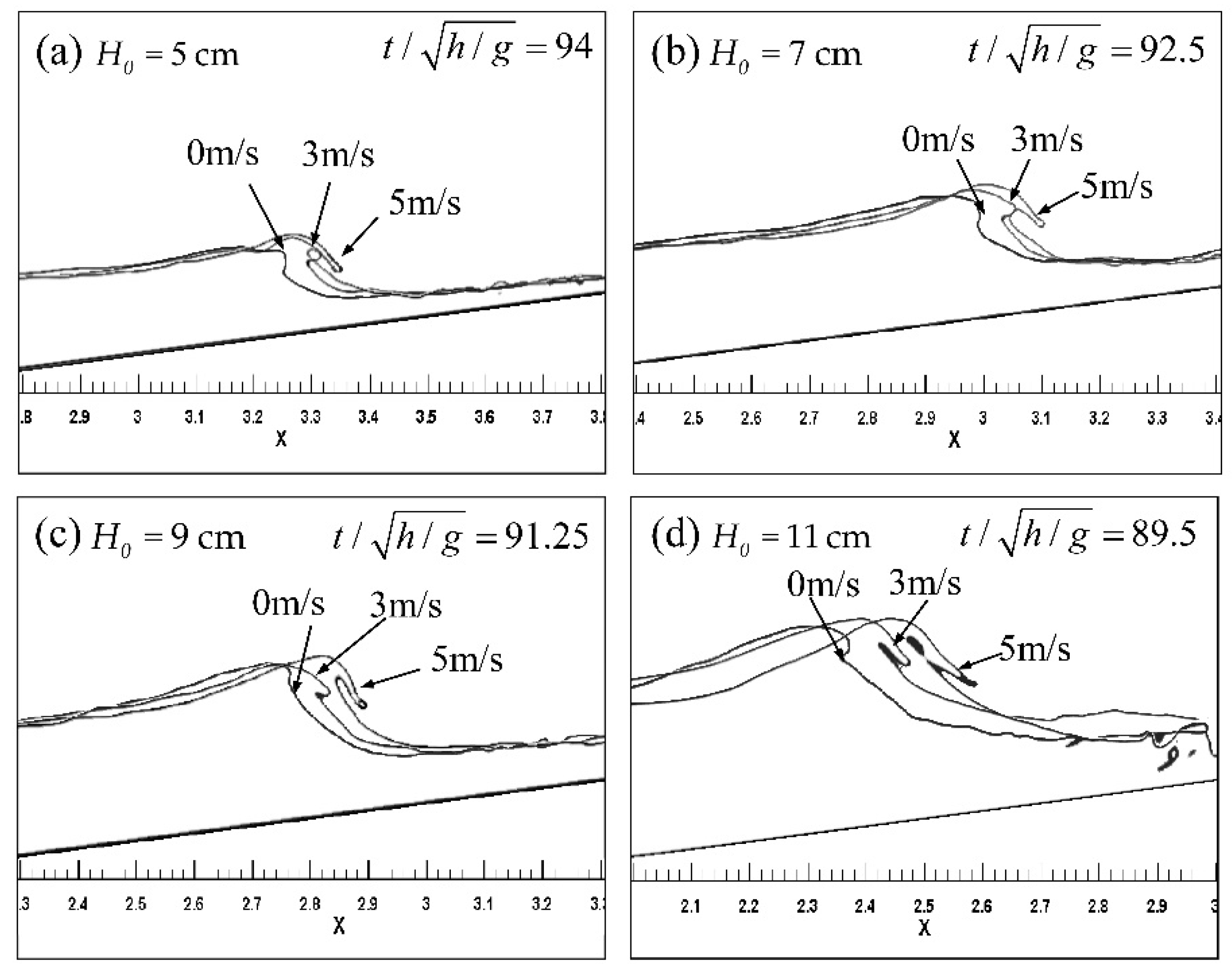
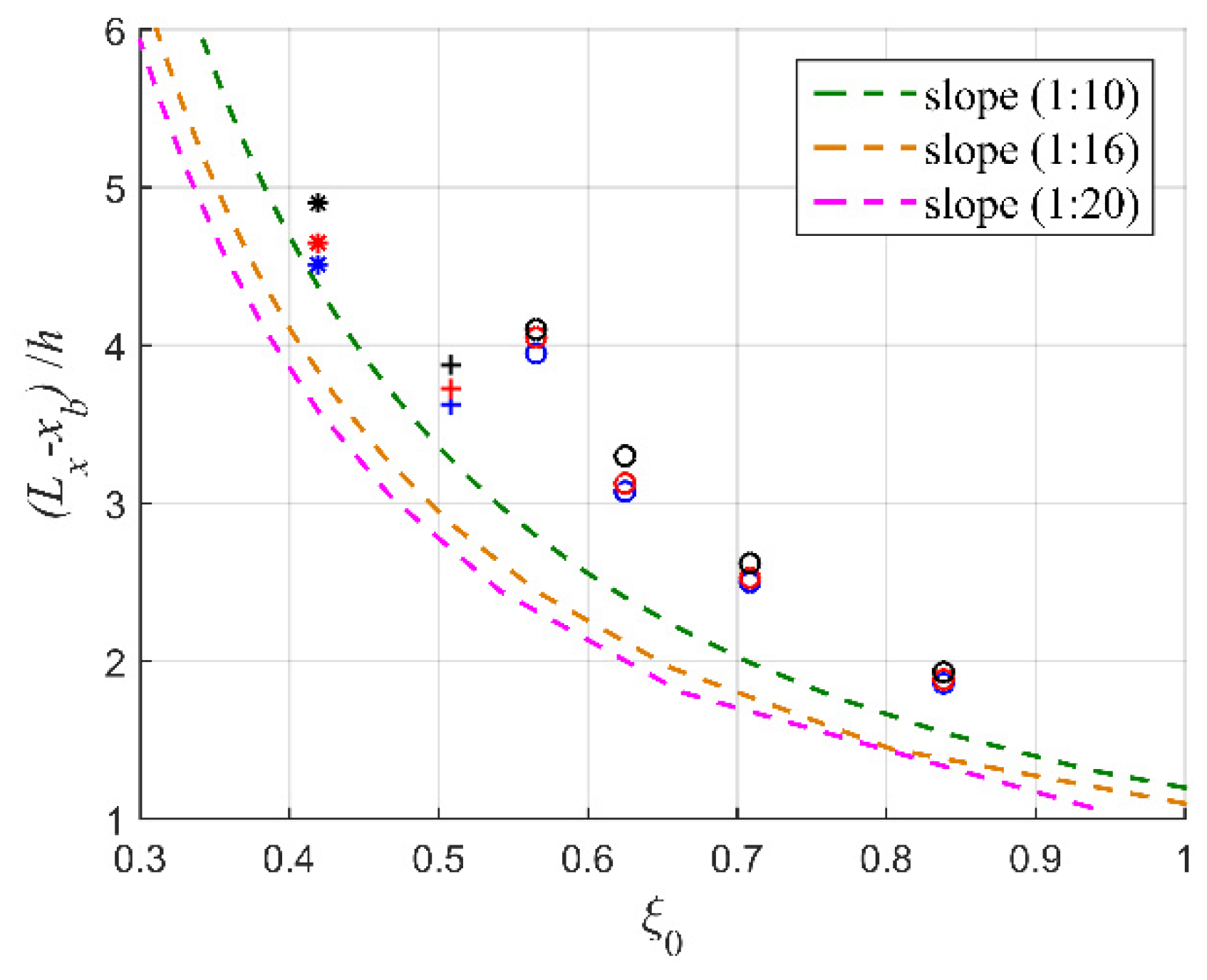
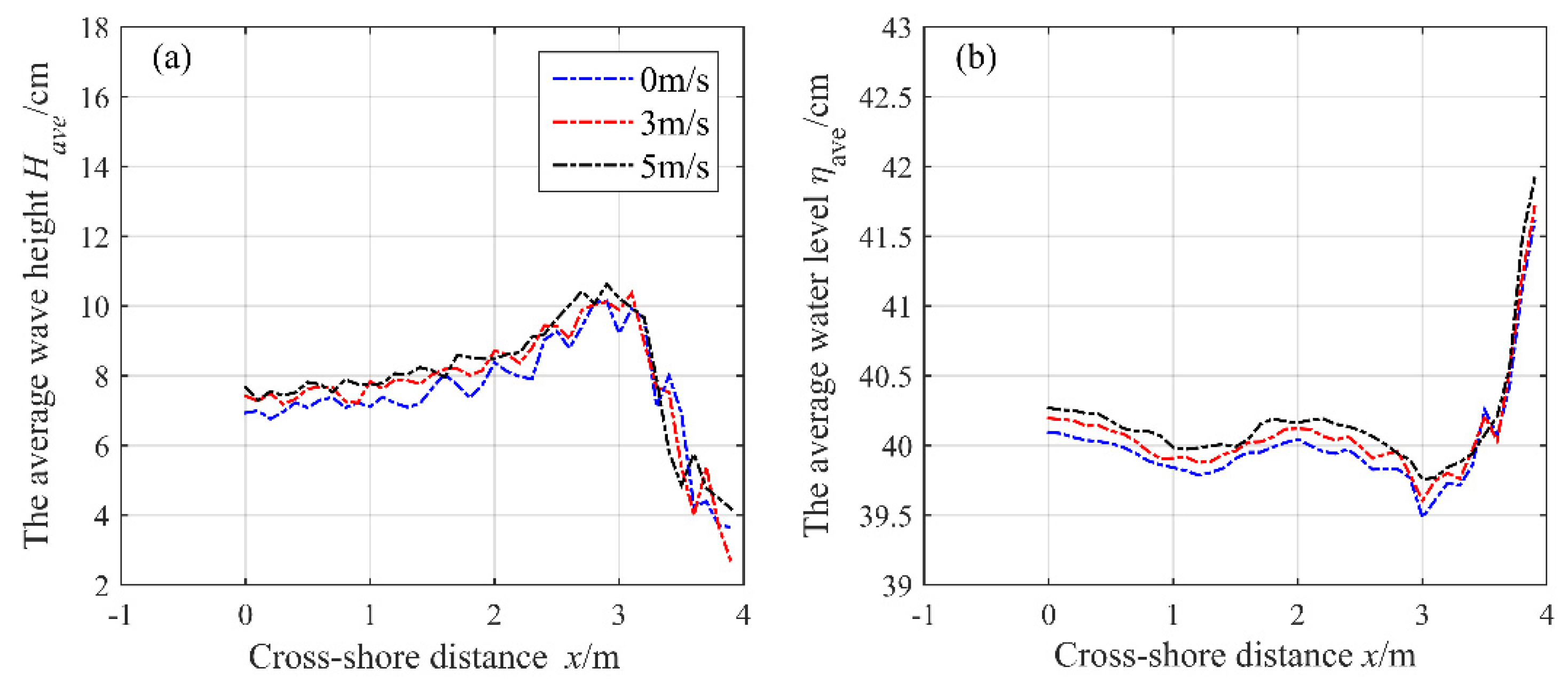

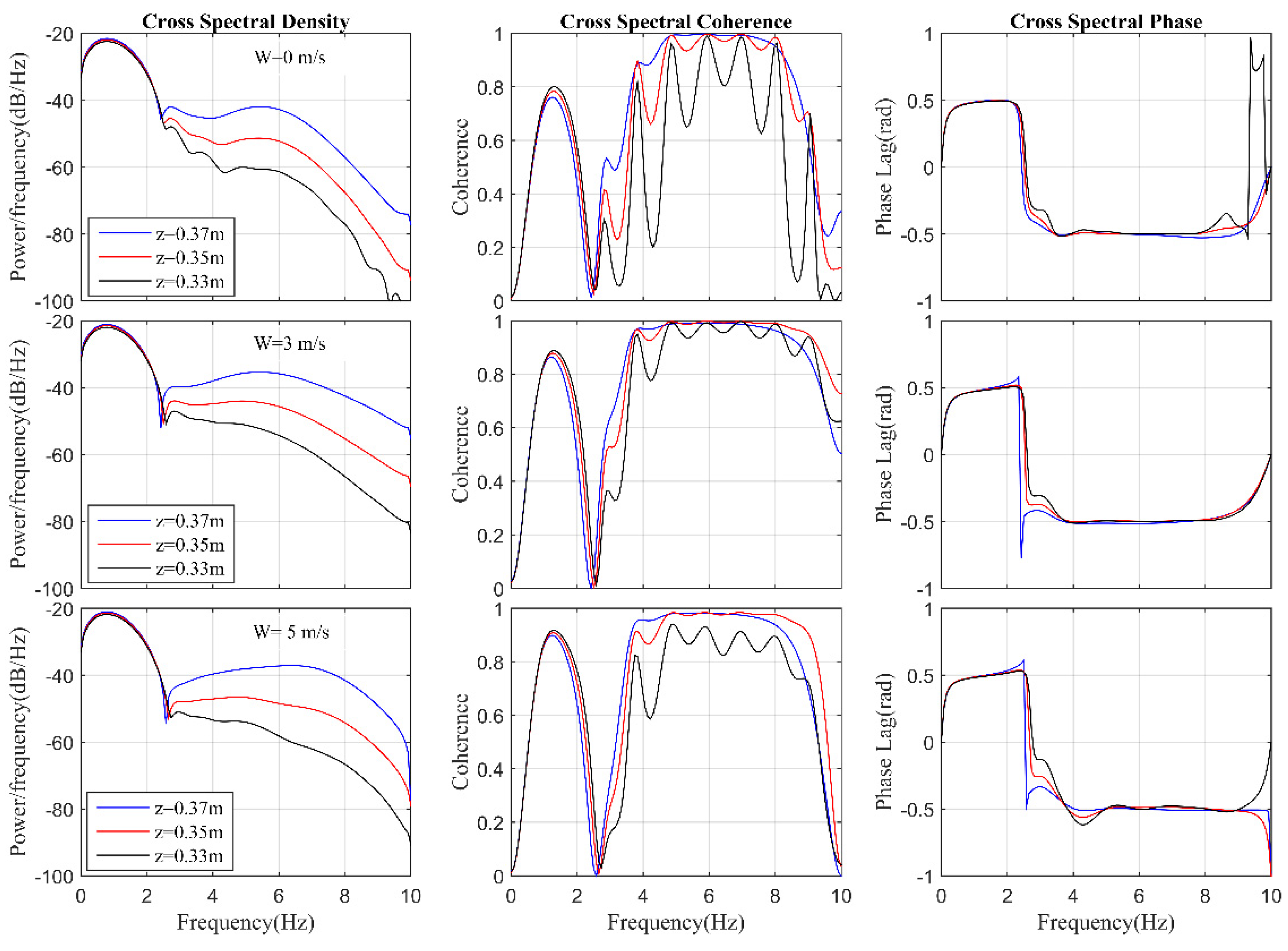
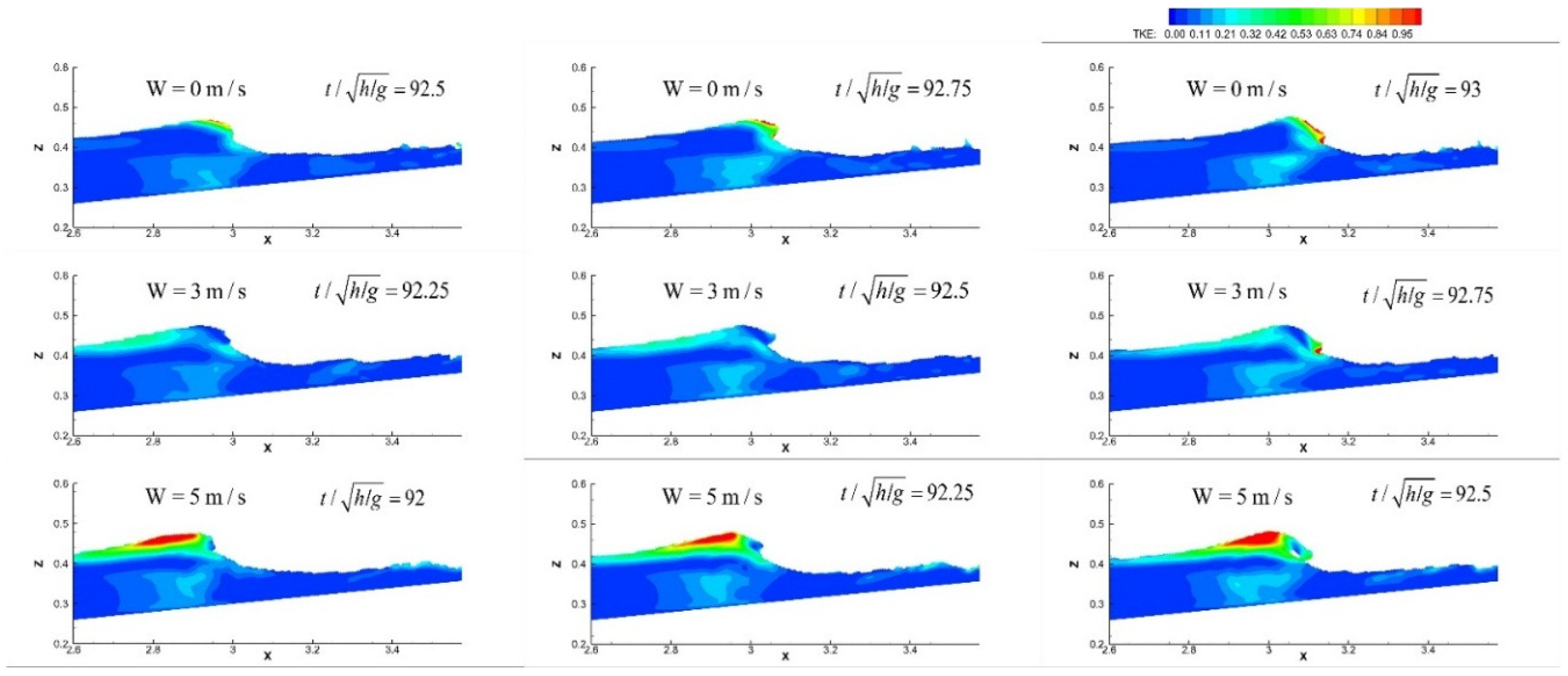

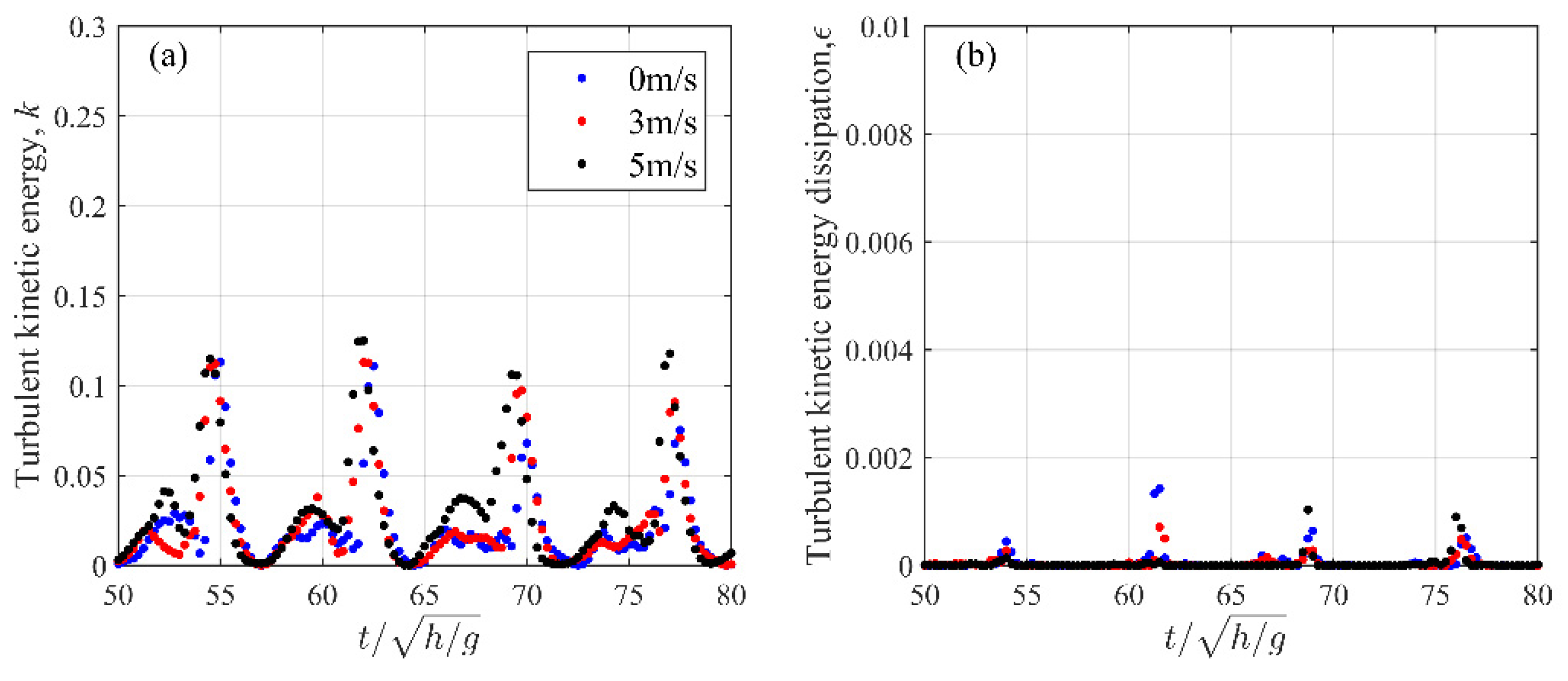
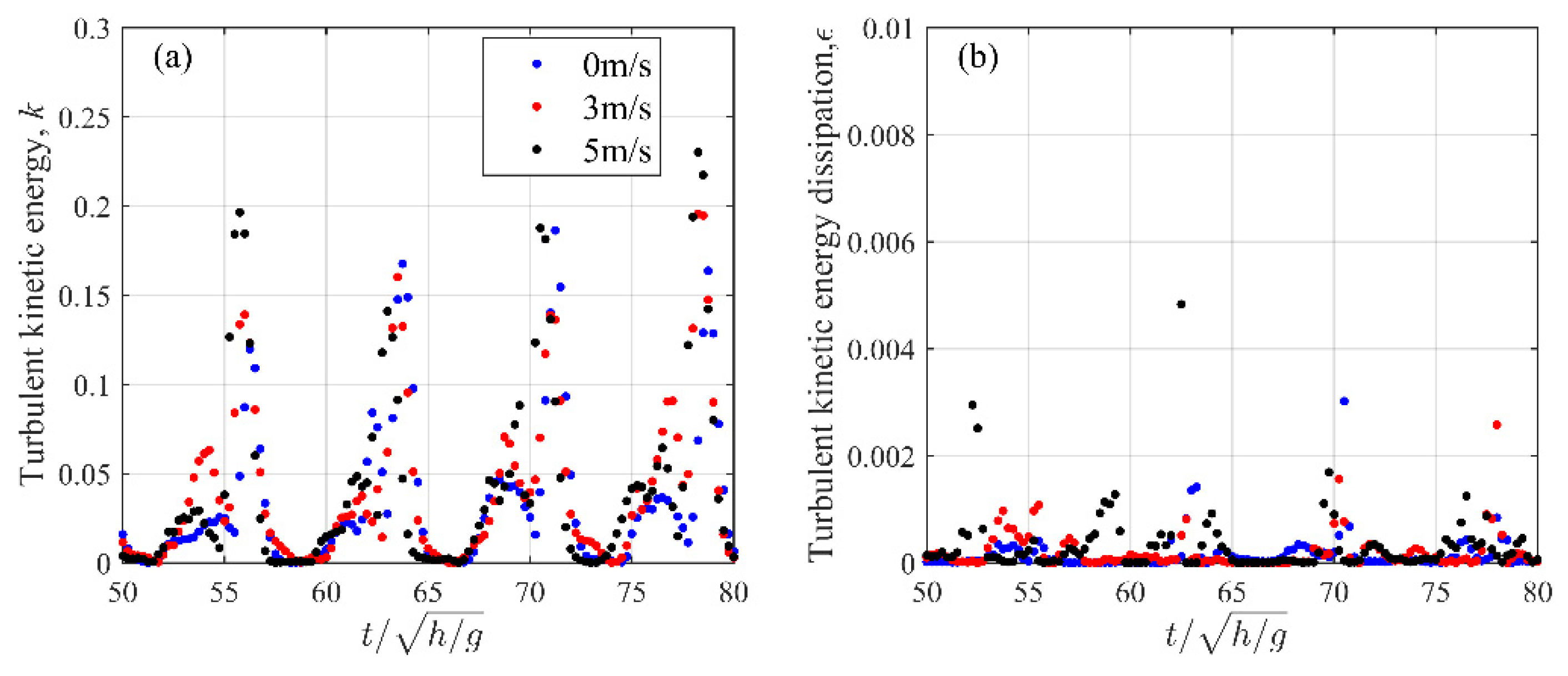

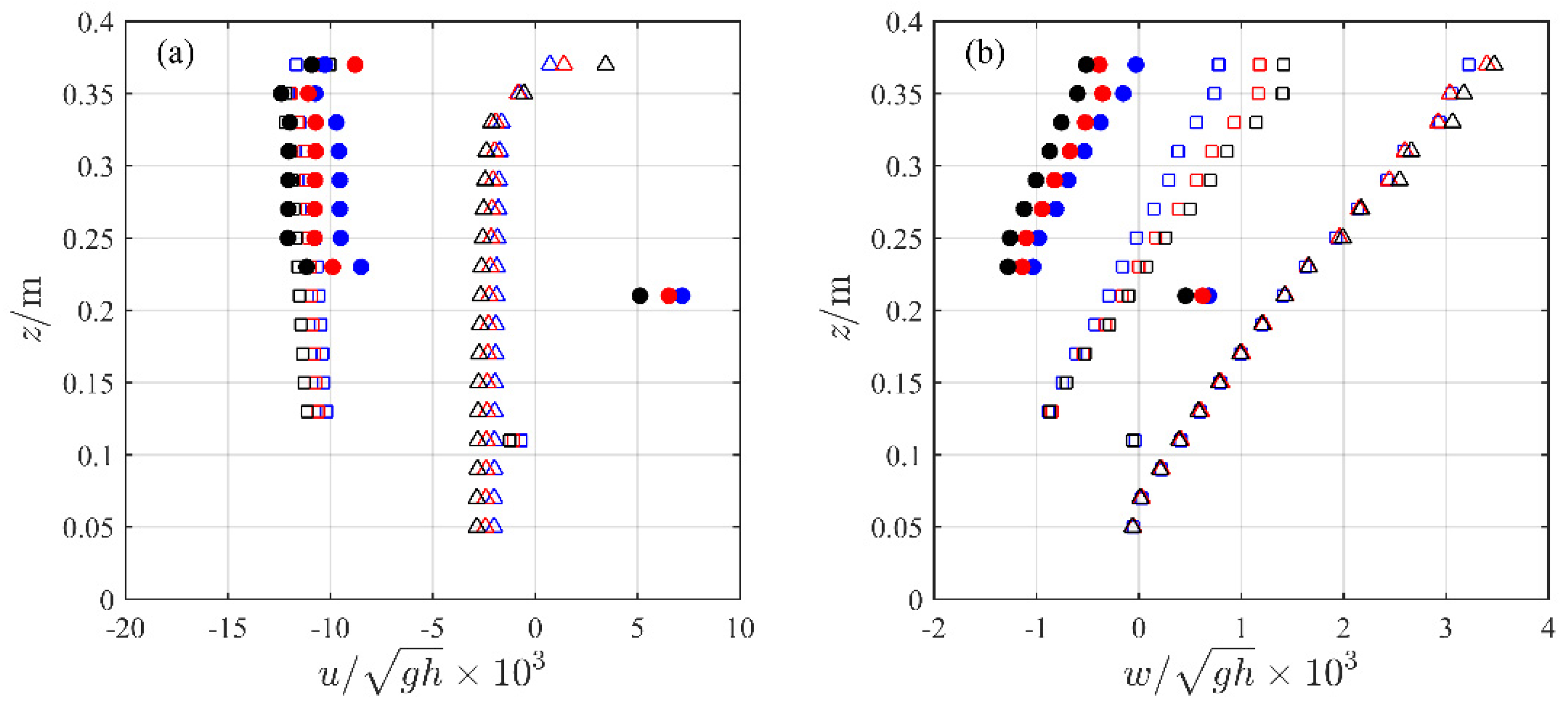
| Case | W (m/s) | H0 (cm) | T (s) | h (m) | ξ0 |
|---|---|---|---|---|---|
| W0H05~W0H11 | 0.0 | 5, 7, 9,11 | 1.5 | 0.4 | plunging |
| W3H05~W3H11 | 3.0 | 5, 7, 9,11 | 1.5 | 0.4 | plunging |
| W5H05~W5H11 | 5.0 | 5, 7, 9,11 | 1.5 | 0.4 | plunging |
| x (m) | hx (m) | W (m/s) | Mean Flow Rate, q (m3/s/m) |
|---|---|---|---|
| 0 | 0.4 | 0, 3, 5 | −0.0011, −0.0014, −0.0016 |
| 1 | 0.3 | 0, 3, 5 | −0.0051, −0.0054, −0.0056 |
| 2 | 0.2 | 0, 3, 5 | −0.0024, −0.0029, −0.0033 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Yang, Y.; Deng, B. Study on the Nearshore Evolution of Regular Waves under Steady Wind. Water 2020, 12, 686. https://doi.org/10.3390/w12030686
Jiang C, Yang Y, Deng B. Study on the Nearshore Evolution of Regular Waves under Steady Wind. Water. 2020; 12(3):686. https://doi.org/10.3390/w12030686
Chicago/Turabian StyleJiang, Changbo, Yang Yang, and Bin Deng. 2020. "Study on the Nearshore Evolution of Regular Waves under Steady Wind" Water 12, no. 3: 686. https://doi.org/10.3390/w12030686
APA StyleJiang, C., Yang, Y., & Deng, B. (2020). Study on the Nearshore Evolution of Regular Waves under Steady Wind. Water, 12(3), 686. https://doi.org/10.3390/w12030686






