Numerical and Experimental Investigation of Wave Overtopping of Barriers
Abstract
1. Introduction
2. The Numerical Model
2.1. Governing Equations
2.2. Numerical Procedure
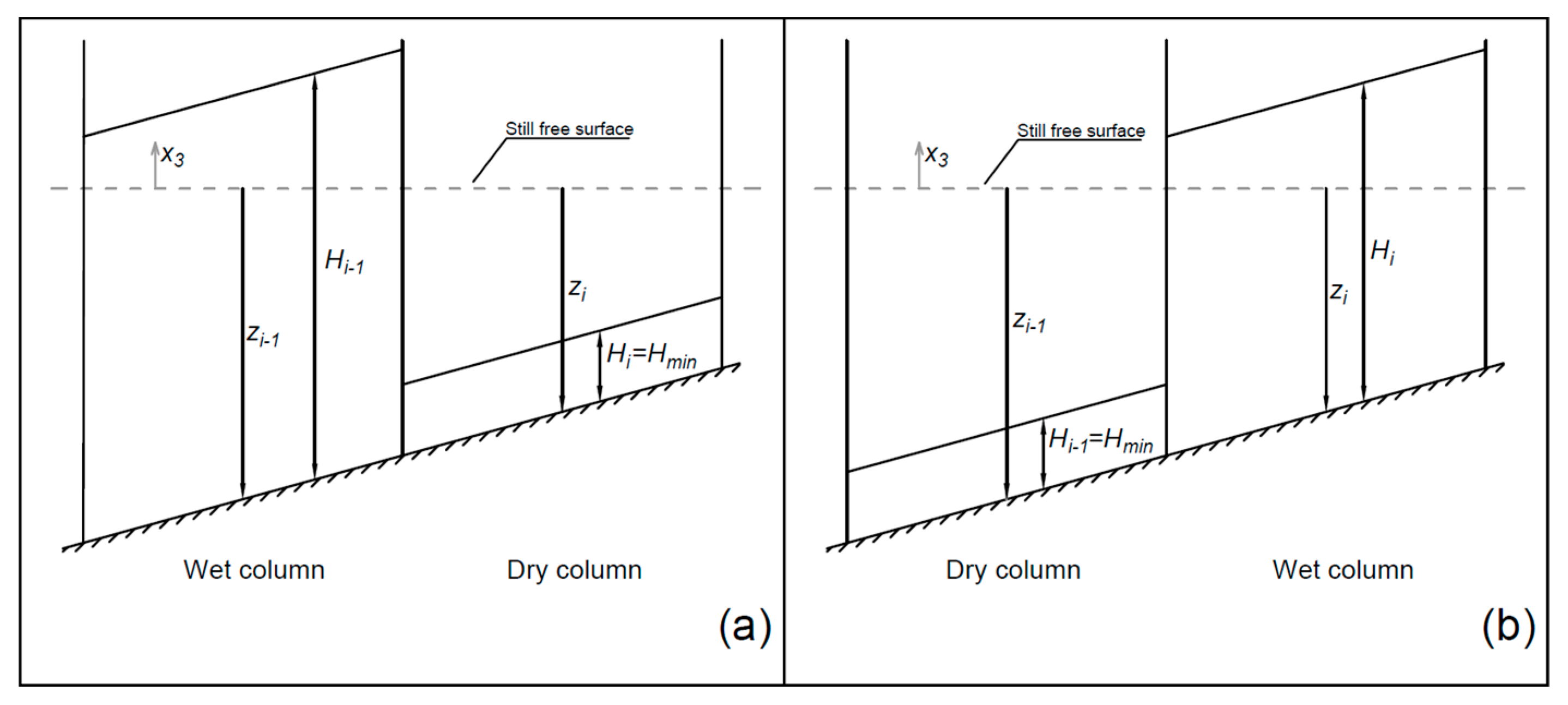
2.3. Wet–Dry Technique
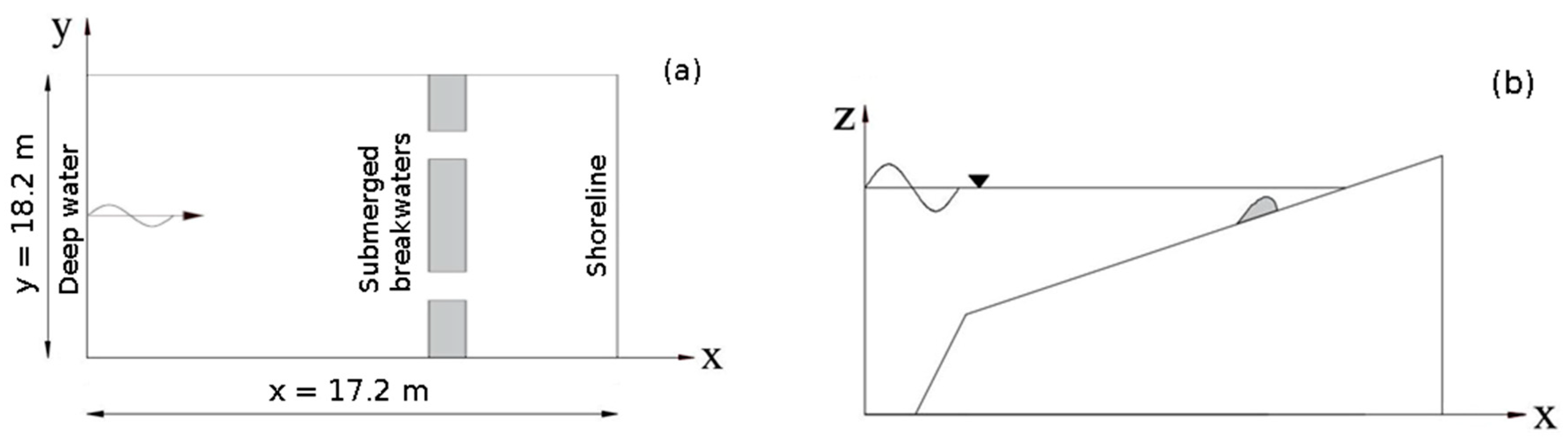
3. Experimental Setup
4. Results and Discussion
4.1. Numerical Simulation Details
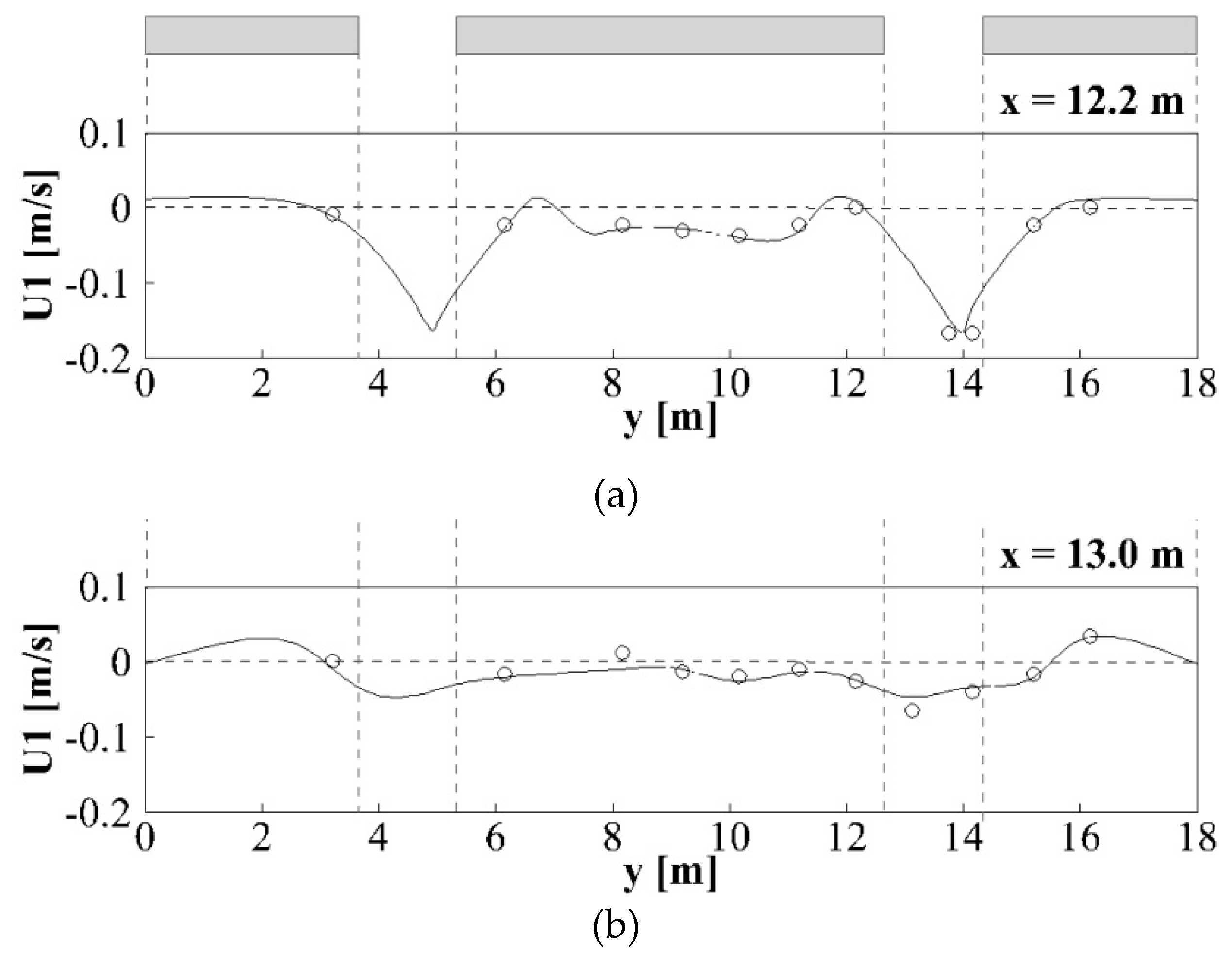
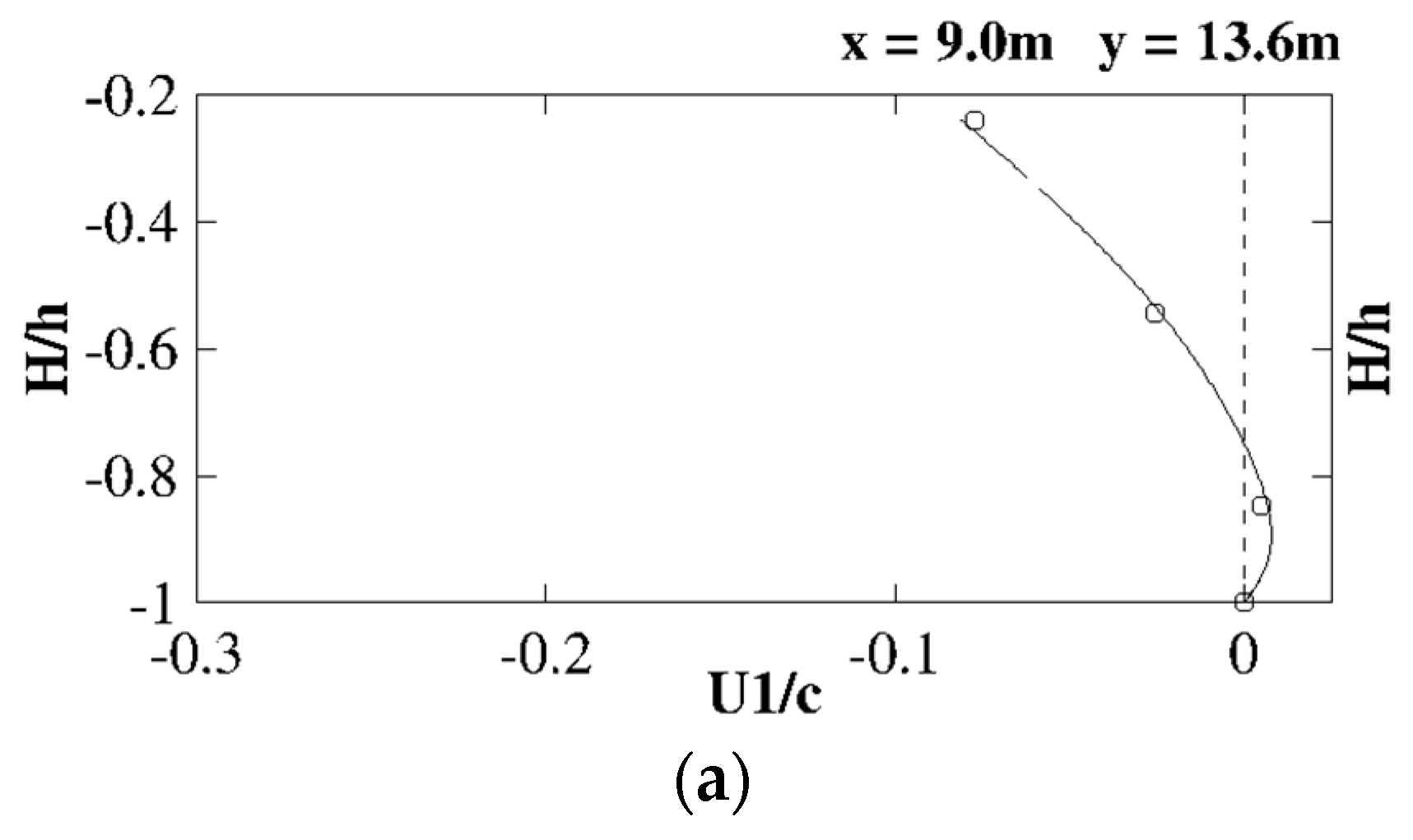
4.2. Three-Dimensional Validation Test
4.3. Wave Overtopping Test
4.3.1. Test T1
4.3.2. Test T2
4.3.3. Test T3
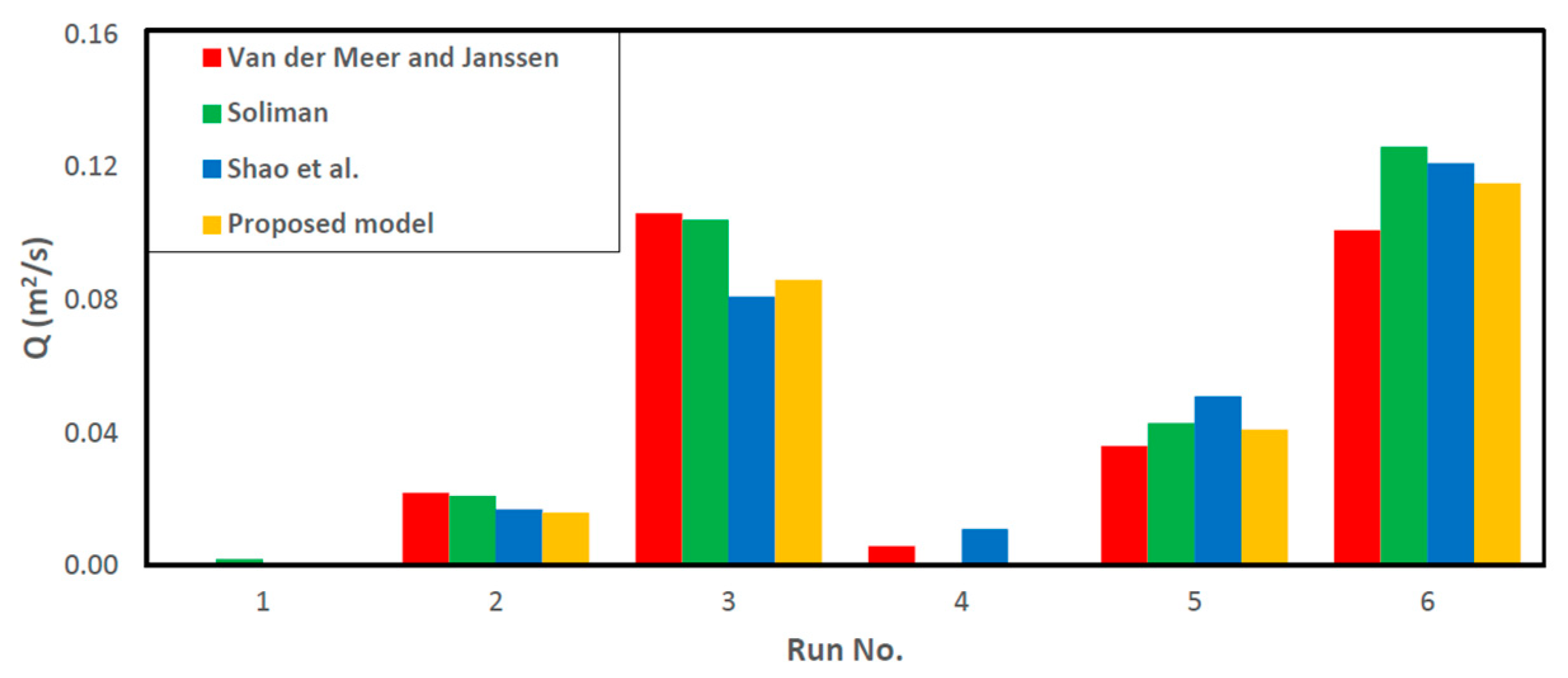
4.4. Random Wave Overtopping Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saville, T. Laboratory Data on Wave Run-Up and Overtopping on Shore Structures; Technical Memorandum. No. 64; U.S. Army, Beach Erosion Board, Document Service Center: Dayton, OH, USA, 1955.
- Van der Meer, J.W.; Janssen, J.P.F.M. Wave run-up and wave overtopping at dikes. In Wave Forces on Inclined and Vertical Structures; Demirbilek, Z., Ed.; American Society of Civil Engineers: New York, NY, USA, 1995; Chapter 1; pp. 1–27. [Google Scholar]
- Lorke, S.; Bornschein, A.; Schuttrümpf, H.; Pohl, R. FlowDike-D – Influence of Wind and Current on Wave Run-Up and Wave Overtopping; Technical Report; Rheinisch-Westfälische Technische Hochschule Aachen and Technische Universität Dresden: Aachen, Germany, 2012. [Google Scholar]
- Donatelli, C.; Ganju, N.K.; Karla, T.S.; Fagherazzi, S.; Leonardi, N. Changes in hydrodynamics and wave energy as a result of seagrass decline along the shoreline of a microtidal back-barrier estuary. Adv. Water Res. 2019, 128, 183–192. [Google Scholar] [CrossRef]
- Tonelli, M.; Fagherazzi, S.; Petti, M. Modeling wave impact on salt marsh boundaries. J. Geophys. Res. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application. 2018. Available online: www.overtopping-manual.com (accessed on 10 November 2019).
- Hu, K.; Mingham, C.G.; Causon, D.M. Numerical simulation of wave overtopping of coastal structures using the non-linear shallow water equations. Coast. Eng. 2000, 41, 433–465. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Fratello, F.; Gallerano, F. A dam-break flood simulation model in curvilinear coordinates. WSEAS Trans. Fl. Mech. 2018, 13, 60–70. [Google Scholar]
- Kozyrakis, G.V.; Delis, A.I.; Alexandrakis, G.; Kampanis, N. A. Numerical modeling of sediment transport applied to coastal morphodynamics. Appl. Numer. Math. 2016, 104, 30–46. [Google Scholar]
- Kazolea, M.; Delis, A.I. Irregular wave propagation with a 2DH Boussinesq-type model and an unstructured finite volume scheme. Eur. J. Mech. B Fluids 2018, 72, 432–448. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Shock-capturing Boussinesq model for irregular wave propagation. Coast. Eng. 2012, 61, 8–19. [Google Scholar] [CrossRef]
- Cannata, G.; Barsi, L.; Petrelli, C.; Gallerano, F. Numerical investigation of wave fields and currents in a coastal engineering case study. WSEAS Trans. Fl. Mech. 2018, 13, 87–94. [Google Scholar]
- Tonelli, M.; Petti, M. Numerical simulation of wave overtopping at coastal dikes and low-crested structures by means of a shock-capturing Boussinesq model. Coast. Eng. 2013, 79, 75–88. [Google Scholar] [CrossRef]
- Chen, X. A fully hydrodynamic model for three-dimensional free-surface flows. Int. J. Numer. Meth. Fl. 2003, 42, 929–952. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Gallerano, F. Numerical integration of the contravariant integral form of the Navier–Stokes equations in time-dependent curvilinear coordinate systems for three-dimensional free surface flows. Continuum Mech. Therm. 2019, 31, 491–519. [Google Scholar] [CrossRef]
- Lara, J.; Losada, I.J.; del Jesus, M.; Barajas, G.; Guanche, R. IH-3VOF: A three-dimensional Navier-Stokes model for wave and structure interaction. In Proceedings of the 32nd Conference on Coastal Engineering, Shanghai, China, 30 June–5 July 2010. [Google Scholar]
- Casulli, V.; Cheng, R.T. Semi-implicit finite-difference methods for three-dimensional shallow flow. Int. J. Numer. Meth. Fl. 1992, 15, 1045–1068. [Google Scholar] [CrossRef]
- Bradford, S.F. Numerical Simulation of Surf Zone Dynamics. J. Waterw. Port. Coast. Ocean Eng. 2000, 126, 1–13. [Google Scholar] [CrossRef]
- Van der Meer, J.W.; Petit, H.A.H.; van den Bosch, P.; Klopman, G.; Broekens, R.D. Numerical Simulation of Wave Motion on and in Coastal Structures. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992. [Google Scholar]
- Berberović, E.; van Hinsberg, N.P.; Jakirlić, S.; Roisman, I.V.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rew. E 2009, 79, 1–15. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Simulating coastal engineering processes with OpenFOAM®. Coast. Eng 2013, 71, 119–134. [Google Scholar] [CrossRef]
- Lin, P.; Li, C.W. A σ-coordinate three-dimensional numerical model for surface wave propagation. Int. J. Numer. Meth. Fl. 2002, 38, 1045–1068. [Google Scholar] [CrossRef]
- Lin, P. A multiple-layer σ-coordinate model for simulation of wave–structure interaction. Comput. Fl. 2006, 35, 147–167. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Cannata, G.; Petrelli, C.; Barsi, L.; Camilli, F.; Gallerano, F. 3D free surface flow simulations based on the integral form of the equations of motion. WSEAS Trans. Fl. Mech. 2017, 12, 166–175. [Google Scholar]
- Cannata, G.; Gallerano, F.; Palleschi, F.; Petrelli, C.; Barsi, L. Three-dimensional numerical simulation of the velocity fields induced by submerged breakwaters. Int. J. Mech. 2019, 13, 1–14. [Google Scholar]
- Armenio, E.; Ben Meftah, M.; Bruno, M.F.; De Padova, D.; De Pascalis, F.; De Serio, F.; Di Bernardino, A.; Mossa, M.; Leuzzi, G.; Monti, P. Semi enclosed basin monitoring and analysis of meteo, wave, tide and current data: Sea monitoring. In Proceedings of the EESMS 2016—2016 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems, Bari, Italy, 13–14 June 2016; p. 7504835. [Google Scholar]
- Bruno, D.; De Serio, F.; Mossa, M. The FUNWAVE model application and its validation using laboratory data. Coast. Eng. 2009, 56, 773–787. [Google Scholar] [CrossRef]
- De Padova, D.; Brocchini, M.; Buriani, F.; Corvaro, S.; De Serio, F.; Mossa, M.; Sibilla, S. Experimental and numerical investigation of pre-breaking and breaking vorticity within a plunging breaker. Water 2018, 10, 387. [Google Scholar] [CrossRef]
- Ferrari, S.; Badas, M.G.; Querzoli, G. A non-intrusive and continuous-in-space technique to investigate the wave transformation and breaking over a breakwater. In Proceedings of the EPJ Web of Conferences, EFM15 – Experimental Fluid Mechanics 2015, Prague, Czech Republic, 17–20 November 2015; p. 02022. [Google Scholar]
- Spiteri, R.J.; Ruuth, S.J. A new class of optimal high-order strong-stability preserving time discretization methods. SIAM J. Numer. Anal. 2002, 40, 469–491. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.W.; Schuller, A. Multigrid; Academic Press: London, UK, 2000. [Google Scholar]
- Toro, E. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley and Sons: Manchester, UK, 2001. [Google Scholar]
- Ferrari, S.; Querzoli, G. Laboratory experiments on the interaction between inclined negatively buoyant jets and regular waves. In Proceedings of the EPJ Web of Conferences, EFM14 – Experimental Fluid Mechanics 2014, Český Krumlov, Czech Republic, 18–21 November 2014; Volume 92, p. 02018. [Google Scholar] [CrossRef]
- Besalduch, L.A.; Badas, M.G.; Ferrari, S.; Querzoli, G. On the near field behavior of inclined negatively buoyant jets. In Proceedings of the EPJ Web of Conferences, EFM13 – Experimental Fluid Mechanics 2013, Kutná Hora, Czech Republic, 19–22 November 2013; p. 02007. [Google Scholar]
- Ferrari, S. Image analysis techniques for the study of turbulent flows. In Proceedings of the EPJ Web of Conferences, EFM16 – Experimental Fluid Mechanics 2016, Marienbad, Czech Republic, 15–18 November 2016; Volume 143, p. 01001. [Google Scholar] [CrossRef]
- Haller, M.C.; Dalrymple, R.A.; Svendsen, I.A. Experimental study of nearshore dynamics on a barred beach with rip channels. J. Geophys. Res. 2002, 107, 1–21. [Google Scholar] [CrossRef]
- Haas, K.A.; Svendsen, I.A. Laboratory measurements of the vertical structure of a rip current. J. Geophys. Res. 2002, 107, 1–19. [Google Scholar] [CrossRef]
- Soliman, A. Numerical Study of Irregular Wave Overtopping and Overflow. Ph.D. Thesis, The University of Nottingham, Nottingham, UK, 2003. [Google Scholar]
- Shao, S.; Ji, C.; Graham, D.I.; Reeve, D.E.; James, P.W.; Chadwick, A.J. Simulation of wave overtopping by an incompressible SPH model. Coast. Eng. 2006, 53, 723–735. [Google Scholar] [CrossRef]


| Test | Mean Water Depth (m) | Wave Height (cm) | Wave Period (s) |
|---|---|---|---|
| T1 | 0.23 | 3.5 | 1.55 |
| T2 | 0.26 | 1 | 1.55 |
| T3 | 0.29 | 2.5 | 0.95 |
| Test | Freeboard (m) | Significant Wave Height (m) | Mean Wave Period (s) | Peak Wave Period (s) |
|---|---|---|---|---|
| R1 | 1.0 | 0.78 | 3.53 | 3.07 |
| R2 | 1.0 | 1.22 | 4.38 | 3.81 |
| R3 | 1.0 | 1.70 | 5.19 | 4.51 |
| R4 | 1.5 | 1.26 | 4.38 | 3.81 |
| R5 | 1.5 | 1.75 | 5.16 | 4.49 |
| R6 | 1.5 | 2.35 | 6.03 | 5.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cannata, G.; Tamburrino, M.; Ferrari, S.; Badas, M.G.; Querzoli, G. Numerical and Experimental Investigation of Wave Overtopping of Barriers. Water 2020, 12, 451. https://doi.org/10.3390/w12020451
Cannata G, Tamburrino M, Ferrari S, Badas MG, Querzoli G. Numerical and Experimental Investigation of Wave Overtopping of Barriers. Water. 2020; 12(2):451. https://doi.org/10.3390/w12020451
Chicago/Turabian StyleCannata, Giovanni, Marco Tamburrino, Simone Ferrari, Maria Grazia Badas, and Giorgio Querzoli. 2020. "Numerical and Experimental Investigation of Wave Overtopping of Barriers" Water 12, no. 2: 451. https://doi.org/10.3390/w12020451
APA StyleCannata, G., Tamburrino, M., Ferrari, S., Badas, M. G., & Querzoli, G. (2020). Numerical and Experimental Investigation of Wave Overtopping of Barriers. Water, 12(2), 451. https://doi.org/10.3390/w12020451







