Abstract
In decision-making with interval numbers, there are problems such as how to reduce the loss of decision information to improve decision accuracy and the difficulty of using interval numbers for sorting. On the basis of fully considering the subjective and objective weights of indexes, the grey entropy method (GEM) is improved by taking advantage of the Mahalanobis-Taguchi System (MTS) in which the orthogonal design has few tests but much obtained information, and the Mahalanobis distance can reflect the correlation between indexes. Then, the signal-to-noise ratio is integrated with the improved degree of balance and approach, and a multi-dimensional interval number decision model based on MTS and GEM is put forth. This model is applied to selecting the optimal scheme of controlling the Pankou reservoir’s water level in flood season. Compared with the decision results of other methods, the optimal scheme selected by the proposed model can achieve greater benefits within an acceptable risk range and thus better coordinate the balance between risk and benefit, which verifies the feasibility and validity of the model.
1. Introduction
Multi-attribute decision-making refers to the process of sorting and selecting among a group of alternatives by using the obtained information [1]. Multi-attribute decision-making methods include Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) [2], set pair analysis (SPA) [3], grey relation analysis (GRA) [4], grey target method (GTM) [5], etc. Under the influence of many factors, the objective things in nature are complex and changeable (e.g., runoff and flood in the hydrological and water resources system), which show great uncertainty like randomness, fuzziness and greyness [6], in addition to the fuzziness of human thinking. In recent years, the multi-attribute decision-making methods with uncertain decision information, especially uncertain attribute values and attribute weights, have become a hot research issue. In general, the priority and also difficulty in solving this kind of problem is to transform uncertain decision-making into definite decision-making. During this process, on the one hand, we should try to avoid or reduce the loss of decision information. The more information loss, the larger deviation caused in the selection of the optimal scheme, which may fail to achieve the expected objectives in scheme implementation and incur risk events. On the other hand, the cumbersome calculation of interval numbers should be reduced, so that the technique is more operable in a practical application. For instance, when using the methods in references [7,8], the comparison of interval numbers only considers their upper and lower boundaries, which loses too much information even though the decision-making efficiency is enhanced. Moreover, the tedious calculation in rough set method [9] and Vlsekriterijumska Optimizacija I Kompromisno Resenje (VIKOR) method [10] makes interval number ranking more difficult.
At present, grey analysis, set pair analysis, stochastic analysis and fuzzy analysis are the four main kinds of hydrologic uncertainty analysis methods. In information theory, a system with some known information and also some unknown information is a grey system, such as the hydrologic and water resources system. Grey relation analysis is a multi-factor analysis method in the grey system theories [11]. Its basic idea is to determine the closeness of relation between a comparison sequence and a reference sequence according to their geometric similarity. Grey relation analysis can overcome the shortcomings of regression analysis, variance analysis and other factor analysis methods in traditional mathematical statistics [12], and has the advantages of a small sample size and simple calculation procedure. Gao and Zhang [13] first used grey relation analysis for scheme selection. However, in the relation coefficient series obtained from the alternatives and the reference scheme, the larger relation coefficient often plays a decisive role in determining the relation degree, while the information implied by other relation coefficients tends to be neglected. As an improvement, Zhang [14] put forward the grey entropy method (GEM) based on the idea that an alternative scheme is better when it is evenly closer to the reference scheme. This method combines the relation degree in grey relation analysis with the balance degree defined in grey entropy by multiplication, and thus, develops the degree of balance and approach for scheme decision-making, which in some way remedies grey relation analysis. The GEM has been widely used in logistics [15], transportation [16], tourism [17] and other industries, with satisfactory results. Grey entropy is a concept that combines grey system theory and information entropy theory. As an effective statistical measurement for information uncertainty [18], it is consistent with the physical meaning of Shannon entropy. Wang et al. [19] defined the grey distance entropy of the real grey number and the interval grey number, respectively, took it as the measurement for the proximity degree of the two grey numbers, and discussed the multi-attribute decision-making methods based on grey distance entropy and TOPSIS. Liu et al. [20] deemed that in the grey entropy method the attribute value is a real number and the attribute weight is not considered, thus they extended the application scope to interval numbers. At present, grey entropy is mainly used to determine the objective weight of indexes in uncertain decision-making, and there are not many in-depth theoretical studies. The comparison of the above decision-making methods is shown in Table 1.

Table 1.
Comparison of the five multi-attribute decision-making methods.
The combination of the Mahalanobis-Taguchi System (MTS) theory and grey entropy can provide a new idea for uncertain multi-attribute decision-making. The Mahalanobis-Taguchi System [21,22], proposed by Japanese engineer Taguchi G. in the 1990s, is a pattern recognition method for unbalanced data. Scholars are becoming gradually more familiar with MTS and constantly try to explore its application or its combination with other theories in different fields. Buenviaje et al. [23] obtained medical patterns from historical data sets through MTS. Huang et al. [24] utilized the data mining function of MTS, combined it with the artificial neural network (ANN) and came up with the MTS-ANN algorithm. Zeng et al. [25] studied how to make the risk decision on power transformer maintenance by using MTS and the grey cumulative prospect theory. Chang et al. [26] employed the three key tools of MTS, namely, orthogonal table, Mahalanobis distance and signal-to-noise ratio, to tackle the problem of multi-attribute decision-making with interval numbers on the basis of TOPSIS. The orthogonal table [27] is a direct test method for multi-factor system optimization. It can be expressed in the form of La(bN), where a is the number of tests, b the number of levels of each factor and N the number of factors that can be arranged at most in the orthogonal table. The orthogonal table is a prepared set of standard tables, from which the suitable one is chosen in actual application according to the number of factors and the number of levels of each factor. The orthogonal table designs a small number of tests and obtains comprehensive information, which can effectively reduce the loss of information. The Mahalanobis distance [28], proposed by Indian statistician Mahalanobis, is a covariance distance that, compared with Euclidean distance, can better reflect the correlation between attributes. The concept of signal-to-noise ratio (SNR) [29] originates from signal transmission and is defined as the ratio of signal power to noise power. Taguchi G. redefined the SNR, regarding the square (μ2) and the variance (σ2) of the expected value of an index (non-negative and continuous) as the signal power and the noise power, respectively. The SNR can be divided into three types: nominal-the-better, smaller-the-better and larger-the-better. The first one means that the closer to the expected value when it is positive, the better; the second one means that the smaller the expected value when it is 0, the better; the third one means that the larger the expected value when it is , the better. The signal-to-noise ratio can be used to measure the volatility of indexes and thereby ensure the accuracy of decision results.
Like other pattern recognition methods, MTS also uses distance to measure the similarity between samples; however, instead of using Euclidean distance, it uses Mahalanobis distance, which is more suitable to distinguish sample similarity. As the theory of MTS has only been developed for the past 20 years and there are few studies on its integration with grey analysis, more work needs to be done to deepen this field of theoretical research and expand its application.
To address the uncertain multi-attribute decision-making problem in which both attribute weight and attribute value are interval numbers, we improved the grey entropy method based on the treatment of interval numbers in reference [26], and put forward a multi-dimensional interval number decision model based on the Mahalanobis-Taguchi System with the grey entropy method (MTS-GEM). The model is applied to the selection of the optimal scheme of controlling the Pankou reservoir’s water level in flood season, which can facilitate reservoir operation research.
2. Multi-Dimensional Interval Number and Mahalanobis-Taguchi System
2.1. Orthogonal Test of Multi-Dimensional Interval Number
Interval number generally refers to the normal interval number in the form of (aL, aU∈R and aU≥aL), where aL and aU are, respectively, the lower and upper bounds of the interval number. Real numbers can be regarded as interval numbers whose lower bounds are equal to their upper bounds. For the basic operation rules of any two interval numbers and , see reference [30].
Suppose that there are n factors (j=1,2,…,n, and n≤N) in a test, which are uniformly distributed within their variation range, and the number of levels of each factor is b. Because n factors can constitute a hypercube in an n-dimensional space, the result of one orthogonal test corresponds to a point on the hypercube.
Take the orthogonal test of three factors as an example. Let the lower bound value of interval number be level 1 and the upper bound value of interval number be level 2, then the orthogonal table of shown in Table 2 can be used for the orthogonal test, and the results are shown in Figure 1.

Table 2.
Orthogonal table of .
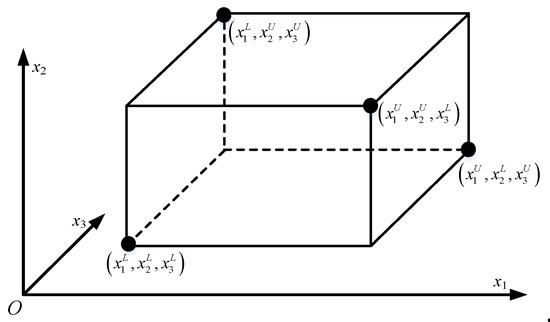
Figure 1.
Orthogonal test results of three-dimensional interval numbers.
2.2. Signal-to-Noise Ratio and Mahalanobis Distance
Let D be the population of a non-negative continuous index, whose signal-to-noise ratio η* is calculated as follows [31]:
where μ2 and σ2 are the mean square and the variance of population D, respectively.
The three types of signal-to-noise ratio for measuring index volatility are calculated as follows.
1 Nominal-the-better (NB) signal-to-noise ratio
According to the knowledge of mathematical statistics, the unbiased estimators of variance σ2 and mean square μ2 of population D are as follows:
where and a is the number of samples.
Put and into Equation (1) and conduct the common logarithmic transformation on η*, then the NB signal-to-noise ratio ηNB can be obtained:
2 Smaller-the-better (SB) signal-to-noise ratio
For an SB index, the smaller μ2 and σ2 are, the better, meaning that the smaller is, the better. The unbiased estimator of D2 is . Take as the signal-to-noise ratio, and the SB SNR ηSB is calculated as follows:
3 Larger-the-better (LB) signal-to-noise ratio
If D stands for an LB index, then D−1 stands for an SB index. From the above derivation process of the ηSB formula, the LB SNR ηLB can be obtained:
Let Z be a population of an n-dimensional real number space, and be the mean vector and the inverse of covariance matrix of Z, respectively. If is one sample of the n-dimensional real number space, then the Mahalanobis distance d from sample x to population Z is:
In scheme decision-making, an alternative scheme is better if its Mahalanobis distance to the reference scheme is smaller, hence, we adopted the SB SNR. If the reference scheme’s sample x and population Z are taken as the input of MTS, then the Mahalanobis distance d between the alternative scheme and the reference scheme is the responding output.
3. Improved Grey Entropy Method by Mahalanobis-Taguchi System
3.1. Grey Entropy
Grey entropy is the entropy of a grey number [32,33]. Grey number refers to a number set with incomplete and uncertain information, in which the numbers are possible values. For a discrete grey number , (where is a finite set and , ), is called the corresponding grey entropy. When , . The more equal are, the greater the grey entropy is, thereby, , and is defined as the balance degree of the grey number.
3.2. The Comparison of Grey Entropy and Information Entropy
Information entropy refers to the entropy of a signal source [34]. A discrete signal source can be expressed as , (where is an infinite set, the probability of random variable is and , , ). Then, is called the information entropy of the signal source.
Accordingly, grey entropy and information entropy have the following similarities and differences.
- Similarities
- With the same form of calculation formula, grey entropy and information entropy share some characteristics, such as symmetry, non-negativity, additivity, convexity and extremum property.
- The physical meanings of grey entropy and information entropy are essentially the same. The former is to measure the fluctuation degree of a grey number, while the latter is to describe the uncertainty of a signal source.
- Differences
- Grey entropy is defined in a finite information space, whereas information entropy is defined in an infinite information space.
- Grey entropy is a kind of non-probability entropy with greyness, that is, is a possible value. On the contrary, information entropy is a type of probability entropy with certainty, that is, is a certain value.
3.3. Fundamentals of Grey Entropy Method
GEM was originally used for scheme decision-making with multi-dimensional real numbers. Suppose an initial decision matrix (I = 1,2,…,m; j=1,2,…,n) composed of m schemes and n indexes. Through weighted standardization, X is converted into , and the alternative scheme is . Given the reference scheme (k = 1,2,…,z), the correlation degree between the alternative scheme and the reference scheme is calculated as follows:
where is the correlation coefficient of index j between and and is the distinguishing coefficient and generally set at 0.5.
The correlation coefficient sequence of and is , whose balance degree is calculated as follows:
where .
The degree of balance and approach of and is calculated as follows:
The greater the degree of balance and approach is, the similar the alternative scheme is to the reference scheme.
It can be seen from Equation (8) that the correlation coefficient reflects the distance between two points. When using the Euclidean distance for calculation, the correlation between indexes, which usually exits in reality, is ignored, making the calculation results of the correlation degree and the balance degree unreasonable. Moreover, there is interaction between indexes, either controllable or uncontrollable. Additionally, the uncontrollable interaction affects the stability of the responding output. Consequently, although the balance degree is an indicator of the volatility of correlation coefficient series, it cannot embody the variability caused by the uncontrollable interaction between indexes. The merit of MTS is that it can not only use the orthogonal table to deal with multi-dimensional real numbers or multi-dimensional interval numbers, taking the interaction among indexes into account, but also use the Mahalanobis distance considering the correlation between indexes to calculate the correlation coefficient. Therefore, using MTS to improve GEM can enhance the decision-making performance of GEM.
4. Multi-Dimensional Interval Number Decision Model Based on MTS-GEM
4.1. Development of the Weighted Standardized Decision Matrix
Suppose that there are m alternative schemes and n indexes, and they constitute the initial interval number decision matrix (i=1,2,…,m; j=1,2,…,n) where . As the dimensions of the indexes are often different, we used Equations (11) and (12) to nondimensionalize different types of indexes, and get the standardized interval number decision matrix , where .
For a benefit index:
For a cost index:
where and .
To make the weight distribution of each index reasonable, the integration of expert scoring (subjective weight) and entropy weight method [35] (objective weight) is used to determine the combined weight of each index.
1 Subjective weight where
Assuming that there are experts who participate in the weight scoring of n indexes, the scoring matrix is (l=1,2,…,; j=1,2,…,n) where , then .
2 Objective weight , where
First, the entropy of the interval number index is calculated based on the standardized interval number decision matrix :
where and are the information entropy of the interval number index’s lower bound and upper bound, respectively; when or , or .
Then, calculate the objective weight of the interval number index :
3 Combined weight , where
Considering both the subjective weight and the objective weight , we obtained the combined weight of the interval number index where and is an empirical factor that reflects the preference of decision makers between subjective experience and objective data [36].
With the standardized decision matrix and the indexes’ combined weight , we used the multiplication algorithm of interval number to obtain the weighted standardized decision matrix , where . Additionally, based on TOPSIS, the positive ideal scheme and the negative ideal scheme were determined:
4.2. Orthogonal Test of Schemes and Calculation of Derivative Indicators
According to the number of indexes, a two-level orthogonal table with N≥n was selected, where n indexes can be arranged in any n columns. For the interval number , take as level 1 and as level 2. The layout matrix of the alternative scheme (i=1,2,…,m) is as follows:
where (g=1,2,…,a) is the distribution point of scheme and , , …, are the components of .
Similarly, the layout matrix of the positive ideal scheme and the layout matrix of the negative ideal scheme can be obtained.
Here, we define derivative indicators as the signal-to-noise ratio and the degree of balance and approach based on square Mahalanobis distance obtained by the initial interval number indexes. According to Equation (6), calculate the square Mahalanobis distance between the alternative scheme’s distribution point and the positive/negative ideal scheme, and we obtain and .
1 Signal-to-noise ratio
The SB signal-to-noise of the scheme i to the positive (negative) ideal scheme is ():
where a is the number of orthogonal tests and , is the square Mahalanobis distance standardized by Equation (18):
2 Improved degree of balance and approach
The correlation degree of the alternative scheme and the positive (negative) ideal scheme is ():
where () is the correlation coefficient of the alternative scheme and the positive (negative) ideal scheme at distribution point g.
Based on the square Mahalanobis distance, the formula of correlation coefficient is revised as follows:
where the distinguishing coefficient is set at 0.5.
The balance degree of the alternative scheme and the positive (negative) ideal scheme is ():
where and .
The degree of balance and approach of the alternative scheme and the positive (negative) ideal scheme is ():
4.3. Scheme Decision-Making
Based on the signal-to-noise ratio and the improved degree of balance and approach, the decision matrix Y is constructed as shown in Equation (23), in which the benefit indicator is and , while the cost indicator is and :
Now, the decision-making problem with multi-dimensional interval numbers is changed into a decision-making problem with multi-dimensional real numbers [37]. The optimal scheme can be selected with the following multi-dimensional real vector space decision-making method (MRVSDM).
- The n-dimensional real numbers are regarded as the points A1,…,Ai,…,Am in an n-dimensional space with O as the origin, and then we can get the vectors ,…,,…,.
- Assuming that the reference scheme vector is , and are the modules of vector ai and vector , respectively. Between vectors ai and , calculate their angle (where is their product), as well as their mapping distance .
- The set of mapping distance can be obtained. According to the principle that the smaller is, the closer vector ai is to vector , the scheme that satisfies the objective is selected as the optimal scheme.
The diagram of decision-making in a three-dimensional real number vector space is shown in Figure 2. The input of the MTS-GEM model is the interval number indexes derived from different schemes. After orthogonal tests and calculation of the Mahalanobis distance, the signal-to-noise ratio, the improved degree of balance and approach, the output is the mapping distance from each scheme to the ideal scheme. The flow chart of this study is shown in Figure 3.
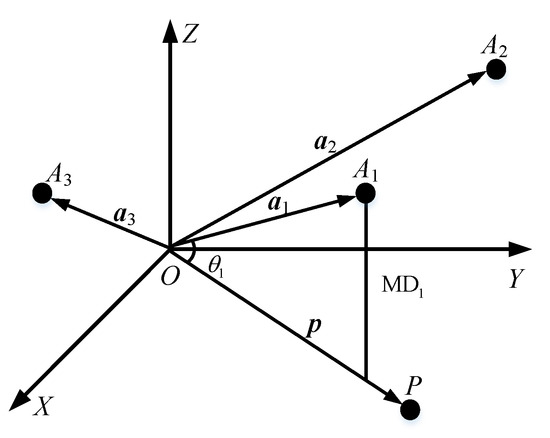
Figure 2.
Diagram of decision-making in a three-dimensional real number vector space.
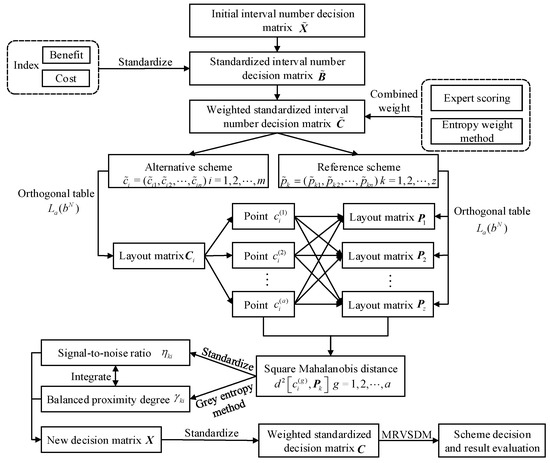
Figure 3.
Flow chart of multi-dimensional interval number decision-making based on Mahalanobis-Taguchi System with grey entropy method.
5. Case Study
5.1. Initial Interval Number Decision Matrix and Its Weighted Standardization
Multi-objective reservoir operation is a multi-dimensional and complicated system engineering issue. Affected by runoff forecast, operation model, solution method and other factors, in the obtained non-inferior solution set, the attribute values are not always a precise real number but an interval number with uncertainty. The Pankou reservoir, located at the upstream of the Du River in China, is an annual-regulating reservoir with comprehensive utilization tasks of power generation, flood control, water supply and so forth. Its basic information is listed in Table 3, and its location map is shown in Figure 4.

Table 3.
Basic information of the Pankou reservoir.
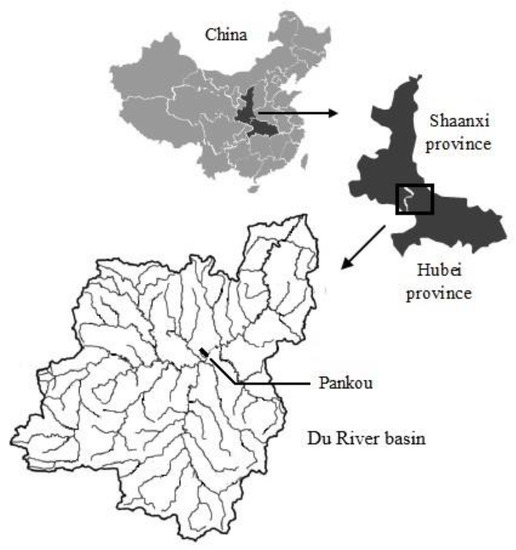
Figure 4.
The location of the Pankou reservoir.
According to the current regulations of the China Yangtze River Flood Control and Drought Relief Headquarters, for the Pankou reservoir, the upper limit of operation water level in flood season (June 20–August 20) is the flood control limit water level (347.6 m), while in other periods it is the normal water level (355 m); the lower limit of operation water level in all periods is the dead water level (330 m), and falling to the lower limit should be avoided during operation.
However, in the actual operation of the Pankou reservoir, it can barely store water to the normal water level in most years, undermining such benefits as power generation and water supply. In order to reasonably adjust the upper limit of water level in flood season and improve the utilization rate of flood resources, in reference [38] the three indexes of flood control risk rate, annual generated power and water storage at the end of flood season were used as the evaluation indexes for selecting the optimal scheme of water level upper limit in flood season. Flood control risk rate was obtained by means of flood stochastic simulation [39]. Firstly, the flood stochastic simulation model was used to simulate n (a large number) pieces of annual maximum flood inflow hydrographs, which can fully reflect the statistical characteristics of the reservoir’s measured flood inflow. Then, a flood operation calculation was conducted to obtain the highest annual water level sequence, and the ratio of times that the water level limit was exceeded to n was taken as the flood control risk rate, the value of which needs to meet people’s acceptable level of risk. Annual generated power refers to the total electricity generated by the hydropower station within a one-year operation cycle, which represents the power generation benefit of the hydropower station. The more annual generated power, the greater the annual power generation benefit. The water storage at the end of the flood season refers to the water storage between the dead water level and the particular water level at the end of flood season, which represents the water supply benefit of the reservoir. The more water storage at the end of flood season, the greater the water supply benefit.
The scheme setting is shown in Figure 5. Currently, Scheme 1 is being adopted as the operation strategy of the Pankou reservoir’s upper water level limit in flood season.
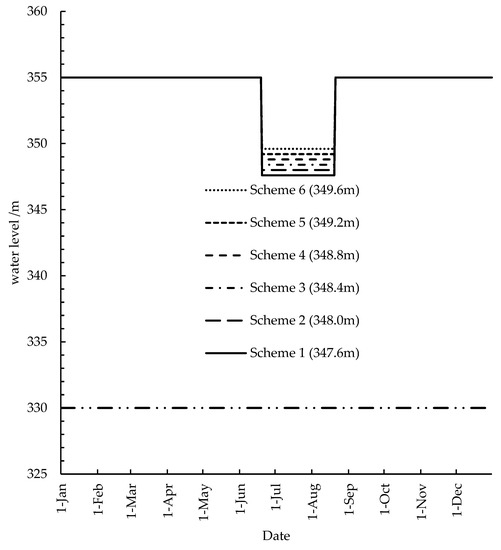
Figure 5.
Scheme setting of the Pankou reservoir’s upper water level limit in flood season.
For the flood control risk rate, the Monte Carlo method was used to randomly simulate 100 groups of 1000 floods corresponding to the 1000-year return period (0.1%). After flood operation calculation of each flood, the number of times that the design flood water level (357.14m) is exceeded in each group of 1000 floods were counted as . The flood control risk rate of each group was , and the flood control risk rate in the form of an interval number was . Similarly, the annual generated power and water storage at the end of flood season were obtained through reservoir operation calculation by using the monthly inflow data of 41 years from 1971 to 2011. Then, the minimum and maximum values of the 41 results formed the interval numbers. The initial interval number decision matrix is shown in Table 4.

Table 4.
Initial interval number decision matrix .
According to Equation (11)–(12), the benefit indexes (annual generated power, water storage at the end of flood season) and the cost index (flood control risk rate) in Table 3 are standardized, resulting in the standardized interval number decision matrix shown in Table 5.

Table 5.
Standardized interval number decision matrix .
According to Lynne [40] who derives the variance formula of interval number sample matrix based on uniform distribution, for , its variance can be expressed as follows:
Based on the definition of the correlation coefficient of two random real number variables in the probability theory and mathematical statistics, the correlation coefficient of two interval variables (h, j=1,2,…,n) is:
From Equation (24)–(25), the correlation coefficient matrix of can be obtained, as shown in Table 6.

Table 6.
Correlation coefficient matrix of the standardized interval number decision matrix.
It is shown in Table 5 that there is positive correlation among the three indexes. The correlation between the flood control risk rate and annual generated power or water storage at the end of flood season is slightly weak. The correlation between annual generated power and water storage at the end of flood season is significant in that their correlation coefficient is 0.971. Thus, it is necessary to consider the correlation between the indexes in the decision-making process of the reservoir water level scheme in flood season.
There are five experts to grade the importance of the indexes, and the subjective weight of the interval number indexes obtained from the scoring matrix is . According to Equation (13), the information entropy weight is and . Thus, the objective weight of the interval number indexes is . Let the empirical factor be 0.5, then the combined weight is . From and , the weighted standardized decision matrix is obtained, as shown in Table 7.

Table 7.
Weighted standardized interval number decision matrix .
Through the matrix , based on TOPSIS and Equation (15), the positive (negative) ideal scheme () is determined as follows:
.
5.2. Orthogonal Test of the Schemes
Since there are three indexes, the orthogonal table is . The alternative scheme’s layout matrix Ci (i=1,2,…,6), the positive ideal scheme’s layout matrix and the negative ideal scheme’s layout matrix are shown in Table 8.

Table 8.
Layout matrixes of the schemes.
5.3. Scheme Decision-Making and Result Evaluation
The square Mahalanobis distance from each point in the layout matrix Ci to the positive ideal scheme’s layout matrix and the negative ideal scheme’s layout matrix is worked out, as shown in Table 9.

Table 9.
Square Mahalanobis distance.
The square Mahalanobis distance is standardized by Equation (18) and the SNR indicator is obtained. The indicator of the degree of balance and approach is worked out by Equation (19)–(22). Accordingly, the decision matrix X is derived, as shown in Table 10.

Table 10.
Derivative indicator decision matrix X.
In accordance with Equation (11)–(12), X is standardized and with the weight of each index being 0.25, the weighted standardized decision matrix C is obtained, as shown in Table 11.

Table 11.
Weighted standardized derivative indicator decision matrix C.
is taken as the reference scheme to calculate the mapping distance from the alternative scheme to the reference scheme.
To verify the feasibility and effectiveness of the method in this paper, the first comparison method of scheme ranking (method 1) is based on the closeness degree of the SNR defined by Equation (26), according to reference [40]:
On the basis of TOPSIS, the improved closeness degree of the degree of balance and approach is defined as follows:
When , , the closer scheme i is to the positive ideal scheme, whereas when , , the farther scheme i is to the positive ideal scheme. This ranking criterion is that the larger is, the better the corresponding scheme i is, which is the second method for comparison (method 2).
The schemes are sorted according to the different ranking criteria of method 1, method 2 and the method in this study. The results are shown in Table 12.

Table 12.
Results of scheme ranking.
It can be seen from Table 11 that Scheme 1 ranks the last in the decision results of all the three methods, meaning that the currently-adopted strategy is far from decent and other schemes need to be selected, which conforms to the status quo of the Pankou reservoir. This study’s method chooses Scheme 3 as the optimal scheme, which raises the upper water level limit in flood season by 0.8 m compared with Scheme 1.
The reasons for the inconsistent scheme ranking results can be explained by the calculation process of the SNR and the improved degree of balance and approach in Section 4.2. The two indicators respectively reflect the output strength and the degree of balance and approach of geometric curves in the alternative and the reference schemes. If method 1 or method 2 is used alone, their decision results will be less likely to be adopted. The method proposed in this paper includes the advantages of both method 1 and method 2, and gets closer to the reference scheme by the mapping distance, producing more accurate and reasonable decision results. Therefore, scheme 3 is recommended as the optimal.
In Table 11, the closeness degree of the SNR and the closeness degree of the balance and approach degree are benefit indicators, whereas the mapping distance is a cost indicator, and therefore converted into a benefit indicator by the range method. After normalizing the three indicators, the decision results of the three methods are illustrated in Figure 6. It can be seen that compared with method 1 and method 2, this study’s method produces more obviously distinct decision results, which proves that the proposed model can effectively mine the hidden rules in data, especially for the analysis of a system with deficient information.
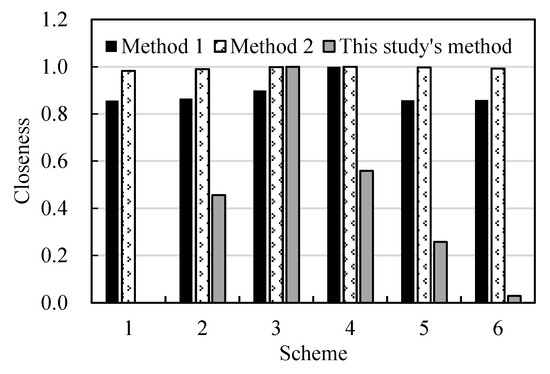
Figure 6.
Comparison of closeness degree of each alternative scheme to the reference scheme.
6. Conclusions
In order to reduce the uncertainty of interval numbers as well as computation work and fully mine the implied information in multi-attribute decision-making, a multi-dimensional interval number decision model based on Mahalanobis-Taguchi System with grey entropy method (MTS-GEM) was proposed and verified by a case study. The principal conclusions are as follows.
- MTS-GEM can effectively reduce the uncertainty created by interval numbers. In the model, the bounded uncertain n-dimensional interval number is expressed quantitatively as a hypercube in the n-dimensional space. Meanwhile, the alternative and reference schemes are all transformed into finite vertices of the hypercube, which realizes the transformation from an interval number decision vector to a real number decision vector.
- MTS-GEM can produce markedly distinctive decision results, which demonstrates the sufficiency of decision information contained in the model. The model not only considers the output response strength and the degree of balance and approach between alternative and reference schemes, but also uses the idea of further approaching the reference scheme by mapping distance, which elevates the accuracy and reliability of the decision results.
- The case study of selecting the optimal scheme of controlling the Pankou reservoir’s water level in flood season shows that the proposed method can pick out the best scheme that better coordinates risk and benefit, which further proves the comprehensive and excellent decision-making performance of the model.
Author Contributions
Conceptualization, C.J. and X.L.; Data curation, X.Y.; Formal analysis, X.L., Y.Z. and X.Y.; Methodology, C.J., X.L. and Y.P.; Validation, X.L., Y.P. and Y.Z.; Writing—original draft, X.L. and J.W.; Writing—review and editing, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This study was financially supported by the National Key Research and Development Program of China (2016YFC0402309), the National Natural Science Foundation of China (51709105) and the Fundamental Research Funds for the Central Universities (2019MS031). The authors are grateful to the reviewers for their valuable comments and constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, Z. Uncertain Multiple Attribute Decision Making: Methods and Applications; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Yoon, K.; Hwang, C.L. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Liu, Y.; Wang, W. Set Pair Analysis and its application to optimization of standard schemes of urban flood control. J. North China Univ. Water Res. Electr. Power (Nat. Sci.) 2018, 39, 77–80. [Google Scholar]
- Tu, E.Q.; Liao, X.Y.; Chen, Z.J.; Wang, H.M. Effects of rainfall on runoff from a small watershed in Three Gorges Reservoir area. Bull. Soil Water Conserv. 2010, 30, 7–11. [Google Scholar]
- Chen, S.; Li, Z.; Xu, Q. Grey target theory based equipment condition monitoring and wear mode recognition. Wear 2006, 260, 438–449. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Jin, J.; Ding, J. Set Pair Analysis for Hydrology and Water Resources Systems; Science Press: Beijing, China, 2010. [Google Scholar]
- Gao, F. Possibility degree and comprehensive priority of interval numbers. Syst. Eng. Theor. Pract. 2013, 33, 2033–2040. [Google Scholar]
- Hou, J.; Li, Y.; Chi, H. An new method of interval numbers ordering in uncertain multiple attribute decision-making. Math. Pract. Theor. 2017, 47, 24–27. [Google Scholar]
- Li, L. Research on Multi-Attribute Decision Making of Interval-Valued Information System based on Rough Set. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 1 March 2014. [Google Scholar]
- Mohammad, K.S.; Majeed, H.; Kamran, S. Extension of VIKOR method for decision making problem with interval numbers. Appl. Math. Model. 2009, 33, 2257–2262. [Google Scholar]
- Deng, J. Grey Theory Basis; Huazhong University of Science & Technology Press: Wuhan, China, 2002. [Google Scholar]
- Wu, Q. System Engineering; Beijing Institute of Technology Press: Beijing, China, 2015. [Google Scholar]
- Gao, X.; Zhang, Q. Gray relational grade rule of uncertain decision making. Oil-Gas Field Surf. Eng. 1995, 14, 57–58. [Google Scholar]
- Zhang, Q.; Li, X.; Deng, J. Grey entropy method of uncertain decision making. J. Manag. Sci. 1995, 6, 37–39. [Google Scholar]
- Shang, L.; Tan, Q. Emergency logistics supplier evaluation based on grey entropy model. Stats. Decis. 2013, 3, 45–47. [Google Scholar]
- Fang, Y.; Li, G.; Du, L. Intercity rail transit system decision-making method based on grey entropy. Syst. Eng. 2015, 33, 152–158. [Google Scholar]
- Guo, Q.; Li, W. Algorithm of tourist routes based on grey entropy decision model. Comput. Eng. Desig. 2017, 38, 1988–1991. [Google Scholar]
- Xia, J. Grey System Hydrology; Huazhong University of Science and Technology Press: Wuhan, China, 1998. [Google Scholar]
- Wang, P.; Fang, Z.; Liu, J.; Chi, Y. Study on grey distance entropy model with application in multiple attribute decision making. In Proceedings of the 2009 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 10–12 November 2009; pp. 1051–1054. [Google Scholar]
- Liu, R.; Gao, X.; Zhang, G. Research on the uncertain multi-attribute decision making methods and application based on grey entropy model with interval-type attribute values and weights. Control Decis. 2018, 1–11. [Google Scholar]
- Taguchi, G.; Jugulum, R. New Trends in Multivariate Diagnosis. Sankhyā Indian J. Stat. Ser. B 2000, 62, 233–248. [Google Scholar]
- Wang, Z.; Lu, C.; Wang, Z.; Liu, H.; Fan, H. Fault diagnosis and health assessment for bearings using the Mahalanobis–Taguchi system based on EMD-SVD. Trans. Inst. Meas. Control 2013, 35, 798–807. [Google Scholar] [CrossRef]
- Buenviaje, B.; Bischoff, J.E.; Roncace, R.A.; Willy, C.J. Mahalanobis–Taguchi System to Identify Preindicators of Delirium in the ICU. IEEE Trans. Inf. Technol. B. 2016, 20, 1205–1212. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Hsu, T.; Liu, C. The Mahalanobis–Taguchi system—Neural network algorithm for data-mining in dynamic environments. Expert Syst. Appl. 2009, 36, 5475–5480. [Google Scholar] [CrossRef]
- Zeng, W.; Hao, Y.; Fan, R.; Yuan, J.; Li, C. Risk decision-making with intervals based on Mahalanobis-Taguchi System and grey cumulative prospect theory for maintenance of power transformers. J. North China Electr. Power Univ. 2015, 42, 100–110. [Google Scholar]
- Chang, Z.; Cheng, L.; Liu, J. Multiple attribute decision making method with intervals on Mahalanobis-Taguchi System and TOPSIS method. Syst. Eng. Theor. Pract. 2014, 34, 168–175. [Google Scholar]
- Zhang, L. Orthogonal Method and Applied Mathematics; Science Press: Beijing, China, 2009. [Google Scholar]
- Mahalanobis, P.C. On the generalized distance in statistics. P. Indian Natl. Sci. A. 1936, 2, 49–55. [Google Scholar]
- Chang, Z. Research progress of Mahalanobis-Taguchi system. Control Decis. 2019, 34, 2505–2516. [Google Scholar]
- Zhou, Z.; Xing, Y.; Sun, H.; Cai, Y.; Yu, X. Interval game analysis of government subsidies on haze governance in Beijing-Tianjin-Hebei. Syst. Eng. Theor. Pract. 2017, 37, 2640–2648. [Google Scholar]
- Wang, W. The Design of the Test and Analysis; Higher Education Press: Beijing, China, 2004. [Google Scholar]
- Zhang, Q.; Qin, H.; Deng, J. New definition of grey number’s grey grade. J. Northeast Petrol. Univ. 1996, 20, 89–92. [Google Scholar]
- Zhang, Q.; Guo, X.; Deng, J. Grey relation entropy method of grey relation analysis. Syst. Eng. Theor. Pract. 1996, 8, 7–11. [Google Scholar]
- Wu, N.; Yuan, S. Maximum Entropy Method; Hunan Science & Technology Press: Changsha, China, 1991. [Google Scholar]
- Li, C.; Zhang, F.; Zhu, T.; Feng, T.; An, P. Evaluation and correlation analysis of land use performance based on entropy-weight TOPSIS method. T. Chin. Soc. Agric. Eng. 2013, 29, 217–227. [Google Scholar]
- Peng, Y.; Ji, C.; Liu, F. Multi-objective optimization model for coordinative dispatch of water and sediment in cascade reservoirs. J. Hydraul. Eng. 2013, 44, 1272–1277. [Google Scholar]
- Zhang, P.; Ji, C. In Multi-Dimensional Vector Space Decision Model and Its Application for Multi-Objective Operation Risk Analysis of Reservoirs, Proceedings of the World Environmental and Water Resources Congress 2017: International Perspectives, History and Heritage, Emerging Technologies, and Student Papers, Sacramento, CA, USA, 21–25 May 2017; Dunn, C.N., Van Weele, B., Eds.; Amer Soc Civil Engineers: New York, NY, USA, 2017; pp. 184–191. [Google Scholar]
- Wang, L.; Yan, X.; Wang, B.; Yu, H.; Ji, C. Interval number grey target decision-making model based on multi-dimensional association sampling and its application. Syst. Eng. Theor. Pract. 2019, 39, 1610–1622. [Google Scholar]
- Xiao, Y.; Guo, S.; Luo, Z.; Xiong, L.H.; Li, W. Estimation of hydrological risk rate for dams. Eng. J. Wuhan Univ. 2005, 38, 10–13. [Google Scholar]
- Lynne, B.; Edwin, D. Symbolic Data Analysis: Conceptual Statistics and Data Mining; John Wiley & Sons Inc.: Chichester, UK, 2006. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).